By raypierre , with the gratefully acknowledged assistance of Spencer Weart
In Part I the long struggle to get beyond the fallacious saturation argument was recounted in historical terms. In Part II, I will provide a more detailed analysis for the reader interested in the technical nitty-gritty of how the absorption of infrared really depends on CO2 concentration. At the end, I will discuss Herr Koch’s experiment in the light of modern observations.
The discussion here is based on CO2 absorption data found in the HITRAN spectroscopic archive. This is the main infrared database used by atmospheric radiation modellers. This database is a legacy of the military work on infrared described in Part I , and descends from a spectroscopic archive compiled by the Air Force Geophysics Laboratory at Hanscom Field, MA (referred to in some early editions of radiative transfer textbooks as the "AFGL Tape").
Suppose we were to sit at sea level and shine an infrared flashlight with an output of one Watt upward into the sky. If all the light from the beam were then collected by an orbiting astronaut with a sufficiently large lens, what fraction of a Watt would that be? The question of saturation amounts to the following question: How would that fraction change if we increased the amount of CO2 in the atmosphere? Saturation refers to the condition where increasing the amount of CO2 fails to increase the absorption, because the CO2 was already absorbing essentially all there is to absorb at the wavelengths where it absorbs at all. Think of a conveyor belt with red, blue and green M&M candies going past. You have one fussy child sitting at the belt who only eats red M&M’s, and he can eat them fast enough to eat half of the M&M’s going past him. Thus, he reduces the M&M flux by half. If you put another equally fussy kid next to him who can eat at the same rate, she’ll eat all the remaining red M&M’s. Then, if you put a third kid in the line, it won’t result in any further decrease in the M&M flux, because all the M&M’s that they like to eat are already gone. (It will probably result in howls of disappointment, though!) You’d need an eater of green or blue M&M’s to make further reductions in the flux.
Ångström and his followers believed that the situation with CO2 and infrared was like the situation with the red M&M’s. To understand how wrong they were, we need to look at modern measurements of the rate of absorption of infrared light by CO2 . The rate of absorption is a very intricately varying function of the wavelength of the light. At any given wavelength, the amount of light surviving goes down like the exponential of the number of molecules of CO2 encountered by the beam of light. The rate of exponential decay is the absorption factor.
When the product of the absorption factor times the amount of CO2 encountered equals one, then the amount of light is reduced by a factor of 1/e, i.e. 1/2.71282… . For this, or larger, amounts of CO2,the atmosphere is optically thick at the corresponding wavelength. If you double the amount of CO2, you reduce the proportion of surviving light by an additional factor of 1/e, reducing the proportion surviving to about a tenth; if you instead halve the amount of CO2, the proportion surviving is the reciprocal of the square root of e , or about 60% , and the atmosphere is optically thin. Precisely where we draw the line between "thick" and "thin" is somewhat arbitrary, given that the absorption shades smoothly from small values to large values as the product of absorption factor with amount of CO2 increases.
The units of absorption factor depend on the units we use to measure the amount of CO2 in the column of the atmosphere encountered by the beam of light. Let’s measure our units relative to the amount of CO2 in an atmospheric column of base one square meter, present when the concentration of CO2 is 300 parts per million (about the pre-industrial value). In such units, an atmosphere with the present amount of CO2 is optically thick where the absorption coefficient is one or greater, and optically thin where the absorption coefficient is less than one. If we double the amount of CO2 in the atmosphere, then the absorption coefficient only needs to be 1/2 or greater in order to make the atmosphere optically thick.
The absorption factor, so defined, is given in the following figure, based on the thousands of measurements in the HITRAN spectroscopic archive. The "fuzz" on this graph is because the absorption actually takes the form of thousands of closely spaced partially overlapping spikes. If one were to zoom in on a very small portion of the wavelength axis, one would see the fuzz resolve into discrete spikes, like the pickets on a fence. At the coarse resolution of the graph, one only sees a dark band marking out the maximum and minimum values swept out by the spike. These absorption results were computed for typical laboratory conditions, at sea level pressure and a temperature of 20 Celsius. At lower pressures, the peaks of the spikes get higher and the valleys between them get deeper, leading to a broader "fuzzy band" on absorption curves like that shown below.

We see that for the pre-industrial CO2 concentration, it is only the wavelength range between about 13.5 and 17 microns (millionths of a meter) that can be considered to be saturated. Within this range, it is indeed true that adding more CO2 would not significantly increase the amount of absorption. All the red M&M’s are already eaten. But waiting in the wings, outside this wavelength region, there’s more goodies to be had. In fact, noting that the graph is on a logarithmic axis, the atmosphere still wouldn’t be saturated even if we increased the CO2 to ten thousand times the present level. What happens to the absorption if we quadruple the amount of CO2? That story is told in the next graph:
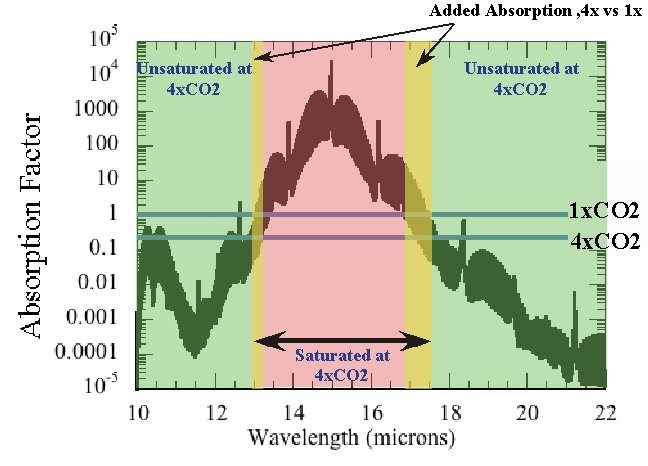
The horizontal blue lines give the threshold CO2 needed to make the atmosphere optically thick at 1x the preindustrial CO2 level and 4x that level. Quadrupling the CO2 makes the portions of the spectrum in the yellow bands optically thick, essentially adding new absorption there and reducing the transmission of infrared through the layer. One can relate this increase in the width of the optically thick region to the "thinning and cooling" argument determining infrared loss to space as follows. Roughly speaking, in the part of the spectrum where the atmosphere is optically thick, the radiation to space occurs at the temperature of the high, cold parts of the atmosphere. That’s practically zero compared to the radiation flux at temperatures comparable to the surface temperature; in the part of the spectrum which is optically thin, the planet radiates at near the surface temperature. Increasing CO2 then increases the width of the spectral region where the atmosphere is optically thick, which replaces more of the high-intensity surface radiation with low-intensity upper-atmosphere radiation, and thus reduces the rate of radiation loss to space.
Now let’s use the absorption properties described above to determine what we’d see in a typical laboratory experiment. Imagine that our experimenter fills a tube with pure CO2 at a pressure of one atmosphere and a temperature of 20C. She then shines a beam of infrared light in one end of the tube. To keep things simple, let’s assume that the beam of light has uniform intensity at all wavelengths shown in the absorption graph. She then measures the amount of light coming out the other end of the tube, and divides it by the amount of light being shone in. The ratio is the transmission. How does the transmission change as we make the tube longer?
To put the results in perspective, it is useful to keep in mind that at a CO2 concentration of 300ppm, the amount of CO2 in a column of the Earth’s atmosphere having cross section area equal to that of the tube is equal to the amount of CO2 in a tube of pure CO2 of length 2.5 meters, if the tube is at sea level pressure and a temperature of 20C. Thus a two and a half meter tube of pure CO2 in lab conditions is, loosely speaking, like "one atmosphere" of greenhouse effect. The following graph shows how the proportion of light transmitted through the tube goes down as the tube is made longer.
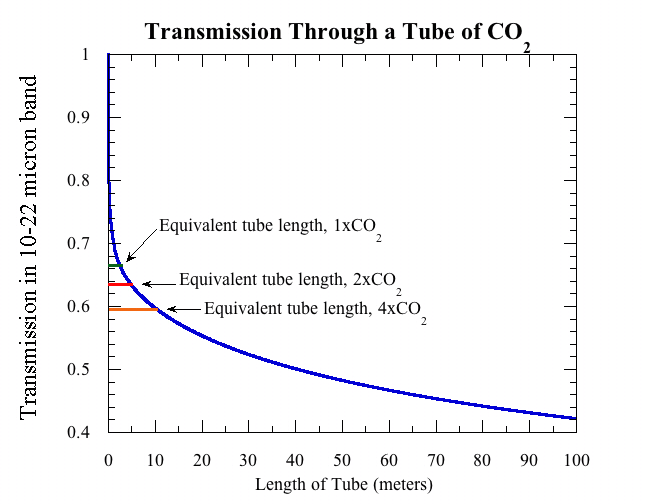
The transmission decays extremely rapidly for short tubes (under a centimeter or so), because when light first encounters CO2, it’s the easy pickings near the peak of the absorption spectrum that are eaten up first. At larger tube lengths, because of shape of the curve of absorption vs. wavelength, the transmission decreases rather slowly with the amount of CO2. And it’s a good thing it does. You can show that if the transmission decayed exponentially, as it would if the absorption factor were independent of wavelength, then doubling CO2 would warm the Earth by about 50 degrees C instead of 2 to 4 degrees (which is plenty bad enough, once you factor in that warming is greater over land vs. ocean and at high Northern latitudes).
There are a few finer points we need to take into account in order to relate this experiment to the absorption by CO2 in the actual atmosphere. The first is the effect of pressure broadening. Because absorption lines become narrower as pressure goes down, and because more of the spectrum is "between" lines rather than "on" line centers, the absorption coefficient on the whole tends to go down linearly with pressure. Therefore, by computing (or measuring) the absorption at sea level pressure, we are overestimating the absorption of the CO2 actually in place in the higher, lower-pressure parts of the atmosphere. It turns out that when this is properly taken into account, you have to reduce the column length at sea level pressure by a factor of 2 to have the equivalent absorption effect of the same amount of CO2 in the real atmosphere. Thus, you’d measure absorption in a 1.25 meter column in the laboratory to get something more representative of the real atmosphere. The second effect comes from the fact that CO2 colliding with itself in a tube of pure CO2 broadens the lines about 30% more than does CO2 colliding with N2 or O2 in air, which results in an additional slight overestimate of the absorption in the laboratory experiment. Neither of these effects would significantly affect the impression of saturation obtained in a laboratory experiment, though. CO2 is not much less saturated for a 1 meter column than it is for a 2.5 meter column.
So what went wrong in the experiment of poor Herr Koch? There are two changes that need to be made in order to bring our calculations in line with Herr Koch’s experimental setup. First, he used a blackbody at 100C (basically, a pot of boiling water) as the source for his infrared radiation, and measured the transmission relative to the full blackbody emission of the source. By suitably weighting the incoming radiation, it is a simple matter to recompute the transmission through a tube in a way compatible to Koch’s definition. The second difference is that Herr Koch didn’t actually perform his experiment by varying the length of the tube. He did the control case at a pressure of 1 atmosphere in a tube of length 30cm. His reduced-CO2 case was not done with a shorter tube, but rather by keeping the same tube and reducing the pressure to 2/3 atmosphere (666mb, or 520 mm of Mercury in his units). Rather than displaying the absorption as a function of pressure, we have used modern results on pressure scaling to rephrase Herr Koch’s measurement in terms of what he would have seen if he had done the experiment with a shortened tube instead. This allows us to plot his experiment on a graph of transmission vs. tube length similar to what was shown above. The result is shown here:
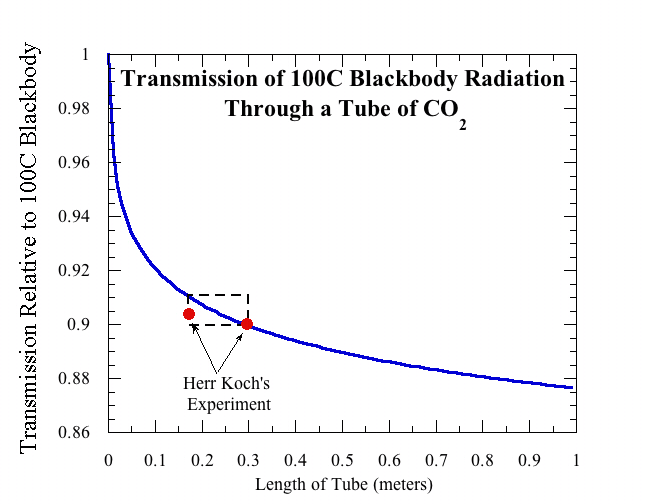
Over the range of CO2 amounts covered in the experiment, one doesn’t actually expect much variation in the absorption — only about a percent. Herr Koch’s measurements are very close to the correct absorption for the 30cm control case, but he told his boss that the radiation that got through at lower pressure increased by no more than 0.4%. Well, he wouldn’t be the only lab assistant who was over-optimistic in reporting his accuracy. Even if the experiment had been done accurately, it’s unclear whether the investigators would have considered the one percent change in transmission "significant," since they already regarded their measured half percent change as "insignificant."
It seems that Ångström was all too eager to conclude that CO2 absorption was saturated based on the "insignificance" of the change, whereas the real problem was that they were looking at changes over a far too small range of CO2 amounts. If Koch and Ångström had examined the changes over the range between a 10cm and 1 meter tube, they probably would have been able to determine the correct law for increase of absorption with amount, despite the primitive instruments available at the time.
It’s worth noting that Ångström’s erroneous conclusion regarding saturation did not arise from his failure to understand how pressure affects absorption lines. That would at least have been forgivable, since the phenomenon of pressure broadening was not to be discovered for many years to come. In reality, though Ångström would have come to the same erroneous conclusion even if the experiment had been done with the same amounts of CO2 at low pressure rather than at near-sea-level pressures. A calculation like that done above shows that, using the same amounts of CO2 in the high vs. low CO2 cases as in the original experiment, the magnitude of the absorption change the investigators were trying to measure is almost exactly the same — about 1 percent — regardless of whether the experiment is carried out at near 1000mb (sea level pressure) or near 100mb (the pressure about 16 km up in the atmosphere).
This may help:
http://eo.ucar.edu/skymath/tmp2.html
_______ begin quote _______
Prior to the 19th century, it was believed that the sense of how hot or cold an object felt was determined by how much “heat” it contained. …
Joule conclusively showed that heat was a form of energy. As a result of the experiments of Rumford, Joule, and others, it was demonstrated (explicitly stated by Helmholtz in 1847), that the various forms of energy can be transformed one into another.
When heat is transformed into any other form of energy, or when other forms of energy are transformed into heat, the total amount of energy (heat plus other forms) in the system is constant.
This is the first law of thermodynamics, the conservation of energy.
…
The energy associated with motion is called Kinetic Energy and this kinetic approach to the behavior of ideal gases led to an interpretation of the concept of temperature on a microscopic scale….
…
Temperature becomes a quantity definable either in terms of macroscopic thermodynamic quantities such as heat and work, or, with equal validity and identical results, in terms of a quantity which characterized the energy distribution among the particles in a system. (Quinn, “Temperature”)
…
The nature of radiation has puzzled scientists for centuries. Maxwell proposed that this form of energy travels as a vibratory electric and magnetic disturbance through space in a direction perpendicular to those disturbances.
…
The great question at the turn of the century was to explain the way this total radiant energy emitted by a black body was spread out into the various frequencies or wavelengths of the radiation. Maxwell’s “classical” theory of electromagnetic oscillators failed to explain the observed brightness distribution. It was left to Max Planck to solve the dilemma by showing that the energy of the oscillators must be quantized, i.e. the energies can not take any value but must change in steps, the size of each step, or quantum, is proportional to the frequency of the oscillator and equal to hv, where h is the Planck constant.
————– end quote ——————-
Timothy, me thinks thou doth psychoanalyze too much. I’ve been asking a simple straight-forward (albeit theoretical) question: Does energy in the vibrational and/or rotational bands increase the temperature (as commonly defined) of the gas? Maybe it’s me, but the question doesn’t sound terribly sinister and encumbered with deep-seated dark motivations to me.
I don’t want to help to do what, exactly? Questions about the temperature of a gas (to which nobody seems to have an answer and seems important to GW theory) or further exploring the claim that IR down-welling is in effect nonexistent (which blows a pretty big hole in GW (not just AGW), at least until scientifically rationalized), what — show I’m not a serious player who just wants to jab folks? Sorry! If you don’t have the answer, that’s perfectly O.K. and carries no negative connotations what-so-ever, but it doesn’t make me the villain. I don’t have the answer either.
Hank, it seems to me that, since gas is all about T, V, P, and n, something directly affecting the temperature (again, as commonly defined) shouldn’t have to be dug out from obscure references and footnotes in papers. Or maybe the answer to my question is just not known for sure — I’ve seen answers both ways from presumably reliable sources.
Nor, Hank, do I fear quantum mechanics (though I’m a long way from expert knowledge), but it does seem to be used to obfuscate or avoid the question at hand at times, even if in a congenial way We could debate the “single molecule has temperature” thing all day without getting any closer to the question at hand.
So, Rod, is this part clear?
“When heat is transformed into any other form of energy, or when other forms of energy are transformed into heat, the total amount of energy (heat plus other forms) in the system is constant.”
— “energy” is not “heat” is not “temperature” —
This also may help:
From: http://galileo.phys.virginia.edu/classes/252/black_body_radiation.html
____________________________
What about Equipartition of Energy?
The point of the rather tedious calculation above, finding exactly how many different modes of vibration, or degrees of freedom, there are in the ovenfull of radiation, was to construct an argument parallel to that applied successfully to understand the properties of gases. The first conclusion would be that there is kT of energy, on average in each wave mode (not ½kT, because the standing wave is like an oscillator with both kinetic and potential energy).
For low frequencies, this is exactly what is observed. The amount of radiation shining out of the oven at low frequencies is correctly predicted by counting modes, as above, and allocating kT of energy to each mode.
The Ultraviolet Catastrophe
The problem is that as we go to higher frequencies, there are more and more possible degrees of freedom. The oven should be radiating huge amounts of energy in the blue and ultraviolet. But it isn’t. For this system, the equipartition of energy isn’t working! ….
____________________________________
Rod B (#502) wrote:
In response to this question: no, the energy in the vibrational and rotational modes does not increase the translational temperature, whereby “commonly defined” implies translational – so longer as the energy in the vibrational and rotational remains in those modes. But it does get reemitted or lost through collision, in which case it will raise the translational temperature assuming one does not already have a local equilibrium.
Rod B (#502) wrote:
I disagree.
The very act of communication on the part of the individual who is listening or reading what someone else has to say is a matter of understanding their intentions – of identifying what it is they intended to communicate. Someone who does not understand this or who is simply disregarding the motivation of others even when those motives become readily apparent is walking blindfolded listening only to the sounds about them.
Someone who is genuinely interested in the promotion of dialogue will be aware of the the psychological elements. So for example, if you engage in internet debates long enough, you come to realize that after a certain point a large part of what continues to fuel a given debate between individuals will be a matter of saving face.
If I am arguing with someone that I care about, I will let them save face – if I consider the results acceptable. If I am arguing with someone that I do not particularly care for, I will let them save face – given the same conditions.
A great deal of argument is about self-assertion which we will tend to view as a form of strength, but there is also strength in self-restraint – and permitting individuals to save face is one of the ways in which one exercises self-restraint. However, I do not believe it is wise to let your act of good will be taken advantage of.
I believe that you are basically a good person. However, you can get rather mischievious. On various occasions, it seemed as if Alastair was going to quit offering his own alternate raditional “theory” – which he is no more qualified to do than either you or I, it seemed quite clear that the questions you were asking and even directing to him were intended to get the whole argument going again. Particularly the further things went along.
To be perfectly honest, I realized you were trying to stir up trouble some time ago, but I didn’t mind so much so long as it was occasional. Not that big of a deal. Up to a point, I could even understand the motivation. But it became a well-established pattern, and then the pattern became tiresome.
However, I was unable to bring it out into to the open so long as I was unwilling to pay the price in terms of how it would affect someone else. Their behavior justified that paying the price. So I decided it was time to bring it out into the open.
At the same time, I believe you had other reasons for being here. I strongly doubt it was all games.
However, when you stated (#495)…
… that did not reflect particularly well on you.
Rod B (#502) wrote:
I believe that you understand enough of the physics to realize what the implications are for future generations. And at the very least you could have ceased in encouraging Alastair to contradict the science.
Rod B (#502) wrote:
Unless I am mistaken, all of the questions you asked regarding temperature were answered by Eli, Ray and Tamino – who have a fair amount of expertise in the area. Additionally, literature was pointed out.
Rod B (#502) wrote:
Who made that claim? Alastair?
You know better – and you have for quite some time.
As I have pointed out to him on numerous occasions, we have infrared images of IR emissions by carbon dioxide at 8 km – and at various other altitudes and at various channels. Likewise, we are flying planes which take measurements demonstrating downwelling IR emissions by carbon dioxide at various altitudes.
Rod B (#502) wrote:
I can understand playfulness, but what you did in terms of your interaction with Alastair went well beyond this. So while I would not consider you a villian, I believe your efforts are misdirected and consciously so.
RE #500 Where Timothy wrote “As it is, theories, lab experiments and empirical measurements of reemission the atmosphere are all in agreement. The science is about as solid as it gets.”
Nowhere in that post is there any reference or citation of a theory, lab experiment, or empirical measurement. This whole thread is based on a the denial of an experiment that was undertaken.
I don’t know whether you have access to the book by Goody and Walker, but it admits that the simple model explained by Gavin does not work for Venus. If you do the sums with an albedo of 80% you will find that the surface temperature is just not feasible. So that theory is wrong!
If you are going to believe everything your are told, of course you will be told the models work. They will gloss over the Venus problem, the Tropical Lapse Rate Problem, and the Energy Balance Closure Problem, and even the Martian polar inversion layer problem (hardly recognised yet) but which Raypierre is going to “eliminate” from his book. See response to #58.
Lectures based on Goody & Walker’s 1972 book Atmospheres:
http://lasp.colorado.edu/~bagenal/3720/CLASS10/10EVM-1.html
“There are multiple different tables of composition – not surprisingly, our understanding of the composition of the atmospheres of Venus and Mars have developed since Goody & Walker wrote Atmospheres in 1972.”
http://lasp.colorado.edu/~bagenal/3720/CLASS14/14EVM-5.html
“… But we just want a simple comparison of Earth, Venus and Mars -Isn’t there a simpler way of looking at this?
For a THIN atmosphere – e.g. Earth, Mars – we can use a simpler model. The book has this…
Rod, part of the problem is that the notion of temperature of a single molecule does not make sense. The fact of the matter is that if you are talking about temperature in the thermodynamic sense, then the presence of molecules is irrelevant, and if you are talking about temperature in the sense of stat mech, you inherently assume a large number of molecules at or near equilibrium.
The relationship between energy and temperature is not as simple as 0.5mv^2 per degree of freedom. For instance, I can add energy to a system of ice, water and water vapor at the triple point and not change the temperature.
Adding energy to the vibrational/rotational excited states will probably increase the gas temperature–but probably through the relaxation process. That is, most of the vibrationally excited atoms will relax via collisions with other molecules (CO2 or other). Some will do so radiatively. A very few of the molecules accelerated by collisions with excited molecules will excite vibrational modes in other CO2 molecules. There is a continual competition between different processes, and small changes (like changes in CO2) can have a big effect on the ultimate balance in that competition. Don’t expect this to be simple.
Alastair, it’s not “denial” to repeat an experiment with better instruments, and to extend the conditions.
The original post is to “discuss Herr Koch’s experiment in the light of modern observations.The discussion here is based on CO2 absorption data found in the HITRAN spectroscopic archive.”
Look again: https://www.realclimate.org/images/TransLongPaths.jpg
That’s science — revisiting the experiment, considering more recent work — not denial.
Alastair McDonald (#505) wrote:
Lets look at lab experiments first:
Then of course you can check the AIP history by Spencer Weart:
Spencer Weart provides the following historical reference:
Martin, P.E., and E.F. Baker (1932). “The Infrared Absorption Spectrum of Carbon Dioxide.” Physical Review 41: 291-303.
… reviewed in:
Smith, R.N., et al. (1968). Detection and Measurement of Infra-Red Radiation. Oxford: Clarendon.
But if you look up what Raypierre mentions, you find that they are performing laboratory measurements and that these measurements are amazingly accurate nowadays:
Barton Paul Levenson also points out that they have even been done with mixtures. (#376)
Now with respect to “empirical measurements of reemission the atmosphere,” I had provided the following earlier in this thread:
#381
NASA AIRS Mid-Tropospheric (8km) Carbon Dioxide
July 2003
http://www-airs.jpl.nasa.gov/Products/CarbonDioxide/
#384
AIRS – Multimedia: Videos: Animations
http://airs.jpl.nasa.gov/Multimedia/VideosAnimations/
Then of course there is the US military article which Allan Ames originally brought to our attention:
USERS’ MANUAL FOR SAMM2,
SHARC-4 and MODTRAN4 MERGED
H. Dothe, J. W. Duff, J. H. Gruninger, P. K. Acharya, A. Berk
AFRL-VS-HA-TR-2004-1145
Environmental Research Papers, No. 1145
http://www.dodsbir.net/Sitis/view_pdf.asp?id=DothH04.pdf
It contains CO2 thermal emission images of the atmosphere as well. And some time ago I pointed out the fact that measurements were even being taken mid-atmosphere by planes and refered you to where you could get the data. Theory? Try quantum mechanics, radiation transfer theory, molecular spectroscopy, etc. You will get plenty of it – at least if you go to a university library.
Alastair McDonald (#505) wrote:
Well, the simple model is simple. Of course it doesn’t work for Venus. Its conceptual. And if you will notice, when Gavin brings it up, he points out that there are some very fundamental problems with attempting to apply it to earth – such as the fact that it doesn’t incorporate the role of moist air convection. In fact its atmosphere is infinitely thin. But the Goddard Institute of Space Studies began by modeling the climates of other planets. They have actually done a fairly good job with Venus, I understand.
Alastair McDonald (#505) wrote:
No, but I tend to trust the experts and I tend to trust in the fallibilistic, self-correcting process of science. Are you suggesting that the experts are untrustworthy? If so, how many different fields? Have they organized a conspiracy? Would you recommend that I trust the opinions of a retired ship captain who has decided to set himself up as an alternate authority on account of his poorly thought-out pronouncements of armchair physics instead?
Alastair McDonald (#505) wrote:
Told the models work? Don’t know if you’ve noticed, but the literature does a pretty good job of pointing out where they are weak. So does Gavin, I believe. Venus? Dealt with it. Tropical Lapse Rate? Don’t know that much about it, but I began digging earlier this weak. It should help in understanding the expansion of the Hadley cells which is bringing drought our way. The things are expanding a bit more as the result of global warming than we initially predicted. Energy Balance Closure Problem? Sounds like a book-keeping issue of checking to make sure that all of the totals add up. Minor, judging from what I’ve seen, but somewhat thorny as you have to take into account all the effects (e.g., turbulence, time of day) and their interaction.
Science doesn’t have all the answers, but just because we don’t know everything doesn’t mean that we know nothing. Science progresses. Incidentally, where are your field experiments?
Raypierre?
I pointed out that you had misread his diagram in #58 with respect to the peaks and #60 with respect to the wavelengths. But normally things are graphed in terms of wavenumber, so perhaps some of your paranoia directed at Raypierre was understandable. However, he would still like to use a better one.
*
I understand the fact that you have questions and problems regarding how it all works. I do too. I am not a physics major, just a philosophy major who is now a computer programmer. But to have questions and problems is not the same thing as having an “alternative theory” and it does not justify arguing as if the physics isn’t well-established, the experts don’t know what they are talking about and somehow you do. Your confusion, the fact that something does not as of yet make sense to you, does not justify your claim to expertise.
*
You have been across the board in terms of your positions.
You claimed that carbon dioxide could not reemit except at the surface. You claimed that it could not reemit in the majority of the atmosphere because local thermodynamic equilibria presumably do not exist in the earth’s atmosphere. So according to you non-LTE prevents reemission. Then you claimed that the top of the atmosphere is non-LTE, and therefore only it could reemit. Then you have claimed that it is the rate of collision being too high which prevents reemission (i.e., hot LTE conditions), but you have also claimed that those parts of the spectra in which reemission would occur get frozen out – meaning that the temperatures are too low for reemission. You have claimed that the emissivity of carbon dioxide will suddenly jump from logarithmic to linear at the surface as the result of higher levels of carbon dioxide – resulting in a catastrophic runaway effect. You have claimed that reemission was due to electrons leaving their excited states when within the context of our atmosphere, reemission is due to molecules leaving their excited states. You have even gone so far as to claim that it was the nucleus which reemits.
The fact that you have jumped from position to position with such speed is itself an admission that you do not know and that you do not understand. And yet you have continued to claim expertise at various points and had been unwilling to ever say what your actual educational and professional background is. I had to look it up.
*
Back in 476 you tried to reverse our positions, claiming for example that I was unaware of some of the more esoteric details of the relevant radiation physics (namely, non-translational temperatures). I didn’t have a problem with this (and indicated as much in 479) – so long as you were willing to quit arguing with what is both theoretically and empirically well-established. I didn’t have a problem with this if it helped you save face – and meant that we could focus on science. The fact is I like you, but I was also willing to let someone else save face rather recently because it seemed the most likely way to get him to go elsewhere.
However, despite all of the evidence and detailed explanations which you have received, despite your desire to avoid conflict and apparent willingness to accept the scientific literature as indicated in 476, you were back to the old game by 489. I’d been played.
Currently your attempts at deligitimizing the advanced state of our knowledge in this area are as bad or worse than what we get from those who would deny that there is such a thing as the greenhouse effect. But you come across as someone who believes that such an effect exists, simply not in the way that the scientific community understands it – and therefore make those who recognize the existence of the greenhouse effect appear confused – when the confusion is entirely of your own making. As such you are giving those who oppose the science a gift which they couldn’t possibly hope to achieve on their own.
There are other effects. For example, when you derail discussions of the actual science into discussions of your ill-informed and often incoherent views. But this is really less important.
*
All of this is so unnecessary.
You have demonstrated the ability to pick up the science, to make the connections, to understand – when you weren’t looking to pick arguments with the experts on anything thath didn’t immediately make sense to you. Honestly you could be quite an asset. You even have been at times. But within the context of the debates in this forum with those who would deny the science, you have often been their greatest ally.
Timothy, me still thinks thou doth analyze too much, and it’s getting tiresome. Sometimes when a student asks a question it’s beneficial to accept it at face value and attempt an answer. Yes, he probably has peer pressure to do stuff, difficulty with his parental relationships, a pile of non-specific teen anxiety and currently really wanting to show off for the cute little Jr. in the first row. But he might just want to know how to factor. Getting yourself all wrapped around the axle and tied up in your jock over secondary sideshows is not particularly helpful. Also, you think Alastair will go quietly into the night if I just stopped goading him??!! Shirley you jest! Or are you just PO’d because he didn’t accept your answers carte blanche, so want to blame me? (There I go! Psychoanalyzing — against all my recommendations [;-) )
I have to go study the rest of the recent post(s); looked like they have some good stuff.
Rod B (#510) wrote (in response to #504, I believe):
Honestly I think both of you could be assets, questions and all. But are you admitting that you have “goaded him” as you have just put it? If so, it would appear that my analysis of you was correct. Would things have gone smoothly without your encouraging him? Probably not, but it would seem that things would have gone a great deal more smoothly, perhaps even on a personal level for him.
But the latter is just sheer speculation on my part. I don’t know enough about him to say. Although I do suspect that he is taking all of this more seriously than you are.
But not even the climatologists would simply expect you to simply take their word for anything. Quite the contrary.
What I would prefer on his part is his acknowledgement that the images of reemission in the mid-troposphere exist, the measurements of absorption and reemission have been performed and that we have graphs of the resulting data. So far every time a link has been provided he has refused to acknowledge that such things were made available. Just stony silence. Then he would make the same claims that no such evidence exists or that such reemission does not take place. It has nothing to do with accepting my answers with or without question. What I would also prefer is his acknowledgement of the fact that he is not an expert any more than I am.
Rod B (#510) wrote:
Frankly there are things that I would much rather be doing than having to deal with this sort of thing – like getting into more of the science. There is a great deal I would like to understand.
Re #509
Timothy,
If you read Spencers Weart’s history, or Bill Bryson’s “A History of Nearly Everything”, you will find that science is littered with mistakes and wrong turns. For instance, either Arhhenius or Angstrom must have been wrong. So what makes you so sure that the current climate theories are correct? The fact that the RealClimate scientists are so confident is no guarantee. Don’t forget what Max Planck wrote:
A new scientific truth does not succeed, generally speaking, because the opponents are convinced and declare themselves educated, but rather because the opponents gradually die out and the following generation is from the start familiar with it.
The skeptics, such as Jack Barrett, are saying “The models are wrong so they are over-estimate the effects of AGW.” The scientists are saying “We know that changes in climate happened in the past due to CO2, therefore our models are correct.” But you, as a philosopher, must know that neither of these assertions is logically correct. There is the possibility that the models are wrong, and that they are underestimating the effects on the way, which is what I believe.
We know that the Dansgaarg-Oeschger events happened but the models cannot reproduce them, therefore the models are wrong. That statement is logically correct. We know that the models were projecting that the Arctic ice would not disappear until 2070. How likely is that now when you see how much the ice has retreated this summer. The models are wrong again. Yes, the models usually get the lapse rate correct, but that does not mean that the models are correct. They are just fitted to the US standard atmosphere! And the models of Venus are fitted to its lapse rate, because the simple models does not work.
What I am saying is that the science produced by the skeptics is correct. That applies to Jack Barret, Christy & Spencer (tropical lapse rate problem), and now Stephen Schwartz. It is the conclusions that they draw from their facts that is wrong.
You wrote “Honestly you could be quite an asset.” That is what I am trying to be, but I am just a lone voice crying in the wilderness. So long as you apply uncritical faith in the scientists of today, then, in the words of Private James Frazer “We’re doomed!”
Re #491 “Dermond (485), I think Planck radiation is dependent only on the temperature of the radiating body, not on any other body or stuff. That’s how a hot sun radiates a bunch into a pretty cold “ether”.”
This is off beam (pun intended) Rod, sorry to put it like this, but if everyone else shares your view there is no way this matter is going to be resolved here. Thermal radiation is no different from any other heat transfer process in the following respect: high energy tends to flows to low; this usually translates as “heat goes from hot to cold”, but the first statement is closer to the 2nd law of thermodynamics than saying “heat”. I notice I have said you are “off beam” about radiative heat and I apologise for this and will try to point you (no more puns) in a suitable direction. The expression used frequently for expressing the radiated energy is, as you know:
Wm2= εσT>4
I have no quarrel with this but we are concerned with the transfer of energy between two places (entities, systems etc.) and the proper expression is:
Wm2= ε σ(T1>4 – T2>4)
because the source (T1) and the sink (T2) temperature play a role, the radiation coupling is reciprocal. When deepspace is involved T>4 is rather small but it should not be forgotten, it matters to somebody. From this expression you can see how the 2nd law of thermodynamics comes into play. Notice that this is for purely radiative transfer, no CO2 or anything else must get in the way. As usual things begin to get rough when you go deeper; since we are dealing with photons there are other considerations that are not immediately obvious, the relevant science concerns the interaction of electromagnetic energy and matter and is called quantum electrodynamics (QED), you probably have heard of this but were not sure how it applied; this article in Wiki. is mainly historical but will lead you however far you want to go http://en.wikipedia.org/wiki/Quantum_electrodynamics .
That word temperature is a big deceiver. I have been watching the debate about “does a molecule of gas have a temperature?” with interest because the basic “thing” is energy. Thermal energy is most happy when it is about atoms, molecules, and particles in general, banging into each other, this is what we think about when we say something is hot or cold. This is a subtle matter and in the world of thermodynamics there is an explanation. In this reference http://en.wikipedia.org/wiki/Talk:Temperature you will find extensive discussion about temperature, in summary it separates the internal energy of the molecules from the kinetic (i.e. translational not rotational etc.) energy. If the definition of temperature seems restrictive it is because this is sometimes necessary when choosing words to identify physical processes.
Alastair, there is more in science than “right” and “wrong”. Indeed, these terms are not particularly useful in scientific discussions because they really never apply. Descriptions are rather “complete” or “incomplete”. A model can be incomplete and still quite usable–viz. classical mechanics. What it boils down to is evidence. There is zero evidence that our current models have serious problems, and there is plenty of evidence that they perform adequately. The fact that we cannot reconstruct events from the distant past is not that troubling, as the outputs of these models are critically dependent on initial conditions, which are poorly constrained. Where we know initial conditions (Mt. Pinatubo, post 9/11/2001, etc.) the models perform well.
Science progresses at its own pace, and that pace is driven by evidence. Classical mechanics was just as incomplete a description of nature pre Michelson-Morley as post, but it was not until we had the evidence that that incompleteness became important. For now, the models do just fine.
Rod, you can always get Alastair going, because he knows Einstein was wrong:
> Blackbody radiation is emitted as a continuous spectrum whereas gases emit line radiation.
This is a guaranteed distraction to any topic at RC — get started in that direction and it goes only in that direction.
On other questions Alastair is often helpful. It’s most likely that current models do underestimate warming, the IPCC is a very conservative group and specifically doesn’t talk about how nature got where it did in past warming events that are known to have happened but aren’t yet showing up in the models.
If you don’t want to talk about how models work and what we may be missing in the way of forcings, bring up radiation transfer, that’s a great way to avoid dealing with what we know has happened in past big warming events that aren’t yet explained or modeled, like the PETM.
As far as I know there aren’t any problems with the models on the “too cold too fast” end —- those work out and seem to be understood. It’s the rapid global warming events that aren’t in the models yet.
RE #511 Timothy Chase
Quote
“What I would prefer on his part is his acknowledgement that the images of reemission in the mid-troposphere exist, the measurements of absorption and reemission have been performed and that we have graphs of the resulting data. So far every time a link has been provided he has refused to acknowledge that such things were made available. Just stony silence.”
Unqoute
Please would you provide details (and/or web refs) of the wavelengths of the emitted radiation in the mid-troposphere? It would be very interesting to compare such figures with the DoE’s statement(re my #419)that CO2 emits only at longer wavelengths than those at which it absorbs.
I believe this statement to be of fundamental importance to consideration of the enhanced GH effect, and so far in this thread it has largely met with “stony silence”.
The problem seems to be that when an excited CO2 molecule emits another photon, it relaxes to a lower energy level in a rotational mode, but the difference in energy is less than the energy of the initially absorbed photon, and so does not match the requirements for further re-absorption by another CO2 molecule. This seems to negate the basis of the multi-layer models of the atmosphere.
Another question is what happens to the energy from the initially absorbed photon remaining in the lower energy rotational mode? Presumably it finds its way by collisions into the atmosphere and so raises the temperature of the atmosphere? Correct, or not???
But this would have been occurring for ever, unless the atmosphere has a way of converting this thermal energy into radiation which can then escape into space.
Mr. Banner, the page you point to is from 1994. The statement you’ve been quoting is one of the few on that page that has no reference/cite/footnote.
I haven’t found that exact statement anywhere else. Maybe it’s outdated, maybe it applies only when both molecules are at the same temperature/pressure/energy level. Offhand it makes sense that on average emission is at a lower energy than absorbtion, as they say — some of the energy will go into other modes. But you could ask:
Page last modified on Wed Jul 17 2002 06:52:51 GMT-0700 (PDT).
URL: http://www.eia.doe.gov/cneaf/alternate/page/environment/appd_a.html
they have a contact link at the bottom of the page
>wavelengths of the emitted radiation in the mid-troposphere
If you look at the links he provided, the photographs specify the elevation and wavelength used in the image.
> the atmosphere has a way of converting this thermal energy into radiation which can then escape into space
That’s the whole point, if you start from the top of this thread and read the original post.
re (511): Timothy, you said (504), “… it seemed quite clear that the questions you were asking and even directing to him [Alastair] were intended to get the whole argument going again…. ” You implied that I am goading Alastair; I never was nor claimed to be.
In 511 you say, “… What I would prefer on his part is his acknowledgement that the images of reemission in the mid-troposphere exist, the measurements of absorption and reemission have been performed and that we have graphs of the resulting data. So far every time a link has been provided he has refused to acknowledge that such things were made available. Just stony silence. Then he would make the same claims that no such evidence exists or that such reemission does not take place.”
Sounds like “…PO’d because he didn’t accept your answers carte blanche…” (my words) to me. You go on to say, “…It has nothing to do with accepting my answers with or without question….” which is directly opposite the words above.
Just though I’d try to clear some things up, as irrelevant as they are.
Dermod (513), I agree with the post. The Sun radiates a pile of energy to the Earth, and the Earth radiates energy to the Sun — but a trivial amount based on their respective surface temperatures (to the 4th power). This also brings up the (your?) question how the colder atmosphere radiates so much back to the earth. Perhaps it’s not classic blackbody radiation?? Perhaps it’s all coming from the low altitude warm troposphere?? I might have misread your post 485; sorry.
Alastair McDonald (#512) wrote:
I notice that what you have written has no acknowledgement of carbon dioxide reemissions in the mid-troposphere and above, something which is demonstrated by the longwave images. Likewise, there is no admission of the data we have from planes or the results that we have obtained in the laboratories. As far as I can tell, you still hold that carbon dioxide can reemit radiation either at the top of the atmosphere, or depending upon your mood, at the surface. Do you acknowledge the images? Do you acknowledge the data? Do you still claim that climatologists and physicists specializing in radiation transfer have next to no understanding of the radiative properties of carbon dioxide? If so, what are they missing?
Alastair McDonald (#512) wrote:
Are you claiming that you have a “new scientific truth” when as I have pointed out:
…?
Are you claiming that your poorly thought-out ideas constitute just such a revolutionary breakthrough? What is your revolutionary idea today? Does it constitute a rigorous scientific theory? What data do you have? What empirical tests have you performed? Are you claiming that you have any background in radiation transfer? Quantum mechanics?
If so, what is this background?
And what specifically are you arguing against with regard to current, mainstream climate theory? That it is not the final theory? That it doesn’t as of yet include all the effects and mechanisms which determine the course of the climate? They make no such claim. Are you claiming that what they are missing is something involving the radiative properties of either carbon dioxide or water vapor? If so, what?
Alastair McDonald (#512) wrote:
Climatologists would not claim that their models are complete. They would however claim to have a great deal of evidence and justification for their understanding of the role that CO2 plays in the evolution of the climate system.
Alastair McDonald (#512) wrote:
I would not claim to be a philosopher.
I would claim that I have a background in philosophy, that I have written eighty page critiques of Descartes’ “Six Meditations on First Philosophy,” “The Critique of Pure Reason” and of early twentieth century empiricism. This does not make me a philosopher or even someone who has the same degree of formal education as those who have obtained a PhD in philosophy.
I would claim some formal background in the history of philosophy. I would claim some formal, graduate level background in ancient greek philosophy.
But this does not make me someone who can offer expert opinion in ancient greek philosophy which is equivilent to that of someone who professionally specializes in ancient greek philosophy.
I would claim some formal background in dialectics. But this does not make me someone who can offer expert opinion in dialectics which is equivilent to that of someone who professionally specializes in dialectics.
As someone who has some graduate-level formal background in epistemology, I also claim to have studied formal and informal logic, to have some background in the relationship between foundationalism and coherentialism, and to have some understanding of the nature of self-referential argumentation. I recognize the fact that neither strong foundationalism nor strong coherentialism is logically defensible. I recognize the fact that a radical skepticism based upon the denial that knowledge exists or upon radical doubt that knowledge exists is self-referentially incoherent. I would claim to have applied self-referential argumentation at a technical level to certain other problems in philosophy, but I would not claim that such results have the same status as that of someone who has obtained a PhD in the relevant fields. I recognize the necessity of admitting corrigible knowledge (i.e., knowledge which lacks cartesian certainty) as a form of knowledge, that lacking this, in logic, no claim to any knowledge is logically defensible.
But even as a whole, this does not constitute a systematic theory of knowledge.
I would claim some formal background in analytic philosophy at the graduate level and I would claim some formal background in the philosophy of science. I would claim that advanced scientific theories are a form of knowledge. I would claim that scientific knowledge is cummulative. I would claim that a conclusion justified by multiple independent lines of investigation is often justified to a far greater degree than it would be if it were justified only by one line of investigation considered in isolation. I would claim that the advanced theories of empirical science cannot be tested in isolation, that there exist interdependencies between various scientific theories.
But this does not make me someone who is in possession of a systematic philosophy of science or who can offer expert level opinion equivilent to that of someone who specializes in the philosophy of science.
*
Do you have a PhD in any field that is relevant to climatology? Do you have a PhD in any advanced field of physics? Can you offer expert level opinion in radiation transfer theory? Do you have any graduate level background in any of this? Do you have any formal background? Have you systematically studied any of these disciplines?
Alastair McDonald (#512) wrote:
What basis do you have for making such claims? Why is it that their claims are correct when you so cavalierly dismiss so much of mainstream climatology? Do you have any formal training which justifies your making such claims as any form of expert level opinion?
Alastair McDonald (#512) wrote:
How can you be an asset if you so cavalierly dismiss so much of mainstream climatology?
Alastair McDonald (#512) wrote:
I recognize that given the current state of our knowledge, we do not understand all the mechanisms which are relevant to understanding the climate system as a whole. I recognize that our knowledge of the evolution of the earth’s climate system is incomplete. But I also recognize that current climate theory is an advanced branch of physics in an advanced state. If this is what you genuinely claim to be an “uncritical faith,” then I have literally no understanding of what you mean by the term.
Re #517
Thank you, Mr Roberts, for your response to my #516. The DoE paper I referred to was updated in 2002. I think the following ref provided by Allan Ames in #464 is of great significance.
http://www.dodsbir.net/sitis/view_pdf.asp?id=DothH04.pdf
It is a joint research paper by Spectral Sciences, Inc., the US Air Force, and Boston College. It is highly authoritative, and immense. Pages 9 and 10 seem to show that an excited Co2 molecule can relax in stages, so that the energy of a particular emitted photon is less than the initially absorbed photons, so making re-absorption impossible. This supports the DoE statement. No doubt someone will wish to correct me on this point.
Another item of interest is that a CO2 molecule can be raised into an excited state by “resonant energy transfer” from a nitrogen molecule.
Ah, that’s a good link, thanks Mr. Banner.
I won’t pretend to follow this. Still hoping to bait one of the real physicists to join in — I wonder if a photon from a lower, warmer CO2 moledule can be absorbed by a higher, cooler CO2 molecule, because I still don’t find a clear argument that it can’t happen. But I’ve just skimmed this huge piece. It is probably worth a read by someone able to handle the physics and explain it. Oh, please?
excerpt——
“When the radiative terms are not negligible compared to the collisional terms and Equation (2) can no longer be used to describe the situation, thermodynamic equilibrium no longer prevails. The situation is said to be in NLTE until the collision terms are much less than the radiative terms. A rule of thumb is that the radiation begins to deviate from LTE when there are less than a million collisions per radiative lifetime. The radiative lifetime of the v = 1 state of NO is about 0.1 s, so the 5.3 μm radiation from NO begins to deviate from equilibrium around 40 km altitude. This is an approximate but helpful rule which is applicable to species that are not produced by chemiluminescence or photodissociation. An exception to this rule of thumb is the 15 μm band of CO2. Due to fast pumping during collisions with oxygen atoms [Sharma, 1988; Sharma and Wintersteiner, 1990], this mode stays in equilibrium up to above 100 km altitude [Rinsland et al., 1992]. At very high altitudes the radiative pumping and loss terms J and A in Equation (1) are much larger than the collisional pumping and loss terms Pc and Lc. The ratio of the excited to ground state densities then becomes
(3) J/A =[M*]/[M]
This situation is described as “radiative equilibrium”. At altitudes greater than about 150 km the ratio of the densities of the CO2 vibrational levels 01101 and 00001 is determined solely by the upwelling earthshine. The frequency of collisions is too small to have any impact and radiative equilibrium prevails. …
The arguments cited above apply to stable species for which normally only the lowest vibrational level is populated and which may be excited by earthshine, sunshine, and collisions. …
…
“We then have a situation where the translational and rotational degrees of freedom can be described by one temperature and the vibrational levels are described by an entirely different temperature. Of course two different vibrational manifolds in the same molecule may be described by two different vibrational temperatures…..”
—– end excerpt ——
For Alastair — do you still agree you can falsify your theory by getting photographs of the limb of the Earth in infrared? Do you agree such photographs would show a fuzzy edge at the stratosphere if CO2 is radiating, as the infrared astronomers believe, but would show a black sky above the top of the clouds/troposphere if CO2 doesn’t radiate as you believe?
If that adequately allows you to test your theory, the images would be available from this system, I expect.
The SEAWIFS satellite system builds true color images for display from “eight (8) different bands in the visible and near infrared part of the electromagnetic spectrum…. the sensor is designed to collect all eight bands at exactly the same time.”
http://oceancolor.gsfc.nasa.gov/SeaWiFS/TEACHERS/TrueColor/
If you think this will let you falsify your theory, you might ask for the various infrared bands that are used to make up some of their many images showing the limb of the planet.
They have lots of imagery taken tangent to the horizon, though the public website images I’ve seen all combine all 8 bands for true color imagery, like these:
http://www.navis.gr/space/greece/images/large_08.jpg
http://www.geog.ucsb.edu/~jeff/wallpaper2/tn_europe_oblq_view_aug14_2001_above_red_sea_6400km_altitude_seawifs_wall_jpg.jpg
http://www.geog.ucsb.edu/~jeff/wallpaper2/cyclone_dina_jan242002seawifs_wall.jpg
Re #523
Hank,
No I do not agree that my theory can be falsified with photographs of the limb of the Earth. I am arguing that a view from outside the atmosphere will be the same as those currently obtained. What I need is a spectrum taken from 100 or 1000 m.
I had a look at the SEAWIFS page, but it is only for visible and near IR. The band I am interested in is the CO2 15 micron band since that has a major effect on the spectrum of the Earth (and Mars.) It is in the far infrared part of the spectrum.
I have performed an experiment which would have falsified my theory, but it didn’t. Unfortunately the results were not good enough to prove my theory. A major problem that I have is, because I am saying the current theory is wrong, no one believes me, and so they are not interested in understanding what my theory is.
I have just been reading James Rodger Fleming’s (Spencer Weart’s rival) book “Historical Perspectives on Climate Change” about Wiiliam Ferrel’s views on the greenhouse effect. Fleming writes: “He [Ferrel] made it clear that one-half of the radiation absorbed in the [atmospheric] envelope would be again radiated back to the [Earth’s] body.”
Fleming goes on to quote Ferrel:
“It is seen, therefore, of what great advantage the atmosphere is in raising the mean temperature of the earth’s surface. This effect is similar to that of the glass covering of a conservatory of plants, which is a diathermanous medium which permits the heat of the sun to pass through with facility, but is almost completely impenetrable by the heat radiated from the air and all bodies within.”[Ferrel, 1884]
I am saying that Ferrel was wrong on both points. The radiation is absorbed by the air and not re-radiated. The glass of a conservatory is transparent to infrared radiation, and in fact it is the band of solar radiation in the UV to which it is opaque!
But then, as I sure Timothy will enjoy pointing out, I do not have the Ferrel Cells named after me so I must be wrong :-(
Re #506 where Hank Roberts Says:
26 August 2007 at 5:39 PM
Lectures based on Goody & Walker’s 1972 book Atmospheres:
http://lasp.colorado.edu/~bagenal/3720/CLASS10/10EVM-1.html
“There are multiple different tables of composition – not surprisingly, our understanding of the composition of the atmospheres of Venus and Mars have developed since Goody & Walker wrote Atmospheres in 1972.”
Since the composition is not what I was discussing I ignored this post, but now having read on I have discovered that if you go to:
http://lasp.colorado.edu/~bagenal/3720/
there are links to PDFs of all the chapters of Goody and Walker.
On pages 14 & 15 of Chapter 3 (pages 57 & 58 of the book) you can find the section to which I was referring. Using the simple model gives an impossible optical depth for Venus.
You quoted?
http://lasp.colorado.edu/~bagenal/3720/CLASS14/14EVM-5.html
“… But we just want a simple comparison of Earth, Venus and Mars -Isn’t there a simpler way of looking at this?
For a THIN atmosphere – e.g. Earth, Mars – we can use a simpler model. The book has this…
But if the models is wrong for Venus, it is wrong. It may give reasonable results for Earth and Mars but it is still wrong. And that is what I am saying – the current models give reasonable results for today’s conditions but they are wrong, and are not predicting the future correctly. Actually, they did not even predict today’s melting Arctic ice correctly. Ray Ladbury may be satisfied with that performance, but I am not.
Alastair,
The physics of melting ice is much less well understood than is that of the atmosphere. If I were to look for the failure of prediction, that is where I would start. And as I have said before, “right” and “wrong” are not particularly useful adjectives when discussing models. Models are simplified approximations of the system under study–by their very nature, they leave out some physics. Models provide insight or they do not. They provide adequate predictions or they do not. If a model does not reproduce the trends seen in the actual system, you look at the physics it leaves out, starting with the least understood aspects. Since I am not a climate scientist, it does not matter what I am satisfied with–what matters is whether they can get meaningful science out of the models. They do.
Alastair, nobody’s “satisfied” or people would have put down the tools and gone home.
“All models are wrong; the practical question is how wrong do they have to be to not be useful” — George Box
Those of us asking for better information are looking for information that can be supported. Yours isn’t yet.
To support your unique theory you need some way it can be falsified or it’s just handwaving.
You need at least one thing that Einstein predicted one way, you predict another way, and is observable by third parties.
Until there’s a difference that can be observed, there’s no difference that makes a difference.
How about those infrared photographs of the horizon from space?
Alastair, your response above appeared after I wrote mine. Care to describe your experiment? I don’t understand what you mean about it not working.
Hank, he uses Real Climate as a platform for his ideas.
It gives him access to a much wider audience than he would have anywhere else. The climatologists who created Real Climate intended it to be used as a platform for teaching climatology to a wide audience. When he is humored as you are doing now, it encourages him in his attempts to undermine the strongest aspects of climatology and to attack the integrity of these climatologists to the point at which it would appear that at certain point they are made uncomfortable participating. He goes so far as to state that they ignore any evidence which suggests that the theories which form a core aspect of their discipline are invalid. And he shows every sign of being willing to do so again in the future.
People who visit here expect the “skeptics.”
They do not expect someone who teaches an alternative greenhouse theory and who knows just enough technical terms to sound convincing – at least for a brief period. He has repeatedly denied the existence of the mountain of evidence which we have on radiation transfer even when we have linked to various pieces of it repeatedly and he continues to do so even now. He shows signs of a willingness to do so in other areas. He derails discussions of the actual science with great frequency and at great length and will do so indefinitely if he is treated with a courtesy that he does not deserve. As such he diminishes the quality of Real Climate, undermines its ability to attract new participants and reach a wider audience.
As a matter of honesty, integrity and honor, I would not claim to have an expertise which I am lacking.
When he attempted to bait me into claiming such expertise I was not tempted for even a small fraction of a second. Nevertheless it opened some old wounds. While latter last even I was able to check the posts at Real Climate and was pleased to see new participants, including at least one that would appear to be a genuine asset, I was unable to participate because I was extremely upset. I am getting over it and will in all likelihood have it under control by the time that some “skeptic” attempts to use it against me. Nevertheless it is a deeply personal issue for me as I devoted a considerable part of my life to the attainment of a level of expertise which I will in all likelihood never achieve.
I do not have a problem with Alastair participating.
However, I at least will have a personal problem with his participating as he does now. Whether he is here or not, I will continue to participate because I believe in Real Climate, consider it to be an extraordinarily generous gift to all those who learn of it and visit it. I will continue to participate because I believe in its mission. I will continue to participate because I believe it is critical that people understand the issues – including the threat of loss of life which lies in the decades ahead. So long as he continues with what he is currently doing, I will not address him directly unless I believe that the conditions especially warrant it – as when he attacked the integrity of one of the climatologists. However, I see little reason in holding back from pointing out that he has no credentials, is entirely lacking of the educational background for any of the claims which he is making, and refuses to acknowledge the evidence which exists.
This is where I stand. I hope that even if you disagree with me that you will at least respect my position.
Oh, I know, Timothy; I often ask Alastair to distinguish statements he makes about the nature of reality that are unique to his theory from those taught in physics classes. I’m sure I’ll continue to ask. It’s the extreme case of the “please give me a cite for why you believe …. and a way to check your sources” request. Good practice anyhow.
Or maybe it’s just recreational typing; when I think that I give up for a while. This is probably one of those times.
As Patrick Moynihan once said, everyone is entitled to their own beliefs, but not to their own facts.
Re #528 Hank, My experiment was very crude so I have been reluctant to report it however …
Near where I live there is The Bournemouth Eye – a tethered balloon. It rises to about 100 m. I aquired an infrared thermometer with a range of 7 to 18 microns and used it to measure the temperature of the surface regularly as the balloon rose and again as it descended. The results showed that the temperature measured fell quickly for the first 50 m above the ground and then remained the same.
Note, what I claim I was reading was not the temperature of the surface which did not change, nor the air temperature which would have fallen by 1F. What I was measuring was the infrared radiation emitted by the surface. The reason the temperature reading fell was because the radiation in the 15 micron band was being absorbed by the air and not being re-emitted, in conflict with Kirchhoff and Einstein.
Convinced?
Re #509
Timothy,
Sorry that I have not replied fully to your posts earlier but they are rather long and I am a slow reader.
Keeping this one short I would just like to mention first that the AIRS maps show CO2 concentration not radiation.
Second, the SAMM2 report is regarding a model not data. However, it does tend to support my view about radiation in the 15 micron band when they write:
Since the 15 μm CO2 band is very strong, its transitions to the ground state and low lying excited states are severely self-absorbed. This fact has important consequences for atmospheric radiation which we will point out as we go along. Similarly, solar radiation has negligible influence on the 15 μm radiation because of the small number of solar photons at this wavelength. The intensity of 15 μm radiation therefore shows no diurnal variation [Wise et al., 1995].
The lack of diurnal variation sort of implies that the 15 micron band originates at the TOA well away from the surface where the solar effect would have an influence.
Their Figure 6 goes against what I am saying, but it is modeled not measured, and it seems that they have forgotten to include the “freezing out” of the vibrational excitation at room temperature (STP) and below.
Cheers, Alastair.
Nope. I just find too many reports of people taking photographs of the atmosphere in the band where you say it can’t happen.
Cameras have long been available in this band, for example this one from Mars Viking:
http://ntrs.nasa.gov/search.jsp?R=81317&id=1&qs=Ne%3D20%26N%3D4294910007%26Ns%3DArchiveName%257C0
http://www.google.com/search?q=%2B%2215+micron%22+%2Binfrared+%2Bsatellite+photos+of+carbon+dioxide
AEBanner (#521) wrote:
Actually from what I can tell you are right.
Transitions from higher to lower states of excitation. But what this means essentially is that the energy becomes split into seperate “parcels,” each of which may be directed towards the surface or towards space. With such partial relaxation this changes the details, no doubt affecting some the atmospheric chemistry (which is part of the subject of the paper) and rendering the “random ladder climb” analogy that I had employed less accurate, but qualitatively things remain much the same. If the radiation reaches the surface, it warms the surface. If it warms the surface, this implies more thermal radiation.
Three points…
The net direct effect of carbon dioxide is to lower the temperature. There is an exception in the lower range where it is active, but this would appear to relatively small. I can look up the diagram a little later. It includes carbon dioxide, water vapor and ozone, showing their local effects in terms of warming or cooling in degrees per day I believe. As I understand it, the atmosphere is directly warmed principally is moist air convection in the lower levels, then both turbulence and diffusion which help to distribute the heat to the upper levels. However, ozone has a fairly broad range over which it has the net effect of warming the atmosphere and its overall net effect is to warm the atmosphere.
Regarding AIRS
AIRS shows CO2 concentration by means of its infrared emissions.
CO2 both absorbs radiation and emits radiation.
RE Alastair (#532),
It helps to keep in mind the fact that the name AIRS is an acronym meaning Atmospheric InfraRed Sounder. Its images of gas concentrations at various altitudes is due to its measurements of infrared emissions. Therefore if it is detecting CO2 at 8 km, this is because CO2 is emitting longwave radiation at 8 km.
If you are unable to lookup this information for yourself, I will gladly look it up for you. However, I am afraid that it will still be up to you to read it. I suppose that would mean that my efforts are wasted.
Re #535
The standard model claims that the CO2 emissions depend on temperature but you are claiming it shows concentration. Who is correct?
To be honest, I am pretty sure it is not the 15 micron emissions that they are using to measure the CO2 concentration. It will be near IR from re-emission of radiation absorbed from the sun.
Alastair McDonald (#537) wrote:
Both.
AIRS does over 2000 different channels. I have mentioned this before. The spectra of carbon dioxide (and other greenhouse gasses) are a function not simply of the gas but of the pressure and temperature. Take enough measurements and you can get a great deal of information out of it.
Incidentally, I notice that your reading speed has suddenly picked up.
re re-emission (534, et al). A repeat of a question/contention I made earlier and tried to remake recently but my post didn’t pass muster (probably too long, redundant and boring, but other than that I thought it pretty good… Or maybe I just botched the posting…). The assertion, refuted by some, that “an excited CO2 molecule can relax in stages, so that the energy of a particular emitted photon is less than the initially absorbed photons, so making re-absorption impossible” makes no sense to me. At a basic level there are near thousands of quanta energy levels (especially in rotation) and a molecule can absorb or emit only at those levels. If a CO2 emits at level “Q”, level Q then exists in every CO2 molecule, and some CO2 molecule will have that level vacant and be able to absorb the re-emitted photonic radiation. It matters not a twit if the first molecule started it all by absorbing a photon at level “X” (all not withstanding other affecting factors.) Is this not correct?
Alastair,
More curious than angry.
Three questions: how long, did Rod know, and most especially, why?
Seen this sort of thing before, but nice twist. That’s what threw me off.
re Timothy (520 et al), I’m disappointed with your attitude. It sounds like you want to assure that RC is a mutual admiration and cooperative cheerleading society — and idea that pops up periodically here. The fact that you believe very strongly in what you profess and even feel you have solid evidence to back up your assertions does not warrant a scientific forum casting out or shunning all who don’t readily subscribe to your dogma. The moderators of RC are not that stringent. It might be O.K., even helpful, to shun the extreme crackpots; but crackpot is not defined by disagreeing with you or challenging your well thought out precepts.
Rod B (#541) wrote:
Rod,
Hank Roberts (#530) gave us a fairly good quote just a little while back:
We have argued a great deal with Alastair and shown him time and time again that the criticisms he has of the mainstream effect don’t work and “his” theory is unworkable. Frustrating, but… whatever.
However, the data that we linked to, thats pretty hard stuff. The reemissions in the mid-troposphere actually recorded via satellite. Then of course there is the data from planes. Couldn’t actually give it to him, but available for purchase nevertheless. And not too expensive. However, he never even acknowledged that we made the images and data available to him time and time again.
And I didn’t like the attack upon the integrity of one of the climatologists. What does your book of “How to Play Fair with the Misinformed” have to say about that?
So yes, if that were what was going on I would have a serious problem with it. Particularly if someone kept on derailing conversations regarding the actual science with his own “theories” which made no sense whatsoever and did everything to undercut the purpose of Real Climate – which is to educate the public about climatology. But I can also see how that sort of thing might appeal to you.
I would also have a serious problem with someone claiming to be an expert – particularly an unacknowledged genius – in a field that he knew very little about. That would be “crackpot” as I understand the term. And I also have a real problem with the anti-science attitude that is so prevailent in certain parts of our society.
Likewise, if I had to weigh someone’s hurt feelings against someone else’s loss of life, let alone a whole lot of other someones’ lives, let’s see, on the one hand, on the other hand,… not much of a choice for me there. I’m sorry if that is a problem for you. However, given BAU for a few more decades I suspect we are going to face some choices that will be a great deal more difficult. Choices I would rather not see anyone have to make.
But I will remind you that I encouraged him to find a more productive role – at numerous points.
Not just trying to jettison him but wanting to see him grow into something more than he was before. As I had written in an essay for a particular audience at one point,
“… while recognizing one’s mistakes may be experienced prospectively as a form of death, the act itself brings a form of rebirth and self-transcendence, giving one the courage to revise one’s beliefs when confronted with new evidence.”
This is a view that I take very much to heart. What we should fear are not our mistakes or even our having to admit our mistakes to ourselves or to others, but our inability to admit our mistakes.
But I figure the following might help as well – at least in terms of understanding where I am coming from….
I don’t expect everyone to agree, but I believe that everyone should be willing to admit their mistakes – particularly when reality stares them right in the face.
Yes, Rod, I am an idealist.
But I also like to think that I am a good student of human nature.
Re #540
Timothy,
my rate of reading has not speeded up. It is still the same at one screenful per day. Thnkfully, your posts have become considerably shorter, and so I can now include them within that ration.
However, when you write “Three questions: how long, did Rod know, and most especially, why?” your brevity has me defeated. To what are you referring?
However, without knowing that, I can still give you an answer to your second question: you will have to ask Rod that! But you may be doing Rod a misjustice. I suspect that he is, like you, searching for the truth. And he, like you, is handicapped by his preconceived ideas. He believes that global warming is all a silly scare. You seem to believe that scientists can make no mistakes. You are both wrong.
Ray and Hank,
You both seem to be making the same point. That although the models are not exactly right that is because no model can be. It is only a simplification of the real world.
But what I am saying is that the model of terrestrial radiation being reflected (or, if you prefer re-emitted) back to the ground is wrong. The air at the surface is not heated by conduction with the ground. It is heated by the radiation from the ground. Either way you get the same result: the air in the atmosphere is heated from below and it convects.
But that is where the similarity between the two systems ends. However, it pointless describing the correct model further if you cannot accept that simple difference.
But I will add that you cannot prove that a transparent colourless gas is acting at the surface of the Earth by using a satellite 100 miles up, no matter how sophisticated its cameras might be.
Gentlemen,
Like Rod B, I have been asking similar questions in all my web postings on this thread but, until recently, have been confused by the answers since several appear to be inconsistent with each other while others answer questions I didn’t ask. However, as the thread has progressed, I believe things are becoming clearer, thanks largely to posts from AEBanner (#454 and 517), Allan Ames (#464), Ike Solem (#457) and Ray Ladbury (#478). Given my propensity to grab the wrong end of the stick, however, I would like to make a series of statements and follow them with a list of questions. I would appreciate advice on the veracity of the former and answers to the latter.
Statements:
1) At the top of the atmosphere, their is escape of long wave radiation which, at equilibrium, matches in energy terms that entering by solar radiation less albedo.
2) There is an “atmospheric window” in the wavelength range of roughly 8.5-13.5 microns where there are no blocking greenhouse gases except for trophospheric ozone. This window allows egress of radiation directly from the surface. However, in energy terms, this represents only about 17% of OLR.
3) Radiant energy absorbed by the atmosphere will be re-emitted in all directions. It will be re-emitted at longer wavelengths than that at which it is absorbed, the re-emitting wavelengths being longer at lower temperatures and pressure. This implies that a species of molecule which absorbs at one wavelength cannot absorb a photon re-emitted by a molecule of its own kind.
4) Approximately two thirds of the energy absorbed by the surface emanates from energy re-emitted in the atmosphere and only one third is attributable to directly absorbed solar energy.
5) Radiative transfer is a much slower energy transport mechanism than convection such that the latter process gets most of the effluent energy to the top of the atmosphere.
6) Radiation leaving the surface has a near blackbody spectrum. OLR does not. There are gaps attributable to greenhouse gases.
7) There is little water vapour in the high atmosphere.
Questions:
1) Will the “atmospheric window” get narrower with increasing CO2? I can picture the possibility of a curtain hanging on the right (long wave) side of the window which may become partly drawn, thus obscuring part of it. I can see this to be particularly likely if energy is leaving a dry surface with little overlying water vapour but less likely over, say, oceans.
2) Ray Ladbury (#478) talks of gaps in the blackbody spectrum in the case of OLR. However, Step 2 of “The CO2 problem in 6 Easy Steps” (Real Climate Archive, August 6th) cites a graph showing IR spectra taken from space. This graph has no explanation. Rightly or wrongly, I interpret it to be showing that Ray’s gaps are attributable to CO2 and ozone but not to water vapour. Is this correct? If so, is it explained by the dry upper atmoshere.
3) How does thermal energy reaching the top of the atmosphere by convection become OLR and make good its escape to space?
4) Various correspondents suggest that infrared in the near-15 micron range can be demonstrated in the high atmosphere. Could this emanate from re-emissions of atmospherically- absorbed solar irradiation, given that re-emissions from lower level CO2 molecules couldn’t apparently be an explanation?
Re #539 Rod B
I can only suggest that the process you described depends upon the absorption cross sections of the molecule for photons of different energies, and so is a matter of probability. The absorption lines adjacent to the 14.99 micron line for CO2 are somewhere between one and two orders down, if I remember correctly. So the chance of the transition happening twice ( in any “chain” ) would be between a factor of 10^2 and 10^4 down.
Gavin,
Quick question. Did you decide not to post something I submitted? Not a problem – light of a new day I am not even sure I would want it to go up. But it helps to know. I know that I have lost an strictly science post or two recently which were probably due to a technical glitch.
Re #547,
Gavin,
Rod has lost a post, and now so has Timothy. I am finding that RealClimate is very slow to respond since it was reconfigured. Moreover now I am no longer able to preview my posts before sending them :-(
The slowness may be due to this thread being too long, or because the RealClimate is now so popular that the server is often overloaded. Are you aware of our difficulties and is it possible you could do something about them?
Regards, Alastair.
Alastair, try turning the other direction — when you can’t cite sources for what you believe, describe a way to test it.
Re #539 and #546
The way the molecules behave is determined by selection rules. for instance see http://www.iop.org/EJ/article/0022-3700/18/22/016/jbv18i22p4481.pdf Selection rules for rotational excitation of polyatomic molecules by slow electron impact
But for an explanation of the principles of electronic and vibrational (vibronic) energy changes see http://en.wikipedia.org/wiki/Franck-Condon_principle