By raypierre , with the gratefully acknowledged assistance of Spencer Weart
In Part I the long struggle to get beyond the fallacious saturation argument was recounted in historical terms. In Part II, I will provide a more detailed analysis for the reader interested in the technical nitty-gritty of how the absorption of infrared really depends on CO2 concentration. At the end, I will discuss Herr Koch’s experiment in the light of modern observations.
The discussion here is based on CO2 absorption data found in the HITRAN spectroscopic archive. This is the main infrared database used by atmospheric radiation modellers. This database is a legacy of the military work on infrared described in Part I , and descends from a spectroscopic archive compiled by the Air Force Geophysics Laboratory at Hanscom Field, MA (referred to in some early editions of radiative transfer textbooks as the "AFGL Tape").
Suppose we were to sit at sea level and shine an infrared flashlight with an output of one Watt upward into the sky. If all the light from the beam were then collected by an orbiting astronaut with a sufficiently large lens, what fraction of a Watt would that be? The question of saturation amounts to the following question: How would that fraction change if we increased the amount of CO2 in the atmosphere? Saturation refers to the condition where increasing the amount of CO2 fails to increase the absorption, because the CO2 was already absorbing essentially all there is to absorb at the wavelengths where it absorbs at all. Think of a conveyor belt with red, blue and green M&M candies going past. You have one fussy child sitting at the belt who only eats red M&M’s, and he can eat them fast enough to eat half of the M&M’s going past him. Thus, he reduces the M&M flux by half. If you put another equally fussy kid next to him who can eat at the same rate, she’ll eat all the remaining red M&M’s. Then, if you put a third kid in the line, it won’t result in any further decrease in the M&M flux, because all the M&M’s that they like to eat are already gone. (It will probably result in howls of disappointment, though!) You’d need an eater of green or blue M&M’s to make further reductions in the flux.
Ångström and his followers believed that the situation with CO2 and infrared was like the situation with the red M&M’s. To understand how wrong they were, we need to look at modern measurements of the rate of absorption of infrared light by CO2 . The rate of absorption is a very intricately varying function of the wavelength of the light. At any given wavelength, the amount of light surviving goes down like the exponential of the number of molecules of CO2 encountered by the beam of light. The rate of exponential decay is the absorption factor.
When the product of the absorption factor times the amount of CO2 encountered equals one, then the amount of light is reduced by a factor of 1/e, i.e. 1/2.71282… . For this, or larger, amounts of CO2,the atmosphere is optically thick at the corresponding wavelength. If you double the amount of CO2, you reduce the proportion of surviving light by an additional factor of 1/e, reducing the proportion surviving to about a tenth; if you instead halve the amount of CO2, the proportion surviving is the reciprocal of the square root of e , or about 60% , and the atmosphere is optically thin. Precisely where we draw the line between "thick" and "thin" is somewhat arbitrary, given that the absorption shades smoothly from small values to large values as the product of absorption factor with amount of CO2 increases.
The units of absorption factor depend on the units we use to measure the amount of CO2 in the column of the atmosphere encountered by the beam of light. Let’s measure our units relative to the amount of CO2 in an atmospheric column of base one square meter, present when the concentration of CO2 is 300 parts per million (about the pre-industrial value). In such units, an atmosphere with the present amount of CO2 is optically thick where the absorption coefficient is one or greater, and optically thin where the absorption coefficient is less than one. If we double the amount of CO2 in the atmosphere, then the absorption coefficient only needs to be 1/2 or greater in order to make the atmosphere optically thick.
The absorption factor, so defined, is given in the following figure, based on the thousands of measurements in the HITRAN spectroscopic archive. The "fuzz" on this graph is because the absorption actually takes the form of thousands of closely spaced partially overlapping spikes. If one were to zoom in on a very small portion of the wavelength axis, one would see the fuzz resolve into discrete spikes, like the pickets on a fence. At the coarse resolution of the graph, one only sees a dark band marking out the maximum and minimum values swept out by the spike. These absorption results were computed for typical laboratory conditions, at sea level pressure and a temperature of 20 Celsius. At lower pressures, the peaks of the spikes get higher and the valleys between them get deeper, leading to a broader "fuzzy band" on absorption curves like that shown below.

We see that for the pre-industrial CO2 concentration, it is only the wavelength range between about 13.5 and 17 microns (millionths of a meter) that can be considered to be saturated. Within this range, it is indeed true that adding more CO2 would not significantly increase the amount of absorption. All the red M&M’s are already eaten. But waiting in the wings, outside this wavelength region, there’s more goodies to be had. In fact, noting that the graph is on a logarithmic axis, the atmosphere still wouldn’t be saturated even if we increased the CO2 to ten thousand times the present level. What happens to the absorption if we quadruple the amount of CO2? That story is told in the next graph:
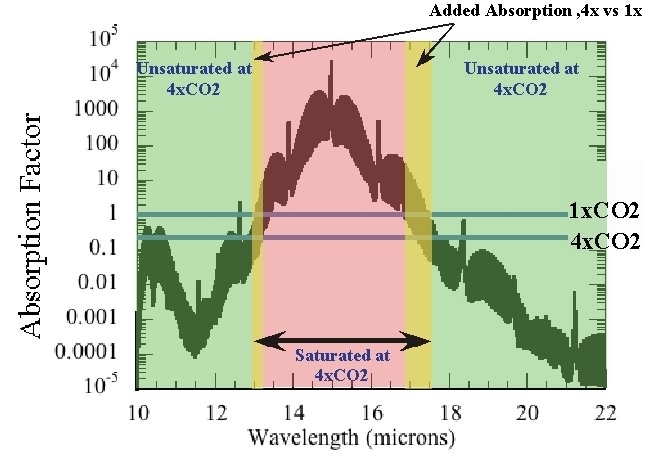
The horizontal blue lines give the threshold CO2 needed to make the atmosphere optically thick at 1x the preindustrial CO2 level and 4x that level. Quadrupling the CO2 makes the portions of the spectrum in the yellow bands optically thick, essentially adding new absorption there and reducing the transmission of infrared through the layer. One can relate this increase in the width of the optically thick region to the "thinning and cooling" argument determining infrared loss to space as follows. Roughly speaking, in the part of the spectrum where the atmosphere is optically thick, the radiation to space occurs at the temperature of the high, cold parts of the atmosphere. That’s practically zero compared to the radiation flux at temperatures comparable to the surface temperature; in the part of the spectrum which is optically thin, the planet radiates at near the surface temperature. Increasing CO2 then increases the width of the spectral region where the atmosphere is optically thick, which replaces more of the high-intensity surface radiation with low-intensity upper-atmosphere radiation, and thus reduces the rate of radiation loss to space.
Now let’s use the absorption properties described above to determine what we’d see in a typical laboratory experiment. Imagine that our experimenter fills a tube with pure CO2 at a pressure of one atmosphere and a temperature of 20C. She then shines a beam of infrared light in one end of the tube. To keep things simple, let’s assume that the beam of light has uniform intensity at all wavelengths shown in the absorption graph. She then measures the amount of light coming out the other end of the tube, and divides it by the amount of light being shone in. The ratio is the transmission. How does the transmission change as we make the tube longer?
To put the results in perspective, it is useful to keep in mind that at a CO2 concentration of 300ppm, the amount of CO2 in a column of the Earth’s atmosphere having cross section area equal to that of the tube is equal to the amount of CO2 in a tube of pure CO2 of length 2.5 meters, if the tube is at sea level pressure and a temperature of 20C. Thus a two and a half meter tube of pure CO2 in lab conditions is, loosely speaking, like "one atmosphere" of greenhouse effect. The following graph shows how the proportion of light transmitted through the tube goes down as the tube is made longer.
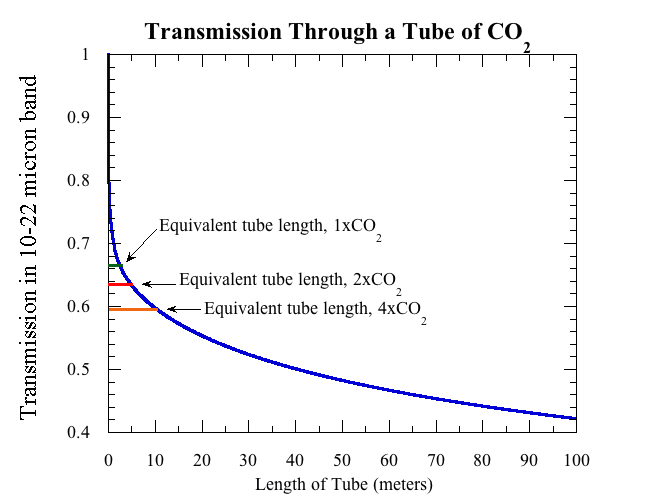
The transmission decays extremely rapidly for short tubes (under a centimeter or so), because when light first encounters CO2, it’s the easy pickings near the peak of the absorption spectrum that are eaten up first. At larger tube lengths, because of shape of the curve of absorption vs. wavelength, the transmission decreases rather slowly with the amount of CO2. And it’s a good thing it does. You can show that if the transmission decayed exponentially, as it would if the absorption factor were independent of wavelength, then doubling CO2 would warm the Earth by about 50 degrees C instead of 2 to 4 degrees (which is plenty bad enough, once you factor in that warming is greater over land vs. ocean and at high Northern latitudes).
There are a few finer points we need to take into account in order to relate this experiment to the absorption by CO2 in the actual atmosphere. The first is the effect of pressure broadening. Because absorption lines become narrower as pressure goes down, and because more of the spectrum is "between" lines rather than "on" line centers, the absorption coefficient on the whole tends to go down linearly with pressure. Therefore, by computing (or measuring) the absorption at sea level pressure, we are overestimating the absorption of the CO2 actually in place in the higher, lower-pressure parts of the atmosphere. It turns out that when this is properly taken into account, you have to reduce the column length at sea level pressure by a factor of 2 to have the equivalent absorption effect of the same amount of CO2 in the real atmosphere. Thus, you’d measure absorption in a 1.25 meter column in the laboratory to get something more representative of the real atmosphere. The second effect comes from the fact that CO2 colliding with itself in a tube of pure CO2 broadens the lines about 30% more than does CO2 colliding with N2 or O2 in air, which results in an additional slight overestimate of the absorption in the laboratory experiment. Neither of these effects would significantly affect the impression of saturation obtained in a laboratory experiment, though. CO2 is not much less saturated for a 1 meter column than it is for a 2.5 meter column.
So what went wrong in the experiment of poor Herr Koch? There are two changes that need to be made in order to bring our calculations in line with Herr Koch’s experimental setup. First, he used a blackbody at 100C (basically, a pot of boiling water) as the source for his infrared radiation, and measured the transmission relative to the full blackbody emission of the source. By suitably weighting the incoming radiation, it is a simple matter to recompute the transmission through a tube in a way compatible to Koch’s definition. The second difference is that Herr Koch didn’t actually perform his experiment by varying the length of the tube. He did the control case at a pressure of 1 atmosphere in a tube of length 30cm. His reduced-CO2 case was not done with a shorter tube, but rather by keeping the same tube and reducing the pressure to 2/3 atmosphere (666mb, or 520 mm of Mercury in his units). Rather than displaying the absorption as a function of pressure, we have used modern results on pressure scaling to rephrase Herr Koch’s measurement in terms of what he would have seen if he had done the experiment with a shortened tube instead. This allows us to plot his experiment on a graph of transmission vs. tube length similar to what was shown above. The result is shown here:
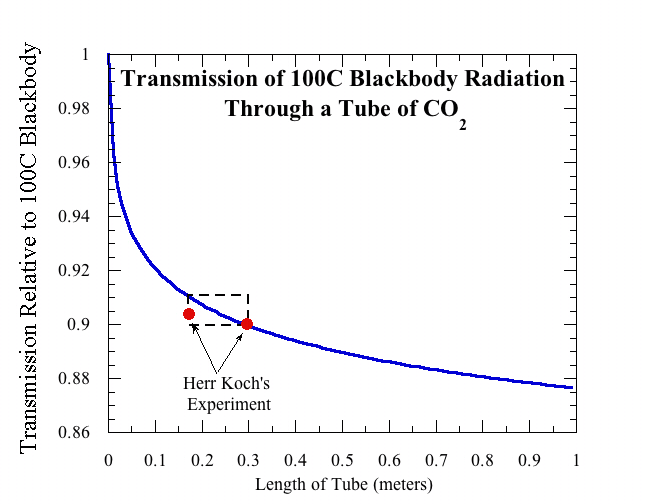
Over the range of CO2 amounts covered in the experiment, one doesn’t actually expect much variation in the absorption — only about a percent. Herr Koch’s measurements are very close to the correct absorption for the 30cm control case, but he told his boss that the radiation that got through at lower pressure increased by no more than 0.4%. Well, he wouldn’t be the only lab assistant who was over-optimistic in reporting his accuracy. Even if the experiment had been done accurately, it’s unclear whether the investigators would have considered the one percent change in transmission "significant," since they already regarded their measured half percent change as "insignificant."
It seems that Ångström was all too eager to conclude that CO2 absorption was saturated based on the "insignificance" of the change, whereas the real problem was that they were looking at changes over a far too small range of CO2 amounts. If Koch and Ångström had examined the changes over the range between a 10cm and 1 meter tube, they probably would have been able to determine the correct law for increase of absorption with amount, despite the primitive instruments available at the time.
It’s worth noting that Ångström’s erroneous conclusion regarding saturation did not arise from his failure to understand how pressure affects absorption lines. That would at least have been forgivable, since the phenomenon of pressure broadening was not to be discovered for many years to come. In reality, though Ångström would have come to the same erroneous conclusion even if the experiment had been done with the same amounts of CO2 at low pressure rather than at near-sea-level pressures. A calculation like that done above shows that, using the same amounts of CO2 in the high vs. low CO2 cases as in the original experiment, the magnitude of the absorption change the investigators were trying to measure is almost exactly the same — about 1 percent — regardless of whether the experiment is carried out at near 1000mb (sea level pressure) or near 100mb (the pressure about 16 km up in the atmosphere).
aaron (#41) said:
This is a bad analogy. What you said is true because warm-blooded animals can control their temperature through evapotranspiration and changing the heat conductance (or resistance if you prefer) of their skin and/or fur.
If you take a cold-blooded animal, like a snake, throw a blanket over it, and shine a heat lamp on it, its temperature will increase more than if it didn’t have a blanket.
[Response: The blanket analogy might still be a useful communication tool if one said simply that the blanket makes you feel warmer, not because it generates energy, but because it insulates you and reduces the rate at which you lose heat. For a mammal, “feel warmer” means that your metabolism doesn’t need to struggle to maintain survivable body temperature. “feel warmer” here doesn’t mean an increase in temperature, but it still conveys the idea that the insulation is the important thing, just like the “insulation” of the Earth by CO2 is the main factor in the greenhouse effect. There are many levels of explanation, and what I’m groping for here in this analogy is the basic one-liner that conveys the essence of the greenhouse effect without doing too much violence to the real physics.
Actually, perhaps the blanket analogy isn’t as bad as all that. True, because your metabolism adjusts, a blanket doesn’t increase your body core temperature, but it does increase your skin temperature and the temperature of the air adjacent to your skin. That’s a big part of why you feel warmer. –raypierre]
#41,51
Although the famous scene in ‘Goldfinger’ is an urban myth, there’s a grain of truth to it.
Anyone wrapped in a space blanket during a heatwave would have pretty poor odds of survival, since heat stroke sets in at a body temperature of 104 F. Go past that point and you will reach thermal equilibrium with your environment forever.
Will the snake increase to a higher temperature with the blanket? (I suppose it depends how windy it is, but it’s not too windy outside of the earth.)
This suggests to me that the effect would warm the atmosphere from the surface out, toward the current surface temperature, until emission is restored and the budget balances. The surface shouldn’t get hotter (not much atleast).
And how how strong is the effect, are we talking about a blanket, or a sheet?
I don’t know if I’m capable of understanding, or even have the time, but I’d like to get into the real physics.
Alastair wrote: “FWIIW I suspect that the data does not exist because when the experimenters measured radiation they found that it did not match the models and so concluded that their data was wrong and did not publish!”
Danger, Alastair! Danger! You are crossing the line into anti-science nutjob territory here. Remember what Isaac Asimov said,
“The most exciting phrase to hear in science, the one that heralds new discoveries, is not ‘Eureka!’, but ‘That’s funny …'”
The goal of experimental science is not to confirm a model, but rather to stretch the model with data until it breaks and the theorists have to fix it. This is their goal. Moreover, there is the issue of accountability: When experimentalists take data, the funding agency expects a report. If no data are forthcoming, there had better be a good explanation. All you do when you make statements like that is demonstrate that you don’t understand how science actually works.
aaron (#53) wrote:
For those who really wish to step into the cathedral of climatology, a basic understanding of the greenhouse effect is all that is required.
The following will give you that:
10 Apr 2007
Learning from a simple model
https://www.realclimate.org/index.php/archives/2007/04/learning-from-a-simple-model/
How far you go in exploring climatology after that is up to you, but this website is a really good place to a great deal of it.
Re #54.
Ray (Ladbury), have you noticed a funny thing on Ray’s (Pierrehumbert) Figure 4.6: Some representative OLR spectra for Mars, observed by the Thermal Emission Spectrometer on Mars Global Surveyor at various times of day. from page 103 (110) of his book?
No matter what the time of day, the CO2 emissions remain the same, with a brightness temperature of around 200 K.
Alastair, I’m afraid I don’t see that in the figure. Yes the variability is les than at other points in the spectrum, but isn’t that what would be expected for a ghg?
Alastair McDonald (#56) wrote:
Pg. 110.
The red is the afternoon, the violet at sunset, and the blue at night.
There is a big difference between them, peaks of 8 x 10^-6, ~5.75 x 10^-6 and 3 x 10^-6 respectively. You were misreading it, Alastair.
Face it: climatology is a great deal more advanced than you thought. Climatology is a branch of physics, a very well developed one at that.
The links I provided above show it, at least with respect to our understanding of spectra.
Climate Forcing by Clouds and Aerosols: Two Years of Field Studies
http://geo.arc.nasa.gov/sgp/radiation/rad1.html
CAVE Publication List (numerous peer-reviewed articles, many of which are directly relevant to this fairly specialized topic)
http://www-cave.larc.nasa.gov/cave/pages/bibliog.html
Sample article from list above:
Introduction to an Online Coupled Ocean-Atmosphere Radiative Transfer Model (2002)
Zhonghai Jin, Thomas Charlock, and Ken Rutledge
http://www-cave.larc.nasa.gov/cave/pdfs/Jin.AGU02.pdf
It is time to quit insisting that you are the only one that really understands how the greenhouse effect works and start learning about it. Put aware your fantasy and start learning about reality. You know some things already, but you could learn a great deal more.
You are bright enough.
[Response: By the way, the Figure 4.6 that’s currently there in the book is just a placeholder pulled from the TES website without modification. Eventually, I’ll re-plot it in consistent form using original data from one of the thousands of TES shots. The night-time curve is just a distraction for the things I’m discussing in Chapter 4, so I’ll eliminate that, but for the stuff you guys are talking about, thinking about why the night-time curve looks the way it does is quite interesting. For educational purposes, it would be nice to have an instrument like TES orbiting the Earth, but so far as I know there isn’t one. A similar instrument was sent to Venus, but unfortunately the sensor got stuck in its blackbody calibration position. –raypierre]
Re Rays response [Response: Alastair, that’s really going too far. There is a figure in Goody and Yung showing the old Tiros top of atmosphere spectra that confirms the standard picture of radiative transfer.]
Ray,
With my model the predicted OLR spectrum at the TOA is the same as yours, and what is measured experimentally. That sort of confirms my picture of radiative transfer :-) What I am saying is that if you measured the CO2 band OLR spectrum at 1000 feet it would look similar to that at the TOA.
I don’t have a copy of Liou’s book (to hand), but on Slide 4 of John Harries’s notes there are two OLR spectra for the tropics and the Arctic. It is funny that both show the same brightness temperature for CO2. It is almost as if CO2 has a fixed brightness temperature that is independent of atmospheric temperature.
I think that you are probably correct when you write “If it sometimes seems like there’s a paucity of downward looking spectral data covering the whole thermal IR, it’s because there really aren’t any serious scientific issues left to settle.” Everyone I speak to thinks that the problem of OLR is well and truly solved. But in A Busy Week for Water Vapor Philipona et al. found that the water vapour near the surface was increasing. That implies that CO2 is acting there, not high in the tropopause as you argue. There, you wrote “In equilibrium, the Earth must lose as much energy out the top of its atmosphere as it gains by absorption of Solar energy” which is true, but you also wrote t “Planets only have one way of losing energy, which is by infrared radiation to space, often called ‘Outgoing Longwave Radiation,’ or OLR.” However, there is another way. Planets can reach equilibrium by producing clouds which reflect the solar energy away, and so match incoming solar radiation to a fixed or even runaway OLR. This is what has happened on Venus, and is the cause of the dust storms on Mars. On Earth it is not dust storms which cool the atmosphere, it is El Nino and hurricanes!
Alastair McDonald (#59) wrote:
The articles I pointed to have charts for mid-atmosphere and they demonstrate the role of the upper atmosphere. The peaks you said looked the same in Raypierre’ book had peaks of 8 x 10^-6, ~5.75 x 10^-6 and 3 x 10^-6 at 20, 22.5 and >25 mu-m respectively.
You have it wrong and the climatologists have it right. You see what you want to see and always look for an easy way to dismiss the rest before really looking at it.
Alastair, please. Raypierre wrote in _A Busy Week …_
> the water vapor feedback discussed in Philipona et al. is not the same water vapor feedback usually discussed in
> connection with global warming. It is instead a surface water vapor feedback which adds additional surface warming
> on top of the usual things we talk about. The effect is already incorporated in the climate models used in IPCC
> forecasts, but the new observational study will be useful as a reality-check.
[[But in A Busy Week for Water Vapor Philipona et al. found that the water vapour near the surface was increasing. That implies that CO2 is acting there, not high in the tropopause as you argue. ]]
It doesn’t imply that at all. Changes in water vapor happen most strongly near the surface because the surface is where the source of the water vapor is — the oceans. And water vapor has a very shallow scale height compared to dry air, 2 km versus 8 km.
Is it oversimple to say ‘the atmosphere warms from the bottom (incident sunlight warms the earth), warm earth warms the lower atmosphere; the atmosphere warms itself by mixing and radiation; the atmosphere cools from the top by radiation to space’?
I believe that after several readings of the two papers(I’m “optically thick” in another sense), I finally grasp the proper response to those who argue fallaciously that additional CO2 would have little or no effect because the absorbtion band in the infra red is near saturation so,(they conclude)there is little absorption of radiation emitted from the surface.
This is a false conclusion because (a) adding CO2 to the atmosphere will cause the thermal radiation emitted to space to originate from higher and colder levels than previously, with less radiation emitted. This disturbs the energy balance until the atmosphere near the surface heats up so that the atmosphere at high levels can radiate enough energy to restore the balance; and (b)adding more CO2 in effect adds more red M&Ms to the conveyor belt by enlarging the width of the spectrum in which CO2 can be absorbed. For the example given by Raypierre,at 1CO2 the band width is almost 3.5 microns (13.5 to 17), while at 4CO2 the band width is about 4.5 microns(13 to 17.5).
If I still don’t have a grasp its through no fault of the authors. Rather that the electromagnetic spectrum and it’s properties are far afield of my own background and experience.But I feel strongly that we’re at a crossroads regarding the future of our planet and it behooves those of us,in the general public to try to comprehend as much as possible.
By the way I try constantly to pretend I believed the opposite of my actual position (what used to be called being on the alarmist side, but now I think is simply the precautionary side and unfortunately may soon be the mainstream), and respond accordingly.
Most denialism is (our) time-wasting deliberate repetition of debunked points for sheer PR purposes (and even to gain mass in search engine results). But some of it, I have to say, is the kind of abuse most scientific ideas should take.
In a similar way, the paper suggesting “most published results are false” I found nonsensical, but useful, for instance.
Now even if I read Knut Ångström very carefully, he only claims:
“Unter keinen Umstunden dorfte die durch die Kohlensure bewirkte Absorption der Erdstrahlung 16 Proc. Ubersteigen, und die Grusse dieser Absorption ändert sich quantitativ mit dem Kohlensuregehalt sehr wenig, solange numlich derselbe nicht weniger als 20 Proc. des vorhandenen betrugt.”
“Under no circumstances will the absorption by CO2 of [IR] terrestrial radiation be larger than 16%, and the amount of this absorption changes quantitatively very little with the CO2 concentration, as long as CO2 concentration remains below 20%.”
IMHO Knut Ångström doesn’t claim saturation in the infrared here, he just contrasts it with the 60% absorption that Arrhenius claimed in 1896.
Furthermore I don’t think that pressure is that effective on absorption if expressed in atm cm (which is in fact 1000 dobson units). Koch measured two absorptions: 10% at 30 atm cm and 9.6% at 20 atm cm, which Ångström extrapolated to 16% for 250 atm cm.
Arhhenius tried to refute this, but in fact the 16% value was confirmed in 1901, by measurements in Berlin. Strangely enough this huge reduction in absorptive power by CO2 (from 60% to 16%) didn’t lead to a change in the climate sensitivity values by Arrhenius.
See the graph: black dots Ångström (1900) red dots Arrhenius (101)
http://home.casema.nl/errenwijlens/co2/angstrom1900/angstromarrhenius.gif
Re: Blanket Analogy
Two things…
First. If its already HOT and you cover yourself with a nice wool blanket even a thin one, you won’t be able to lose heat fast enough and you’ll experience the wonderful symptoms of Heat Stroke, the proverbially “flu-like symptoms” of fatigue, nausea, vomiting, delirium, fever, death… So, I think the blanket analogy works quite well.
Second. A better analogy might be attic/wall insulation in a home. You still need a furnace to warm the house – but if you have better insulation the furnace needs to provide less heat to maintain a nice comfy temperature. But in our case, our furnace (sun) isn’t linked to a thermostat here on Earth and so doesn’t reduce its output despite our improved insulation – and so our house gets hotter. See above…
To the best of my knowledge, no one has yet answered the question posed at the beginning of this paper, that when an infrared flashlight of one watt is flashed at sea level, what fraction would be received by an astromanut above the atmosphere. Maybe because the answer is obvious to most, but I’ll take a crack at it anyway.
Using the graph of ‘Transmission Through a Tube of CO2’ shown in this paper, at 300 ppm concentration of CO2 and a temperature of 20C,and sea level pressure, a 1.0 meter tube filled with pure CO2 would be needed to simulate one atmosphere of equal cross section, when pressure broadening and the fact that pure CO2 collisions are different from the,mainly nitrogen and oxygen composition of the air. This would be equivalent to a column of air from the surface to the top of the atmosphere. The amount of light getting through would by about .66 watt. At 2xCO2, a length of tube of 5 meters would be needed to simulate the atmosphere and the amount of light received is about .64 watt. The amount drops to .6 watt at 4xC02.
These numbers are a lot less than the 4 watt deficit given in the first paper, from the 240 watts/m^2 entering as given in Gavin’s paper ‘Learning from a simple model’. This is because(I hope) of the fact that the watt originates from sea level and does not undergo the cooling and mixing that takes place in the greenhouse process. If I’m still in the dark(pun intended)its back to the drawing board.
Laurence, what is the frequency and bandwidth of the flashlight? Is it cloudy? You need that information.
I really liked your detailed analysis in Part 2 of how the absorption of infrared depends on CO2 concentration. Enjoyed Part 1 as well.
Thank you, Eli. I only left out three critical elements?! Not too good. I’ll have to make an assumption on frequency( wavelength) and, if allowed, assume that the light shines with equal intensity throughout the bandwidth. Assuming cloudlessness is pretty idealistic and doesn’t simulate the real world, but I thought it was an implied in the initial question at the beginning of the paper. Anyhow, I appreciate knowing that these factors have to be taken into account.
How does the mesosphere and thermosphere above and with (much) higher temperatures than the stratosphere play into all of this? Is it that the density/pressure is so low as to be near non-existant and the so few molecules with high kinetic energy just don’t count other than in pristine theory?? If so, what would be a more scientific way of describing it? If not, why isn’t their radiation into space at a temp similar to or even greater than the surface?
67. Those are both good. I’d refine the first one though. Instead of “if it’s already HOT” change it to “if you (or another person) are already hot”. If it’s hot out, the blanket won’t cause you to overheat, it might even keep you from being overheated.
Rod B. I think you answered your own question. The international space station orbits in the upper part of the thermosphere–not much there.
re 33: “…the more times each parcel of energy is absorbed and re-emitted, the higher the temperature will be.”
I just can’t get this. Take two molecules that keep exchanging a photon. Why does the temperature (average of the two) increase? Or change at all? Also, for the most part, the absorption of IR radiation by a molecule ends up as energy stored in its internal bonds or electron levels, neither of which increases the temperature of that molecule…does it?? What am I missing here?
Rod B (#75) wrote:
Its not that you have one photon bouncing back and forth between two molecules, its that the energy is slowed down before it finally escapes to space while energy keeps coming in at the same rate. At some point the rate at which energy leaves the system (the photons leaving the Earth and its atmosphere) has to be balanced with the energy which is entering the system (the new photons just keep coming in at the same rate). The only way to do this is to raise the temperature of the Earth to the point that its increased temperature raises the rate of energy loss enough to compensate form the decreasing of the rate of energy loss due to the greenhouse gases.
The more energy that is in the system at any given time, the higher the temperature at the surface and the higher the temperature in the lower atmosphere. Greenhouse gases require a higher level of energy to be in the system to achieve a balance between the rate at which energy enters the system and the rate at which energy leaves the system. More energy essentially means more photons at any given time where each photon will tend to take longer to get out.
A bit of an oversimplification (Ray will probably be pulling out his wooly hair when he reads this), but close enough.
[Response: It’s actually not so bad, so I guess I guess I get to keep my hair (wooly or not):) Fourier himself used an analogy with a bucket (actually he used “vase” not “seau”) with a hole near the bottom. Put it under a faucet and the bucket will fill up until the pressure forces water out the hole at the same rate it’s coming in. The amount of water in the bucket is analogous to temperature, the faucet in is analogous to sunlight (fixed supply) and the leak through the hole is the loss to space by infrared. Though he didn’t take the analogy further, in modern terms we’d say that if you decrease the size of the hole you need more water in the bucket in order to force water out at a rate that balances the input. You can sort of think of the bucket analogy as applying to photons, I suppose, but then you have to think harder to get the connection with temperature. –raypierre]
If equal numbers of water molecules and carbon dioxide molecules are put into the tube, who gets most of the IR photons? The water molecules by far because water molecules have a permenant electric dipole and carbon dioxide molecules do not. In fact carbon dioxide is a fairly weak absorber of IR energy as compared to water.
I think you guys are suffering from severe carbon dioxide anoxia.
What you guys are claiming is that the recent trend in global warming is due to the increase of the concentration of carbon dioxide from 0.033% by volume in 1980 to present value of 0.038% by volume. That claim, in the words of the late Senator Everett M. Dirksen, “Ole Golden Throat”, “is just so much hogwash”. Google, Gobal Warming: A closer Look at the numbers” Monte Hieb is mine safety engineer, knows a lot about gases and gives the correct computation re role of the water vapor and carbon dioxide, etc in the greenhouse effect. My advice: don’t challenge an engineer, they are never wrong.
The reason the last 10 years out of 12 have been the warmest on record is that period has been dominated by a strong El Nino cycle which has now come to an end. A La Nina cycle has started and the climate is going to cool down big time.
[Response: Far be it for me to start the whole engineers vs. scientists thing again, but Monte Hieb’s calculations are, to quote Senator Dirksen, “hogwash” and are almost as wrong as it is possible to be! – see: https://www.realclimate.org/index.php/archives/2006/01/calculating-the-greenhouse-effect/ . I hope that the rigour he applies to his mine safety calculations is significantly higher. – gavin]
Gavin: You are just flat out wrong about carbon dioxide’s role in climate. At ca. 0.038% by volume carbon dioxide does diddly squat. Your article on “Water Vapor: Forcing or Feedback” is nonsense. Water is always present in real air and it does not matter how it gets there. Water molecules are light, agile, swift, frisky and pesky. Carbon dioxide molecules are slugs and dumbells. I’m an organic chemist and have been duking it out with water molecules at the bench for 40 years.
Here are agents that move enormous amounts of water into the atmosphere over land that is independent of carbon dioxide: Microbes, insects, plants, and animals. All surfaces have adsorbed and absorbed water, and large volumes are exchanged with the atmosphere that depends on only pressure and temperature. Climate and weather are strongly influenced by heating air over the of the land and humidity of the air over that land.
Gavin You just don’t know the personalities of these molecules.
[Response: Errr…. You might want to think about getting out of the lab a little more often…. – gavin]
Harold, how many water molecules have you duked it out with in the stratosphere? Pretty dry up there last data I saw. And the CO2 band is a lot less saturated up there. Being an organic chemist does not mean you are an expert in atmospheric physics. I’m a physicist with >20 years experience. Here, I am a student. Join us and learn.
Take Timothy’s text:
“the photons leaving the Earth and its atmosphere) has to be balanced with the energy which is entering the system (the new photons just keep coming in at the same rate). The only way to do this is to raise the temperature of the Earth to the point that its increased temperature raises the rate of energy loss enough to compensate form the decreasing of the rate of energy loss due to the greenhouse gases.”
Now _why_ to do this, the only way is to raise the temperature of the Earth —
Photons coming in: solar output, energy transferred in a whole lot of ways, but what heats the surface of the Earth is photons.
Photons come in specific energies, not a sliding scale, but stepwise. About the same number of each energy, on average, all the time, comes in from the Sun.
All of them that hit the ground basically end up as heat energy. The ground gets warmer. The ground warms the air.
The ground is at a temperature — an energy level — that’s going to be emitted in the infrared range. The photons coming off the ground in the infrared are in the band (the set of energies) that, when they hit a greenhouse gas molecule, get grabbed and turned into another kind of energy (the bond vibrates? stretches? the angle changes?) and that then causes another photon in the same infrared range to be emitted (or the molecule bumps another one and transfers the energy by bumping it a bit harder while it’s vibrating).
So we get energy in, over the Sun’s range of output. If there weren’t any greenhouse gases in our atmosphere, the ground would be radiating heat right into space, and be a lot colder. As more greenhouse gases accumulate, they’re floating around in the atmosphere and as they pick up energy from photons in the infrared (or by being bumped) they can emit infrared photons, which go in any random direction. Most of those hit another greenhouse gas molecule or hit Earth, lather rinse repeat.
Some don’t hit anything on their way off the planet — those remove heat energy. Nothing else does. Only outgoing infrared.
So —- more heat energy in the system bouncing around the more greenhouse gas molecules there are, and at the very top of the atomosphere, while there are a few more molecules of CO2 (and almost no water), they aren’t magically picking up the extra energy that’s bouncing around below.
The whole atmosphere’s expanded as it’s being heated from the bottom up. So at the top of the atmosphere the molecules get lifted up, and cool as they get further apart. The top of the atmosphere cools, because the lower atmosphere has heated and lifted up the top of the total atmosphere.
What’s happening with the energy leaving the planet? It was at a level matching solar input (in total, emitted as infrared energies). It still is, and the greenhouse gases at the top got lifted up, and they cooled (higher, thinner, fewer collisions).
Where’s the outgoing energy now, since we recently added a lot of greenhouse gas? It’s bouncing around in the Earth/Atmosphere, and in the oceans. Heat is penetrating the ground, as the drilling work has detected.
Over the next few centuries, all the heat bouncing around is going to mean there will be on average more faster (hotter) molecules zipping to the top of the atmosphere, whacking a greenhouse gas molecule harder, bumping it up to a higher energy than it had there in the high thin cold air (which can go into its bonds, and its bond energy can punch out a higher energy, hotter, shorter wavelength photon that before the GHG era).
The molecules at the new higher top of the expanded upper atmosphere eventually warm up to where the total energy being emitted into space is again equal to the total coming from the sun.
Still too many polysyllables, can someone make this simpler?
re 76: Sounds like trivia but it might help to understand what’s going on. My contention (question) is that the IR radiation absorbed by atmospheric gasses does NOT raise the temperature of the gasses/atmosphere, though I understand how sequential emission-absorption-re-emission eventually raises the temp of the earth surface. I also understand the temp of the atmosphere changes for a slew of other reasons, one of which might be the collision of gas molecules and the coincident exchange/conversion of bond energy to kinetic energy (=temp) — but not from IR absorption per se.
re 80: “Still too many polysyllables, can someone make this simpler?”
I’m dubious over some of the details (especially upper atmos stuff), but overall I think your description is quite good!
Rod B in #81
If you think of temperature as being a function only of the kinetic energy of the gas molecules, then absorption of a photon does not immediately raise the gas temperature. However, IIRC, you have to consider the various internal modes of the molecules as additional degrees of freedom over which to distribute energy. That’s why the heat capacity of a diatomic gas is higher than the heat capacity of a monatomic gas and the heat capacity of a polyatomic gas is higher yet. So a more general definition of temperature which takes into account the total energy of the system would say that the temperature does indeed go up when a photon is absorbed. I think. It’s been a long time since I had thermo, but I did look up gas heat capacities the other day. Google is your friend.
Rod B (#81) wrote:
Well, there is some warming do to the conversion of captured photons into kinetic energy, but it can go the other way as well, and this really isn’t where the main action is as far as heating the atmosphere goes, or so I have picked up while here. Evidently, much of the warming of the atmosphere is largely do to water vapor as the result of evaporation.
But I am still try to sort out the details.
I will be going over the two posts, the comments, etc.. Plus I have started on Ray’s book and have some other material. One thing I definitely want to get right.
Hank Roberts thanks, thats supercalifragilisticexpialidocious!
There have been a variety of predictions of the mismatch between CO2 equilibrium temperature and present day temperature based around standardised futures a la IPCC, but is anybody actually keeping track of the sensibly expected emissions looking forwards say five to ten years?
With 140+ coal fired power plants lighting their boilers this year alone and no doubt even more predicted for the next few years we are not going to hit any sort of flattening of CO2 emissions for a while. Not until something very messy hits the fan in a way that will reverse this trend. India, China and co are just hitting their straps and no amount of proselytising is going to stop that any time soon � at least not until we are all suffering a lot.
So if we look at say the next 10 to 20 years of vigorous anthropogenic CO2 addition, plus some reasonably likely carbon from drying forests and tundra, what is the likely CO2 in 2020 and 2030, and what is the equilibrium temperature for that awful state?
I think THATS the answer we need to be waving around on our placards.
#85 Nigel
I suspect what you’re looking for is the IPCC Special Report on Emissions Scenarios http://www.grida.no/climate/ipcc/emission/ and probably Chapter 10 of AR4 (http://ipcc-wg1.ucar.edu/wg1/wg1-report.html)… Can’t give you a summary, since I haven’t read them myself.
[[My contention (question) is that the IR radiation absorbed by atmospheric gasses does NOT raise the temperature of the gasses/atmosphere,]]
Then your contention is wrong. Does blacktop heat up in the sun? Same process as the atmosphere heating up in IR light.
When an IR photon is absorbed by a carbon dioxide molecule, it raises that molecule’s energy. It is most likely to lose that energy in collision with a neighboring molecule. The neighboring molecule will move a little faster. Faster molecular motion = higher temperature.
RE #78 Retired five years ago. My idea of a green enviroment is the hall or the cardroom at the rock in Richmond, BC. This place is fantastic and has 25 tables going 24/7/356.
I get plenty of exercise doing yardwork.
re 83: Thanks, DeWitt. My understanding is that velocity is the only thing that determines temperature (mv^2 ala 0.5mv^2 = 1.5kT (the 1.5 factor might be off — I’m too lazy right now to look up a confirmation)). You can add heat energy without increasing temp (evaporation, e.g.) and raise temp without adding heat energy (air conditioning compressors, e.g.). Would you concur? Or point me in the right direction?
re 87 (Barton): “…Then your contention is wrong. Does blacktop heat up in the sun? Same process as the atmosphere heating up in IR light.”
But aren’t the processes different? Sunlight hitting almost any solid or liquid material, if not reflected, will excite the motion of the entirew molecule and this, and only this, determines temperature. Because of the strangeness of material science, sunlight hitting a gas molecule does nothing (with some exceptions, but mostly ionization or molecular breakup). However, IR radiation, again inexplicably, does interact with some gas molecules, but through absorption of the E-M energy by the (predominately) intra-molecular bonds with no temperature increase. An entirely different process.
“…When an IR photon is absorbed by a carbon dioxide molecule, it raises that molecule’s energy. It is most likely to lose that energy in collision with a neighboring molecule. The neighboring molecule will move a little faster. Faster molecular motion = higher temperature…”
I agree with this, but note it is the collidee not the absorber that gets hotter. BTW, I think the most likely loss/transfer of energy comes from emission, not collision, but this is just a quibble.
Re: #89 (Rod B)
Velocity is not the only thing that determines temperature. Temperature is (roughly speaking) proportional to the average energy per mode in the system. The modes can include velocity, internal vibration, potential energy, rotation, even magnetic field strength (one of the ways used to achieve ultra-low temperatures in a laboratory is “magnetic relaxation”).
The exact definition of temperature is: the rate of change of energy with respect to entropy, when volume and particle number are held constant. Not a very insightful definition for this discussion … but precise.
Rod,
Temperature has a precise thermodynamic definition as Tamino indicated. Consider a monoatomic gas. It has 3 degrees of freedom, and indeed its energy is 3kT/2. Now consider a diatomic gas–we’ve added new degrees of freedom, including rotation and vibration. Unlike kinetic energy, which is not quantized, these new energy modes are quantized, although the bands tend to be broad, and deform in response to surrounding molecules. Although these are INTERNAL to the molecule, they are motion. Indeed, if the atoms were part of a solid, they would share teh vibration with all their neighbors. Thus, I believe that in a collision, the energy may thermalize and add to the kinetic energy of the atoms. So, I don’t think it’s 100% correct to view the vibrational bands of CO2 as frozen out and isolated from the other types of energy. Indeed, given that a photon carries momentum, even in a radiative porcess, there is some change in momentum (albeit small) and therefore energy of the absorbing or emitting molecule.
In any case, the energy is not escaping, and it has to have some effect.
Also, when you evaporate water, your molecules of water in vapor form are moving faster, and those in liquid form are moving slower; when you freeze water, the molecules are moving much slower yet. You can say there’s no temperature change on some large average total basis — but any glider pilot knows to look for places where nice puffy white cumulus clouds are forming, because heat is transferred to the surrounding air as the molecules of water vapor glom together into droplets. The air rises faster as the heat of condensation is released.
Now I”m hoping for some wild idea from the people who specialize in tuning microwave pumping to favor particular chemical reaction paths. Is here any way to do something analogous with favoring particular vibration/bond energy paths, somehow find something to tune in the upper atmosphere to make it more probable that an already common interaction will kick out an infrared photon?
Bypass the whole middle atmosphere, run the radio transmitters on solar power and tickle the CO2 or whatever else is handy= at the top of the atmosphere into turning a bit more of its energy into infrared, going out where we need it to go?
Just daydreaming.
Rod B in #89
I really can’t explain in any more detail than tamino did (#91) why you are wrong about only molecular translational kinetic energy determining temperature without the equivalent of a semester course in thermodynamics and statistical mechanics. I will add some numbers, though. For molar heat capacity in J/mole K at constant pressure, argon is 20.8, nitrogen is 28.8 and CO2 is 37.84. The atomic weight of argon and the molecular weight of CO2 are similar (40 and 44), so it’s not just a function of mass.
Hank Roberts in #93 said:
Over thirty years ago some of the people in the lab where I worked built a CO2 laser with the idea of trying to influence specific reaction rates by activating selected molecular bonds. The idea became dead in the water when it was found that the absorbed energy redistributed internally much (like orders of magnitude IIRC) faster than the rate of any chemical reaction. So you can’t in general, as far as I know, change the path of a chemical reaction by exciting a particular chemical bond in a molecule consisting of more than two atoms. To stimulate IR emission, you need a population inversion as in a laser, again IIRC.
Is there any net energy transferred to the surrounding air molecules when carbon dioxide absorbs infrared radiation? This Wikipedia article suggests any energy absorbed is subsequently re-radiated.
Five percent over what time period? And how is this relationship affected by changing temperature, pressure, or greenhouse gas concentrations? My feeling is that direct warming of the air is not a factor in the greenhouse effect, but I am not sure about that.
I’ve found a new toy for on line spectral modeling and am using it to illustrate the saturation fallacy. The Spectral Calculator allows separation of the various parameters being discussed here, such as temperature, pressure and composition. The first post is on temperature. The approach is to simplify by isolating one factor at a time.
Eli Rabett (#94) wrote:
I would strongly recommend checking it out.
Eli is kind enough to walk you through using the tool and how it may be used. I was able to follow just fine – and then ended up playing around with it a bit. There are more features if you subscribe, and the prices are a little high for my shoe-string budget, but the free features are more than enough to insure that I will be returning more than a few times.
Blair Dowden (#95) wrote:
You are probably right that ir heating of the atmosphere isn’t a major mechanism, but I suspect that warmer air will result in additional emissions where kinetic energy is transformed into longwave emissions. In Raypierre’s inline to your comment #37, he stated that “infrared absorbtion-emission has a cooling effect, which balances convective heating” where the latter is moist air convective heating due to evaporation. If I am not mistaken, this implies that some of the energy which is resulting in emission isn’t from absorption, but is the result of convective heating – and therefore molecular collisions.
Timothy, I think that you are right that there’s not a lot of atmospheric heating. It is mainly that some of the IR photons eventually make it back to the ground and are reabsorbed, further heating the surface. But the basic issue is that the amount of radiation escaping decreases, so the system must heat up until a new equilibrium (energy out=energy in) is established.
My understanding of the process is that when Sunlight is absorbed by the Earth’s surface,the surface warms and emits radiation in the mostly infra red part of the spectrum.The infra red is strongly absorbed by C02 and H2O.The molecules absorb this energy transmit part of this into motion and collide with the predominant N2 and 02 gases of the atmosphere, increasing their velocity.This increase in motion of all the molecules raises the temperature of the air .
If we treat the atmosphere as layers through which the infra red radiation passes on its journey into space,half of the flow of the photons is up and half down.Layers close to the ground are warmer because they receive the direct radiation from the ground and also the re-transmitted radiation from the warmer layers above. This results in a thermal structure where the warmest air is at low altitudes and gets progressively cooler in the upper regions.This is oversimplified since I haven’t included convection but it’s basically why the thermal structure is what it is.
Since as the above paper shows, the air is not near saturation, adding more CO2 means more IR radiation is absorbed, more heating takes place and the cycle continues with more intensity. The differential temperature between the surface and the top to the troposphere is now greater and more layers have to be warmed at the top for the same amount of energy to escape. There are less polysyllables here but is it right?