 Many of you will have seen the obituaries (MIT, NYT) for Ed Lorenz, who died a short time ago. Lorenz is most famous scientifically for discovering the exquisite sensitivity to initial conditions (i.e. chaos) in a simple model of fluid convection, which serves as an archetype for the weather prediction problem. He is most famous outside science for the ‘The Butterfly Effect’ described in his 1972 paper “Predictability: Does the Flap of a Butterfly’s Wings in Brazil Set Off a Tornado in Texas?”. Lorenz’s contributions to both atmospheric science and the mathematics of dynamical systems were wide ranging and seminal. He also directly touched the lives of many of us here at RealClimate, and both his wisdom, and quiet personal charm will be sorely missed.
Many of you will have seen the obituaries (MIT, NYT) for Ed Lorenz, who died a short time ago. Lorenz is most famous scientifically for discovering the exquisite sensitivity to initial conditions (i.e. chaos) in a simple model of fluid convection, which serves as an archetype for the weather prediction problem. He is most famous outside science for the ‘The Butterfly Effect’ described in his 1972 paper “Predictability: Does the Flap of a Butterfly’s Wings in Brazil Set Off a Tornado in Texas?”. Lorenz’s contributions to both atmospheric science and the mathematics of dynamical systems were wide ranging and seminal. He also directly touched the lives of many of us here at RealClimate, and both his wisdom, and quiet personal charm will be sorely missed.
Ed Lorenz had a reputation of being shy and quiet, and this was indeed the impression he gave on first meeting. Indeed raypierre was interviewed by Ed at MIT in 1979 for his first faculty job — and remembers having to ask most of the questions as well as answer them. But he also remembers a lot of timely support from Ed that helped smooth over the somewhat rocky transition from basic turbulence theory to atmospheric science. The longer you were around Ed, the more you came to appreciate his warmth and sense of humor. He was an avid hiker, and many in the community (our own Mike Mann included) have recollections of time on the trail with him around the hills of Boulder and elsewhere.
Lorenz launched the modern era of the study of chaotic systems, which has profound implications both within and beyond atmospheric science. We’ll say more about that in a bit, but the monumental work on chaos should not leave Lorenz’s other contributions to atmospheric science completely in its shadow. For example, in a 1956 MIT technical report, Ed introduced the notion of “empirical orthogonal functions” to atmospheric science, and this technique now plays a central role in diagnostic studies of the atmosphere-ocean system. He also pioneered the study of angular momentum transport in the atmosphere, and of atmospheric energetics. Among other things, he introduced the important notion of “available potential energy,” which quantifies the fact that not all of the potential energy can be tapped by allowable rearrangements of the atmosphere. Later, he pioneered the concept of resonant triad instability of atmospheric waves, an idea that has repercussions for the sources of atmospheric low frequency variability. As if that weren’t enough Ed also introduced the concept of the “slow manifold” — a special subset of solutions to a nonlinear system which evolve more slowly than most solutions. The atmospheric equations support a lot of very quickly changing solutions, like sound waves and gravity waves, but on the whole what we think of as “weather” or “climate” involves more ponderous motions evolving on time scales of days to years. Ed’s work on this subject launched the study of how such slowly evolving solutions can exist, and how to initialize a numerical model so as to minimize the generation of the fast transients. This is now part and parcel of the whole apparatus of data assimilation and numerical weather forecasting.
Ed was not a user of general circulation models. His essential approach was to crystallize profound phenomena into very small sets of equations for how a handful of variables change with time. He left behind him a dozen or so such models, each of which would repay many lifetimes of study. He was indeed a master of “seeing the world in a grain of sand.” You can read about some of these models in the talk raypierre gave at the 1987 Lorenz ‘retirement’ symposium — not that this slowed him down!
Now let’s take a closer look at that butterfly effect. Despite the fact that there are no butterflies or tornadoes in climate models, Lorenz’s discoveries and their implications played a central role in climate modelling efforts and in the most recent IPCC report.
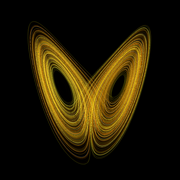 The notion of the butterfly effect itself was drawn from a simple but astute observation of the way the solutions of certain nonlinear equations behave when they are solved using a computer. Start with a greatly simplified representation of thermal convection, first formulated by Barry Saltzman using a technique called “low order modelling.” If you run a simulation using these equations and then try and replicate it using starting values that only differ in the last decimal place, you will find that the simulations quickly diverge from one another – and by quickly, it means that the differences grow exponentially fast. Lorenz found this phenomenon by accident, but quickly recognised the profound implications. If the real weather system displayed the same behaviour, it meant that since however well one knew the initial conditions of the atmosphere, there would always be some uncertainty, that uncertainty would be quickly magnified, rendering weather forecasts useless after a few exponential doubling times. The practical implication is that – even if you had a perfect model – for every halving of the error in the initial conditions you only get one extra time period of useful forecast. Given this time period is only a few hours in many cases, the practicality of true weather forecasts for periods longer than two weeks or so, is vanishingly small.
The notion of the butterfly effect itself was drawn from a simple but astute observation of the way the solutions of certain nonlinear equations behave when they are solved using a computer. Start with a greatly simplified representation of thermal convection, first formulated by Barry Saltzman using a technique called “low order modelling.” If you run a simulation using these equations and then try and replicate it using starting values that only differ in the last decimal place, you will find that the simulations quickly diverge from one another – and by quickly, it means that the differences grow exponentially fast. Lorenz found this phenomenon by accident, but quickly recognised the profound implications. If the real weather system displayed the same behaviour, it meant that since however well one knew the initial conditions of the atmosphere, there would always be some uncertainty, that uncertainty would be quickly magnified, rendering weather forecasts useless after a few exponential doubling times. The practical implication is that – even if you had a perfect model – for every halving of the error in the initial conditions you only get one extra time period of useful forecast. Given this time period is only a few hours in many cases, the practicality of true weather forecasts for periods longer than two weeks or so, is vanishingly small.
The mathematically inclined reader who takes a look at Ed’s early papers on what is now called the “Lorenz Attractor” will be astonished at the depth and modernity of his ideas about chaos. This line of work was no mere remark on a numerical exercise. Lorenz actually teased out the geometry of chaos — the many-leaved structure of the attractor — realizing that it was no simple geometric entity like a sphere or a folded sheet of paper. It was indeed “strange” in a sense which he made geometrically precise. This is why the work had such lasting impact on the area of pure mathematics known as dynamical systems theory. He went beyond that to develop or apply many fundamental concepts in chaotic systems, quantitatively formulating various measures of predictability and connecting the Lyapunov exponent — a certain precise mathematical characterization of chaos — with the structure of strange attractors. But that’s for the mathematicians. What makes Lorenz’s work interesting to the entity on the Clapham omnibus is the notion of sensitive dependence on initial conditions. Some have even seen in this deterministic chaos the resolution to the problem of free will!
The idea that small causes can have large and disproportionate effects is not at all new of course. The poem: “For the want of a nail, the battle was lost” (medieval in origin) encapsulates that well, and popular culture is full of such examples, “It’s a wonderful life” (1946) and Ray Bradbury’s “A Sound of Thunder” (1952) for instance. Curiously, Bradbury’s story also involves a butterfly, and since it predates Lorenz’s coining of the phrase by a decade or so, people have speculated that there was a connection to Lorenz’s choice of metaphor (he started off with a seagull in his 1963 Trans. N.Y. Ac. Sci. paper). But that doesn’t appear to be the case (see here for a history). It’s worth adding that all of Lorenz’s papers were exceptional in their clarity and are well worth tracking down as an example of science writing at its best.
However, the difference between the long-standing popular conception and Lorenz’s work is that he demonstrated this effect in a completely deterministic system with no random component. That is, even in a perfect model situation, useful predictability can be strongly limited. Strictly speaking, Poincaré first described this effect in the classic three-body problem in the early 1900s, but it was only with the onset of electronic computers, as used by Lorenz, that this became more widely recognised. To throw in another popular culture reference, Tom Stoppard’s Arcadia has a character, Septimus, who drives himself mad trying to calculate chaotic solutions to the logistic map by hand.
So what does this have to do with the IPCC?
Even though the model used by Lorenz was very simple (just three variables and three equations), the same sensitivity to initial conditions is seen in all weather and climate models and is a ubiquitous phenomenon in many complex non-linear flows. It is therefore usually assumed that the real atmosphere also has this property. However, as Lorenz himself acknowledged in 1972, this is not directly provable (and indeed, at least one meteorologist doesn’t think it does even though most everyone else does). Its existence in climate models is nonetheless easily demonstratable.
But how can climate be predictable if weather is chaotic? The trick lies in the statistics. In those same models that demonstrate the extreme sensitivity to initial conditions, it turns out that the long term means and other moments are stable. This is equivalent to the ‘butterfly’ pattern seen in the figure above being statistically independent of how you started the calculation. The lobes and their relative position don’t change if you run the model long enough. Climate change then is equivalent seeing how the structure changes, while not being too concerned about the specific trajectory you are on.
Another way of saying it is that for the climate problem, the weather (or the individual trajectory) is the noise. If you are trying to find the common signal that is a signature of a particular forcing then averaging over a number of simulations with different weather works rather well. (There is a long standing quote in science – “one person’s noise is another person’s signal” which is certainly apropos here. Climate modellers don’t average over ensemble members because they think that weather isn’t important, they do it because it gives robust estimates of the signal they are usually looking for.)
The ensemble approach, and indeed the multi-model ensemble approach, used in IPCC then derives directly from Lorenz’s insights into his serendipitous numerical problem.
Re 19 again – it occurs to me that, in general, along portions of a strange attractor, one could have regions where there is local contraction in all dimensions, or local expansion in all dimensions – so long as it is in a limited portion of phase space. Interestingly, this would have to include not just the direction but the speed – one may discuss the velocity field in phase space. I suppose one could map the one phase space into another phase space where the divergence of the velocity field is everywhere zero, so then you’d have your complementary contracting and expanding components relative to the attractor itself.
Re 50,51 – here’s another interesting visualizing – when a system (such as the atmosphere-ocean, or atmosphere-ocean-biosphere, or atmosphere-ocean-biosphere-crust, or…) has variation on different timescales, one could imagine a strange attractor that is slowly being deformed and/or moved about (this could include time components – speeding up, slowing down, each in different parts, etc.). The shape (and timing, or including timing) of the attractor could be represented as a subset of the coordinates in a different phase space; On a longer timescale, the attractor’s shape (and/including timing) would trace out another attractor.
Roger Pielke Sr. is mistaken, but it will take a little while to explain why:
First, here is a good discussion of the mathematics of the basic Lorenz attractor and also of the related phenomenon of Taylor-Couette flow – a long studied example of the onset of turbulence.
http://hmf.enseeiht.fr/travaux/CD9899/travaux/optmfn/hi/99pa/hydinst/report03.htm
There is a nice user-operated online java program that shows the time evolution of those same Lorenz equations. http://www.geom.uiuc.edu/java/Lorenz/
Try to predict the number of consecutive cycles on either “wing”.
Lorenz was the first to provide a quantitative description of what had been until then a purely qualitative argument – and this work absolutely relied on using a computer to carry out the large numbers of calculations. David Ruelle says this in his short book, Chance and Chaos (1991)
Ruelle also says this about attractors and hydrodynamic turbulence:
One can see this in action by playing with the Lorenz java applet linked above – no matter where a trajectory begins, it is drawn onto the attractor. Each point on the attractor represents the entire system in different states – a big job for a little point! (climate models now have some 10 million dynamic variables, I believe)
The notion of dissipation is important here. In the supercooled water example, the heat of ice formation is immediately dissipated in the sub-freezing water, allowing for rapid ice growth – that’s just a dramatic example of a carefully prepared dissipative system. More generally, a dissipative system is a thermodynamically open system, which operates far from thermodynamic equilibrium, while exchanging energy and matter with its surroundings. That’s what Lorenz was working with.
Now, Roger Pielke Sr. makes at least two incorrect claims about this:
The first claim is just plain wrong – see
http://www.atmos.umd.edu/~ekalnay/nwp%20book/nwpchapter7/Ch7_2.html
As for the second – they are going to revisit David Ruelle 1979, “Microscopic fluctuations and turbulence”? Here is Ruelle on this (Chance & Chaos pg. 182)
Compare that to say, http://www.renewamerica.us/columns/hutchison/070711
– a curious article on the uselessness of computers for modeling climate that has a certain similarity to Roger Pielke Sr.’s and Roy Spencer’s themes.
In the world of physics, a microscopic fluctuation is something like the collision between two molecules (very sub-millimeter scale). Any radiative transfer of energy will not necessarily damp out a perturbation on those scales. A water molecule that absorbs or emits an infrared photon will vibrate differently; that will slightly change the result of the next collision it has, and so on – creating enough of a perturbation that two near-identical states will generate wildly different behavior at some time T in the future.
In the practical case of a hurricane, the energy budget depends on the thermal difference between the sea surface and the top of the troposphere. No butterfly flaps will have much effect on that. What they will affect is the timing of easterly waves. The damping or amplification of convection by a few hours could affect the timing of an easterly wave by a day; a day’s difference over the Atlantic could make all the difference for favorable hurricane conditions (no wind shear, say).
Finally, let’s return to Lorenz (Essence of Chaos) himself to clear up a few points about the dissipative (open!) system he was working with – and let’s also note that his discovery was not an accident, but rather the result of remarkable tenacity:
For a real example of modern work on estimating the predictability of chaotic systems, from the European Centre for Medium-Range Weather Forecasts (1999), see:
http://www.ecmwf.com/newsevents/training/lecture_notes/pdf_files/PREDICT/Uncert.pdf
Here is another final (promise, that’s all on this) Edward N. Lorenz quote to sleep on:
RE: #29 Hello Roger!
The earth is a closed thermodynamic system: it gains and looses essentially no mass with its surroundings i.e., outer space, but gains and looses large amounts of energy in such a way that the average surface temperature of the system is about 288 K (Mass loss is confined to hydrogen, helium, space probes and their expelled fuel exhaust while mass gain is from meteors, space snowballs and particles from the solar
wind and deep space).
Since the earth is a sphere comprised of three phase of heterogenous and honogenous matter of enormous mass whose spatial and temporal composition and properties are never constant, it is not possible that the flap of a single small butterfly wing will have any discernible effect on the system whatsoever. Even the effects on system earth of the very violent wing flappings of the large butterfly Mt. Pinitubo disspated after a short period of time.
Harold Pierce Jr writes:
The Earth is NOT a closed thermodynamic system, since closure of a thermodynamic system involves energy as well as matter.
Non sequitur. The conclusion does not follow from the premises.
“Pinatubo.” And the fact that it dissipated doesn’t mean it was never there.
Surely the flapping of a butterflies wings would be dampened down by the other millions of small perturbations taking place a the same time. In a real world scenario there would be literally millions are small uncertain perturbations at any one time. How could anyone assign probability to a single one of these events ?
[Response: As a practical matter, you couldn’t, though the mathematics still says the effect of all these perturbations is there. For that matter, the uncertainties that matter most in weather prediction are the uncertainties in observation of the initial state of the atmosphere, not the actual butterfly-scale forcing uncertainties, which almost certainly contribute less to error growth over time scales of ten days or so. The butterfly statement is just a vivid way of expressing the notion of sensitive dependence on initial conditions. That said, there is a lot of interesting mathematics and physics in the question of the nature of the ensemble of trajectories you get when you represent all those unknown perturbations by stochastic noise. How sensitive are the results to the details of the noise? How much is the long term mean state affected by the presence of noise? What is the probability distribution of the ensemble of trajectories? All these are very deep and difficult questions, but very interesting ones. Good results are available for fairly simple systems like iterated nonlinear 1D maps, but things rapidly get intractable when you go further up the hierarchy of models. –raypierre]
Re: Ike Solem #53,
The differences between predictions of the first and second kind might be more theoretical than practical, as stated in Palmer’s uncertainty memorandum which you cited:
“In practice, as discussed below, it is not easy to separate the predictability problem into a component associated with initial error and a component associated with model error.”
The paper acknowledges “our limited knowledge of the current state of the climate system (especially the deep ocean), and the limited natural predictability that may in fact exist on decadal to centennial timescales”
Uncertainties introduced by parameterizations and other model formulations might be assessed explicity by stocastic methods: “A principal uncertainty in climate change prediction lies in the uncertainties in model formulation, e.g as discussed in Section 4. As discussed in Section 4, such uncertainty may necessarily imply some stochastic representation of the inßuence of sub-grid scale processes within the model formulation.”
But they are not addressed that way currently by the IPCC. “At present, such stochastic representations have not been used in the context of climate simulation. Rather, the representation of model uncertainty in ensemble integrations has been based on the multi-model ensemble.” This was circa 1999, but I saw no evidence that this was different in the FAR.
But there is the problem that the “the pdf spanned by the use of the different sets of models is ad hoc, and may not cover all of the uncertainties in model formulation. Moreover, in practice the models are not truly independent of one another; there is a tendency (possibly for pragmatic rather than scientiÞc reasons) for groups to adopt similar sets of parametrisations.”
Given the number of degrees of freedom, perhaps it is not suprising that there are some documented correlated errors in the AR4 model. Unfortunately, the paper didn’t treat what the threshold of significance of these errors must be before the meta-ensemble can no longer be said to address the pdf of uncertainty in model formulations. Furthermore, the consideration of validation of the model or ensemble skill was very event oriented. Even if good skill is validated for the prediction of certain events, there still remains the question of whether that would imply that the models are also skillful in non-events such as attribution.
Let me say in advance that any similarity in my comments to those available at:
http://www.renewamerica.us/columns/hutchison/070711
are a mere coincidence, or if particularly strong, must be due to a convergence of some sort, since I have never read the site.
Pete, As Raypierre said, the butterfly reference is just a poetic way of saying “a small perturbation”. Sometimes the metaphor in poetry will communicate to the laymen a concept that would otherwise take several pages of math–which the layman wouldn’t read anyway. Scientists tend to look at controlled systems–partial derivatives, admonitions of “ceteris paribus” (meaning other things being equal), etc. We know that ceteris is rarely paribus, but the controlled experiment is much easier to interpret. One can then look at 2 simultaneous perturbations, etc. as needed to understand the system. Fortunately, physical systems are rarely so complicated that multiple simultaneous perturbations are essential to understanding. This does occur in ecology, though.
Maybe the butterfly effect is simply an artifact of the capacity to run sets of parameters through a function and observe the difference. Nobody but a tort lawyer would attempt to do the same in “real life”. The events of “real life” seem over-determined.
There is a religious difference between physicists and chemists on what a closed system is. Physicists describe a closed system as one that exchanges nada with the surroundings. Chemists differentiate between closed systems that can exchange energy but not mass, and isolated ones that can exchange neither with the surroundings.
Before discussing the matter, one does well to inquire what the faith of your partner is.
The butterfly could be the catalyst. The straw that broke the camels back (so to speak). But this is not like the cigarette that started the forest fire. It is more like emergence that would explain how it could be a contributing factor.
However, it would easier to explain how evolution produced the butterflies holometabolism than is would to explain how a single butterflies wings creates a tornado half way around the world. But it is certainly a great question and contribution by Lorenz.
Some confusion here revolves around the issue of chaos in mathematical models vs. chaos in nature. This is also a topic that Lorenz discussed, starting with an overview of the mathematical model:
One could also construct a detailed model of a tornado – and the grid scale of the model would miss microscale perturbations that will influence the future course of the system. For example, the strongest tornadoes are generated by rotating supercell thunderstorms. This is another example of sensitive dependence on initial conditions, because not all supercells lead to tornadoes (only about 20%), and not all tornadoes become real monsters.
As far as the parameterizations of sub-model grid scale process (like thunderstorms), I don’t believe that there are any reported realistic parameterizations that don’t result in sensitive dependence.
The key point here is that chaos is a mathematical phenomenon – but down the centuries, we’ve found that nature follows mathematical rules – so is the chaos in models also found in nature? That’s the hard-to-analyze question (see raypierre’s response to #56).
Once again, Lorenz clarifies the situtation:
One other thing – “dissipative” has a technical meaning here that doesn’t match the normal use of the term. For example, a category 5 hurricane is a very active dissipative system that is dissipating like crazy – that doesn’t mean “weakening and falling apart”, as the normal usage, but rather that the system of interest is open and is far from thermodynamic equilibrium, as opposed to a “Hamiltonian” system. Thus, the issue here is Hamiltonian vs. general dynamical systems. In Hamiltonian systems, forces are not dependent on velocity (unlike say, friction). In this view, all life forms including ourselves are non-Hamiltonian dissipative systems – it’s not a moral judgement on character. :)
Fluid systems are never Hamiltonian, because the theorem is that “If the system is Hamiltonian (no friction) then the fluid is incompressible”. Lorenz explains it like this:
A very interesting question now is to what degree the ocean circulation is chaotic – what is the predictability scale for the ocean circulation? In other words, what kind of reliable long-term ocean weather forecasts can we make?
I have a question for the experts here. I think it’s somewhat related to the thread topic because it has to do with modeling dynamic systems. A colleague at my institution, a physicist, claims that climate science is junk science because climatologists are not experts in nonlinear dynamical systems analysis. He claims that because they don’t publish in the top peer-reviewed journals of nonlinear dynamics, such as PhysicaD, Physical Review E, International Journal of Bifurcations and Chaos, or Chaos, that their models are meaningless, and it is impossible to separate the human contribution to climate from natural variations in climate. I’m a physical chemist, not an expert on nonlinear dynamic systems, but I know enough to realize that modeling such systems is very difficult. What is the best way to respond to my colleague? Are there any good resources I could read on this? Thanks in advance.
[Response: You left out Phys. Rev. Letters. Actually, many of us (myself included) have published in some or all of those journals, when the subject material is appropriate. I think I have at least one paper in each, except for Physica D, and I know Stefan has a couple of things in PRL. That’s beside the point, though. Following the tradition of Ed Lorenz, climate scientists pay close attention to the dynamical systems literature, and make use of it in their own work where appropriate. You can find lots of dynamical systems stuff cited in work in Journal of Climate, Journal of Atmospheric Sciences, and elsewhere. When the main applications are to atmospheres/oceans we tend to publish in our own journals, since that’s the audience. We only turn to the basic physics journals when a result has broader interest to the community of physicists. Most importantly, there are relatively few results in dynamical systems theory that in and of themselves help you distinguish natural variabilty from trends due to a changing control parameter (CO2, say). That requires an understanding of the physics of the particular system you are working on, not of generic properties of dynamical systems. Given that issue, I’m not sure exactly what readings to point you to, though if all you’re looking for is a selection of climate science papers that show an awareness of and contribution to the dynamical systems literature, I’m sure I or the RC readership could help out with that. –raypierre]
Climate Science has posted a weblog on the topic of the “Butterfly Effect“.
Re 21 – I think some of what you are describing is the butterfly effect. Besides that, you mentioned the persistence of droughts.
(An aside, it occurs to me that one might expect droughts to tend to propogate downwind? (as gauged by the boundary layer where the soil moisture would have the most direct impact on humidity) as well as to some extent downstream, though not as fast as floods since water flows faster when there is more of it, generally speaking – in the ecosystem concept of weather/climate, is a drought migrating or continually giving birth to daughter droughts that overlap the area … the two descriptions would be mathematically equivalent and useful for different purposes, I expect, … And the persistence of drought might be a case of a ‘compositional genome’, which may also have been involved in the origin of life – PS I think a simple population model x(n+1) = k*[x(n) * [1 – x(n)]] also exhibits chaotic behavior for some values of k; as k is increased, the single point attractor bifurcates several times and then goes ‘haywire’; interestingly the chaos is interupted by brief intervals where there are 3 or some other number of point attractors that each bifurcate again… although there if k and x(0) are not within certain ranges, the solution goes to +/- infinity… As a sample of ‘population climatology’, I was thinking one might define the set of all extratropical storms which inhabited similar habitats from genesis to lysis, with similar life histories, along the same storm track, for some season or month of the year, during periods defined by NAO, ENSO, etc. indices … for some period of n years… and then consider the collective metabolism, etc. of this population – PV transport, APE conversion, latent heat intake and precipitation, etc… and whether these are balanced by other populations of weather/climate phenomena or not – ecological succession would be triggered by imbalances, then – because there may have been many such periods during the n years, the ecological succession may have recurred many times, etc…)
The drought persistence would be from the temporary memory in the soil moisture (or effects on vegetation). But if a drought can be triggered by the butterfly effect, then that is an aspect of the longer term climate that the potential for chaotic drought initiation exists (if a drought of some particular magnitude only happens once, then maybe the climate system only momentarily crossed a threshold, or crossed two successive thresholds – or maybe it was just one of those rare things when some of the butterfies randomly lined up). Such droughts would be aspects of internal variability, the longer term weather of an even longer term climate, and the soil moisture’s role would be similar to an SST anomaly’s role in other low-frequency variability.
Re 53 – those transients die out – I expect the butterfly effect exists because the chances are essentially zero of picking a perturbation that dies out to the where it would have been on the attractor as opposed to somewhere else?
[Response: The last comment is very well put. To rephrase it in more mathematical language, a random perturbation has zero probability of projecting ONLY on contracting dimensions. –raypierre]
RE: #36
Since there is no uniform spatial and temporal distribution of CO2 and of All other gases including water vapor in the atmosphere as expressed in absolute concentarion units such as moles/cu meter, how is this taken into account in the various computer modeling experiments?
I saw some recent sat images of the distribution of CO2 in the mid-trophosphere and its distibution is not uniform specially over the continents.
[Response: The variations in CO2 are of interest to carbon cycle people, and are therefore tracked in models that are aimed at understanding sources and sinks. However, the variations are small enough that they are not radiatively significant, so in most climate models CO2 is treated as a well-mixed gas for the purposes of radiative transfer. As you note, more variable greenhouse gases, such as water vapor, are treated as inhomogeneous in the radiative calculation. Some models have begun doing this for methane as well. There would be no particular difficulty in doing the same for CO2 if anybody wanted to but it’s really a very small effect, radiatively. By the way this is way off topic, which is probably why your earlier comments were deleted. I’d suggest this is not the right thread for further discussion of your query, but I hope my information helps. –raypierre]
Re, Re,# 56; Therefore Raypierre you are surely using statistical averages or many averages spread across the system in question at certain resolutions to model the initial conditions, say 10×10 or 100×100 mile grid?
I have read that this is why with millions more spent on attemtping to improving the long range climate temperature (sensitivity) your error bars are roughly the same as they were in the first IPCC report. The uncertainty in black carbon, aerosols, clouds etc makes for a possible range of temperatures that has not lent itself to be much better refined.
These uncertainties lead to the reason why we have temperature rise ranges?
[Response: Not really. I was mainly talking about the accuracy of medium range forecasts in my remark. You are talking about the long term response of climate to change of a control parameter (CO2, mainly), and you should be talking about forecast uncertainty rather than “error bars”. The forecast uncertainty represents the likely range of future climates given what we know today, and that’s the range policy planners have to live with and deal with. The range hasn’t narrowed because as our understanding of climate has improved we’ve discovered new phenomena at about the same rate we settle older issues. In addition, most of the uncertainty (for a given emission scenario) is still due to difficulties in nailing down cloud feedbacks. Although the forecast range of warming hasn’t narrowed much, we have a much greater understanding of the nature of the uncertainty. Clouds are just a hard problem, and I don’t think anybody has much expectation that the uncertainty range in that area is going to go down much in the next decade or two, though we may well get better at using paleoclimate data to get an idea of what kinds of cloud feedbacks are most likely to be correct. –raypierre]
Re inline response to #56 “there is a lot of interesting mathematics and physics in the question of the nature of the ensemble of trajectories you get when you represent all those unknown perturbations by stochastic noise. How sensitive are the results to the details of the noise? How much is the long term mean state affected by the presence of noise? What is the probability distribution of the ensemble of trajectories? All these are very deep and difficult questions, but very interesting ones. Good results are available for fairly simple systems like iterated nonlinear 1D maps, but things rapidly get intractable when you go further up the hierarchy of models.” –raypierre
By “intractable”, I guess you mean analytically so? Do you know if anyone is working on simulations of systems that are intermediate between nonlinear 1D maps and real-world complexity? I believe statisticians use simulations to get distributions for analytically intractable stochastic processes.
[Response: By “intractable” I meant it’s a hard thing to prove theorems about. It’s even hard to show that a probability distribution on some general attractor actually exists, let alone compute it. Nonlinear systems subject to stochastic noise are certainly amenable to simulation, though. –raypierre]
Re 65, Patrick, I’m not sure why the population of storms can be expressed as a series although weather forecasters always like to relate storms to previous ones based on track, season, ENSO and many of the other factors you listed. But each successive storm has no relationship to the previous one except in the cases where there is some persistent effect. So although your model would exhibit the required chaotic behavior, I don’t think it has a basis in reality. I agree about the soil moisture persisting the drought and propagation downwind. Those should be quite easy to model. The end of the drought is what concerns me. How is the pattern change modeled when it has (AFAIK) chaotic origins?
Thanks, Raypierre, that helps some. I think my colleague’s main objection is that because climate is an “aperiodic nonlinear system” (his words), it’s impossible to quantify the extent of human contribution. If you (or the readership) can suggest some references for how the numbers are extracted, that would be useful. (For example, IPCC WG1, Feb. 2007, FAQ 2.1, Fig. 2 shows that total net human activities have a radiative forcing of ~1.5 +/- ~1 W/m2. How is that number determined?)
[Response: Even aperiodic nonlinear systems vary within a limited range — call that the “natural variability.” When the observed variations are different in character and magnitude from the “natural variability” then you know they are caused by a trend in some control parameter. When, moreover, the trend agrees with the computed response to changing the control parameter (CO2) you have an even stronger argument. If you had an identical twin Earth with constant CO2, you could determine the natural variability without a model. We don’t really have that; recent paleoclimate provides some evidence, but there are problems with reconstructing past global temperatures and with correcting for past “forcings” like volcanic activity or solar fluctuations. Hence, it is necessary to us models of one sort or another to help understand natural variability, as well as to determine the response to changing forcing. Think of it as a “signal to noise” problem. You can send information by modulating a radio wave even though the radio transmitter generates a certain amount of chaotic, aperiodic noise. For climate, it’s CO2 that’s doing the modulation (and civilization which is doing the speaking). The IPCC report does a quite good job of explaining this, I think — look at their graphs of observed temperature, simulated temperature with natural forcings, and simulated temperature with both natural and anthropogenic forcings. Lee Kump is doing a very elementary book interpreting the IPCC results for the lay audience, and Dave Archer and Stefan Rahmstorf have a somewhat more advanced book coming out. Either of those will help for people who don’t want to slog through the whole IPCC report. By the way,the radiative forcing numbers you quote come from using observed trends in atmospheric constituents (long-lived greenhouse gases and aerosols) and running them through radiation models. There is little uncertainty in the radiation models. The main uncertainty comes from the effect of aerosols on clouds, and the high end of the possible range of that effect is what gives you the low end of your range of anthropogenic forcing. –raypierre]
Mark (70) — I suggest “Plows, Plagues and Petroleum” for W.F. Ruddiman’s popular account of his hypothesis regarding the climate of the past. His papers then go into greater detail with regard to the agreement with ice core, etc., data.
re 70, (can’t resist some bad humor here)
Shouldn’t the more important questions be:
What is the total net butterfly activty radiative forcing?
What caused the butterfly to flap his wings?
If butterflies in Brazil are causing these Texas tornados then shouldn’t we spray the heck out of the Amazon?
[Response: And please, let’s not forget the butterfly-albedo feedback! –raypierre]
Re 69 –
I’m not an expert on droughts specifically, but I would say:
If a drought has a lot of trouble ending but was easily started, it was probably during the course of a shift in climate. In the extreme, if desertification was becoming likely, the butterfly effect would have some role in the exact timing.
Otherwise, though, I would answer with this question: if lack of soil moisture gives inertia to a drought, why didn’t a previous higher level of soil moisture prevent the drought? I suspect the ending of a drought can be part of the same overall chaotic process that is ‘low-frequency variability’.
Oh, and I wasn’t saying that each storm along a storm track is related to each other in the sense of a lineage (However, one could try to make that analogy); also, I was refering to a hypothetical subset of such storms, which may not be grouped in time. What I meant was just a population of similar phenomena – although timing might be used as defining characteristic (winter storms (seasonal timing), El Nino storms, storms that started during the start of a blocking event at some distance x to the west or … whatever (relative timing)), the population need not occur in one continuous unit of time. It is a population that is a part of an ecosystem that occupies some region of the atmosphere’s (and possibly the ocean’s) phase space, and ecological succession occurs when trajectories enter or leave that phase space, and one way of looking at why that happens is that the ecosystem is not balanced – and possibly this is because of fluxes of potential vorticity or other things are not balanced, and that may involve the population in question.
The ‘fitness’ of such phenomena would just be their tendency to recur – that’s not to say they are reproducing themselves autocatalytically (although thunderstorms can seed new thunderstorms via gust fronts). One might also try fitting ‘carrying capacity’ and ‘niche’ to the situation… And coevolution occurs: one population affects the fitness of another.
PS I wasn’t suggesting that the x(n+1) formula given earlier was to be used in this case (or any particular case that I know of), that was just a familiar example (PS if one charts the x point attractors in a k by x graph, the pattern is fractal).
PS each storm along a storm track must have some effect on the conditions of the track; though some of those effects will be advected away from the next cyclogenisis, the previous storm will help shape the environment of the next storm.
—
There are some other clarifications/add-ons I’d like to make to my previous comments:
Earlier I suggested that very small perturbations might be somewhat or partly superfluous given quantum uncertainty. However, while quantum uncertainty makes the trajectories probabilistic rather than perfectly deterministic, the idea the other very small perturbations would be superfluous would be like saying that the other butterflies’ flaps are superfluous.
Another point from the second paragraph: the butterfly effect can be involved in the timing of a threshold being crossed (and on occasions when the threshold would otherwise only just be crossed or not, the butterfly effect could make the difference); on the small scale, icebergs may calve off a glacier at some rate, but the precise moment of calving at each instance may be affected by butterflies at some time in the past. On the larger scale, global warming has a longer term trajectory towards a sea ice-free arctic summer, but interannual variability introduces a range of possible timing for first occurence of that state.
One key point about the butterfly effect is that it may be possible to know it exists, but it is next to impossible to actually trace events back to butterflies. It is unnoticed because it doesn’t cause big surprises (or, big surprises are just rare – which I guess is circular, but anyway…).
Another key point is timing. If the butterfies with significant effect on the details of a tornado at time t0 (small variations in timing, strength, track) flapped at time t1 before the tornado, then the butterflies with larger influences happened at t2, t2 before t1, and the butterflies which decided whether that tornado would occur happened before then, and the butterflies that had sizable influence on the entire 100 tornado outbreak happened before that, and the butterflies that affected whether their would be a tornado outbreak at all before that (they happenned before the proximate recognizable causes, like wind shear, dew points, divergence aloft, dryline, etc.) … and the butterflies that had influence on whether parts of Scotland and Ireland would end up on the coast of North America or not must have occured some time before that part of the break-up of Pangea…
And when a large event does occur, it may use up some amount of energy or transport something somewhere, and could have a negative feedback regarding the likelihood of such an event happenning again soon. This doesn’t shut down the butterfly effect – butterflies still have influence on when the next such event occurs.
The shape of a strange attractor, and the velocity field of the phase space, can be such that, for given boundary conditions there is an average tendency to be drawn preferentially into certain parts of phase space. This may or may not include the time average of all trajectories; the trajectories may loop around their center. There are positive, negative, and ‘sideways’ feedbacks, but outside of some region (but within the attractor’s basin), the feedbacks may be overall negative. This isn’t the same as negative feedback in climate change – changes in boundary conditions may cause by themselves some forcing of the climate, for example, by moving the center of the attractor through phase space, but then positive feedbacks may amplify that initial change, but if/when a new equilibrium is reached, negative feedbacks would tend to draw trajectories toward the new region of the attractor.
PS the shape of the attractor and the velocity field in it’s region may also change. Climate is a multidimensional thing. Some people may then point out that keeping track of something like global average surface temperature is not of much value. However, that ignores tendencies for correlations between such simple variables and the more complex aspects of climate (although there are also differences in changes in shape that can be correlated to solar vs greenhouse vs various types of aerosol forcing – fingerprints of causes of climate change).
On that note, examples of the potential for complexity of climate:
The same average value of some variable, say x (x may be T, the spatial gradient of T, humidity, wind, or some higher-level variable like the ENSO index)may occur with different variation about the average – for example, the standard deviation is not specified. Even if the standard deviation is specified, the actual shape of the distribution is not specified – is it a bell curve or are their multiple peaks? And even if the distribution is specified for a given time interval, the arrangment is not specified. And that can have real effects: for example, if spikes in evaporation tended to follow immediately after spikes in precipitation, average soil moisture would tend to be low, whereas the reverse would be expected if spikes in evaporation tended to immediately precede spikes in precipitation. … Speaking of which, of course runoff will tend to peak after precipitation peaks, in uplands, but lower in a basin, runoff may initially be negative (water flows in from upslope)… anyway, runoff is one reason why shorter periods of more intense precipitation would matter.
PS I also had an argument with someone over whether or not all these statistics (climate) is real or just an abstraction (as if an abstraction like 2+2=4 would cease to be true?). But of course it has real effects, as can be seen by the insensitivity of large lakes to short term precipitation/runoff/evaporation variations, or that a tropical rainforest won’t spring up overnight after a warm rainy day (nor will it spring up if all the precipitation came in 1 minute or if the temperature started at -50 and rose to 100 (deg C)), whereas longer term variations will have significant effects on such things.
Anyway, finding a way to justify the above: The shape (and velocity field) of attractors in phase space are a handy way of thinking of those kinds of issues.
—
I wanted to put all that out there because I won’t be able to get back to this for a few weeks at least. (And remember: The stars do affect people. Exhibit A: telescopes. And UFOs do exist – millions of them are in the Amazon rainforest. We’ve narrowed them down to insects, but beyond that…)
PS thanks for the inline comment in my last post.
Mark, What is your colleague’s specialty in physics? Certainly not nonlinear dynsmics. The naivete in his argumens belies his having looked into climate science (or nonlinear dynamics) in any detail. I think he is purveying organic matter of bovine fabrication, and as such will be reluctant to admit his mistake. Rather than backing him into a corner, the best strategy would be to provide a graceful way for him to back down.
Most nonlinear systems tend to exist near equilibrium and their behaviour is nominal and nothing special happens. However push that equilibrium system out of its equilibrium and interesting things can happen. In simple one parameter or two parameter systems behaviour is unpredictable and can turn chaotic once the system is pushed far enough from equilibrium.
The interesting behaviour occurs somewhere in between but it terms of climate there are many drivers and hence many parameters and a combination of factors can lead to so called interesting climate behaviour although that interesting behaviour could kill a few million of us in terms of the four horses.
Re #73, Patrick, your rhetorical question “why didn’t a previous higher level of soil moisture prevent the drought?” is answered by the large scale factors that change the weather patterns. If the small scale factors were dominant, then the authorities should mandate lawn watering during a drought rather than ban it. The current negative NAO is not affected by the wetness of the mid-Atlantic, but could change based on one butterfly in one yard around here. But that change is just “low frequency variability” by which I believe you mean a small change in timing compared to large periodicity and large variations in that periodicity and doesn’t matter to the model. Other effects are easy to model, soil moisture from distribution of rainfall, gust fronts, local SST changes from storms, etc, given sufficient model resolution. I’m still not sure that there is any tendency to be drawn into any part of the phase space. That seems more likely to be the psychology of weather forecasters (e.g. for storm tracks).
We know from Ike in that the waves coming off of Africa can be parameterized into a 3-5 period without having to model the mountains and convection that are the ultimate source. However, the pattern changes that promote or inhibit convection on those mountains would have to be fed back into the period and distribution parameters for the waves. But going further Ike asks if the fraction of energy that organizes itself into hurricanes will remain constant. I think not. The reason is the same as with the convection, measured or submodeled parameterization no longer holds in the new, higher energy environment. In fact the large scale patterns will be quite different with positive or negative consequences for hurricane formation and strength.
Likewise I disagree with the distinction that Ike quotes in #53, initial value problems (e.g. forecasting El Nino) versus changes in forcing. The forecast is never necessary in climate models (I realize they are talking about weather forecasts), but the modeling of El Nino as it may change with climate changes is necessary. That modeling is agnostic of any particular conditions (i.e. initial) at any time, but does require fidelity to the effect on El Nino by those conditions, and the effect of the climate model on those conditions. A lack of periodicity or a some statistical distribution of periodicity due to amplification of chaotic changes does not invalidate models, but only forces modelers to do more real world measurements and submodels and create dynamic parameters from those.
Likewise about #62, I don’t think that unpredictability due to chaos needs to be resolved (implicitly) by resorting to energy equations. Yes, energy is increasing, along with water vapor, etc. But the models can have fidelity to those changes by applying appropriate real-world measurements or results from detailed submodels. To me this seems to be a solvable problem.
Eric, I think you are missing the point entirely. There are irregular and regular components of the climate system, and there are also thermodynamic limits – the system is open, but that doesn’t mean conservation of energy doesn’t apply.
Weather predictions of the first kind display sensitive dependence on initial conditions. The predictive ability of a model of nature is not some set quantity, but varies with the system itself and also spatially. Parts of the tropics are far more predictable than mid-latitude regions where frontal systems are mixing – but the limits are anywhere from a few days to a few weeks.
Climate predictions of the first kind are similar in that they look a bit like ocean circulation forecasts – an impending El Nino or La Nina can be predicted some months in advance, for example. Discussions of the chaotic elements of El Nino have shown up in the normal “dynamical systems” journals: Power-law correlations in the southern-oscillation-index fluctuations characterizing El Niño – M Ausloos, K Ivanova – Physical Review E, 2001 (pdf)
The ability to forecast El Nino over the short term goes back some time – see Science 1988, Barnett et. al: http://www.sciencemag.org/cgi/content/abstract/241/4862/192
For current La Nina & SOI conditions: http://www.bom.gov.au/climate/enso/
Now, what about climate predictions of the second kind? These are far more general questions, in that if we have a solid understanding of climate, than we should be able to estimate what the climate of any rocky planet with a known atmospheric composition and surface characteristics is. If we find a rocky planet around some distant star, and we know how much sunlight it gets, what its orbit is like, what its atmosphere is made of, and the distribution of landmasses and oceans, can we predict what the basic climate will be like? The answer there is yes – within limits.
Take the hurricane situation. Can we accurately predict hurricanes a month away right now? Take a look at the surface temperature field on the satellite view of the Atlantic basin right now.
Compare that to the very similiar current sea surface temperature: http://weather.unisys.com/surface/sst.html
(anomalies are at http://www.osdpd.noaa.gov/PSB/EPS/SST/climo.html but are not so useful).
The basic element needed for hurricane formation is a SST of at least 26.5C – and the surface layer has to be warm to a depth of some 50 meters. If you look at current conditions from 10 to 30 N latitude, there is no way for a hurricane to form, no matter how many perturbations are introduced.
However, if we increase SSTs and the depth of the warm mixed layer, we change the basic thermodynamics of the system, and we can predict, that if all other factors are held equal, that the warmer than 26.5C SSTs will appear earlier in the spring, will persist later into the fall, and will have a greater area of extent. We can also predict that the warm surface layer will be deeper – perhaps the most important factor, as that is really what allows a hurricane to reach maximum intensity.
It may very well be that there will be compensating changes in wind shear, but that’s highly uncertain – and it is very unlikely that such compensations would be constant. Thus chances are higher for stronger hurricanes in a warmer world.
Unfortunately, Gray & Klotzbach at Colorado are still claiming that current trends are all due to a “positive phase of the AMO” which is resulting in more rapid northward spread of warm water – implying that we will see a cooling trend in SSTs “some 5-20 years from now”. That is basically nonsense, regardless of any AMO effect, but that’s what their latest hurricane predictions claim, as covered at ScienceDaily:
There is some evidence of this AMO in climate models…
http://www.agu.org/pubs/crossref/2006…/2006GL026242.shtml
So. . . the models are showing that the AMO is actually real and is having an influence – I hear applause from Pielke and Gray already – except that they say that the models are bogus and can’t be trusted, and that they have no “predictive skill.” – and this paper relies heavily on model runs as “calculated observations” – a procedure that should have the skeptics screaming bloody murder, I think.
The AMO and its cousin the PDO are recently recognized “oscillations” (with periods of from 5-20 years… on the basis of one century’s worth of time series analysis data? A “periodic oscillation” – with an apparently inexplicable oceanic mechanism driving it?) – but let’s look at how HadCM3 deals with El Nino – EL Ninos show up, but frequency and timing is off, indicating some degree of sensitive dependence:
http://www.agu.org/pubs/crossref/2007/2007JD008705.shtml
One claim that you will see often is this: “The El Niño-Southern Oscillation (ENSO) phenomena are the largest natural interannual climate fluctuation in the coupled ocean-atmosphere system. Warm (El Niño) and cold (La Niña) ENSO events occur quasi-periodically.”
Do they really? (Quasi-periodic functions are finite combinations of periodic functions) Or is the incidence of El Nino events chaotic on the scale of years? Could El Ninos triggered by whales, in other words? This is probably one of the more interesting questions in ocean science today – what is the scale of predictablity for ocean circulation?
The point is that in making any prediction of weather or climate, one has to be aware of whether it is a weather prediction of the first kind, a climate prediction of the first kind, or a climate prediction of the second kind. Climate predictions of the second kind do not appear to display sensitive dependence on initial conditions. Any discussion of climate predictions thus has to involve at least some understanding of this whole topic.
Climate predictions, in this language, consist of efforts to predict how the regular components of the land-ocean fluid dynamic system will change due to changes in the overall structure of the system itself – changes in atmospheric composition, changes in ice cover, changes in forest cover, and so on.
What skeptics appear to be doing is trying to muddy the waters by claiming that there are no regular or predictable components of the system over the long run – which is clearly not the case.
Ray, (#74) well, my colleague’s PhD thesis title is “On Nonlinear Time Series Analysis”, and he has published on complexity of multichannel EEGs, and nonlinear time series analysis of sunspots. He certainly knows very little about climate scientists, and you are correct that giving him a graceful way out is more likely to be effective than direct confrontation.
Thanks, Raypierre and David Benson for reading suggestions.
Mark (78) — I’ll also suggest “The Discovery of Global Warming”,
http://www.aip.org/history/climate/index.html
hoping that your colleague will take the time to read it.
During all this discussion I’m not sure anyone asked whether the actual climate system is in fact chaotic, in the sense that it has at least one positive Lyapunov exponent. I have always been struck by a comment I once heard a pretty good numerical hydrodynamicist make. He did Galerkin simulations. WIth say N=N1 Galerkin modes at Reynolds number R=R1 he would see exponential divergence of nearby trajectories (chaos). Holding R fixed but increasing the number of Galerkin modes (from N1 to say N2) resulted in behavior that did not display exponential divergence of nearby trajectories. Increasing the reynolds number from R1 to R2 would result in exponential divergence with N=N2 and so on. I have no idea if this stuff was ever published. I’ve never really known what to make of it. It isn’t clear that the higher dimensional but nonchaotic system is even more predictable than the lower dimensional chaotic one.
Re 63 and 78: I occasionally fancy myself a dynamicist of sorts but I sure as hell wouldn’t be dissing these climate fellers for their lack of understanding of dynamics.
Re #76, Ike, there’s 26.5 water right now, but no hurricanes (the charts don’t show the depth of the warm water). In the other links, El Ninos are predicted, where possible, from related periodic factors. These oscillations may bounce between states without any particular periodicity, but it will always be an ocean weather (and related climate) prediction of the first kind. As for the second kind of prediction, I believe that’s mainly an abstraction, rather than a reality. One reason is that the second kind of prediction depends on accurate modeling (not predictions) of the first kind of effects. Without those models, the first kind of effects have to be parameterized preventing them from changing as the climate changes. We can model El Nino in today’s climate, but what about a warmer climate?
I don’t think a planet with water and land in a particular configuration and known atmospheric composition can have a predicted temperature range to any useful precision without a sufficient model of the first kind of effects. Earth’s history shows as much. Water is the problem, predictions can only be as good as the prediction of the distribution of water vapor in all dimensions and clouds. In current global models these are heavily parameterized based on detailed models and real world measurements to get decent accuracy. The good news for all concerned is the fidelity and computer power (model resolution) is constantly increasing and will make this whole discussion moot.
Lorenz was certainly a very smart guy. However, for most people his “butterfly effect” creates the wrong impression. It implies the butterfly *causes* the tornado, which would be remarkable if true. But what if there are a thousand butterflies all in the same area. Which one causes the tornado?
You can try and run a kind of counterfactual argument, whereby you say something like: “on all trajectories where the butterfly does not flap his wings, but all other boundary/initial conditions are the same, the tornado doesn’t happen; on all trajectories where the butterfly flaps his wings, but all other boundary/initial conditions are the same, the tornado does happen”, but that is unlikely to be true.
The best you can probably say is: “if the butterfly flaps his wings exactly *this* way (for some precise specification of “this”), and all other boundary/initial conditions are equal, the tornado happens; if the butterfly does not flap his wings exactly *that* way (for some precise definition of “that”), the tornado does not happen”. But this is just comparing two single trajectories – it is a very weak notion of causality. For if this is what we mean by the “butterfly causing the tornado”, then we can equally find any other pair of trajectories, one with a tornado and one without that differ by a single event and claim that it is that event that causes the tornado. In other words, by this definition of causality, any number of other butterfly wing flaps “cause” the tornado, as do an uncountable number of other events ranging from my choice to eat cereal instead of toast for breakfast through to the individual decisions made by the cockroaches on my street.
Most people take from Lorenz’s analogy that the butterfly causes the tornado. But on any sensible definition of causality it does not, hence I think the analogy does more harm than good.
Mark (#70), your colleague is correct, but only half-way. While there are all indications that the climate is indeed an “aperiodic nonlinear system”, it should be possible to quantify the extent of human contribution. But to do so, one needs a correct model of natural climate variations first. It is quite obvious that during 99.9% of available climate records (from various sediments and ice cores) there was no human contribution, because the industry simply didn’t exist. These are purely natural variations. Yet the climatology is quite short of delivering a model of natural long ice ages and fast deglaciations. Given the absence of such model of natural variations, the claim of anthropogenic influence on current state of climate has no scientific foundation so far.
[Response: This is equivalent to arguing that since we don’t know the precise cause of every wildfire throughout history, we can’t convict an arsonist whose actions were caught on tape. It’s a complete fallacy. – gavin]
Roger (#64):
Part of your final construction reads: “However, this kinetic energy is dispersed over progressively larger and larger volumes such that it will quickly dissipate into heat as the magnitude of the disturbance to the flow at any single location becomes smaller”. This assertion fails to take into account the general and well documented effect of hydrodynamic instability, when, under certain (even uniform) stress conditions above certain threshold of forcing, generic infinitesimal perturbations grow into a macroscopic global flow pattern by _drawing_ its energy from otherwise smooth velocity (and/or temperature) field. If the flow is far from being stable and already turbulent, there are several known effects of “coherent structures”, who’s appearance resembles the process of original instability in many respects.
The original Saltzman equation system of 1962 does not contain accounting of dissipation of fluid motions into thermal energy; see Equation (4) of the paper. The same approximation obtains for the Lorenz system of 1963. The original Saltzman 7-equation system does not produce chaotic response for the range of parameters and initial conditions investigated in the paper. Saltzman used more modes in the expansions, and then reduced these to 7 for calculations. Lorenz found a subset of these 7 equations and a range of parameters for which he investigated chaotic response. So far as I am aware, no Lorenz-like modeling approach has included viscous dissipation in the thermal energy balance model.
Both the Saltzman and Lorenz systems are zeroth-order models for the onset of motion for a fluid contained between horizontal planes; the Rayleigh-Benard problem is a convenient designation. Similar systems of equations are obtained also for flows in closed loops; thermosyphons, also here. The fluid motions for the original Saltzman and Lorenz problem are driven by a temperature difference between the planes bounding the flow. The Boussinesq approximation is used in the momentum-balance model for the vertical direction.
The temperature difference between the planes is required to be maintained in order for the flow to continue. In the presence of frictional losses all fluid motions require that energy be constantly added to the system for the flow to maintain. Likewise, in a very rough analogy with small perturbations and turbulence, a driving force is required in order for the small-scale motions to be maintained. In many flows, the driving potential is provided through the shear in the mean flow by the power supplied to maintain the mean flow.
Periodic motions, not chaotic motions, have been observed for the Lorenz system for some values of the parameters appearing in the system; see Tritton, Physical Fluid Dynamics, for example, and the closer analyses such as that linked above. It is equally well-known that chaotic response can be obtained due solely to inappropriate numerical methods applied to PDEs and ODEs that cannot produce chaotic response in their solutions. When numerical solution methods are important aspects of any analysis, the effects of these methods on the calculated numbers require deep investigations so as to eliminate spurious effects that are solely products of the numerical methods.
Changes in the parameters in the model system produce the same kinds of effects that are observed when the initial conditions are changed. There are some ranges of the parameters that do not show sensitivity to initial conditions nor chaotic response. The focus on sensitivity to initial conditions and chaotic response seems to always miss the fact that simply invoking ‘the Lorenz model’ is not sufficient to ensure that chaotic response is obtained.
Dynamical systems theory predicts that the differences between the dependent variables will grow exponentially for two different values of initial conditions, no matter how small. Statements about the time required for a perturbation to be effective over various ranges of temporal and spatial extent in the physical world should be addressed from the viewpoint of physical phenomena and processes; not by what a few calculations using a model/code indicate. Again, aphysical properties of calculated fluid flows can frequently be traced to improper numerical solution methods and the implementation of these into computer software.
The demonstration linked to in the original post for this thread led to the introduction of more questions than answers. The effects of the size of the discrete time interval was an issue. As were the effects of the numerical solution methods. A comment over there mentions that the calculated response might in fact be controlled by model equations and numerical solution method in contrast to chaotic response. Additional discussions of step-size effects have been presented here for both NWP and GCMs. The presence, or absence, of chaotic response in the model/code cannot be ascertained by use of a few calculations. The possibility of causality linked to the model equations and/or numerical solution method should be determined first. The mere possible existence of the potential for chaotic response is not sufficient for concluding chaotic response.
A demonstration by a calculation of an idealized model equation system never says anything about the actual response of the modeled world; especially when as in the case of GCMs the model equations are acknowledged to be approximations and simplifications of the complete fundamental equations. A calculation by a GCM demonstrates the properties of that GCM for that calculation and can provide no information relative to the chaotic response of the real world climate.
Neither sensitivity to initial conditions nor non-linearity nor complexity, either separately or all together, provide necessary and sufficient conditions for a prior determination of chaotic response. Analyses of the complete system of continuous equations, plus careful consideration of numerical solution aspects, combined with analyses of calculated results are all necessary for determination of chaotic response. A model of a complex physical system, comprised of a system of nonlinear equations, the numerical solutions of which show sensitivity to initial conditions, and the calculated output from which ‘looks random’ does not even mean that the calculation exhibits chaotic response. ‘Looks random’ in itself is not a description that is consistent with chaotic response. And the properties and characteristics of the calculated results cannot ever be attributed to be properties and characteristics of the modeled physical system.
Heuristic appeals to Lyapunov exponents should be verified by calculations of the numerical values of these numbers. So far as I know that has yet to be carried out for any GCM model equations. As the numerical values of the exponents generally requires use of numerical methods, convergence of these methods for the exponenst must also be demonstrated. The results of application of numerical solution methods are well known to be very capable of producing results that appear to have the same characteristics of positive Lyapunov exponents.
There are many papers dealing with generalization of the Lorenz model equations, primarily by including more modes in the expansions. Three recent papers by Roy and Munsielak here, here, and here, provide a good review and summary of these investigations. The authors rightly conclude that some of the generalizations are not properly related to the original Lorenz model systems. As noted by Roy and Munsielak, there are two important characteristics of the continuous Lorenz equations are (1) they conserve energy in the limit of no viscosity (energy conserving in the dissipationless limit) and (2) the systems have solutions that are not unbounded. Some generalizations of the Lorenz model system that do not conform to these requirements show routes to chaos that are different from those for the Lorenz system. Is it clear that the continuous equations, expansions, and associated numerical solution methods, used in NWP and GCMs are consistent with the original basis of the Lorenz-like models?
It would seem that in order to say that GCMs are producing chaotic response in the sense of the Lorenz model system, the continuous equations should be investigated to ensure that each complete continuous system of model equations has the properties of the original Lorenz system. Hasn’t yet been done as far as I know.
It seems to me that the hypothesis that GCM calculations are demonstrating chaotic response is not well founded. Especially whenever the original Lorenz model system is invoked as the template for chaotic response.
As noted in response to Comment 39 and Comment 56 above, the analytical properties of equation systems comprised of PDEs plus ODEs plus algebraic model equations relative to chaotic response are for all practical purposes unknown (my summary). I think there is a proof of the existence of the Lorenz attractor by Warwick Tucker since about 2000.
I think maybe Comment #45 above is referring to papers and reports by D. Orrell on model error vs. chaotic response of complex dynamical systems.
All corrections to the above will be appreciated.
[Response: All GCMs as written can be considered to be deterministic dynamical systems. All of them display extreme sensitivity to initial conditions. All of them have positive Lyapunov exponents (though I agree it would be interesting to do a formal comparison across models of what those exponents are). All are therefore chaotic. Your restriction of the term chaotic to only continuous PDEs where it can be demonstrated analytically, is way too restrictive and excludes all natural systems – thus it is not particularly useful. Since the main consequence of the empirical determination that the models are chaotic is that we need to use ensembles, I don’t see how any of your points make any practical difference. The GCMs can be thought of as the sum total of their underlying equations, their discretisation and the libraries used (and that will always be the case). It is certainly conceivable, nay obvious, that these dynamical systems are not exactly the same as the one in the real world – which is why we spend so much time on evaluating their responses and comparing that to the real world. But as a practical matter, the distinction (since it can never be eliminated) doesn’t play much of a role. – gavin]
Will you please take a look at this curious blog by an italian negationist?
http://omniclimate.wordpress.com/2008/04/24/realclimate-raises-the-bar-against-climate-models/
It says “your” models are unfalsifiable, and therefore not science at all. So, “climate change” is an entity that can only become observable in the long, long term. And since there is little concern for the “specific trajectory”, there literally exists NO possible short-term sets of observations that can falsify the climate models.
Ohm, and he ends with In further irony, the above pairs up perfectly well with RC’s “comments policy” that can be summarized more or less into “we will censor everything we do not like“.
Maybe a short answer will silence him. Once and for all, although I doubt it.
Thanks
[Response: I doubt it too. But really, what is so hard with the concept of short term noise and long term signal? Does a single toss of a coin that lands on heads mean the coin is unfair? No. How about 2 heads in a row? No. However, if you get a really long series of heads the chances that it is fair coin become smaller. The same is true for models – a head here or a tail there are interesting but do not determine the long term accuracy of the model. It is the long term trends that do. I apologise if that’s inconvenient for people who think that one La Niña event implies the onset of a new ice age, but them’s the breaks. – gavin]
Dan (#85): Your introductory premise is incorrect. The original Saltzman equation system was derived from an approximation of Navier-Stockes system with finite viscosity, see Eq. (1)-(3), which means that the dissipation is accounted, and therefore the rest of truncation represents a dissipative system.
Gavin,
In regards to your reply in #86, a long series of heads is NOT a sign of an unfair coin in itself. You have an equal chance of getting a sequence of heads as you do any other sequence. Reminds me of the Richard Feynman quote “You know, the most amazing thing happened to me tonight. I was coming here, on the way to the lecture, and I came in through the parking lot. And you won’t believe what happened. I saw a car with the license plate ARW 357. Can you imagine? Of all the millions of license plates in the state, what was the chance that I would see that particular one tonight? Amazing!”
[Response: Agreed for the sequence, but I’m only interested in the distribution (the ratio of heads to tails). – gavin]
Gavin, regarding your comment to #83: Isn’t it true that dominant cause of wildfires is natural, from thunders? Then, if your goal is to restrict global fires, convicting one or two arsonist would accomplish nothing, correct? Also, who would you like to convict for wildfires a million years ago, some lemurs?
There is a simple way to settle the falsifiability issue. Could anybody at RC please post a blog clearly stating what would falsify the climate models? Say (just as a way of example) “if temperatures will be cooler than today’s in 2020” or “if there is a sustained negative trend over the course of 25 years”. Those statements are simplistic: I am sure you can come up with something more sophisticated.
Alternatively, if such a clear-cut answer has already been the topic of one of your blogs, could you please provide the link. thanks in advance.
The idea of a climate model being falsifiable strikes me as naive. The statement that “climate sensitivity to CO2 doubling is 3 degrees C per doubling” is certainly falsifiable. However, the evidence currently favors the proposition, and even if it were falsified, the climate model would persist more or less in the same form with a different sensitivity. New forcers might be discovered, but that would not change the form of the climate model dramatically.
There is more to the philosophy of science than Karl Popper, folks.
The hypothesis that humans are behind the current warming epoch is certainly falsifiable–all you have to do is 1)show that all the independent lines of evidence constraining CO2 sensitivity are wrong; 2)come up with a model that explains the current warming without this sensitivity; and 3)show why physics is wrong and somehow the greenhouse contribution stops magically at 280 ppmv. And do let us know how you progress with that.
Which particular model are you talking about, Maurizio?
Or are you talking about the known physics?
Or the forcings?
You can fix a problem in a component by understanding it, rather than deciding the entire engine is unusable because something is wrong with how it works.
http://www.google.com/search?q=%22falsify+the+climate+models%22
Re: #89 Al Tekhasski wrote: “Isn’t it true that dominant cause of wildfires is natural, from thunders?”
In the United States. somewhere between 2 and 10 percent of wildfires are caused by lightning. The vast majority of wildfires is due to human causes, intentional or accidental. In some places, coastal California for example, lightning is relatively uncommon.
http://www.bellmuseum.org/wildfire.html
#86 THe models in general are extraordinary in precision, until Chaos, as per Lorenz butterflies, take over. I defy anyone who thinks otherwise to come up with a 4 day forecast having accurate temperatures for say 1000 locations simultaneously… Or for someone to come up with a better long range climate temperature projection than from Nasa GISS or other proven models. What some people call model “errors” are simply mathematical interpretation or application mistakes, one of which should be corrected in the near future. I give three letters, DWT, a clue, whole atmosphere temperature trends work, for those who want to see proof, check out my website….
Re #90: Somebody posted two ways to falsify the climate models on your web site.
(1)Perform lab experiment with the result that CO2 doesn’t absorb/emit the way the climate models assume.
(2)Perform lab experiment in which fluid flow is observed that contradicts the Navier Stokes equations.
I could go on and on. It’s trivial to come up with experiments that could falsify the climate models in the short term. It isn’t the fault of the climate models that they’re based on very well established physics.
Regarding #91 and #92: well folks it was the RC people that spoke in this blog about “predictability” and finding the “common signal that is a signature of a particular forcing”. Maybe that’s where the falsifiability lies. It’s not just a matter of changing a parameter’s value though, as it could very well be that not all parameters, and not all physical relationships have been identified yet.
I am sure Gavin is clever enough to know that there must be a prediction made, and a measurement done regarding that prediction, otherwise it’s not “science”, it’s useless.
Please don’t be “more loyalist than the King”…
Eric says: “One reason is that the second kind of prediction depends on accurate modeling (not predictions) of the first kind of effects.”
That’s like saying that a prediction that June in the U.S. will be warmer than February depends on accurate modeling of atmospheric and oceanic weather systems in February! Obviously it does not.
Breaking the problem into atmospheric weather forecasts of the first kind, ocean weather forecasts of the first kind, and climate forecasts of the second kind seems reasonable when discussing the overall ocean-atmosphere-land-ice fluid dynamics system. More generally, the overall system has regular and irregular components, and the regular components are predictable on far longer timescales than the irregular components.
The big uncertainty here is carbon cycle feedbacks, which require an understanding of the biosphere and cryosphere responses – and that requires an ability to predict future carbon emission and uptake by soils, the biosphere, and oceans – and also by people.
At this point, it seems fair to say that the greatest uncertainty in predictions of future climate change is now future human behavior.
P.S. Regarding “causality” it helps to think about trying to recover the past behavior of a system from a measurement of its current state. This is really the paleoclimate perspective – and it turns out that the present state of the system isn’t of much use in recovering a record of its past state – for that, paleoclimate scientists turn to sediment records, ice core records, and the like. This is the other side of “sensitive dependence on initial conditions.” What does the Euclidean “proof” mean in such a situation?
For example, if we take the current state of the atmosphere, can we say what it was like yesterday based on that alone? Only to a point, and the backwards limit dies out as fast as the forward one does. During the 18th and 19th century, many people believed that perfect knowledge of the universe would allow one to predict the future and know the past, completely. That notion is now only of historical interest. People are still working out the “philosophical implications” – meaning that there are a lot of people running around with 18th-19th century physical models of the world in their heads, unfortunately. Sad to say, most courses in differential equations at colleges today are largely taught from that archaic perspective.
Maurizio, Why did your reading of philosophy of science stop with Popper in the mid 1900s? GCMs are complicated entities with many interacting parts. Yes you could try to falsify any one of those parts, but the new model will look very much like the old one–with perhaps slightly different parameters.
You say that perhaps “not all parameters, and not all physical relationships have been identified yet.”
Yes, and there could be a pink unicorn in my car trunk when I go to the parking lot today as well. Do you have a concrete suggestion for a missing parameter or relationship. If so, propose it. If not, then I’m not sure what your admonition adds to the discussion.
So, let’s see, you don’t understand GCMs or philosophy of science. What else do you not understand…?
Maurizio,
I think your comment is an example of popular misconceptions about basic scientific issues. If you wanted a prediction, and went to your relevant expert, and you were told that your system was actually not predictable, or had a small degree of predictability, wouldn’t that be valuable information about the system?
You seem to be claiming that studies of probablility are not scientific, in other words? If so, you would really be saying that most of 20th century science is not actually science!
What a certain class of skeptics are trying to do is to claim that since one cannot predict the irregular components of the climate system, one can’t predict the regular components either. This is a highly ridiculous claim, but an apparent lack of scientific knowledge among the general public allows them to get away with it.
It’s true that some systems do have such a large irregular component that they are essentially random over any but the shorter timescale – “econometric” predictions really do seem useless, for example – but climate is clearly predictable. It’s also clear that the composition of the atmosphere affects the climate, and it’s also clear that we’ve added a lot of heat-trapping gases to the atmosphere, mainly from fossil fuel combustion, so yes, we are changing the climate, slowly on the human timescale, but incredibly quickly on the geologic timescale.
From an outward observer’s perspective, climate science seems interesting in that you can make lots of predictions but the time scale implies that validation extends over one’s career. I suppose it requires some patience…