It is a good tradition in science to gain insights and build intuition with the help of thought-experiments. Let’s perform a couple of thought-experiments that shed light on some basic properties of the statistics of record-breaking events, like unprecedented heat waves. I promise it won’t be complicated, but I can’t promise you won’t be surprised.
Assume there is a climate change over time that is U-shaped, like the blue temperature curve shown in Fig. 1. Perhaps a solar cycle might have driven that initial cooling and then warming again – or we might just be looking at part of a seasonal cycle around winter. (In fact what is shown is the lower half of a sinusoidal cycle.) For comparison, the red curve shows a stationary climate. The linear trend in both cases is the same: zero.
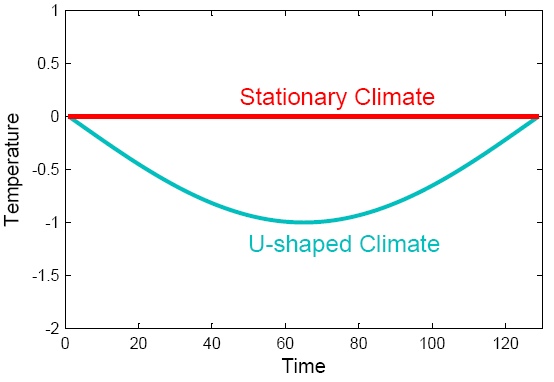
Fig. 1.Two idealized climate evolutions.
These climates are both very boring and look nothing like real data, because they lack variability. So let’s add some random noise – stuff that is ubiquitous in the climate system and usually called ‘weather’. Our U-shaped climate then looks like the curve below.
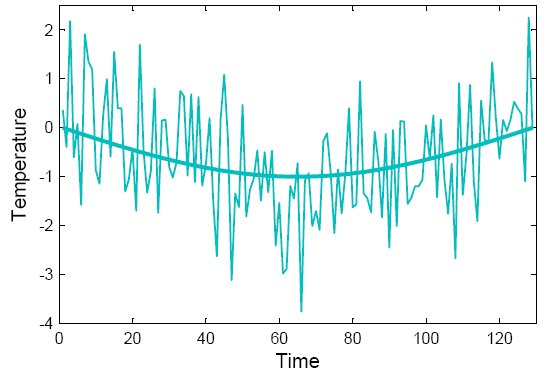
Fig. 2. “Climate is what you expect, weather is what you get.” One realisation of the U-shaped climate with added white noise.
So here comes the question: how many heat records (those are simply data points warmer than any previous data point) do we expect on average in this climate at each point in time? As compared to how many do we expect in the stationary climate? Don’t look at the solution below – first try to guess what the answer might look like, shown as the ratio of records in the changing vs. the stationary climate.
When I say “expected on average” this is like asking how many sixes one expects on average when rolling a dice a thousand times. An easy way to answer this is to just try it out, and that is what the simple computer code appended below does: it takes the climate curve, adds random noise, and then counts the number of records. It repeats that a hundred thousand times (which just takes a few seconds on my old laptop) to get a reliable average.
For the stationary climate, you don’t even have to try it out. If your series is n points long, then the probability that the last point is the hottest (and thus a record) is simply 1/n. (Because in a stationary climate each of those n points must have the same chance of being the hottest.) So the expected number of records declines as 1/n along the time series.
Ready to look at the result? See next graph. The expected record ratio starts off at 1, i.e., initially the number of records is the same in both the U-shaped and the stationary climate. Subsequently, the number of heat records in the U-climate drops down to about a third of what it would be in a stationary climate, which is understandable because there is initial cooling. But near the bottom of the U the number of records starts to increase again as climate starts to warm up, and at the end it is more than three times higher than in a stationary climate.
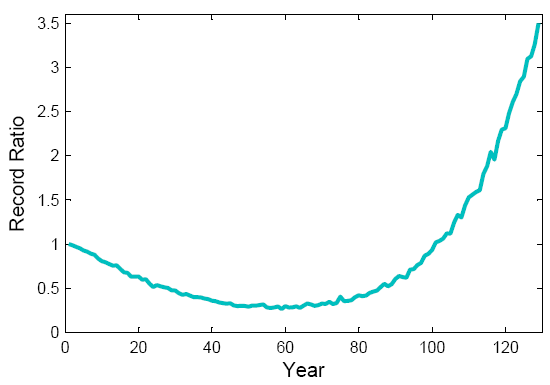
Fig. 3. The ratio of records for the U-shaped climate to that in a stationary climate, as it changes over time. The U-shaped climate has fewer records than a stationary climate in the middle, but more near the end.
So here is one interesting result: even though the linear trend is zero, the U-shaped climate change has greatly increased the number of records near the end of the period! Zero linear trend does not mean there is no climate change. About two thirds of the records in the final decade are due to this climate change, only one third would also have occurred in a stationary climate. (The numbers of course depend on the amplitude of the U as compared to the amplitude of the noise – in this example we use a sine curve with amplitude 1 and noise with standard deviation 1.)
A second thought-experiment
Next, pretend you are one of those alarmist politicized scientists who allegedly abound in climate science (surely one day I’ll meet one). You think of a cunning trick: how about hyping up the number of records by ignoring the first, cooling half of the data? Only use the second half of the data in the analysis, this will get you a strong linear warming trend instead of zero trend!
Here is the result shown in green:
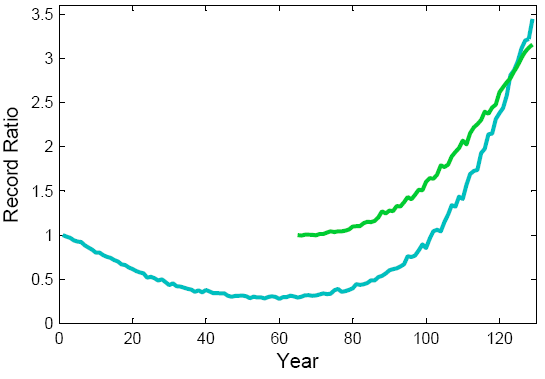
Fig. 4. The record ratio for the U-shaped climate (blue) as compared to that for a climate with an accelerating warming trend, i.e. just the second half of the U (green).
Oops. You didn’t think this through properly. The record ratio – and thus the percentage of records due to the climatic change – near the end is almost the same as for the full U!
The explanation is quite simple. Given the symmetry of the U-curve, the expected number of records near the end has doubled. (The last point has to beat only half as many previous points in order to be a record, and in the full U each climatic temperature value occurs twice.) But for the same reason, the expected number of records in a stationary climate has also doubled. So the ratio has remained the same.
If you try to go to even steeper linear warming trends, by confining the analysis to ever shorter sections of data near the end, the record ratio just drops, because the effect of the shorter series (which makes records less ‘special’ – a 20-year heat record simply is not as unusual as a 100-year heat record) overwhelms the effect of the steeper warming trend. (That is why using the full data period rather than just 100 years gives a stronger conclusion about the Moscow heat record despite a lesser linear warming trend, as we found in our PNAS paper.)
So now we have seen examples of the same trend (zero) leading to very different record ratios; we have seen examples of very different trends (zero and non-zero) leading to the same record ratio, and we have even seen examples of the record ratio going down for steeper trends. That should make it clear that in a situation of non-linear climate change, the linear trend value is not very relevant for the statistics of records, and one needs to look at the full time evolution.
Back to Moscow in July
That insight brings us back to a more real-world example. In our recent PNAS paper we looked at global annual-mean temperature series and at the July temperatures in Moscow. In both cases we find the data are not well described by a linear trend over the past 130 years, and we fitted smoothed curves to describe the gradual climate changes over time. In fact both climate evolutions show some qualitative similarities, i.e. a warming up to ~1940, a slight subsequent cooling up to ~ 1980 followed by a warming trend until the present. For Moscow the amplitude of this pattern is just larger, as one might expect (based on physical considerations and climate models) for a northern-hemisphere continental location.
NOAA has in a recent analysis of linear trends confirmed this non-linear nature of the climatic change in the Moscow data: for different time periods, their graph shows intervals of significant warming trends as well as cooling trends. There can thus be no doubt that the Moscow data do not show a simple linear warming trend since 1880, but a more complex time evolution. Our analysis based on the non-linear trend line strongly suggests that the key feature that has increased the expected number of recent records to about five times the stationary value is in fact the warming which occurred after 1980 (see Fig. 4 of our paper, which shows the absolute number of expected records over time). Up until then, the expected number of records is similar to that of a stationary climate, except for an earlier temporary peak due to the warming up to ~1940.
This fact is fortunate, since there are question marks about the data homogeneity of these time series. Apart from the urban adjustment problems discussed in our previous post, there is the possibility for a large warm bias during warm sunny summers in the earlier part, because thermometers were then not shaded from reflected sunlight – a problem that has been well-documented for pre-1950 instruments in France (Etien et al., Climatic Change 2009). Such data issues don’t play a major role for our record statistics if that is determined mostly by the post-1980 warming. This post-1980 warming is well-documented by satellite data (shown in Fig. 5 of our paper).
It ain’t attribution
Our statistical approach nevertheless is not in itself an attribution study. This term usually applies to attempts to attribute some event to a physical cause (e.g., greenhouse gases or solar variability). As Martin Vermeer rightly said in a comment to our previous post, such attribution is impossible by only analysing temperature data. We only do time series analysis: we merely split the data series into a ‘trend process’ (a systematic smooth climate change) and a random ‘noise process’ as described in time-series text books (e.g. Mudelsee 2010), and then analyse what portion of record events is related to either of these. This method does not say anything about the physical cause of the trend process – e.g., whether the post-1980 Moscow warming is due to solar cycles, an urban heat island or greenhouse gases. Other evidence – beyond our simple time-series analysis – has to be consulted to resolve such questions. Given that it coincides with the bulk of global warming (three quarters of which occurred from 1980 onwards) and is also predicted by models in response to rising greenhouse gases, this post-1980 warming in Russia is, in our view, very unlikely just due to natural variability.
A simple code
You don’t need a 1,000-page computer model code to find out some pretty interesting things about extreme events. The few lines of matlab code below are enough to perform the Monte Carlo simulations leading to our main conclusion regarding the Moscow heat wave – plus allowing you to play with the idealised U-shaped climate discussed above. The code takes a climate curve of 129 data points – either half a sinusoidal curve or the smoothed July temperature in Moscow 1881-2009 as used in our paper – and adds random white noise. It then counts the number of records in the last ten points of the series (i.e. in the last decade of the Moscow data). It does that 100,000 times to get the average number of records (i.e the expected number). For the Moscow series, this code reproduces the calculations of our recent PNAS paper. In a hundred tries we find on average 41 heat records in the final decade, while in a stationary climate it would just be 8. Thus, the observed gradual climatic change has increased the expected number of records about 5-fold. This is just like using a loaded dice that rolls five times as many sixes as an unbiased dice. If you roll one six, there is then an 80% chance that it occurred because the dice is loaded, while there is a 20% chance that this six would have occurred anyway.
To run this code for the Moscow case, first download the file moscow_smooth.dat here.
----------------------
load moscow_smooth.dat
sernumber = 100000;
trendline = (moscow_smooth(:,2))/1.55; % trendline normalised by std dev of variability
%trendline = -sin([0:128]'/128*pi); % an alternative, U-shaped trendline with zero trend
excount=0; % initialise extreme counter
for i=1:sernumber % loop through individual realisations of Monte Carlo series
t = trendline + randn(129,1); % make a Monte Carlo series of trendline + noise
tmax=-99;
for j = 1:129
if t(j) > tmax; tmax=t(j); if j >= 120; excount=excount+1; end; end % count records
end
end
expected_records = excount/sernumber % expected number of records in last decade
probability_due_to_trend = 100*(expected_records-0.079)/expected_records
----------------------
Reference
Mudelsee M (2010) Climate Time Series Analysis. Springer, 474 pp.
“Given that it coincides with the bulk of global warming (three quarters of which occurred from 1980 onwards) and is also predicted by models in response to rising greenhouse gases, this post-1980 warming in Russia is, in our view, very unlikely just due to natural variability.”
Using this simply time-series analysis…is it not possible to pepper PNAS with reams of analyses that describe “very unlikely just due to natural variability” conditions because of what has occurred primarily since 1980? What if there was a spot on Earth that may have stayed flat (or even cooled) since 1980? Would these, using similar analysis, when published, mean anything?
I appreciate the way all this is explained, and it makes a lot of sense. However, I have a comment about this part:
“This is just like using a loaded dice that rolls five times as many sixes as an unbiased dice. If you roll one six, there is then an 80% chance that it occurred because the dice is loaded, while there is a 20% chance that this six would have occurred anyway.”
I don’t think it makes sense to talk about an individual event having x% chance of occurring with the bias or trend, and y% without. Probabilities can really only be about sets of data, not individual data points. It makes sense to say that we have, for example, 50% more warm records in the last two decades than the previous two decades, or that we can expect warm records to increase by 10% per decade on average, but not that any particular event has 80% chance of being due to global warming – that’s meaningless.
It’s OK to make a general statement about the consequences of the warming trend, like “events of this magnitude are now 80% more likely to occur in any given decade”, but it’s not OK to say “this particular event was 80% likely to have been due to the warming trend”. The real world just doesn’t work that way.
I hope this makes some kind of sense to everyone.
[Response: I don’t agree. You have two possibilities: the climate is either roughly stationary (constant mean and variance over time), or it is not. Similarly, your die/coin/whatever is either fair (equal probs of all possible outcome), or it is not. The analysis allows you to determine the relative likelihoods of the two possibilities. Very straight forward.–Jim]
Thank you for the code. I’m a SAS programmer, and at my age, the thought of learning a new language is unappealing, so I translated this to SAS (below).
My point in this posting is to follow up on my comments at the end of the Moscow warming thread.
You have made it clear that you are looking at warming from all causes. My issue is that this is being widely interpreted as showing the effect of global warming (loosely defined), while the actual observed warming in this region may have other significant components. My main concern was AMO, under the assumption that the AMO might account for a significant fraction of the recent temperature trend observed in Moscow.
I wanted a simple sensitivity analysis: What would the results have looked like if we had merely experienced the temperature trend of the 1930s again. Obviously this is crude, yet I think it has some natural appeal for determining how different the present situation (reflecting global warming) is from the past. Obviously, the actual observed 1930s data is a poor proxy for the AMO signal, so I’ll also test for a peak that’s half-a-degree below the 1930’s peak.
In short, I’ll compare the data as presented, a peak matched to the 1930s (trend ends at 0.5C below then 2009 value), and a further test case (trend ends at 1C below the 2009 value).
The results are 81% (replicating your main result), 72% (replaying the 1930s peak) and 54% (for 0.5C below the 1930s peak).
My conclusion is that any temperature trend for this geographic region that looked similar to the 1930s — here, plus or minus half a degree C — would generate a substantially increased likelihood of new high temperature records. In particular, if there is a strong cyclical component due to AMO (impossible to determine empirically, but useful at least as a straw man), then it is proper to attribute the increased odds to warming, but possibly not proper to attribute them to global warming.
SAS code follows. Vastly wordier than Matlab, but this is not was SAS was designed to do.
* In SAS, comments are set off by asterisks, every command must end with a semicolon ;
* DATA is the file you are creating, SET or CARDS is what you are reading from ;
* Read the columns of data, output as one record with 129 temperature observations in moscow_smooth_1 to moscow_smooth_129 ;
data temp ; input year temperature ; cards ; * your dataset went here ; run ;
data temp ; set temp ; counter = year – 1880 ; * for use in transpose step ; run ;
proc transpose data = temp out = temp1 prefix = moscow_smooth_ ; var temperature ; run ;
* Run the analysis ;
data temp2 ; set temp1 ;
array moscow_smooth (*) moscow_smooth_1 – moscow_smooth_129 ;
* to mimic a replay of the 1930s warmth, deflate the series so that the 2009 values matches the 1930s peak ;
* Let A be a factor to be used to test even lower peaks ;
A = 0 ;
array moscow_adjusted (*) moscow_adjusted_1 – moscow_adjusted_129 ;
adjuster = 1 – ((moscow_smooth(57)-A)/moscow_smooth(129)) ;
* = 1 – 19.04/19.54 for the base case, the factor to deflate the 2009 trend down match the 1930s peak ;
do j = 1 to 129 ;
moscow_adjusted(j) = moscow_smooth(j) ; * fill the cells with the originals, then deflate them ;
if (57 <= j tmax then do ;
tmax=t ;
if j >= 120 then excount=excount+1;
end ;
end ;
expected_records = excount/i ;
end ;
probability_due_to_trend = 100*(expected_records-0.079)/expected_records ;
put probability_due_to_trend ; * write it to the log file ;
* *********************************modified so that 2009 trend value matches 1930s peak ;
excount2 = 0 ;
do i = 1 to 100000;
tmax = -99 ;
do j = 1 to 129 ;
t = moscow_adjusted(j) + rannor(-1) ; * trend plus normal variate mean zero variance 1, -1 tells SAS to read the clock for the seed value ;
*put moscow_smooth(j) t ;
if t > tmax then do ;
tmax=t ;
if j >= 120 then excount2=excount2+1;
end ;
end ;
expected_records2 = excount2/i ;
end ;
probability_due_to_trend2 = 100*(expected_records2-0.079)/expected_records2 ;
put probability_due_to_trend2 ; * write it to the log file ;
run ;
Oddly, something about the process of posting garbled the lines in the SAS code above. What’s posted is gibberish (e.g., there are unclosed parentheses, logic aside it would not run as written). I won’t bother to try to post the correct code unless somebody else wants to work with it. The results as stated are correct, the SAS code is garbled.
I’m agitated that this group, for whom I have the greatest respect, have not mentioned, even in passing that the debate is over. It’s been over for a hundred years.
1. CO2 was discovered 150 years ago.
2. It’s properties -it inhibits passage of electro-magnetic-radiation in the ‘heat’ range- were discovered 100 years ago.
3. The buildup of CO2 in the atmosphere was discovered 50 years ago.
There’s nothing to discuss! This interminable debate of the ‘hair on the flea on the dog’ may be considered PC but it certainly is not as important as reporters and some contributors make it out to be.
An important question is this: How do you feed a million people whose homeland has been inundated?
This massive aggregation of brain-power could absolutely be put to better use.
the link to the NOAA website should be:
http://www.esrl.noaa.gov/psd/csi/events/2010/russianheatwave/
Re: #3 (Christopher Hogan)
That’s quite an assumption. I see no more evidence that AMO is responsible for warming than that Leprechauns are.
I suggest you take that up with those who are making that interpretation.
Thanks for an interesting article. Your paper isn’t one I’ve come across before, I’ll read it properly tomorrow on the bus – so apologies if any of the following is actually explained by the paper, on an initial perusal it doesn’t seem so.
As far as the above article goes: The extreme rise in ratio at the end of the series in both figures 3 & 4 initially reminded me of research I’ll get onto below. However as I don’t think we can say with confidence what the trend would be in the real world I’m not sure about the utility of this in terms of whether or not we are seeing a strong increase of natural disasters in our climate. It seems to me that the primary cause of the massive increase in ratio at the end of the series is due to the decreasing probability of new records as the stationary series gets longer.
On a related matter I’ve been discussing on the recent open thread (if people have nothing to add on this matter here I’ll let it drop – this issue isn’t in the field I’m most interested in):
Over at Tamino’s ‘Open Mind’ blog there was a discussion about extreme weather events using . I commented about some research from EMDAT about trends in European floods, “Three decades of floods in Europe : a preliminary analysis of EMDAT data.” PDF here.
Figure 1 of the EMDAT report shows an exponetial rise in floods from 1973 to 2002. This is against a background in the EMDAT database of a rise in reported flood and storm disasters that is over and above the trends in reported non-hydrometeorological disasters, ref – note in particular the difference between wet and dry earth movements. This would at face value appear to suggest an increase in hydrometeorological disasters and the most plausible explanation for that would be the intensification of the hydrological cycle due to AGW. However figure 2 of the EMDAT report shows that a change in reporting sources from 1998 accounts for much of the recent rise in reported disasters.
The question I’ve not been able to work out is whether the change in reporting wholly explains the recent increase in floods, or whether there is indeed an underlying increase in floods. If changes in technology (e.g. internet) and reporting ‘fashions’ wholly accounts for this increase then at some stage it should saturate. By that I mean that the press can only report what is happening, if they report an increasing percentage of events then at some stage they’ll near 100% coverage, at which point if the series is stationary the increasing trend will not sustain and will level out.
I suspect that whilst reporting bias and increasing urbanisation (e.g. building on flood plains) accounts for some of the post 1980 increase, I also suspect there is an underlying element due to the intensified hydrological cycle. If anyone can clarify this, or point to research that does I’d be grateful.
Blue7053,
I agree that the debate as to the reality and ongoing nature of AGW is over. However the debate as to it’s progression in terms of impacts (the most important metric for humanity) is not over.
Christopher, you shouldn’t overestimate the role of AMO. I don’t know if you have bought into the mistaken belief that the ‘S-shape’ of the 20th century temperature curve is largely caused by the AMO — it is not. The peak-to-peak of the AMO in global temperatures is no more than some 0.1C (e.g., Knight et al. 2005). Compare this to a total temperature increase over the 20th century (from Rahmstorf & Coumou) of 0.7C, with an interannual variability of +/-0.09C.
[Response: Indeed. This is a key finding of Knight et al (2005) (of which I was a co-author) as well as Delworth and Mann (2000) [the origin of the term ‘Atlantic Multidecadal Oscillation’ (AMO) which I coined in a 2000 interview about Delworth and Mann w/ Dick Kerr of Science]. The AMO, defined as a 40-60 year timescale oscillation originating in coupled North Atlantic ocean-atmosphere processes, is almost certainly real. It is unfortunate however that a variety of phenomena related simply to the non-linear forced history of Northern Hemisphere temperature variations have been misattributed (see e.g. Mann and Emanuel Eos 2006) to the “AMO”. In this sense, I fear I helped create a monster. I talk about this in my up-coming book, The Hockey Stick and The Climate Wars. –Mike]
It gets worse looking at Moscow: there, while both the total temperature increase and (perhaps) the impact of AMO are about double that of the global case, the interannual variability is a whopping +/-1.7C. Any AMO effect would find it hard to stand out against this background.
About your code: Perhaps put it on a web site and give a link to it in a comment here.
I tested Stefan’s code in octave and it works. Octave is free and easily installed even on Windows ;-)
Icarus62, Your interpretation of probability is one possible interpretation (namely, the frequentist), but it is not one that is universally accepted. And what would you say about a probability in quantum mechanics, where the probability of a measurement is well defined in terms of the wave function?
Generally, however, in my experience, even Frequentists have no trouble assigning probability to a single event.
Re: #8 (Chris R)
I looked at the EM-DAT data some time ago. There are obvious, and very strong, effects due to changes in both the likelihood of reporting and the way that effects (e.g. estimated number of fatalities) are estimated. These seem to be extreme for the older data, but likely continue even to more modern times. I concluded, as you suggest, that it’s very difficult to disentangle observational effects from physical changes. So I fear that those data, at least, aren’t sufficient to answer your questions. And that’s a real pity.
5blue7053 says:
6 Nov 2011 at 1:01 PM
“I’m agitated that this group, for whom I have the greatest respect, have not mentioned, even in passing that the debate is over. It’s been over for a hundred years.”
If one is unwilling to re-examine one’s assumptions, analysis, and conclusions, learning and discovery stops. Regardless of what the preponderance of the evidence says, the debate is NOT over, because there is always more to learn, deeper understandings and insights to gain, and the occasional surprise. Have the confidence in your thinking to be willing to question it – always and forever.
RE:3
Hey Christopher,
As you are solving for the observation in 2009/10 you probably should not use those values in the analysis.
Next, (as you are likely comfortable with current statistical methods, this may not apply to you), basically in statistics, no outlier should be greater then 100% of the range of the population in a normalized distribution. (If we incorporate the 2009/10 anomalies we should re-calculate the median of the population.) In order to determine the probability that a value could be part of a population is whether it is contained in the data set defined by its maximum range. (This is very different from trying to determine the probability that a value is possibly the median of the population.)
The value above the rolling median in this case, is the maximum temperature above the changing mid-range value or is the “extreme value”. By removing the changing mid-range (normalizing the data as though it represented a stationary climate) and simply plotting the maximum values, it still describes a parabola. The tilted form of the resulting parabola, where the fixed point can be the median and the resulting tilt of the “fixed line”, describes the change from a stationary climate.
Cheers!
Dave Cooke
(Note: In this case, we likely could describe 2 parabolas, if we could extend the data set back another 70 years, with a regional equivalent site/proxy, it may reveal some useful information as to weather pattern oscillations…)
Are we seeing a second effect also perhaps. Posulate that instead of just the average trending upwards, that the standard deviation is increasing as well. Then the effect would be even more pronounced. In fact if you had a flat average, but the standard deviation went up, you’d still get a lot of records. So do we have data on whether the standard deviation, which represents some sort of weather variability measure is changing?
Stefan — I thought this quite a good and clar exercise. But I now, on physical grounds, wish to doubt the white noise assumption. Obviously one could rerun the exerise for 1/f^a noise, pink noise, for various values of a between 0 and 2. Rather than doing so I’ll simply ask if that changes much.
Thomas – that’s not right. A larger standard deviation leads to less record-breaking. It’s one of the main findings of the Rahmstorf and Coumou paper (building on earlier work in this regard). That’s why the Moscow July temp series sees less record-breaking warm events, than the GISS global temp series. Moscow in July warms at 1.8°C over the 100 year period, but the year-to-year variability is 1.7°C. GISS on the other hand, has 0.7°C over 100 yrs, but an interannual variability of only 0.088°C.
The same deal applies to the MSU satellite vs surface temperature datasets. The satellites have larger interannual variability than the ground-based network and therefore a smaller probability of record-breaking. This is explained in the paper, which is freely available here.
Re: #16 (Rob Painting)
I don’t think Thomas was referring to a larger standard deviation series having more records than a smaller one (as was addressed in Rahmstorf & Coumou), but to an increase in standard deviation within a single series leading to more records.
Geno “more to learn, deeper understandings and insights to gain, and the occasional surprise” has no relevance to the central debate being over, any more than it does to evolution science, where exactly the same phrase could be used.
Did anyone thought yet about applying memristive functions, to model nonlinearity behavior?
5 blue7053: “How do you feed a million people whose homeland has been inundated?”
You don’t. They die. The difficult part may be realizing what is possible and what is not possible. Do what you can and don’t try to do what you can’t. The action to take is to stop the Global Warming. You could also try to stop the growth of population.
The point of continuing to tell people what has already been discovered is that the people have not become convinced enough to act on GW yet. The sooner we act, the more people will be saved. The later we act, the fewer people will be saved. Scientists cannot dictate policy.
Justice is a human invention found nowhere in Nature. There will be no justice. Excessive altruism will lead you into more of what you don’t want.
Climate change is not an isolated event, as many come to recognise there are cyclical changes, occasionally the phasing is such (with relevant delays) that is likely to produce a cumulative extreme. One of the rare occasions happened in the late 1690s-early 1700s. If the current decadal period is one, time will tell.
Here:
http://www.vukcevic.talktalk.net/CET-NV.htm
I have made an attempt (again time will tell if successful) to capture some of those oscillations related to the North Atlantic, the home of the AMO, which according to the BEST team is of the global importance:
We find that the strongest cross-correlation of the decadal fluctuations in (global) land surface temperature is not with ENSO but with the AMO.
http://berkeleyearth.org/Resources/Berkeley_Earth_Decadal_Variations (pages 4&5).
Something to watch:
http://capitalclimate.blogspot.com/2011/11/indirect-effects-arctic-ice-loss-has.html
Will circumstances render the math unnecessary?
To Tamino,comment 7. I don’t have a model that decomposes the local temperature change into a global warming (broadly defined) and other. But neither does anybody here. So ignore my ham-handed exercise in trying to parse out the marginal effects of global warming. There’s still an issue here.
Nobody can take serious issue with the arithmetic. The observed warming at that location creates substantially higher odds of a new record. Some of the statistically-oriented comments above have noted, maybe that could have been done better, but I think that’s unlikely to be empirically important.
What’s a little sketchy is that the writeup is of two minds about causality. Formally, it clearly states that it’s not attribution, and ignores the outlier 2010 year when calculating trend. Informally, it’s a tease. Look at the last sentence in “It ain’t attribution” paragraph. I paraphrase: It ain’t attribution (but we all know it’s global warming). Alternatively (but what else could it be). Or compare the temperature trend graph in the prior posting to the data actually used. The graph boosts the 2009 value about 1C relative to the data. That the graph and data differed was noted in the text, yet I’ve never before seen that sort of visual exaggeration used on Realclimate.
So here’s my technical question. Why? Why do you have to tease about the causality here, rather than test it in some formal way? Was it just a time constraint, or is there some fundamental barrier to doing more than just hint as to cause?
I can think of any number of naive things to do, other than comparing the current trend to prior peak as I did above.
So here’s one. Why not take the median temperature prediction from an ensemble of GCMs for this area, with and without GHG forcing, monte carlo with the actual observed distribution of residuals, and attribute the marginal increase in likelihood under the GHG scenario to the impact of GHGs on temperature records. Is that too much like the Dole analysis? Are the models insufficiently fine-grained to allow this? Do they do such a poor job at local temperature prediction? I’m not suggesting the burden of developing the distribution of temperatures via iterated runs of the ensembles, just taking (what I hope would be) canned results and hybridizing them with the current method to parse out to which GHG-driven warming has raised the odds of a new high temperature.
To me, as this stands, the writeup is unsatisfying. You have unassailable arithmetic that, by itself, strictly interpreted, has little policy content. Then you have not-quite-attribution material wrapped around that – clearly distinguished from the formal analysis. I’m just wondering if there was some fundamental barrier to combining the two, or whether there is no formal (yet easily implemented) way to put the policy context on some firmer ground.
[Response: Our goal with this paper was to understand better how the number of extremes (both record-breaking and fixed-threshold extremes) changes when the climate changes. We derived analytical solutions and did Monte Carlo simulations; our goal was not to create any “policy content”. To give the abstract solutions we found some real-life meaning, we did not confine it to the 100-point synthetic data series we originally worked with but added two simple examples, one of them was the Moscow data. This got much bigger than expected since during the review process the Dole et al. paper came out, and the reviewers asked us to elaborate on the Moscow data – that is how this became a much larger aspect of the paper than originally intended. Our goal was not to revisit the question of what causes global warming. There is plenty of scientific literature on that. -stefan]
Vukcevic,
Could you expand on the North Atlantic precursor in your graph. Is it related to the NAO, AMO, or some other factor?
I have a question on language and testing and language. If say we have a loaded dice that will roll a 6, 5 out of 6 times, then it seems if a 6 were to be rolled we can say the 6 had the probability of (5-1)/5 = 80% being a result of the loading. Is there a better term than do to loading the dice? If we role a 2 it was less likely on the loaded dice, and I’m hopeing for some better language to explain this to people that don’t understand statistics.
On the substance of the paper there is modeling of the variability of the temperatures and trend line. It seems fairly straight forward to test this model on a fairly large number of data points. The last decade was fairly hot. Has this been tested on a number of regions with historical data and verified to be a good predictive model of records?
thanks
[Response: Sure, we’ve tested this globally on over 150,000 time series, but that paper is still in review. -stefan]
24 Dan H. says:
7 Nov 2011 at 10:21 AM
Vukcevic,
Could you expand on the North Atlantic precursor in your graph. Is it related to the NAO, AMO, or some other factor?
I would qualify it the other way around:
The NAO, and some years later AMO, are related to North Atlantic Precursor.
See the last graph in:
http://www.vukcevic.talktalk.net/NAOn.htm
but it is related to the SSN as you can see here:
http://www.vukcevic.talktalk.net/CET-NV.htm
this is a relationship that current science may have a bit of a problem verifying, data is there, but mechanism is not so clear cut as the graph may suggest.
Getting a record ratio curve like that just because you made the climate U-shaped is astounding. It is so counter-intuitive that I predict a lot of people won’t believe it. What happens if you invert the U? Same as the half U?
[Response: Easy enough to try – that is why we provided the code, so our readers can play… -stefan]
Thanks, an excellent post that knocked some rust off of my stats and probability, and answered some questions in my mind about this kind of study.
I’ve been thinking for a while that it isn’t any single unusual event that will create the most serious kinds of problems, it is the risk that more than one event happens in the same year. As unusual events become less unusual, that risk goes up. It was convenient that the US farmers had a good year at the same time the Russian farmers had a bad one, and still, one could conjecture that the Arab Spring was sparked by high food prices resulting from Russia not exporting any wheat to that region that year. Probably that fire was already prepared, but it might have needed a spark.
Which leads me to comments #5 and #20. If the 100 million are isolated by geography, they die, but if they are not, then they inundate whatever nearby areas there are. Then, depending on political and economic conditions of those regions, they either die, are fed, or trigger social upheaval that could potentially result in more deaths than if they had been isolated. I believe all scenarios (with smaller numbers) have played out in history, but it is damnably hard to predict because so much depends on the decisions of those in power at the time. Not that those in power can be blamed always; there are no-win scenarios.
Unless Moscow was chosen a priori the analysis is highly suspect. Run a Monte Carlo simulation of 100 cities and a posteriori pick the city with the largest record and I’m sure you could get a similar result just due to randomness.
[Response: I think you may not quite understand our analysis. All the Monte Carlo simulations tell us is that with the given (nonlinear) climate trend, the chances of hitting a new record are five times larger than without the climate trend. This conclusion would remain true even if there had not been a record in Moscow in the last decade. Our analysis finds that the chances of a record in the last decade were 41%. It might as well have not occurred. But it is five times as large as the 8% that you would expect in an unchanging climate.
Think of the loaded dice (by the way, do you native speakers now call the singular a die or a dice??): a large number of tries might show you that your loaded dice rolls twice as many sixes as a regular dice. This information would remain true whether you have just rolled a six or not. But IF you have just rolled a six, you can say there is a 50% chance that this would not have happened with a regular dice. That is just another way of saying that a regular dice on average would only produce half as many sixes. -stefan]
(by the way, do you native speakers now call the singular a die or a dice??)
Die-hards (pun intented) still use die as the singular noun for that little cube with spots on it, and this is still considered correct as listed in all the main dictionaries I believe.
However, the Oxford dictionaries (online at least), and possibly others, now list dice as “a small cube with each side having a different number of spots on it”; i.e. use in the singular is approved usage. And under die usage they note “In modern standard English, the singular die (rather than dice) is uncommon. Dice is used for both the singular and the plural”.
Oxford dictionaries have made this change to common usage at some time since 1994 (which is the date of my edition of the SOED in which “die” is the only singular version given). Time for me to update my SOED!
So, both versions are now considered correct, and so confusion and arguments will no doubt reign.
Stefan, some of us still use the singular forms “die”, “datum”, and “phenomenon”, but we appear to be in danget of extinction.
“. . . by the way, do you native speakers now call the singular a die or a dice??”
“Die” is correct, though I think this is something people often get wrong.
re: die/dice, see Ambrose Bierce’s Devil’s Dictionary. :-)
> …but that paper is still in review. -stefan
And you haven’t even held the press conference yet? You’re falling behind the times. :-)
@ Edward Greisch 7 Nov 2011 at 11:47 PM re inverting the curve
Mathematics says that probability of high temperatures with a convex upward curve is the same as the probabilities of record LOWS, with a concave up curve. If you plotted high and low probabilities on the same graph, it (probably &;>) would look like this.
Yes: die is old-school singular. But then I also remember when “inflammable” meant “burns easily”, non-flammable meant it wouldn’t, and you couldn’t find “flammable” in the dictionary.
So (to get back on topic, sort of…) a heat wave and very dry vegetation would create highly-inflammable conditions…
[Response: Good example. The use of “inflammable” has caused me problems more than once in reading the old fire literature…how exactly was this forest “inflammable” if it just went up in smoke?? :) Jim]
“…do you native speakers now call the singular a die or a dice?”
It depends on the audience. My friends in academia prefer “data are”; those in industry, “data is”. “Indexes” is a verb (seldom used) and “indices” is a noun to the academics, but “indices” is sometimes not received well by customers in industry, etc. To some it merely sounds correct, to others, it sounds pretentious. To me, it is just simpler to think of datum/die as singular and data/dice as plural, but then, I am feeling somewhat like a dinosaur. (#31 ;-) )
It is the nature of knowledge that it is never completely certain, because the contents of our mind is limited by our human abilities to perceive, analyze, and conceive. To make statements like “the debate is over” with reference to scientific discussions is to betray a fundamental lack of understanding regarding epistemology. David Horton is simply demonstrating this lack of understanding, as did 5blue7053 before him. To refuse to debate is to tread into the realm of dogma, not science.
Re: #39 (Geno Canto del Halcon)
To make statements like “the debate is not over” with reference to some scientific topics — say, the health risk of smoking for example — is not an exercise in epistomological purity. It’s a despicable, and rather pathetic, excuse to deny reality, usually for the most loathesome of motives.
It’s also recorded history. Concerning global warming, we are watching history repeat itself.
Please spare us your haughty appeal to philosophical uncertainty.
re: “the debate is over”:
Some debates are over. (There’s no such thing as phlogiston; the Earth orbits the Sun; CO2 is a greenhouse gas; it’s increasing; the increase comes from human activities.)
Some aren’t. This post, for instance, is related to a current debate among reasonable people over whether a particular heat wave could have been anticipated based on past trends. That question, in turn, is related to the no less debated question how particular events can be ascribed to man-made global warming.
I hereby declare the debate over the debate being over, over.
Geno Canto del Halcon wrote: “To make statements like ‘the debate is over’ with reference to scientific discussions is to betray a fundamental lack of understanding regarding epistemology.”
To make statements like “Regardless of what the preponderance of the evidence says, the debate is NOT over” (your words in comment #12) without stating specifically what particular “debate” or what particular “scientific discussion” you are talking about, is vacuous.
Yes “die” is the singular. It is forgotten because dice nearly occur in pairs. Other singulars are “addendum”, “agendum” and “stadium”. The word “cattle” is notable for not having a singular. We have words for a single male or female of the species but if you see one some way off and can’t tell the gender we don’t have a word for it.
Stefan, you have doubtless noted that aridity is spreading (see the papers of Dai for instance.) And where it is not arid there are more floods, and where neither of the above is happening precipitation is still more concentrated in fewer stronger events. As these all seem to be ongoing trends, agriculture is going to have a large problem in the future. If drought and floods keep increasing then by 2030 say, if there is a “good year” for both drought and flooding at the same time, there may be a very large famine. How would you compute the cumulative risk of this? [for perhaps a 1 million person starves famine, 10 million and 100 million, for 2030, 2040, 2050 …]
This is the information humanity needs. Has it been published? Are you working on it?
Geno Canto del Halcon, look at it this way: scientists are constantly striving for a deeper understanding of gravity. However, new discoveries in this area are not going to make satellites fall out of the sky, nor will Newtonian calculations be any less successful when calculating how to launch a rocket to Mars. Likewise new discoveries in atmospheric physics will not make all the usual processes of energy exchange stop happening.
Climate science the working out of standard physics and chemistry on a planetary scale. A planet as a whole can gain or lose energy in very few ways. On a planet like ours a big portion of the daily energy loss (to compensate for the energy gain from our star) takes the form of longwave infrared radiation. Certain gases intercept and re-radiate this radiation through the atmosphere. The energy is finally lost to space from the cold thin upper atmosphere. The whole process is mediate by certain gases and is called the greenhouse effect. This is not going to change, just as satellites are not going to fall out of the sky on account of new discoveries. But scientists hardly consider all questions answered. Why do you suppose they keep on doing research?
In the area of climate change we have not only an interesting application of physics, we also have a very large slowly developing human problem. There is something obvious we can do to keep the problem from getting too large and harmful. We can change the way we get usable energy. The reason this change is delayed is so that the current top energy companies can continue to accumulate large sums of money. Please don’t help them.
Pete Dunkelberg @43 — … precipitation is still more concentrated in fewer stronger events. I’ve certaqinly seen this expressed several times but have not read a definitive study.
Pete:
It’s taken a long, long time but English, in recent decades, has finally decided it’s not Latin after all … and that we’re free to throw the shackles and have the language that we want. :)
And as has been pointed out above, “dice” as the singular is accepted by linguistic authorities (such as the Oxford Dictionary).
If people think that English must be a dead language, then surely they reject words like “internet”, and all that follows?
Geno Canto del Halcon,
I look forward to your bibliography of recent papers on the luminiferous aether.
#47–Not even trying to resist the OTness of this linguistic stuff. . .
“how exactly was this forest “inflammable” if it just went up in smoke??”
Well, it presumably went up “in flame” too–and I think “inflammable” was originally meant to convey “capable of becoming inflamed.” Which now sounds exclusively medical–but I think it was not always thus.
One question; Does the above data simulation for heat records hold true when looking only at the minimum values (regarding winter records in the the same manner).
[Response: If you’re asking if the same type of analysis could be applied to records, regardless of which end of the scale they’re on, the answer is yes.–Jim]
Stafan, thanks for the reply, I look forward to seeing the statistics . I side with the evolving English part of the debate and prefer the term loaded dice, but die is certainly acceptable ;-)
From a thought experiment point of view, variation will give similar results as directional change. Is this correct as long as the variation is similar to your curve and is bigger than the directional change. Jumping back to the real world, and the paper, it seems that the trend line includes both local climate change and low frequency climate variation. There definitely appears to be some climate variation in the 130 year trend line. Would it not be more proper to say that the dice is then loaded with both local climate change and climate variation, and the comparison model had no cyclical climate variations? This would make the event more likely due to climate change and variation, which seems easy to grasp. The interesting thing is not the direction but the probabilities.
Following up on the language part, say the January low in oklahoma this year had similar loaded dice against it. Would the probability be (1-5)/1 = -400% that the low was due to climate change? Or would it be better to say since it is a negative number climate change is unlikely to have had anything to do with causation of this record low?