My co-authors and I have just published an article in Nature Geoscience (advance online publication here; associated press release here) which seeks to explain certain enigmatic features of tree-ring reconstructions of Northern Hemisphere (NH) temperatures of the past millennium. Most notable is the virtual absence of cooling in the tree-ring reconstructions during what ice core and other evidence suggest is the most explosive volcanic eruption of the past millennium–the AD 1258 eruption. Other evidence suggests wide-spread global climate impacts of this eruption [see e.g. the review by Emile-Geay et al (2008)]. We argue that this–and other missing episodes of volcanic cooling, are likely an artifact of biological growth effects, which lead to a substantial underestimation of the largest volcanic cooling events in trees growing near treeline. We speculate that this underestimation may also have led to overly low estimates of climate sensitivity in some past studies attempting to constrain climate model sensitivity parameters with proxy-reconstructed temperature changes.
Tree rings are used as proxies for climate because trees create unique rings each year that often reflect the weather conditions that influenced the growing season that year. For reconstructing past temperatures, dendroclimatologists typically seek trees growing at the boreal or alpine treeline, since temperature is most likely to be the limiting climate variable in that environment. But this choice may also prove problematic under certain conditions. Because the trees at these locations are so close to the threshold for growth, if the temperature drops just a couple of degrees during the growing season, there will be little or no growth and therefore a loss of sensitivity to any further cooling. In extreme cases, there may be no growth ring at all. And if no ring was formed in a given year, that creates a further complication, introducing an error in the chronology established by counting rings back in time.
We compared simulated temperature of the past millennium derived by driving theoretical climate models with estimated natural (volcanic+solar) and anthropogenic forcings for the past millennium. We employed two different climate model simulations: (1) the simulation of the NCAR CSM 1.4 coupled atmosphere-ocean General Circulation Model (GCM) analyzed by Ammann et al (2007) and (2) simulations of a simple Energy Balance Model (EBM). While the GCM provides a more comprehensive and arguably realistic description of the climate system, the computational simplicity of the EBM lends itself to extensive sensitivity tests. As the target for our comparison, we used a state-of-the-art tree-ring based Northern Hemisphere (NH) mean temperature reconstruction of D’Arrigo et al (2006). The reconstruction was based on a composite of tree ring annual ring width series from boreal and alpine treeline sites across the northern hemisphere, and made use of a very conservative (“RCS”) tree-ring standardization procedure designed to preserve as much low-frequency climatic information as possible.
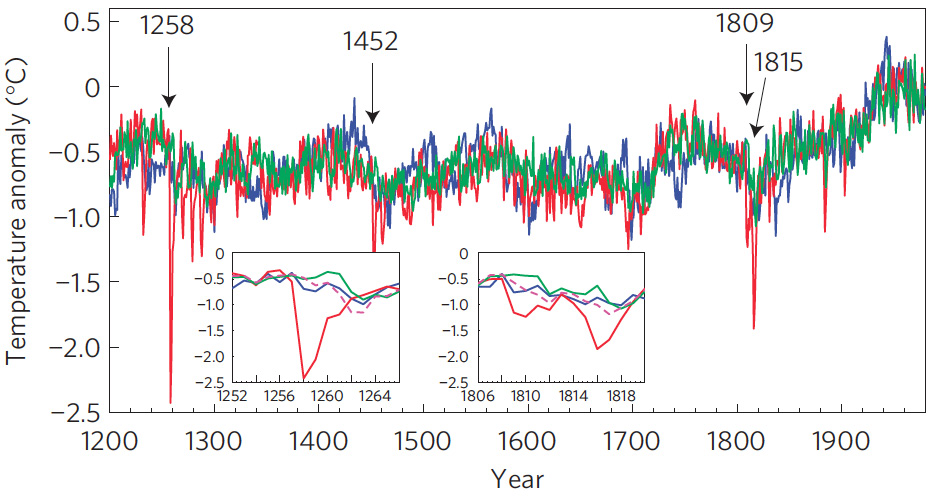
Interestingly, the long-term variations indicated by the model simulations compared remarkably well with those documented by the tree-ring reconstruction, showing no obvious sign of the potential biases in the estimated low-frequency temperature variations that have been the focus of much previous work (see e.g. this previous RealClimate review). Instead, the one glaring inconsistency was in the high-frequency variations, specifically, the cooling response to the largest few tropical eruptions, AD 1258/1259, 1452/1453 and the 1809+1815 double pulse of eruptions, which is sharpy reduced in the reconstruction relative to the model predictions. Indeed, this was found to be true for any of several different published volcanic forcing series for the past millennium, regardless of the precise geometric scaling used to estimate radiative forcing from volcanic optical depth, and regardless of the precise climate sensitivity assumed.
Following the AD 1258 eruption, the climate model simulations predict a drop of 2C, but the tree ring-based reconstruction shows only about a 0.5C cooling. Equally vexing, the cooling in the reconstruction occurs several years late relative to what is predicted by the model. The other large eruptions showed similar discrepancies. An analysis using synthetic proxy data with spatial sampling density and proxy signal-to-noise ratios equivalent to those of the D’Arrigo et al (2006) tree-ring network suggest that these discrepancies cannot be explained in terms of either the spatial sampling/extent or the intrinsic “noisiness” of the network of proxy records.
However, using a tree growth model that accounts for the temperature growth thresholding effects discussed above, combined with the complicating effects of chronological errors due to potential missing growth rings, explains the observed features remarkably well.
Show in the above figure (Figure 2d from the article) is the D’Arrigo et al tree-ring based NH reconstruction (blue) along with the climate model (NCAR CSM 1.4) simulated NH mean temperatures (red) and the “simulated tree-ring” NH temperature series based on driving the biological growth model with the climate model simulated temperatures (green). The two insets focus on the response to the AD 1258 and AD 1809+1815 volcanic eruption sequences. The attenuation of the response is produced primarily by the loss of sensitivity to further cooling for eruptions that place growing season temperatures close to the lower threshold for growth. The smearing and delay of the cooling, however, arises from another effect: when growing season lengths approach zero, we assume that no growth ring will be detectable for that year. That means that an age model error of 1 year will be introduced in the chronology counting back in time. As multiple large eruptions are encountered further back in time, these age model errors accumulate. This factor would lead to a precise chronological error, rather than smearing of the chronology, if all treeline sites experienced the same cooling. However, stochastic weather variations will lead to differing amounts of cooling for synoptically distinct regions. That means that in any given year, some regions might fall below the “no ring” threshold, while other regions do not. That means that different chronological errors accumulate in synoptically-distinct regions of the Northern Hemisphere. In forming a hemispheric composite, these errors thus lead to a smearing out of the signal back in time as slightly different age model errors accumulate in the different regions contributing to the composite.
Including this effect, our model accounts not only for the level of attenuation of the signal, but the delayed and smeared out cooling as well. This is particularly striking in comparing the behavior following both the AD 1258 and AD 1809 eruptions (compare the green and blue curves in the insets of the figure). Our model, for example, predicts the magnitude of the reduction of cooling following the eruptions and the delay in the apparent cooling evidence in the tree-ring record (i.e. in AD 1262 rather than AD 1258). We have also included a minor additional effect in these simulations. While volcanic aerosols cause surface cooling due to decreased shortwave radiation at the surface, they also lead to increased indirect, scattered light at the surface. Plant growth benefits from indirect sunlight, and past studies show that e.g. a Pinatubo-sized eruption (roughly -2W/m^2 radiative forcing) can result in a 30% increase in carbon assimilation by plants. This effect turns out to be relatively small because it is proportional in nature, and thus results in a very small absolute increase when growth is suppressed i the first place by limited growing seasons. However, not including this effect results in a slightly less good reproduction (purple dashed curves in the two insets of the figure) of the observed behavior.
As noted earlier, our main conclusions are insensitive to the precise details of the forcing estimates used, the volcanic scaling assumptions made, and the precise assumed climate sensitivity. They were also insensitive to the details of the biological tree growth model over a reasonable range of model assumptions. The conclusion that tree-ring temperature reconstructions might suffer from age model errors due to missing rings is bound to be controversial. A few points are worth making here. First of all, our conclusion is quite specific to temperature-sensitive trees at treeline, and it does not imply more general problems in the larger discipline of dendrochronology. Secondly, the conclusion at this stage simply a hypothesis, a hypothesis that can account for these key enigmatic features in the actual tree-ring hemisphere temperature reconstruction: the attenuation, and the increasing (back in time) delay and temporal smearing of the cooling response to past volcanic forcing. Were an equally successful and more parsimonious hypothesis to be provided for these observations, I would be the first to concede and defer to this alternative explanation.
One argument against the specific conclusion of missing growth rings is that trees are carefully cross-dated when forming regional chronologies, and this precludes the possibility of chronological errors. That, however, assumes that there are at least some trees within a particular region that will not suffer a missing ring during the years where our model predicts it. Yet our prediction is that all trees within a region of synoptic or lesser scale where growing season temperatures lie below the growth threshold will experience a missing ring. Thus, cross-dating within that region, regardless of how careful, cannot resolve the lost chronological information. It is my hope that dendroclimatologists will reassess raw chronologies more carefully and critically assess the extent to which the predicted features might indeed be present in the underlying tree-ring data. Again, this paper presents a hypothesis for explaining some enigmatic features of existing tree-ring temperature reconstructions. It is hardly the last word on the matter.
Finally it is worth discussing the potential wider implication of these findings. Climate scientists use the past response of the climate to natural factors like volcanoes to better understand how sensitive Earth’s climate might be to the human impact of increasing greenhouse gas concentrations, e.g. to estimate the equilibrium sensitivity of the climate to CO2 doubling i.e. the warming expected for an increase in radiative forcing equivalent to doubling of CO2 concentrations. Hegerl et al (2006) for example used comparisons during the pre-industrial of EBM simulations and proxy temperature reconstructions based entirely or partially on tree-ring data to estimate the equilibrium 2xCO2 climate sensitivity, arguing for a substantially lower 5%-95% range of 1.5–6.2C than found in several previous studies. The primary radiative forcing during the pre-industrial period, however, is that provided by volcanic forcing. Our findings therefore suggest that such studies, because of the underestimate of the response to volcanic forcing in the underlying data, may well have underestimated the true climate sensitivity.
It will be interesting to see if accounting for the potential biases identified in this study leads to an upward revision in the estimated sensitivity range. Our study, in this regard, once again only puts forward a hypothesis. It will be up to other researchers, in further work, to assess the validity and potential implications of this hypothesis.
From the paper:
Two naive questions:
1) How is the solar dependent factor analyzed? Wouldn’t g_E be dependent on cloud parameters?
2) Would a carbon-dioxide factor g_C(t) (derived perhaps from stomata studies) be a useful inclusion? Is it a factor in the ‘divergence’?
What is your estimate as to how much the “accounting” may have to be revised? Are we talking a few minor revisions of interest to experts in the field or significant revisions that affect public policy, risk management, planning, and engineering?
I’m wondering several things (And, Yes, I will read your Nature GeoSci Item, and no doubt find the answers – though you can still take this, from a RealClimate Fan Constructive Editorially Criticising This Item POV, as just that):
Where, exactly, where did the AD 1258 Eruptions Occur, and what other evidence is there for there apparent severity?
Could it be that the Eruptions in question occured during, say, a certain season – during, say, a Monsoon of great fierceness – that diverted a disproportionate amount of material onto the sampling sites?
Is there any evidence thatthese AD1258 Eruptions may have been, say, low in Sulfate Emissions – and, thus, low in generation of upper stratospheric aerosols?
Love.
Only tangentially related to this article but….
Do you know about, or can you refer me to someone who may know about, the climate effects of the other Tambora-scale volcanic eruption (VEI=7) of the last millenium — from Changbaishan (Baitoushan) on the China-NKorea border (42oN latitude) sometime between 960-1025 AD? The magma had an unusual chemical composition (=comendite) and its eruption is calculated to have released 100 km3 of particulates into the stratosphere, ~1800 megatons of H2O, 45 megatons each of Cl and F, but only 2 megatons of S. Seems odd for something of this magnitude to have little climate consequence. I have studied aspects of this eruption for some years.
“42oN latitude”
That’s a key factor. Surely you can understand why.
comments?
[edit]
[Response:Sure. Don’t waste our time.–Jim]