Climate sensitivity is a perennial topic here, so the multiple new papers and discussions around the issue, each with different perspectives, are worth discussing. Since this can be a complicated topic, I’ll focus in this post on the credible work being published. There’ll be a second part from Karen Shell, and in a follow-on post I’ll comment on some of the recent games being played in and around the Wall Street Journal op-ed pages.
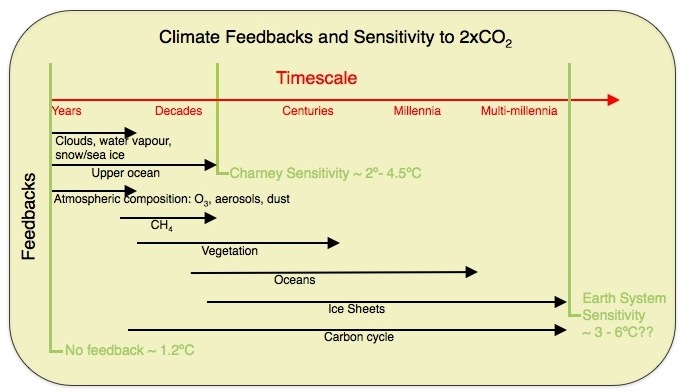
What is climate sensitivity? Nominally it the response of the climate to a doubling of CO2 (or to a ~4 W/m2 forcing), however, it should be clear that this is a function of time with feedbacks associated with different components acting on a whole range of timescales from seconds to multi-millennial to even longer. The following figure gives a sense of the different components (see Palaeosens (2012) for some extensions).
In practice, people often mean different things when they talk about sensitivity. For instance, the sensitivity only including the fast feedbacks (e.g. ignoring land ice and vegetation), or the sensitivity of a particular class of climate model (e.g. the ‘Charney sensitivity’), or the sensitivity of the whole system except the carbon cycle (the Earth System Sensitivity), or the transient sensitivity tied to a specific date or period of time (i.e. the Transient Climate Response (TCR) to 1% increasing CO2 after 70 years). As you might expect, these are all different and care needs to be taken to define terms before comparing things (there is a good discussion of the various definitions and their scope in the Palaeosens paper).
Each of these numbers is an ’emergent’ property of the climate system – i.e. something that is affected by many different processes and interactions, and isn’t simply derived just based on knowledge of a small-scale process. It is generally assumed that these are well-defined and single-valued properties of the system (and in current GCMs they clearly are), and while the paleo-climate record (for instance the glacial cycles) is supportive of this, it is not absolutely guaranteed.
There are three main methodologies that have been used in the literature to constrain sensitivity: The first is to focus on a time in the past when the climate was different and in quasi-equilibrium, and estimate the relationship between the relevant forcings and temperature response (paleo constraints). The second is to find a metric in the present day climate that we think is coupled to the sensitivity and for which we have some empirical data (these could be called climatological constraints). Finally, there are constraints based on changes in forcing and response over the recent past (transient constraints). There have been new papers taking each of these approaches in recent months.
All of these methods are philosophically equivalent. There is a ‘model’ which has a certain sensitivity to 2xCO2 (that is either explicitly set in the formulation or emergent), and observations to which it can be compared (in various experimental setups) and, if the data are relevant, models with different sensitivities can be judged more or less realistic (or explicitly fit to the data). This is true whether the model is a simple 1-D energy balance, an intermediate-complexity model or a fully coupled GCM – but note that there is always a model involved. This formulation highlights a couple of important issues – that the observational data doesn’t need to be direct (and the more complex the model, the wider range of possible constraints there are) and that the relationship between the observations and the sensitivity needs to be demonstrated (rather than simply assumed). The last point is important – while in a 1-D model there might be an easy relationship between the measured metric and climate sensitivity, that relationship might be much more complicated or non-existent in a GCM. This way of looking at things lends itself quite neatly into a Bayesian framework (as we shall see).
There are two recent papers on paleo constraints: the already mentioned PALAEOSENS (2012) paper which gives a good survey of existing estimates from paleo-climate and the hierarchy of different definitions of sensitivity. Their survey gives a range for the fast-feedback CS of 2.2-4.8ºC. Another new paper, taking a more explicitly Bayesian approach, from Hargreaves et al. suggests a mean 2.3°C and a 90% range of 0.5–4.0°C (with minor variations dependent on methodology). This can be compared to an earlier estimate from Köhler et al. (2010) who gave a range of 1.4-5.2ºC, with a mean value near 2.4ºC.
One reason why these estimates keep getting revised is that there is a continual updating of the observational analyses that are used – as new data are included, as non-climatic factors get corrected for, and models include more processes. For instance, Köhler et al used an estimate of the cooling at the Last Glacial Maximum of 5.8±1.4ºC, but a recent update from Annan and Hargreaves and used in the Hargreaves et al estimate is 4.0±0.8ºC which would translate into a lower CS value in the Köhler et al calculation (roughly 1.1 – 3.3ºC, with a most likely value near 2.0ºC). A paper last year by Schmittner et al estimated an even smaller cooling, and consequently lower sensitivity (around 2ºC on a level comparison), but the latest estimates are more credible. Note however, that these temperature estimates are strongly dependent on still unresolved issues with different proxies – particularly in the tropics – and may change again as further information comes in.
There was also a recent paper based on a climatological constraint from Fasullo and Trenberth (see Karen Shell’s commentary for more details). The basic idea is that across the CMIP3 models there was a strong correlation of mid-tropospheric humidity variations with the model sensitivity, and combined with observations of the real world variations, this gives a way to suggest which models are most realistic, and by extension, what sensitivities are more likely. This paper suggests that models with sensitivity around 4ºC did the best, though they didn’t give a formal estimation of the range of uncertainty.
And then there are the recent papers examining the transient constraint. The most thorough is Aldrin et al (2012). The transient constraint has been looked at before of course, but efforts have been severely hampered by the uncertainty associated with historical forcings – particularly aerosols, though other terms are also important (see here for an older discussion of this). Aldrin et al produce a number of (explicitly Bayesian) estimates, their ‘main’ one with a range of 1.2ºC to 3.5ºC (mean 2.0ºC) which assumes exactly zero indirect aerosol effects, and possibly a more realistic sensitivity test including a small Aerosol Indirect Effect of 1.2-4.8ºC (mean 2.5ºC). They also demonstrate that there are important dependencies on the ocean heat uptake estimates as well as to the aerosol forcings. One nice thing that added was an application of their methodology to three CMIP3 GCM results, showing that their estimates 3.1, 3.6 and 3.3ºC were reasonably close to the true model sensitivities of 2.7, 3.4 and 4.1ºC.
In each of these cases however, there are important caveats. First, the quality of the data is important: whether it is the LGM temperature estimates, recent aerosol forcing trends, or mid-tropospheric humidity – underestimates in the uncertainty of these data will definitely bias the CS estimate. Second, there are important conceptual issues to address – is the sensitivity to a negative forcing (at the LGM) the same as the sensitivity to positive forcings? (Not likely). Is the effective sensitivity visible over the last 100 years the same as the equilibrium sensitivity? (No). Is effective sensitivity a better constraint for the TCR? (Maybe). Some of the papers referenced above explicitly try to account for these questions (and the forward model Bayesian approach is well suited for this). However, since a number of these estimates use simplified climate models as their input (for obvious reasons), there remain questions about whether any specific model’s scope is adequate.
Ideally, one would want to do a study across all these constraints with models that were capable of running all the important experiments – the LGM, historical period, 1% increasing CO2 (to get the TCR), and 2xCO2 (for the model ECS) – and build a multiply constrained estimate taking into account internal variability, forcing uncertainties, and model scope. This will be possible with data from CMIP5, and so we can certainly look forward to more papers on this topic in the near future.
In the meantime, the ‘meta-uncertainty’ across the methods remains stubbornly high with support for both relatively low numbers around 2ºC and higher ones around 4ºC, so that is likely to remain the consensus range. It is worth adding though, that temperature trends over the next few decades are more likely to be correlated to the TCR, rather than the equilibrium sensitivity, so if one is interested in the near-term implications of this debate, the constraints on TCR are going to be more important.
References
- . , "Making sense of palaeoclimate sensitivity", Nature, vol. 491, pp. 683-691, 2012. http://dx.doi.org/10.1038/nature11574
- J.C. Hargreaves, J.D. Annan, M. Yoshimori, and A. Abe‐Ouchi, "Can the Last Glacial Maximum constrain climate sensitivity?", Geophysical Research Letters, vol. 39, 2012. http://dx.doi.org/10.1029/2012GL053872
- P. Köhler, R. Bintanja, H. Fischer, F. Joos, R. Knutti, G. Lohmann, and V. Masson-Delmotte, "What caused Earth's temperature variations during the last 800,000 years? Data-based evidence on radiative forcing and constraints on climate sensitivity", Quaternary Science Reviews, vol. 29, pp. 129-145, 2010. http://dx.doi.org/10.1016/j.quascirev.2009.09.026
- J.D. Annan, and J.C. Hargreaves, "A new global reconstruction of temperature changes at the Last Glacial Maximum", 2012. http://dx.doi.org/10.5194/cpd-8-5029-2012
- A. Schmittner, N.M. Urban, J.D. Shakun, N.M. Mahowald, P.U. Clark, P.J. Bartlein, A.C. Mix, and A. Rosell-Melé, "Climate Sensitivity Estimated from Temperature Reconstructions of the Last Glacial Maximum", Science, vol. 334, pp. 1385-1388, 2011. http://dx.doi.org/10.1126/science.1203513
- J.T. Fasullo, and K.E. Trenberth, "A Less Cloudy Future: The Role of Subtropical Subsidence in Climate Sensitivity", Science, vol. 338, pp. 792-794, 2012. http://dx.doi.org/10.1126/science.1227465
- M. Aldrin, M. Holden, P. Guttorp, R.B. Skeie, G. Myhre, and T.K. Berntsen, "Bayesian estimation of climate sensitivity based on a simple climate model fitted to observations of hemispheric temperatures and global ocean heat content", Environmetrics, vol. 23, pp. 253-271, 2012. http://dx.doi.org/10.1002/env.2140
Great overview, thanks. I think it is important to stress that with the current growth of fossil fuel emissions we are above the highest IPCC emissions scenario (RCP 8.5), at least for fossil fuel combustion. If this persists in the future we will be in the 3 degree range in 2100 even with the lowest CS estimates.
Gavin Schmidt, could you maybe have a look at a catastrophic “paper” by the economist Alan Carlin that got lost in the scientific literature? One of his reasons to claim that “the risk of catastrophic anthropogenic global warming appears to be so low that it is not currently worth doing anything to try to control it” is that he uses a very low value for the climate sensitivity based on non-reviewed “studies”, while ignoring the peer-reviewed work.
[Response: As pointed out by Hank in the comment below, we’ve already wasted enough of our neurons on Carlin. See here. –eric]
Very illuminating, thank you. I agree with Guido, and would add that it would be helpful to stress how critical constraining ECS is. It’s not necessarily obvious to the uninitiated what a huge effect this ~2ºC uncertainty in ECS estimates has on scenarios that attempt to predict the magnitude and timing of climate change impacts (e.g. the AR5 RCPs). Also I found some possible minor typos:
“strongly dependent [on?] still unresolved issues”
“has been looked at before of course, but [efforts?] have been severely hampered”
“are more likely to follow to be correlated to the TCR” [remove “to follow”?]
It also might be helpful to spell out Aerosol Indirect Effect.
[Response: thanks! – gavin]
Victor Venema links to his own blog above. RC’s link on Carlin:
https://www.realclimate.org/index.php/archives/2009/06/bubkes/
I think what really matters are the changes we can expect in the world in terms of livability, including the ability to grow adequate food. Using the change in temperature from the last glacial maximum as a ruler, if the change in temperature from that is near 6 Kelvin, then 2 K warmer than pre-industrial means a certain level of effects. If that change is only 4 K, then 2 K warmer means a higher level of change ecologically.
The 2 K limit generally accepted as a dangerous limit would mean something different if the change in temperature from the last GM is 6 K (approximately 1/3 change again) versus 4 K (approximately 1/2 change again). In other words, if climate sensitivity is toward the low end, 2 K is more dangerous than we currently give it credit for, and arguments for low risk because of low sensitivity are less valid because that means that more ecological changes occur for a given temperature change than currently thought.
Quite helpful Gavin. Well done.
A useful post.
Correct me if I am wrong, but this appears to be walking back the CS numbers a bit. ~3C seems to be heading towards ~2.5C. I am encouraged as I have been a somewhat vocal critic that when models have been over estimating the temps fairly consistently that it somehow wasn’t translating into lower CS estimates, or constraining the upper range. Many forcings were being twiddled to account for observations (namely aerosols), but the main CO2 forcing seemed to be the third rail.
[Response: Huh? Forcing is not the same as sensitivity. For reference, GISS-ModelE had a sensitivity of 2.7ºC, and GISS-E2 has sensitivity of 2.4ºC to 2.8ºC depending on version. All very mainstream. – gavin]
Thanks for this crucial science on sensitivity. A crucial subject for understanding. This leads to questions about micro-sensitivity. People are thinking about their individual impact to global warming. Generalities of carbon footprint try to package the message but fail. We might want to know the impact of specific actions.
Certainly operating a carbon fueled car has real consequences, although for any one vehicle they are very slight. A single cylinder emission is the lowest unit of micro-sensitivity. One person in a car might have a few million per day – or a pound of CO2 per mile traveled. It’s like pissing in a trout stream, one person may not do more harm than scare away the fish, but with millions along the shores all streaming away all day, pretty soon it is the yellow river of death.
Somewhere we need to measure cognitive sensitivity to human impacts of global warming. Perhaps the visual display would be like a car’s tachometer – it would measure ineffectual use of CO2. The micro-sensitivity meter would indicate how effectively carbon fuel is used to deploy clean energy. It would sit right on the dashboard.
Tom Scharf wrote: “models have been over estimating the temps fairly consistently”
That’s simply not true.
Contrary to Contrarian Claims, IPCC Temperature Projections Have Been Exceptionally Accurate
27 December 2012
SkepticalScience
This was just posted at SkSc:
“Time-varying climate sensitivity from regional feedbacks
Time-varying climate sensitivity from regional feedbacks – Armour et al. (2012) [FULL TEXT]
Abstract:”The sensitivity of global climate with respect to forcing is generally described in terms of the global climate feedback—the global radiative response per degree of global annual mean surface temperature change. While the global climate feedback is often assumed to be constant, its value—diagnosed from global climate models—shows substantial time-variation under transient warming. Here we propose that a reformulation of the global climate feedback in terms of its contributions from regional climate feedbacks provides a clear physical insight into this behavior. Using (i) a state-of-the-art global climate model and (ii) a low-order energy balance model, we show that the global climate feedback is fundamentally linked to the geographic pattern of regional climate feedbacks and the geographic pattern of surface warming at any given time. Time-variation of the global climate feedback arises naturally when the pattern of surface warming evolves, actuating regional feedbacks of different strengths. This result has substantial implications for our ability to constrain future climate changes from observations of past and present climate states. The regional climate feedbacks formulation reveals fundamental biases in a widely-used method for diagnosing climate sensitivity, feedbacks and radiative forcing—the regression of the global top-of-atmosphere radiation flux on global surface temperature. Further, it suggests a clear mechanism for the ‘efficacies’ of both ocean heat uptake and radiative forcing.”
Citation: Kyle C. Armour, Cecilia M. Bitz, Gerard H. Roe, Journal of Climate 2012, doi: http://dx.doi.org/10.1175/JCLI-D-12-00544.1.”
http://www.skepticalscience.com/new_research_52_2012.html
And this:
“Late Pleistocene tropical Pacific temperatures suggest higher climate sensitivity than currently thought
Late Pleistocene tropical Pacific temperature sensitivity to radiative greenhouse gas forcing – Dyez & Ravelo (2012)
Abstract: “Understanding how global temperature changes with increasing atmospheric greenhouse gas concentrations, or climate sensitivity, is of central importance to climate change research. Climate models provide sensitivity estimates that may not fully incorporate slow, long-term feedbacks such as those involving ice sheets and vegetation. Geological studies, on the other hand, can provide estimates that integrate long- and short-term climate feedbacks to radiative forcing. Because high latitudes are thought to be most sensitive to greenhouse gas forcing owing to, for example, ice-albedo feedbacks, we focus on the tropical Pacific Ocean to derive a minimum value for long-term climate sensitivity. Using Mg/Ca paleothermometry from the planktonic foraminifera Globigerinoides ruber from the past 500 k.y. at Ocean Drilling Program (ODP) Site 871 in the western Pacific warm pool, we estimate the tropical Pacific climate sensitivity parameter (λ) to be 0.94–1.06 °C (W m−2)−1, higher than that predicted by model simulations of the Last Glacial Maximum or by models of doubled greenhouse gas concentration forcing. This result suggests that models may not yet adequately represent the long-term feedbacks related to ocean circulation, vegetation and associated dust, or the cryosphere, and/or may underestimate the effects of tropical clouds or other short-term feedback processes.”
Citation: Kelsey A. Dyez and A. Christina Ravelo, Geology, v. 41 no. 1 p. 23-26, doi: 10.1130/G33425.1.”
In general, as we get better and better data and as models include more and more feedbacks, are studies moving toward higher and higher sensitivities?
That had been my impression, but perhaps this is the result of selective reading on my part.
[Response: I would need to check, but I think this is a constraint on the Earth System Sensitivity – not the same thing (see the first figure). – gavin]
I’m increasingly thinking that what we really need is an estimate of the sensitivity of the system to an injection of carbon dioxide including the feedback from the carbon cycle etc. I suppose that is the Earth System Sensitivity in this terminology. Using sensitivities where carbon dioxide concentrations is an exogenous variable could underestimate the cost of emissions impacts.
Surely the models described are all lagging behind the real world. The CMIP5 models seem to predict an Arctic free of summer sea ice in a few decades but the real world trend is for this to happen in the next few summers.
So why should policy makers care what these models predict as climate sensitivity? I suppose it is an interesting scientific problem but we should bear in mind that most or all of them are on the optimistic side.
Quite apart from the known underestimated feedbacks – more forest fires, melting permafrost, the decomposition of wetlands – new possibilities turn up. What if we see more Great Arctic Cyclones pop up in coming years to speed very unwelcome climate changes?
Don’t you think we’re seeing changes that exceed predictions already. Lots of droughts, floods and snow.
I would be interested in your take on frankenstorm Sandy. A sign of climate change or just blowing in the wind?
Since the AGU/Wiley publishing switchover seems to have anihilated the Hargreaves et al paper (hopefully only temporarily!), here’s my own copy of it.
[Response: James — thanks. One of my papers disappeared this way too. Mildly annoying! I added a link in the post which we’ll remove once AGU sorts things out. –eric]
Thanks for this interesting post.
If “sensitivity” is the response to a given injection of CO_2, how can we measure this directly when the CO_2 level is constantly increasing?
[Response: That isn’t the point. Sensitivity is a measure of the system, and many things are strongly coupled to it – including what happens in a transient situation (although the relationship is not as strong as one might think). The quest for a constraint on sensitivity is not based on the assumption that we will get to 2xCO2 and stay there forever, but really just as a shorthand to characterise the system. Thus for many questions – such as the climate in 2050, the uncertainties in the ECS are secondary. – gavin]
“Palaeosens (2012)” — the reference in footnote 1 — is
http://www.nature.com/nature/journal/v491/n7426/abs/nature11574.html
Making sense of palaeoclimate sensitivity
PALAEOSENS Project Members
(Paywalled, but the Supplementary Information (4.8M) PDF is available
Geoff Beacon #13: You may indeed be able to cite cases where models are “lagging behind the real world”. Arctic sea ice measurements below a past prediction do constitute such a case. But comparing different *future* predictions of “an Arctic free of summer sea ice” cannot, logically, be cited today as a discrepancy between a past prediction and the real world, as measured. Please don’t confuse these 2 situations, which are quite different. If you want to bet on an ice-free Arctic, by some appropriate definition, by some date in a couple years, you can probably find a place to do it, but that’s a different thing from pointing out how a past prediction missed something in the real world.
Ric Merritt #18
I actually did make money betting on the Arctic sea ice this year – but I would like to point out the bets were motivated more by anger than avarice.
Just look at the plots taken from CMIP4 and CMIP5 models when they are compared with measured extents from NSIDC data then tell us where you would place your bet for a summer free of sea ice.
I’d expect to see the Arctic essentially free of ice during September within three years.
What’s your bet?
Neven’s Sea Ice Blog has some pieces that will help :
The real AR5 bombshell
Models are improving, but can they catch up?
> Ideally, one would want to do a study across all
> these constraints with models that were capable of
> running all the important experiments – the LGM,
> historical period, 1% increasing CO2 (to get the TCR),
> and 2xCO2 (for the model ECS) – and build a multiply
> constrained estimate taking into account internal
> variability, forcing uncertainties, and model scope.
> This will be possible with data from CMIP5 ….
How soon? Is there any coordination among those doing this, before papers get to publication, so you know what’s being done by which group, and all the scientists are aware of each other’s work so they, taken as a group, can nail down as many loose ends as possible?
Volume has a more immediate signal than extent. In other words, measuring extent masks the problem. Since we now can talk with either term, it is a disservice for the IPCC to speak extent. I suggest the whole sea ice section be re-written with a volume-centric view. I’m betting all those “models more or less worked for extent up to 2011” would turn into “models were way off on volume through 2012”.
Oops, I see that’s been answered:
http://www.metoffice.gov.uk/research/news/cmip5
“… (CMIP5) is an internationally coordinated activity to perform climate model simulations for a common set of experiments across all the world’s major climate modelling centres….
…. and deliver the results to a publicly available database. The CMIP5 modelling exercise involved many more experiments and many more model-years of simulation than previous CMIP projects, and has been referred to as “the moon-shot of climate modelling” by Gerry Meehl, a senior member of the international steering committee, WGCM…..”
How does this submitted paper by Hansen et al fit in:
http://arxiv.org/ftp/arxiv/papers/1211/1211.4846.pdf
Do I understand correctly that this paper suggests a current CS of about 4 degrees C and earth system sensitivity of about 5 degrees, and seems to rule out CS-values lower than 3 degrees?
They also speak about sea level sensitivity as being higher than current ice sheet models show. It seems about 500 ppm CO2 could eventually mean an ice free planet, much lower than the circa 1000 ppm that ice sheet models seem to estimate.
Any thoughts on this approach and these conclusions?
Splendid word, I’d guess a typo, in the Hansen conclusion:
“16×CO2 is conceivable, but of course governments would not be so foolhearty….”
Gavin
This is not the subject but it seems that, in AR5 (sorry it is the leaked version), the mean total aerosol forcing is less (30%) than this same forcing in AR4.(-0.9W/m2 against -1.3W/m2)
On this link, http://data.giss.nasa.gov/modelforce/RadF.txt ,NASA-GISS provides a total aerosol forcing, in 2011, of -1.84W/m2.
I think that, if it is easy to conciliate a 3°C sensitivity with -1.84W/m2, it seems impossible with -0.9W/m2 (the new IPCC mean forcing), maybe a 2°C sensitivity works better.
So, is there another aerosol effect (different of the adjustment) accounted by the models, or other things?
[Response: That file is the result of an inverse calculation in Hansen et al, 2011. You need to read that for the rationale. The forcings in our CMIP5 runs are smaller. – gavin]
On the studies of sensitivity based on the last glacial maximum, what reduction in solar forcing is used based on the increased Albedo of the ice-sheets, snow and desert. It doesn’t appear to be outined in the papers.
This is off topic, but I was wondering about the Alaska earthquake this morning and its impact on the methane hydrates along the continental shelf. Info on this would be helpful.
Geoff,
My bet would be the opposite. Historically, a new low sea ice extent (area) is set every five years, with small recoveries in-between. My bet would be that 2012 was an overshoot, and that the next three years will show higher extents and areas. The next lower sea ice will occur sometime thereafter.
Looking again at Hansen’s submitted paper leaves me guessing his earth system sensitivty in the current state a little more than 5 degrees C, more like 6-8 degrees. Any other interpretations?
26 Paul W asked, “On the studies of sensitivity based on the last glacial maximum, what reduction in solar forcing is used based on the increased Albedo of the ice-sheets, snow and desert. It doesn’t appear to be outined in the papers.”
Yes, the obvious questions that make the most sense are often missing. What’s the total watts/m2 of the initial orbital push from LGM to HCO (totally silent on this), and what’s the total increase in temperature (4-6C?)?
Combine the two and you’ve got a total system sensitivity for conditions during an ice age. I’ve heard that sensitivity for current conditions is probably higher, but regardless, isn’t that the first thing one would want answered about climate sensitivity?
1. What was the initial push historically?
2. What was the final result (pre-industrial temps)?
3. What is the current push?
RC often touches on the last two, but the answer to the all-important first question is rarely (if ever – I don’t ever remember seeing an answer) mentioned even though it seems to be the best way to derive some sort of prediction about the future that doesn’t rely on not-ready-for-prime-time systems.
Has anybody ever heard of an estimate of the initial orbital forcing from LGM to HCO?
#28–Dan H wrote:
Maybe. But didn’t we have a conversation here on RC, not so long ago, about the virtues and vices of extrapolation?
I’m looking at the winter temps from 80 N this year (continuing toasty, relatively), and thinking about ENSO–neutral is now favored through spring–and remembering a) that the weather last year was rather unremarkable for melt and b) we’re still at the height of the solar cycle, more or less.
Throw in a quick consult with some chicken entrails, and I’ve concluded that I wouldn’t bet on Dan’s extrapolation.
Jim Larsen #30,
I think Jim Hansen mentions the initial orbital forcing for glaciation-deglaciation to be less than 1 W/m2 averaged over the planet, maybe just a few tenths of a W/m2. The resulting slow GHG and albedo feedbacks are about 3 W/m2 each, in his calculation.
So what happens if the initial GHG forcing now is about 4 W/m2? Would that mean slow feedbacks would total tens of W/m2? Or less? It seems Hansen thinks less, about 4 W/m2 as well, but I don’t really understand why. Does it have to do with the initial orbital forcing being much stronger or effective locally, at the poles?
It seems to me Hansen is really still struggling to understand this himself, and as a consequence his papers are not fully clear yet. Or maybe I just don’t understand clearly enough myself.
> Historically, a new low sea ice extent (area) is set every five years
What planet equates extent and area, and has this 5-year cycle?
Re- Comment by Lennart van der Linde — 6 Jan 2013 @ 4:20 AM
You say- “Does it have to do with the initial orbital forcing being much stronger or effective locally, at the poles?”
The northern hemisphere has much more land than the southern hemisphere and they are therefore affected differentially by orbital forcing.
Steve
Dan H #28: I wouldn’t be so sure that 2012 is an outlier. Look at the second animation here. The last few years show ice thickness consistently below previous levels. The pattern is oscillation with a downward trend but around 2007, the previous record year for minimum extent, there’s a big drop, then another one in 2010. With increasingly less multi-season ice, rebuilding previous sea ice extent gets harder and harder. I’m sure some people also thought 2007 was an outlier.
Of course you could be right that there’s some oscillation before it dips again, but I wouldn’t bet on it. There was nothing special about 2012 conditions to have caused a big dip (e.g. SOI index didn’t show any big El Niño events over the year).
Kevin,
Fair enough. However, looking at the decrease in sea ice minimum over the past decade or so, both the 2007 and 2012 minima crashed through the preious lows in a typical overshoot pattern. Recently, a new low has been set every five years (2002, 2007, & 2012), with modest recoveries in-between. Last year, looks remarkably similar to 2007.
Doesn’t -3.5 W/m2 from the ice age Albedo forcing seem like an awfully low figure.
The Arctic sea ice melting out above 75N would have almost no impact at all if that is the forcing change of glaciers down to Chicago and sea ice down to 45N (at lower latitudes where the Albedo has much more impact).
Paul Williams,
I can’t tell where you got the figure but -3.5W/m2 is about right for current understanding of “boundary condition” land albedo change between pre-industrial and LGM. In LGM simulations land albedo changes are prescribed (at least in regards to ice sheets and altered topography due to sea level; there are feedback land albedo changes) so are a forcing, whereas sea ice is determined interactively by the model climate, so is a feedback in this framework.
Geoff Beacon #19: To answer your question, if you mean you expect the NSIDC to announce a September arctic sea ice minimum below, say 1M sq km, by 2015, I would bet against, but not a huge amount, because of uncertainty.
This is not due to any denialist illness, or any reluctance to put my money where my mouth is. Over the last several years, when irritated by trolls on DotEarth, Joe Romm’s site, or the like, I have repeatedly offered to bet more than my current middle-class salary, indexed to the S&P 500 at time of settling up, on the course of global temperatures over decades. Strangely enough, I never got a serious bite.
But my previous point, which you kinda ignored, was that future expectations, which are of course what folks make bets about, are fundamentally different from pointing out a difference between carefully recorded past expectations and carefully recorded (probably recent) past measurements. I think the conversation is clearer if we keep that straight.
#36–“Last year, looks remarkably similar to 2007.”
Only in terms of the magnitude of the extent drop. But if there’s one thing I’ve learned about watching sea ice melt, it is that it ‘loves’ to confound.
#37–Maybe, but IIRC, I saw an estimate of .7 w/m2 for an ice-free Arctic summer. So, maybe not–though the .7 estimate was probably somewhat of a ‘spherical cow in a vacuum’ deal.
@James Annan (#14). Thanks for posting your paper. I think there is a disconnect between the modeling and paleodata community that is affecting your estimates. The data community (geochemical proxies) would argue that we’ve solidly established the 2.5-3 deg cooling level for the deep tropics during the LGM. The MARGO data is dominated by older foram transfer function estimates, which even its most ardent practitioners would agree do not record tropical changes accurately. This is an important point that is affecting a number of recent estimates of sensitivity using MARGO data.
[Response: David, thanks for dropping by. I take it you mean that the Margo data is resulting in underestimates of climate sensitivity? –eric]
@Eric: Yes, that’s the implication. if you look at Fig. 2 in Hargreaves et al, the observational band for LGM tropical cooling they use, based on MARGO, is -1.1 to -2.5 deg C, equating to a sensitivity of about 2.5 deg. Using an estimate of the mean tropical cooling based on geochemical proxies of 2.5-3 deg would yield a sensitivity closer to 3.5 deg (but perhaps Julia will comment).
Paul Williams @37 — The ice sheets become dirtier over time.
Do the ‘older foram transfer function estimates’ make different calculations but using the same original material? Or is this new field data? How did the geochemists come by the ‘geochemical proxies of 2.5-3’ now favored?
@Hank Roberts #45. I believe that the transfer function estimates used in MARGO are based on the traditional method used in CLIMAP, rather than newer approaches. And I also believe it is largely the same data set used in CLIMAP. As for the geochemical data, it is based on Mg/Ca in foraminifera, alkenone unsaturation in sediments and some sparse data from other techniques such as Ca isotopes, clumped isotopes and TEX86. The -2.5 to -3.0 deg cooling value is my subjective estimate based on knowledge of the data and various published compilations. Although LGM oxygen isotope changes cannot be used to independently assess cooling, they provide a useful additional constraint that is difficult to reconcile with a cooling much less than 3 deg.
Thanks Dr. Lea for coming by,
It would be interesting to have someone do a post on the history of LGM ocean-temperature reconstructions following CLIMAP, including the Sr/Ca evidence.
There’s a lot to it (and I think is one of the initial pushes for Lindzen in developing his faith in a low climate sensitivity).
This helps (I’d heard some of the terms, I’d have to look up all of ’em again as most of what I know is decades out of date)
Please go on at as much length as you have patience for.
> affecting a number of recent estimates
> of sensitivity using MARGO data.
Time to invite all the authors whose work is affected to a barbeque?
How hard is it to revise a paper if the author (or reviewer, or editor) decides this change should be made? Simple, or complicated?
Dan H #28:
Not sure where you get the idea that a record low extent is set every five years. The previous record to 2007 was in 2005. As I recall the 2007 record resulted from very favourable weather conditions, so it would have been unlikely for another record to be set for several years (and it wasn’t). I think we can say that the 2007 melt made it more likely that another record smashing melt season would occur eventually given the right conditions, and that we can say the same about 2012.
http://nsidc.org/arcticseaicenews/2012/10/poles-apart-a-record-breaking-summer-and-winter/