As part of the IPCC WG1 SPM (pdf) released last Friday, there was a subtle, but important, change in one of the key figures – the radiative forcing bar-chart (Fig. SPM.4). The concept for this figure has been a mainstay of summaries of climate change science for decades, and the evolution over time is a good example of how thinking and understanding has progressed over the years while the big picture has not shifted much.
The Radiative-Forcing bar chart: AR5 version
The earliest version of a bar-chart that shows radiative forcing is this chart from one of Jim Hansen’s papers (Hansen et al, 1981):
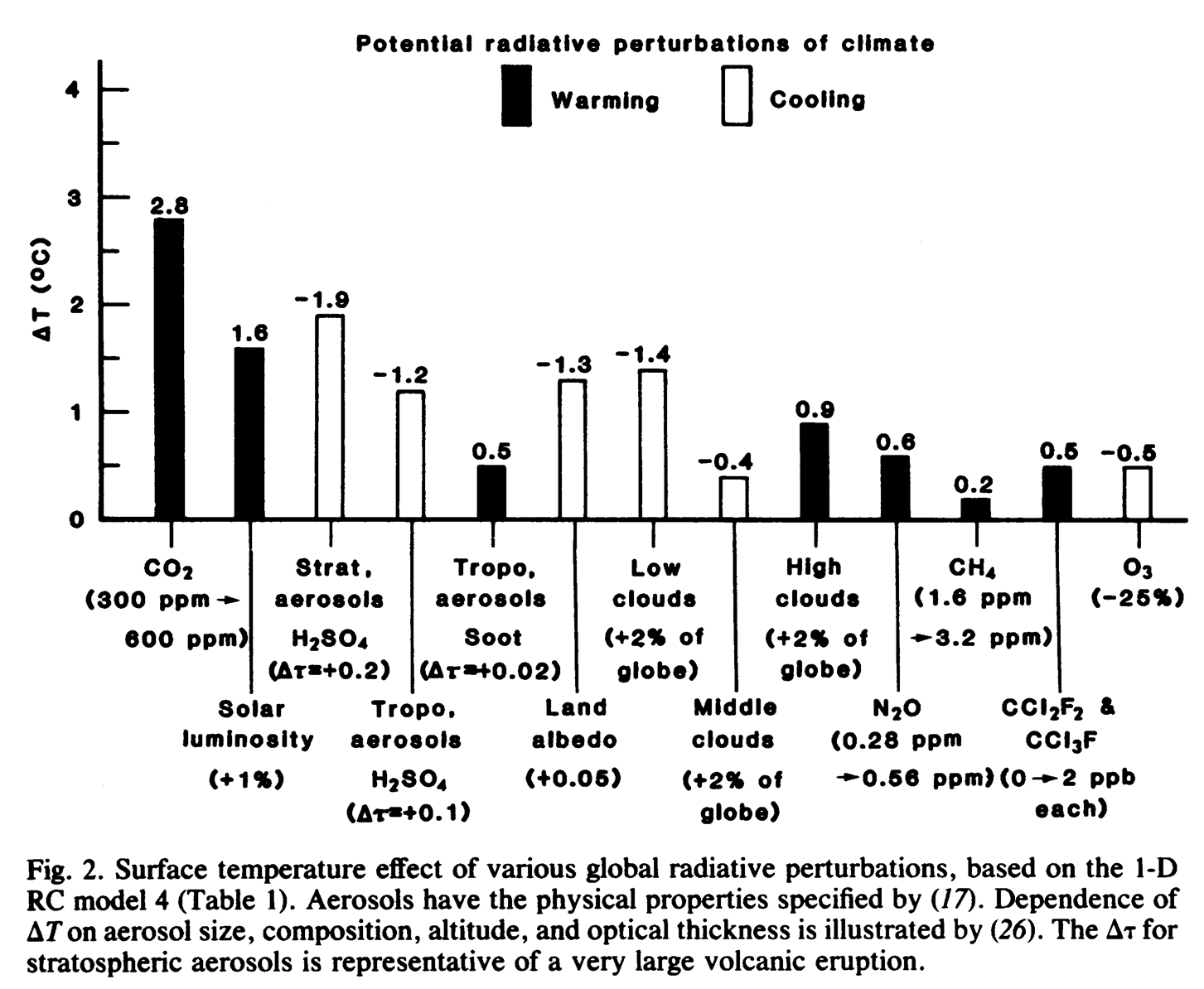
In it, they demonstrate the relative importance – cooling or warming – of a number of relevant changes in radiatively important components (CO2, CH4, the sun, aerosols etc.). While the y-axis is the no-feedback surface temperature response, and the changes aren’t with reference to the pre-industrial, this might qualify as the ‘ur’-figure – the one from which all the others below are derived. (Note, if you know of an earlier version, please let me know and I’ll update the post accordingly).
I can’t find any examples for a decade or so, and in the First Assessment Report (FAR) (1990) there wasn’t such a figure either, even in the main text. (Again, please let me know if I’ve missed one). However, in the early 1990s, the figure appears in a form much closer to what we’ve come to expect. For instance, in Hansen et al (1993), the forcings in 1990 with respect to 1850 are given:
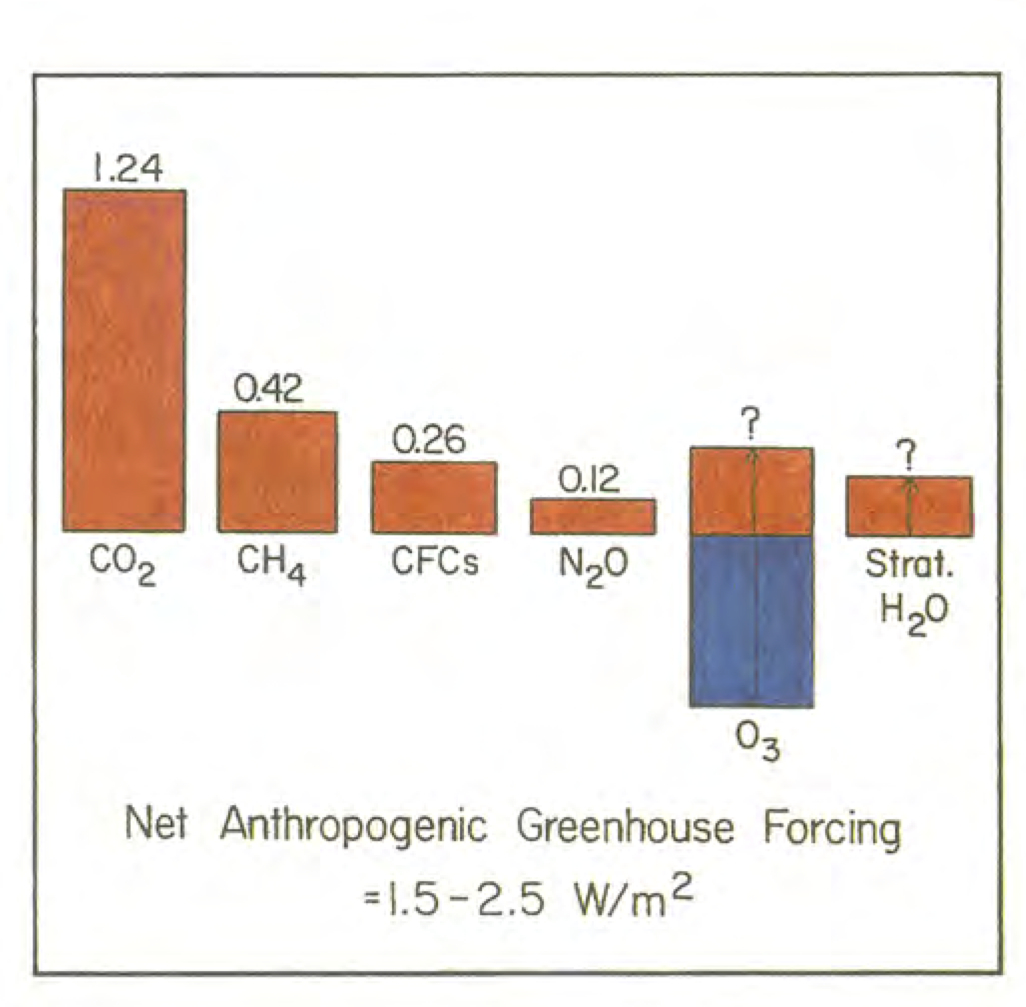
The transition to W/m2 as the unit has now been made, different greenhouse gases are separated, and an acknowledgement of more complicated issues associated with ozone and stratospheric water vapor is included. The main conclusion is that CO2 had been historically the most important forcing (around 1.24 W/m2). Shortly thereafter, the 1995 IPCC Second Assessment Report (pdf) added a couple of innovations:

Namely, an assessment of confidence, and the addition of aerosol forcings, while lumping the well-mixed gases all together. There is also the addition of the non-anthropogenic solar term. The figure was updated in 1998 and 2000 by Hansen and colleagues:
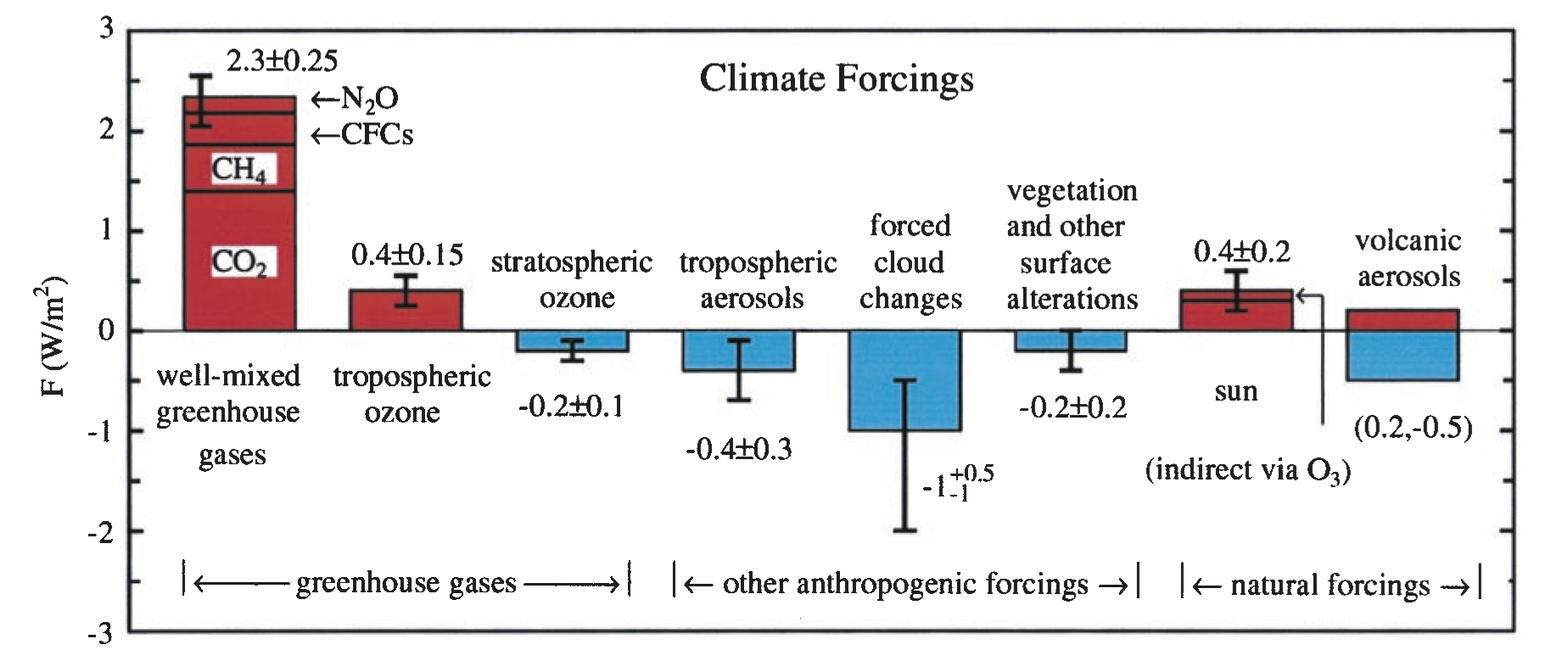

These updates added land use/land cover changes to albedo, decadal trends in volcanoes, and (in 2000) made the subtle point that the greenhouse effect from CFCs was offset a little by the impact CFCs were having on the ozone layer. An analogous diagram was very prominent in the 2001 IPCC Third Assessment report (TAR):
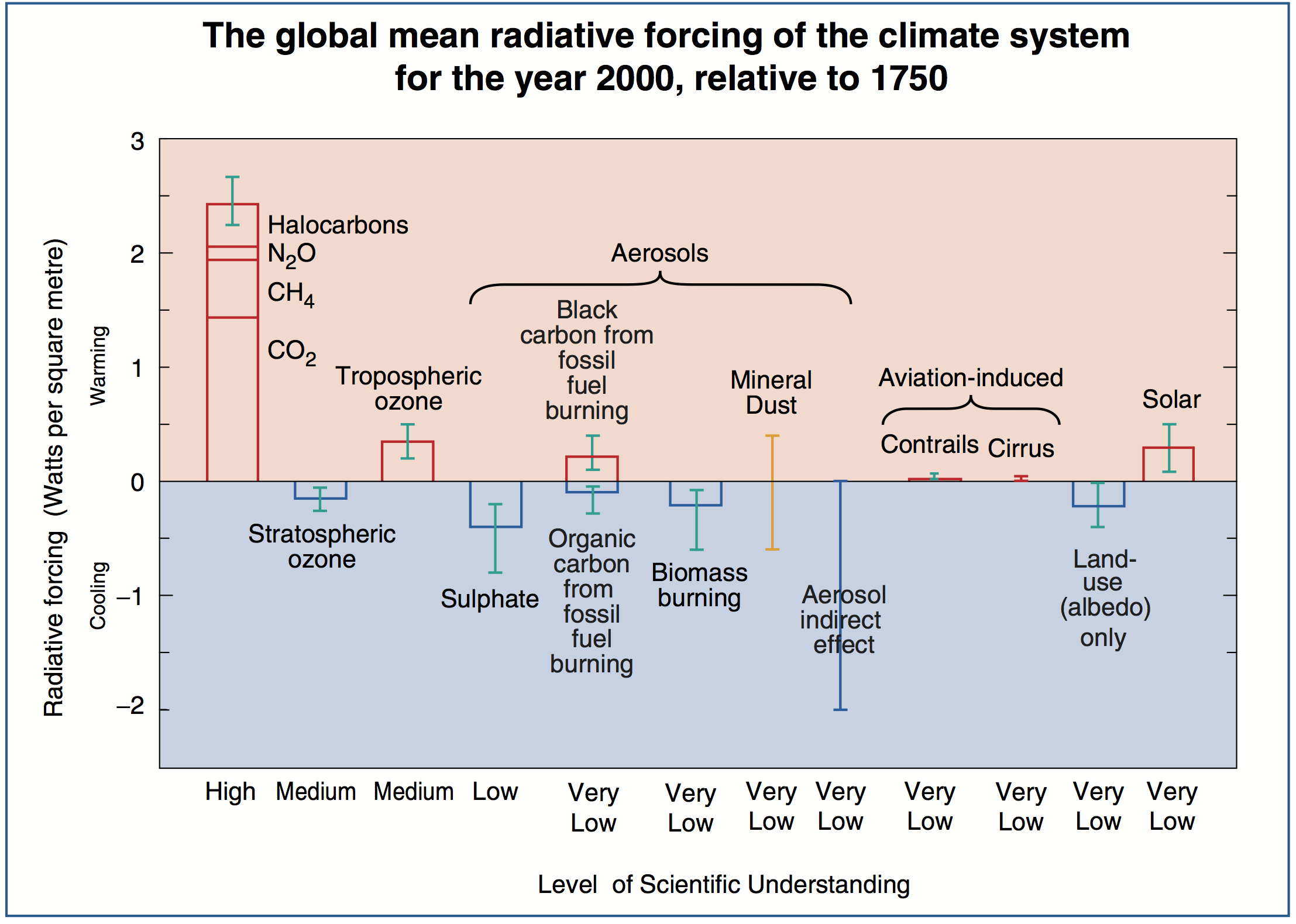
As with the SAR version, the confidence levels are present, there has been a switch from 1850 as a baseline in the SAR version, to 1750 in order to capture the beginning of the industrial rise in the GHGs, and again additional items were included: some aerosol related (sulphates, mineral dust, biomass burning, carbonaceous aerosols (incl. black carbon)), and two associated with aviation (via contrails and enhanced cirrus cloud formation). Concurrently, the Hansen et al (2001) version:
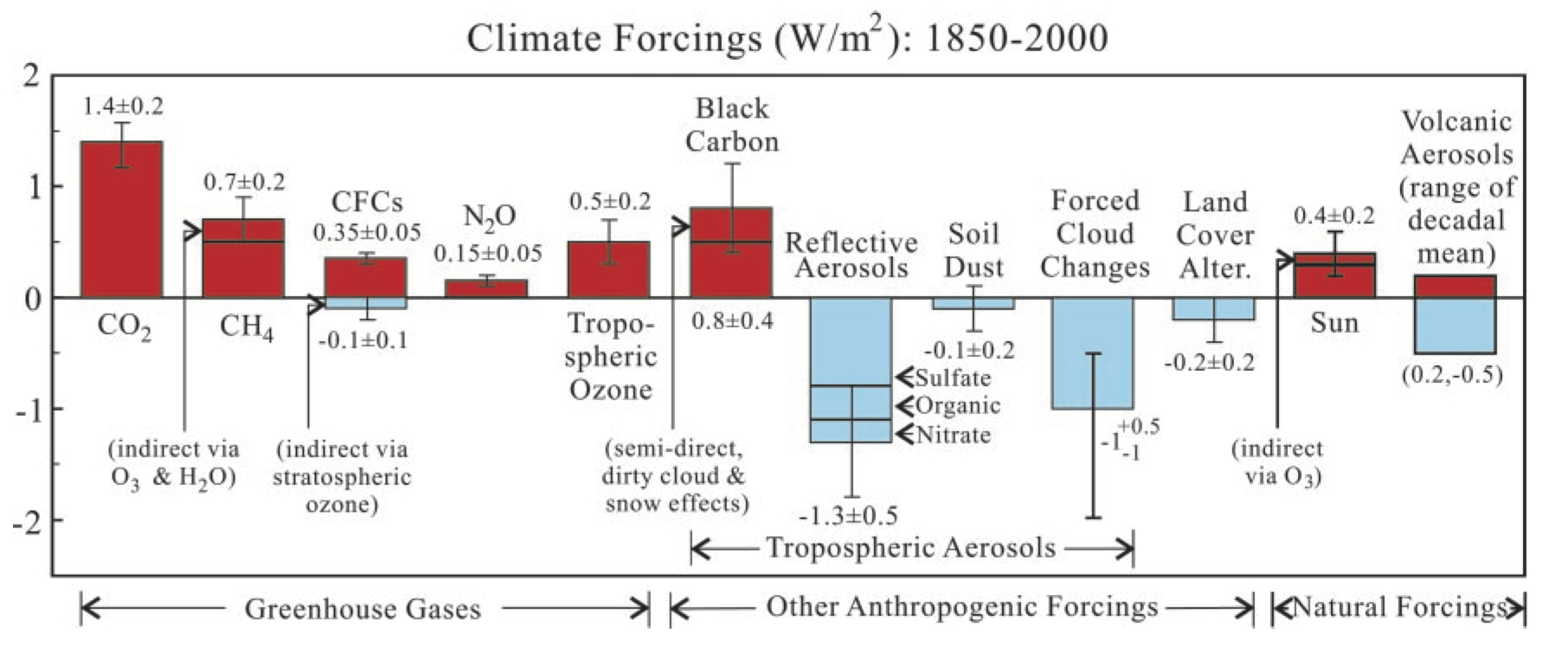
included even more details – the effect of black carbon on snow, nitrate aerosols, and an enhancement of the solar effect via ozone changes.
In the 2007 AR4 SPM, the main innovation was to rotate the axes by 90º and to add a bit more colour:
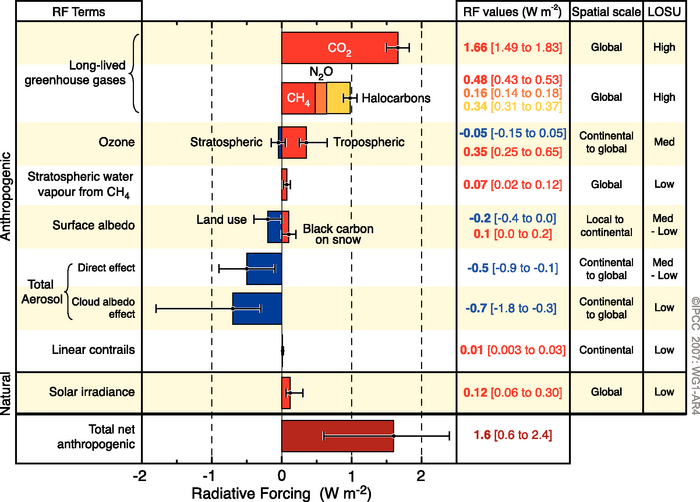
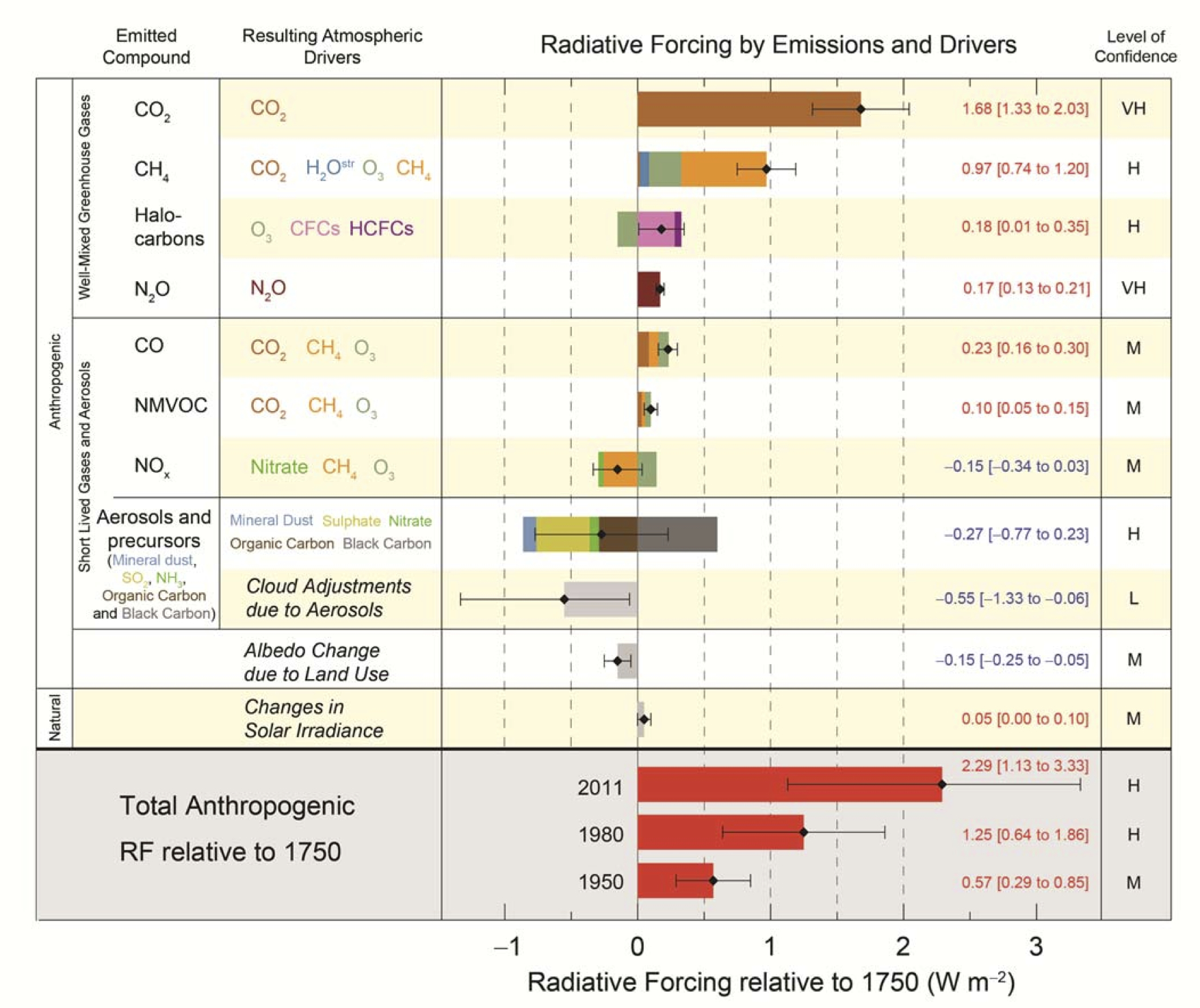
Though stratospheric water vapour makes a comeback, and the indirect effect of black carbon on snow makes an entrance for IPCC. In the AR5 SPM though, something more interesting happened…

The effects are now grouped by emissions, rather than by concentrations. This too has it’s antecedents, Fig 2.21 in the AR4 full report did the same thing, but was little noticed. In turn, that figure was drawn from work by Shindell et al (2009). This allows many of the indirect effects to be seen clearly. A particular point of interest is that the forcing by emission for CH4 is twice as large than its forcing by concentration, because of the important indirect effects on ozone and aerosols. The inclusion of CO, VOCs and NOx – normally considered as air quality issues – which affect climate via their indirect effects on ozone etc, is a salient reminder that the two issues are very much connected.
Summary
The most obvious change over time is that the visual styling of the graphs has improved over time. The latest version is far more comprehensive – including more effects, more connections, more error bars – and is, arguably, more useful. This follows from the fact that it is emissions that can be potentially moderated, and the latest iteration shows explicitly what the key emissions are (as opposed to what their consequences are after atmospheric chemistry has done it’s thing).
A key change over time is of course the increasing forcing from CO2. In 1993 it was 1.24 W/m2, in 2001, 1.4 W/m2, to today’s 1.7 W/m2.
The treatment of aerosols – and particularly the difference between absorbing (i.e. black carbon) and scattering (sulphates, nitrates) – has varied a lot. This is partly because of new information (on sources, concentrations, effects), but also because the aerosol issue has been reframed many times. The situation of black carbon is the most complicated. BC on it’s own is strongly warming, and it’s additional indirect effects on snow albedo amplify that. However, BC is almost always emitted in combination with organic carbonaceous aerosols (and/or secondary organic aerosol precursors), and so with respect to the emission-producing activity, the net effect on temperature is partially compensated (see the TAR version for instance). BC is chiefly associated with incomplete combustion of fossil fuel, or alternatively with biomass burning (through deforestation, land clearance or naturally occurring forest fires), and these two classes of sources have sometimes been grouped (2007), and sometimes separated (2001). The AR5 version groups all the aerosol factors into one bar with each of the separate constituents delineated. A further breakdown of this into contributions by activity would be useful, but as I understand it, this was considered not within the scope of WG1.
One final example is also worth noting. In all of the pre-AR5 figures (except Hansen in 2000), tropospheric and stratospheric ozone were considered separately. But while there are two separate effects going on (ozone precursors increasing in the lower atmosphere, and ozone depletion due to CFCs above), there is not a clean separation between changes in the troposphere and stratosphere. Thus the AR5 version correctly shows the ozone changes as indirect effects of the different emissions without delineating where the changes in ozone are occurring. This is a definite conceptual improvement among many.
References
- J. Hansen, M. Sato, R. Ruedy, A. Lacis, and V. Oinas, "Global warming in the twenty-first century: An alternative scenario", Proceedings of the National Academy of Sciences, vol. 97, pp. 9875-9880, 2000. http://dx.doi.org/10.1073/pnas.170278997
- D.T. Shindell, G. Faluvegi, D.M. Koch, G.A. Schmidt, N. Unger, and S.E. Bauer, "Improved Attribution of Climate Forcing to Emissions", Science, vol. 326, pp. 716-718, 2009. http://dx.doi.org/10.1126/science.1174760
Re 49 WebHubTelescope – okay; when I looked at your equation I was puzzled so I had to go through it myself.
and another correction (bold in following) (I’m just restating the end of my 46, with corrections):
————————-
dP = 3*OLR/T * dT; for OLR ~= 240 W/m2, that’s
2.5, 2.8, 3.3 W/m2 per K , or 0.40, 0.35, 0.31 K per W/m2, @220, 255, 288 K (zero non-Planck feedback equilibrium climate sensitivity, setting aside the matter of the stratosphere, etc.).
1 W/m2 of TSI -> ~ 0.175 W solar forcing TOA -> 0.070, 0.062, 0.053 K @three Temps (see above), not taking into account stratospheric portion, feedbacks, or time for equilibration.
dP/P = 3 * (OLR,TSI*0.175)/T * dT / (OLR,TSI*0.175) = 3*dT/T
———————-
(where dP is either the change in OLR required to restore equilibrium or it is the solar forcing TOA ; they would be equal, of course, when the only forcing is solar; P is OLR, but can be expressed in terms of TSI(hence the OLR,TSI*0.175 parts) (I’m not sure if I originally just forgot the 0.175 factor in the above equation or if I didn’t included it because the cancelation.))
then, manipulating the last equation:
dP/dT = 3*P/T ~= 3*(5.67E-8 W/(m2*K4) * T^4) / T = d/dT (5.67E-8 W/(m2*K4) * T^4)
(as a double check that dP/dT = 3*P/T , and of the prior equation)
dT = (1/3)*T/P * dP
= (1/3)*T/OLR * d(OLR) in general
= (1/3)*T/(TSI*0.175) * d(TSI*0.175)
= 1/3 * T/TSI * d(TSI) for solar forcing.
Patrick, We are very close to being in agreement. I don’t think it is a 1/3 factor but a 1/4 factor for scaling.
We may need someone else to make a ruling and act as a tiebreaker.
It is time to really think about what the graphs mean.
Circa 1750, we started burning the geologic carbon, increasing the amount of greenhouse gases in the atmosphere and warming the surface of the Earth. We also released trivial amounts of methane. These small methane releases have preoccupied modelers that should have been thinking about the big picture.
The big picture is simple. The concentration of CH4 in the atmosphere is the partial pressure of CH4 in equilibrium with a large number of reservoirs of solid methane clathrate. Each clathrate reservoir has its local equilibrium dependent on local temperature, total pressure, and the CH4 concentration in the reservoir’s local environment.
Thus, as long as there are clathrates, we can expect them to control the partial pressure of methane in the atmosphere. The legal and diplomatic fiction of a low global warming potential for methane is based on an incorrect definition and bounding of the methane system that fails to recognize the equilibrium relationship between small flows (megatonnes) of methane in the atmosphere/ biosphere and large (gigatonnes) reservoirs of methane clathrates.
Circa 1750, conditions had been stable for a relatively long period, and all clathrate reservoirs were in equilibrium with atmospheric concentrations of CH4 on the close order of 0.7 ppmv to 0.4 ppmv. As the Earth started to warm, the equilibrium point for some clathrate reservoirs moved from solid to gas, and they released methane into their environments. As the methane equlibrium moves toward gas, we are seeing atmospheric CH4 concentrations approaching 2 ppmv. This produces a radiative forcing of almost 200 ppm of CO2 ,and thus our effective green house gas concentration is now on the close order of 600 ppm CO2e.
Since clathrate/ methane gas is an equilibrium system, as methane is removed from the oceans & atmosphere by oxidation, and the partial partial pressure of methane declines, then methane clathrate in the reservoirs will dissociate to restore the equilibrium partial pressure of methane for that temperature. As the Earth continues to warm, the equilibrium will continue to move from solid clathrate to methane gas resulting in higher atmospheric partial pressures of methane. I am as sure of this as I am that the atmosphere will hold more water vapor as it warms. It is the same physics.
I have oversimplified the methane cycle. Still, the subject chart does not tell the big picture.
RealClimate has been here before as in:
https://www.realclimate.org/index.php/archives/2012/01/much-ado-about-methane/ .
However, in parts of the Arctic, we are now separated from sea floor clathrates by only a hundred meters of ocean that is becoming increasingly storm mixed. It is time to see the oceans as circulating fluid, that helps bring the system to equilibrium.
re WebHubTelescope @ 52 – my 1/3 factor came directly from taking the derivative of sigma*T^4. Does your 1/4 … OMG! Duh. How could I have missed that! :) OOPS!!!!
Sure, if the Undergravel Filter of Doom* model proves true.
Assuming drilling and military seabed activity have perforated the permafrost, and warm water circulates down in the sediments laterally between faults in a way not seen during past glacial cycles.
Assuming new clathrate doesn’t form to plug up the holes within the temperature/pressure stability zone, or doesn’t form fast enough to limit the process.
Assuming the seabed surprises us — could it be unstable like the ice caps, and for the same reason — heat moving by circulation not diffusion?
I feel lucky. I doubt it’s happening. But hey, the Russian and ex-USSR records from their petroleum operations and Arctic navy ought to give some idea. Betcha their Navy (and likely ours and several others) have hydrophone sound files going back decades that would be searchable for sounds indicating outbursts of bubbles, for example. Is anyone looking?
_______
*UFOD: Some guy on the Internet
Question re: Relationship between forcing, CO2 concentrations and Temperatue.
Where’s the error:
CO2 forcing abatement = 5.35 ln (Concentration 1 / Concentration 2).
Keeping PPM levels to 409 versus 410 results in a reduction in forcing by 0.013 watts per square meter.
Multiply by sensitivity (of temps to forcing), and you get 0.44×0.013 = 0.057 Degrees C.
1 ppm CO2 (by volume), or 1.6 ppm by mass corresponds to 1.6×10^-6 x mass of atmosphere, or 1.6×10^-6 x 5×10^18 = 8×10^12 kg or 8 billion tons.
Thus to reduce the temperature increase by one fifteenth of a degree you have to reduce CO2 levels by 8 billion tons, or one ton per person on the Earth. Because of the logarithmic relationship, the next fifteenth of a degree will require an even greater reduction.
… which is to say it’s 1/4; thanks for bringing it up again, I might never have gone back to the matter. (Maybe part of my brain was trying to integrate instead?).
corrected versions:
P = 5.67 E-8 W/(m2 K4) * T^4
dP = 4*[5.67 E-8 W/(m2 K4) * T^3] * dT
= 4*P/T * dT
dP/P = 4 dT/T
dT = 1/4 * T/P * dP
= 1/4 * T * dP/P
For the sun, assuming T =
57805778 K http://en.wikipedia.org/wiki/Sun (isothermal photosphere is an approximation, of course),dT per W/m2 of dP is 1.06 K
For the Earth, with OLR ~=240 W/m2 (I think I saw 235 W/m2 once; if 240 W/m2 is 5 W/m2 too great, dT values will be ~ 2.1 % too small)
@ 288 K (global average surface T), 255 K (effective broadband emission T), 220 K (at or near tropopause, roughly)
dT per W/m2 of OLR change (in response to SW (solar) forcing) or recovery (in response to LW forcing)
0.300 K, 0.266 K, 0.229 K
per 1 W/m2 change in TSI (~0.175 W/m2 solar forcing TOA)(one can substitute change in TSI in place of solar forcing TOA if TSI replaces OLR in the equation; the 0.175 factor drops out)
0.0525 K, 0.0465 K, 0.0401 K
per doubling of CO2 (based on 3.7 W/m2 – which is actually the tropopause level forcing after stratospheric adjustment)
1.11 K, 0.983 K, 0.848 K
Notice the sensitivity …
(this is equilibrium climate sensitivity with no non-Planck feedbacks, based on T^4 proportionality (which doesn’t generally apply to specific absorption/emission bands, and may be a little off due to horizontal and temporal T variations (I don’t think that’s a big factor, though… not entirely sure; I estimated once that the variations at the surface over a year may cause the surface to emit as if it were 1 K warmer than it is; higher highest cloud tops and greater low-level H2O tend to be in warmer places (making them look cooler from above) and upper troposphere has smaller variations but …))
… decreases with decreasing T. It would be the other way around, if the OLR were proportional to T^4, but I am using the same OLR. I used 3 temps in an attempt to find a range of possible sensitivities, since at some parts of the spectrum much OLR comes from near the surface (absent higher clouds, etc.) while at other parts it comes more from the upper troposphere or higher. However, there is also the spectral variation in n for T^n (for blackbody P(T), peak over wavelength n=5, peak over frequency n=3, peak over (log or ln)(wavelength or frequency) n=4, longest wavelengths n approaches 1, shorter wavelengths n gets larger).
Also, this excludes the effect that a portion of the forcing is realized in the stratosphere … my first approximate guess is half, or a bit less than half, of that adds to the tropopause level forcing when the stratosphere adjusts (via warming or cooling and changes in downward LW flux as a result) (the fraction depends on where in the stratosphere the warming or cooling occurs, of course, but if enough of the downward LW flux is from bands with small stratospheric optical depth, the fraction is less sensitive to that distribution).
So I’d go with a more refined model. The no non-Planck feedback response for CO2 doubling is supposed to be a bit over 1 K, and I think my range of values above didn’t quite reach as high. The OLR response to the imposed decrease (after stratospheric adjustment) would tend to be excluded from the center of the CO2 band …
(and also, I’d expect, possibly some of the highest cloud tops, via the FAT hypothesis (I don’t have time just now to reread the link completely (I may have left off before finishing, now that I think about it) but I think it’s specifically about tropical cirrus)- but wait, this is before considering such feedbacks)
… But it’s not as if the OLR increase in response to the imposed decrease is coming entirely from the surface in the tropics.
… also exluded taking into account portion of OLR from stratosphere (solar heating there would tend to equal a net contribution to OLR from there, so the net upward flux at the tropopause would be smaller, which would increase the calculated dT values.
… but I think that’s wandering outside of the territory where such a simple relationship would hold anyway (the total LW flux upward at the tropopause will be larger than the net upward LW flux, and in the spirit of the relationship derived, the gross flux may be more appropriate). But obviously it was intended as a rough approximation.
… but the last 2 comments (of mine) are at least in some contexts moot as forcing at tropopause level and at TOA are the same after stratospheric adjustment; so OLR does have to increase (after strat.sph. adjustment) by the amount of forcing at tropopause level (excluding any SW feedbacks); change in gross upward flux at tropopause level will probably exceed that.
Aaron Lewis (#53) wrote:
“Circa 1750, we started burning the geologic carbon …”
Not in significant amounts, especially compared to the burning of wood.
Ice cores and methane reconstructions seem to show something exceptional happened in the 18th century. And it seems tracable to the Northern hemisphere. But it’s not clear it started around 1750 and in any case can not possibly be explained by the burning of minute amounts of geologic carbon.
Furthermore, your theory doesn’t seem to explain either the mid-16c. methane spike or the slow rise in atmospheric methane concentrations between high antiquity and 1000 years ago. And certain human activities which do not necessarily involve fossil fuels are known to cause methane emissions…
Re 53 Aaron Lewis wrote that an increase of 2ppmv pf methane = 200ppmv of co2. Surely methane has a forcing of approx. 20 times the equivalent amount of co2. So 2ppmv of methane = 40ppmv of co2, not 200.
re 56 Marc Opie “Where’s the error:”
I found three.
“Multiply by sensitivity (of temps to forcing), and you get 0.44×0.013 = 0.057 Degrees C.”
If climate sensitivity is ~ 3 K/doubling of CO2 ~ 3/3.7 K/(W/m2) = 0.81 K/(W/m2); using that value I get 0.0106 K (using unrounded 3/3.7); using 0.7 K/(W/m2) instead I get 0.0091 K. 0.057 K seems a bit too high, even after slow-acting feedbacks. (But I just realized that 0.0057 K is the result of 0.44 K/(W/m2) * 0.013 W/m2, so you’re decimial point was just one point off.)
“Thus to reduce the temperature increase“… “you have to reduce CO2 levels by 8 billion tons, or one ton per person on the Earth. Because of the logarithmic relationship, the next fifteenth of a degree will require an even greater reduction.”
Actually a larger reduction is required because some is going into the ocean. On the flip side, you’ll be reducing ocean acidification as well.
But the next 0.01 K will require a smaller reduction if you’re going from 409 to 408 ppm. Or did you meant it will be even harder to go from 411 ppm to 410 ppm? That of course assumes a constant airborne fraction per unit emission, which isn’t really what’s going on; some part of the rate of CO2 uptake out of the atmosphere should be an ongoing response to prior emissions, but also there’s potential for a response to climate change itself.
… ie absent climate feedback on C-cycles, a slower rate of emission would tend to reduce the peak atmospheric CO2 because the removal by the ocean, etc, would keep up a little bit more – of course, that only goes so far in the short term, since a return to the initial atmospheric CO2 level requires some very slow-acting processes. (I’m under the impression that to some extent a ‘climate fate’ is insensitive to the exact rate of release of the same given total CO2 (maybe because of the slow feedbacks?); I assume that’s only true for a limited range (relative to Earth’s time) – I mean, if we took 1 Trillion tons and spaced it out over the next 4 billion years, rather than a century or so, I’d have to think it wouldn’t be to much of a problem…)