By raypierre , with the gratefully acknowledged assistance of Spencer Weart
In Part I the long struggle to get beyond the fallacious saturation argument was recounted in historical terms. In Part II, I will provide a more detailed analysis for the reader interested in the technical nitty-gritty of how the absorption of infrared really depends on CO2 concentration. At the end, I will discuss Herr Koch’s experiment in the light of modern observations.
The discussion here is based on CO2 absorption data found in the HITRAN spectroscopic archive. This is the main infrared database used by atmospheric radiation modellers. This database is a legacy of the military work on infrared described in Part I , and descends from a spectroscopic archive compiled by the Air Force Geophysics Laboratory at Hanscom Field, MA (referred to in some early editions of radiative transfer textbooks as the "AFGL Tape").
Suppose we were to sit at sea level and shine an infrared flashlight with an output of one Watt upward into the sky. If all the light from the beam were then collected by an orbiting astronaut with a sufficiently large lens, what fraction of a Watt would that be? The question of saturation amounts to the following question: How would that fraction change if we increased the amount of CO2 in the atmosphere? Saturation refers to the condition where increasing the amount of CO2 fails to increase the absorption, because the CO2 was already absorbing essentially all there is to absorb at the wavelengths where it absorbs at all. Think of a conveyor belt with red, blue and green M&M candies going past. You have one fussy child sitting at the belt who only eats red M&M’s, and he can eat them fast enough to eat half of the M&M’s going past him. Thus, he reduces the M&M flux by half. If you put another equally fussy kid next to him who can eat at the same rate, she’ll eat all the remaining red M&M’s. Then, if you put a third kid in the line, it won’t result in any further decrease in the M&M flux, because all the M&M’s that they like to eat are already gone. (It will probably result in howls of disappointment, though!) You’d need an eater of green or blue M&M’s to make further reductions in the flux.
Ångström and his followers believed that the situation with CO2 and infrared was like the situation with the red M&M’s. To understand how wrong they were, we need to look at modern measurements of the rate of absorption of infrared light by CO2 . The rate of absorption is a very intricately varying function of the wavelength of the light. At any given wavelength, the amount of light surviving goes down like the exponential of the number of molecules of CO2 encountered by the beam of light. The rate of exponential decay is the absorption factor.
When the product of the absorption factor times the amount of CO2 encountered equals one, then the amount of light is reduced by a factor of 1/e, i.e. 1/2.71282… . For this, or larger, amounts of CO2,the atmosphere is optically thick at the corresponding wavelength. If you double the amount of CO2, you reduce the proportion of surviving light by an additional factor of 1/e, reducing the proportion surviving to about a tenth; if you instead halve the amount of CO2, the proportion surviving is the reciprocal of the square root of e , or about 60% , and the atmosphere is optically thin. Precisely where we draw the line between "thick" and "thin" is somewhat arbitrary, given that the absorption shades smoothly from small values to large values as the product of absorption factor with amount of CO2 increases.
The units of absorption factor depend on the units we use to measure the amount of CO2 in the column of the atmosphere encountered by the beam of light. Let’s measure our units relative to the amount of CO2 in an atmospheric column of base one square meter, present when the concentration of CO2 is 300 parts per million (about the pre-industrial value). In such units, an atmosphere with the present amount of CO2 is optically thick where the absorption coefficient is one or greater, and optically thin where the absorption coefficient is less than one. If we double the amount of CO2 in the atmosphere, then the absorption coefficient only needs to be 1/2 or greater in order to make the atmosphere optically thick.
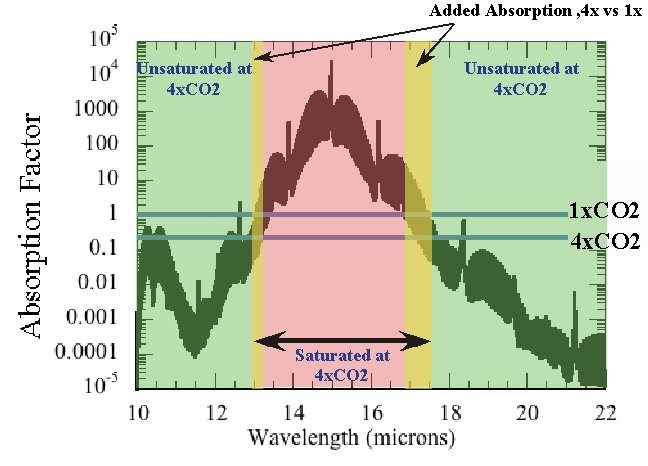
The absorption factor, so defined, is given in the following figure, based on the thousands of measurements in the HITRAN spectroscopic archive. The "fuzz" on this graph is because the absorption actually takes the form of thousands of closely spaced partially overlapping spikes. If one were to zoom in on a very small portion of the wavelength axis, one would see the fuzz resolve into discrete spikes, like the pickets on a fence. At the coarse resolution of the graph, one only sees a dark band marking out the maximum and minimum values swept out by the spike. These absorption results were computed for typical laboratory conditions, at sea level pressure and a temperature of 20 Celsius. At lower pressures, the peaks of the spikes get higher and the valleys between them get deeper, leading to a broader "fuzzy band" on absorption curves like that shown below.
We see that for the pre-industrial CO2 concentration, it is only the wavelength range between about 13.5 and 17 microns (millionths of a meter) that can be considered to be saturated. Within this range, it is indeed true that adding more CO2 would not significantly increase the amount of absorption. All the red M&M’s are already eaten. But waiting in the wings, outside this wavelength region, there’s more goodies to be had. In fact, noting that the graph is on a logarithmic axis, the atmosphere still wouldn’t be saturated even if we increased the CO2 to ten thousand times the present level. What happens to the absorption if we quadruple the amount of CO2? That story is told in the next graph:
The horizontal blue lines give the threshold CO2 needed to make the atmosphere optically thick at 1x the preindustrial CO2 level and 4x that level. Quadrupling the CO2 makes the portions of the spectrum in the yellow bands optically thick, essentially adding new absorption there and reducing the transmission of infrared through the layer. One can relate this increase in the width of the optically thick region to the "thinning and cooling" argument determining infrared loss to space as follows. Roughly speaking, in the part of the spectrum where the atmosphere is optically thick, the radiation to space occurs at the temperature of the high, cold parts of the atmosphere. That’s practically zero compared to the radiation flux at temperatures comparable to the surface temperature; in the part of the spectrum which is optically thin, the planet radiates at near the surface temperature. Increasing CO2 then increases the width of the spectral region where the atmosphere is optically thick, which replaces more of the high-intensity surface radiation with low-intensity upper-atmosphere radiation, and thus reduces the rate of radiation loss to space.
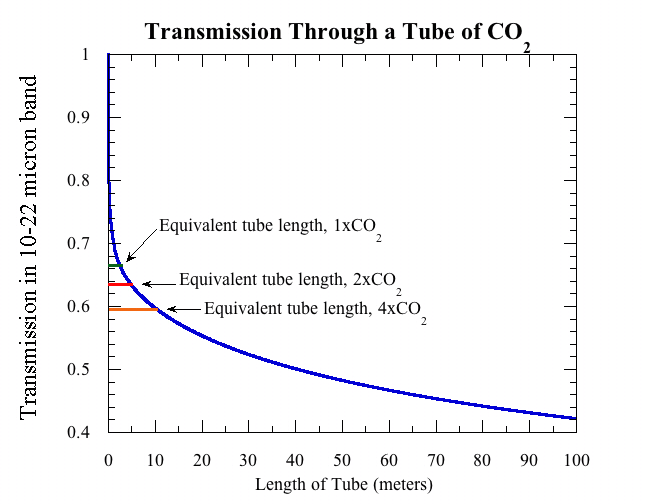
Now let’s use the absorption properties described above to determine what we’d see in a typical laboratory experiment. Imagine that our experimenter fills a tube with pure CO2 at a pressure of one atmosphere and a temperature of 20C. She then shines a beam of infrared light in one end of the tube. To keep things simple, let’s assume that the beam of light has uniform intensity at all wavelengths shown in the absorption graph. She then measures the amount of light coming out the other end of the tube, and divides it by the amount of light being shone in. The ratio is the transmission. How does the transmission change as we make the tube longer?
To put the results in perspective, it is useful to keep in mind that at a CO2 concentration of 300ppm, the amount of CO2 in a column of the Earth’s atmosphere having cross section area equal to that of the tube is equal to the amount of CO2 in a tube of pure CO2 of length 2.5 meters, if the tube is at sea level pressure and a temperature of 20C. Thus a two and a half meter tube of pure CO2 in lab conditions is, loosely speaking, like "one atmosphere" of greenhouse effect. The following graph shows how the proportion of light transmitted through the tube goes down as the tube is made longer.
The transmission decays extremely rapidly for short tubes (under a centimeter or so), because when light first encounters CO2, it’s the easy pickings near the peak of the absorption spectrum that are eaten up first. At larger tube lengths, because of shape of the curve of absorption vs. wavelength, the transmission decreases rather slowly with the amount of CO2. And it’s a good thing it does. You can show that if the transmission decayed exponentially, as it would if the absorption factor were independent of wavelength, then doubling CO2 would warm the Earth by about 50 degrees C instead of 2 to 4 degrees (which is plenty bad enough, once you factor in that warming is greater over land vs. ocean and at high Northern latitudes).
There are a few finer points we need to take into account in order to relate this experiment to the absorption by CO2 in the actual atmosphere. The first is the effect of pressure broadening. Because absorption lines become narrower as pressure goes down, and because more of the spectrum is "between" lines rather than "on" line centers, the absorption coefficient on the whole tends to go down linearly with pressure. Therefore, by computing (or measuring) the absorption at sea level pressure, we are overestimating the absorption of the CO2 actually in place in the higher, lower-pressure parts of the atmosphere. It turns out that when this is properly taken into account, you have to reduce the column length at sea level pressure by a factor of 2 to have the equivalent absorption effect of the same amount of CO2 in the real atmosphere. Thus, you’d measure absorption in a 1.25 meter column in the laboratory to get something more representative of the real atmosphere. The second effect comes from the fact that CO2 colliding with itself in a tube of pure CO2 broadens the lines about 30% more than does CO2 colliding with N2 or O2 in air, which results in an additional slight overestimate of the absorption in the laboratory experiment. Neither of these effects would significantly affect the impression of saturation obtained in a laboratory experiment, though. CO2 is not much less saturated for a 1 meter column than it is for a 2.5 meter column.
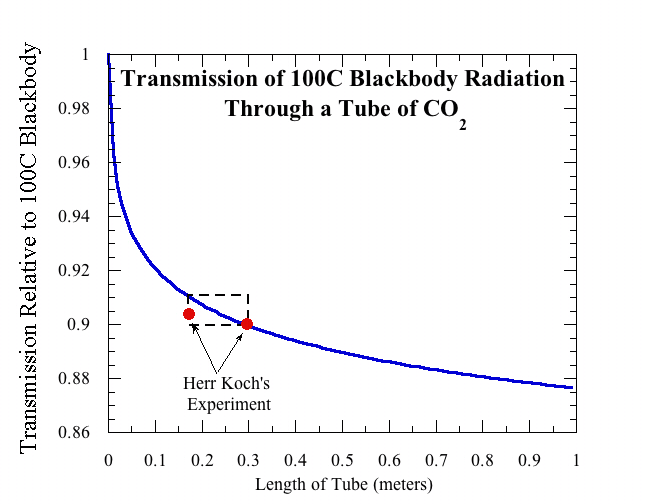
So what went wrong in the experiment of poor Herr Koch? There are two changes that need to be made in order to bring our calculations in line with Herr Koch’s experimental setup. First, he used a blackbody at 100C (basically, a pot of boiling water) as the source for his infrared radiation, and measured the transmission relative to the full blackbody emission of the source. By suitably weighting the incoming radiation, it is a simple matter to recompute the transmission through a tube in a way compatible to Koch’s definition. The second difference is that Herr Koch didn’t actually perform his experiment by varying the length of the tube. He did the control case at a pressure of 1 atmosphere in a tube of length 30cm. His reduced-CO2 case was not done with a shorter tube, but rather by keeping the same tube and reducing the pressure to 2/3 atmosphere (666mb, or 520 mm of Mercury in his units). Rather than displaying the absorption as a function of pressure, we have used modern results on pressure scaling to rephrase Herr Koch’s measurement in terms of what he would have seen if he had done the experiment with a shortened tube instead. This allows us to plot his experiment on a graph of transmission vs. tube length similar to what was shown above. The result is shown here:
Over the range of CO2 amounts covered in the experiment, one doesn’t actually expect much variation in the absorption — only about a percent. Herr Koch’s measurements are very close to the correct absorption for the 30cm control case, but he told his boss that the radiation that got through at lower pressure increased by no more than 0.4%. Well, he wouldn’t be the only lab assistant who was over-optimistic in reporting his accuracy. Even if the experiment had been done accurately, it’s unclear whether the investigators would have considered the one percent change in transmission "significant," since they already regarded their measured half percent change as "insignificant."
It seems that Ångström was all too eager to conclude that CO2 absorption was saturated based on the "insignificance" of the change, whereas the real problem was that they were looking at changes over a far too small range of CO2 amounts. If Koch and Ångström had examined the changes over the range between a 10cm and 1 meter tube, they probably would have been able to determine the correct law for increase of absorption with amount, despite the primitive instruments available at the time.
It’s worth noting that Ångström’s erroneous conclusion regarding saturation did not arise from his failure to understand how pressure affects absorption lines. That would at least have been forgivable, since the phenomenon of pressure broadening was not to be discovered for many years to come. In reality, though Ångström would have come to the same erroneous conclusion even if the experiment had been done with the same amounts of CO2 at low pressure rather than at near-sea-level pressures. A calculation like that done above shows that, using the same amounts of CO2 in the high vs. low CO2 cases as in the original experiment, the magnitude of the absorption change the investigators were trying to measure is almost exactly the same — about 1 percent — regardless of whether the experiment is carried out at near 1000mb (sea level pressure) or near 100mb (the pressure about 16 km up in the atmosphere).

Rod, technically, it’s not a blackbody spectrum as such, but if you place a black body at that point, it will heat up to roughly that temperature.
Harold, OK, so arrogating to yourself an aura of expertise based on your experience in a field related to climate studies by only the slimmest of threads–that’s OK. Calling you on it is a cheap shot. Whatever, dude, just trying to understand the rules of engagement here.
Re: #150 (Harold Pierce Jr)
Your post #120 is so full of the most basic falsehoods that it’s impossible to take your claim of expertise seriously. It seems to me that Ray Ladbury was pretty easy on you.
Re 153: I’m a slave to my generous nature.
tamino (#153) wrote:
I suppose I should really thank him…
I have been working on a page devoted to climate change fallacies as part of something a bit larger, and the material he wrote looks like good source material! What do you think: should credit him as a source?
re 151: absolutely true, Ray. […but you can’t seem to admit that electrostatic and magnetic flux (radiation) itself has no temperature…]
From the AMS http://amsglossary.allenpress.com/glossary/search?id=local-thermodynamic-equilibrium1
local thermodynamic equilibrium�(Abbreviated LTE.) A condition under which matter emits radiation based on its intrinsic properties and its temperature, uninfluenced by the magnitude of any incident radiation.
LTE occurs when the radiant energy absorbed by a molecule is distributed across other molecules by collisions before it is reradiated by emission. LTE is needed for Planck’s law and Kirchhoff’s law to apply, and is typically satisfied at atmospheric pressures higher than about 0.05 mb. Laser radiation is an example of non-LTE emission.
Eli Rabett (#154) wrote:
Thank you, Eli. That answers a number of questions.
Actually, I had done a little reading earlier today, and I ran across the fact that a local thermodynamic equilibrium requires the local kinetic temperature to be equal to the Planckian temperature.
Please see:
Local Thermodynamic Equilibrium — from Eric Weisstein’s World of Physics
http://scienceworld.wolfram.com/physics/LocalThermodynamicEquilibrium.html
Given what you have just said, a few pieces have started to fall together for me. If the matter corresponding to the kinetic temperature and the radiation corresponding to the Planckian temperature are strongly interacting, in all likelihood we have a local thermodynamic equilibrium.
I had been wondering how moist air convection would enter into this, whether it would result in a violation of the local thermodynamic equilibrium – but given what you have just stated, it would appear to be irrelevant since the local thermodynamic equilibrium would be a very good approximation on a small timescale (which is all that would be required for it to be considered as being applicable within a given environment) and convection would become important only over much greater time scales.
The same link above includes a link to a piece on Kirchoff’s law which argues that it is still “applicable” even under non-equilibrium conditions – if one performs a suitable averaging over all wavelengths. Of course, it is strictly applicable, that is, under LTE, it is applicable at each individual wavelength considered independently of the other wavelengths. Incidently, if I remember correctly, Gavin (?) mentioned at one point that it was by means of treating each wavelength independently of the rest that Kirchoff was first able to derive the law in the first place. This would seem to be a fairly weak derivation – if one were under the assumption that local thermodynamic equilibria were few and far between rather than realizing that they were the rule, not the exception.
Rod B.,
The concept of temperature in a radiation field is useful–photons interact after all and so have a thermodynamics of their own. BTW, you do realize that it’s possible to have a negative temperature (e.g. a population inversion), and if you do, it corresponds to a higher energy state than a positive temperature. Of course, left to itself, such a negative temperature state will quickly decay to a normal Arrhenius distribution, but you need to remember that all thermodynamic concepts are somewhat subtle–not to mention widely applicable. Do you remember the results from the last run at the Relativistic Heavy Ion Collider at Brookhaven? They were talking about the temperature of a quark-gluon plasma created by slamming uranium atoms together. That surely goes beyond anything Boltamann envisioned.
Re #149: Ray, your comments on thermodynamic equilibrium did help me to re-think about how the atmosphere behaves. I might have found my missing link. This is where I am now:
When we follow the radiative process of the greenhouse effect, we see the Earth radiates infrared radiation, which is absorbed by greenhouse gases. This gets converted into kinetic energy, which means the air is warmer. The kinetic energy in turn excites the greenhouse gas molecules which causes them to emit infrared radiation in all directions. Some of this (ie. 324 watts per square meter) reaches the ground and warms the surface of the Earth.
So the air and the surface are being warmed by this process. But most of it takes place in the lower atmosphere, where there is ten times more water vapor than carbon dioxide, and water vapor absorbs over a wider spectrum. It seems that carbon dioxide can only contribute a few percent to the greenhouse effect.
But Raypierre makes a startling statement: If there was no temperature gradient in the atmosphere there would be no greenhouse effect. Lets construct that world and see what happens, by confining all the greenhouse gases to the lower atmosphere. All the same absorption and re-radiation of longwave energy will take place as it does now. The surface will receive the same 324 W/m2 of infrared radiation. The only difference is that those greenhouse gas molecules that radiate into space will do so at a higher temperature, the same as that at the surface. The higher temperature means more energy is being lost.
Where does that energy come from? It has to come from the surface of the Earth, and get there by convection. That would mean a lot more convection than what we have today. It appears that in this world the greenhouse gases do not lead to any warming, all they do is make the atmosphere a lot more violent. Instead of heat energy we get wind energy.
If we let our greenhouse gases seep higher into the atmosphere, they get cooler and radiate at a lower temperature. Less energy is lost, and there is less convection from the surface to compensate. More heat energy is retained, and the Earth gets warmer.
Relatively more carbon dioxide makes it to the upper atmosphere than water vapor, which condenses at lower temperatures. Therefore carbon dioxide plays a larger role in raising the altitude at which the atmosphere radiates into space. This explains why it appears to punch above its weight, contributing about 20 percent of the greenhouse effect instead of 2 or 3 percent.
Does this make sense?
Blair (160), a quicky while I digest the rest of your post: If the molecule heats up with IR absorption, why wouldn’t it cool down with later IR emission??
Blair,
Let’s think of it this way. First how does energy get where it’s going. Well, the surface warms because sunlight hits it. Water evaporates and the surface heats the air. Water vapor and air rise, transporting lots of energy to the mid to upper troposphere–this is the dominant process for transporting energy to levels up to the stratosphere. Energy in the stratosphere gets there mainly from incoming UV sunlight being absorbed by O3 molecules, but there’s a small contribution from outgoing longwave radiation–OLR–(infrared or IR). OK, so how does the upper troposphere and stratosphere get rid of energy. Well, it can go back to the surface as wind or storms, but that keeps the energy in the system. The only way the climate loses energy is by OLR. Now OLR is not a very efficient energy transport mechanism. You only get it two ways: A collision excites a rotational or vibrational mode that relaxes via OLR or an OLR photon from below excites a mode that then decays via OLR. Collisional excitation is not common at atmospheric temperatures (only a few percent of molecules have such energies at these temperatures), but there are still lots and lots of molecules, so it happens. Only half the photons emitted on average will still be outbound. Moreover, if the atmosphere is sufficiently dense, there’s a good chance that the excited molecule will decay collisionally rather than radiatively. So, basically, near the surface, where the atmosphere is dense, there’s virtually no chance that an IR photon in the sensitive band of a greenhouse molecule will escape.
OK. Let’s look at Earth from a satellite. Where are the photons we see coming from. Looking at a spectral range far from any absorption lines, we’re seeing photons coming right from the surface. Now what about a photon in the absorption region of water (too broad to be a “line”)–any chance it came from the lower troposphere? Nope. It would be gobbled up again immediately–it had to come from the cloud tops. above which there’s virtually no water. What about CO2’s absorption lines–well CO2 is present and well mixed into the lower stratosphere at least, so a photon in this band is unlikely to escape before another CO2 molecule gobbles it up. And so the OLR in this band has to be coming from very high up, where the CO2 concentration is feeble enough that the probability of the photon being absorbed is small. But it’s very cold at the top of the troposphere/bottom of the stratosphere, so far fewer molecules will be excited collisionally, and the OLR in the CO2 band will be weak here. So the IR radiation in the CO2 band is an LTE process.
To summarize: The probability of an IR photon from the surface in the absoprtion region of a ghg escaping the atmosphere is virtually nil. It will be absorbed and a lower flux (decreased by 1/2 by the direction of the photon and by nonradiative relaxation) will be emitted, consistent with the temperature of the gas where this takes place. The process will repeat until the density of the greenhouse gas is sufficiently low above that the photon has a chance of escaping without being reabsorbed. Thus the intensity in this band will look like it comes from a source with the temperature of the region where the ghg peters out. Add more CO2 and the region where this density occurs rises and gets cooler so the emission in the band is more feeble. Less radiation overall escapes, so the planet warms until the OLR again equals the incoming radiation.
Does this make sense, Blair?
A quick question. I have been having a hard time finding a good reference that characterizes the CO2 content vs altitude in the stratosphere. Spencer states that CO2 is well mixed well into the stratosphere. I’ve found a couple of references that say that at the troposphere/stratosphere boundary the CO2 content drops by 5-7 ppmv, but I have one guy contending that at the stratosphere boundary the CO2 content drops to 52 ppmv and one contending there is zero CO2 in the stratosphere. The references I’ve found on line are abstracts from rather old Nature articles. Anyone got anything better?
Re #162: On a macro scale, energy is absorbed near the surface, and lost in the upper atmosphere. Convection is the connection between them. Am I right to say that this is the process that drives the convection?
How about this: The greenhouse effect drives convection in the atmosphere by separating the region of heat gain near the surface from the region of heat radiation into space higher in the atmosphere. The lapse rate (fall in temperature with altitude), not primarily caused by the greenhouse effect, is responsible for greenhouse warming, because a colder greenhouse gas radiates less energy. A smaller lapse rate would mean more energy lost from the upper atmosphere, leading to more turbulence and less warming. A higher lapse rate means less energy is lost, thus more warming and less energy differential to drive turbulence.
On a micro level, I want to examine this statement:
The first sentance seems meaningless to me without a time scale. I expect to see something like “5 percent collisional excitation per second at 15 deg. C.”
Are you also saying that in a denser atmosphere there is less collisional excitation? Implying it goes up with temperature but down with pressure?
To clarify what I said above, the main driver in the atmosphere is the temperature difference between the equator and poles. This is a horizontal force, as opposed to the vertical force caused by the greenhouse effect.
The difference in solar radiation reaching the equator and polar regions is roughly the same as the 235 watts per square meter that need to be transported up into the atmosphere to be dumped into space, but the distance is smaller. I wonder how these forces compare in magnitude?
[[Blair (160), a quicky while I digest the rest of your post: If the molecule heats up with IR absorption, why wouldn’t it cool down with later IR emission?? ]]
Again, individual molecules don’t have a temperature, groups of molecules do. But extrapolating the question to a whole layer of atmosphere, you can have radiative balance at many different possible temperatures. The more IR a layer is absorbing, the higher the temperature at which it will achieve radiative equilibrium. (Or in the real atmosphere, radiative-convective equilibrium.)
Barton, I think I have a word problem —- when they cool a single atom, what is it being measured in this work if not temperature? The words make it hard for me to grok. Maybe others are having the same language trouble as well. It’s likely the ‘physics for poets’ problem — using words where only math really explains what’s happening. When they cool a single atom, if it doesn’t have a temperature, what does it have less of after the procedure?
P Maunz, T Puppe, I Schuster, N Syassen, et alâ�¦ – Nature, 2004 – nature.com
… Cavity cooling of a single atom ….. Cooling of a single atom in an optical trap inside a resonator.
Hello:
I have a climate-change skeptic who has asked me to detail his misconceptions based on his inability to understand why man-made CO2 is the cause of global warming and how warming can be stopped by limiting CO2 emissions. I don’t want to take up or detract from the threads of both Parts I and II, which I have read and will reread to try to understand the arguments, but I’m not an atmospheric physicist/chemist and can’t adequately respond to his questions. I assume my email address can be “seen” by the moderator, and if he/she would be willing to discuss this with me “off-line”, I’d be much obliged. Thanks.
Hank, In a single-atom trap, what they are doing is decreasing the kinetic energy of a single atom to the point where it can be confined with a laser and magnetic field. It’s kinetic energy, not temperature, per se. This is done to look at excitation/relaxation or radioactive decay properties of that single atom.
In a Bose-Einstein condensation experiment, they use similar techniques to cool an assemblage of atoms to the point where their quantum nature as bosons becomes apparent. Here, it is adequateto talk temperature.
Thanks Ray; I nitpick at this because I think “cooling” and “warming” make people think of “temperature” — it’s a word problem, that the word doesn’t apply to cooling a single atom, or to what changeswhen a single molecule absorbs or emits an infrared photon, yet when all the kinetic energy that can be removed is removed, we’re still approaching “absolute zero” and, again, “zero” makes people think it’s a temperature.
Just foraging for simpler terms that still explain what’s meant.
I thought we (well, many of us) had concluded/agreed that an individual gas molecule has kinetic energy and temperature, which is pretty much defined by kinetic energy. Now I’m reading again that single molecules have no temperature. Can we get this figured out? How about a vote, maybe leading to a consensus?
re 157, 158: If the Planckian and Maxwellian components are in equlibrium, would we not expect that a thermometer dressed in black would read the same as one in white?
Or does “local” mean “narrow region of frequency”?
Rod, “temperature” is a word problem. I think it’s clear that temperature is an average, in macroscopic work.
Microscopic and submicroscopic work is different. Excerpts below from various definitions:
Temperature is a measure of the average kinetic energy of the particles in a sample of matter.
en.wikipedia.org/wiki/Temperature
In thermodynamics, the integrating factor of the differential equation referred to as the first law of thermodynamics.
In statistical mechanics, a measure of translational molecular kinetic energy (with three degrees of freedom).
http://www.novalynx.com/glossary-t.html
… the measurement of how fast the molecules are moving back and forth.
http://www.uwsp.edu/cnr/wcee/keep/Mod1/Unitall/definitions.htm
temperature is what you measure with a thermometer (this is kind of an operational definition).
… the temperature of a system tells how much the internal energy of the system grows upon a given increase of entropy
http://www.maxwellian.demon.co.uk/faq/glossary.html
Temperature refers to the temperature of the ambient air excluding direct heating of the sensor by solar radiation.
http://rps.uvi.edu/WRRI/glossary.html Glossary of Meteorological Terms
#168 Tabor:
Have a look at this:
http://gristmill.grist.org/skeptics
for clarification on common skeptic views. (RealClimate isn’t well suited to this sort of work ;-) )
I wanted to provide more detail on my previous request. I have a scientific background (Ph. D. in plant ecology) and a research background in paleoecology. So, I understand climate history, but lack training in atmospheric chemistry and physics. I work for a non-profit conservation organization and have been having conversations with a donor about climate change. He is insistent that CO2 does not matter for current warming (he also argues for saturation, which is amply covered here). Here is an excerpt of how he describes the greenhouse effect:
“CO2 is well mixed with the other gases and is present from ground level to high altitudes. No radiation from the earth is reflected back. At altitude the air is colder, so the radiation is absorbed by a cold gas. Gore states that there is enough CO2 to absorb all the radiation in the opaque regions of the CO2 and none escapes – it just warms the CO2. There is also a radiative transfer between the warm earth and the cold gas which warms the gas and cools the earth, but this may be small.”
He cannot follow “Gore’s scheme” – Gore “says that adding CO2 will make the earth’s radiation warm the CO2 at lower altitudes, thus causing a slight warming. This in turn allows the atmosphere to hold more water vapor. This causes major global warming. Here is why I disagree. The earth’s radiation goes equally in all directions, so only the nearly vertical rays are absorbed at altitude, and the lower portion gets the most heat. Adding CO2 should not change this.”
My skeptic goes on to say that “CO2 makes up about .0003 of the atmosphere. Heating this one degree raises the temperature of the atmosphere by .0003 degrees..”
Having read through both parts I and II and read the responses, I have little trouble seeing the errors in his thinking. Take the last paragraph – I have read elsewhere, CO2 contributes app. 25% or more of the warming effect (with a range around that number) – most of the gas in the atmosphere N2 and O2 are not radiative gases and don’t contribute to greenhouse warming. So, the thinking that greenhouse warming is directly and simply proportional to CO2 relative concentration not to mention that the greenhouse effect is a consequence of “warming: CO2 are off base.
He also is wrong in stating that no radiation from the earth is reflected back. As was described in Part I, some of the absorbed IR is re-radiated in all directions. And, his description of Gore’s “scheme” is off.
This thread describes in detail how the greenhouse effect works, and how adding CO2 will lead to more warming, but I wanted to make sure I’m not missing anything, or that my friend is not raising something that hasn’t been covered here.
Thanks.
#174
I’ve checked that out, and provided more detail in my next post, realizing that my post was not specific enough to warrant comment. The grist site does not address the issues that are being discussed here, as far as I can tell, for example, that site has not posted anything on saturation.
Hank, I realize this is starting to sound like an arcane philosophical debate, but I think the concept is important. I didn’t see any of your sources in 173 that prohibited the state of just one molecule. Though they all implied/stated the predominately practical situation of moles of molecules. E.g. “the average kinetic energy of the particles in a sample of matter.”: how large a sample? 1023molecules? 10,000? Two? Hey, how about one? Average kinetic energy comes from a bunch of individual molecules all having their own individual kinetic energy (per Boltzman distribution for gasses). Now I recognize that its pretty hard to get a Boltzman distribution average when you get down to 2 or 3 molecules. But those 2 or 3 (or ONE) still have kinetic energy and hence temperature.
This seems important to me to get my hands around the process of radiation absorption/emission, energy transfer (to what in the sub-molecular or even sub-atomic level), variations of temperature for all of these processes, etc. I need to understand how it works at the molecular/atomic level — and that means ONE. That’s really the only way (for me at least) to understand the physics. Start with one electron, neutron, atom, molecule, photon, unit charge, etc. and go from there. If one molecule doesn’t get hotter, none do. The common accepted usage of the term not withstanding.
Taber, if you can find out your donor’s source for his beliefs, it may be helpful. I tried some searches using phrases from your description and didn’t get a hit. In general it’s a familiar denial statement, but knowing more particularly if he’s relying on a PR site or a political source or one of the sites that claims to be science info may help clarify what he’s thinking and why.
Re #163
Ray,
This is more recent than your old Nature articles. It hasn’t been published yet! Figure 3 shows the vertical (and latitudinal) distribution of CO2.
Atmos. Chem. Phys. Discuss., 7, 9973-10017, 2007
http://www.atmos-chem-phys-discuss.net/7/9973/2007/
© Author(s) 2007. This work is licensed under a Creative Commons License.
MIPAS reference atmospheres and comparisons to V4.61/V4.62 MIPAS level 2 geophysical data sets
J. J. Remedios1, R. J. Leigh1, A. M. Waterfall2, D. P. Moore1, H. Sembhi1, I. Parkes1, J. Greenhough1, M.P. Chipperfield3, and D. Hauglustaine
http://www.atmos-chem-phys-discuss.net/7/9973/2007/acpd-7-9973-2007.html
I think that the sudden drop in concentration above 80 km is due to the CO2 molecule being heavier than other air molecules. See http://www.atmos-chem-phys-discuss.net/7/9973/2007/acpd-7-9973-2007.pdf
[Response: I don’t think so – I think it is related to the photolytic destruction of CO2 in the mesosphere. (i.e. http://www.cosis.net/abstracts/EGU04/05569/EGU04-J-05569.pdf ) – gavin]
Touche Gavin!
But over 70 km is in the ignorosphere, where the atmosphere begins to become non-uniform, with the scale heights of chemical species differing by their molecular weights. See http://en.wikipedia.org/wiki/Mesosphere
Rod, some of the cites define temperature as an “average” — can you get an average temperature for a single molecule? Perhaps with multiple measurements.
Other cites define temperature in terms of the solution to the thermodynamic equation, the sum of kinetic energy.
This is a poetry question, not a physics argument:
http://www.newscientist.com/blog/shortsharpscience/
Tuesday, July 10, 2007 The poetry of science
What do poets and scientists have in common?
“… the need to communicate new and unfamiliar concepts â�� for which appropriate words and metaphors may not already exist â�� without resorting to lazy clichés that may distort the meaning….so much science now happens at a level we canâ��t see, so science depends more and more on metaphor and analogy to communicate itself.”
Clearly when people above say a molecule doesn’t have a temperature they mean they can’t calculate an average with one item. Clearly other writers use the word temperature to mean the kinetic energy in the one item.
Recall the 11th Commandment: “You do too know what I mean!” Doesn’t it apply to this discussion?
Taber Allison — I’m probably more of an amateur at this than you, but to me it appears that you have the essentials, and haven’t missed anything important for your purposes.
Hank, it’s more fundamental than that. Remember the precise physical definition of temperature–partial derivative of energy wrt entropy (holding # of particles and volume constant). You can’t define the entropy of a single particle, so the definition breaks down when you have a single particle. There is more to temperature than kinetic energy.
Re #175: Taber, most of the statements made by your skeptic are wrong, including some of those attributed to Gore. But there is one main misconception behind it all. The simplest model used to explain the greenhouse effect is that it acts like a blanket to keep the Earth warm. And that is fine if you are willing to take the scientist’s word for it and have no inclination to explore further.
But as soon as you look at the actual composition of the atmosphere the blanket model falls apart. As I am sure you realize from reading here, it is a lot more complicated than that. Your head is probably spinning from all the detail. Mine is.
Basically, the greenhouse does not work simply by absorbing heat and warming the air. If it did, your skeptic would be right that carbon dioxide can only play minor role and doubling it would not make much difference.
Instead, it works by changing the temperature at which the Earth loses energy into space. So while a great number of greenhouse gas molecules may absorb and re-radiate energy, the one that matters is the one that radiates it into space. That is more likely to happen in the upper atmosphere, where it is colder. The lower the temperature, the less energy is lost, and the more the Earth warms.
Cold air can hold less water vapor, so it decreases with altitude. So while on average there is ten times as much water vapor, there is relatively a lot more carbon dioxide in the upper atmosphere where it matters.
There are probably gaps in this explanation that you do not quite follow. If so, then ask. That is what this forum is about. I am still having trouble connecting the heat gain at the surface and lower atmosphere with the heat loss in the upper atmosphere. I am sure the answer is convection, but the details are not clear.
Alastair (and Gavin), thanks for the references–just what I needed. They guy on the other end of this debate is using science that is about 50 years out of data–i’t like he spent the last 50 years in a coma. Damn, I forgot to ask him if he knew who Milli Vanilli (sp) was. ;-)
This horse is still kicking. It’s not obvious to me that I can’t get the average of one thing, unless I’m constrained by an arbitrary (for good reason maybe) construct of the definition. One house sold in all of Podunk County last year; what was the average sale price of houses in Podunk last year? None??? I’ll have to think about it.
So I can’t have temp with one molecule, but I can with TWO??? What if I start with one (no temp) and then add another from a distant unconnected place which had/has no temp (’cause it was/is just one), do I now have two molecules with no temp? Gets me back to the earlier post — if I have just one molecule and it has no temperature, does it have no kinetic energy? And if it crashes elastically into a wall, no energy/temp is transferred??? I certainly understand the usefulness of the “average” concept. But taken to the extreme of “one molecule can not have temp” creates absurdity after absurdity. And I want to know exactly what happens, say, when one photon is absorbed by one CO2 molecule. Does its energy and temperature not increase (from nothing?!?!) if its up there by itself? Does it increase if other molecules are in the vicinity (BTW, how near do the others have to be to count??)? It’s starting to sound a lot like the magical enigma of particle/quantum physics…
This is why the Buddha said the first thing is the rectification of names (wry grin).
“Hotter” — can mean for one molecule, an increase in energy? But “hotter” not in temperature beacuse for temperature you need more than one molecule; “hotter” as in, er, livelier, more energetic, more spread out, whatever. Stirred up.
Two molecules, the one that got stirred up can pass some of that excitedness by bumping it, or by passing a photon from the one to the other. Have we got “temperature” with two molecules?
I’m banging on the words because Rod’s having trouble seeing how one molecule can absorb a photon, get more excited, then bump into another molecule and pass th at excitation on. Let’s try it for the fifth grader level and see if there are words that can be helpful.
We know it _happens_ so we know it’s real, but real means mathematics; finding words is up to us.
Let me introduce the idea of an ensemble. Take your one molecule. Put it in a box (this turns out to be important if you actually do the exercise) whose walls are at temperature T. Now imagine you have an infinite number of such boxes, so that the molecule is moving at all possible velocities subject to the constraint that the walls are at temperature T. You will find that the translational, vibrational and rotational average energy distributions are specified by the temperature T.
and remember: http://lemoncustard.com/media/rf8.gif
Rod B (#186) wrote:
For me the idea of a single molecule having a temperature is sounds like that Zen Koan question of,
“What is the sound of one hand clapping?”
I think for pretty much the same reason. When you are talking about temperature, you are speaking of a distribution of velocities, but if there is only one molecule, there can be no distribution or spread.
It makes about as much sense as the fact that you can’t have someone be a parent without their being the parent of someone. That with only one straight line, you can’t have something which is crooked. That to make a right angle with straight lines, you need more than one straight line. Temperature seems to be a quality when you first think of it, at least with human-scale objects, and structure might seem to be the same sort of thing, at least when one considers a single large object. But the structure of a thing consists of the relationships which exist among its parts, their positions and how they are connected.
Consider me with my four limbs and counting my neck and head as a fifth. Now rotate each in the same way so that my left arm is where my left leg used to be, and my left leg is where my right leg used to be. Now that is something that seems especially absurd.
The relationships matter. But to have a relationship requires two or more things.
“Distribution” sounds like a spatial concept, and that is roughly how they handle the “velocity distribution” in “phase space.”
#177 There’s no doubt that Boltzmann defined his thermodynamic laws on the basis of statistical mechanics, as was Einstein’s study of Brownian motion in 1905. If you start looking at the internal energies of molecules, you need to look at how energy is bound up in the bonds between atoms, if you start looking at individual atoms you need to start looking at spin and quantum electron states. Sooner or later, you’ll end up with the Standard model of QCD and perhaps have to get into debates about String theory!
However, I think this is all going in the wrong direction.
The point is that earth can only receive and lose heat via electromagnetic radiation at its boundary layer. The “messenger” is always the photon.
So it’s more important to look at the top of atmosphere radiation balance than go delving into the debates in fundamental high energy physics.
Re #187
Actually a molecule has four temperatures: kinetic, electronic, vibrational, and rotational. The average of the kinetic temperatures of all the molecules in a volume of gas is the Maxwellian temperature of the gas, i.e. its temperature measured with a thermometer. According to the Equipartition Theorem, when the gas is in thermodynamic equilibrium all four average temperatures will be the same. In other words the average kinetic, electronic, vibrational, and rotational temperatures will all be equal. But any two molecules in the gas will have different kinetic temperatures, and their other temperature will not necessarily be equal to their kinetic temperatures.
For instance, if a CO2 molecule absorbs a photon, then its vibrational temperature will increase, but its kinetic temperature will initially remain unchanged. If it is relaxed by a collision with an air molecule, then the air molecule will have a higher kinetic temperature, and so the air will have a higher Maxwellian temperature. In other words, the air warms (but not by much!)
[[My skeptic goes on to say that “CO2 makes up about .0003 of the atmosphere. Heating this one degree raises the temperature of the atmosphere by .0003 degrees..”]]
The increased energy of the greenhouse gas is almost immediately distributed throughout local air by collisions. You don’t have CO2 heating up by 1 degree and everything else staying the same temperature. The whole atmosphere heats up.
Rod B.,
First, the concept of an average doesn’t make sense if you are talking about averaging over a sample size of one. There, you are dealing with exact measurements. For a sample size of 2, you can come up with a meaningful average, but the concept of the average is not very useful, since two states may have the same average properties, but very different energy distributions for the two molecules. And so on. Remember in statistics class, the place where you could start approximating various distributions (Poisson, binomial…) as Normal was sample size of ~30. The larger the ensemble the harder it becomes to specify the system in terms of the energies of the indivicual molecules, but the more meaningful the average properties start to be.
Second thing to keep in mind. The concept of temperature dates from the very early history of thermodynamics–when heat was considered a kind of fluid. Temperature was the gradient that said which direction heat flowed. As thermodynamics became more formal, the temperature came to mean something very specific in the relation between energy and entropy–specifically it was the partial derivative (or slope) in the change in energy for a change in entropy (other variables held constant). The relationship between average energy (kinetic, potential, etc.) and temperature comes out of Maxwell’s (or more generally the Arrhenius) distribution, which relates temperature and average energy. Also, keep in mind that it’s not just kinetic energy, we’re talking about here–that only holds for billiard-ball molecules with no internal degrees of freedom. And don’t forget that tempearature applies to solids as well, where it relates to the energy levels of the oscillations between atoms in the solid (and that’s elastic potential and kinetic, not just kinetic).
So what you are dealing with is a concept that has 3 different meanings in 3 different models, all of which are related but just a little different.
Eli is right–you can think of things in terms of ensembles if that helps, but it’s the box-molecule system that really has the temperature in that case. When speaking of a single particle–or even 2 particles, it just makes much more sense to speak in terms of the indivudual energies of the two particles.
So there’s a common problem in explanation here —– a CO2 molecule can absorb an infrared photon, then pass the energy along to other gases, warming the atmosphere. Even though there are relatively few, they are transferring the energy.
This latter argument seems like “the straw holds only an ounce of water, there’s no way you could drink a quart of water through it — or pump a hundred gallons through it.”
I am a retired research veterinarian,ignorant of physics, and hope that I may receive a little help from correspondents to this site. To facilitate this, I would like to put the following proposition which others may rubbish at will, thus providing illumination to me:
For a stable temperature balance at ground level, it is generally argued that influent energy (from the sun) should equal effluent energy (by convection/conduction and by infra red radiation). This appears to ignore planetary sequestration of energy and its subsequent release into the atmosphere. Until recent times, some surplus energy was being locked away “in the cellar”(fossil fuels). We’ve now found the key and are gorging on the goodies we’ve discovered. We have developed technology which has enabled a massive population increase and has been accompanied by unprecedended release of heat into the atmosphere. Would this alone not be sufficient to destabilise the climate, leaving aside possible indirect greehouse effects?
I find it hard to believe that this possibility has not been previously considered. It may be so facile that it was dismissed years ago, explaining my not having heard anything of the possibility in recent debates on the subject. In any event, I would appreciate enlightenment.
If there is any merit at all in my hypothesis, the direct effect on climate may or may not summate with the indirect greenhouse effects of CO2. (I remain to be convinced of the magnitude of the latter effects despite having been impressed with Raypierre’s arguments on absence of waveband saturation in qualititave terms.)
Of course, in the unlikely event that I have made a valid case, replacement of fossil fuel with a non carbon source of energy (such as nuclear)in equal amount wouldn’t have a mitigating effect on climate change.
Douglas, Welcome. Earth recieves 1.740Ã�10^17 W from the Sun–that’s 24/7/365.25. Compare that to global energy consumption of 1.5 x 10^13 W, and you can see we’ve still got quite a lot of catching up to do. Your basic point, though is valid–energy consumption cannot increase exponentially indefinitely.
Mr. Wise, that’s been considered. The total heat produced by all human energy use (let alone the total energy stored in fossil fuels over the longer term) is extremely tiny compared to the total energy reaching the planet from the Sun. Photosynthesis just doesn’t store sunshine all that efficiently!
One source: http://www.nd.edu/~philinst/pdfs/CHAPTER6.pdf
“… Superimposing the steeply climbing curve for fossil fuel upon the gradually rising curve for biomass energy, we see an increase from roughly 960 million metric tons annual oil-equivalent consumed in 1900 to roughly 10,600 million in the late 1990s. This constitutes approximately an eleven-fold increase in overall human energy use during the 20th century.
“…. In 1750, humankind consumed roughly 260 million oil-equivalent tons of energy. By 1900, the annual total had grown to about 900 million. This amounts to something less than a 4 fold increase in 150 years. The corresponding increase for
the 100 years between 1900 and 2000 was three times greater. If we were to graph this increase on the millennium scale employed in Figure 6.1, the line of increase would show an almost vertical rise.”
It’s a lot, but not compared to sunshine: “… in 1970 the total energy consumed in the U.S. was equal to the energy of sunlight received by only 0.15% of the land area of the continental U.S.” http://adsabs.harvard.edu/abs/1974STIA…7512425W
#196 Doug Wise
I’m not certain of the answer to your question but I suspect that the answer is that the heat directly realised by humanity is small compared to the heat arriving from the sun but the effect of the carbon dioxide realised is more significant.
The appropriate analogy is probably along the lines that burning your blanket gets you a small amount of heat in the short term but keeping it in an uncombusted form will keep you warm night after night!
#196 We consume around 13 terawatts of energy per year, but the amount of solar energy incident on the planet is estimated at around 600 terawatts.
giving a ratio of roughly 2.16%.
But it gets worse, because the 13 terawatts includes hydroelectric and nuclear power production.
So human thermal energy production is probably less than 1% of incident solar radiation.
The other way of looking at it is, what was the climate like when C02 levels were much higher e.g. in the early Carboniferous before sequestration of the coal seams?
Pretty damn hot with average temperatures of around 22C compared to about 12 C today.
Later on in the middle carboniferous, conditions were not unlike today and the CO2 levels were also similar.
Cool geological periods with high C02 levels coincide with continental drift and super continents allowing ice cap formation.