By raypierre , with the gratefully acknowledged assistance of Spencer Weart
In Part I the long struggle to get beyond the fallacious saturation argument was recounted in historical terms. In Part II, I will provide a more detailed analysis for the reader interested in the technical nitty-gritty of how the absorption of infrared really depends on CO2 concentration. At the end, I will discuss Herr Koch’s experiment in the light of modern observations.
The discussion here is based on CO2 absorption data found in the HITRAN spectroscopic archive. This is the main infrared database used by atmospheric radiation modellers. This database is a legacy of the military work on infrared described in Part I , and descends from a spectroscopic archive compiled by the Air Force Geophysics Laboratory at Hanscom Field, MA (referred to in some early editions of radiative transfer textbooks as the "AFGL Tape").
Suppose we were to sit at sea level and shine an infrared flashlight with an output of one Watt upward into the sky. If all the light from the beam were then collected by an orbiting astronaut with a sufficiently large lens, what fraction of a Watt would that be? The question of saturation amounts to the following question: How would that fraction change if we increased the amount of CO2 in the atmosphere? Saturation refers to the condition where increasing the amount of CO2 fails to increase the absorption, because the CO2 was already absorbing essentially all there is to absorb at the wavelengths where it absorbs at all. Think of a conveyor belt with red, blue and green M&M candies going past. You have one fussy child sitting at the belt who only eats red M&M’s, and he can eat them fast enough to eat half of the M&M’s going past him. Thus, he reduces the M&M flux by half. If you put another equally fussy kid next to him who can eat at the same rate, she’ll eat all the remaining red M&M’s. Then, if you put a third kid in the line, it won’t result in any further decrease in the M&M flux, because all the M&M’s that they like to eat are already gone. (It will probably result in howls of disappointment, though!) You’d need an eater of green or blue M&M’s to make further reductions in the flux.
Ångström and his followers believed that the situation with CO2 and infrared was like the situation with the red M&M’s. To understand how wrong they were, we need to look at modern measurements of the rate of absorption of infrared light by CO2 . The rate of absorption is a very intricately varying function of the wavelength of the light. At any given wavelength, the amount of light surviving goes down like the exponential of the number of molecules of CO2 encountered by the beam of light. The rate of exponential decay is the absorption factor.
When the product of the absorption factor times the amount of CO2 encountered equals one, then the amount of light is reduced by a factor of 1/e, i.e. 1/2.71282… . For this, or larger, amounts of CO2,the atmosphere is optically thick at the corresponding wavelength. If you double the amount of CO2, you reduce the proportion of surviving light by an additional factor of 1/e, reducing the proportion surviving to about a tenth; if you instead halve the amount of CO2, the proportion surviving is the reciprocal of the square root of e , or about 60% , and the atmosphere is optically thin. Precisely where we draw the line between "thick" and "thin" is somewhat arbitrary, given that the absorption shades smoothly from small values to large values as the product of absorption factor with amount of CO2 increases.
The units of absorption factor depend on the units we use to measure the amount of CO2 in the column of the atmosphere encountered by the beam of light. Let’s measure our units relative to the amount of CO2 in an atmospheric column of base one square meter, present when the concentration of CO2 is 300 parts per million (about the pre-industrial value). In such units, an atmosphere with the present amount of CO2 is optically thick where the absorption coefficient is one or greater, and optically thin where the absorption coefficient is less than one. If we double the amount of CO2 in the atmosphere, then the absorption coefficient only needs to be 1/2 or greater in order to make the atmosphere optically thick.
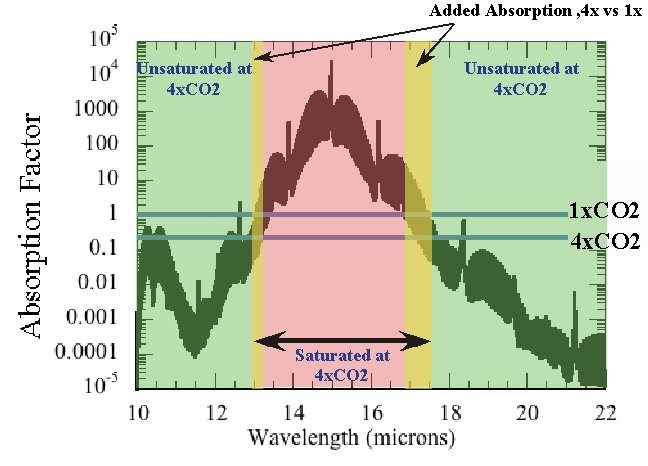
The absorption factor, so defined, is given in the following figure, based on the thousands of measurements in the HITRAN spectroscopic archive. The "fuzz" on this graph is because the absorption actually takes the form of thousands of closely spaced partially overlapping spikes. If one were to zoom in on a very small portion of the wavelength axis, one would see the fuzz resolve into discrete spikes, like the pickets on a fence. At the coarse resolution of the graph, one only sees a dark band marking out the maximum and minimum values swept out by the spike. These absorption results were computed for typical laboratory conditions, at sea level pressure and a temperature of 20 Celsius. At lower pressures, the peaks of the spikes get higher and the valleys between them get deeper, leading to a broader "fuzzy band" on absorption curves like that shown below.
We see that for the pre-industrial CO2 concentration, it is only the wavelength range between about 13.5 and 17 microns (millionths of a meter) that can be considered to be saturated. Within this range, it is indeed true that adding more CO2 would not significantly increase the amount of absorption. All the red M&M’s are already eaten. But waiting in the wings, outside this wavelength region, there’s more goodies to be had. In fact, noting that the graph is on a logarithmic axis, the atmosphere still wouldn’t be saturated even if we increased the CO2 to ten thousand times the present level. What happens to the absorption if we quadruple the amount of CO2? That story is told in the next graph:
The horizontal blue lines give the threshold CO2 needed to make the atmosphere optically thick at 1x the preindustrial CO2 level and 4x that level. Quadrupling the CO2 makes the portions of the spectrum in the yellow bands optically thick, essentially adding new absorption there and reducing the transmission of infrared through the layer. One can relate this increase in the width of the optically thick region to the "thinning and cooling" argument determining infrared loss to space as follows. Roughly speaking, in the part of the spectrum where the atmosphere is optically thick, the radiation to space occurs at the temperature of the high, cold parts of the atmosphere. That’s practically zero compared to the radiation flux at temperatures comparable to the surface temperature; in the part of the spectrum which is optically thin, the planet radiates at near the surface temperature. Increasing CO2 then increases the width of the spectral region where the atmosphere is optically thick, which replaces more of the high-intensity surface radiation with low-intensity upper-atmosphere radiation, and thus reduces the rate of radiation loss to space.
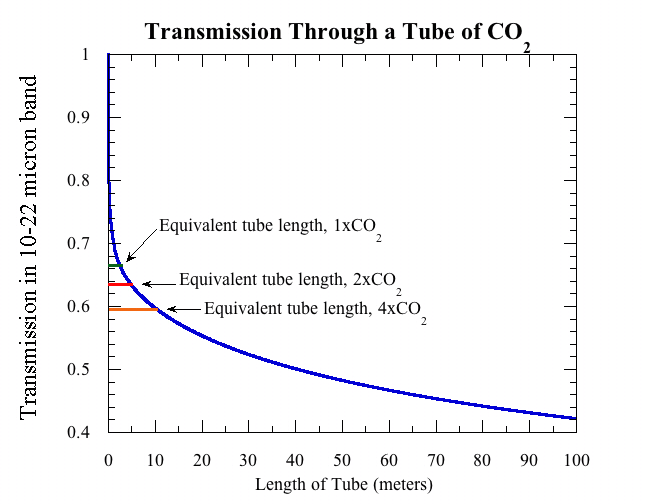
Now let’s use the absorption properties described above to determine what we’d see in a typical laboratory experiment. Imagine that our experimenter fills a tube with pure CO2 at a pressure of one atmosphere and a temperature of 20C. She then shines a beam of infrared light in one end of the tube. To keep things simple, let’s assume that the beam of light has uniform intensity at all wavelengths shown in the absorption graph. She then measures the amount of light coming out the other end of the tube, and divides it by the amount of light being shone in. The ratio is the transmission. How does the transmission change as we make the tube longer?
To put the results in perspective, it is useful to keep in mind that at a CO2 concentration of 300ppm, the amount of CO2 in a column of the Earth’s atmosphere having cross section area equal to that of the tube is equal to the amount of CO2 in a tube of pure CO2 of length 2.5 meters, if the tube is at sea level pressure and a temperature of 20C. Thus a two and a half meter tube of pure CO2 in lab conditions is, loosely speaking, like "one atmosphere" of greenhouse effect. The following graph shows how the proportion of light transmitted through the tube goes down as the tube is made longer.
The transmission decays extremely rapidly for short tubes (under a centimeter or so), because when light first encounters CO2, it’s the easy pickings near the peak of the absorption spectrum that are eaten up first. At larger tube lengths, because of shape of the curve of absorption vs. wavelength, the transmission decreases rather slowly with the amount of CO2. And it’s a good thing it does. You can show that if the transmission decayed exponentially, as it would if the absorption factor were independent of wavelength, then doubling CO2 would warm the Earth by about 50 degrees C instead of 2 to 4 degrees (which is plenty bad enough, once you factor in that warming is greater over land vs. ocean and at high Northern latitudes).
There are a few finer points we need to take into account in order to relate this experiment to the absorption by CO2 in the actual atmosphere. The first is the effect of pressure broadening. Because absorption lines become narrower as pressure goes down, and because more of the spectrum is "between" lines rather than "on" line centers, the absorption coefficient on the whole tends to go down linearly with pressure. Therefore, by computing (or measuring) the absorption at sea level pressure, we are overestimating the absorption of the CO2 actually in place in the higher, lower-pressure parts of the atmosphere. It turns out that when this is properly taken into account, you have to reduce the column length at sea level pressure by a factor of 2 to have the equivalent absorption effect of the same amount of CO2 in the real atmosphere. Thus, you’d measure absorption in a 1.25 meter column in the laboratory to get something more representative of the real atmosphere. The second effect comes from the fact that CO2 colliding with itself in a tube of pure CO2 broadens the lines about 30% more than does CO2 colliding with N2 or O2 in air, which results in an additional slight overestimate of the absorption in the laboratory experiment. Neither of these effects would significantly affect the impression of saturation obtained in a laboratory experiment, though. CO2 is not much less saturated for a 1 meter column than it is for a 2.5 meter column.
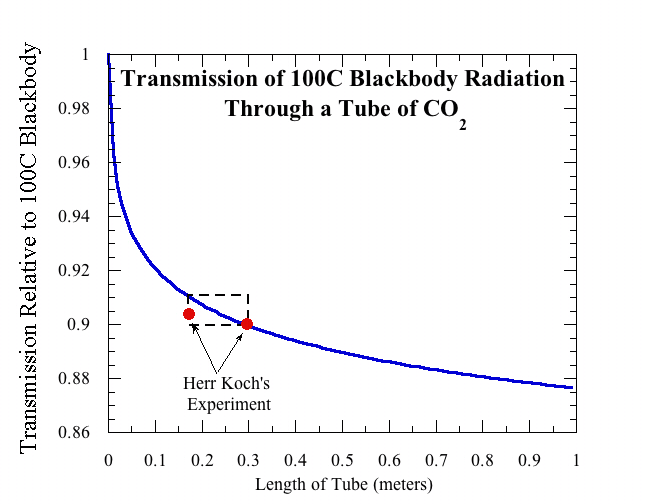
So what went wrong in the experiment of poor Herr Koch? There are two changes that need to be made in order to bring our calculations in line with Herr Koch’s experimental setup. First, he used a blackbody at 100C (basically, a pot of boiling water) as the source for his infrared radiation, and measured the transmission relative to the full blackbody emission of the source. By suitably weighting the incoming radiation, it is a simple matter to recompute the transmission through a tube in a way compatible to Koch’s definition. The second difference is that Herr Koch didn’t actually perform his experiment by varying the length of the tube. He did the control case at a pressure of 1 atmosphere in a tube of length 30cm. His reduced-CO2 case was not done with a shorter tube, but rather by keeping the same tube and reducing the pressure to 2/3 atmosphere (666mb, or 520 mm of Mercury in his units). Rather than displaying the absorption as a function of pressure, we have used modern results on pressure scaling to rephrase Herr Koch’s measurement in terms of what he would have seen if he had done the experiment with a shortened tube instead. This allows us to plot his experiment on a graph of transmission vs. tube length similar to what was shown above. The result is shown here:
Over the range of CO2 amounts covered in the experiment, one doesn’t actually expect much variation in the absorption — only about a percent. Herr Koch’s measurements are very close to the correct absorption for the 30cm control case, but he told his boss that the radiation that got through at lower pressure increased by no more than 0.4%. Well, he wouldn’t be the only lab assistant who was over-optimistic in reporting his accuracy. Even if the experiment had been done accurately, it’s unclear whether the investigators would have considered the one percent change in transmission "significant," since they already regarded their measured half percent change as "insignificant."
It seems that Ångström was all too eager to conclude that CO2 absorption was saturated based on the "insignificance" of the change, whereas the real problem was that they were looking at changes over a far too small range of CO2 amounts. If Koch and Ångström had examined the changes over the range between a 10cm and 1 meter tube, they probably would have been able to determine the correct law for increase of absorption with amount, despite the primitive instruments available at the time.
It’s worth noting that Ångström’s erroneous conclusion regarding saturation did not arise from his failure to understand how pressure affects absorption lines. That would at least have been forgivable, since the phenomenon of pressure broadening was not to be discovered for many years to come. In reality, though Ångström would have come to the same erroneous conclusion even if the experiment had been done with the same amounts of CO2 at low pressure rather than at near-sea-level pressures. A calculation like that done above shows that, using the same amounts of CO2 in the high vs. low CO2 cases as in the original experiment, the magnitude of the absorption change the investigators were trying to measure is almost exactly the same — about 1 percent — regardless of whether the experiment is carried out at near 1000mb (sea level pressure) or near 100mb (the pressure about 16 km up in the atmosphere).

Re #196: Doug, a unit of fossil fuel is only burned once, but the carbon dioxide produced remains in the atmosphere for tens or hundreds of years contributing the to greenhouse effect. The direct heat from combustion is negligible, so it is ignored.
Something I’ve been wondering about, and this seemed as good a place as
any to ask:
I’ve heard it claimed a few times (not by particularly authoritative
sources) that because CO2 higher in the atmosphere has a greater effect
on greenhouse warming (true?), emissions from aircraft have more of an
effect (per molecule) than emissions from cars, etc. Other than in the
very short term, is this true, or does the CO2 get mixed fast enough that
the difference is negligible?
Jeremy,
It’s been looked at, although the concern is not really CO2 which stay’s pretty well mixed well into the stratosphere (See Alastair’s link in response (#179) to my query above), but soot, other aerosols, water vapor, uncombusted fuel and so on could be a concern.
Many thanks to those of you who so clearly and courteously addressed the concern I raised in posting 196 – one less thing for me to be sceptical about! Before raising another, I would like to mention in passing that the two graphs in the first reference suggested to me by Hank Roberts (198)would be sufficient in themselves to convince most sceptics that we constitute a threat to the planet, even if not through the medium of CO2.
Back to the CO2 story. Can any of you take the trouble to put me right over a few other matters? I have had bad experiences of models in my own field. Perhaps climate models are more robust – they’re certainly more sophistated and complex. Nevertheless, I note that one of your lead authors has also expressed misgivings on the subject (see “The Lure of Solar Forcing”) so, perhaps, I may be allowed to question the basis for assumptions in the greenhouse gas models? I will raise a few questions which have largely been provoked by Raypierre’s lead article to this Section and a graph in Wikipedia headed, “Radiation Transmitted by the Atmosphere” in a Section entitled, “Greenhouse Gas”.
1) It is sometimes stated that, without greenhouse gasses, we’d be 33 deg C colder (all to do with equilibrium, blackbody radiation and an albedo of 0.3 as I vaguely understand it). However, why does the Royal Society suggest that we’d only be 20-30 deg C colder and why the broad range? It doesn’t suggest a great deal of certainty with the present situation and thus doesn’t inspire a huge amount of confidence in predictions of future scenarios.
2) My concern primarily rests with the subject of wavelength saturation. Clearly, reducing atmospheric CO2 would make us colder. However , will increasing it make us hotter and, if so, by how much? I am not sure whether the answers solely emanate from modellers and, if they do, whether it would be possible to test their findings by direct experimentation.
3) It is my understanding that 60% of heat escaping the earth does so by convection to the top of the atmosphere (wherever that is – top of clouds, top of stratosphere, troposphere/stratosphere interface?)where there is conversion to OLR and escape to space. This process is essentially unaffected by greenhouse gasses. The remaining 40% of escaping heat leaves the earth’s surface as IRR but only 30% of this 40% (12%) ever gets out, the rest being absorbed by greenhouse gasses. Is my understanding correct even if naively expressed, partly correct or hopelessly wrong?
4) The Wikipedia graph shows practically all escaping IR being routed through a waveband frequency of 8.5 to 15 microns (assertion based on “eyeballing” the data only). Below 8.5, water vapour alone is sufficient to absorb all IR. Above about 15 microns, overlapping absorption bands of CO2 and water vapour prevent escape. Is this correct?
5) The Hitran spectroscopic archive relating to CO2 was used to generate the graph shown by Raypierre in the lead article to this Section. A second graph was generated to show what would happen if atmospheric CO2 quadrupled. This translated to about 10% extra absorption – about 3% at 13 microns and 7% at 17 microns.
6) My problem is that I don’t know whether the Hitran data already incorporate the effects of water vapour over the 10-22 micron range shown in the graph because I don’t know how the graph was generated. If they don’t, then the 7% potential extra absorption by CO2 around the 17 micron wavelength will be irrelevant except in very dry air while the 3% around the 13 micron area will, in reality, be much less, given water vapour. My judgement here is based on the Wikipedia graph.
7) This leads me to the conclusion that, if CO2 and water vapour at current levels are considered together, addition of more atmospheric CO2 will only provide very few of Raypierre’s extra red M and Ms. In other words, it is possible that the upside of potential warming is much more constrained than has been suggested.
8) Because I have no access to numbers (not bright enough to use them if I had) and no knowledge of the assumptions of climate models, I’m probably being ridiculously naive. However, I hope you can understand the logic behind my current scepticsm.
9) Raypierre invokes a virtual female experimenter (why female – is he a romantic as his name might suggest or merely being politically correct) with a tube of CO2 and a blazing torch of IR in the 10-22 micron bandwidth. It seems a pity that she couldn’t have had a torch blasting out a true blackbody spectrum and a tube with both CO2 and water vapour in it. Better still, would it be possible actually to carry out a genuine experiment (experimenter of either sex acceptable) to allow a test of model assumptions with respect to increasing CO2 against a background of an otherwise fixed current atmosphere?
10) If surface temperatures rise, won’t increasing convection rate act as a negative feedback?
If any of you out there have the patience to give me one more push, my scepticism may finally fall away and I’ll be able to concentrate on being totally depressed by contemplating the consequences of your projections!
Can’t answer all of your questions, but I’ll try the first two:
[[1) It is sometimes stated that, without greenhouse gasses, we’d be 33 deg C colder (all to do with equilibrium, blackbody radiation and an albedo of 0.3 as I vaguely understand it). However, why does the Royal Society suggest that we’d only be 20-30 deg C colder and why the broad range? It doesn’t suggest a great deal of certainty with the present situation and thus doesn’t inspire a huge amount of confidence in predictions of future scenarios.]]
The 255 K figure for Earth’s equilibrium temperature is based on its current albedo of about 0.3. The uncertain figures are probably based on the fact that we don’t know what Earth’s albedo would be without the atmosphere. The current albedo is mostly from clouds.
[[2) My concern primarily rests with the subject of wavelength saturation. Clearly, reducing atmospheric CO2 would make us colder. However , will increasing it make us hotter and, if so, by how much? I am not sure whether the answers solely emanate from modellers and, if they do, whether it would be possible to test their findings by direct experimentation.]]
Radiative forcing by CO2 (at least for concentrations similar to those at present) appears to be logarithmic:
RF = 5.35 ln (C/C0)
where RF is in watts per square meter and concentration C and original concentration C0 are in parts per million by volume (ppmv). For doubling CO2, this gives RF = 3.7 watts per square meter. For a climate sensitivity of 0.75 K per watt per square meter, this would bring about a 2.8 K temperature increase.
Douglas, Barton does a good job on the treatment of CO2 forcing. I thought I’d chime in and correct a few misimpressions. First, convection is indeed the dominant mechanism for transporting heat–in the troposphere. However, it does not remove energy from the climate system–the energy is still in the atmosphere. The only way you lose energy is via longwave radiation that exits the atmosphere entirely (outgoing longwave radiation or OLR). Water vapor is important for many reasons. In the troposphere it is the dominant greenhouse gas, but it also drives much of the energy transport, since the heat of condensation puts a lot of energy high in the troposphere. Very high in the troposphere and into the lower stratosphere, the situation is very different. Here there is very little water vapor and much less convection (especially in the stratosphere–as the name implies).
So the question is how does the energy get from the upper troposphere where convection manages to transport it to space–and it’s here that adding CO2 makes a difference. In the upper troposphere and stratosphere, where most of the water vapor has condensed out of the atmosphere, CO2 is the dominant greenhouse gas. This is where the second blanket analogy comes from. Increase the weight of the blanket, and you are going to get warmer, because more energy will be re-radiated back into the troposphere. Does this help?
Consider that heat escaping into space has to have some form, and we call that infrared photons.
With zero greenhouse gases, the infrared photons produced when sunshine heats the surface of the planet get radiated out into space (see the link I posted earlier on measuring the temperature of the Moon during an eclipse, sorting out the heat from the surface regolith vs. the heat from the underlying rock, noting the measurement was done through the upper part of Earth’s atmosphere so correcting for water vapor here.)
With some greenhouse gases, the infrared photons coming from the heated planet get involved in the atmosphere, the heat moves among various modes, most of which can be transferred to other gases by sideswiping and bouncing off them (and no, I haven’t a clue about the quantum mechanics of those interactions, but I’m sure I’m using poetry here not math — since we’re talking about atoms and small molecules, we’re talking probabilities not freeway or billiards interactions).
The other processes make gases move in bulk; weather.
At the top of the troposphere, the bulk motion from local heating quits rising in the temperate zones; in the tropics, and over very large volcanos, the atmosphere can billow up into the cold dry stratosphere; aircraft and rockets can deposit water up there as well. Note the attention given to the increase in number and location of “polar stratospheric clouds” which are being seen further away from the poles. We’ve changed that part of the atmosphere, not for the better.
At the top of the _stratosphere_ though, we’re faced with the question of how the heat energy escapes into space.
It can’t escape very much by conduction; nothing to touch. It can’t escape much by convection; nowhere to go, except for the very small light atoms. Hydrogen can get off the planet carrying some heat as velocity, but it’s trivial.
What can escape? Infrared photons.
Where do they come from? Some made it all the way from the ground, which “glows” in the infrared range. We see satellite infrared photos, and we can see both the water vapor and the ground as brighter where they’re hotter.
Some come from water vapor emitting infrared — photons that were emitted from where the water vapor is, almost all in the troposphere, and that happened to be headed upward and continued without interacting and left the planet.
Some come from CO2, which is well mixed in the lower atmosphere and which doesn’t freeze out so isn’t removed from the stratosphere like water vapor is. Most of those infrared photons are energy that has been working its way up through the atmosphere. Remember the atmosphere is always glowing in the infrared band —- curse of the infrared astronomers, the sky is _bright_ day and night for them.
I don’t know how long it takes an infrared photon on average to go from the ground to space; but the physics predicted that when the ground got warmer as CO2 increased, the stratosphere would get colder — the lower atmosphere warms up, the gases expand, the whole atmosphere gets a bit bigger, pushing the top of it a bit higher, and as it gets higher it expands and cools.
At the top, that cooler CO2 is getting bumped and jostled by other molecules, and it’s taking it a bit more interaction to accumulate enough energy that it can cough out an infrared photon. Which can go up, down, or sideways …..
Last questions of a skeptic …
I’ve been following this website for six months, learning about climate change. I also bought several books on Amazon by Houghton and Hartmann and have checked out the AIP website. I have learned a lot, and every objection I had has been answered.
These two articles, which get to the basic spectroscopic underpinnings of the model, are excellent. I wish they had been out there when I got first got motivated to see what all the fuss was about. Most of what is available is either way too dumbed down (which only raises educated non-specialist’s skepticism) or are the original papers, themselves (which are too expensive, and too terse to understand) . Writing an article at a level to explain things in a technically correct way is very difficult without writing and entire textbook. (Yes I have downloaded Raypierre’s book and am working through it). The authors have done a great service. Thanks.
However, I still have a few remaining questions. As I understand things, the best analogy of what is happening with CO2 absorption is it is like a Venetian blind slowly closing. Yes, the line centers are totally opaque, pushing the height where radiation at those frequencies can escape so high and cold they don’t contribute much at all to the total radiation budget. This just puts more burden on th frequencies in between, in the skirts of the lines, which much radiate more power, thus requiring a higher near surface temperature.
My questions, then, are:
1) How accurate is the model of a Lorentzian for a collisoned broadened lineshape far down in the wings?
What are the basic asumptions? Yes it works for the width at half-maximum (or 1/e^2 width), but what about way way down, far from line center, in the case of very high optical density?
2) Have any direct measurements been down in the far wings on these lines (since Koch 100 yrs ago)? The spectral plots I see in these articles (and in Houghton’s book) are calculated extrapolations of fits based on two parameters: full width at half maximum (FWHM) and oscillator strength.
3) I expect the short answer to 2)is : yes, the HITRAN database. But what is the HITRAN database for? Was is designed and measured to be used for chemical identification? If so, center wavelength (CW), line strength, and a FWHM may be OK to identifiy peaks. But a full spectrum for broadband radiation models may need more measurements at widely varying concentrations to see the actual shape of the wings. Far in the wings, details of the statistics of the phase interruptions which cause the spectal broadening may be important. What if the actual absoption differs from the Lorentzian by 20%, (or 50%)? What would that mean for the temperature predictions? I was a little surprised that one author seems not to know much about the origins of HITRAN. Is this uncertainty widespread among the climate modelling community? (Hey, I realize there is an awful lot of stuff to know …)
I fully expect to find out this is a non-issue
(as all my other ideas have turned out to be!).
I probably expect that the phase kicks from collisons happen over a timescale on the order of the center frequency, and therefore the deviations would appear so far fom line center whee the absorption is so ridiculously low it is not in the picture. The phase modulations from passing molecules may be slower, though. I have to ask these questions because the consequenes for reducing CO2 by the necessary 70% (!) are very serious. Before people start writing checks with their mouths about what emission caps should be, they better be sure they can pay up when the time comes. And that we are very very sure of the physics that we CAN check.
Thanks for any thoughts on this stuff.
Re #208
Dave,
The wings of the lines are still being investigated. In April I was talking to a scientist who was working on the effects of the mixing ratios from the wings of two different absorbing gases.
You can find the story of HITRAN here at http://in-cites.com/papers/LaurenceRothman.html but note that he says that water vapour could block out the infrared radiation from a jet engine through absorption. Just think how quickly the weaker emissions of infra-red from Earth’s surface are blocked out by the thicker lower atmosphere.
In the 15 micron band cited by Ray Pierrehumbert, the optical dense lines do not get more than 30 m above the surface of the Earth. They certainly do not reach the top of the atmosphere, by definition. In that band, pretty well the only radiation that reaches the TOA is in the gaps between the lines where no absorption takes place. When you average the gaps and lines you get the band absorption. But the absorption mainly happens near the surface. It does not cascade up the atmosphere driven by falling temperatures. For CO2, Planck’s function is irrelevant, as is re-emission to the surface. Only water vapour and clouds acts in that way. But the rate of evaporation, and so the concentration of water vapour, depends amongst other things, on the concentration of CO2, and so the gross greenhouse effect does depend on CO2.
Because CO2 only acts near the surface it also affects the ice cover. The latest high levels of CO2 have led to the melting of the Arctic sea ice. See how the ice melt is almost a month earlier than previous years at http://www.abmcdonald.freeserve.co.uk/north.htm
When the ice has gone, the CO2 will act on the sea water and the global climate will return to the balmy days of the Eemian or even perhaps the Eocene.
[[In the 15 micron band cited by Ray Pierrehumbert, the optical dense lines do not get more than 30 m above the surface of the Earth. They certainly do not reach the top of the atmosphere, by definition.]]
Gee, and I get 7,800 meters. Are we talking about the same thing? If you’re talking about exactly the line at 14.99 microns, I think you’ll find that very little IR energy from the Earth, or at least a very tiny fraction of it, is emitted between 14.98 and 15.00 microns.
If you use the band from 13 to 17 microns, you’ve got lines all through there, and a certain absorption coefficient, and the 99% depression only occurs at 7.8 km. Not 30 meters.
Alistair,
I agree about the extremly high optical densities near the line centers. That is what makes the wing shape so important. If it is just being investigated now, it seems to me that this whole field is way way out on a limb. If the lineshape were a square box function, with infinitely steep sidewalls, they GW would have the same saturation dependence as you get for a smeared out gray body model. (Which is wrong I have been told.)
I need to find the papers for the radiatve forcing vs. CO2 concentration expressions in the IPCC report. Several different complicated expressions by different authors were included. If you plot them, they are not so different. Though they are functions of log(CO2 conc.), when you plot them over the range of doubling CO2, you are not way off from a simple linear increase. The reason for this dependence, I thought, had to do with the shape of the wings, which give a much softer (but more pernicious since it can go up and up) saturation (with concentration) behavior to the forcing. I have a suspicion that even if I pay $100 for them, I still won’t get a straight answer. I’d bet they never checked whether the HITRAN linshapes represent reality at all. They just cranked away on their *line by line* codes on their computers.
Raypierre’s plot of the transmission for broadband light vs propagation distance is essentially the same phenomenon. Note that he is just calculating the trsnmission assuming the lines are lorentzian.
I have found the website for the HITRAN:
http://cfa-www.harvard.edu/hitran
In the original 1973 paper, the authors directly state that *the precise lineshape is a matter of some uncertainty … but it customary to start from a Lorentz shape. … All lineshapes in HITRAN are assumed to be Lorentzian* Later it states that some paper question the validity of the 1/(v-v0)^2 dependence in the far wings. I will try to find these old (1964 and 1969) papers I guess.
The whole thing is just a table of fits for line center wavelength, FWHM, and oscillator strength. Reference was made to fits using a third order polynomial. That would definitely be a fit just to the top of the lineshape. They 2004 paper on the site references this paper by Rothman as the latest word on the lineshapes:
L. S. Rothman, R. L. Hawkins, R. B. Wattson, and R. R Gamache, Energy levels, intensities, and
linewidths of atmospheric carbon dioxide bands, JQSR 48, 537-566 (1992).
I would pay for it, but I can’t seem to get access to pay the $30 from Science Direct. ( I is such a scam that taxpayer funded research is handed over for a song to these academic publishing houses. This stuff should be free … dammit.)
What we need to see is the raw spectral data for a few of the lines, and see how they fit it in the wings. I really think this database is for applications like chemical identification or order of magnitude visibility estimates of targets (missile plumes) through the atmosphere.
This really bugs me. This stuff should be measured and re-measured with the latest modern detectors and sources (quantum cascade lasers etc.) Relying on data from the 1970s is ludicrous for such an important and subtle problem CO2 induced GW seems to be. This is the only part of the whole GW problem that can be measured with decent accuracy! (The CO2 conc. is the only other one.) It sound to me like the modelers just took this database on faith and ran much too far with it. I have seen no references to the need for further experimental determination of detailed lineshapes anywhere.
Even if Lorentzian fits turn out to be OK, it will be like being right the same way a stopped clock gives the correct time twice a day. Not very confidence inspiring about the underpinings of the rest of the GW story.
If I have to stomach being lectured by Cameron Diaz and Ed Begley Jr. on TV, then the researchers better get out the glass tubes and re-measure, or at least re-fit, some of these lines. If Lorentzians are OK in the wings, then tutorials should address why this is so, since the HITRAN data seems to be fit only at line center.
> For CO2, Planck’s function is irrelevant, as is re-emission to the surface. Only water vapour and clouds acts in that way.
Cite, please?
I’m still trying to grasp what happens with absorption/emission on a molecular scale to molecular energy, and have gotten mixed messages here. Does the absorbed IR radiant energy all go to the intramolecular bonding energy? and does this get distributed over the translational stretching, bending, or molecular rotation following some process that is energy and/or molecular makeup dependent? Does this bond energy appear as “regular” exo-molecular (is that a word??) kinetic energy (translation velocity)? Or, can the molecule transfer some of its bond energy to “regular” kinetic energy. What I’m getting at, does bond energy, directly or indirectly, tend to increase a molecule’s “pudding”? Pudding being a molecular quality that if it were evidenced in a lot of molecules would be temperature. Can the bond energy transfer as kinetic with a collision with another molecule. Finally when a molecule emits radiant energy does it all come from the bonds or can “regular” kinetic energy provide some? Finally (really), do electron energy levels play any part in infrared radiation absorption/emission?
Anyone care to help?
Re #213
Rod, One would think that chemistry is simple, with atoms made of protons, neutrons and electrons. That explains atomic number, isotopes, atomic weight, electrical conduction, and the chemical composition of molecules. However, when you go into quantum mechanics it all becomes horribly complicated.
by
There are not just one, but four ways in which a gas molecule can be “heated.” (Solids and liquids have a different way, which is inter-molecular vibration which generates blackbody radiation.) Those four ways are the kinetic energy of the molecule, its electronic excitation, its vibrational state, and its rotational state. When one of the molecule’s electron gets excited, either by the absorption of a photon or collision with a free high energy electron, then the molecular electron can return to its ground state by emitting a photon, or the energy can be dissipated into kinetic, rotational and vibrational energy. The vibrational energy can emit a photon or be dissipated into kinetic and rotational energy. The rotational energy can be emitted as a photon or be dissipated into kinetic energy.
In general, electronic excitation (absorption) and relaxation (emission) involve visible and ultra violet (UV) photons. Vibrational excitation and relaxation involve infra red photons, and rotational excitation and relaxation involves microwave photons. This means that solar radiation is neded for electronic excitation, whereas terrestrial blackbody radiation only causes vibrational and rotational excitation. A further complication is that the high energy UV radiation from the Sun can break molecular bonds and provide the energy for new ones. This is how the ozone layer is formed.
In order for a molecule to absorb or emit a wave of electromagnetic radiation it must oscillate so that there is a change in the balance of its electromagnetic field. Carbon dioxide is a symmetrical linear molecule so its rotations do not generate a field. However, the water vapour molecule is bent so its rotations do produce a field and it can be rotationally excited by radiation of the appropriate frequency.
In general, an excited molecule can lose its energy without emitting a photon. “The most common mode of return is by thermal decay involving radiation-less transitions.” [Atkins, P.W. “Molecular Quantum Mechanics 2nd edn.” 1983] Thus the idea that the greenhouse effect works by the excited gases re-emitting back to the surface is nonsense!
Alastair, please. Posting these statements overthrowing contemporary physics isn’t fair to new readers who may believe you.
Be fair: warn new readers that there are counterexamples in hardware to what you believe. I refute it thus:
“… lasers (e.g. dye lasers, carbon dioxide lasers) where the laser medium consists of complete molecules, and energy states correspond to vibrational and rotational modes of oscillation of the molecules….”
http://en.wikipedia.org/wiki/Carbon_dioxide_laser
“…. the laser is achieved by the following sequence:
1. Electron impact excites vibrational motion of the nitrogen. Because nitrogen is a homonuclear molecule, it cannot lose this energy by photon emission, and its excited vibrational levels are therefore metastable and live for a long time.
2. Collisional energy transfer between the nitrogen and the carbon dioxide molecule causes vibrational excitation of the carbon dioxide, with sufficient efficiency to lead to the desired population inversion necessary for laser operation.
…
“the laser transitions are actually on vibration-rotation bands of a linear triatomic molecule [O=C=O], the rotational structure of the P and R bands can be selected …..”
The math Dr. Weart describes being done in the 1950s led to the carbon dioxide laser before it led to our understanding of how the energy flows in the atmosphere. It’s the same physics though.
Thanks, Alastair. A couple of follow-ups: Do gasses not emit blackbody/Planck-type radiation? How about the Sun, or is its gas so compressed, even at the “surface”, that it acts like a liquid? Does bond energy change in liquids and solids? Do bond energy or electron levels affect heat (temperature) levels? If the predominate relaxation of gasses is other than re-emission of IR radiation, does that mean the temperature increase in the earth’s surface mainly comes from conduction or convection of heated greenhouse gasses down to the surface? Sounds a little shaky (but what do I know??!!) Does this apply to CO2 (and maybe other GH gasses???) but not H2O as I think you said above? Or is it that molecule #1 absorbs the IR and mainly relaxes by transferring its absorbed energy to molecule #2 as kinetic energy, then molecule #2 can relax by emitting radiation, ala “local thermodynamic equilibrium” mentioned above by Eli??? If molecule #2 can easily emit, why doesn’t molecule #1??
As I understand it, only a molecule with a dipole moment can absorb radiation and convert it directly to rotational energy. But other molecules (with other restrictions) can absorb IR directly into vibrational bond energy. Is this right and what you said in #214?
Given that electron energy levels are considerably less (in number) and higher (in level) than bond energy levels, is that why electron excitation is very discrete and comes generally from higher energy visible/UV/X-ray radiation?, while gas bonds can absorb a much wider range of photon energy (hf) levels and in the infrared?
Alastair, on speculation, I figured the problem may be that CO2 is not a homonuclear molecule (more than one kind of element).
So, I tried a search for: non-homonuclear triatomic molecule
That search (either Google or Scholar) finds this: http://www.aiaa.org/content.cfm?pageid=406&gTable=mtgpaper&gID=67474
Abstract: http://pdf.aiaa.org/preview/1979/PV1979_1041.pdf
That may help. It’s early but it’s on the point you’re wrestling with.
Re #210
Barton, Tour results do not agree with Messerole, C.A., Mulcahy, F.M., Lutz, J., and Yousif, H.A. (1997) �CO2 Absorption of IR Radiated by the Earth� Journal of Chemical Education, 74 p. 316-7 who calculate that transmission of CO2 in the 2390 to 2275 cm^-1 band is less than 1% at a height of 25 m. I would be interested to see your calculations.
Regards, Alastair.
Re #211
Dave,
There is some information on line shapes in this document http://www.ecmwf.int/newsevents/training/rcourse_notes/PARAMETRIZATION/RADIATION_TRANSFER/Radiation_transfer4.html#999581
Note that the number of lines makes the careful treatment of the wings both impractical and irrelevant.
Re #212
Hank,
I thought that this document stated that water vapour emits at a low level of continuum radiation. I don’t think there is any doubt that clouds do!
Re #215
Hank,
The physics that I am attacking is not contemporary. It is based on the 19th century concept of Kirchhoff’s Law which can be paraphrased as emitted radiation equals absorbed radiation on a per wavelength basis, or more formally as: “The emissivity of a medium is the ratio of the emitted energy to the Planck function at the temperature of the medium for a given wavelength. If the absorptivity is defined as the amount of energy absorbed at that wavelength divided by the appropriate Planck function, Kirchhoff’s law states that the two quantities are equal.” [Morcrette, J-J. “Radiation Transfer” ECMWF, 2000]
The laser is based on the concept of stimulated emission first proposed by Einstein in 1917. Stimulated emission occurs when the absorption of one photon results in two being emitted. This is in direct conflict with Kirchhoff’s law. Moreover, the initial CO2 molecules are not excited by radiation, but rather by the collision with an excited Nitrogen molecule. Nor does the CO2 emit a photon with the same energy that it absorbed from the N2. Moreover, it requires the aid of collision with a Helium molecule to return to its ground state.
So, it is nothing like Kirchhoff’s law at all :-(
Hi Rod,
Blackbody radiation is emitted as a continuous spectrum whereas gases emit line radiation. In the same paper in which Einstein proposed stimulated emission, he proved that Kirchhoff�s Law applied to gases, and that they emit according to Planck�s function. For the proof, he used the Equipartition Theorem/ Boltzmann Distibution, but that does not apply to the vibrational energies of greenhouse gases at room temperature. They are �frozen out� due to quantum effects. He had already got the specific heats wrong and had been corrected by Debye in 1907. That was before Einstein was famous. Now of course, no-one would dare to correct Einstein, so if he did make a second error then it is not surprising that it has persisted.
The Sun emits continuous radiation that follows Planck�s function except for the Fraunhofer lines created by the gases of the chemical elements. It is argued that in the Sun these lines are so broadened by temperature and pressure that they are smeared out into blackbody radiation. I believe that your suggestion that the gases are so compressed that they behave like liquids has also been proposed. Inspection of the surface of the Sun tends to suggest that it is a liquid, but you have to be pretty brave or foolish to claim that it is molten!
When the energy of the molecules in a solid exceed a threshold they become liquid. This requires latent heat. Increase the energy further and it becomes the kinetic energy of the gas molecules. The temperature of the surface of the Earth is 99.9% due to the absorption of solar radiation, but if the air is cooler than the surface then it will be heated by conduction. When the air is warmer it will be cooled by conduction. Warming and cooling by convection is restricted to the atmosphere itself, (and the oceans.)
But, what I am saying is that most of the heating of the air at the surface is due to the greenhouse effect of the Earth�s blackbody radiation being absorbed by the greenhouse gases. That causes convection during the day only. H2O is more complicated because it also causes convection by being less dense than air, and it carries latent heat up into the atmosphere. Thus water provides a further method of cooling the surface by evaporation and warming the atmosphere by condensation.
I think LTE is a red herring. It only applies to stellar bodies where there is substantial emission from the gases and no other form of heating. There is a region called non-LTE where the solar radiation heats the gases and they are unable to cool because of a lack of collisons. However as far as outgoing longwave radiation is concerned, in the Earth�s atmosphere, the greenhouse gas molecules are de-excited by collisions before they can re-emit their absorbed energy, (but I may revise that view.) The point is that molecule 1 is a greenhouse gas molecule which can re-emit but it loses it energy to an air molecule, which cannot re-emit the energy. Molecule 2 will share its kinetic energy with other air molecules. In theory one of those will collide with Molecule 1 and re-excite it, but before it can emit it will be hit by another air molecule.
The radiation can be absorbed as rotational energy, vibrational energy, or electronic energy depending on it frequency of the photon. For rotational absorption you need a polar molecule, such as the bent water vapour molecule O / H O, in order to have and oscillating field. A rotating symmetrical molecule O = C = O does not create a field because it is neutral. But both polar and non-polar molecules can produce oscillating fields by stretching and bending, as can ozone O = O = O a triatomic homonuclear molecule.
Electronic levels are not fewer, just require more energy � higher frequency photons. Look up Hydrogen lines and you will find that there are several sets for the simplest of molecules.
Hope this answers your couple of questions :-)
BTW, Alastair, I thought your referenced links in #210,220 offered a very good explanation of the basics of radiation transfer at the molecular level.
There are continua associated with water and CO2 emission at very low levels.
Re.
222. Alistair. You must be aware that just about everyone thinks your stand on LTE is a bit odd. Including the US air force…please see http://www.dodsbir.net/Sitis/view_pdf.asp?id=DothH04.pdf
Re #217.
Hi Hank,
That is an intriguing link you posted, but I cannot get to the full paper, nor to the paper to which they refer by Simmons and Lindquist. I have found the technical report on the NASA server which has lots of goodies. Try searching for carbon dioxide. It brings up Moon forming collisions and a Hadean Earth!
The trouble is the report only has absorption coefficients for 300 K but what I need is 200 K thru 300 K. Anyway, as they say, back to the drawing board :-)
Re #205
I don’t think that the US Air Force has heard my views on LTE yet. I only came to the conclusion that it was irrelevant to OLR today!
Alastair, thanks. This is great! But, a couple more followups. I would have guessed that electron energy levels number in the many hundreds and bonding energy levels, with their numerous combinations, in the many thousands, and which is one of the bases for “spreading”. Not correct?
If the GH gasses re-emit very little (in any direction) what causes the ultimate emission of about 240 W/m2 or so into outer space? Radiation making it directly from the surface to 60km or so seems screwy (most IR radiation is (first?) absorbed within 100m). Is it blackbody-type radiation? [I couldn’t tell from #222, 1st para. if gasses do or do not emit radiation ala Planck. As an aside, how thick/deep can a surface be and still be a radiating surface?]
“most of the heating of the air at the surface is due to the greenhouse effect of the Earth’s blackbody radiation being absorbed by the greenhouse gases. That causes convection during the day only.” Since the Earth radiates 24 hrs/day, why “during the day only”??
Your referenced link is faulty.
I have a request: would people responding to previous comments please reference the poster and time as well as the number? or at least quote enough of the text so as to make an unambiquous determination ? the numbers seem to change and it is difficult to scroll back and forth for visually and physically challenged readers.
I also notice that the php/sql engine has some difficulty at times, or i would suggest implementing a threaded comment system a la Usenet, but that might be too much to ask.
i suppose i could volunteer to code such an extension…
Re #228
Glad you like it Rod.
I will push the boat out a little here because I am not sure if the following is true but …
Gaseous elements when vapourised tend to be atomic, or even plasmic and so can have no vibrational or rotational excitation levels. However, with just one electron hydrogen has 12 lines. But those electronic levels are never stimulated by infra-red photons, so they are irrelevant to the greenhouse effect. They are relevant to the interior of stars, and they are what Einstein considered. Milne, who came up with the idea of LTE was also thinking about electronic excitation and astrophysics. That is why LTE is not relevant to the Earth’s atmosphere.
The main greenhouse gases are H2O and CO2. Nitrogen and Oxygen do not absorb or emit infra-red radiation but do get heated by collisions with the excited greenhouse gas molecules. If they collide with a greenhouse gas at the same time as a photon then the the absorption line of the greenhouse gas is broadened. Obviously, high in the atmosphere where the air is thinner there are less collisions and less broadening.
Although the CO2 cannot absorb photons which produce pure rotation, the energy levels of the vibratiosn can be modfied by rotations. So a vibration line becomes a vibration band ie a series of lines for the different rotations that can be associated with the vibration. There are also several pure vibration lines due there being different isotopic versions of the greenhouse gas molecules. For instance 12C 16O 16O, 13C 16O 16O, 14C 16O 16O, 12C 16O 17O, etc. Then each of these has a full series of rotational variations.
I am arguing that the emissions to space come from between the lines and from between the bands. But I am also saying that there is a lot of radiation to space from the tops of clouds near the tropopause. That radiation is blackbody and there is no water vapour above it to prevent it escaping to space. The heat for that radiation is provided by the condensation of water vapour which was carried there by convection not by radiation.
You ask why is there convection] during the day only? A good question :-)
Without the Sun or the back radiation from the atmosphere which I have demolished then in a clear sky state the surface cools very quickly, and since the power of the radiation depends on the fourth power of the temperature, there is a big drop in the heating of the lower air which is also being cooled by conduction. There is also a little back radiation from water vapour cooling the air.
The link for hydrogen lines should be http://iapetus.phy.umist.ac.uk/Teaching/IntroAstro/Hydrogen.html
So, Alastair, someone on Alpha (the International Space Station) or using an infrared imaging satellite could aim an infrared film camera at the horizon — from there they can clearly see the top of the troposphere and the clear stratosphere above it — and you’d predict that, viewed in the infrared, the stratosphere seen edge-on would not be emitting any infrared at all, it’d be black on the picture, and the clouds would show up as very bright in the infrared?
Is that a fair summary? If so you’ve got a falsifiable prediction.
Possibly it’s already been done and you can find an image somewhere.
re 230,231 (Alastair and Hank): I ran across a doc that kinda confirms the infrared radiation into space comes directly from the surface (between the lines so to speak, or, more accurately, mostly through the “window”), and (primarily) the clouds. Very little presumably comes from re-emitting greenhouse gasses. I have to go contemplate.
Alastair McDonald (#222) wrote:
The common view is that as long as the electromagnetic field and matter are strongly interacting, there is a local thermodynamic equilibrium. This is a view that was expressed by Eli Rabett back in #153:
But of course you go on to explain why you don’t think that the radiation and matter strongly interact:
Interesting approach, Alastair. Greenhouse gas molecules (such as carbon dioxide) can always be de-excited by collisions before they re-emit, but they can never be excited to re-emission by collisions. The energy only goes in one direction.
This is the “law” if you will which in your view prevents the electromagnetic field and matter from strongly interacting.
In the common view, nature would have no preference for de-excitation versus excitation. Thus the Planckian temperature of the electromagnetic field will follow like the tail the dog which is the Maxwellian temperature of matter – resulting in Local Thermodynamic Equilibrium (LTE). But you maintain that the only place where this sort of strong interaction can take place is in stars. But why would such strong interaction take place there? Couldn’t we simply impose the same sort of “filter,” declaring that molecules always get de-excited by collision before re-emission even under those circumstances? If not, why not?
http://radix.net/~bobg/climate/halpern.on.radiation.html
I would like to wade in on Alastair’s side generally, though perhaps not in all details. In particular, I would assure Timothy Chase that radiation and absorption go together. If there is one, there is the other, though other processes may compete to make it difficult to measure.
I also say that isolated CO2 molecules inside a hot sphere will have detectable radiation — this is what it means to be in complete thermal equilibrium, as opposed to LTE which can have either higher or lower thermal radiation compared to the vib-rot-tran components.
BTW, please note that the Einstein coefficients are kinetic, and apply with or without equilibrium.
Allan Ames (#235) wrote:
Well, Alastair believes that he has some sort of integrated alternative theory of the greenhouse effect. All of the elements are strongly-coupled. However, the inability of carbon dioxide to absorb and re-emit except when it is close to the ground plays an essential role in his view – at least as far as I understand it.
In the mainstream view, the strong interaction between the greenhouse gases and the atmosphere (which exists in all parts of the atmosphere except the uppermost parts of the stratosphere where pressure is too low) is what results in the coupling of the electromagnetic field of thermal radiation and the atmosphere itself. The atmosphere is opaque to thermal radiation, and molecules can be both excited to re-emission and de-excited so that they fail to re-emit. The electromagnetic field and the atmosphere are strongly interacting. Such strong interaction implies strong coupling – and the achievement of a local thermodynamic equilibrium in which the Planckian temperature of the longwave radiation and the Maxwellian temperature of the atmosphere are equal.
Moreover, since greenhouse gases can absorb and re-emit in all the lower layers of the atmosphere (that is, beneath the highest layers of the stratosphere) and re-emit in all directions, they can absorb and re-emit between neighboring layers, and higher layers will indirectly interact with the surface via the intermediary layers. As such, in the mainstream view, water vapor dominates in the lower levels of the troposphere, but in higher layers which are especially dry, carbon dioxide dominates and plays the role of a greenhouse gas, the effects of which is to regulate the amount of water vapor which is in the lower atmosphere through water vapor feedback – since any given parcel of carbon dioxide stays in the atmosphere much longer than an equivilent parcel of water vapor.
But in Alastair’s view, it is precisely this strong interaction which prevents the electromagnetic field and greenhouse gases from becoming strongly coupled – because energy which might be re-emitted by greenhouse gas molecules is always lost in collisions, never gained. In his view, it is only within stars that a local thermodynamic equilibrium will be achieved. Assuming Alastair is correct about strong interaction preventing strong coupling in planetary atmospheres, I have to wonder whether the achievement of a local thermodynamic equilibrium would be even “less likely” in a stellar atmosphere.
PS to Allan Ames…
Anyway, I believe that at a certain level, talk about a local thermodynamic equilibrium is still just an approximation. For example, there is the electromagnetic field of the sun – solar radiation – then the electromagnetic field of the atmosphere – its thermal radiation. We can speak of these as separate fields and we can distinguish between them, their temperatures, their spectra, but it isn’t exactly as if each and every photon bears a label designating it as belonging to one field or the other.
Obviously solar radiation isn’t in local thermodynamic equilibrium (LTE) with the atmosphere, and thus the whole of the electromagnetic radiation within any given part of the atmosphere won’t be in LTE with the atmosphere. But the thermal radiation of the earth will be, for the most part – and it is something that we can distinguish from solar radiation – particularly at night. The atmosphere is transparent to visible light (mostly), and solar radiation is principally in the visible part of the spectrum. The atmosphere is opaque to the earth’s thermal radiation (for the most part), and so it makes sense to treat this thermal radiation as being in local thermodynamic equilibrium with the atmosphere. But a thermometer wrapped in black linen is something else – that’s why we speak of albedos.
Now is this good enough? Well, yes – as an approximation. If you want to get into the really detailed equations, that is possible, too. Hank Roberts pointed to a source which shows how the general direction. But while Einstein is more accurate, most people stick to Newton – because it is easier to work with the equations and they don’t need that kind of accuracy. The same works here, I believe. As for the greenhouse effect itself, the central issue is fairly basic, in my view at least: greenhouse gas molecules can gain or lose energy in collisions, and consequently, they can and do absorb and re-emit radiation throughout most of the atmosphere.
Re #224 where Eli Rabett wrote “There are continua associated with water and CO2 emission at very low levels.”
I have now found the reference to contiuum radiation that I was looking for. It is chapter 9 of “Principles of remote sensing of atmospheric parameters from space” February 1998 By R. Rizzi and updated by R. Saunders which can be found at
http://www.ecmwf.int/newsevents/training/rcourse_notes/DATA_ASSIMILATION/REMOTE_SENSING/Remote_sensing10.html
or downloaded as a PDF from http://www.ecmwf.int/newsevents/training/rcourse_notes/pdf_files/Remote_sensing.pdf
It is a little confused because it says first that the continuum is mainly due to H2O, perhaps due to its dimers. Then states that CO2, N2 and O2 also produce a continuum emission, but as far as I know these gases do not produce dimers.
The full document is worth reading if you want blackbody radiation, vibro-rotational bands, and line shapes and broadening explained with more authority than me. OTOH I do not endorse his view that atmospheric gases obey Kirchhoff’s Law!
Re #231 Hank,
Thanks for that suggestion of a limb spectrum. I am just trying to remember where I saw such a diagram recently, but I cannot find it. An accurate < 1/cm downward spectrum for clear skies would also work. The problem is finding one.
re 236, Timothy: I’m asking a quicky question without having read the entire post; couldn’t wait.
“…the achievement of a local thermodynamic equilibrium in which the Planckian temperature of the longwave radiation and the Maxwellian temperature of the atmosphere are equal.”
Maybe I missed a turn somewhere, but isn’t Planck temperature determined by Maxwell temperature and always equal to it, at least on the “surface” of the gasses??
[ps I trust I’m not reopening the debate over the “temperature” of the actual E-M radiation…!]
re 237, by Timothy: a quicky quibble and a clarification:
The photons do too bear a label by virtue of the hf energy level.
I halfway buy the “close enough” (for the girls I go with [;-)) argument, but am bothered by its conclusive nature. While just an partially educated hunch, my basis for being a skeptic rests greatly on the molecular/atomic/sub-atomic very precise physics that goes on between radiation and gas molecules. A physics that I gather is still based a bunch on assumptions and reasonable scientific guesses.
It appears to me that Hank Roberts’s posts # 66 and 67 under Friday roundup belong in this thread.
Rod B (#239) wrote:
Well, at this point I will gladly defer to the American Meteorological Society:
If there isn’t enough interaction, the local thermodynamic equilibrium breaks down. But I was unclear as to why exactly this happens. But the example of a laser is a good clue. If the particles are colliding infrequently, then the electromagnetic field which arises from absorption and re-emission will tend to destroy the Boltzmann distribution of velocities which exist between those particles.
Please see:
Thermal Radiation in the Upper Atmosphere
A. R. Curtis, R. M. Goody
Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, Vol. 236, No. 1205 (Aug. 2, 1956), pp. 193
http://links.jstor.org/sici?sici=0080-4630%2819560802%29236%3A1205%3C193%3ATRITUA%3E2.0.CO%3B2-C&size=LARGE&origin=JSTOR-enlargePage
The derivation of Planck’s and Kirchoff’s laws presuppose the persistance of a Boltzmann distribution – but if the latter breaks down, the other two go out the window – which is why a gas laser is able to emit radiation at a precise frequency, etc., the radiation overwhelms the dis-order that would normally exist within matter and which would therefore be imposed upon the electromagnetic field. In essence, a laser is an instance of the tail wagging the dog.
Rod B (#240) wrote:
I was thinking the same thing, too.
You have the wavelength or frequency, the directionality in the case of solar radiation (unless there is scattering), etc.. But an individual photon could belong to one or the other far wing of the Planckian distribution. The sun, afterall, emits some longwave radiation. Similarly, there will be some photons emitted within the visible part of the spectrum even by objects at room temperature.
Actually the “close enough” is more or less implicit in the phrase “local thermodynamic equilibrium” itself, assuming the LTE is a stable one. If it is to persist, there must be interaction between the local neighborhood and the outside world. Sunlight being absorbed by the ground and re-emitted into the atmosphere as thermal radiation is a good example of this.
“… A physics that I gather is still based a bunch on assumptions and reasonable scientific guesses.”
Well, one could argue that we know of radiation only because we know of matter. Then again, one could make the opposite argument. Seems all pretty mysterious to me. Then again, as a former philosophy major, I came to think that knowledge itself was pretty mysterious. It took me ten years to arrive at a satisfactory definition of it, or rather, definitions of the terms in which it is defined.
At least on the surface, it seems to me that there is a fairly big divide between philosophy and empirical science. Descartes could go round in circles over whether what he was staring at was actually his hand or not or whether he could trust an argument which seemed to suggest that he existed at the time he held it firmly in mind. Empirical science, on the otherhand, attempts to ground itself in evidence and testability. None of the arguments are deductively certain except insofar as we aren’t really sure whether they apply only to our mental constructs. Euclid is a good example of this.
But what empirical science has going for it is justification from many different lines of inquiry – where the tentative conclusions which it arrives at are tested again and again – and improved upon as needed. The justification received by a conclusion which is justified by multiple lines of inquiry can be far greater than that which it receives from any one line of inquiry considered in isolation.
In contrast, when you have a single individual sitting in a small warm room staring at his hand by the light of a fire, there isn’t that much evidence for him to work with, certainly not in any systematic fashion. If he is especially inclined towards radical doubt, he is pretty much limited to that single line of inquiry which he happens to be thinking about at the moment.
After a while, it can get to be a pretty strange brew – the result of the tail of thought wagging the evidence on which it would otherwise be based.
In #236 Tim wrote Well, Alastair believes that he has some sort of integrated alternative theory of the greenhouse effect. All of the elements are strongly-coupled. However, the inability of carbon dioxide to absorb and re-emit except when it is close to the ground plays an essential role in his view – at least as far as I understand it.
It is not correct that I am arguing that CO2 is only able to to absorb near the ground. It can absorb at all altitudes, and when clouds emit blackbody radiation, the CO2 lines will be absorbed in the regions around them. However, in most of the atmosphere there is no radiation in the frequencies at which CO2 absorbs because it has already been absorbed by CO2 near the surface of the Earth (or around the clouds.)
OTOH, I am postulating that CO2 does not emit at any altitude because it is deactivated by collisions before it can do so. However, that does raise an interesting point. In the region where Goody & Jung (G&Y) say non-LTE exists i.e. where the time between collisions is greater than relaxation times, then CO2 emissions will occur. In other words, greenhouse gas emissions will come from the G&Y non-LTE region of atmosphere. Since this non-LTE region is at the top of the atmosphere, there is no surprise that is where emissions to space originate.
In #237 Tim wrote Assuming Alastair is correct about strong interaction preventing strong coupling in planetary atmospheres, I have to wonder whether the achievement of a local thermodynamic equilibrium would be even “less likely” in a stellar atmosphere.
The radiation from the surface of the Sun and from stars is blackbody radiation caused by the vibration of the atoms. The relative movement of the positively charged nuclei of the atoms generates a continuum oscillating electromagnetic field. Therefore there is no delay between a molecule becoming excited and its relaxation. (That delay only occurs in the much cooler planetary atmosphere where line radiation is generated by molecular vibrations, not atomic vibrations.) In the region of the Sun which is generating blackbody radiation, obviously the Maxwellian and Planckian temperatures are equal, and so that region is in LTE. Above that region is the Chromosphere where the Fraunhofer lines are produced.
So for strict LTE you need part of the the atmosphere to be a blackbody, which in the case of the Earth’s atmosphere it is not!
[[Barton, Tour results do not agree with Messerole, C.A., Mulcahy, F.M., Lutz, J., and Yousif, H.A. (1997) “CO2 Absorption of IR Radiated by the Earth” Journal of Chemical Education, 74 p. 316-7 who calculate that transmission of CO2 in the 2390 to 2275 cm^-1 band is less than 1% at a height of 25 m. I would be interested to see your calculations.
Regards, Alastair. ]]
Certainly. Transmissivity in a column of gas is
T = exp(-k c L)
where k is absorption coefficient, c greenhouse gas concentration, and L path length. The k c L term is, of course, the optical thickness. We can use Beer’s Law here because for infrared light in Earth’s atmosphere, scattering is negligible.
Essenhigh (2001) gives a mean absorption coefficient from 13 to 17 microns of 1.48 reciprocal meter atmospheres. For a carbon dioxide concentration of 0.04% of an atmosphere, the path length needed for transmissivity to drop to 1% is about 7,800 meters.
For a blackbody at 288 degrees K (the Earth’s surface, although it’s actually a graybody with a mean emissivity around 0.95), 8.5% of the radiation is from 13 to 17 microns, using the Planck distribution.
The discrepancy may be from considering different bandwidths. If you calculate it from, say, 14.98 to 15.00 microns, of course the needed path length will be much smaller. Your miscalculation may be in assuming that the infrared radiation from the Earth is only in the exact bands that carbon dioxide absorbs. There is plenty that gets through. There are CO2 absorption line wings all over the spectrum, but they are only highly concentrated at a few points, like the 4.3 and 15 micron bands.
Re #244
Barton.
I should have remembered that you were using Essenhigh’s values :-( They are from Hottel, H. C. and Egbert. R. B. Trans. Am. Soc. Mech. Engrs. 1941, 63, 297. See
http://pubs.acs.org/subscribe/journals/ci/31/i12/html/12box.html#refb
That document goes back to 1941 when it was believed that greenhouse gases absorbed bands of radiation. We now know that those bands are in fact groups of lines. The absorption only happens to the lines. When these lines are totally absorbed and not re-emitted no more absorption can occur. If these lines are totally absorbed in the first 50 m say, and on average they are 30% of the band width, then the absorption at 50 m will be 30% and the transmission 70%. However and 100 m, the absorption will not double to 60% nor will the transmission be 40%. They will still be 30% and 70% respectively.
Your calculation of a 1% transmissity at 7,800 does not happen, otherwise there would be no radiation emitted at the top of the atmosphere in the 13 to 17 micron band at all, but we know that the brightness temperature there is 215 K. I am arguing that 215K is the average of lines with a brightness temperature of 0K and others with a brightness temperature of 300K.
Alastair McDonald (#245) wrote:
Well now, that changes everything!
Everyone knows that when a new theory comes along and supplants an older theory, it replaces it whole. Perfect example: Einstein’s gravitational theory and Newton’s gravitational theory. Not even the geometry of space remains the same, and absolute time? Well, we know what happened to that.
Then again, there is that correspondence principle. Looking at Schwarzchild’s solution, the only way that Schwarzchild was able to derive the last constant left in his equations was by reference to how how curved spacetime approached the flat employed by Newton if one followed a straight line far enough.
The bands are groups of lines, but the bands and the lines broaden as the result of pressure and temperature. Likewise, there is lifetime broadening of a single line simply as the result of the uncertainty principle as it applies to energy and time.
Like you I enjoy physics.
I am looking forward to learning more about it. The neat thing about it is that it seems there is always more to learn.
RE: 237 Timothy Chase
There are two issues. As regards the physics, since we are talking about the transfer of many joules of energy through a kilogram/sq.m. each day, a small error in the transport parameters can lead to large errors in temperature. So, we need the most accurate portrayal we can put together.
Then there is the further question of how to embed the physics in a broader climate model in a way that can be calculated in reasonable time. Have you seen a detailed analysis of what heat flow (and error) the best LBL models predict?
If Rod_B is still wondering about the temperature of single atoms, in non-LTE, temperature is the number that gives you the correct vibration population distribution, which presumes that a single atom can have a temperature.
I cannot find the post, but the reference to SAMM2 is very good. http://www.dodsbir.net/Sitis/view_pdf.asp?id=DothH04.pdf
A useful reference on LTE is http://edoc.ub.uni-muenchen.de/archive/00001056/01/Goussev_Oleg.pdf
It seems consistent to say that LTE is equilibration in the mechanical modes, but not necessarily in or with the radiation modes.
I still mostly agree with Alastair. And lines get narrower as the altitude goes up until you are in the nonLTE region.
Allan Ames (#247) wrote:
I agree – accuracy is a good thing. Then again, it also helps to keep in mind that there are negative feedback processes involved in the establishment of equilibria. Not all errors grow large – and some errors average out. Tamino had a good essay on this a while back. Much of climatology is based upon this sort of principle.
Not offhand. Then again I am a philosophy major turned coder.
I thought that “population” normally refered to more than one.
That looks like something worth reading.
I might recommend the following:
I found the following to be of interest:
I didn’t know, for example, that non-LTE effects become important in the middle of the Earth’s atmosphere and the above, but it suggests that LTE is a good approximation below this – as does the passage from the earlier paper.
I also found this interesting:
Across some parts of the spectra, (partial-)LTE will still hold up – as suggested in the first passage I cited.
It seems fair to say that LTE is a good approximation in a variety of circumstances. However, as I pointed out in what you were responding to, one may perform more exact calculations which dispenses with this sort of approximation all together. But it will still be an approximation to one degree or another.
So you have stated.
But you have never actually said what it is that you agree with. That LTE doesn’t hold at all in planetary atmospheres? That the greenhouse effect occurs only in the lowest part of the atmosphere? That greenhouse gases are incapable of re-emission?
Actually I believe you already acknowledged that you disagree with the last of these, and as it is quite central to his “theory.”
In any case, it would help if you would be more specific – for the sake of accuracy if nothing else.
But as the papers you have cited would suggest, LTE is a fair approximation throughout much of the atmosphere in one band or another. Therefore Kirchoff’s law is applicable in many contexts – and greenhouse gases are able to perform their role as greenhouse gases throughout much of the atmosphere.
Given the emphasis which you place on accuracy, I would expect you to prefer a theories which recognize the fact that the greenhouse effect occurs throughout much of the atmosphere over a theory which holds that it only occurs near groundlevel.
In the piece that you were responding to I acknowledged the fact that LTE breaks down at the upper reaches. But it seems that I have learned a little more.
Thank you for suggesting the articles.
PS to 248
What is most interesting about the second paper which Allan Ames pointed out:
Non-LTE diagnostics of the infrared observations of the planetary atmosphere
Oleg Goussev an der Fakultat für Physik der Ludwig–Maximilians–Universitat
Munchen 2002
http://edoc.ub.uni-muenchen.de/archive/00001056/01/Goussev_Oleg.pdf
… is the existence of “non-Local Thermodynamic Equilibria,” where opacity and emissivity are functions of the frequency which are not strictly equal. Kirchoff’s Law is violated – but its violation is a matter of degree and specific to particular bands. Interestingly, the effect is partly dependent upon direction. In the lower atmosphere (including the layers where carbon dioxide is most important), the effects appear to be fairly minor. Judging from the literature I have seen so far, the effects (or deviations from Kirchoff’s Law) appear to be most important in plasma physics and mid to upper levels of the atmosphere. In essence, non-local thermodyanmic equilibria simply adds a new level of detail and precision in terms of our account of the atmosphere. Likewise, we have been taking this sort thing into account in some climate models at least as far back as 1999.
For those who might be interested, I think it is worth checking out. But in any case, it is probably best to learn Euclid before moving on to Riemann (that particular analogy seems especially apt) – just as you should learn differential calculus prior to integral. (I came in through the backdoor in both cases, but then in the former it was youth and in the latter ignorance. Oh well…)
Timothy (re 242), I didn’t see anything in the post that contradicted what I said in 239 and 240. In any case I agree with you. Now to read what comes later….