By raypierre , with the gratefully acknowledged assistance of Spencer Weart
In Part I the long struggle to get beyond the fallacious saturation argument was recounted in historical terms. In Part II, I will provide a more detailed analysis for the reader interested in the technical nitty-gritty of how the absorption of infrared really depends on CO2 concentration. At the end, I will discuss Herr Koch’s experiment in the light of modern observations.
The discussion here is based on CO2 absorption data found in the HITRAN spectroscopic archive. This is the main infrared database used by atmospheric radiation modellers. This database is a legacy of the military work on infrared described in Part I , and descends from a spectroscopic archive compiled by the Air Force Geophysics Laboratory at Hanscom Field, MA (referred to in some early editions of radiative transfer textbooks as the "AFGL Tape").
Suppose we were to sit at sea level and shine an infrared flashlight with an output of one Watt upward into the sky. If all the light from the beam were then collected by an orbiting astronaut with a sufficiently large lens, what fraction of a Watt would that be? The question of saturation amounts to the following question: How would that fraction change if we increased the amount of CO2 in the atmosphere? Saturation refers to the condition where increasing the amount of CO2 fails to increase the absorption, because the CO2 was already absorbing essentially all there is to absorb at the wavelengths where it absorbs at all. Think of a conveyor belt with red, blue and green M&M candies going past. You have one fussy child sitting at the belt who only eats red M&M’s, and he can eat them fast enough to eat half of the M&M’s going past him. Thus, he reduces the M&M flux by half. If you put another equally fussy kid next to him who can eat at the same rate, she’ll eat all the remaining red M&M’s. Then, if you put a third kid in the line, it won’t result in any further decrease in the M&M flux, because all the M&M’s that they like to eat are already gone. (It will probably result in howls of disappointment, though!) You’d need an eater of green or blue M&M’s to make further reductions in the flux.
Ångström and his followers believed that the situation with CO2 and infrared was like the situation with the red M&M’s. To understand how wrong they were, we need to look at modern measurements of the rate of absorption of infrared light by CO2 . The rate of absorption is a very intricately varying function of the wavelength of the light. At any given wavelength, the amount of light surviving goes down like the exponential of the number of molecules of CO2 encountered by the beam of light. The rate of exponential decay is the absorption factor.
When the product of the absorption factor times the amount of CO2 encountered equals one, then the amount of light is reduced by a factor of 1/e, i.e. 1/2.71282… . For this, or larger, amounts of CO2,the atmosphere is optically thick at the corresponding wavelength. If you double the amount of CO2, you reduce the proportion of surviving light by an additional factor of 1/e, reducing the proportion surviving to about a tenth; if you instead halve the amount of CO2, the proportion surviving is the reciprocal of the square root of e , or about 60% , and the atmosphere is optically thin. Precisely where we draw the line between "thick" and "thin" is somewhat arbitrary, given that the absorption shades smoothly from small values to large values as the product of absorption factor with amount of CO2 increases.
The units of absorption factor depend on the units we use to measure the amount of CO2 in the column of the atmosphere encountered by the beam of light. Let’s measure our units relative to the amount of CO2 in an atmospheric column of base one square meter, present when the concentration of CO2 is 300 parts per million (about the pre-industrial value). In such units, an atmosphere with the present amount of CO2 is optically thick where the absorption coefficient is one or greater, and optically thin where the absorption coefficient is less than one. If we double the amount of CO2 in the atmosphere, then the absorption coefficient only needs to be 1/2 or greater in order to make the atmosphere optically thick.
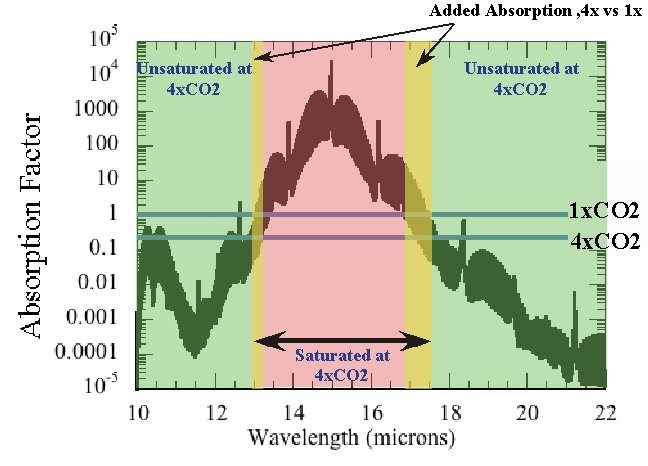
The absorption factor, so defined, is given in the following figure, based on the thousands of measurements in the HITRAN spectroscopic archive. The "fuzz" on this graph is because the absorption actually takes the form of thousands of closely spaced partially overlapping spikes. If one were to zoom in on a very small portion of the wavelength axis, one would see the fuzz resolve into discrete spikes, like the pickets on a fence. At the coarse resolution of the graph, one only sees a dark band marking out the maximum and minimum values swept out by the spike. These absorption results were computed for typical laboratory conditions, at sea level pressure and a temperature of 20 Celsius. At lower pressures, the peaks of the spikes get higher and the valleys between them get deeper, leading to a broader "fuzzy band" on absorption curves like that shown below.
We see that for the pre-industrial CO2 concentration, it is only the wavelength range between about 13.5 and 17 microns (millionths of a meter) that can be considered to be saturated. Within this range, it is indeed true that adding more CO2 would not significantly increase the amount of absorption. All the red M&M’s are already eaten. But waiting in the wings, outside this wavelength region, there’s more goodies to be had. In fact, noting that the graph is on a logarithmic axis, the atmosphere still wouldn’t be saturated even if we increased the CO2 to ten thousand times the present level. What happens to the absorption if we quadruple the amount of CO2? That story is told in the next graph:
The horizontal blue lines give the threshold CO2 needed to make the atmosphere optically thick at 1x the preindustrial CO2 level and 4x that level. Quadrupling the CO2 makes the portions of the spectrum in the yellow bands optically thick, essentially adding new absorption there and reducing the transmission of infrared through the layer. One can relate this increase in the width of the optically thick region to the "thinning and cooling" argument determining infrared loss to space as follows. Roughly speaking, in the part of the spectrum where the atmosphere is optically thick, the radiation to space occurs at the temperature of the high, cold parts of the atmosphere. That’s practically zero compared to the radiation flux at temperatures comparable to the surface temperature; in the part of the spectrum which is optically thin, the planet radiates at near the surface temperature. Increasing CO2 then increases the width of the spectral region where the atmosphere is optically thick, which replaces more of the high-intensity surface radiation with low-intensity upper-atmosphere radiation, and thus reduces the rate of radiation loss to space.
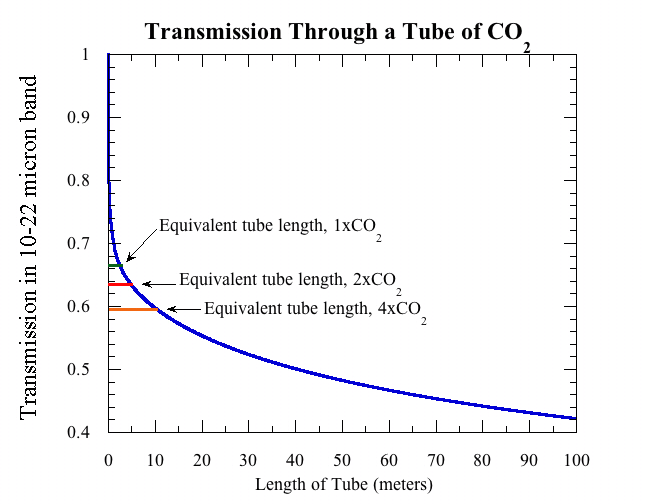
Now let’s use the absorption properties described above to determine what we’d see in a typical laboratory experiment. Imagine that our experimenter fills a tube with pure CO2 at a pressure of one atmosphere and a temperature of 20C. She then shines a beam of infrared light in one end of the tube. To keep things simple, let’s assume that the beam of light has uniform intensity at all wavelengths shown in the absorption graph. She then measures the amount of light coming out the other end of the tube, and divides it by the amount of light being shone in. The ratio is the transmission. How does the transmission change as we make the tube longer?
To put the results in perspective, it is useful to keep in mind that at a CO2 concentration of 300ppm, the amount of CO2 in a column of the Earth’s atmosphere having cross section area equal to that of the tube is equal to the amount of CO2 in a tube of pure CO2 of length 2.5 meters, if the tube is at sea level pressure and a temperature of 20C. Thus a two and a half meter tube of pure CO2 in lab conditions is, loosely speaking, like "one atmosphere" of greenhouse effect. The following graph shows how the proportion of light transmitted through the tube goes down as the tube is made longer.
The transmission decays extremely rapidly for short tubes (under a centimeter or so), because when light first encounters CO2, it’s the easy pickings near the peak of the absorption spectrum that are eaten up first. At larger tube lengths, because of shape of the curve of absorption vs. wavelength, the transmission decreases rather slowly with the amount of CO2. And it’s a good thing it does. You can show that if the transmission decayed exponentially, as it would if the absorption factor were independent of wavelength, then doubling CO2 would warm the Earth by about 50 degrees C instead of 2 to 4 degrees (which is plenty bad enough, once you factor in that warming is greater over land vs. ocean and at high Northern latitudes).
There are a few finer points we need to take into account in order to relate this experiment to the absorption by CO2 in the actual atmosphere. The first is the effect of pressure broadening. Because absorption lines become narrower as pressure goes down, and because more of the spectrum is "between" lines rather than "on" line centers, the absorption coefficient on the whole tends to go down linearly with pressure. Therefore, by computing (or measuring) the absorption at sea level pressure, we are overestimating the absorption of the CO2 actually in place in the higher, lower-pressure parts of the atmosphere. It turns out that when this is properly taken into account, you have to reduce the column length at sea level pressure by a factor of 2 to have the equivalent absorption effect of the same amount of CO2 in the real atmosphere. Thus, you’d measure absorption in a 1.25 meter column in the laboratory to get something more representative of the real atmosphere. The second effect comes from the fact that CO2 colliding with itself in a tube of pure CO2 broadens the lines about 30% more than does CO2 colliding with N2 or O2 in air, which results in an additional slight overestimate of the absorption in the laboratory experiment. Neither of these effects would significantly affect the impression of saturation obtained in a laboratory experiment, though. CO2 is not much less saturated for a 1 meter column than it is for a 2.5 meter column.
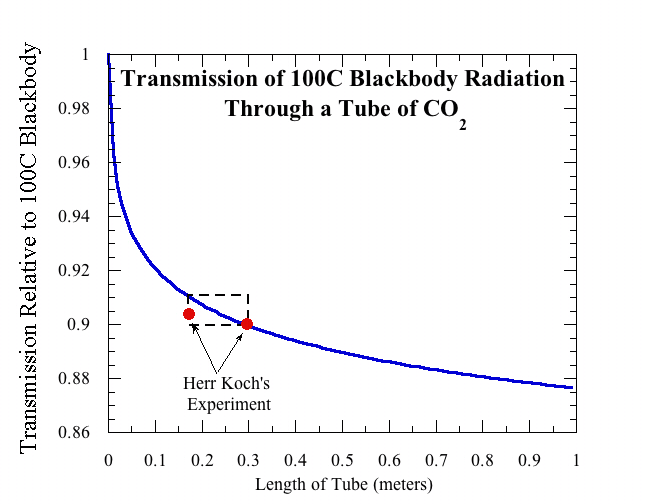
So what went wrong in the experiment of poor Herr Koch? There are two changes that need to be made in order to bring our calculations in line with Herr Koch’s experimental setup. First, he used a blackbody at 100C (basically, a pot of boiling water) as the source for his infrared radiation, and measured the transmission relative to the full blackbody emission of the source. By suitably weighting the incoming radiation, it is a simple matter to recompute the transmission through a tube in a way compatible to Koch’s definition. The second difference is that Herr Koch didn’t actually perform his experiment by varying the length of the tube. He did the control case at a pressure of 1 atmosphere in a tube of length 30cm. His reduced-CO2 case was not done with a shorter tube, but rather by keeping the same tube and reducing the pressure to 2/3 atmosphere (666mb, or 520 mm of Mercury in his units). Rather than displaying the absorption as a function of pressure, we have used modern results on pressure scaling to rephrase Herr Koch’s measurement in terms of what he would have seen if he had done the experiment with a shortened tube instead. This allows us to plot his experiment on a graph of transmission vs. tube length similar to what was shown above. The result is shown here:
Over the range of CO2 amounts covered in the experiment, one doesn’t actually expect much variation in the absorption — only about a percent. Herr Koch’s measurements are very close to the correct absorption for the 30cm control case, but he told his boss that the radiation that got through at lower pressure increased by no more than 0.4%. Well, he wouldn’t be the only lab assistant who was over-optimistic in reporting his accuracy. Even if the experiment had been done accurately, it’s unclear whether the investigators would have considered the one percent change in transmission "significant," since they already regarded their measured half percent change as "insignificant."
It seems that Ångström was all too eager to conclude that CO2 absorption was saturated based on the "insignificance" of the change, whereas the real problem was that they were looking at changes over a far too small range of CO2 amounts. If Koch and Ångström had examined the changes over the range between a 10cm and 1 meter tube, they probably would have been able to determine the correct law for increase of absorption with amount, despite the primitive instruments available at the time.
It’s worth noting that Ångström’s erroneous conclusion regarding saturation did not arise from his failure to understand how pressure affects absorption lines. That would at least have been forgivable, since the phenomenon of pressure broadening was not to be discovered for many years to come. In reality, though Ångström would have come to the same erroneous conclusion even if the experiment had been done with the same amounts of CO2 at low pressure rather than at near-sea-level pressures. A calculation like that done above shows that, using the same amounts of CO2 in the high vs. low CO2 cases as in the original experiment, the magnitude of the absorption change the investigators were trying to measure is almost exactly the same — about 1 percent — regardless of whether the experiment is carried out at near 1000mb (sea level pressure) or near 100mb (the pressure about 16 km up in the atmosphere).

Correction to 398 regarding the NEC Earth Simulator
32 teraflops – where a teraflop is a trillion floating-point calculations per second – and that was back in 1998. Ancient history as far as computers are concerned – given the doubling of chip speed every six months.
Please see:
Rod, “temperature” is not a Platonic ideal object.
It’s a choice from a list of definitions.
You need to pick one. That means pointing to which dictionary you are using. Once people know what meaning you are choosing for the word, it’s possible to try to talk about the physics.
For most definitions of “temperature” it’s an average.
Note also that most definitions of “velocity” are: direction and speed.
The speed of computer instructions is not linearly related to finishing an application. As the speeds have increased (and the supercomputer speed has not come anywhere near doubling every six months since 1998) the number of OPS or FLOPS to complete the same process has also gone up significantly. For instance much of the speed is garnered through multiprocessing and the instructions just to coordinate and communicate within the multiprocessor goes up exponentially.
But, you might be right — maybe they can run a detailed comprehensive model in a few weeks. Though “streamlining algorithms” could also include taking some gross shotcut estimations — ‘let’s not numerically integrate every line; let’s just assume the answer is… 4.7…. [;-}
Hank, when you say doubling CO2 will heat the earth by 2.4 degrees, which of the many alternate temperatures are you referring to??
I wouldn’t say something like that. It’d be uninformative at best.
I’d point to a source in a science site that would include a definition of the term used. Same as I’m suggesting you do.
http://www.usclivar.org/Newsletter/Variations_V3N3/Wehnerarticle.pdf
Rod, you know by now that you’re banging on a question that’s written about extensively, and the answer depends on how you set up the question.
Forty years ago:
http://prola.aps.org/abstract/PR/v150/i1/p153_1
One year ago:
http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6TVG-4JD0FT7-2&_user=10&_coverDate=09%2F15%2F2006&_rdoc=16&_fmt=summary&_orig=browse&_srch=doc-info(%23toc%235534%232006%23996309997%23627528%23FLA%23display%23Volume)&_cdi=5534&_sort=d&_docanchor=&view=c&_ct=61&_acct=C000050221&_version=1&_urlVersion=0&_userid=10&md5=f260a899d45f2ec37b94fb1f08fe85ea
Utterly spooky, talking about condensation, from the same issue:
http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6TVG-4JCBJS4-C&_user=10&_coverDate=09%2F15%2F2006&_rdoc=40&_fmt=summary&_orig=browse&_srch=doc-info(%23toc%235534%232006%23996309997%23627528%23FLA%23display%23Volume)&_cdi=5534&_sort=d&_docanchor=&view=c&_ct=61&_acct=C000050221&_version=1&_urlVersion=0&_userid=10&md5=c3e9f252ab9d8e19b6d3afe057b39718
Rod B (#404) wrote:
They tend to use just about the best chips on the market at the time that they are constructed, but they aren’t constructed every six months. It would be interesting to find out what the most recent machine is and its specs. Of course, I can’t wait for the qubits, but that kind of tech still looks like it might take a while.
Wild guess, but I would expect something logarithmic rather than exponential. We are talking about addresses where the length of the address would go up logarithmically with the number of addresses. Probably 2 to the power of something for the number of processors, that sort of thing. And oddly enough, Google has discovered that they can get away with doing what they do by stringing together a bunch of PCs.
True, but we have every reason to expect them to compare algorithms to test for accuracy and the effects upon the results from a given scenario – much like testing a new supercomputer with the calculation of pi out to so many decimal places.
In any case, these guys seem pretty detail oriented – if you check Gavin’s paper on the latest model.
Thanks to those who attempted to address my concerns expressed in posts #382 and #386. I will need time to study the links I have been given (and, possibly, professional help).
I was reassured to read the statement from Timothy Chase (#387)to the effect that modellers take account of the absorptive effects of water vapour/CO2 mixtures by using line by line analysis in up to 15 layers of atmosphere although the statement was subsequently queried by Rod B (#396).
However, I was confused by another of Timothy’s statements: He stated that “saturation from a given layer of atmosphere means that emissivity at a particular wavelength is 1, or alternatively, that it is opaque to that wavelength.” This seems to correspond to Raypierre’s definition: “Saturation refers to the condition where increasing the amount of CO2 fails to increase the absorption, because the CO2 was already absorbing essentially all there is to absorb at the wavelengths where it absorbs at all.” However, Timothy goes on to state that all the radiation absorbed will be re-emitted isotropically, that is, in all directions, thus explaining why higher level CO2 will not be irrelevant. He now appears to be singing from the same hymn sheet as Hank Roberts (#384) with his mud analogy.
Raypierre’s original essay appears to contradict this. He states that if you shine infrared of a particular wavelength up from the surface and there is sufficient CO2 and/or water vapour to saturate it by the time it has reached 4km, “essentially” none will get through. This must mean that higher level CO2 will be redundant with respect to that wavelength.
Am I being stupid or are Hank and Timothy contradicting Raypierre? Surely opaque is opaque is opaque? Alternatively, why describe a given wavelength as saturated if infrared of the same wavelength is re-emitted (albeit in haphazard directions). If the latter occurs, some of it will be up and thus higher level CO2 will obviously not be redundant at that wavelength. I am beginning to think that the answer may lie in Raypierre’s use of the word “essentially”, possibly implying that a tiny amount might get through the saturated layer. If this is the case, then higher level CO2 would be expected to have a tiny effect.
Please note that I am not disagreeing that increasing CO2 will cause more absorption “in the wings” thus reducing the bandwidth of infrared that can escape (with consequent global warming). Am I wrong to be thinking “horizontally” rather than “vertically”?
> Am I being stupid or are Hank and Timothy contradicting Raypierre?
Neither, I think. Remember that the wide range of sunlight once it reaches the ground becomes heat. Heat keeps the lower atmosphere moving. Eventually that motion is going to carry the warmth above the lower atmosphere, to the point where a photon can get away into the stratosphere.
Perhaps it’s time to urge Raypierre to help us out?
Douglas Wise (#408) wrote:
I will give it a shot, although if Raypierre wishes to step in and correct me, no problem…
Thing of it is, we are dealing with several issues at the same time.
Now what Raypierre is dealing with primarily is why adding carbon dioxide at a given layer does not result in saturation. While the peak becomes saturated, the wings are not saturated due to spreading where the spreading is both line spreading and band spreading due to pressure and temperature. Its not all at the same wavelength – which is why we get the logarithmic relationship between the partial pressure and temperature. That is, for every doubling the temperature goes up so many degrees. This argument holds whether you are dealing with water vapor or carbon dioxide.
However, it does not work for carbon dioxide at the same layer as were water vapor is dominant, because for all relevant wavelengths water vapor dominates and swamps out the effects of any additional carbon dioxide since carbon dioxide exists in much smaller quantities.
Now this is the point at which the absorption and reemission comes in.
The lower atmosphere is already opaque to any additional carbon dioxide at all relevant frequencies – unless you are talking about it being brought up to about the same level percentage wise as water vapor. Not bloody likely.
However, the longwave radiation which is absorbed and re-emitted at the layer where water vapor is dominant gets re-emitted and reaches the layer which is especially dry and where carbon dioxide is dominant. This layer is only partially opaque to longwave radiation – principally at the peak. Doubling the partial pressure of carbon dioxide at this level will increase the amount of longwave radiation which – rather than escaping to space heads in the direction of the surface. Some of this will be absorbed, and the direct effect will be (due to the greenhouse feedback between the atmosphere and the surface which I explained earlier) will be to raise the temperature of the surface by 1.2 degrees Celsius.
However, this increases the partial pressure of water vapor – another feedback. Then there are some additional feedbacks involving the albedo effect, the expansion of the atmosphere, etc., so that after all of the feedbacks the net result once the entire system reestablishes an equilibrium will that a doubling of the partial pressure of carbon dioxide implies an increase in temperature of 2.8 degrees.
So raising the partial pressure of carbon dioxide won’t increase the greenhouse effect if it is added at the same layer where water vapor is dominant (the lower troposphere) because that part of the atmosphere is already opaque – being dominated by water vapor. However, raising the partial pressure of carbon dioxide in the upper troposphere will increase the greenhouse effect with regard to a particular wavelength so long as that wavelength is not saturated in that upper layer. That was Hank’s point – as he was responding to your query regarding a specific wavelength.
But even if that particular wavelength (the peak) is saturated in the dry upper troposphere, the wings won’t be. That is one of Raypierre’s points. But then another one of Raypierre’s points is that the atmosphere expands due to the warming of the atmosphere which diminishes the density and degree of saturation of the uppermost layers where carbon dioxide plays an active role in the greenhouse effect. However, it takes a while for the uppermost layers to warm up after the adiabatic expansion and consequent cooling of those layers – where the process of warming up takes place by means of the relatively inefficient process of thermal diffusion.
These layers will have to warm up to the point at which they can more effectively absorb (due spreading) and reemit longwave radiation before they can fully participate in the greenhouse effect. This is the main reason why there is such a lag time before the climate system is able to achieve equilibrium again. And this I believe was another one of Raypierre’s points – although it came up in the comments, I believe.
I hope this helped!
Timothy (407), certainly not log related, though maybe 2N as opposed to exponential. Address length has little to do with it; coordinating, sync-ing, timing, and controlling many processors, each running a tidbit of the appl, does. Google’s appl, as complex as it is, is not the same as modeling.
“but we have every reason to expect them to compare algorithms to test for accuracy…” You can’t really test for accuracy without running the algorithm. We inherently know the value of pi to a jillion places, and it will never differ. We don’t “know” (at least with similar precision) what to check our shortcut against in global climate modeling.
A perhaps useful quote I’ve borrowed below — this is taken from one of the nonfiction columns in the online magazine Jim Baen’s Universe may help. I’ll claim fair use for this bit; attribution and information about the author follows. Full text by subscription at http://baens-universe.com/articles/The_Perpetual_Electron
People keep trying to describe what’s happening as Newtonian classical physics.
——— begin excerpt ———-
“… trying to imply and/or apply a classical idea of a ball oriented about an axis spinning and there being motion involved really has nothing to do [with] a quantum particle. Classical reality is completely meaningless and different and does not apply.” …
“Saying that electrons are fundamental particles is not sufficient to lay their behavior to rest. They have properties, and all properties are caused by something. There is no level below which we can stop searching for causes. We may not be able to find the causes, but they are there, waiting for us. Waiting for the day when we improve the power or subtlety of our equipment or the power or subtlety of our intellectual models.”
…” it is very likely that an electron is simply a manifestation of an actual piece of spacetime that cannot be reduced to anything else unless it is converted to a photon which would be another manifestation of spacetime.” … “we know diddly about the universe and will continue to peel back the layers …. Electrons are just manifestations of spacetime that emit certain unusual properties that when described via macroscopic ideas such as spinning balls confuses the living hell out of most people.” …“We must really and truly put our minds outside the classical ideas box and start thinking along the path of the weirdness that is quantum physics.”
—————-end quote; continuing excerpt identifying the author quoted ———————
— Doctor Travis S. Taylor is a scientist and engineer, as well as an author of fiction and non-fiction. His primary occupation is as a contractor working on projects for NASA, the Department of Defense and the intelligence community.
His current projects include advanced propulsion systems, ideas to help win the global war on terrorism, engineering future combat systems and helping to design the crew exploration vehicle for NASA’s return to the moon. He has a doctorate in optical science and engineering, a bachelor’s in electrical engineering, and three master’s degrees: one in astronomy, one in physics and one in aerospace engineering. He’s known as Doc Travis to readers of his hard science fiction novels. ….
Hank, written about extensively, but not with exactness. Maybe some of these papers use shorthand that is recognized by their professional circle, but it’s not by me. For instance, one of your sources (BTW, I couldn’t access two of them) said something like ‘temperature from kinetic energy being equivalent to the temp from the “total” energy; Is “total” vibration, rotation, electron, chemical and nuclear? (I’m just using this as a typical example; they might have well defined it in the whole specific article.) I’ve seen credible sources that said rotational and vibration energy directly affects temperature; and equally credible sources that said the opposite. We’ve had this in this thread! And I’m wanting to avoid the obscure and mysterious. Shirley you don’t think that if only I ask the question in a certain way that we are not experiencing global warming, aka temperature increases….
[[Raypierre’s original essay appears to contradict this. He states that if you shine infrared of a particular wavelength up from the surface and there is sufficient CO2 and/or water vapour to saturate it by the time it has reached 4km, “essentially” none will get through. This must mean that higher level CO2 will be redundant with respect to that wavelength.
Am I being stupid or are Hank and Timothy contradicting Raypierre? Surely opaque is opaque is opaque?]]
The radiation from the ground doesn’t get through, but the greenhouse gases that have absorbed it radiate, and the IR from them goes up higher, and so on, and so on. All the layers affect all the other layers, even if not directly. (Though again, as I have been saying, there is IR that gets through the lowest layer. There is IR from the surface that goes all the way to space, though not a great amount of it — about 40 watts per square meter.)
Re #397 Where Rod B Says:
‘ … absorbed radiation can increase the temperature of a gas only after it gets transferred from virotation to translation, either in the same molecule or another via a collision. Secondly, emission decreases the temperature of a gas only if the source energy of virotation was just transferred from some molecule’s translation. Radiation being absorbed and immediately re-emitted (with whatever probability that happens) without any intervening energy transfer does not affect the temperature of a gas what-so-ever. Is this correct?’
Yes! It is correct.
However, I think it may help if I explain the difference between heat and temperature. Heat is energy. For solids it is the energy of atomic vibrations. These are three dimensional, causing the contents of the bulb of a mercury thermometer to expand and increase the height of the column that is used to register temperature. But that temperature is what a mercury thermometer indicates. Let me call that the ‘Real’ temperature.
For all solids, the atomic vibrations of the positively charged nucleii and the negative electron clouds generates a continuum radiation which increases in intensity and average frequency with temperature. This radiation obeys the Stefan-Boltzmann Law http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/stefan.html , and can also be used to measure the temperature. This temperature is called the Planckian temperature since it is based on Planck’s function for blackbody radiatiors. If the solid is not an ideal blackbody, then its Planckian temperature and its ‘Real’ temperature may not be the same. NB The blackbody radiation is sometimes called thermal radiation since it depends on temperature. But the temperature measured that way is called the blackbody or Planckian temperature, not the thermal temperature.
If you place a monatomic gas such as Helium in a heated container, then the gas molecules (atoms) will collide with the walls of the container and share their kinetic energy with the atomic vibrations of the container. Eventually thermodynamic equilibrium will be reached where a mercury thermometer will register the same temperature whether placed in the gas or on the container. This temperature is called the kinetic or Maxwellian temperature since it is due to the kinetic energy of the molecules, and corresponds to what I called the Real temperature of solids. At room temperature helium cannot emit vibrational or rotational photons since it consists of neutral atoms. Diatomic homogeneous molecules such as N2 and O2 have a similar problem with emitting photons since they too are neutral. Those gases have a zero Planckian temperature since they do not radiate.
The diatomic heterogeneous molecules such as carbon monoxide do absorb and emit by stretching.
Triatomic molecules, both homogeneous O3 and heterogeneous H20 & CO2, can absorb and emit vibrational energy
Polar triatomic molecules such as H2O can also absorb rotational energy. So even at this simple level it gets quite complicated.
The separate energies contained in vibrations and rotations cannot be measured directly with a thermometer, but the radiation emitted can, which leads to a Planckian or brightness temperatures for each line. A gas is then assumed to have four temperatures, due to its four types of energy: translational, electronic, vibrational, and rotational.
According to the Equipartition theorem http://en.wikipedia.org/wiki/Equipartition_theorem (ET) these four temperature should correspond, but the ET is a classical theory and does not apply to the quantum mechanics of low temperature gases such as the greenhouse gases on Earth.
That is where Raypierre and I fall out.
Thanks, Hank (#409), Timothy (#410) and Barton (#414) for answering my queries in post #408. As you are all more or less singing from the same hymn sheet, I deduce that you must be right (or all instructed by a bad teacher!). In other words, ground effluent photons of wavelengths that match the absorption bands of greenhouse gases can be blocked at a low level of the atmosphere if there are enough of those gases present. This is defined as saturation. However, at the top of this low level there is re-emission of apparently the eqivalent number of photons of the same wavelength, carrying the same amount of energy, albeit directed in random directions.
If this is correct, why confuse a simple layman like myself by talking about saturation which implies that the photons of a given wavelength have had all their energy taken from them and been effectively finished off for good. Surely, scattering would be a more appropriate word to use.
As soon as one accepts that photons are just pinging about like pinballs in areas of so-called saturation but that , eventually, they all get out, one can readily understand why high altitude CO2 can be thought of as a second blanket.
However, if this is all there is to it and, if greenhouse gases are at a constant level such that one has eqilibrium, one would expect infrared to be emerging from the top of a saturated column of atmosphere at the same rate that it is going in. Under such circumstances, one would measure 100% transmission and zero saturation. This, therefore, must be wrong.
Perhaps the photons don’t get re-emitted in quite the way I envisage. Perhaps most end up hitting the surface of the earth, changing wavelength and trying an alternative escape route.
Hank mentioned convection. Perhaps there may be an explanation here but I can’t quite figure what it is.
It is clear that I have no understanding of physics and I appreciate that it must therefore be hard to explain to me what is really going on. It was Raypierre’s tube which blocked egress of infrared that doesn’t seem to tie in with your explanations. It seems you are all suggesting that there should be re-emission from the top of the tube such that, if I waited for an equilibrium situation, egress should match input.
Help!
Alastair McDonald (#415) wrote:
Actually I believe I was the only one who argued for the equality of the different temperatures on the basis of the equipartition theorem – although I knew that it was an approximation in partial- and non- local thermodynamic equilibria. (Actually, I don’t believe Rayspierre has ever really mentioned equipartition on RealClimate – or for that matter distinguished between the different kinds of temperatures.) However, I didn’t know that the equipartition theorem broke down quite so badly at the quantum level, at least with respect to specific heat. Thank you for bringing this to my attention.
Anyway, outside of rocket nozzles, cryogenics and lasers, there doesn’t seem to be much research devoted to rotational temperatures, or in the case of carbon dioxide, rovibrational temperatures. The literature will distinguish between different vibrational temperatures for carbon dioxide above 50 km, but as of yet I don’t see anything related to other temperatures as the result of non-vibrational or rotational-vibrational molecular states of greenhouse gases.
Perhaps this is something we could both look for in the time ahead. A bit esoteric, but since it seems to interest both of us, I think it would be worth digging into. Likewise we could both dig into partial- and non-local thermodynamic equilibria – as this is another interest we would seem to share.
Douglas Wise (#416) wrote:
Well, it really is a different process from scattering. I myself wondered the same thing a few weeks ago, though. But for example, the temperature of the radiation absorbed and re-emitted tends to be the same as the temperature of the atmosphere itself so long as the atmosphere is (roughly) in local thermodynamic equilibrium – which for the vibrational states of carbon dioxide is from 50 km to below.
This is because energy tends to be equally distributed between the translational and vibrational for greenhouse gases. This is due to the fact that collisions are happening at a rate that is roughly two orders of magnitude or more above the rate of relaxation for the molecular states of excitation. And because it is actually absorption and re-emission, it is inelastic.
Energy is exchanged and a thermal equalibrium tends to be achieved between the thermal radiation and the atmosphere. The inelasticity of the interaction is likewise important in terms of the reradiation being isotropic, and the fact that the radiation is emitted becomes important once we get to moist air convection.
Additionally, as others have pointed out, the photon which is absorbed is actually finished off. When a photon is emitted, it will generally be after a large number of collisions, and will probably be emitted by a different molecule altogether.
In fact, the reemission is reemission of radiation, not of the same photon, and it is reemission by the gas, not by a given molecule since the molecule which emits is different from the molecule which absorbs. Alastair helped clarify this issue not too long ago.
The pinging about like pinballs is a great analogy. In this, the carbon dioxide acts like bumpers. The more bumpers, the longer pinballs will remain in play, and assuming they enter at a constant rate, the more pinballs which will be in play assuming one has a larger number of bumpers. It is a good analogy, but as suggested above, it has its limitations.
Well, there are a couple of problems here actually.
The thermal radiation is entering at the bottom of the column, not the top. Solar radiation comes in through the top, but if it is scattered either at the clouds or the surface rather than being absorbed at the surface, then it isn’t part of the climate system’s thermal radiation. To become thermal radiation which is part of the climate system, it has to be absorbed by the surface and radiated as thermal radiation.
Secondly, 100% transmission would imply that no radiation is being reradiated towards the ground – but approximately half of the reradiated thermal radiation is downwelling, half upwelling. And downwelling radiation gets the chance to be absorbed by the surface, raising the temperature of the surface before being reradiated. This is what leads to the feedback.
Well, convection is a major part of the equation. At nearly all levels of the atmosphere, carbon dioxide and water vapor have a local direct cooling effect. They raise the temperature, but they raise the temperature primarily at the surface. The lower atmosphere is warmed principally by moist air convection and the upper atmosphere is warmed primarily by the slow process of the diffusion of thermal energy.
The one major exception to this is the case of ozone – which is able to absorb radiation in the ultraviolet part of the spectrum. Since it tends to absorb most of its energy from solar radiation, in the lower part of the atmosphere where it is active, it tends to have a net warming effect.
I knew less a couple of months ago – so you are not doing that bad…
The thermal energy entering at the bottom and the thermal energy leaving at the top will match – once the new equilibrium is established. The rate at which energy enters and the rate at which energy leaves will be equal at equilibrium. But these rates become equal only because the temperature at the surface is high enough that it is able to radiate more radiation and thus compensate for the increased opacity of the atmosphere.
I found this passage recently in a piece from the Energy Information Administration of the US Department of Energy
http://www.eia.doe.gov/cneaf/alternate/page/environment/appd_a.html
“What happens after the GHG molecules absorb infrared radiation? The hot molecules release their energy, usually at lower energy (longer wavelength) radiation than the energy previously absorbed. The molecules cannot absorb energy emitted by other molecules of their own kind. Methane molecules, for example, cannot absorb radiation emitted by other methane molecules. This constraint limits how often GHG molecules can absorb emitted infrared radiation. Frequency of absorption also depends on how long the hot GHG molecules take to emit or otherwise release the excess energy.”
Surely, this cannot be correct?
Please can someone advise?
Re #419: AEBanner — I am not a physicist. However, I found a paper on-line in Proc. N. A. S. , vol. 12, 1927 by Joseph W. Ellis giving the longest absorption band at 7.67 microns, with presumeably the next being a 6.58 micron band. A paper from the Proc. Royal Society (?) in 1965 gives the only emission band for methane of import in the upper atmosphere as the 7.65 micron band.
Perhaps more usefully for you, I found that there exists a book entitled “The Physics and Chemistry of the Upper Atmosphere” by MH Rees.
re 419. This is a BOMB that I trust is a DUD. The words blow a battleship sized hole into the absorption / re-emission process, don’t they?? Also: (Individual) Molecules are hot?? Molecules emit only at different frequencies than they absorb?? Am I reading this wrong? Or, as AEBanner implies, is DOE out to lunch? — which would be a helluva note!
Re #419
I have e-mailed DoE for confirmation of this paragraph, and I really hope they reply.
By “hot” molecules, I assume they simply mean molecules which have absorbed photons and are therefore in an excited state.
Re #419 What the DoE are saying is quite correct. Let’s face it, if I had mentioned this earlier you would not have believed me.
What happens is that when a photon is absorbed is that the excited state first partly relaxes via a radiationless transition. See http://www.garfield.library.upenn.edu/classics1981/A1981LY47300001.pdf
Then it can emit the remaining energy as a photon, but the emitted photon will be at a longer wavelength than the absorbed one because it has less energy.
The climate modelers like Gavin are still working with Kirchhoff’s Law based on a paper by Einstein in 1917, but radiationless transfers have been known about since 1968, four years after the first edition of Goody’s bible Atmospheric Radiation was published!
422 AEBanner and 421 Rod B Yes, hot just means a photon has been absorbed and that the energy has not yet been lost to collision or radition. And Alastair is probably right about the models, though I have not been able to tell for sure. Gavin or someone needs to verify exactly what state they are in for us. The current basis for such things is NLTE radiative transfer theory — http://www.ssec.wisc.edu/library/coursefiles/05_rte.pdf would be a start. Its fig 5.1 is quite interesting.
You can backtrack this thread to various discussions on LTE, which will have some other recent references. Or search for line by line transfer models or radiative transfer models. The problem for GCM’s is that LBL models can suck up a whole computer by themselves, so various levels of approximation are used in the GCM’s and these vary substantially as to accuracy. OCO and CH4 do not work the way a lot of people think they do, or even the way many models do, which I believe is one of Alastair’s points. But they do assuredly bring about interactions between the radiation fields and the kinetic motion, just not the way some people expect.
WOW you guys are still at this.!! I repeat my comment from Part I, before I even knew that part II existed.
Re 278 (from Part I, or 419 form here). The first 3 DOE sentences are valid. The rest is true but irrelevant since it is not constraining on the total process.
When the CO2 absorbs the energy & returns it to the air mostly by collisions but a little by re-emission, (once a hot CO2 collides once, then it loses enough energy that it canNOT reemit a photon of the specific wavelength that can be absorbed by another CO2) the surrounding air reabsorbs the energy within microseconds and within centimeters (at ground level) and since the air’s temperature is unchanged (conservation of energy) then the air will reemit IR energy per Wein & Stefan-Boltzmann in the wavelength range that CAN be absorbed or reabsorbed by the CO2, continuously, forever. This is HOW CO2 transports energy to higher elevations & out to space. Since the air & CO2 density is lower at higher elevations. a photon travels further going up than it does going down, hence energy is transported out to space. (in a zig-zag process of many absorbtions, at one microsecond per absorbtion, you can get a million absorbtions in a second!!)
Another comment on saturation. When CO2 absorbs a (typical IR) photon, the molecule goes to ~900K. (so said Eli years ago!) THEREFORE, the only way all the CO2 can be saturated is WHEN all the air is at ~900K. Otherwise the CO2 will collide with the air and cool back down to unsaturated conditions. OR looking at it in another way, IF all the CO2 DID stay saturated, then CO2 could not absorb photons, and the IR radiated photons would go directly to space faster, and hence cool down the air. We will not survive too well at ~900K. The saturation concept is a waste of energy!
A side comment- the concept that CO2 “TRAPS” photons is totally absurd. There is NO way in the world, that a ~900K CO2 molecule can exist for more than a few microseconds aurrounded by 288K air molecules. Besides if CO2 traps the energy & doesn’t give it back, then how does the energy warm the air? CO2 “catches and releases” energy. It just slows the transport to space process down, which is why GHGs cause warming.
My next question is since the air is now warmer, why doesn’t the Stefan-Boltzmann equation, that says that the energy transported out (either as a black body or gray – it doesn’t matter) is proportional to T^4, simply transport out MORE energy faster at the warmer temperature, to return the air to the original equilibrium temperature? ie Mother Natures natural compensation process for the greenhouse effect?
re 419 – 425: This is getting out of control! I’ll tentatively accept most of this, but a couple of things do not compute. 1) If the (numerous) discrete rotational and/or vibrational energy levels are precise for every (say) CO2 molecule, then the molecule can absorb or emit, or can transfer to translation energy at only one of those discrete levels. In the event of re-emission (assume at a lower frequency than the original absorption), it is not anywhere near obvious why another CO2 molecule can not absorb this photon as it has an energy level that exactly matches the re-emission. Can anyone explain why not? Moreover it seems much less likely that a different molecule from CO2 will absorb a CO2 molecules emission…
2) How do we come back around to a gas of normal density now emitting blackbody radiation ala Stefan-Boltzmann? For the umpteenth time, does it or not?
A follow up query: Does IR energy absorbed into the rotational or vibration levels have to relax almost immediately? Does a molecule never re-emit directly, as opposed to very seldom? Wouldn’t the average CO2 molecule absorb a number of photons near simuntaneously? Do/can collisions transfer energy from translation to rotation/vibration?
One last quibble/clarification for John. I assume you mean that when a molecule absorbs a typical IR photon, and then transfers its energy from rotation/vibration to translation, the temperature goes up ~900K. Am I correct? (And put your helmet on — the one-molecule-cannot-have-temperature contigent might be ready to fire…)
Re #426
If you refer to #423 you will see that Alistair McDonald explained that an excited CO2 molecule can lose some energy by means of a “radiationless transition”, and he gave a reference to this effect which apparently has been known since 1968. Therefore, the energy of a new photon when emitted is less than the energy of the photon which initially excited the molecule. However, the energy of the new photon is then too small to excite another molecule, and its energy is presumably transferred into kinetic energy of other molecules, or the photon goes to ground, or escapes into space.
This seems to be OK, except that I simply do not understand how a “radiationless transition” works, and I should be very grateful for further explanation.
Re relaxation time for an excited CO2 molecule, I have been informed that 100 picoseconds (10^-10 sec) would probably be a top end figure, and it would more likely be 10ps.
re #427, et al: But there are thousands of discrete energy levels in a CO2 molecule. I also assume that a radiationless transistion/transfer does not have to transistion the full energy of whichever level, but can transistion say half of it (to translation) and half of it to a lower rotational level. [note, translation energy levels are far more numerous, near continuous, and almost do not exhibit similar quanta — other than via Planck’s constant.] This new 2nd rotational level then might re-emit but at a quanta that is 100% of its energy, which is half the energy of the original absorbed level, and thence at a lower frequency. But the energy quanta of this second level exactly matches a potentially available level in another — (actually every other, CO2 molecule. So why can’t the next molecule absorb that emitted energy quanta? Secondly, that particular quanta/level is less likely to exist in a non-CO2 molecule.
re #427-II. If the relaxation interval is ~10psec, doesn’t that mean that the rotation and vibration levels absorb energy, but effectively never have any energy? If that’s correct how can the heat capacity (“n”kT) ever vary?
http://link.aip.org/link/?JCPSA6/122/044112/1
Ok, clearly Angstrom is spinning by now …
A general formula for the rate of resonant transfer of energy between two electric multipole moments of arbitrary order using molecular quantum electrodynamics
A. Salam
Department of Chemistry, Wake Forest University, Winston-Salem, North Carolina 27109
(Received 14 July 2004; accepted 19 October 2004; published online 12 January 2005)
A general expression is derived for the matrix element for the resonant transfer of energy between an initially excited donor species and an acceptor moiety in the ground state, with each entity possessing an electric multipole moment of arbitrary order. In the quantum electrodynamical framework employed, the coupling between the pair is mediated by the exchange of a single virtual photon. The probability amplitude found from second-order perturbation theory is a product of the electric moments located at each center and the resonant multipole-multipole interaction tensor. Using the Fermi golden rule, a general formula for the rate of energy transfer is obtained. As an illustration of the efficacy of the theory developed, rates of excitation energy exchange are calculated for systems interacting through dipole-quadrupole, dipole-octupole, quadrupole-quadrupole, and the familiar dipole-dipole coupling. For each of the cases examined, the near- and far-zone limits of the migration rate are calculated from the result valid for all donor-acceptor separations beyond wave function overlap. Expression of the octupole contribution to the transfer rate in terms of its irreducible components of weights 1 and 3 leads to new features. The octupole weight-1 term is found to contribute only when the interaction is retarded, while the dipole-octupole weight-1 contribution appears as a higher-order correction term to the dipole-dipole rate. Order of magnitude estimates are given for the contributions of dipole-quadrupole and dipole-octupole terms relative to the leading dipole-dipole rate for near-, intermediate-, and far-zone separations to further understand the role played by higher multipole moments in the transfer of excitation and the mechanism dominating the process. ©2005 American Institute of Physics.
Allen Ames (#424) wrote:
Thank you, Allen. This looks fun!
*
AEBanner,
One point to keep in mind: if a molecule can lose energy during a collision, it can also gain energy in a collision. This is a large part of what goes on, actually, as what tends to raise the temperature of the lower atmosophere isn’t the absorption of radiation but moist air convection. The energy from this tends to be radiated both to space and to the surface by greenhouse gases. As such greenhouse gases have a net direct tendency to cool the atmosphere and tend to warm the atmosphere primarily by means of re-emitted radiation warming the surface which promotes moist air convection.
In any case, Allen, Alastair and I take an interest in how reality breaks from local thermodynamic equilibrium, but they may be a little farther than myself at this point.
Douglas asked in 382: “When climate modellers determined climate sensitivity for a doubling of CO2, did they take into account the possibility of …” and “… have they addressed the possibility that the formula would have to change as CO2 levels significantly exceed those experienced in the previous one million years …”
If you use the Find function for the words “climate sensitivity” in the topic I think you’ll get some help here; you’re thinking that climate sensitivity is something modelers come up with from physics calculations, I gather.
This may help clarify where the modelers get the estimates for climate sensitivity: http://julesandjames.blogspot.com/2006/03/climate-sensitivity-is-3c.html
On the second question, one million years isn’t much:
http://www.globalwarmingart.com/wiki/Image:Carbon_Dioxide_400kyr_Rev_png
if you’re willing to go four hundred million years, you can get some big numbers: http://www.globalwarmingart.com/wiki/Image:Phanerozoic_Carbon_Dioxide_png
Note the climatologists never did agree on whether to have their temperature scales run left-right or right-left; the zero point on one of those charts is on the right, and on the other one it’s on the left. Up is always more and down is always less, fortunately.
Re #428
You make a good point, Rod B, and I’ve wondered about that myself. I can only suggest that the process you described depends upon the absorption cross sections of the molecule for photons of different energies, and so is a matter of probability. The absorption lines adjacent to the 14.99 micron line for CO2 are somewhere between one and two orders down, if I remember correctly. So the chance of the transition happening twice ( in any “chain” ) would be between a factor of 10^2 and 10^4 down.
Hopefully, someone who really knows will provide a proper reply, because I believe this to be of great significance.
John Dodds (#425) wrote:
When the CO2 absorbs the energy & returns it to the air mostly by collisions but a little by re-emission, (once a hot CO2 collides once, then it loses enough energy that it canNOT reemit a photon of the specific wavelength that can be absorbed by another CO2) the surrounding air reabsorbs the energy within microseconds and within centimeters (at ground level) and since the air’s temperature is unchanged (conservation of energy) then the air will reemit IR energy per Wein & Stefan-Boltzmann in the wavelength range that CAN be absorbed or reabsorbed by the CO2, continuously, forever. This is HOW CO2 transports energy to higher elevations & out to space. Since the air & CO2 density is lower at higher elevations. a photon travels further going up than it does going down, hence energy is transported out to space. (in a zig-zag process of many absorbtions, at one microsecond per absorbtion, you can get a million absorbtions in a second!!)
Generally it doesn’t even make sense to speak of a photon being absorbed and reemitted. This is actually something which Alastair has pointed out on some occasions. The collisions and consequent transfers of energy simply occurs too often. I remember his running the equations once, and the figure was that collisions would occur at roughly a thousand times the rate of emission. Instead what we know as the result of quantum mechanics, experiments in the labs and infrared imaging of the atmosphere is that when radiation gets absorbed by the gas, it raises the temperature of the gas resulting in the reemission of energy which takes essentially a random path – if one were to track parcels of it.
Eventually some of that radiation will reach the surface and some will reach space. That which reaches the surface will warm the surface, either resulting in moist air convection which raises the tends to raise the temperature of the atmosphere or is reemitted in the form of thermal radiation. Eventually the energy gets out, and in fact at some point an equilibrium will be established where thermal radiation being emitted by the surface and thermal radiation leaving the atmosphere will be equal.
*
Incidently, Alastair brought up something called radiationless transfer at one point, but that is a very specialized phenomena which I believe has nothing to do with the atmosphere. But climatologists would know as they work with radiation physicists who can model this sort of thing: they have even incorporated the fairly esoteric non-local thermodynamic equilibria. But I wouldn’t worry about that for a little while. Throughout most of the atmosphere it isn’t that relevant, and where it does occur it is a matter of gradual deviation from what are called local thermodynamic equilibria.
*
When it cools by collision, it “heats up” other molecules by collision. At some point some of the molecules which recieve energy by collision will be greenhouse gas molecules which reemit.
Actually, throughout most of the atmosphere the radiation has the net tendency of cooling the atmosphere. But some of the radiation which is emitted by greenhouse gases will reach the surface, warming it and resulting in more thermal radiation or in moist air convection and some will escape to space. The moist air convection is what tends to raise the temperature of the atmosphere.
Well, we aren’t talking about black body or gray body as the emissivity will differ in different parts of the spectra, meaning that the capacity to absorb and reemit will be different for different parts of the spectra. But with greenhouse gases being involved, a new equilibria is reached at a higher temperature roughly according to the T^4 where the thermal radiation entering the system from the surface will be equal to the thermal radiation escaping to space.
In essence, the higher temperature is the compensation for the presence of greenhouse gases in the atmosphere – as this is what makes it possible for the amount of thermal radiation entering the system to equal the thermal radiation which is leaving the system. Or to put it in terms of the problem you posed, the equilibria at the higher temperature will be reached before the even higher temperature which would be necessary to reemit radiation at a high enough rate to bring the temperature back down to the original temperature.
Hank (430), are you describing a transfer between quantized states, which for all practical purposes exist only in the rotation and vibration energy levels? If it’s from a quantized level to a non-quantized level (translation) then it would seem your analysis ala resonance doesn’t apply. (But the reverse, from translation to quantized levels, I’m not sure…) Between quantized states between different molecules, while following your rules of allowability, isn’t this transfer always with photons, i.e. emission/absorption of radiation?
Timothy (434), a couple of nits, though like bacteria can be terribly important: You say radiation absorption raises the temperature of the gas. I though we finally concluded that this is not correct, as absorption is only into rotation or vibration levels, which, until that absorbed energy gets transferred to translation, has no effect on temperature. Likewise emission per se from a greenhouse gas does not cool anything, other than emitted virotional energy which came from a transfer of energy from translation. And that transfer, not the emission, causes the cooling.
Isn’t radiationless transfer the transfer of energy from a virotional to another vibration/rotation level within the same molecule or from virotional to translation within the same or, maybe??, to a different molecule, none of which involves photons? Isn’t this important because the exchange between vibration/rotation levels and translation allows radiation to, indirectly, cause temperature changes in the gas. Alastair?
[Is there an industry accepted word that combines “vibration” and “rotation”??]
I had stated in #434:
Rod B (#435) wrote:
No problem.
When molecules have vibrational, rotational or vibrorational energy, they may also have translational energy which makes it possible for them to collide. When they collide, they may lose or gain these other forms of energy. Now I said “heats up” basically as a shorthand for any of these forms of energy since each also corresponds to a temperature. For example, depending upon the type of vibration (stretching, bending, etc) a given molecule of carbon dioxide may have several different vibrational temperatures at the same time – or rather, the aggregate of such molecules will, that is, the gas as a whole. Normally these are equal, that is, below 50 km, but above 50 km collisions will happen less often and thus they will tend to diverge. And since these are temperatures, emission actually does cool the gas.
Now one of the questions that is puzzling me is whether this is the case with rotational (which does not apply to carbon dioxide) and vibrorotational (which does) temperatures as well: are they equal to the vibrational and translational temperatures below 50 km? I honestly don’t know the answer as of yet. However, I suspect that if I stay here long enough I will have the answers to this and a great many other questions.
Rod, the text in 430 is not my analysis.
You wrote
> isn’t this transfer always with photons
That explanation invokes “virtual photons” — click the link to see the original: http://link.aip.org/link/?JCPSA6/122/044112/1
Radiation transfer articles in the physics journals are written almost entirely in math, that I make no pretense to handle.
This may be why Spencer Weart’s AIP History section on radiation physics ends with the 1980s, because it was at that point good enough to be useful for climate work.
What matters for this issue is that the heat does move and the models describe how it moves well enough to be useful.
re 423 Alastair: I think the original radiationless transfer is Forster Transfer (with an umlauted o) (~Furster)
http://www.everything2.com/index.pl?node_id=625957
Such transfer can take place when the spectra overlap and the molecules are close, as between dye molecules adsorbed to a surface. It can be inter- or intra- molecular, like chlorophyll. Radiationless transfer is also what happens in a solid, where the spectral overlap is nearly total, and energy belongs to the whole solid, not just an atom. The relevance here is that close coupling between many molecules gives rise to bands, not lines, and many coupled molecules can have a continuum where energy is shared, just like a solid. This makes blackbody radiative properties. As far as I know right now, only OHO has enough heat of association that multimers are at all likely. Also see http://en.wikipedia.org/wiki/Dark_quencher
As for LTE and photons, the references back around #250 are worth a look if you have not done so recently. A lot of current discussion is covered in them.
Note to Douglas Wise: I see a big difference between the physics as expressed by radiation transfer theory, and what seems to be in the heads of a lot of people who think they know about GW. I sympathize because the older band theories support much misconception, and the pre quantum theories are still around.
Hank, Timothy: Rod B certainly has come a long way, has he not?
> a long way
Definitely a long way into territory I’d never imagined (grin). I continue to hope Raypierre will come tell us where we’re getting to!
“It’s a long way from Isaac Newton,
It’s a long way to us …”
With apologies to http://www.ediacara.org/songs.html
I agree with Timothy and Allan that radiationless transfers are just a red herring, and are probably irrelevant to the greenhouse effect.
Allen Ames (#438) wrote:
I don’t mean to embarass him, but I pretty much always knew that he was/is special. And frankly I think a fair number of us have learned a great deal. Personally, that is one of my two biggest priorities. I am not sure what comes in first, though.
Rod 423,
Yes, when a molecule absorbs energy into a rotational etc mode IT HAS to gain energy. It HAS to heat up. Otherwise conservation of energy does not work.
If it gains energy it will be hotter, & one way or another (mostly collisions (as Eli said years ago, as Timothy said above), the energy will be returned to the rest of the air.
If you visualize a CO2 absorbing the smallest possible photon of energy, then it can only either reemit, of hit and lose some energy to the an other molecule (mostly N2 & O2.) If it hits then it cannot reemit.
Timothy (436), I think that rotation and vibration “temperature” should be properly called characteristic temperature to distinguish it from “real” temperature. (Much like the “characteristic temperature” of the electro-magnetic energy wave coming of a (black)body that has “real temperature”. If you add a pile of energy to vibration/rotation it does not increase the “real” temperature of the gas, as measured with a thermometer. It took me a long time to assimilate this and change my earlier opposite belief — thanks to a lot of helpful pounding form RC posters. Only translation (zipping around) energy affects the temperature of a gas. Please tell me I’m correct.
I also understand that energy can transfer among the three gasseous energy states (and can exchange rotation/vibration with translation from another molecule) and it works toward some equitable distribution within the molecule among the three states (equipartition). Secondly, with very few and insignificant exceptions, longwave radiation is directly absorbed and/or emitted into/from vibration or rotation energy.
I haven’t absorbed all of the posts yet, but I’ll jump to the question that’s really bothering me. There is a credible assertion going around that greenhouse gasses hardly ever gets to re-emit absorbed photons, except at very high altitudes. Question: where does the roughly 325 watts/square meter of downwelling longwave radiation that the earth has to absorb come from???
ROD B We are all grappling to some degree with what is meant by “temperature”. For sure in RT theory the LTE temperature presumes equilibrium between kinetic energy and the analogs of harmonic motion. If these were in equilibrium with the external radiation field it would be a “colored body” equilibrium, depending on the emitters/absorbers present. (There are very few black gases.) As LTE begins to fail for lack of collisions, the last one left is, I think, the kinetic, since it holds the most energy. To change kinetic energy requires a collision of some kind, but (I think) the rot-vib’s have some internal conversions.
If the various energy components are not in equilibrium, it is reasonable to talk about average energy and so average temperature. “Apparent” might depend on how you were looking at the system. The emission from a set of nearly regular vibration levels will have an apparent temperature that depends on the separation and collisions driving the excitation. You may have noticed the OCO emission at 15 microns which seems to always have a temperature around 260. This is a sort of temperature (NLTE maybe). The only unambiguous definition seems to be, as said earlier, the proportionality between delta heat/delta entropy.
As you will no doubt hear, the primary source of it all is the sun.
Don’t think “re-emit absorbed photons” — I had trouble with this. It’s not a solid entity that’s caught and thrown like a football.
The photon is a bookkeeping entry — an amount of energy transfer — not an entity; there’s no photon that exists after the molecule captured the energy — the energy then is in some other form. The molecule is doing a lot of other energy transactions all along. Those may include an outgoing photon, carrying away some energy.
Re 443
Types of temperature -Baloney!- er excuse me – a bright rosy red herring!
Conservation of energy is the key. Energy is either in a photon or in matter (or in a mag field) Going from the ground to space it goes from in matter (heat, translational or rotational or potential or binding energy in the atom or whatever, to photon. Conservation of energy requires one or the other & it can’t get lost on the way. You can’t NOT count it. (unless you are repealing E=mc^2) Since there is no nuclear fission or fusion in the air, AND since there ARE mechanisms to tranlate rotational etc to translational energy (eg a “hotter” CO2 with photon takes more space (higher energy state, vibrates in a larger space etc) than one without the photon- the larger hotter CO2 will perturb the nearest cooler molecules, to move energy to cooler molecules (collisions) then the energy is going to find its lowest state (ie equilibrium),- warm CO2 will cool down to warm the air. OR don’t you believe that the GHE warms the air? If the hot CO2 does not lose its eneregy to the air then how does the air warm up?
This is NOT even physics. It is plain ordinary common sense.
Sorry, but you guys are getting ridiculous.
This is kind of a continuous clarification…. John (442), I have to disagree (though it has been only a couple of weeks since I vociferously argued your point!) Adding energy, even “heat” energy, does not necessarily affect temperature. Otherwise there would be no differing specific heats (the amount of energy to raise one mass unit one degreeK: deltaQ = C*deltaT), which there are with gasses. Specifically the specific heat of a gas increases as vibration and rotation energies start to exceed their ground level. Nor, I guess, would you have things like heat of vaporization or fusion. I agree that rotation and vibration can be transferred to translation, and changes in translation energy, by definition changes temperature.
Allen, I agree the entropy equation (~ Q=ST) is valid, but I’m not comfortable with it as the ultimate say — entropy itself is not exactly unambiguous! Plus, I understand this can proven to be exactly as temperature defined by the Center-of-Mass kinetic energy. And, I agree the definition, or which “temperature” are we talking about, has to be clear. That’s why I call it “real” temperature as opposed to “characteristic” temperature, which is not real temperature but a characteristic that has some relevance to some related temperature. Talking of the “temperature” of an “E-M wave” or a “vibration level”, while physically accurate in the right contex, is not helpful, most pointedly because this entire blog is devoted to assessing REAL temperature.
John (446), you’re being too loose with your terminology. The absorption of a photon by a GHG into its vibration/rotation energies DOES NOT increase the temperature of the gas. The transfer of (some of) that vibration/rotation energy to translation energy DOES increase the temperature, maybe a microsecond or so down the line.
Rod Re where does the 325 watts come from?
The models say that the stratosphere (15-50+Km) gets cooler by transferring energy to the troposhere (0-15Km). (see Hansen et al 2005 figure 1.e)
So then why doesn’t the SBL (hotter air rises faster! hotter (gray)objects radiate more energy) just move the extra energy back to the stratosphere to cancel out the GHE & return to equilibrium? or doesn’t equilibrium work. Funny, every day the earth goes from cooling at night to warming when the sun comes up. IT IS REQUIRED that it pass thru equilibrium at the TOA twice every day! and since the energy gets all the way to the ground then it is required that the air be at equilibrium at all elevations every day also. (it takes under a second for a photon to go from ground to space via multiple CO2 absorbtions – so the SBL maintains AIR equilibrium VERY VERY quickly!) The cooler stratosphere & warmer ground is impossible if we are at equilibrium. BUT THAT temperature reality is confirmed by measurements. So HOW????
You might try adding energy to the ground from energy stored in the ocean/land per Hansen Nazarenko 2005 (which would also warm the stratosphere since we are adding energy that is not from the sun & not included in the models,) AND you might try subtracting energy from the stratosphere (because the earth mag field which has decreased for the last 100+ years no longer transfers as much energy to the charged particles in the stratosphere to send them towards the poles?- also not included in the models!
OR you might try continuing to think about it. You are doing well- Just don’t believe everything you hear – question everything. especially from the experts here! including Gavin’s step ONE of six, that the GHE is unchallengeable. (according to me- the GHE works, but the SBL just cancels it out almost immediately so there is no long term CO2 effect. CO2 can’t cause warming! The GHE doesn’t add energy. Arrhenius failed to account for the (gray body) SBL.-ie that hotter air radiates more energy faster to compensate for the slow down in transporting energy due to the increased absorbtions.)
John, I can’t recall or figure out what “SBL” stands for…