Guest post by Tamino
In a paper, “Heat Capacity, Time Constant, and Sensitivity of Earth’s Climate System” soon to be published in the Journal of Geophysical Research (and discussed briefly at RealClimate a few weeks back), Stephen Schwartz of Brookhaven National Laboratory estimates climate sensitivity using observed 20th-century data on ocean heat content and global surface temperature. He arrives at the estimate 1.1±0.5 deg C for a doubling of CO2 concentration (0.3 deg C for every 1 W/m^2 of climate forcing), a figure far lower than most estimates, which fall generally in the range 2 to 4.5 deg C for doubling CO2. This paper has been heralded by global-warming denialists as the death-knell for global warming theory (as most such papers are).
Schwartz’s results would imply two important things. First, that the impact of adding greenhouse gases to the atmosphere will be much smaller than most estimates; second, that almost all of the warming due to the greenhouse gases we’ve put in the atmosphere so far has already been felt, so there’s almost no warming “in the pipeline” due to greenhouse gases already in the air. Both ideas contradict the consensus view of climate scientists, and both ideas give global-warming skeptics a warm fuzzy feeling (but not too warm).
Despite the celebratory reaction from the denialist blogosphere (and U.S. Senator James Inhofe), this is not a “denialist” paper. Schwartz is a highly respected researcher (deservedly so) in atmospheric physics, mainly working on aerosols. He doesn’t pretend to smite global-warming theories with a single blow, he simply explores one way to estimate climate sensitivity and reports his results. He seems quite aware of many of the caveats inherent in his method, and invites further study, saying in the “conclusions” section:
Finally, as the present analysis rests on a simple single-compartment energy balance model, the question must inevitably arise whether the rather obdurate climate system might be amenable to determination of its key properties through empirical analysis based on such a simple model. In response to that question it might have to be said that it remains to be seen. In this context it is hoped that the present study might stimulate further work along these lines with more complex models.
What is Schwartz’s method? First, assume that the climate system can be effectively modeled as a zero-dimensional energy balance model. This would mean that there would be a single effective heat capacity for the climate system, and a single effective time constant for the system as well. Climate sensitivity will then be
S=τ/C
where S is the climate sensitivity, τ is the time constant, and C is the heat capacity. Simple!
To estimate those parameters, Schwartz uses observed climate data. He assumes that the time series of global temperature can effectively be modeled as a linear trend, plus a one-dimensional, first-order “autoregressive” or “Markov” or simply “AR(1)” process [an AR(1) process is a random process with some ‘memory’ of its previous value; subsequent values y_t are statistically dependent on the immediately preceding value y_(t-1) through an equation of the form y_t = ρ y_(t-1) + ε, where ρ is typically required to be between 0 and 1, and ε is a series of random values conforming to a normal distribution. The AR(1) model is a special case of a more general class of linear time series models known as “Autoregressive moving average” models].
In such as case, the autocorrelation of the global temperature time series (its correlation with a time-delayed copy of itself) can be analyzed to determine the time constant τ. He further assumes that ocean heat content represents the bulk of the heat absorbed by the planet due to climate forces, and that its changes are roughly proportional to the observed surface temperature change; the constant of proportionality gives the heat capacity. The conclusion is that the time constant of the planet is 5±1 years and its heat capacity is 16.7±7 W • yr / (dec C • m^2), so climate sensitivity is 5/16.7 = 0.3 deg C/(W/m^2).
One of the biggest problems with this method is that it assumes that the climate system has only one “time scale,” and that time scale determines its long-term, equilibrium response to changes in climate forcing. But the global heat budget has many components, which respond faster or slower to heat input: the atmosphere, land, upper ocean, deep ocean, and cryosphere all act with their own time scales. The atmosphere responds quickly, the land not quite so fast, the deep ocean and cryosphere very slowly. In fact, it’s because it takes so long for heat to penetrate deep into the ocean that most climate scientists believe we have not yet experienced all the warming due from the greenhouse gases we’ve already emitted [Hansen et al. 2005].
Schwartz’s analysis depends on assuming that the global temperature time series has a single time scale, and modelling it as a linear trend plus an AR(1) process. There’s a straightforward way to test at least the possibility that it obeys the stated assumption. If the linearly detrended temperature data really do behave like an AR(1) process, then the autocorrelation at lag Δt which we can call r(Δt), will be related to the time constant τ by the simple formula
r(Δt)= exp{-Δt/τ}.
In that case,
τ = – Δt / ln(r),
for any and all lags Δt. This is the formula used to estimate the time constant τ.
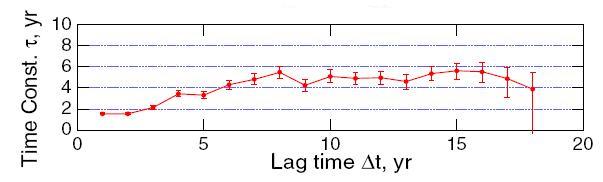
And what, you wonder, are the estimated values of the time constant from the temperature time series? Using annual average temperature anomaly from NASA GISS (one of the data sets Schwartz uses), after detrending by removing a linear fit, Schwartz arrives at his Figure 5g:
Using the monthly rather than annual averages gives Schwartz’s Figure 7:
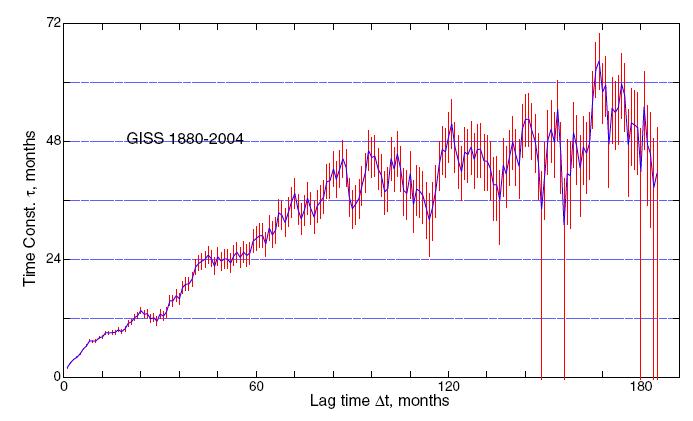
If the temperature follows the assumed model, then the estimated time constant should be the same for all lags, until the lag gets large enough that the probable error invalidates the result. But it’s clear from these figures that this is not the case. Rather, the estimated τ increases with increasing lag. Schwartz himself says:
As seen in Figure 5g, values of τ were found to increase with increasing lag time from about 2 years at lag time Δt = 1 yr, reaching an asymptotic value of about 5 years by about lag time Δt= 8 yr. As similar results were obtained with various subsets of the data (first and second halves of the time series; data for Northern and Southern Hemispheres, Figure 6) and for the de-seasonalized monthly data, Figure 7, this estimate of the time constant would appear to be robust.
If the time series of global temperature really did follow an AR(1) process, what would the graphs look like? We ran 5 simulations of an AR(1) process with a 5-year time scale, generating monthly data for 125 years, then estimated the time scale using Schwartz’s method. We also applied the method to GISTEMP monthly data (the results are slightly different from Schwartz’s because we used data through July 2007). Here’s how they compare:
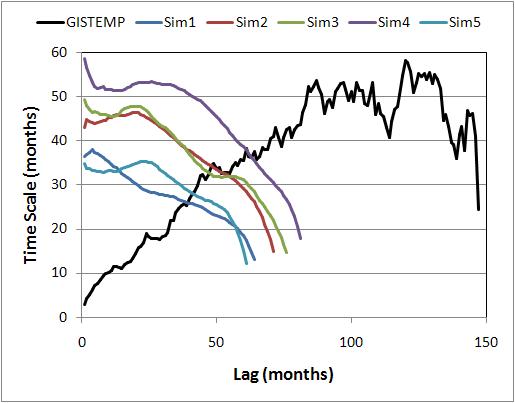
This makes it abundantly clear that if temperature did follow the stated assumption, it would not give the results reported by Schwartz. The conclusion is inescapable, that global temperature cannot be adequately modeled as a linear trend plus AR(1) process.
You probably also noticed that for the simulated AR(1) process, the estimated time scale is consistently less than the true value (which for the simulations, is known to be exactly 5 years, or 60 months), and that the estimate decreases as lag increases. This is because the usual estimate of autocorrelation coefficients is a biased estimate. The word “bias” is used in its statistical sense, that the expected result of the calculation is not the true value. As the lag gets higher, the impact of the bias increases and the estimated time scale decreases. When the time series is long and the time scale is short, the bias is negligible, but when the time scale is any significant fraction of the length of the time series, the bias can be quite large. In fact, both simulations and theoretical calculations demonstrate that for 125 years of a genuine AR(1) process, if the time scale were 30 years (not an unrealistic value for global climate), we would expect the estimate from autocorrelation values to be less than half the true value.
Earlier in the paper, the AR(1) assumption is justified by regressing each year’s average temperature anomaly against the previous year’s and studying the residuals from that fit:
Satisfaction of the assumption of a first-order Markov process was assessed by examination of the residuals of the lag-1 regression, which were found to exhibit no further significant autocorrelation.
The result for this test is graphed in his Figure 5f:
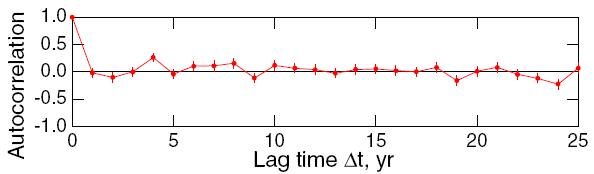
Alas, it seems this test was applied only to the annual averages. For that data, there are only 125 data points, so the uncertainty in an autocorrelation estimate is as big as ±0.2, much too large to reveal whatever autocorrelation might remain. Applying the test to the monthly data, the larger number of data points would have given this more precise result:
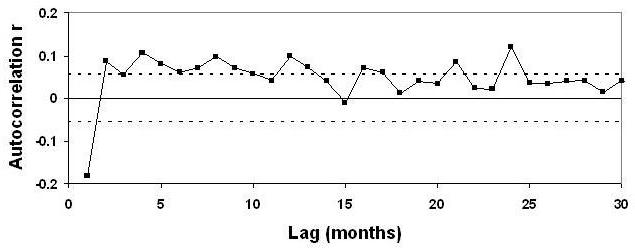
The very first value, at lag 1 month, is way outside the limit of “no further significant autocorrelation,” and in fact most of the low-lag values are outside the 95% confidence limits (indicated by the dashed lines).
In short, the global temperature time series clearly does not follow the model adopted in Schwartz’s analysis. It’s further clear that even if it did, the method is unable to diagnose the right time scale. Add to that the fact that assuming a single time scale for the global climate system contradicts what we know about the response time of the different components of the earth, and it adds up to only one conclusion: Schwartz’s estimate of climate sensitivity is unreliable. We see no evidence from this analysis to indicate that climate sensitivity is any different from the best estimates of sensible research, somewhere within the range of 2 to 4.5 deg C for a doubling of CO2.
A response to the paper, raising these (and other) issues, has already been submitted to the Journal of Geophysical Research, and another response (by a team in Switzerland) is in the works. It’s important to note that this is the way science works. An idea is proposed and explored, the results are reported, the methodology is probed and critiqued by others, and their results are reported; in the process, we hope to learn more about how the world really works.
That Schwartz’s result is heralded as the death-knell of global warming by denialist blogs and Sen. Inhofe, even before it has been officially published (let alone before the scientific community has responded) says more about the denialist movement than about the sensitivity of earth’s climate system. But, that’s how politics works.
David, if I understand the definition, we’re taking the period after the end of the last ice age until the 1800s or so as stable. The amount of CO2 going in and out of the atmosphere was stable, biogeochemical cycling was maintaining the level.
Then people started burning fossil fuels:
Climate Forcing
By altering the global energy balance, such mechanisms “force” the climate to change. Consequently, scientists call them “climate forcing” mechanisms. …
http://www.ace.mmu.ac.uk/eae/Climate_Change/Older/Climate_Forcing.html
Er, duh, “use the Search box, Hank …”
https://www.realclimate.org/index.php?p=186
What is a first-order climate forcing?
“… climate forcings (the changes that affect the energy balance of the planet) …”
Hank Roberts (301, 302) — Thanks for the link to the older Real Climate thread and especially your first (301) sentence. So I think I now have it right:
Taking 1750 CE as the beginning of the industrial age, by 1850 CE the forcing was some X W/m^2 due to a modest increase in CO2 concentration. Then by 2007 CE it is X + 1.485 W/m^2 due to an immodest increase in CO2 concentration.
My concern is whether I can just add these this way. (Upon some reflection, even that now appears to be wrong.) :(
Aha! Just have to be careful about what is added:
C0: base concentration
C1: concentration later
C2: concentration even later
then
ln(C1/C0) + ln(C2/C1) = ln(C2/C0)
so the addition is ok, provided we remember that this is only an approximation to reality…
Now I think you’re describing why people are writing coupled climate models, David. Lots of forcings, lots of feedbacks, all at once.
David, by mathematical definition the formula compares today’s forcing due to today’s CO2 concentration, to the forcing of the concentration whenever you choose — CO20. It’s a relative forcing, but since it’s a log function, relative to itself is zero, ’cause log1 = 0.
Rod B (306) — I don’t think so, one several grounds. The most important is that the so-called relative forcing is in physical units, say W/m^2. Ratios are dimensionless so it is not a ratio comparison. (Which is why I find ‘Relative Forcing’ to be a poorly chosen term.)
David, that’s an old chestnut that I got beat up badly over (though still think I’m correct [;-) The units are put in with the 5.35 (or whatever) multiplying factor. though it’s still mathematically equivalent to a unitless exponent of the concentration ratio…. Duck! Incoming!
Rod B (308) — Consider yourself bashed once again. :)
Well, in any case, I agree with Barton (297)….
David B. Benson (#300) wrote:
“Additional Forcing” would work for me so long as one kept in mind the fact that “forcing” does not exist where the system is in equilibrium. I believe that what the climatologists assume as an approximation: the base year is in equilibrium (one is after all concerned with the evolution of the climate system as it evolves over time due to being disturbed), and as such there is no forcing in the base year. But another way of saying this would be that the forcing was zero in the base year.
Incidentally, in the past I have viewed the “series” of absorptions and reemissions of thermal radiation between the atmosphere and the surface (where a given “packet” of energy may be absorbed by the atmosphere, undergo collisions, emission, absorption by the surface, emission, etc) as feedback. From a certain perspective it is, but not as climatology understands it. In climatology, “feedback” is always understood in relation to “forcing.”
Given the near instantaneous nature of the amplification (that is, prior to amplification by means of such processes as water evaporation), this initial amplification is simply considered part of the initial forcing. The forcing itself is defined essentially as the deficit between radiation as the deficit between the thermal energy entering the system and the thermal energy which is leaving the system at the top of the atmosphere.
Re forcings and so on: I wonder if it might not make more sense (to those of us without a major background in atmospheric science, anyway) to use a different concept. Anyone who has done much home remodeling is probably familiar with insulation R values. So what’s the R value of the atmosphere? And how much does adding X amount of CO2 increase the effective R value?
Aha! RF abbreviates ‘Radiative Forcing’. That is just fine. And as pointed out in comment #297, for any given C0,
RF = 5.35 ln(C0/C0) = 0,
appropriate for an equilibrium C0.
With reference to Table 1 of the paper:
Dividing the “rate of change of heat content with time” by the “rate to change of temperature with time” does give an instantaneous “rate of change of heat content with temperature” what it does not guarantee is to give a constant and generally it doesn’t as is the case here.
Inspection of the data will show that the ocean is warming much more slowly than the surface temperature. The two are only weakly coupled. This is a bit of a problem if you are going to use the derived heat capacity as if it were tightly coupled to the surface as is done in this paper.
This has more general significance for anyone seeking to use the ocean as a significant drag on surface temperature rise. The weak coupling means that the ocean is not absorbing a high proportion of the current forcing the largest value given being .205 W/m^2 this value is likely to rise with increasing disparity between surface and water temperatures at depth. In the same way it is likely that it was smaller in the past not just absolutely but as a proportion of the forcing.
Appealing to a weakly coupled heatsink, no matter how big, is unlikely to produce a significant brake on, or delay in rising temperatures.
Best Wishes
Alexznader Harvey
Suppose a steady stream of non-radiant heat energy is fed into the atmosphere. How is the proportion lost to space calculated?
[[Suppose a steady stream of non-radiant heat energy is fed into the atmosphere. How is the proportion lost to space calculated?]]
What is “non-radiant heat energy?” And what direction is it going?
I’ll assume that what you mean is that a region of the atmosphere is being spontaneously heated by some unknown mechanism. It would then radiate more than before since its temperature would be higher, according to the modified Stefan-Boltzmann law:
F = ε σ T4
where F is the flux density emitted (in watts per square meter in the SI), ε the emissivity of the body doing the radiating (a figure which must be between 0 and 1), σ the Stefan-Boltzmann constant (5.6704 x 10-8 W m-2 K-4 in the SI), and T the temperature (K in the SI).
For a beam of light going straight up, the amount that gets through would be determined by the optical thickness of the medium in the way:
F = F0 e-τ
The optical thickness τ is the product of the absorption coefficient k for the wavelength of the light in question (in m2 kg-1 in the SI), the density ρ of the absorbing medium (kg m-3) and dz the path length (m):
τ = k ρ dz
Complications are induced by the facts that emitted radiation is usually at many wavelengths, that absorption coefficients vary by wavelength, and that the density and composition of the medium change with altitude.
For a broad order-of-magnitude example, consider that of the 390 watts per square meter emitted by the Earth’s surface on average, only about 40 W m-2 survive to get out to space. The Earth radiates about 240, the other 200 coming from the atmosphere.
Re #316
Thank you for the reply, but by the steady input stream of energy to the atmosphere I meant heat energy such as sensible and latent heat, not infrared radiation.
Off-topic, but ought to be interest to climatologists, both professional and amateur:
http://www.alternet.org/environment/64445/
regarding controversy about hydropower and methane release.
Barton and AEBanner, I’m trying an answer, but mostly as a question/test of my knowledge — correct or incorrect?
There is about 559 watts/square meter entering the atmosphere: 390 from the surface (of which 40 goes straight out the top), 67 from incoming solar (none of which goes straight out the top — going the wrong direction), and 102 from latent/thermal heat from the surface, none of which can go straight out the top, by definition — only radiation can leave the atmosphere. All of that incoming gets bounced around, transferred, radiated and reabsorbed among the molecules (except for the 40 that get out directly), and eventually gets radiated out (~42% or 235, including the straight 40), or radiated down and “reabsorbed” by the earth’s surface (~58%). So the answer is that the non-radiative heat source (thermals and latent) get absorbed entirely by the atmosphere, then lose their identity as such and become part of the molecular atmospheric energy stew.
A.E. Banner posts:
[[Thank you for the reply, but by the steady input stream of energy to the atmosphere I meant heat energy such as sensible and latent heat, not infrared radiation.]]
Well, neither conduction, convection, nor changes of state get outside the atmosphere. Earth’s only thermal connection with space is through radiation.
What the mechanism was heating an area of atmosphere doesn’t matter. The radiation will still proceed as described.
I’m puzzled by Mr. Banner’s assumption that “sensible heat” and “latent heat” can be “input” — perhaps that means “added” or “created” or perhaps that means “rearranged” — is there an example of that in whatever you’re relying on as the basis for these questions?
Ask the people there what they mean.
Rod —
Yes, I think you have it right. The non-radiative fluxes (conduction, convection, latent heat) only transfer energy from surface to atmosphere and within the atmosphere. The only way the Earth system interacts with outer space is through radiation. (To a reasonable degree of accuracy, anyway.)
Re #319 and #320
Thank you, Rod B and Barton, for your replies.
OK, agreed. Energy can escape to space from Earth only as electromagnetic radiation.
So does this mean that the only way sensible and latent heat in the atmosphere can escape to space is through inter-molecular collisions exciting molecules into higher energy levels, with subsequent infrared photon emission? And does this apply only to the greenhouse gases, or does it include nitrogen and oxygen radiating as a “black body”?
Re #321 Hank
Just trying to get some ideas sorted out. Please humour me for now.
Good question AEBanner. I’d like to 2nd it — can’t answer it but have had the same question. Why wouldn’t O2 and N2 radiate out with normal blackbody (Planck function) radiation? I contend they do, but there is much disagreement ala gases radiating Planck function E-M waves. It further seems that, if they do, the radiation would be very small/light/weak. First off, I’m not sure where one would pick the boundary for radiating into space. The top of the thermosphere where it is very hot — but hardly anything there? The top of the stratosphere or mesosphere where it is very cold (and would radiate little Planck stuff)? Plus radiating gases have a lower emissivity as the density decreases, don’t they?
Rod B., There is a lot of misunderstanding of blackbody radiation–and a tendency to confuse it with “thermal radiation”. A blackbody spectrum is just the spectrum you get when a photon gas is in equilibrium. However, photons do not interact with each other, so the only way a gas of photons can come to equilibrium is by interacting with the materials around it–the walls of a container, gasses therein, etc. However, these materials themselves can only absorb and radiate at energies corresponding to differences between their energy levels. Now these energy “lines” can get broadened. In solids, nearby lines can even coalesce into “energy bands” (hence the conduction and valence bands). However, for any single molecule type, you will not have a continuum of energies as you do for a black-body spectrum. It is a grey body, instead of a black body.
The things to remember:
1)Where a molecule can’t absorb, it can’t radiate either. There have to be energy transitions that correspond to the energy of the radiation.
2)Blackbody radiation is what you get for equilibrium in the radiation field–but it is via interactions with matter that the radiation field reaches equilibrium.
WRT your other question–the level at which the planet radiates is that at which the probability of the upwelling LWIR photon being captured is significantly less than 1–that is at which its interaction length becomes long compared to the distance to space.
Re #326 Ray Ladbury
Very interesting, thank you.
So oxygen and nitrogen cannot emit photons.
But can photons be generated by collisions between O2 and/or N2 molecules, and then escape to space?
If not, then it would seem that non-radiant heat energy put continuously into the atmosphere would be largely retained, since the only escape route is via the low concentrations of greenhouse gases.
This would cause an increase in atmospheric temperature.
Ray Ladbury (#326) wrote:
Quick clarification.
Unless I am mistaken, while the above is undoubtedly true, what we are typically concerned with in terms of “where the planet radiates from” is the layer of the atmosphere which radiates at the effective temperature of the planet – the temperature that the earth appears to have at a distance given the thermal radiation which escapes the atmosphere. This is the so-called “effective radiating layer.” This is where as much energy will escape to space as is radiated back to the surface in the form of backradiation. The effective radiating layer is at roughly 6 km and rising, but well within the troposphere.
#316, Barton, thanks for the very enjoyable writing as usual. It brings to mind: if there is so little radiation escaping to space, how are actual observations, measurements done in accounting for the true heat radiation book? Theory seems fine, but I believe that there is more heat energy in the tropsphere than estimated, this would explain the recent Polar ice great melt (not modelled to happen till about 2038). Is there a way for the theory to miss out on something still not formally observed?
Or put this another way, is the heat radiation accounting always balanced to the satisfaction of our certified atmospheric accountants?
Timothy Chase–it’s a little more complicated than that. At wavelengths where there is little absorption, the radiation is effectively coming directly from the surface, so the “temperature” of the radiation is the surface temperature. For LWIR, the radiation can’t escape until the optical free path is of order the remaining atmospheric thickness, so, there, the temperature will be characteristic of that level. If the atmosphere becomes thicker at a particular wavelength, then the temperature of the region where it effectively escapes must increase–along with the temperature of the atmospher and the planet as a whole.
A. E. Banner, the symmetry of O2 and N2 can be broken by intermolecular interactions, resulting in some absorption and emission. But they would mostly lose energy by colliding with molecules that could radiate at roughly thermal energies.
> AEBanner wrote: “… oxygen and nitrogen cannot emit photons”
You need to state limited conditions for that to be correct.
http://odin.gi.alaska.edu/FAQ/#color
Ray, I really hate to disagree with you expertise, so I’ll just “reclarify”. What doesn’t add up in 326 is the sea of photons. They just didn’t arrive out of nowhere; they were generated by the same body that you say is now having trouble absorbing some of them. Secondly, I thought so-called blackbody radiation was in fact (prettin’ near) “thermal” radiation, both terms originating (mostly) from Planck figuring out what heated bodies do. (The formula for total radiated power has only T as an independent variable.) Blackbody radiation is those photons escaping through the little hole, not reabsorbing into the inside walls; and they display a continuous spectrum as shown in the jillions of graphs. Thirdly, I thought the convention is “greybody” is continuous (for all practical purposes) but with an emissivity less than 1.0, though it is also used to describe matter with variable (by wavelength) emisivity… and, it seems, to confuse people.
Your last statement implies that the atmosphere (including O2 and N2) does not emit blackbody radiation (per my definition) but that the exitance is only from either 1) the temperature dependent blackbody-type radiation that makes it all the way from the earth’s surface, or 2) some (per your and Timothy’s calculus) of the discrete radiation ala translation and rotational energy levels (and not directly temperature dependent) in radiating (re-emitting) atmospheric molecules, which include only “greenhouse” gases. Is that what you contend?
Ray Ladbury (#330) wrote:
Glad to hear it — means I will learn something.
Somewhat different problem from what I was considering, then. But this helps to explain how the infrared sounders work – and why it helps to have them looking at over 2000 different “channels” – and how this gives them the ability to peel away layers of the atmosphere, looking at the concentration of different greenhouse gases at different altitudes.
A.E. Banner posts:
[[If not, then it would seem that non-radiant heat energy put continuously into the atmosphere would be largely retained, since the only escape route is via the low concentrations of greenhouse gases.
This would cause an increase in atmospheric temperature.]]
Right, but since latent and sensible heat transfer to the atmosphere is pretty much a continuous process, the atmosphere would have to heat up indefinitely.
It doesn’t because the greenhouse gases radiate away the heat energy as infrared radiation, proportionate to the fourth power of the temperature.
Wayne Davidson posts:
[[ It brings to mind: if there is so little radiation escaping to space, how are actual observations, measurements done in accounting for the true heat radiation book?]]
They have to write a model to account for where everything goes. Here’s an example:
http://www.atmo.arizona.edu/students/courselinks/spring04/atmo451b/pdf/RadiationBudget.pdf
Note that, although some of the figures can be checked by observation, there is some room for error and different studies come up with slightly different numbers.
The contention that there is more heat energy in the troposphere than known is unlikely. We can calculate how much heat energy is present from the temperature:
H = m cp T
where m is the mass of the substance (say, a layer of air) in kg, cp the specific heat at constant pressure (Joules per Kelvin per kilogram), and T the temperature (K). H comes out in Joules. Vertical temperature profiles are easily measured with balloons. It’s unlikely that the troposphere heat content is substantially greater than estimated.
Rod, you write above “Your last statement implies … either 1) … or 2) …” — you seem to be trying to derive some kind of natural law by logic.
Nature’s more complicated, between the extremes.
Discrete emission lines from gases in the upper atmosphere where there’s less interaction between molecules.
Emission bands where there’s more interaction in gases at ‘one atmosphere’ of pressure at the bottom of the atmosphere and the surface of the planet.
Emissions from interaction with the enormous mass of other material _in_ the atmosphere, all the dust and soot and water as liquid and as vapor.
That’s where this ‘photon cloud’ interacts. It’s not a nice simple either/or situation.
The number and kind of interactions are enormous. You’re going to have a little of everything, statistically, in the result.
# 334 thanks Barton, The resolution coverage of radiosondes may be better at Southern lattitudes,
but in the Polar regions they are few and far apart. If T is the weighted temperature of the entire troposphere, and average T needs to be calculated from all radiosonde profiles then, if this is the heat calculation which is monitored, there is plenty room for error as from the gaps between the great distances between Upper Air stations. But I have yet to meet an atmospheric heat budget “accountant” yet…
Ron, you’re asking the same question in several different threads now, and getting attention from people in several places with the same question. Can you pick one place or ask our hosts to give you one place, rather than spread it around? It’d help focus, else we keep repeating the same answers over and over, recreational typing.
I want to try to get an estimate for the proportion of a continuous, steady supply of initially non-radiant heat energy put into the atmosphere which can subsequently escape to space as radiation following inter-molecular collisions in the atmosphere between greenhouse gases and the oxygen and nitrogen.
Assume that the concentration of GHGs including water vapour is an average of 2%, then the GHGs would acquire about 2% of the energy if shared out equally, and this 2% would escape to space as infrared photons from the GHGs. The oxygen and nitrogen cannot radiate, so the remaining approx 98% of the steady input supply goes into heating the atmosphere.
Correct, or perhaps not? But, if not, why not?
I still haven’t figured out what you mean by “non-radiant heat energy put into the atmosphere” — can you give an example?
Something like a geyser? ignoring the fact that it too radiates heat, just considering it as emitting superheated water that immediately condenses into a cloud? That would release latent heat into the atmosphere. Or something like Chernobyl, ignoring the radiant energy from that and just considering the hot gases produced?
But once you’ve added heat, of any form, it continues to change form. It doesn’t sort out one way or the other and rush away as photons or else stick around as kinetic energy, it’s going back and forth between all those forms all the time.
Here (aside from using ‘reradiate’ — ubiquitous but nitpickable),
this may help:
http://fsi.ucf.edu/Brandenburg/SS_22GlobalWarming.ppt
Photons don’t just rush away from the planet, they’re not neutrinos.
They interact; they interact more as CO2 increases; each interaction transfers that packet of energy into another form.
“Thermal Photon Diffusivity”
“Diffusivity is lowered by increased CO2”
“20 cm mean free path at 15 microns”
Re #339 and #340
Thank you, Mr Roberts.
Yes, the two examples you provided will serve very well.
The question remains, though. How is the proportion lost to space calculated, or what is the figure if known?
Re #339 and my reply
No, sorry. Please cancel the example of Chernobyl, because this was not a continuous supply.
The geyser is still OK.
[[Assume that the concentration of GHGs including water vapour is an average of 2%, then the GHGs would acquire about 2% of the energy if shared out equally, and this 2% would escape to space as infrared photons from the GHGs. The oxygen and nitrogen cannot radiate, so the remaining approx 98% of the steady input supply goes into heating the atmosphere.
Correct, or perhaps not? But, if not, why not?]]
Because the hotter the greenhouse gases get, the more they radiate, disproportionately (a fourth-power law).
Re #338, AEB; and #343 Barton Paul Levenson
The Stefan-Boltzmann Law to which you referred gives the output power from a black body. Infrared emission rate from GHGs also follows this law, but only if sufficient power is being supplied to the GHGs in the first place. These gases are not, of themselves, power generators.
The power I am concerned with is that which might, perhaps, be transferred to the GHGs by increased atmospheric inter-molecular collisions resulting from extra energy from sensible or latent heat supplied continuously to the atmosphere.
If this mechanism exits, it would be interesting to know the efficiency, since this could have an effect on the temperature of the atmosphere.
AEBanner,
OK, let’s think about this in terms of what these different energies mean.
First latent heat. This is just the energy that you have to supply to take the substance from an energetically favorable state to one that is less energetically favorable–e.g. solid to liquid or solid to gas or liquid to gas. The only way this energy does anything is by being liberated as the substance transforms to the energetically favorable state again. That is, it has to become thermal energy.
Thermal energy can be transformed into latent heat, into vibrational energy/rotational energy, etc. as long as there are molecules energetic enough to cause such transitions. Since we are dealing with >10^30 molecules, you’ll certainly have a few that are. Sensible heat is just thermal energy (including kinetic, vibrational, rotational etc. degrees of freedom).
Ultimately almost all of this energy comes from the Sun–whether it goes into latent heat of water vapor, thermal energy, green plants or whatever. So you have a pretty good idea of the energy input to the system if you know the incident solar energy and the planetary albedo. The only other substantial energy source that has much importance is the energy from within Earth (latent heat of condensation of liquid iron onto the solid iron core, radioactive decays, etc.) and this is negligible compared to solar inputs. The following link gives some discussion.
http://en.wikipedia.org/wiki/Earth's_energy_budget
Re #345 Ray Ladbury
Thank you for your reply, but I wanted to concentrate on non-radiant energy entering the atmosphere, eg your idea of condensation of liquid iron, or Hank Roberts’s geyser. These sources are clearly far less important than solar energy, but probably do deserve some consideration.
Is there any method of calculating how much power can be transferred by molecular collisions from the atmosphere to the 2% GHG components, and which can then be re-emitted to space as infrared photons
Yes, Mr. Banner. That point’s been gone over repeatedly in multiple topics, each time you ask the question.
All of it can be transferred.
All of it will be, over several hundred years.
That’s what’s meant by the planet reaching a new equilibrium temperature. That’s the reason it takes a long while for the effects of a given amount of CO2 increase to stabilize once CO2 stops being added.
Re #347 Hank Roberts
You say the point has already been dealt with, but no real answer has been forthcoming, although much has been said. In your post, you imply all of the added energy will be lost to space, but no explanation for the mechanism is given. It is very easy to say that is dealing with the point, but it does not get us any further forward. Also, remember that I want to concentrate on initially non-radiant energy. Your last paragraph is dealing with standard GHG theory, and so is not on point.
I repeat below a paragraph from my #338, and ask anyone to show why they think it’s wrong.
[[Assume that the concentration of GHGs including water vapour is an average of 2%, then the GHGs would acquire about 2% of the energy if shared out equally, and this 2% would escape to space as infrared photons from the GHGs. The oxygen and nitrogen cannot radiate, so the remaining approx 98% of the steady input supply goes into heating the atmosphere.]]
AEB posts, again:
[[I repeat below a paragraph from my #338, and ask anyone to show why they think it’s wrong.
[[Assume that the concentration of GHGs including water vapour is an average of 2%, then the GHGs would acquire about 2% of the energy if shared out equally, and this 2% would escape to space as infrared photons from the GHGs. The oxygen and nitrogen cannot radiate, so the remaining approx 98% of the steady input supply goes into heating the atmosphere.]]]]
Okay, you didn’t like my last explanation, try this one. The atmosphere is NOT steadily getting hotter and hotter to a noticeable degree, aside from the very slow creep due to global warming. If it’s not getting rapidly warmer, despite the fact that a tremendous amount of energy pours into it every day, then THERE MUST BE SOME WAY OF GETTING RID OF THE ENERGY. Okay? If it DIDN’T get rid of the energy, IT WOULD HEAT UP QUICKLY.
The atmosphere gets rid of heat energy by radiating it to space.
RE #349 Barton Paul Levenson
[[Okay, you didn’t like my last explanation, try this one. The atmosphere is NOT steadily getting hotter and hotter to a noticeable degree, aside from the very slow creep due to global warming. If it’s not getting rapidly warmer, despite the fact that a tremendous amount of energy pours into it every day, then THERE MUST BE SOME WAY OF GETTING RID OF THE ENERGY. Okay? If it DIDN’T get rid of the energy, IT WOULD HEAT UP QUICKLY.
The atmosphere gets rid of heat energy by radiating it to space.]]
I completely agree with your statement above. There is no question about how the enormous amount of solar energy received is radiated back to space.
But, I am concerned with a different problem which I’ve tried to state on several occasions now, without being properly understood.
This is the item in my #338. In no way does it raise the subject of solar energy.
It’s not a question of “not liking your explanation”. In common with other replies, it simply did not address the problem I posed.