Guest post by Tamino
In a paper, “Heat Capacity, Time Constant, and Sensitivity of Earth’s Climate System” soon to be published in the Journal of Geophysical Research (and discussed briefly at RealClimate a few weeks back), Stephen Schwartz of Brookhaven National Laboratory estimates climate sensitivity using observed 20th-century data on ocean heat content and global surface temperature. He arrives at the estimate 1.1±0.5 deg C for a doubling of CO2 concentration (0.3 deg C for every 1 W/m^2 of climate forcing), a figure far lower than most estimates, which fall generally in the range 2 to 4.5 deg C for doubling CO2. This paper has been heralded by global-warming denialists as the death-knell for global warming theory (as most such papers are).
Schwartz’s results would imply two important things. First, that the impact of adding greenhouse gases to the atmosphere will be much smaller than most estimates; second, that almost all of the warming due to the greenhouse gases we’ve put in the atmosphere so far has already been felt, so there’s almost no warming “in the pipeline” due to greenhouse gases already in the air. Both ideas contradict the consensus view of climate scientists, and both ideas give global-warming skeptics a warm fuzzy feeling (but not too warm).
Despite the celebratory reaction from the denialist blogosphere (and U.S. Senator James Inhofe), this is not a “denialist” paper. Schwartz is a highly respected researcher (deservedly so) in atmospheric physics, mainly working on aerosols. He doesn’t pretend to smite global-warming theories with a single blow, he simply explores one way to estimate climate sensitivity and reports his results. He seems quite aware of many of the caveats inherent in his method, and invites further study, saying in the “conclusions” section:
Finally, as the present analysis rests on a simple single-compartment energy balance model, the question must inevitably arise whether the rather obdurate climate system might be amenable to determination of its key properties through empirical analysis based on such a simple model. In response to that question it might have to be said that it remains to be seen. In this context it is hoped that the present study might stimulate further work along these lines with more complex models.
What is Schwartz’s method? First, assume that the climate system can be effectively modeled as a zero-dimensional energy balance model. This would mean that there would be a single effective heat capacity for the climate system, and a single effective time constant for the system as well. Climate sensitivity will then be
S=τ/C
where S is the climate sensitivity, τ is the time constant, and C is the heat capacity. Simple!
To estimate those parameters, Schwartz uses observed climate data. He assumes that the time series of global temperature can effectively be modeled as a linear trend, plus a one-dimensional, first-order “autoregressive” or “Markov” or simply “AR(1)” process [an AR(1) process is a random process with some ‘memory’ of its previous value; subsequent values y_t are statistically dependent on the immediately preceding value y_(t-1) through an equation of the form y_t = ρ y_(t-1) + ε, where ρ is typically required to be between 0 and 1, and ε is a series of random values conforming to a normal distribution. The AR(1) model is a special case of a more general class of linear time series models known as “Autoregressive moving average” models].
In such as case, the autocorrelation of the global temperature time series (its correlation with a time-delayed copy of itself) can be analyzed to determine the time constant τ. He further assumes that ocean heat content represents the bulk of the heat absorbed by the planet due to climate forces, and that its changes are roughly proportional to the observed surface temperature change; the constant of proportionality gives the heat capacity. The conclusion is that the time constant of the planet is 5±1 years and its heat capacity is 16.7±7 W • yr / (dec C • m^2), so climate sensitivity is 5/16.7 = 0.3 deg C/(W/m^2).
One of the biggest problems with this method is that it assumes that the climate system has only one “time scale,” and that time scale determines its long-term, equilibrium response to changes in climate forcing. But the global heat budget has many components, which respond faster or slower to heat input: the atmosphere, land, upper ocean, deep ocean, and cryosphere all act with their own time scales. The atmosphere responds quickly, the land not quite so fast, the deep ocean and cryosphere very slowly. In fact, it’s because it takes so long for heat to penetrate deep into the ocean that most climate scientists believe we have not yet experienced all the warming due from the greenhouse gases we’ve already emitted [Hansen et al. 2005].
Schwartz’s analysis depends on assuming that the global temperature time series has a single time scale, and modelling it as a linear trend plus an AR(1) process. There’s a straightforward way to test at least the possibility that it obeys the stated assumption. If the linearly detrended temperature data really do behave like an AR(1) process, then the autocorrelation at lag Δt which we can call r(Δt), will be related to the time constant τ by the simple formula
r(Δt)= exp{-Δt/τ}.
In that case,
τ = – Δt / ln(r),
for any and all lags Δt. This is the formula used to estimate the time constant τ.
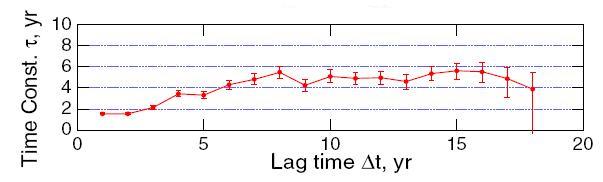
And what, you wonder, are the estimated values of the time constant from the temperature time series? Using annual average temperature anomaly from NASA GISS (one of the data sets Schwartz uses), after detrending by removing a linear fit, Schwartz arrives at his Figure 5g:
Using the monthly rather than annual averages gives Schwartz’s Figure 7:
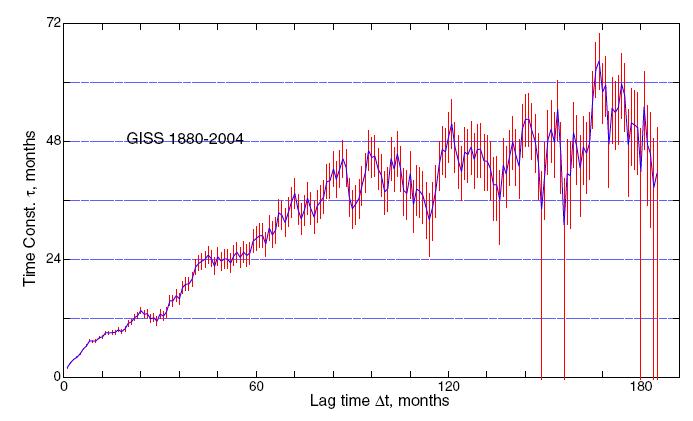
If the temperature follows the assumed model, then the estimated time constant should be the same for all lags, until the lag gets large enough that the probable error invalidates the result. But it’s clear from these figures that this is not the case. Rather, the estimated τ increases with increasing lag. Schwartz himself says:
As seen in Figure 5g, values of τ were found to increase with increasing lag time from about 2 years at lag time Δt = 1 yr, reaching an asymptotic value of about 5 years by about lag time Δt= 8 yr. As similar results were obtained with various subsets of the data (first and second halves of the time series; data for Northern and Southern Hemispheres, Figure 6) and for the de-seasonalized monthly data, Figure 7, this estimate of the time constant would appear to be robust.
If the time series of global temperature really did follow an AR(1) process, what would the graphs look like? We ran 5 simulations of an AR(1) process with a 5-year time scale, generating monthly data for 125 years, then estimated the time scale using Schwartz’s method. We also applied the method to GISTEMP monthly data (the results are slightly different from Schwartz’s because we used data through July 2007). Here’s how they compare:
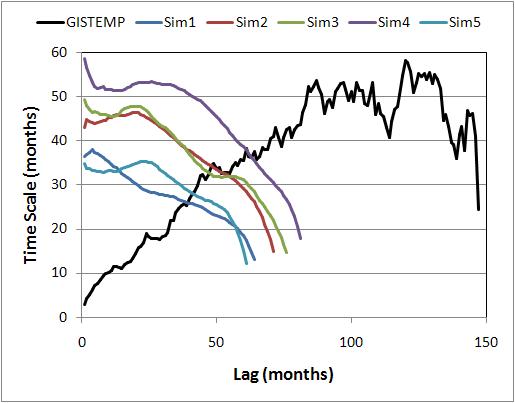
This makes it abundantly clear that if temperature did follow the stated assumption, it would not give the results reported by Schwartz. The conclusion is inescapable, that global temperature cannot be adequately modeled as a linear trend plus AR(1) process.
You probably also noticed that for the simulated AR(1) process, the estimated time scale is consistently less than the true value (which for the simulations, is known to be exactly 5 years, or 60 months), and that the estimate decreases as lag increases. This is because the usual estimate of autocorrelation coefficients is a biased estimate. The word “bias” is used in its statistical sense, that the expected result of the calculation is not the true value. As the lag gets higher, the impact of the bias increases and the estimated time scale decreases. When the time series is long and the time scale is short, the bias is negligible, but when the time scale is any significant fraction of the length of the time series, the bias can be quite large. In fact, both simulations and theoretical calculations demonstrate that for 125 years of a genuine AR(1) process, if the time scale were 30 years (not an unrealistic value for global climate), we would expect the estimate from autocorrelation values to be less than half the true value.
Earlier in the paper, the AR(1) assumption is justified by regressing each year’s average temperature anomaly against the previous year’s and studying the residuals from that fit:
Satisfaction of the assumption of a first-order Markov process was assessed by examination of the residuals of the lag-1 regression, which were found to exhibit no further significant autocorrelation.
The result for this test is graphed in his Figure 5f:
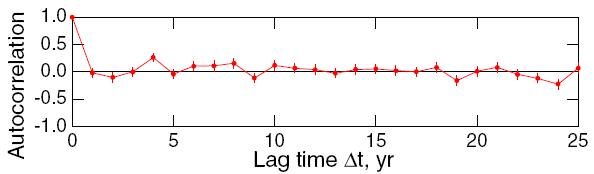
Alas, it seems this test was applied only to the annual averages. For that data, there are only 125 data points, so the uncertainty in an autocorrelation estimate is as big as ±0.2, much too large to reveal whatever autocorrelation might remain. Applying the test to the monthly data, the larger number of data points would have given this more precise result:
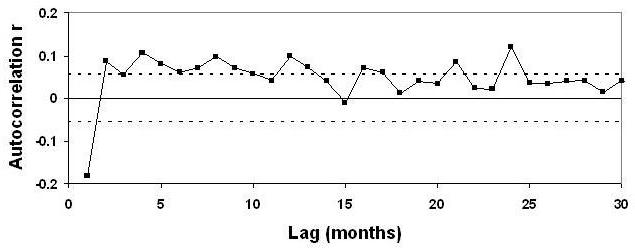
The very first value, at lag 1 month, is way outside the limit of “no further significant autocorrelation,” and in fact most of the low-lag values are outside the 95% confidence limits (indicated by the dashed lines).
In short, the global temperature time series clearly does not follow the model adopted in Schwartz’s analysis. It’s further clear that even if it did, the method is unable to diagnose the right time scale. Add to that the fact that assuming a single time scale for the global climate system contradicts what we know about the response time of the different components of the earth, and it adds up to only one conclusion: Schwartz’s estimate of climate sensitivity is unreliable. We see no evidence from this analysis to indicate that climate sensitivity is any different from the best estimates of sensible research, somewhere within the range of 2 to 4.5 deg C for a doubling of CO2.
A response to the paper, raising these (and other) issues, has already been submitted to the Journal of Geophysical Research, and another response (by a team in Switzerland) is in the works. It’s important to note that this is the way science works. An idea is proposed and explored, the results are reported, the methodology is probed and critiqued by others, and their results are reported; in the process, we hope to learn more about how the world really works.
That Schwartz’s result is heralded as the death-knell of global warming by denialist blogs and Sen. Inhofe, even before it has been officially published (let alone before the scientific community has responded) says more about the denialist movement than about the sensitivity of earth’s climate system. But, that’s how politics works.
AEBanner (344) says, “The Stefan-Boltzmann Law to which you referred gives the output power from a black body. Infrared emission rate from GHGs also follows this law, but only if sufficient power is being supplied to the GHGs in the first place. These gases are not, of themselves, power generators.”
Not exactly on your point, but it reopens the door for an old chestnut. Why do GHG need “sufficient power” to emit ala Stefan-Boltzmann? And why don’t all atmospheric gases emit as such? The cosmic backgrounds presumably radiates about 4.5 microwatts/m2. Aren’t the GHG (and others??) molecular and, to a lesser extent, atomic vibrations sufficient?
On your point (which I too am interested in but haven’t fully followed…), two points: 1) the latent and sensible heat energy picked up by the GHGs can radiate either up and out, or back down (actually isotropic, but same-same); 2) after a GHG radiates away the energy that it picked up from molecular collision, can it not pick up some more? Do either of these points have an effect on your thinking?
All of the added energy will eventually be lost to space.
Here’s how. You have a thousand people on a sports field. They can all catch and hand off softballs.
The softball is the energy being moved around, whether it’s a photon or a collision, it’s a transfer of energy.
Twenty of these thousand people, besides handing off, also have the strength to throw a softball. They throw it hard enough that if it doesn’t get caught by someone else, it will go right over the fence, to get it completely out of play.
The other 9,980 people can only hand the softball back and forth — they aren’t able to throw it. They just hand it to another person.
There’s been a steady rain of softballs into the stadium, and the people who catch them get rid of them promptly. Those who can throw them do throw them; anyone who can’t throw will hand them off in any random direction immediately.
There has been an equilibrium, for the last eight thousand years or so — the people with strong arms have been throwing softballs out of the stadium at about the same rate they’ve been raining into the stadium. They don’t always throw them, sometimes they just hand them off. When they do throw them, they don’t throw them out of the stadium, they just throw them randomly. Most of them get caught by someone else in the stadium.
Now, you’ve begun to upset the balance.
You’re inside the stadium with a big bag, and you’re tossing more softballs into play that were just in the bag up til now.
You toss them at random, to any of the thousand people in the stadium.
9,980 of those people just hand them on again to any other person at random.
20 of those people, remember, have the strong arms and when they get a softball, they can throw it. Sometimes they do throw it. Sometimes when it’s thrown it goes right out of the stadium completely.
All these people catch and hand off or throw all the time, so your adding a few more softballs to the total number in play speeds up the catching and handing off and throwing slightly. As you continue to add more softballs, the catching, handing off, and throwing speeds up.
For a while, there are slightly more softballs being handed and thrown around inside the stadium. You’ve added only a very few to the total, so almost all of them are just going back and forth. The odds are pretty low that they’ll get handed to someone with a strong arm.
And most of the people with strong arms are in the middle of the crowd anyhow, no clearance around them even if they throw, just more people in the way.
But one or two of the strong-armed people are near the edge of the field where the people thin out.
Sometimes one of those people is handed or catches a softball. They randomly pass or throw it. They’re near the edge. So every time one of the strong-armed people catches a softball and happens to throw it toward the outfield fence, it goes clear out of the park. It’s gone.
Eventually, all the softballs you added are going to get into the hands of one of the strong-armed people. Eventually each of those people will happen to throw a softball over the fence. Not every time.
Once your bag is empty (your geyser or volcano runs out of heat) you stop adding more softballs to play.
But almost all of the softballs you added are still going from hand to hand. For a few hundred years or so.
Eventually every one you added gets thrown out of the park.
Analogy: a weak thrower can only “hand off” energy — like a nitrogen or oxygen molecule, it can only take energy and bounce it on to another molecule by physically banging into it (whatever that means at the scale of molecular interactions, these aren’t really softballs).
A strong thrower is a molecule that — in addition to being able to absorb energy and pass it on by contact, can also emit photons — can throw.
A player who can only hand off the ball can catch one of those throws, but all that does is make them spin around or bounce off another person in the crowd while passing on the softball.
So the strong-arm throwers aren’t “Maxwell’s Demons” — they aren’t selectively getting rid of the extra softballs you put into play. But their throws are strong enough that they _can_ leave the stadium.
Whew.
Re #351 Rod B
Thank you for your interesting and encouraging comments.
Greenhouse gases do not generate power, and so if they are to radiate they must first be provided with the power, either by absorbing infrared photons of the appropriate wavelength (energy), or by kinetic energy from inter-molecular collisions. The required energy is quantised, and must match the change of vibrational/rotational energy level in the GHG molecule.
We then have the basic old rule: energy out = energy in
As for the atmosphere, I, myself, should appreciate an explanation of why the emission follows the S.B. Law. But then, again, the supply stream of photons TO the GHGs comes from the Earth’s surface which is radiating as a black body and so obeys Stefan_Boltzmann. Since this is a fourth power Temperature law, this effect probably greatly outweighs any contribution from collisional contributions (?? first power??), and so the emission rate from the GHGs must also follow the S.B. equation. It cannot be greater.
With regard to oxygen and nitrogen, their molecular structures do not permit absorption of photons. But, this brings us to my original question, which is whether inter-molecular collisions can induce appropriate energy absorption in these gases, and if so how much? Rather than repeat the whole thing in detail here, please go to #338.
Yes, I have taken on board the isotropic nature of the emission, and this could affect results by a factor of 2, if we ever get that far.
And yes, I see no reason why the collision/emission process should not be repeated continuously if it indeed happens at all.
Re #352 Hank Roberts
Thank you, Mr Roberts. Nice analogy, I like it.
So more softballs in play means a higher temperature, right?
So before the supply bag gets empty, if the softballs are tossed into play at a high enough rate (numbers per second), greater than they are being thrown out of the field, then the total number in play keeps on getting larger. That is, the temperature keeps on increasing. OK so far?
Until the supply bag is empty.
Now suppose there is a continuous delivery of new, full supply bags to the centre of the field!
AEBanner, no, I contend the S-B (Planck function) radiation is sourced completely different from the infrared emission “powered by” the quantum vibration/rotational energy levels within the molecule. The latter is not a function of the 4th power of the “molecular temperature”. The fact that the same molecule can absorb radiation into those internal levels even if the source of that radiation is S-B emanating from the earth’s surface is not a contradiction. Once the radiation is “out there” the recipient can not tell one emission source from another, other than it might like certain wavelengths.
I think you are making too much of the latent/sensible heat source. After the surface emission travels a few centimeters, gets its energy absorbed by a GHG into rotational/vibration internal energy, and, within probably less than a microsecond (some say picosecond), gets transferred to another molecule of any heritage as translation energy, it’s all part of the same stew. When some of that energy finally gets “bumped” into a high altitude GHG and then emitted out of the atmosphere, it is impossible (other than statistics) to determine the initial source of that energy packet.
Hank, your description of the process is, well, descriptive. But I do think it misses the point. If the softballs represent heat and the stadium guys are throwing far more softballs into the mix than the edge throwers can toss out, wouldn’t the temperature of the field increase? And the possibility of catching up in a hundred years (though I can’t see how) not make any real difference?
Re #353 AEB
Sorry, mistake in penultimate paragraph.
Instead of “these gases”, please read “the greenhouse gases”.
Re #355 Rod B
Sorry, but you have mis-understood my thinking. The GHGs are clearly NOT powered by vibrational/rotational energy levels within the molecules!!! They can only emit energy previously absorbed either from Earth’s surface-emitted photons, or perhaps(???) from inter-molecular collisions.
It is this last possible alternative I’m concerned with, and only then from additional collisions arising from extra non-radiant heat added within the bulk of the atmosphere.
However, I think your last paragraph has hit the proverbial nail on the head. Hank’s excellent and poetic analogy seems to me to have shown very clearly that the temperature of the atmosphere would, indeed, increase. Moreover, this would go on as long as the supply of softballs continued.
The temperature of the atmosphere will continue to increase while the (non-radiant) energy is still supplied.
AEBanner (357), I think I’m with you…, but still maybe fail to understand your question. The rotational/vibrational energy in a GHG starts at the “zero” level. (Doesn’t mean 0 energy, but at the lowest possible energy in each mode and incapable of emission). Energy is then added from either IR radiation or transfer from translation energy via collision. From other posts the latter is not “perhaps” but mostly (though the posts generally refer to losing energy by either emission or collision transfer), until at high altitudes the path length (between collisions) gets much longer, or it emits back to the earth(??). At the first low level it would seem it is (only) the sensible and latent heat raising the temp of the low atmosphere and creating the energy transferring collisions, though GHGs can pick up sensible heat directly, and I guess water vapor is the primary recipient of latent heat.
I’m starting to get wrapped around the axle here, but the point is that the energy sources (latent, sensible, IR radiation, some solar radiation) all eventually look alike and would tend to raise the temperature of the atmosphere at low levels and taper off as the altitude increases (except for the small solar radiance). The temperature of the atmosphere then tends to decrease virtually only through IR radiation, some going into space (about 235 watts worth) and about 325 watts reabsorbed by the ground. The long-term balance determines the temperature profile of the atmosphere and the temperature of the surface.
Am I being any help here, or have I missed your question entirely?
Re #358 Rod B
Thanks for that, but I think you are trying to look too deeply into this matter.
What I am saying, and Hank’s post has illustrated brilliantly, is simply that a continuous supply of heat energy into the atmosphere will increase the temperature, because it cannot escape to space as quickly as it is supplied. This is because the energy can escape to space only through photon emission from the GHGs, which may be present only at the 2% concentration level, including water vapour, and so the GHGs can acquire only 2% of the additional heat input stream, if shared out equally.
Therefore, the atmospheric temperature will continue to increase as long as the additional heat supply is maintained.
I’m trying to prepare the ground in order to avoid an expected shower of mortar bombs in the near future.
re 359
I understand your point, and it is a curiously interesting question. I think (and need second guessing) GHG can emit (up or down) far more than the energy percent equal to the concentration percentage, through the multiple photon emission from a single molecule mentioned above. In equilibrium conditions GHGs account for (have to) emitting out (again, up or down) virtually 100% of the non-reflective “heat” (radiance, latent, or sensible) added to the atmosphere — even though their concentration is 2% or less. The relative amount of heat added from each source (radiance, latent, sensible, etc.) has virtually no effect, since, in the general sense “heats is heats” (not really, but it sounds good and makes the point.) In your scenario adding a lot of GHGs seems like it ought to cool the atmosphere, even at the surface.
AEB writes:
[[What I am saying, and Hank’s post has illustrated brilliantly, is simply that a continuous supply of heat energy into the atmosphere will increase the temperature, because it cannot escape to space as quickly as it is supplied. This is because the energy can escape to space only through photon emission from the GHGs, which may be present only at the 2% concentration level, including water vapour, and so the GHGs can acquire only 2% of the additional heat input stream, if shared out equally. ]]
What you are saying is wrong, and contradicts what science has learned about electromagnetic radiation and climatology for the past 200 years or so. There has always been a continuous supply of heat energy into the atmosphere, but the heating does not run away because radiation by the greenhouse gases increases as the fourth power of temperature. Your fixation on the 2% figure misleads you. The fact is, the Earth’s temperature, and the temperature of any given planet or moon we know of, does not rise continuously. Your argument says that they should.
Specifically, your phrase “it cannot escape to space as quickly as it is supplied” is just wrong. Conservation of energy means it does just that. The energy from the sun is balanced by the energy emitted from the planet. That’s true of all planets at all times. You can have discrepancies while the temperature of a planet is changing, but over one day or one year they are negligible, and in the long run all such imbalances are corrected by the Stefan-Boltzmann mechanism.
Let’s say there’s an input stream of energy added to the atmosphere from nowhere. It’s being teleported in by sinister aliens, probably either Grays or Reptoids. The temperature of the atmosphere goes up. The greenhouse gases only get 2%. They radiate it away. Then they pick up more energy from molecular collisions. They radiate that away. The heating only continues up to a given point at which the radiation out matches all the heat sources in. The 2% of the energy held by the greenhouse gases is not always the same 2% of the energy. That’s where your mistake lies. You’re mistaking a short-term snapshot for an overall process.
Re #360 Rod B
Thank you for helping to clarify my ideas.
I think we have to distinguish between two different effects;
1. heating due to solar radiation
2. atmospheric temperature increase due to “hot air” being added to the body of the atmosphere.
In the first case, the power involved is, of course, enormous. It is radiated from the Earth’s surface, and is handled by the huge numbers of GHG molecules in the atmosphere. It is important to understand that it is not the GHG concentration, per se, which matters. It is the very number of participating GHG molecules which enables this huge power to be absorbed and radiated again!! If you consider a closed gas jar full of air, the GHG concentration is the same as that in the outside atmosphere, but clearly the molecule numbers are very, very different!
In the second case, a continuous stream of “hot air” is added into the bulk of the atmosphere, and rises in accordance with convection to higher altitudes, so heating the atmosphere generally, in line with Hank’s analogy. This extra energy does not come from the Earth’s surface, and so does not take part in the standard GHG effect.
The extra “hot air” energy is shared out equally by inter-molecular collisions between the molecules in the atmosphere, so that the only ones capable of emitting electromagnetic radiation, namely the GHGs, receive only their fare share which does, indeed, depend upon their concentration of about 2%. However, it does not follow that even this 2% share of the extra energy is all absorbed into the molecular energy levels and so become capable of being re-radiated to some extent. The shared-out energy may simply become increased kinetic energy of the GHGs, with no extra photon emission possible. It would be interesting, but not vital, to know the factor involved in this process.
Re #361 Barton Paul Levenson
Thank you for your comments, but I am unable to accept them. I think you have not fully understood the point I have been trying to get across. Hopefully, my reply to Rod B, #362, will have helped to make things more clear.
In your first paragraph where you say that the radiation by the GHGs increases as the fourth power of the (Absolute) temperature, you are clearly referring to electromagnetic radiation emitted from the Earth’s surface. Of course, I do agree with that. Then you go on to say that the temperature of the Earth does not rise continuously but, I ask, what has been happening to it since the beginning of the industrial revolution??? I hope to be able to offer an explanation which could compliment the enhanced greenhouse theory.
Your second paragraph is simply wrong. Conservation of Energy is satisfied if you take into account the extra energy stored in the atmosphere.
The energy received from the Sun is certainly balanced by the usual energy emitted by the planet, no question, but you have not treated the additional supply of “hot air” which I am suggesting is being continuously added to the bulk of the atmosphere. Please refer to my reply to Rod B above.
In your third paragraph, you seem to be neglecting the idea that more and more “hot air” is being continuously supplied to the bulk of the atmosphere, and that this will rise to higher altitudes without heating the Earth’s surface. The added heat is spread throughout the atmosphere, and the GHGs get their fair share according to their concentration, about 2%.
Even if the whole of their share were converted by collisions into excited state energy within the GHG molecules, then their subsequent rate of photon energy emission would still be only 2% of the input power of the “hot air” being added to the atmosphere. Therefore, the temperature of the atmosphere will continue to rise.
re AEBanner’s 362
Others are better at this since I’m partly parroting what I’ve picked up here.
Well, maybe as the onion layers get peeled back. But within a microsecond after a GHG molecule’s initial absorption of surface radiation all energy is essentially the same.
You’re correct that the preponderance of energy/heat added to the atmosphere comes from earth surface blackbody radiation, about 350 watts/m2. The other sources are not tiny however: about 100 watts from latent and sensible heat and about 65 watts from direct solar absorption. (And I suppose the latent heat, predominately from water vapor, is not realized as temperature affecting until the vapor condenses.) Also you’re correct that the absolute number, not the percent concentration that is the bigger effect in absorption, in addition to GHGs capability of “turning the energy over”.
This is where it starts to fall apart. The “extra energy” does so take part (in some fashion) in the GH effect. It is initially realized as translation kinetic energy. Through collision it can transfer (some of) that energy to another molecule, including GHGs. That molecule, by virtue of its tendency to equipartion, can transfer the energy from its translation to its vibration or rotation energy. (Some say the energy can transfer directly from #1’s translation to #2’s rotation, e.g.). A GHG is the only molecule that can absorb the surface radiation, and always into either vibration or rotation energy. From there it can 1) emit the energy in the infrared spectrum — up or down, or 2), most likely at lower altitudes, transfer the absorbed energy to its own translation or, directly or indirectly, to another molecule’s (likely O2 or N2) translation. Now it can reabsorb more surface radiation or transfer in some translation energy. In any case the energy is basically all in one pot and gets pretty much distributed equally without regard to its initial source — with the minor limitation that vibration and rotation energy levels are discrete/quantized.
Am I helping or hurting?
Re #364
Thank you for your helpful comments.
I think that there is no significant difference between our ideas on this matter. I do accept that a GHG molecule, after absorbing kinetic energy and subsequently emitting a photon, is fully capable of receiving more electromagnetic energy from the Earth’s surface, and so continue to take part in the GH effect. No problem.
Your comments are helpful in that they have given a clear picture of the energy transfer system within the atmosphere, but when you say that the energy is basically all in one pot, this simply serves to support my idea that added “hot air” tends to raise the temperature of the atmosphere. I am suggesting that it cannot escape to space as quickly as it is supplied because of the low concentration of GHGs and the fact that they can only get their fair share of the extra energy through molecular collisions.
On this last point, it would be helpful to know more details about the collision/energy absorption process in a GHG molecule, and the “efficiency” with which it occurs, since this will affect the amount of energy emitted to space. But I can’t see how it can exceed the 2% share.
AEBanner (365):
My understanding: a GHG can “accept” energy from either IR radiation or from molecular collision, not just IR alone. The IR radiation must go into the internal vibration or rotation energy states. Only these energy states can emit the quantized IR radiation energy. (To the picky I might be using “states” incorrectly, but bear with me.) The incoming collision (translation) energy can 1) go into the GHG translation, 2) go into translation and then to vibration/rotation as the GHG has a tendency to more or less equitably distribute its energy among its various states (stores?), 3) go directly into the GHG vibration/rotation energy stores. Which it actually does is known only statistically. The GHG inherently tries to return its vibration or rotation energies to their lowest level, all things being equal. It can release this energy through emission, collision, or, to a lesser degree, redistribution. Collisions predominate at low altitudes. It does not inherently want to decrease its translation energy.
Now I will use a couple of constructs that will raise the ire of some, but can be helpful for discussion. (I believe them to be correct but don’t really want to resurrect the debate…) 1) Individual molecules have real temperature ala nkT = 1/2mv2. 2)Vibration and rotation internal energies do not affect the real temperature (though they can be assigned a characteristic temperature, like radiation); though this is not critical to my point.
When a GHG molecule and a regular molecule, say N2, collide, energy is transferred to the N2 molecule if the GHG is hotter. N2 gets a little hotter; the GHG gets a little cooler, though this might now be mitigated by the GHG molecule redistributing some internal energy to its translation energy. If the N2 molecule is hotter (say form latent or sensible heat transfer) energy will transfer to the GHG. The N2 cools (and spreads the latent/sensible heat a bit) and the GHG heats, though this likewise is mitigated with maybe redistribution of some of its received translation energy to internal energy. The internal energy gets more antsy and increases slightly the probability to relax its internal energy through IR emission. BTW, it’s actually a little more complex ala the Maxwell-Boltzmann distribution, but this doesn’t alter the point.
Quickly jumping form the ridiculous (micro) to the sublime (macro), the very small number of GHG molecules are more than sufficient to emit all the radiation energy, up or down, that all inputs, earth IR, solar, latent, and sensible, can give it. Mostly because of a GHG molecule’s capability to turn it’s internal energy over and over very fast, and convert translation energy to emittable internal energy. And even if it goes through a jillion collisions and exchanges before it finally emits some energy forever.
BTW this is the area that causes a lot of my skepticism (me being a card-carrying skeptic, of course), but not in the particular process we’re discussing.
Re #361 Barton Paul Levenson
And #366 Rod B
After consideration of your posts above, I accept the point you are both making concerning the capability of the GH gases to radiate to space all the energy they receive by collisions with oxygen and nitrogen molecules.
As I have already indicated though, it would be very interesting to know the relevant data; eg the conversion rate from the kinetic energy of these collisions into increased energy levels within the water and CO2 molecules, respectively, and the maximum rate of photon emission from these GHGs.
Any chance of references, please?
Re: #334 Tamino on Friday roundup #3 (closed, so posting here instead).
I’ll respond to your comments one at a time.
I get the impression you’re having fun exploring the surface temperature record, and reporting your findings here as you go along. That’s a good thing.
Quite true.
But bear in mind you’re not the first to do so. In a previous comment you expressed surprise that I had responded so quickly. I suspect you thought that I was overly eager to contradict your model. This is not so, the reason for the quickness of my response is that I had done the analysis already; I’ve been looking at these data for a long time. I had even explored the “jump” model (which I usually call a “step-change” model) myself. And this isn’t even my field of research; there are many others who have been looking at it longer than I have.
Ah I see; in addition you may be a faster worker than me, or have more time available.
I am not an ideological frequentist, in fact my work (which is unrelated to climate science) requires a lot of Bayesian analysis. In my opinion it’s a mistake to marry oneself to either approach.
I agree with you, but I was thrown by your not appearing to understand the factor of 8.8 which I had produced.
I do indeed know of ways to calculate the likely significance of the difference between two competing models, and my earlier calculations indicated that it was in fact not significant.
As for my earlier claim of acceleration of global warming recently, that opinion was formed in response to a specific question (a long time ago in a galaxy far, far away) about the time interval 1970 to the present. But I regard 1975 to the present as the “modern global warming era,” and for that time frame I have lately reversed my opinion, as I expressed in tamino.wordpress.com.
Yes, I have now read that article, and found it very interesting. So I have resiled from step changes (when outliers are deleted) and you have resiled from acceleration in the data. “Resile” was apparently one of Tony Blair’s favourite words; perhaps I’d better stop using it now that he’s out of fashion!
Estimating error ranges based on the red-noise character of data doesn’t depend on assuming an AR(1) model, although that is a common approach. I use a different method, which takes into account the full autocorrelation structure of the available data. That’s what was done in the aforelinked post. It seems to me that the response to Schwartz’s analysis actually proves that the data do not follow an AR(1) model adequately to derive an accurate value for the time constant of the global climate, even if there is one (and it’s overwhelmingly likely that there is more than one applicable time constant).
You did attract comments in your blog asking for details of the calculations. For standard regression without autocorrelation, you rightly pointed out that standard statistical texts explain this. However, I don’t think the same is true for your auto-correlation analysis (or you use different standard texts from me). So, if I might press you, please could you supply a reference or details of your procedure, so that I can attempt to analyze the monthly data too. Personally, I don’t think there is much extra “real” information in the monthlies over the yearlies, but applying a sound statistical analysis to them might change my mind.
I think your assigning the monikers “co2 brigade” and “solar brigade” is misleading (but not an intentional deception). Those who agree that greenhouse gases are the primary cause of modern warming do not deny the solar influence. Those who argue that the primary cause is solar variations have to overcome the difficult fact that solar variations simply don’t fit the bill, and have yet to offer any explanation that I’ve heard, how greenhouse gases can fail to warm the planet significantly.
These were the names that sprang to my mind when I first started reading the blogs on both sides of the argument. I preferred them to “warmers” and “denialists”; the latter has too close an association to Holocaust denialists, where the evidence is (in my humble opinion of course) far more incontrovertible. Anyway, since then I have seen, as you say, CO2 brigaders who certainly acknowledge solar influence, but likewise I have seen solar brigaders who ackowledge a CO2 influence, but they don’t agree with, or remain to be convinced by, the magnitude of the effect IPCC is claiming, mainly relating to the thorny question of climate sensitivity – which I am not yet ready to address myself.
I have several objections to the “jump” model. First, it has no basis (that I’m aware of) in physics; given two models which are statistically indistinguishable, it seems logical to prefer the one which has a sound physical interpretation.
I agree that a linear trend is more plausible a priori. But something close to a jump could occur from sudden heat exchange with the oceans. So a La Nina might flatten off a rising trend for a while, and then an El Nino gives a big bump. As for “statistically indistinguishable”, I believe that the correct calculation on yearly data would show 5% significance in favour of the smaller error squared from the jump model (but I cannot currently prove that). This is not so important given your next point.
Second, in order to isolate the long-term signal it helps to remove the known short-term factors as much as possible, i.e., to remove the el Nino and Mt. Pinatubo (and el Chicon, etc.) signal; doing so seriously undercuts the jump model.
I agree; with removal of these effects I have “resiled” from the jump model.
Third (for me, most persuasive), even without removing the el Nino signal the period 1997-2007 shows a statistically significant (even within stringent red-noise limits) deviation from flatness, rejecting this hypothesis.
I did not find that was true for the yearly data, and I have not been able to analyze the monthly data in the same way as you, so cannot comment on that.
I encourage your continued exploration of the data.
Thanks, we all need encouragement – it is certainly fascinating stuff.
Rich.
Hi there…Thanks for the nice read, keep up the interesting posts..what a nice Friday
I’m late to the party, but then again, I wasn’t reading climate blogs back in October.
Unless I totally screwed up, if you account for in-field measurement uncertainty and reprocess the annual data the result is a ~18 years.
In terms of the language everyone seems to be using:
* The earth’s climate is the AR(1) process and the model earth’s temperature, T, would follow this process.
* Uncertainty in measurement due to imprecise thermometers, lack of station coverage etc. is white noise.
Using this language, GISS temperature measurements, Tm, are Tm = T+ e, where e is “noise”.
The analysis also provides a fiduciary check on itself by giving an estimate of the magnitude of ‘e’– the uncertainty of the in field measurements. I get the 1-sigma error in ‘e’~ 0.08K, which is a bit higher than the 0.05K attributed to current level uncertainty due to lack of station coverage. However, the real infield uncertainty since 1880 is likely higher than the 0.05K expected with more recent instrumentation.
So, basically, if you account for uncertainty in the data, this really simple model doesn’t look quite so bad. However, the time constant is much higher– and nearer 18 years.