There has been a lot of discussion about decadal climate predictions in recent months. It came up as part of the ‘climate services’ discussion and was alluded to in the rather confused New Scientist piece a couple of weeks ago. This is a relatively “hot” topic to be working on, exemplified by two initial high profile papers (Smith et al, 2007 and Keenlyside et al, 2008). Indeed, the specifications for the new simulations being set up for next IPCC report include a whole section for decadal simulations that many of the modelling groups will be responding to.
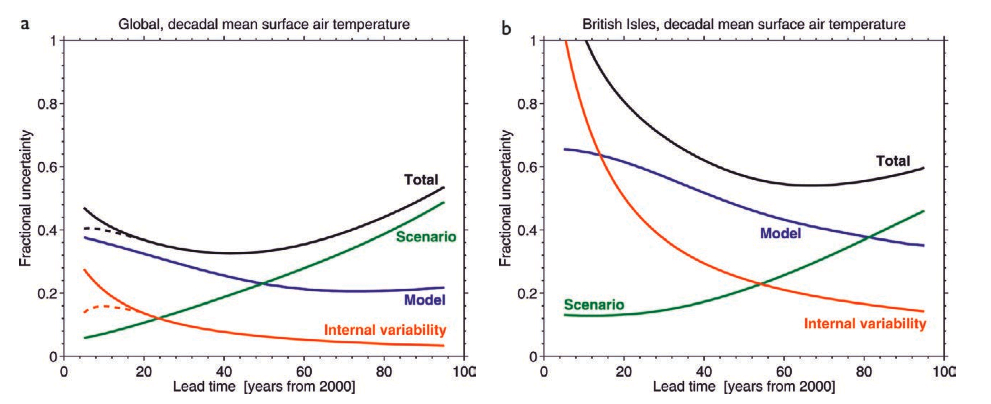
This figure from a recent BAMS article (Hawkins and Sutton, 2009) shows an estimate of the current sources of prediction error at the global and local scale. For short periods of time (especially at local scales), the dominant source of forecast uncertainty is the ‘internal variability’ (i.e. the exact course of the specific trajectory the weather is on). As time goes by, the different weather paths get averaged out and so this source of uncertainty diminishes. However, uncertainty associated with uncertain or inaccurate models grows with time, as does the uncertainty associated with the scenario you are using – ie. how fast CO2 or other forcings are going to change. Predictions of CO2 next year for instance, are much easier than predictions in 50 years time because of the potential for economic, technological and sociological changes. The combination of sources of uncertainty map out how much better we can expect predictions to get: can we reduce error associated with internal variability by initializing models with current observations? how much does uncertainty go down as models improve? etc.
From the graph it is easy to see that over the short term (up to a decade or so), reducing initialization errors might be useful (the dotted lines). The basic idea is that a portion of the climate variability on interannual to decadal time scales can be associated with relatively slow ocean changes – for instance in the North Atlantic. If these ocean circulations can be predicted based on the state of the ocean now, that may therefore allow for skillful predictions of temperature or rainfall that are correlated to those ocean changes. But while this sounds plausible, almost every step in this chain is a challenge.
We know that this works on short (seasonal) time scales in (at least some parts of the world) because of the somewhat skillful prediction of El Niño/La Niña events and relative stability of teleconnections to these large perturbations (the fact that rainfall in California is usually high in El Niño years for instance). But our ability to predict El Niño loses skill very rapidly past six months or so and so we can’t rely on that for longer term predictions. However, there is also some skill in seasonal predictions in parts of the world where El Niño is not that important – for instance in Europe – that is likely based on the persistence of North Atlantic ocean temperature anomalies. One curious consequence is that the places that have skillful and useful seasonal-to-interannual predictions based on ENSO forecasts are likely to be the places where skillful decadal forecasts do worst (because those are precisely the areas where the unpredictable ENSO variability will be the dominant signal).
It’s worth pointing out that ‘skill’ is defined relative to climatology (i.e. do you do a better job at estimating temperature or rainfall anomalies than if you’d just assumed that the season would be just like the average of the last ten years for instance). Some skill doesn’t necessarily mean that the predictions are great – it simply means that they are slightly better than you could do before. We should also distinguish between skillful (in a statistical sense) and useful in a practical sense. An increase of a few percent in variance explained would show up as improved skill, but that is unlikely to be of good enough practical value to shift any policy decisions.
So given that we know roughly what we are looking for, what is needed for this to work?
First of all, we need to know whether we have enough data to get a reasonable picture of the ocean state right now. This is actually quite hard since you’d like to have subsurface temperature and salinity data from a large part of the oceans. That gives you the large scale density field which is the dominant control on the ocean dynamics. Right now this is just about possible with the new Argo float array, but before about 2003, subsurface data in particular was much sparser outside a few well travelled corridors. Note that temperature data are not sufficient on their own for calculating changes in the ocean dynamics since they are often inversely correlated with salinity variations (when it is hot, it is often salty for instance) which reduces the impact on the density. Conceivably if any skill in the prediction is simply related to surface temperature anomalies being advected around by the mean circulation, it could be possible be useful to do temperature only initializations, but one would have to be very wary of dynamical changes and that would limit the usefulness of the approach to a couple of years perhaps.
Next, given any particular distribution of initialization data, how should this be assimilated into the forecasting model? This is a real theoretical problem given that models all have systematic deviations from the real world. If you simply force a model temperature and salinity to look exactly like the observations, then you risk having any forecast dominated by model drift when you remove the assimilation. Think of a elastic band being pulled to the side by the ‘observations’, but having it snap back to it’s default state when you stop pulling. (A likely example of this is the ‘coupling shock’ phenomena possibly seen in the Keenlyside et al simulations). A better way to do this is via anomaly forcing – that is you only impose the differences from the climatology on the model. That is guaranteed to have less model drift, but at the expense of having the forecast potentially affected by systematic errors in, say, the position of the Gulf Stream. In both methods of course, the better the model, the less bad the problems. There is a good discussion of the Hadley Centre methods in Haines et al (2008) (no sub reqd.).
Assuming that you can come up with a reasonable methodology for the initialization, the next step is to understand the actual predictability of the system. For instance, given the inevitable uncertainties due to sparse coverage or short term variability, how fast do slightly differently initialized simulations diverge? (Note that we aren’t talking about the exact path of the simulation which will diverge as fast as weather forecasts – a couple of weeks, but the larger scale statistics of ocean anomalies). This appears to be a few years to a decade in “perfect model” tests (where you try and predict how a particular model will behave using the same model but with an initialization that mimics what you’d have to do in the real world).
Finally, given that you can show that the model with its initialization scheme and available data has some predictability, you have to show that it gives a useful increase in the explained variance in any quantities that someone might care about. For instance, perfect predictability of the maximum overturning streamfunction might be scientifically interesting, but since it is not an observable quantity, it is mainly of academic interest. Much more useful is how any surface air temperature or rainfall predictions will be affected. This kind of analysis is only just starting to be done (since you needed all the other steps to work first).
From talking to a number of people working in this field, my sense is that this is pretty much where the state of the science is. There are theoretical reasons to expect this to be useful, but as yet no good sense for actually how practically useful it will be (though I’d welcome any other opinions on this in the comments).
One thing that is of concern are statements that appear to assume that this is already a done deal – that good quality decadal forecasts are somehow guaranteed (if only a new center can be built, or if a faster computer was used). For instance:
… to meet the expectations of society, it is both necessary and possible to revolutionize climate prediction. … It is possible firstly because of major advances in scientific understanding, secondly because of the development of seamless prediction systems which unify weather and climate prediction, thus bringing the insights and constraints of weather prediction into the climate change arena, and thirdly because of the ever-expanding power of computers.
However, just because something is necessary (according to the expectations of society) does not automatically mean that it is possible! Indeed, there is a real danger for society’s expectations to get completely out of line with what eventually will prove possible, and it’s important that policies don’t get put in place that are not robust to the real uncertainty in such predictions.
Does this mean that climate predictions can’t get better? Not at all. The component of the forecast uncertainty associated with the models themselves can certainly be reduced (the blue line above) – through more judicious weighting of the various models (perhaps using paleo-climate data from the LGM and mid-Holocene which will also be part of the new IPCC archive), improvements in parameterisations and greater realism in forcings and physical interactions (for instance between clouds and aerosols). In fact, one might hazard a guess that these efforts will prove more effective in reducing uncertainty in the coming round of model simulations than the still-experimental attempts in decadal forecasting.
You write, “uncertainty associated with uncertain or inaccurate models grows with time,” but the graphs both show model uncertainty declining with increasing time. Or, am I interpreting them wrong?
[Response: The graphs show the fractional uncertainty compared to the signal, specifically: “The relative importance of each source of uncertainty in decadal mean surface temperature projections is shown by the fractional uncertainty (the 90% confidence level divided by the mean prediction) relative to the warming from the 1971–2000 mean” – gavin]
I assume that a decade is a running mean of ten years. Is this correct?
Re #1:
As the author of the referenced paper, I know that this can be a confusing picture! There is another version here:
http://ncas-climate.nerc.ac.uk/research/uncertainty/exFig1.jpg
which I think clarifies the growth of uncertainty, and it’s components.
Ed Hawkins.
“Predictions”
[Response: cough.. fixed. – gavin]
Thanks for another informative post!
Typo in heading: “predicitions” for “predictions.”
The link to the World Modelling Summit for Climate Prediction at the end of the article doesn’t mention decadal forecasting. As far as I know (I wasn’t invited to it!) that meeting was more about how to improve the representation of regional climate and extreme weather in climate models, partly by increasing the resolution of climate models, and partly by testing climate models by performing weather forecasts and seasonal to decadal predictions (seamless prediction) with them.
I agree wholeheartedly with your assessment of the challenges to producing skillful and useful decadal predictions, but I think you’re possibly missing out by not mentioning that they might be extremely useful tools for evaluating the representation of processes within climate models (e.g. can trying to forecast ENSO with a climate model tell you anything about how well the model represents ENSO?).
Cheers
Len Shaffrey
[Response: Thanks for the comment. I’m certainly not suggesting that research on decadal predictions is not worthwhile – it is and for the reasons you suggest. However, this is more a caution against people thinking this is a mature field of research which it certainly isn’t. There is however a link between regional predictions and decadal predictions – which is highlighted by the figure from Hawkins and Sutton – and that is the role of internal variability. Statements about ‘necessary’ improvements to regional forecasts (which depend on greater predictability of the internal variability) without proper assessments of its feasability, I find to be somewhat jumping the gun. – gavin]
well, so if we expect some more years of no warming and perhaps some cooling, we must be “prepared” for the media, the politics and the own credability, not to loose.
having the same globale temperature at 2020 as around 2000, it will show again, that the proposed climate sensivity for CO2 is not well calculated and any stated future scenario must be wrong.
I’m sure you want to update this
It’s got some problems.
https://www.realclimate.org/index.php/archives/2004/12/how-do-we-know-that-recent-cosub2sub-increases-are-due-to-human-activities-updated/
How do we know that recent CO2 increases are due to human activities?
— 22 December 2004
Another, quite independent way that we know that fossil fuel burning and land clearing specifically are responsible for the increase in CO2 in the last 150 years is through the measurement of carbon isotopes.
One of the methods used is to measure the 13C/12C in tree rings, and use this to infer those same ratios in atmospheric CO2. This works because during photosynthesis, trees take up carbon from the atmosphere and lay this carbon down as plant organic material in the form of rings, providing a snapshot of the atmospheric composition of that time.
Sequences of annual tree rings going back thousands of years have now been analyzed for their 13C/12C ratios. Because the age of each ring is precisely known** we can make a graph of the atmospheric 13C/12C ratio vs. time. What is found is at no time in the last 10,000 years are the 13C/12C ratios in the atmosphere as low as they are today. Furthermore, the 13C/12C ratios begin to decline dramatically just as the CO2 starts to increase — around 1850 AD. This is exactly what we expect if the increased CO2 is in fact due to fossil fuel burning.
[Response: Not following your point at all. What do you think is wrong with this? – gavin]
In addition to economic, technological and sociological changes as sources of uncertainty related to knowing the level of carbon dioxide in the atmosphere over time, there are also uncertainties in our understanding of the carbon cycle where, even if emissions and deforestation were perfectly known, uptake or release of carbon dioxide from or to natural carbon pools is also unclear. And, while direct anthropogenic effects dominate now, an exponential feedback could take over as the dominant term and thus may dominate the scenario uncertainty in the longer timescale. The only way to control for this is to avoid perturbations which might trigger such a feedback. In other words, good models may only be possible for a reduced emissions regime.
This?
[edit]
[Response: Not even close. Carbon isotope analyses in well-dated tree rings have absolutely nothing to do with tree rings used as climate proxies. In this context the only thing that matters is that the carbon in the wood is independently datable. – gavin]
Following up on the points raised in #6….
The internal variability of climate on regional scales is, of course, an important issue. We can still potentially significantly improve projections of regional climate for later in the century, where the internal variability component is a smaller fraction of the total uncertainty. Projections of regional details and changes in extreme temperatures in the mid-21st century should still be useful(?), and that is likely to require higher resolution. To predict regional changes for the next decade or two will probably require both higher resolution and initialised predictions.
Of course, we have a long way to go to realise this potential. And, as #9 has suggested, there is additional uncertainty in the carbon cycle on the longer timescales.
Ed.
When will you be posting on the implications of the BAS Antarctic survey?
Here’s more from Gavin on this important issue. He’s been warning about inflated expectations for a long time on short-term prediction:
> http://dotearth.blogs.nytimes.com/2008/08/20/making-climate-forecasting-more-useful/
> http://j.mp/nytIPCC
now a had a better look at the graphs above. what would you tell us with that “uncertanities”?
the black curve lies globaly arround 0,5, so what, can be right, can be true, we dont know.
at british islands by 0,7, ok. that means we dont know, but we have a chance, that the “predictions” (better simulations!) could be ok.
thank you guys, thats what we wont explain to you for many years.
I’m only a public health sociologist, but I can make one decadal prediction with a high degree of certainty. If there is no clear warming trend for the next ten years, the chance of getting anything meaningful done politically in the United States, whether it concerns greenhouse gas emissions or mitigation, is going to be 1+(e^(i*pi)). Just sayin.
Agree with #15.
At the risk of driving Gavin crazy, if possible to reduce model uncertainty just a bit, would be very helpful. Backcasting explanations make it all look so easy.
We can deal with scenario uncertainty and “weather.”
With regards to model predictions and uncertain variables like CO2 emissions.
Why not freeze the models along with the model runs?
So instead of just posting the output of a model run on a scenario, the model code itself should be frozen, so it can be rerun with updated emissions scenarios.
What confusing graphs !!!
Very very hard to read…(thank you Ed Hawkins, the other graph helps a lot, but I still can’t link it to the two on this page)
For example I don’t understand why the fractional uncertainty does not start from more than 1 for the global temp…
I had understood that for less than 30 years, the natural variations (or “noise”) can hide the long term trend. So it means that you even cannot tell if it will warm or cool down.
It that light, was does mean the total fractional uncertainty of 0.4 at ten years ?
I understand we are talking about decadal mean temperature, but still…
@15 cervates:
I’m only a public health sociologist, but I can make one decadal prediction with a high degree of certainty. If there is no clear warming trend for the next ten years, the chance of getting anything meaningful done politically in the United States, whether it concerns greenhouse gas emissions or mitigation, is going to be 1+(e^(i*pi)). Just sayin.
3-5 years stedy or slightly cooling will be enought and they are almost affraid, that it will be happen and the co2 climatesensivity is said to be completely wrong!
MikeN, the reason they don’t keep outdated models running after improvements are added is — just from what I’ve gathered as an ordinary reader, mind you:
— old models are less useful than improved ones
— each model uses all available computer and time resources
— all models are wrong.
Do you know the rest of that 3rd line?
[Response: Actually, these days it’s pretty easy to find old versions of the models. EdGCM was bascially the old Hansen model from 1988, and I think you could still find the previous public releases of the NCAR models. There are issues with software libraries and compilers of course. – gavin]
#18 Naindj –
The graphs are for 10-year average temperature predictions relative to the 1971-2000 mean (not the forecast starting year of 2000). So middle time of the first data point (2001-2010) is already 20 years past the middle time of the baseline. Decadal-scale uncertainty is competing with 20 years of global warming, and the global warming is larger by a factor of two than the 90% spread of the model sample.
Approximate numerical example: mean model forecast for 2001-2010 = +0.28 C relative to 1971-2000. 90% range of model forecasts: +/- 0.14. Fractional uncertainty 0.14/0.28 = 0.5.
In their paper, they also estimate fractional uncertainty in predicting 2001-2010 temperatures relative to a year 2000 baseline, and that’s quite a bit higher initially (0.9).
So, regional applications of global models show that northern California will warm as a result of global climate change, especially during the winter and spring, resulting in decreased snowpack and increased stress on the statewide water system.
At the same time, increased warming will result in more frequent El Nino conditions as the Pacific ocean looks to dump heat back into the atmosphere. This means more rain in southern California.
So, if Southern California water managers get their act together, they can swap snowpack losses for El Nino gains.
Is this right?
[Response: Hmm… not really. The big issue is of course what ENSO will do – and this is not well understood. I don’t think you can safely say that “increased warming will result in more frequent El Nino” – the projections and credibility for this aspect of climate are very varied. The snow pack changes are more reliable. – gavin]
cervates (15) & franz mair (19) — Here are the decadal averages from the HadCRUTv3 global temperature product:
http://tamino.files.wordpress.com/2008/04/10yave.jpg
Almost fifty of steady, very fastm warming ought to be enough to spur action, don’t you think?
Re #18, Naindj,
Hopefully the graphs make more sense if you read the whole paper linked to by Gavin! I agree that they are not easy to read at first, but are updates of a similar graph made by Cox & Stephenson (2007, Science). There are other versions in the paper as well which may be easier to understand, like this one:
http://ncas-climate.nerc.ac.uk/research/uncertainty/Fig4c.jpg
where the colours are the same as in the graphs in the article and show the fraction of the total uncertainty due to each source.
Internal variability can indeed hide the warming for a decade or so, as we are experiencing at the moment, but not for 30 years globally.
Re: the fractional uncertainty – it does not start from more than 1 because, as you say, we are considering a decadal mean temperature which reduces the uncertainty in the internal variability component, and importantly, the temperatures are always measured relative to the mean temperature from 1971-2000. We can therefore be confident that the temperature in the next decade will be warmer than the average of 1971-2000.
As the fractional uncertainty is the total uncertainty divided by the temperature change above 1971-2000, the uncertainty would have to be quite large to make this quantity greater than 1. [In fact, it is very close to 1 for an annual prediction 1 year ahead]. A value of 0.4 for the fractional uncertainty means that if the temperature prediction is 0.5K above 1971-2000 then the uncertainty is 0.2K, and so on.
Hope this helps!
Ed.
Re #18 (again)
Also, of course regionally the internal variability is much larger and so we can be less confident in our projections of the next decade on regional scales, as shown by the second panel in the article, where the fractional uncertainty is indeed larger than 1 for the next decade for the UK.
This does not make the projections useless, but it is important to realise the uncertainties in short term projections. It is hoped that the decadal predictions may help in this respect, though much more research is needed.
Ed.
It very much looks like the model predictions are just about hanging in there when compared to the real world measurements. If temperatures continue to fall or flatten out then observations will break out of the lower band and then it will be interesting to see where the modellers go then.
Is it just me or is there a lot less certainty surrounding this subject recently, shrill nonsense stories in the lead up to Copenhagen notwithstanding.
Re #21, #24 and #25 (John and Hank)
Yes it helped!
(I’m slow but not a desperate case)
Quite interesting graph indeed. (once you understand it!)
Thanks!
I think that it would help many of us understand the basis of the discussion if “decadal predictions” were defined and that was contrasted with climate change predictions (or projections if that be a better word) whose scale can be “decadal”.
[Response: The projections that are usually talked about (and that are the basis of the IPCC figures for instance) are all from long simulations that hindcast from the 19th Century using only the external forcings (CO2, methane, aerosols, volcanoes, solar etc.). By the time they get to 2010 or 2020 there is a wide range of ‘states’ of the internal variability. For instance, one realisation might have a big El Nino in 2009, another would be having a La Nina event and more would be ENSO-neutral. Similarly, some might have an anomalously strong circulation in the North Atlantic, others would have an anomalously weak circulation etc. Thus the projections for the next decade from these sets of runs encompass a wide range of internal variability which has no relationship to the state of internal variability in the real world right now. Thus their future simulations are generally only used to forecast the element of climate change that is forced by the continuing rise in greenhouse gases etc. and to give an assessment of the range of possible departures from the forced change that result from different internal variability.
The difference that the decadal predictions make is that they try and sync up the state of internal variability from the real world with an analogous state in the model, and thus attempt to predict the unforced variability and the forced variability together. In theory, this should be closer to what actually happens – at least for the short time period. – gavin ]
A bit OT here, but speaking of changing the energy mix, Ontario, Canada’s largest province, has just enacted feed-in-tariffs a la Spain–and we may be seeing the first corporate impacts from that. It should be noted that Ontario plans to phase out coal by 2014. (Coal was 23% of the energy mix five years ago, and is now just 7%.)
http://www.cleantech.com/news/5077/feed-tariff-spurs-canadian-hydro
> sync … with an analogous state in the model
Does that mean picking from the simulations run from 1900 to the present a few that (now? year after year from the start?) happened to stay the closest to observed reality in as many ways as possible?
Some of that closeness would be happenstance (getting the volcanos right); is the notion that some of the closeness would be meaningful and those scenario runs would happen to have picked values within the ranges that are …..
I’ll stop guessing now. But before the topic derails, if you can, or some of the visiting authors can, please do set out a 7th-grade-level description of what’s done?
David Harrington (26) — Tempatures continue to rise. There is a nice graphic here:
http://climateprogress.org/2009/09/22/new-york-times-andrew-revkin-suckered-by-deniers-to-push-global-cooling-myt/
and here are the decadal averages from the HadCRUTv3 global temperature product:
http://tamino.files.wordpress.com/2008/04/10yave.jpg
On trends and 30 year ‘windows’.
I’m not a scientist, nor a mathematician.
Dipping into RC from time to time I have learned that climate is determined by 30 year time spans; anything less is natural variations – or ‘weather’. Variations tends to obscure trend. So far, so good.
So how can I put faith in the work of scientist and modelers in the continuing, if slightly erratic, upward trend.
This would help me.
If one were to take every 30 time span from 1850 (reasonable start point?), so that’s 1850 – 1879, then 1851 – 1880, blah, blah, etc finally ending at 1979 – 2008, are all these year on year 30 year trends level or upward?
Essentially, I am looking for something that would satisfy my (always doubting) mind.
I really would like to get an answer to this.
IF not, what do people on this site say.
__________________
PS. Above, where I wrote “always doubting” I would have preferred to have used the word ‘sceptical’, but that word, ‘sceptical’, sees to have become poisoned.
From the web article referenced in your article its all about natural variability being so overwhelming on the relatively short time scales of the oscillations of natural phenomena (ENSO, La nina, el nino etc). In order for climate science to tease a viable projection of a specific trend shorter than a statistically significant time line is much harder than knowing what will most likely happen over a entire century period (100 years) ?
If we BAU for as long as we can on fossil fuels at the annual rise rate of 2% then we double our usage in 35 years (log2/2) which also means an additional 1.6 Trillion tonnes will have been releasd by 2045. If sinks falter then upto 1 trillion tonnes remains in the atmosphere.
Do anyone know the billion tonnes of CO2 to Co2 ppmv in the atmosphere at all? I did read 50 ppmv per 200 billion tonnes which would mean a 250 ppmv rise in CO2 by 2045.
I have the impression that this discussion on decadal prediction is ignoring natural external forcing:
for the very next decades, it seems to me that the potential for major volcanic eruption(s) and the unknowns regarding solar activity are absent from the BAMS figures – or at least, I wonder where it could be : this is not internal variability (it is short term fluctuations in external forcing), it is not model error, and it is probably not included in the “scenario” uncertainty (it might have been, but a quick look at the paper suggests that it is not the case).
Thus my impression is that this is a theoretical view about models, but it does not fully answer the question “what do we know about the climate within x decades”, at least for short term prediction. Right ?
[Response: Not really. For natural forcings that are somewhat predictable (i.e. the existence of the solar cycle – if not its precise magnitude), this can be included. Volcanoes are obviously a wild card. In some sense this can be likened to scenario uncertainty – but it would be a greater magnitude than the scenario uncertainty addressed by Hawkins. – gavin]
Theo Hopkins (33) — The graph of decadal temperature averages linked in comment #32 starts in 1850 CE. You can estimate the 30 year averages from that. Of the more recent such intervals 1940–1969 might be flat or even down a bit; certainly not after that.
Theo, that’s a great project. I think that, in order to achieve maximum reassurance for your mind–doubting, skeptical, or just questioning–you should do the plotting yourself. Woodfortrees offers a wonderful tool to do this. I’ve done the first 30-year span for you; knock yourself out!
(And let us know what you find.)
http://www.woodfortrees.org/plot/hadcrut3vgl/from:1850/to:1879/trend
– old models are less useful than improved ones
Of course. But the old models still have some use.
– each model uses all available computer and time resources
No they don’t. Only when they are running. I’m asking for the code to be stored.
– all models are wrong.
but some are more wrong then others?
Theo Hopkins says:
29 September 2009 at 1:51 PM:
No. Why would you expect them to be?
1851 – 1880
1881 – 1910
1911 – 1940
1941 – 1970
1971 – 2000
1851 – 2008
I used hadcrut3 because it goes back to 1851. GISSTEMP is similar, but only goes back to 1880. (It has been argued that from 1851 – 1880 hadcrut3 only represents the NH well.)
Here’s GISTEMP:
1881 – 1910
1911 – 1940
1941 – 1970
1971 – 2000
1880 – 2008
Theo, Kevin’s right, you should do it yourself rather than just trust some stranger on a blog somewhere to do it for you.
This may help:
http://scienceblogs.com/stoat/2007/05/the_significance_of_5_year_tre.php#
MikeN — you can look it up. You know how.
Theo Hopkins (#32),
http://moregrumbinescience.blogspot.com/2009/01/results-on-deciding-trends.html
What you’re looking for (though 20- or 25-year trends rather than 30-year) is in figures 3, 4 and 5, but do read the whole post, or you’ll miss out.
Re #30 (Hank)
The ‘syncing’ of the models to the internal variability is done by inserting (or ‘assimilating’) ocean observations into the climate model (this type of thing is done for weather forecasting too) to force the climate model to be close to the current state. It is then let to run free without being given any more observations, and is then a prediction.
Ed.
Our Stefan is pumping up the volume:
Gavin in #28,
Is it not possible to test with presently available model runs if the idea of detailed predictions can be hoped for? There must be instances when model and observation make a pretty good match in the hindcasts. Do they then stay close for a period longer than just being temporary neighbors might produce? Is there extended coherence between model and observation when they get close? If so, then there is hope. If not, then the models are not close enough in detail to the world yet.
Jim Galasyn #43, note that the two metres is not a forecast for 2100AD. Just in case someone tries to pull a Gore on Stefan…
I would like to ask you a general question – How accurate are the GCM’s in predicting reality?
You have said that for temperature, the output from single GCM runs will not match the data as well as a statistical model based purely on the forcings, but that the mean of many simulations is better at predictions than any individual simulation.
I am puzzled by this. If a single simulation is not a good predictor of reality how can the average of many simulations, each of which is a poor predictor of reality, be a better predictor, or indeed claim to have any residual of reality?
[Response: Any single realisation can be thought of as being made up of two components – a forced signal and a random realisation of the internal variability (‘noise’). By definition the random component will uncorrelated across different realisations and when you average together many examples you get the forced component (i.e. the ensemble mean). Just as in weather forecasting, the forecast with the greatest skill turns out to be this ensemble mean. i.e. you do the least badly by not trying to forecast the ‘noise’. This isn’t necessarily cast in stone, but it is a good rule of thumb. – gavin]
Should we really treat “scenario uncertainty” as an uncertainty (part of the noise), or as sensitivity to an independent variable (part of the signal)?
[Response: It is not part of the noise, it is part of the uncertainty in the forced signal and so is very different in kind from internal variability. – gavin]
I’ve put a new page on my climatology web site dealing with the successful predictions of the models. I cribbed a great deal from earlier posts at places like RealClimate and Open Mind. Here it is:
http://BartonPaulLevenson.com/ModelsReliable.html
Can anyone who knows any of these details send me a citation for a prediction and/or the observation(s) which confirmed it? I have some of this information already, but not all of it. If I can get a comprehensive list together I’ll put it all into that web page as an appendix to prove I’m not just blowing smoke.
Paul in 48. It is all very well to trumpet the success of the models at predicting this or the other but where is the model that can predict at least a fair number of these results in its own right? Model “a” got this right and model “b” got that right but on the whole the process is an amalgamation or average and on this basis it is not going that well. Cherry picking is not science.
[Response: Fair general point, but not actually a propos. Publishing particular results with a particular model is normal, publishing repetitions of the same result with a different model tends to be less common – but it certainly happens. And in assessments such as the IPCC or the CCSP reports, the results tend to be taken over multiple models. – gavin]
#32 Theo Hopkins
30 years with attribution helps. In other words, look at the period after WWII. There was about a 33 year cooling trend, but that trend is generally attributed to the effects of industrial aerosols masking the global warming effect during that period.
The industrial output at that time had some downsides, like the destruction of the ozone and acid rain. So the Montreal protocol was put in place and the industrial output of those pollutants was reduced and the CO2 pollutant then became more dominant and warming resumed.
PS I’m still a skeptic.