Arctic Sea Ice Volume: PIOMAS, Prediction, and the Perils of Extrapolation

Guest Commentary by Axel Schweiger, Ron Lindsay, and Cecilia Bitz

We have just passed the annual maximum in Arctic sea ice extent which always occurs sometime in March. Within a month we will reach the annual maximum in Arctic sea ice volume. After that, the sea ice will begin its course towards its annual minimum of both extent and volume in mid-September. This marks the beginning of the ritual of the annual sea ice watch that includes predictions of the extent and rank of this year’s sea ice minimum, as well as discussion about the timing of its eventual demise. One of the inputs into that discussion is the “PIOMAS” ice-ocean model output of ice volume – and in particular, some high-profile extrapolations. This is worth looking at in some detail.

Prediction methods for the sea ice minima range from ad-hoc guesses to model predictions, from statistical analyses to water-cooler speculation in the blogosphere. Many of these predictions are compiled in the SEARCH-sponsored “sea ice outlook“.

This year’s discussions however will be without the input of the father of modern sea ice physics, Norbert Untersteiner, who recently died at the age of 86. Much of the physics in PIOMAS and global climate models can be traced to Norbert’s influence. Norbert was sober-minded and skeptical about the prospects of skillful short-term sea ice predictions, but even he couldn’t help but be drawn into the dubious excitement around the precipitous decline of arctic sea ice and regularly added his own guestimate to the sea ice outlook. Norbert’s legacy challenges those of us who engage in predictions to prove our skill and to understand and explain the limitations of our techniques so they are not used erroneously to misinform the public or to influence policy…more about that later and here.

PIOMAS

PIOMAS is the Panarctic Ice Ocean Modeling and Assimilation System. It belongs to the class of ice-ocean models that have components for the sea ice and the ocean, but no interactive atmosphere. There is an active community (AOMIP) engaged in applying and improving these types of models for Arctic problems. Without an atmosphere, inputs that represent the atmospheric forcing (near surface winds, temperature, humidity, and downwelling short and longwave radiation) need to be provided. Typically those inputs are derived from global atmospheric reanalysis projects. The advantage of such partially-coupled models is that they can be driven by past atmospheric conditions and the simulations match well the observed sea ice variability, which is strongly forced by the atmosphere.

This is in contrast to fully-coupled models, such as those used in the IPCC projections, which make their own version of the weather and can only be expected to approximate the mean and general patterns of variability and the long-term trajectory of the sea ice evolution. Another advantage of ice-ocean models is that they don’t have to deal with the complexities of a fully-coupled system. For example, fully-coupled models have biases in the mean wind field over the Arctic which may drive the sea ice into the wrong places, yielding unrealistic patterns of sea ice thickness. This has been a common problem with global climate models but the recent generation of models clearly shows improvement. Because sea ice is strongly driven by the atmosphere, model predictions depend on the quality of the future atmospheric conditions. Therefore an ice-ocean model, like PIOMAS, is much more accurate at hindcasts, when the atmospheric conditions are simply reconstructed from observations, than for forecasts, when atmospheric conditions must be estimated. That is not to say that PIOMAS can’t be used for predictions, it can (Zhang et al. 2008, Lindsay et al. 2008 , Zhang et al. 2010) but it is important to recognize that performance at hindcasts does not necessarily say much about performance at forecasts. This point often gets confused.

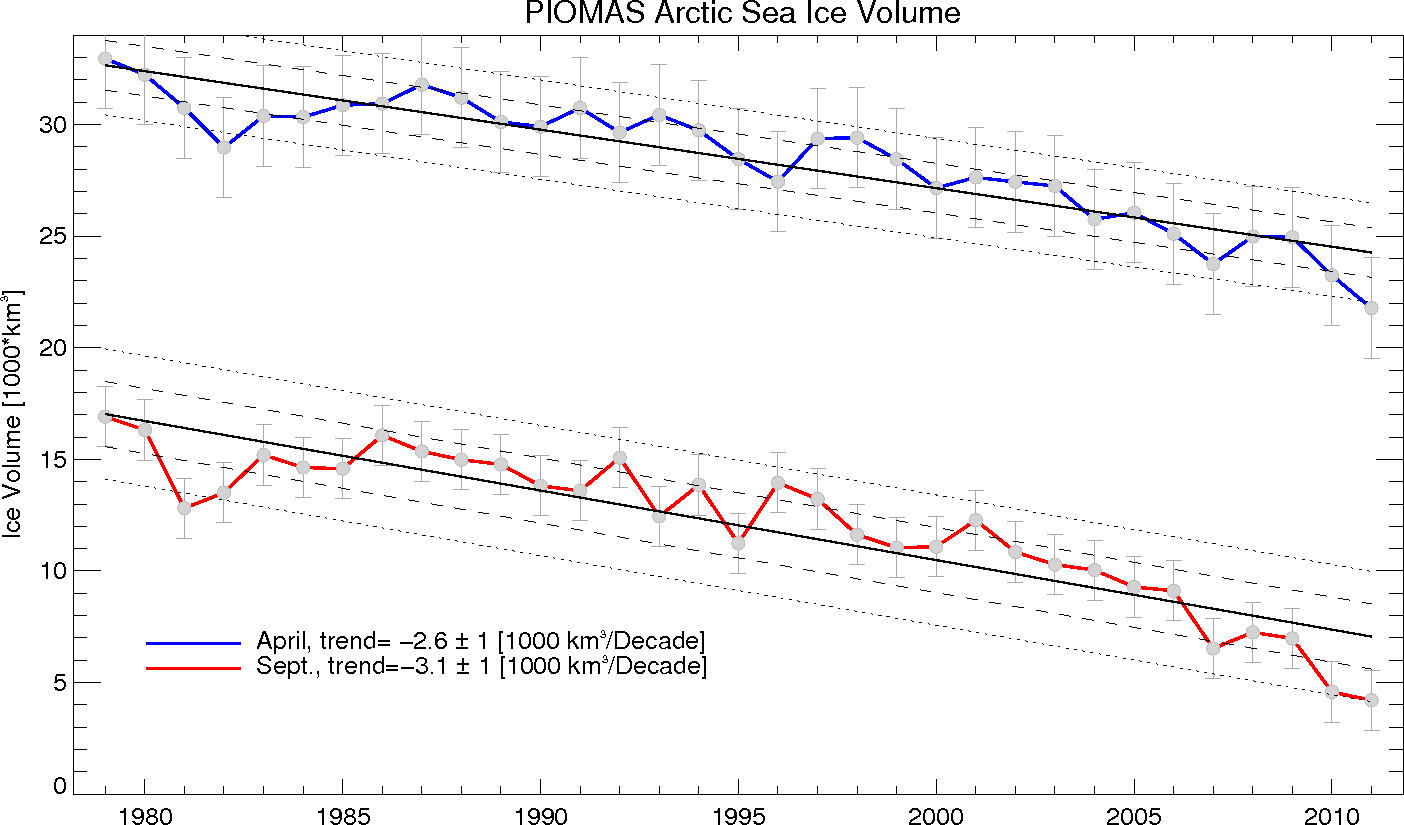
Figure 1: PIOMAS mean monthly arctic sea ice volume for April and September. Dashed lines parallel to linear fits represent one and two standard deviations from the trend. Error bars are estimated based on comparison with thickness observations and model sensitivity studies (Schweiger et al. 2011)

PIOMAS was developed and is operated by Jinlun Zhang at the University of Washington. It is the regional version of the global ice-ocean model of Zhang and Rothrock (2003). The sea ice component represents sea ice in multiple categories of thickness and accounts for changes in thickness due to growth and melt as well as mechanical deformation of ice (Thorndike et al. 1975, Hibler 1980).
It has evolved with continual improvements, including the addition of data assimilation capabilities (Zhang et al. 2003, Lindsay et al. 2006) and the development of sister models for new applications (BIOMAS for biology) or specific regions (BESTMAS for the Bering Sea and GIOMAS for the entire globe) (publications). As a modeler working among observationalists from a variety of disciplines, Jinlun has never been short of tire-kickers who probe, push, and challenge his model from all sorts of different angles and identify warts and beauty spots. This is one of the reasons why PIOMAS has evolved into one of the premier ice-ocean models (Johnson et al. 2012), particularly when it comes to the representation of the sea-ice cover.

PIOMAS has been used in a wide range of applications but arguably the most popular product has been the time series of total Arctic sea ice volume which we have been putting out since March 2010 (see also Fig 1). The motivation for this time series is to visualize the fact that the long term Arctic-wide loss of sea ice is not only happening in extent, which is well measured by satellites, but also in thickness, which isn’t. Ice volume, the product of sea ice area and thickness, is a measure for the total loss in sea ice and the total amount of energy involved in melting the ice. Though this is a very small part of the change of global energy content, it is regionally important and investigations into the cause of sea ice need to pin down the sources of this energy.

But why use PIOMAS to show the decline in ice volume when our group of researchers has been involved in measuring, rescuing, and collecting sea ice thickness data from in-situ observations for 30-some years? The answer is that even though wide-spread thickness losses from observations alone have been apparent for some areas or time periods, Arctic-wide thickness losses are more difficult to document because of the sparse sampling in time and space. The problem can be visualized by constructing a “naïve” sea ice thickness time series from in-situ observations:

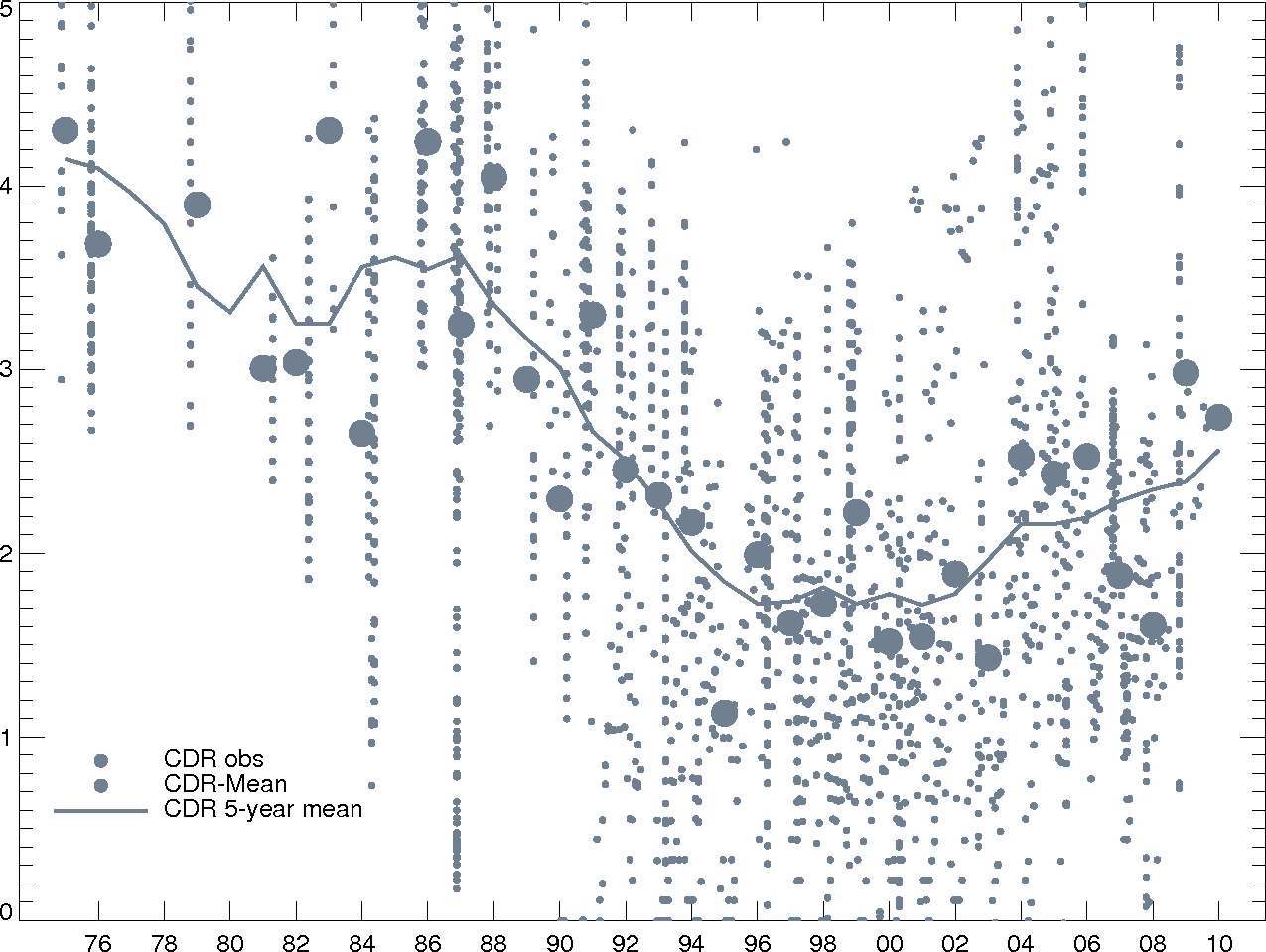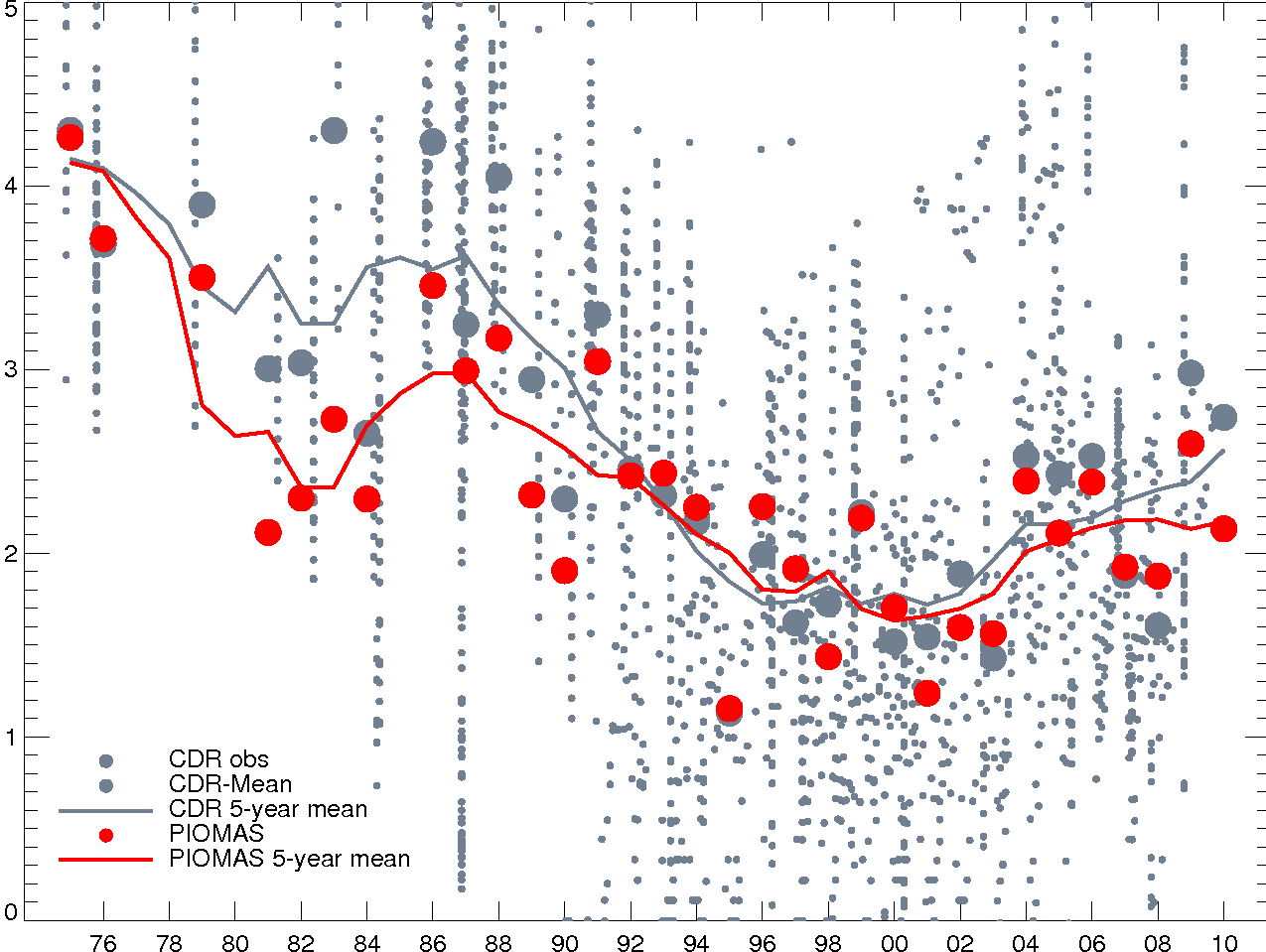
Figure 2 Naïve sea ice thickness time series. Sea ice thickness observations from the sea ice thickness climate data record (small grey dots), averages for all observations in a given year (large grey dots), and 5-year running mean through those observations. The same calculation for the corresponding PIOMAS simulations at the location and time of observation is shown by the big red dots and line.

Before those claiming that global warming stopped in 1998 have a field day with this figure, they should appreciate that our total volume time series and the naïve thickness time series are entirely consistent. The sampling issues arise from the fact that sea ice is highly dynamic with lots of spatial and seasonal variability so that measurements from individual moorings, submarine sonar tracks, and aircraft flights can only construct an incomplete picture of the evolution of the total Arctic sea ice volume. Progress towards establishing ice thickness records from satellite (ICESat, Envisat, and CryoSat-2) will change this over time, but these sources won’t yield a record before these measurements began and satellite retrievals of ice thickness have their own issues.

PIOMAS is not normally run as a freely-evolving model, but rather it assimilates observations. Ice concentration and sea surface temperature are currently assimilated and we have experimented with the assimilation of ice motion (Zhang et al. 2003, Lindsay et al. 2006). Assimilation helps constrain the ice extent to observations and helps improve the simulation of sea ice thickness. Ice thickness observations are not assimilated into the model. Instead, ice thickness and buoy drift data are used for model calibration and evaluation. So using a model constrained by observations is quite possibly the best we can do to establish a long-term ice volume record.

Model calibration is of course necessary. We need to determine parameters that are not well known, deal with inadequately modeled physics, and address significant biases in the forcing fields. Parameters changed in PIOMAS calibration are typically the surface albedo and roughness, and the ice strength. Once calibrated, the model can be run and evaluated against observations not included in the calibration process. Evaluation does not only mean showing that PIOMAS says something useful but also establishes the error bars on the estimated ice thickness. To establish this uncertainty in the ice-volume record (Schweiger et al. 2011), we spent a significant effort drawing on most types of available observations of ice thickness thanks to a convenient compilation of ice thickness data (Lindsay, 2010). We have also compared PIOMAS estimates with measurements from ICESat and conducted a number of model sensitivity studies. As a result of this evaluation our conservative estimates of the uncertainty of the linear ice volume trend from 1979-present is about 30%. While there is lots to do in improving both measurements and models to reduce the uncertainty in modeled ice volume, we can also say with great confidence that the decline in observed ice thickness is not just an effect of measurement sampling and that the total sea ice volume has been declining over the past 32 years at astonishing rates (for instance a 75% reduction in September volume from 1979 to 2011).

Prediction

The seasonal prediction issue and the prediction of the long-term trajectory are fundamentally different problems. Seasonal prediction, say predicting September ice extent in March, is what is called an initial value problem and the September ice extent depends both on the weather, which is mostly unpredictable beyond 10 days or so, and the state of the ocean and sea ice in March. Improving observations to better characterize that state, and improving models to carry this information forward in time is our best hope to improve seasonal predictability. The prediction of the long-term trajectory, depends on the climate forcing (greenhouse gases, aerosols, solar variability) and how the model responds to those forcings via feedbacks. A recent model study showed that the crossover between initial-value and climate-forced predictability for sea ice occurs at about 3 years (Blanchard-Wrigglesworth et al. 2011). In other words, a model forgets the initial sea ice state after a few years at which point the main driver of any predictable signal is the climate forcing. In fact, coupled model simulations have shown that even removing all the sea ice in a particular July has little lasting impact on the trajectory of the ice after a few years (Tietsche et al. 2011).

PIOMAS has been run in a forward mode (and hence without data assimilation) to yield seasonal predictions for the sea ice outlook (Zhang et al. 2008) and has also provided input to statistical forecasts (Lindsay et al. 2008) and fully-coupled models. We have also done experiments with PIOMAS in a climate projection mode by scaling atmospheric forcing data from a reanalysis to 2xC0₂ projections from the CMIP3 models (Zhang et al. 2010). This setup provides more realistic wind fields and spatial thickness distribution but cannot account for important atmosphere-ocean feedbacks.

Global climate model projections (in CMIP3 at least) appear to underestimate sea ice extent losses with respect to observations, though this is not universally true for all models and some of them actually have ensemble spreads that are compatible with PIOMAS ice volume estimates and satellite observations of sea ice extent. With error bars provided, we can use the PIOMAS ice volume time series as a proxy record for reality and compare it against sea-ice simulations in global climate models. This provides another tool in addition to more directly observed properties for the improvement and evaluation of these models and is in our view the best use of PIOMAS in the context of predicting the long-term trajectory of sea ice.

Predictions of a seasonally ice-free Arctic Ocean

The eventual demise of the summer sea ice is a common feature of nearly every climate model projection (the exceptions are models with very inappropriate initial conditions). But the question of when the Arctic will be ‘ice-free’ is imprecise and calls for a clear definition of what ice-free means. Does it mean completely ice-free, or is there a minimum threshold implied? Does it mean the first time the summer sea ice goes beneath this threshold or does it imply a probability of encountering low-ice conditions over a period of time? (e.g. high likelihood of Septembers with less than 10⁶ km² of ice in a 10-year period). Regardless of whether the concept is actually useful for any practical purpose (say for planning shipping across the Arctic), it is nevertheless a powerful image in communicating the dramatic changes that are under way in the Arctic.

Once defined, predictions of when an ice-free Arctic will occur seem justified. In the published literature there are several papers specifically targeting such predictions (Zhang and Walsh, 2006, Wang and Overland, 2009, Boe et al. 2009, Zhang et. al. 2010) while others include discussion about the timing of ice-free summers (e.g. Holland et al. 2006). Some address the fact that the CMIP3/IPCC AR4 simulations show sea ice declines less rapid than the observations and attempt to correct for it. Published projections, though with varying definitions of what constitutes ice-free, all project an ice-free Arctic ocean somewhere between 2037 (Wang and Overland, 2009) and the end of the century. Predictions of earlier ice-free dates so-far seem to be confined to conference presentations, media-coverage, the blogosphere, and testimony before to the UK parliament.

Extrapolation

A different class of predictions are based on simple extrapolation using historical sea ice extent, concentration, or volume. An example is included in the materials presented by the so-called ‘Arctic Methane Emergency Group’ who show extrapolations of PIOMAS data and warn about the potential of a seasonally ice-free Arctic ocean in just a few years. So does it make sense to extrapolate sea ice volume for prediction? In order to do a successful extrapolation several conditions need to be met. First, an appropriate function for the extrapolation should be chosen. This function needs to either be based on the underlying physics of the system or needs to be justified as appropriate for future projections beyond just fitting the historical data.

But what function should one choose? Since we don’t really have data on how the trajectory of the Arctic sea ice evolves under increased greenhouse forcing, model projections may provide a guide about the shape of appropriate function. Clearly, linear, quadratic or exponential functions do not properly reflect the flattening of the trajectory in the next few decades seen for example in the CCSM4 (Fig 3). The characteristic flattening of this trajectory, at first order, arises from the fact that there is an increasingly negative (damping) feedback as the sea ice thins described by Bitz and Roe (2004) and Armour et al. (2011). The thick ice along the northern coast of Greenland is unusually persistent because there are on-shore winds that cause the ice to drift and pile-up there. So extrapolations by fitting a function that resembles a sigmoid-shaped trajectory may make more sense, but even that, as shown in the figure, yields a much earlier prediction of an ice-free Arctic than can be expected from the CCSM4 ensemble.

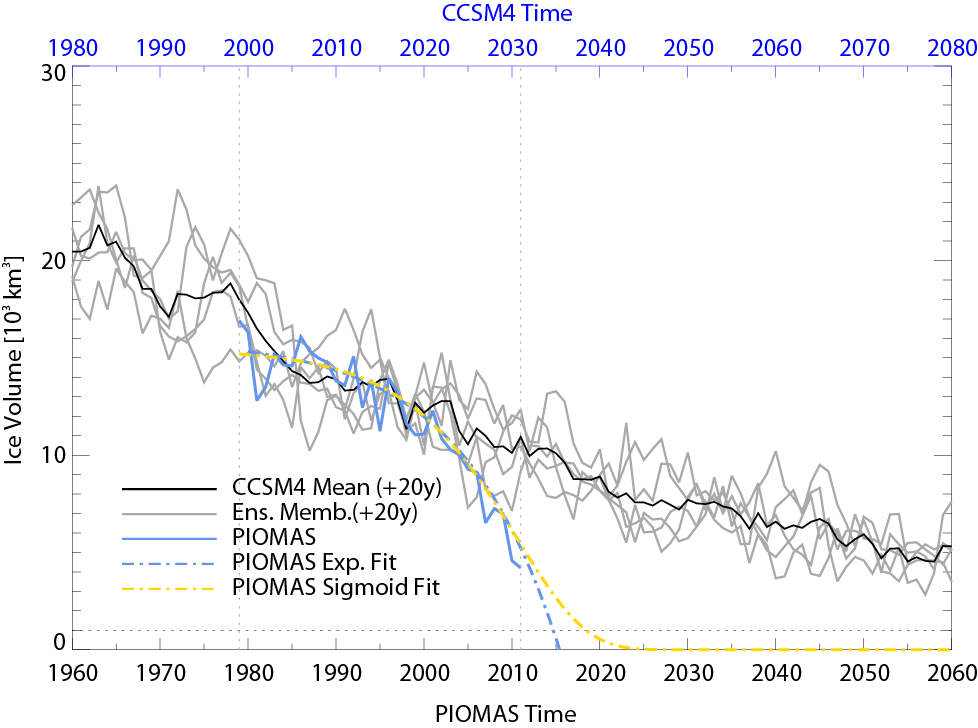
Figure 3. CCSM4 AR4 ensemble and PIOMAS September mean arctic ice volume. Exponential and sigmoid (Gompertz) fits to PIOMAS data are shown. Note that the 1979-2011 September mean of the CCSM4 ensemble has about 30% higher sea ice volume than PIOMAS. To visualize the difficulty in choosing an appropriate extrapolation function based on PIOMAS data we shifted the CCSM4 time series forward by 20 years to roughly match the mean ice volume over the 1979-2011 fitting period.

But there is a second issue that may foil prediction by extrapolation: The period over which the function is fit must be sufficiently long to include adequate long-term natural variability in the climate system. The goodness of fit over the fitting period unfortunately may be misleading. Whether or not this is the case for sea ice extent or volume is an open question. The sea ice trajectory shows considerable natural variability at various time scales on top of the smoother forced response to changes in greenhouse gases. Periods of rapid decline are followed by slower periods of decline or increases. By fitting a smooth function to a sea ice time series (e.g. PIOMAS) one might easily be tempted to assume that the smooth fit represents the forced (e.g. greenhouse) component and the variation about the curve is due to natural variability. But natural variability can occur at time scales long enough to affect the fit. We have to remember that part of the observed trend is likely due to natural variability (Kay et al. 2011, Winton, 2011) and may therefore have little to do with the future evolution of the sea ice trajectory. This is visualized in figure 4 where ensemble members from the CCSM4 AR4 runs are fit with S-shaped (Gompertz) functions using the 1979-2011 period to estimate the parameters. The differences between the ensemble members, reflecting natural variability, yield vastly different extrapolated trajectories. Natural variability at these time scales (order of 30 years) may very well make prediction by extrapolation hopeless.

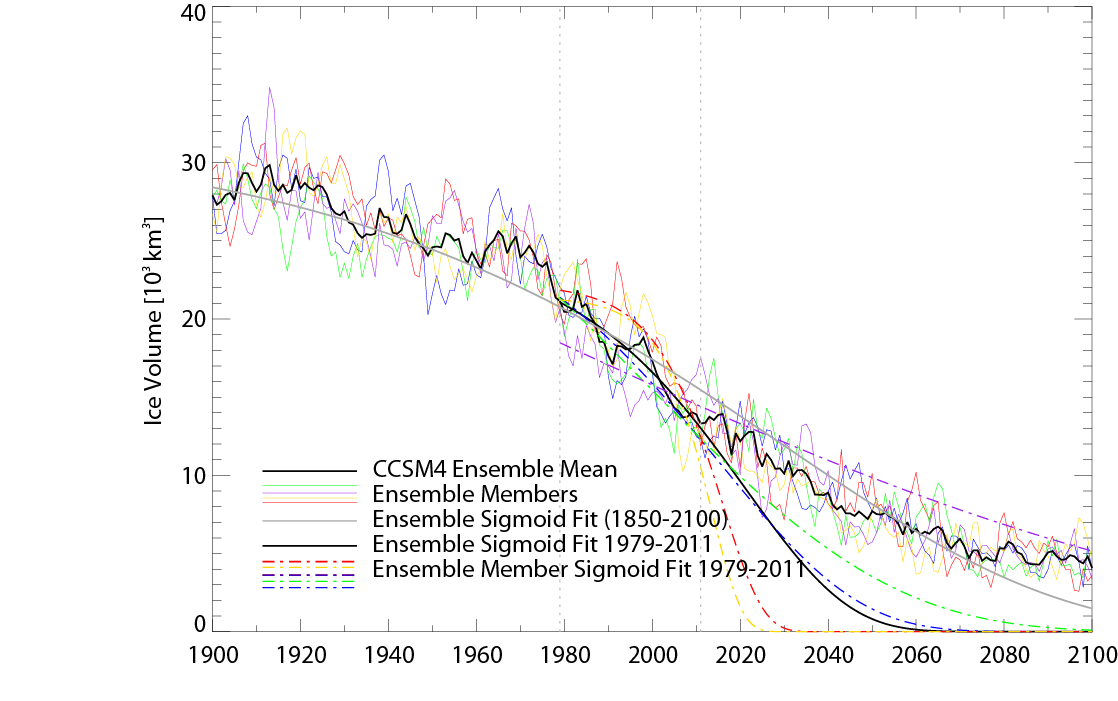
Figure 4. CCSM4 AR4 ensemble with sigmoid (Gompertz) fits. Light vertical lines represent fitting period for ensemble members (1979-2011).

In summary, we think that expressing concern about the future of the Arctic by highlighting only the earliest estimates of an ice-free Arctic is misdirected. Instead, serious effort should be devoted to making detailed seasonal-to-interannual (initial-value) predictions with careful evaluations of their skill and better estimates of the climate-forced projections and their uncertainties, both of which are of considerable value to society. Some effort should also target the formulation of applicable and answerable questions that can help focus modeling efforts. We believe that substantially skillful prediction can only be achieved with models, and therefore effort should be given to improving predictive modeling activities. The best role of observations in prediction is to improve, test, and initialize models.

But when will the Arctic be ice free then? The answer will have to come from fully coupled climate models. Only they can account for the non-linear behavior of the trajectory of the sea ice evolution and put longer term changes in the context of expected natural variability. The sea ice simulations in the CMIP5 models are currently being analyzed. This analysis will reveal new insights about model biases, their causes, and about the role of natural variability in long-term change.It is possible that this analysis will change the predicted timing of the “ice free summers” but large uncertainties will likely remain. Until then, we believe, we need to let science run
its course and let previous model-based predictions of somewhere between “2040 and 2100″ stand”

References

Bitz, C. M., and G. H. Roe (2004), A mechanism for the high rate of sea ice thinning in the Arctic Ocean, J Climate, 17(18), 3623-3632.
Boe, J. L., A. Hall, and X. Qu (2009), September sea-ice cover in the Arctic Ocean projected to vanish by 2100, Nature Geoscience, 2(5), 341-343.
Hibler, W. D. (1980), Modeling a Variable Thickness Sea Ice Cover, Monthly Weather Review, 108(12), 1943-1973.
Holland, M. M., C. M. Bitz, and B. Tremblay (2006), Future abrupt reductions in the summer Arctic sea ice, Geophys. Res. Lett, 33(23), 5.
Johnson, M., et al. (2012), Evaluation of Arctic sea ice thickness simulated by Arctic Ocean Model Intercomparison Project models, J. Geophys. Res., 117, C00D13.
Kay, J. E., M. M. Holland, and A. Jahn (2011), Inter-annual to multi-decadal Arctic sea ice extent trends in a warming world, Geophys. Res. Lett, 38.
Lindsay, R. W. (2010), New Unified Sea Ice Thickness Climate Data Record, Eos Trans. AGU, 91(44), 405-416.
Lindsay, R. W., J. Zhang, A. J. Schweiger, and M. A. Steele (2008), Seasonal predictions of ice extent in the Arctic Ocean, J.Geophys.Res., 113(C2), 11.
Lindsay, R. W., and J. Zhang (2006), Assimilation of ice concentration in an ice-ocean model, Journal of Atmospheric and Oceanic Technology, 23(5), 742-749.
Rothrock, D. A., Y. Yu, and G. A. Maykut (1999), Thinning of the Arctic sea-ice cover, Geophys. Res. Lett, 26(23), 3469-3472.
Schweiger, A. J., R. Lindsay, J. Zhang, M. Steele, H. Stern, and R. Kwok (2011), Uncertainty in modeled Arctic sea ice volume, J. Geophys. Res., 116, C00D06.
Tietsche, S., D. Notz, J. H. Jungclaus, and J. Marotzke (2011), Recovery mechanisms of Arctic summer sea ice, Geophys. Res. Lett, 38.
Thorndike, A. S., D. A. Rothrock, G. A. Maykut, and R. Colony (1975), Thickness Distribution of Sea Ice, J.Geophys.Res., 80(33), 4501-4513.
Wang, M. Y., and J. E. Overland (2009), A sea ice free summer Arctic within 30 years?, Geophys. Res. Lett, 36, 5.
Winton, M. (2000), A reformulated three-layer sea ice model, Journal of Atmospheric and Oceanic Technology, 17(4), 525-531.
Winton, M. (2011), Do Climate Models Underestimate the Sensitivity of Northern Hemisphere Sea Ice Cover?, J Climate, 24(15), 3924-3934.
Zhang, J., D. R. Thomas, D. A. Rothrock, R. W. Lindsay, Y. Yu, and R. Kwok (2003), Assimilation of ice motion observations and comparisons with submarine ice thickness data, J.Geophys.Res., 108(C6), 3170, DOI: 3110.1029/2001JC001041
Zhang, J., and D. A. Rothrock (2003), Modeling global sea ice with a thickness and enthalpy distribution model in generalized curvilinear coordinates, Monthly Weather Review, 131(5), 845-861.
Zhang, X. D., and J. E. Walsh (2006), Toward a seasonally ice-covered Arctic Ocean: Scenarios from the IPCC AR4 model simulations, J Climate, 19(9), 1730-1747.
Zhang, J., M. Steele, and A. Schweiger (2010), Arctic sea ice response to atmospheric
forcings with varying levels of anthropogenic warming and climate variability, Geophys.
Res. Lett, 37 (L20505)