Guest Commentary by Axel Schweiger, Ron Lindsay, and Cecilia Bitz
We have just passed the annual maximum in Arctic sea ice extent which always occurs sometime in March. Within a month we will reach the annual maximum in Arctic sea ice volume. After that, the sea ice will begin its course towards its annual minimum of both extent and volume in mid-September. This marks the beginning of the ritual of the annual sea ice watch that includes predictions of the extent and rank of this year’s sea ice minimum, as well as discussion about the timing of its eventual demise. One of the inputs into that discussion is the “PIOMAS” ice-ocean model output of ice volume – and in particular, some high-profile extrapolations. This is worth looking at in some detail.
Prediction methods for the sea ice minima range from ad-hoc guesses to model predictions, from statistical analyses to water-cooler speculation in the blogosphere. Many of these predictions are compiled in the SEARCH-sponsored “sea ice outlook“.
This year’s discussions however will be without the input of the father of modern sea ice physics, Norbert Untersteiner, who recently died at the age of 86. Much of the physics in PIOMAS and global climate models can be traced to Norbert’s influence. Norbert was sober-minded and skeptical about the prospects of skillful short-term sea ice predictions, but even he couldn’t help but be drawn into the dubious excitement around the precipitous decline of arctic sea ice and regularly added his own guestimate to the sea ice outlook. Norbert’s legacy challenges those of us who engage in predictions to prove our skill and to understand and explain the limitations of our techniques so they are not used erroneously to misinform the public or to influence policy…more about that later and here.
PIOMAS
PIOMAS is the Panarctic Ice Ocean Modeling and Assimilation System. It belongs to the class of ice-ocean models that have components for the sea ice and the ocean, but no interactive atmosphere. There is an active community (AOMIP) engaged in applying and improving these types of models for Arctic problems. Without an atmosphere, inputs that represent the atmospheric forcing (near surface winds, temperature, humidity, and downwelling short and longwave radiation) need to be provided. Typically those inputs are derived from global atmospheric reanalysis projects. The advantage of such partially-coupled models is that they can be driven by past atmospheric conditions and the simulations match well the observed sea ice variability, which is strongly forced by the atmosphere.
This is in contrast to fully-coupled models, such as those used in the IPCC projections, which make their own version of the weather and can only be expected to approximate the mean and general patterns of variability and the long-term trajectory of the sea ice evolution. Another advantage of ice-ocean models is that they don’t have to deal with the complexities of a fully-coupled system. For example, fully-coupled models have biases in the mean wind field over the Arctic which may drive the sea ice into the wrong places, yielding unrealistic patterns of sea ice thickness. This has been a common problem with global climate models but the recent generation of models clearly shows improvement. Because sea ice is strongly driven by the atmosphere, model predictions depend on the quality of the future atmospheric conditions. Therefore an ice-ocean model, like PIOMAS, is much more accurate at hindcasts, when the atmospheric conditions are simply reconstructed from observations, than for forecasts, when atmospheric conditions must be estimated. That is not to say that PIOMAS can’t be used for predictions, it can (Zhang et al. 2008, Lindsay et al. 2008 , Zhang et al. 2010) but it is important to recognize that performance at hindcasts does not necessarily say much about performance at forecasts. This point often gets confused.
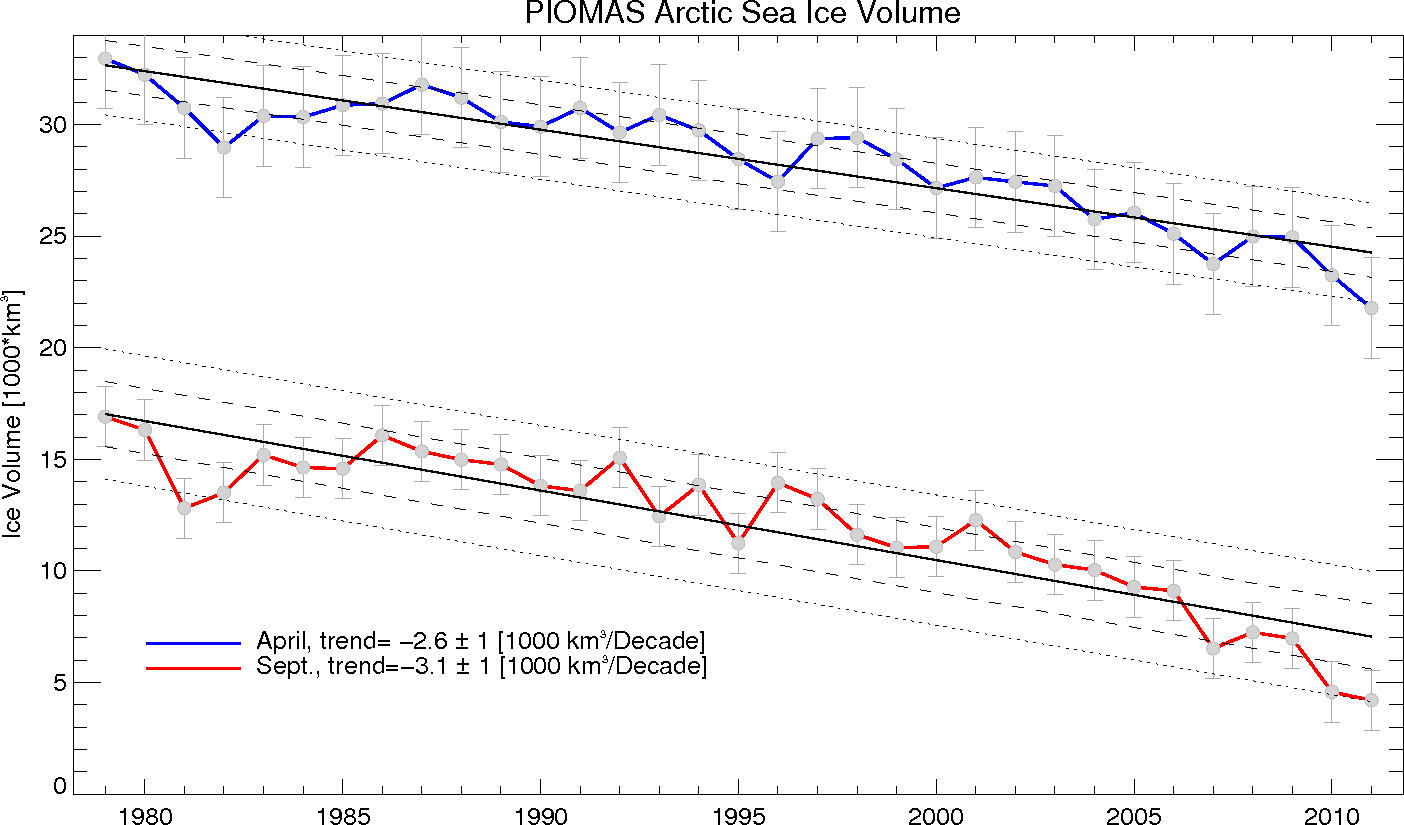
Figure 1: PIOMAS mean monthly arctic sea ice volume for April and September. Dashed lines parallel to linear fits represent one and two standard deviations from the trend. Error bars are estimated based on comparison with thickness observations and model sensitivity studies (Schweiger et al. 2011)
PIOMAS was developed and is operated by Jinlun Zhang at the University of Washington. It is the regional version of the global ice-ocean model of Zhang and Rothrock (2003). The sea ice component represents sea ice in multiple categories of thickness and accounts for changes in thickness due to growth and melt as well as mechanical deformation of ice (Thorndike et al. 1975, Hibler 1980).
It has evolved with continual improvements, including the addition of data assimilation capabilities (Zhang et al. 2003, Lindsay et al. 2006) and the development of sister models for new applications (BIOMAS for biology) or specific regions (BESTMAS for the Bering Sea and GIOMAS for the entire globe) (publications). As a modeler working among observationalists from a variety of disciplines, Jinlun has never been short of tire-kickers who probe, push, and challenge his model from all sorts of different angles and identify warts and beauty spots. This is one of the reasons why PIOMAS has evolved into one of the premier ice-ocean models (Johnson et al. 2012), particularly when it comes to the representation of the sea-ice cover.
PIOMAS has been used in a wide range of applications but arguably the most popular product has been the time series of total Arctic sea ice volume which we have been putting out since March 2010 (see also Fig 1). The motivation for this time series is to visualize the fact that the long term Arctic-wide loss of sea ice is not only happening in extent, which is well measured by satellites, but also in thickness, which isn’t. Ice volume, the product of sea ice area and thickness, is a measure for the total loss in sea ice and the total amount of energy involved in melting the ice. Though this is a very small part of the change of global energy content, it is regionally important and investigations into the cause of sea ice need to pin down the sources of this energy.
But why use PIOMAS to show the decline in ice volume when our group of researchers has been involved in measuring, rescuing, and collecting sea ice thickness data from in-situ observations for 30-some years? The answer is that even though wide-spread thickness losses from observations alone have been apparent for some areas or time periods, Arctic-wide thickness losses are more difficult to document because of the sparse sampling in time and space. The problem can be visualized by constructing a “naïve” sea ice thickness time series from in-situ observations:
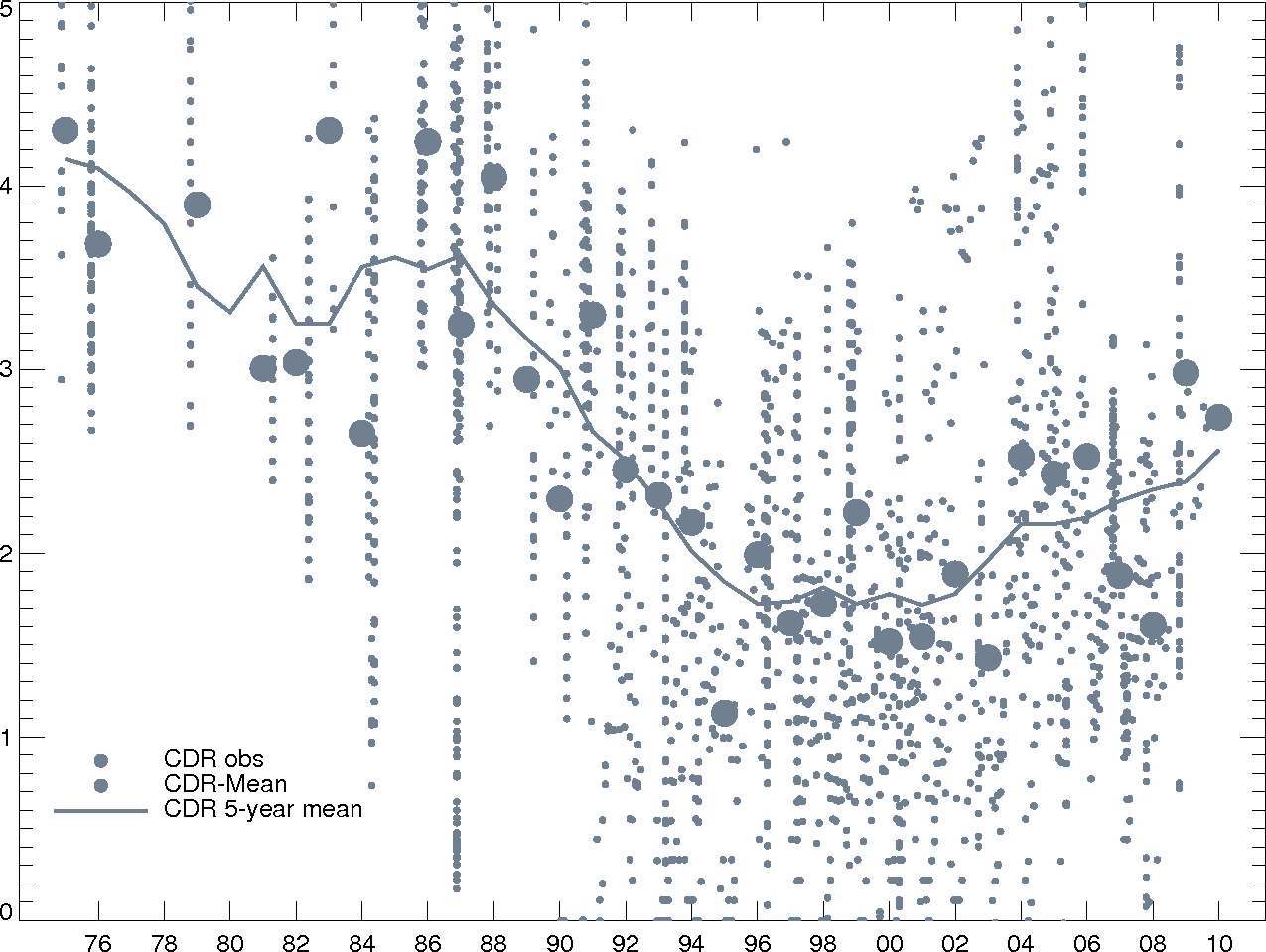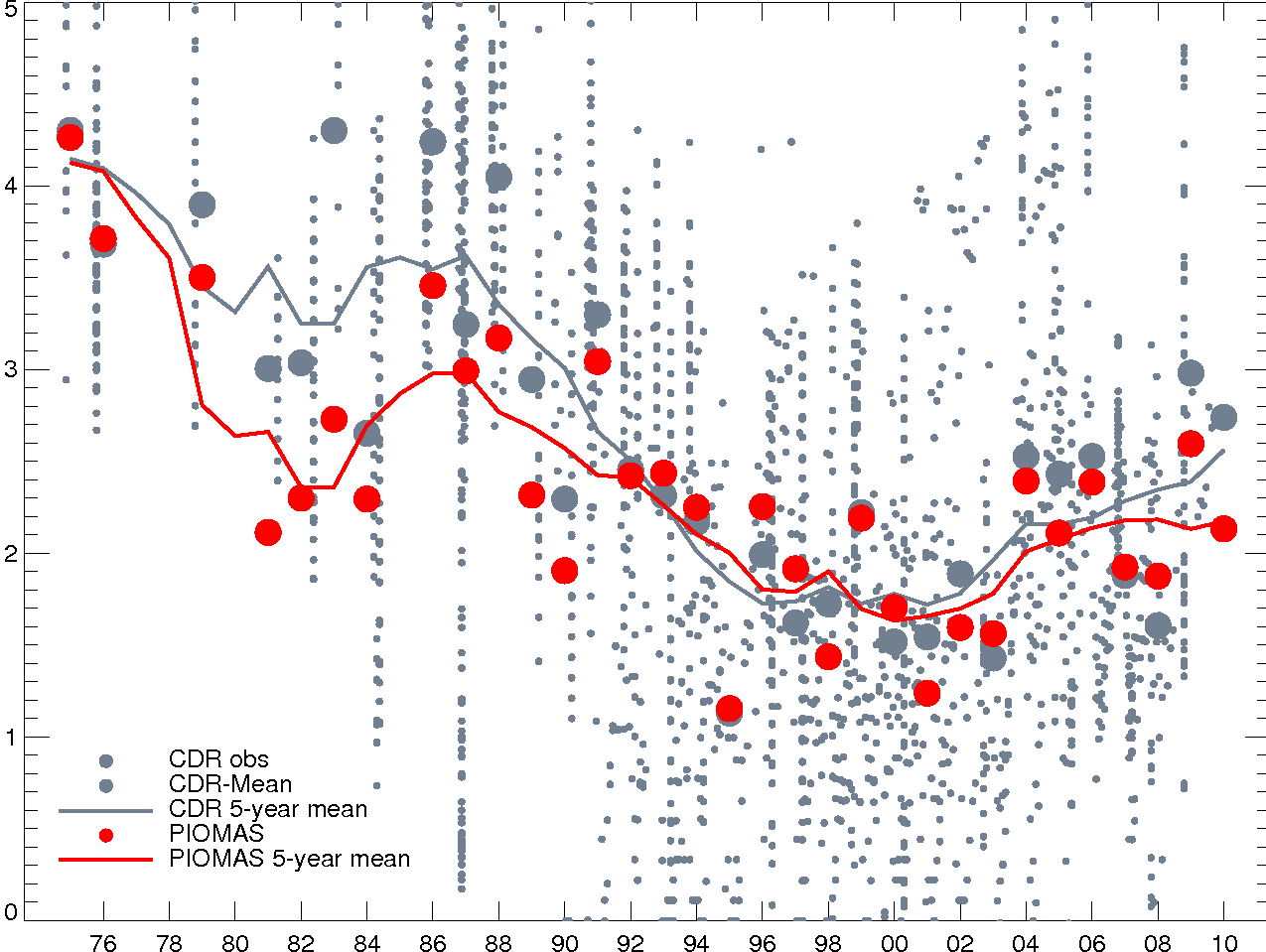
Figure 2 Naïve sea ice thickness time series. Sea ice thickness observations from the sea ice thickness climate data record (small grey dots), averages for all observations in a given year (large grey dots), and 5-year running mean through those observations. The same calculation for the corresponding PIOMAS simulations at the location and time of observation is shown by the big red dots and line.
Before those claiming that global warming stopped in 1998 have a field day with this figure, they should appreciate that our total volume time series and the naïve thickness time series are entirely consistent. The sampling issues arise from the fact that sea ice is highly dynamic with lots of spatial and seasonal variability so that measurements from individual moorings, submarine sonar tracks, and aircraft flights can only construct an incomplete picture of the evolution of the total Arctic sea ice volume. Progress towards establishing ice thickness records from satellite (ICESat, Envisat, and CryoSat-2) will change this over time, but these sources won’t yield a record before these measurements began and satellite retrievals of ice thickness have their own issues.
PIOMAS is not normally run as a freely-evolving model, but rather it assimilates observations. Ice concentration and sea surface temperature are currently assimilated and we have experimented with the assimilation of ice motion (Zhang et al. 2003, Lindsay et al. 2006). Assimilation helps constrain the ice extent to observations and helps improve the simulation of sea ice thickness. Ice thickness observations are not assimilated into the model. Instead, ice thickness and buoy drift data are used for model calibration and evaluation. So using a model constrained by observations is quite possibly the best we can do to establish a long-term ice volume record.
Model calibration is of course necessary. We need to determine parameters that are not well known, deal with inadequately modeled physics, and address significant biases in the forcing fields. Parameters changed in PIOMAS calibration are typically the surface albedo and roughness, and the ice strength. Once calibrated, the model can be run and evaluated against observations not included in the calibration process. Evaluation does not only mean showing that PIOMAS says something useful but also establishes the error bars on the estimated ice thickness. To establish this uncertainty in the ice-volume record (Schweiger et al. 2011), we spent a significant effort drawing on most types of available observations of ice thickness thanks to a convenient compilation of ice thickness data (Lindsay, 2010). We have also compared PIOMAS estimates with measurements from ICESat and conducted a number of model sensitivity studies. As a result of this evaluation our conservative estimates of the uncertainty of the linear ice volume trend from 1979-present is about 30%. While there is lots to do in improving both measurements and models to reduce the uncertainty in modeled ice volume, we can also say with great confidence that the decline in observed ice thickness is not just an effect of measurement sampling and that the total sea ice volume has been declining over the past 32 years at astonishing rates (for instance a 75% reduction in September volume from 1979 to 2011).
Prediction
The seasonal prediction issue and the prediction of the long-term trajectory are fundamentally different problems. Seasonal prediction, say predicting September ice extent in March, is what is called an initial value problem and the September ice extent depends both on the weather, which is mostly unpredictable beyond 10 days or so, and the state of the ocean and sea ice in March. Improving observations to better characterize that state, and improving models to carry this information forward in time is our best hope to improve seasonal predictability. The prediction of the long-term trajectory, depends on the climate forcing (greenhouse gases, aerosols, solar variability) and how the model responds to those forcings via feedbacks. A recent model study showed that the crossover between initial-value and climate-forced predictability for sea ice occurs at about 3 years (Blanchard-Wrigglesworth et al. 2011). In other words, a model forgets the initial sea ice state after a few years at which point the main driver of any predictable signal is the climate forcing. In fact, coupled model simulations have shown that even removing all the sea ice in a particular July has little lasting impact on the trajectory of the ice after a few years (Tietsche et al. 2011).
PIOMAS has been run in a forward mode (and hence without data assimilation) to yield seasonal predictions for the sea ice outlook (Zhang et al. 2008) and has also provided input to statistical forecasts (Lindsay et al. 2008) and fully-coupled models. We have also done experiments with PIOMAS in a climate projection mode by scaling atmospheric forcing data from a reanalysis to 2xC02 projections from the CMIP3 models (Zhang et al. 2010). This setup provides more realistic wind fields and spatial thickness distribution but cannot account for important atmosphere-ocean feedbacks.
Global climate model projections (in CMIP3 at least) appear to underestimate sea ice extent losses with respect to observations, though this is not universally true for all models and some of them actually have ensemble spreads that are compatible with PIOMAS ice volume estimates and satellite observations of sea ice extent. With error bars provided, we can use the PIOMAS ice volume time series as a proxy record for reality and compare it against sea-ice simulations in global climate models. This provides another tool in addition to more directly observed properties for the improvement and evaluation of these models and is in our view the best use of PIOMAS in the context of predicting the long-term trajectory of sea ice.
Predictions of a seasonally ice-free Arctic Ocean
The eventual demise of the summer sea ice is a common feature of nearly every climate model projection (the exceptions are models with very inappropriate initial conditions). But the question of when the Arctic will be ‘ice-free’ is imprecise and calls for a clear definition of what ice-free means. Does it mean completely ice-free, or is there a minimum threshold implied? Does it mean the first time the summer sea ice goes beneath this threshold or does it imply a probability of encountering low-ice conditions over a period of time? (e.g. high likelihood of Septembers with less than 106 km2 of ice in a 10-year period). Regardless of whether the concept is actually useful for any practical purpose (say for planning shipping across the Arctic), it is nevertheless a powerful image in communicating the dramatic changes that are under way in the Arctic.
Once defined, predictions of when an ice-free Arctic will occur seem justified. In the published literature there are several papers specifically targeting such predictions (Zhang and Walsh, 2006, Wang and Overland, 2009, Boe et al. 2009, Zhang et. al. 2010) while others include discussion about the timing of ice-free summers (e.g. Holland et al. 2006). Some address the fact that the CMIP3/IPCC AR4 simulations show sea ice declines less rapid than the observations and attempt to correct for it. Published projections, though with varying definitions of what constitutes ice-free, all project an ice-free Arctic ocean somewhere between 2037 (Wang and Overland, 2009) and the end of the century. Predictions of earlier ice-free dates so-far seem to be confined to conference presentations, media-coverage, the blogosphere, and testimony before to the UK parliament.
Extrapolation
A different class of predictions are based on simple extrapolation using historical sea ice extent, concentration, or volume. An example is included in the materials presented by the so-called ‘Arctic Methane Emergency Group’ who show extrapolations of PIOMAS data and warn about the potential of a seasonally ice-free Arctic ocean in just a few years. So does it make sense to extrapolate sea ice volume for prediction? In order to do a successful extrapolation several conditions need to be met. First, an appropriate function for the extrapolation should be chosen. This function needs to either be based on the underlying physics of the system or needs to be justified as appropriate for future projections beyond just fitting the historical data.
But what function should one choose? Since we don’t really have data on how the trajectory of the Arctic sea ice evolves under increased greenhouse forcing, model projections may provide a guide about the shape of appropriate function. Clearly, linear, quadratic or exponential functions do not properly reflect the flattening of the trajectory in the next few decades seen for example in the CCSM4 (Fig 3). The characteristic flattening of this trajectory, at first order, arises from the fact that there is an increasingly negative (damping) feedback as the sea ice thins described by Bitz and Roe (2004) and Armour et al. (2011). The thick ice along the northern coast of Greenland is unusually persistent because there are on-shore winds that cause the ice to drift and pile-up there. So extrapolations by fitting a function that resembles a sigmoid-shaped trajectory may make more sense, but even that, as shown in the figure, yields a much earlier prediction of an ice-free Arctic than can be expected from the CCSM4 ensemble.
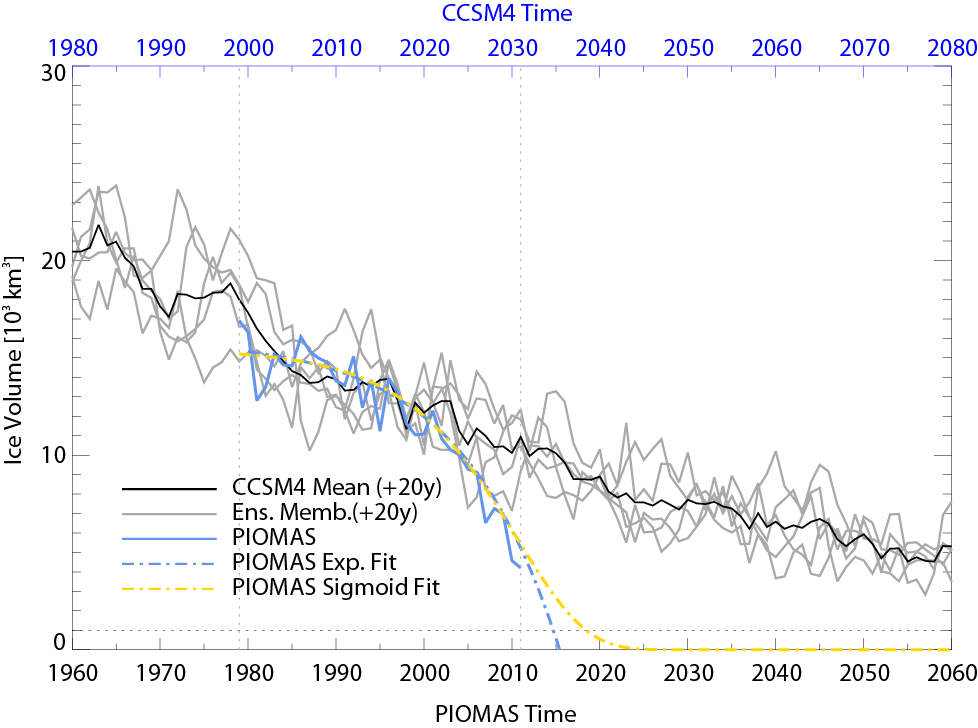
Figure 3. CCSM4 AR4 ensemble and PIOMAS September mean arctic ice volume. Exponential and sigmoid (Gompertz) fits to PIOMAS data are shown. Note that the 1979-2011 September mean of the CCSM4 ensemble has about 30% higher sea ice volume than PIOMAS. To visualize the difficulty in choosing an appropriate extrapolation function based on PIOMAS data we shifted the CCSM4 time series forward by 20 years to roughly match the mean ice volume over the 1979-2011 fitting period.
But there is a second issue that may foil prediction by extrapolation: The period over which the function is fit must be sufficiently long to include adequate long-term natural variability in the climate system. The goodness of fit over the fitting period unfortunately may be misleading. Whether or not this is the case for sea ice extent or volume is an open question. The sea ice trajectory shows considerable natural variability at various time scales on top of the smoother forced response to changes in greenhouse gases. Periods of rapid decline are followed by slower periods of decline or increases. By fitting a smooth function to a sea ice time series (e.g. PIOMAS) one might easily be tempted to assume that the smooth fit represents the forced (e.g. greenhouse) component and the variation about the curve is due to natural variability. But natural variability can occur at time scales long enough to affect the fit. We have to remember that part of the observed trend is likely due to natural variability (Kay et al. 2011, Winton, 2011) and may therefore have little to do with the future evolution of the sea ice trajectory. This is visualized in figure 4 where ensemble members from the CCSM4 AR4 runs are fit with S-shaped (Gompertz) functions using the 1979-2011 period to estimate the parameters. The differences between the ensemble members, reflecting natural variability, yield vastly different extrapolated trajectories. Natural variability at these time scales (order of 30 years) may very well make prediction by extrapolation hopeless.
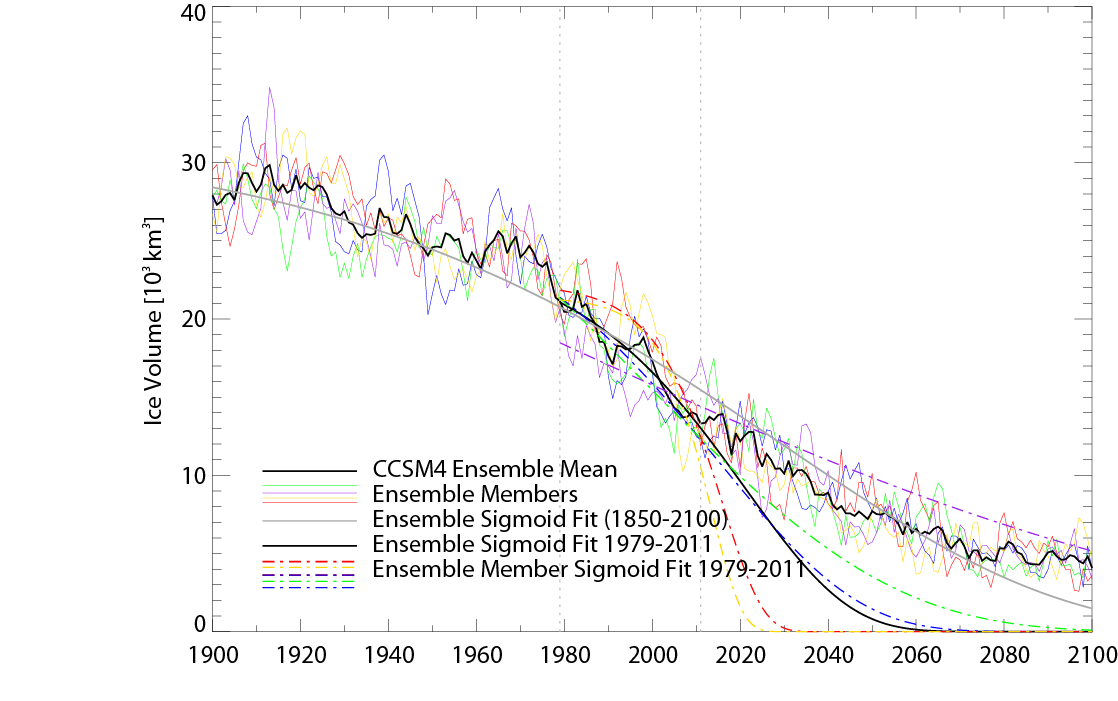
Figure 4. CCSM4 AR4 ensemble with sigmoid (Gompertz) fits. Light vertical lines represent fitting period for ensemble members (1979-2011).
In summary, we think that expressing concern about the future of the Arctic by highlighting only the earliest estimates of an ice-free Arctic is misdirected. Instead, serious effort should be devoted to making detailed seasonal-to-interannual (initial-value) predictions with careful evaluations of their skill and better estimates of the climate-forced projections and their uncertainties, both of which are of considerable value to society. Some effort should also target the formulation of applicable and answerable questions that can help focus modeling efforts. We believe that substantially skillful prediction can only be achieved with models, and therefore effort should be given to improving predictive modeling activities. The best role of observations in prediction is to improve, test, and initialize models.
But when will the Arctic be ice free then? The answer will have to come from fully coupled climate models. Only they can account for the non-linear behavior of the trajectory of the sea ice evolution and put longer term changes in the context of expected natural variability. The sea ice simulations in the CMIP5 models are currently being analyzed. This analysis will reveal new insights about model biases, their causes, and about the role of natural variability in long-term change.It is possible that this analysis will change the predicted timing of the “ice free summers” but large uncertainties will likely remain. Until then, we believe, we need to let science run
its course and let previous model-based predictions of somewhere between “2040 and 2100″ stand”
References
Bitz, C. M., and G. H. Roe (2004), A mechanism for the high rate of sea ice thinning in the Arctic Ocean, J Climate, 17(18), 3623-3632.
Boe, J. L., A. Hall, and X. Qu (2009), September sea-ice cover in the Arctic Ocean projected to vanish by 2100, Nature Geoscience, 2(5), 341-343.
Hibler, W. D. (1980), Modeling a Variable Thickness Sea Ice Cover, Monthly Weather Review, 108(12), 1943-1973.
Holland, M. M., C. M. Bitz, and B. Tremblay (2006), Future abrupt reductions in the summer Arctic sea ice, Geophys. Res. Lett, 33(23), 5.
Johnson, M., et al. (2012), Evaluation of Arctic sea ice thickness simulated by Arctic Ocean Model Intercomparison Project models, J. Geophys. Res., 117, C00D13.
Kay, J. E., M. M. Holland, and A. Jahn (2011), Inter-annual to multi-decadal Arctic sea ice extent trends in a warming world, Geophys. Res. Lett, 38.
Lindsay, R. W. (2010), New Unified Sea Ice Thickness Climate Data Record, Eos Trans. AGU, 91(44), 405-416.
Lindsay, R. W., J. Zhang, A. J. Schweiger, and M. A. Steele (2008), Seasonal predictions of ice extent in the Arctic Ocean, J.Geophys.Res., 113(C2), 11.
Lindsay, R. W., and J. Zhang (2006), Assimilation of ice concentration in an ice-ocean model, Journal of Atmospheric and Oceanic Technology, 23(5), 742-749.
Rothrock, D. A., Y. Yu, and G. A. Maykut (1999), Thinning of the Arctic sea-ice cover, Geophys. Res. Lett, 26(23), 3469-3472.
Schweiger, A. J., R. Lindsay, J. Zhang, M. Steele, H. Stern, and R. Kwok (2011), Uncertainty in modeled Arctic sea ice volume, J. Geophys. Res., 116, C00D06.
Tietsche, S., D. Notz, J. H. Jungclaus, and J. Marotzke (2011), Recovery mechanisms of Arctic summer sea ice, Geophys. Res. Lett, 38.
Thorndike, A. S., D. A. Rothrock, G. A. Maykut, and R. Colony (1975), Thickness Distribution of Sea Ice, J.Geophys.Res., 80(33), 4501-4513.
Wang, M. Y., and J. E. Overland (2009), A sea ice free summer Arctic within 30 years?, Geophys. Res. Lett, 36, 5.
Winton, M. (2000), A reformulated three-layer sea ice model, Journal of Atmospheric and Oceanic Technology, 17(4), 525-531.
Winton, M. (2011), Do Climate Models Underestimate the Sensitivity of Northern Hemisphere Sea Ice Cover?, J Climate, 24(15), 3924-3934.
Zhang, J., D. R. Thomas, D. A. Rothrock, R. W. Lindsay, Y. Yu, and R. Kwok (2003), Assimilation of ice motion observations and comparisons with submarine ice thickness data, J.Geophys.Res., 108(C6), 3170, DOI: 3110.1029/2001JC001041
Zhang, J., and D. A. Rothrock (2003), Modeling global sea ice with a thickness and enthalpy distribution model in generalized curvilinear coordinates, Monthly Weather Review, 131(5), 845-861.
Zhang, X. D., and J. E. Walsh (2006), Toward a seasonally ice-covered Arctic Ocean: Scenarios from the IPCC AR4 model simulations, J Climate, 19(9), 1730-1747.
Zhang, J., M. Steele, and A. Schweiger (2010), Arctic sea ice response to atmospheric
forcings with varying levels of anthropogenic warming and climate variability, Geophys.
Res. Lett, 37 (L20505)
It will be interesting to see which “skeptic” site or blog will be the first to show your naïve sea ice thickness time series WITHOUT the accompanying caveat, and maybe even use it to accuse POIMAS of cheating in preparing their volume trends.
Can’t see figure 3 at all. Not even a gap where the image should be.
(Firefox)
[Response: Fixed. – gavin]
can’t see Fig 3. Maybe it’s my browser, I can see the others. Nice post.
Sea ice thickness varies by many many factors, from ocean salinity, temperatures, sea temperature convection, mirrored by atmospheric similar variations from above, is a complex issue made simple by the equation result in the form as simple as frozen water, we try to reverse engineer this result without having all the equation variables at every spot over an extremely wide area.
Given that there this much work about sea ice which will take a while to resolve, there is another method of sensing its decline, another equation like the one giving ice thickness which has nothing to do with looking at the sea. Another way would be to look at boundary layers, which are no mere strictly local product, but rather the result of the ice to air dynamic. This I literally do. It agrees that there are natural variations, but the whole underlying trend is that low troposphere boundary layers are rapidly changing looking like Southward ones. I again emphasize that a comprehensive compilation of Upper air low thermal layer trends will show what I mean… But there is another way, more powerful and sensitive than with radio sondes.. More on this in a few weeks. Mean time why not study boundary layers while having fun with a good mystery like the Titanic? http://eh2r.blogspot.ca/ We the people of “unsinkable earth” of infinite resources need to study.
I wonder, given the arguments presented here that six month projections are weather and three year projections are climate, if the sigmoid is properly applied to September ice volume? The amplitude of the April to September variation seems fairly steady so far suggesting that weather influences are not changing all that much. The slopes shown in fig. 1 are similar and if anything are divergent rather than convergent as an emergent sigmoid behavior in September would require.
Might in not be better to introduce a effective negative ice volume of warmer water that delays in refreezing to produce the April maximum? Then the problem of trying to meet zero volume with an artificial fitting function would not provide and artificial constraint. In that case, linear extrapolation could be performed. Extrapolating based on date from 1980 to the present yields and estimate around the 2040 for zero September ice volume while using an apparent steeper trend since 2000 yields an estimate around 2015 for the lower curve in fig. 1 or around 2020 using the upper curve as a guide.
The argument about piling up seems a little weak to me. You need a source to pile from, and that source is diminishing according to the upper curve in fig. 1. Sigmoids certainly do occurs in nature. But, I’d expect it to turn up in the April data eventually rather than the September data simply because the September data is mostly dependent on the April data as an initial condition and we certainly do not expect that drop to level off anytime soon. Shallow coastal waters that cool quickly may provide lingering April ice in the Arctic in 120 years or so, justifying a sigmoid treatment of the source function at that time, but perhaps it is not appropriately applied to September data now.
One could do worse than to quote Mark Twain:
“In the space of one hundred and seventy-six years the Lower Mississippi has shortened itself two hundred and forty-two miles. That is an average of a trifle over one mile and a third per year. Therefore, any calm person, who is not blind or idiotic, can see that in the Old Oolitic Silurian Period, just a million years ago next November, the Lower Mississippi River was upwards of one million three hundred thousand miles long, and stuck out over the Gulf of Mexico like a fishing-rod. And by the same token any person can see that seven hundred and forty-two years from now the Lower Mississippi will be only a mile and three-quarters long, and Cairo and New Orleans will have joined their streets together, and be plodding comfortably along under a single mayor and a mutual board of aldermen. There is something fascinating about science. One gets such wholesale returns of conjecture out of such a trifling investment of fact.”
– Life on the Mississippi
[Response: Wonderful. Thanks for the quote. – axel]
Chris,
The piling up comes mostly from the Greenland glaciers, with minor contributions from other land forms. These will remain long after the Arctic becomes ice-free. The winds and currents will have an even greater impact as the ice retreats from open areas near the North Atlantic towards the Canadian islands.
Figure 4 may be the most telling, with 2040 being an extreme low end for estimates of an ice-free Arctic.
Ray,
I like the analogy. I reminds me of the headlines in my hometown when the annual murder rate increased 100%. Two people were killed that year.
Also good to remember is that there is a high probability that the effects of Arctic sea ice decline are felt before the Arctic becomes effectively ice-free (below 1 million km2 sea ice area at the end of a melting season). And it’s those effects that are interesting to us, not some satellite picture showing a small blot of ice north of Greenland and Ellesmere Island (however spectacular a sight it will be).
Excellent article. I was just speaking with someone yesterday about the difference between possibility and probability regarding arctic ice. At least now I can speak with slightly more understanding of the difficulties in predicting when.
The take away here is that ‘if it be not in the morrow then it be yet to come’.
We did something rather ‘big’ here.
It should be noted that there is such a mismatch between the ice volume shown in the lower curve in fig. 1 and that shown in fig. 4 that is seems unlikely that they represent the same time period. According to the PIOMAS website, the average ice volume in September between 1979 and 2010 was 12,300 km^3 in apparent agreement with fig. 1. In the models shown in fig. 4 however, the corresponding value appears to be about 18,000 km^3. This suggests that the extrapolations in fig. 4 are not for an ice-free September, but perhaps for an ice-free July. If we are not comparing apples with apples, worries about fitting functions are a little premature. It is virtually certain that the first ice-free July will occur some years later than the first ice-free September. Earlier projections for September are not inconsistent with later predictions for July and there seems to be little evidence for the perils indicated in the title.
Dan, do you have a source for your contention that “piling up comes mostly from the Greenland glaciers, with minor contributions from other land forms”?
It’s in direct contradiction to the post, which specifically states that:
“The thick ice along the northern coast of Greenland is unusually persistent because there are on-shore winds that cause the ice to drift and pile-up there.”
A quick Google search didn’t provide any support for your suggestion, though it did turn up a blog which may well be of interest to watchers of the Arctic sea ice:
http://icyseas.org/tag/greenland/
And of course, the implication would be that most of the sea-ice along the northern coast of Greenland originates as glacial ice, becomes part of an ice shelf, then calves off to become sea ice. To engage in a little hand-waving of my own, that seems highly implausible to me–the areas of ice shelf are much smaller than the area of sea ice.
Relevant:
http://journals.cambridge.org/action/displayAbstract;jsessionid=EFBE60832F058E258DF1AABF4D5BC289.journals?fromPage=online&aid=5415316
http://www.sciencedirect.com/science/article/pii/S0277379110002994
http://nsidc.org/cryosphere/sotc/iceshelves.html
In general, my impression is that your suggestion is an instance of “the tail attempting to wag the dog.” Of course, I’m open to actual evidence suggesting otherwise–though perhaps a tad skeptical that it will be forthcoming. ;-)
Ah, now I can see fig. 3. An arbitrary time-shift has been introduced to deal with the volume mismatch I noted above. Yet, even so, the data diverge rather dramatically and significantly from the models. This most likely suggests a deficiency in the models. It would be good to know how much volume they predict in April. In any case, they do not seem to have skill yet and do not seem useful for extrapolation for this purpose. If the authors had adopted a volume shift rather than a time-shift, the models would predict zero ice volume around 2060. But, the models still would not get the observed slope right. So, again, what perils?
[Response: Chris, I agree that the mismatch in total volume suggests that the CCSM4 overestimates the total ice volume. I am much less sure that the divergence between the PIOMAS ice volume and the CCSM4 ensemble mean (after shift) has anything to say about the whether CCSM4 is deficient or not. For the first 20 years of the time series PIOMAS and the CCSM4 ensemble mean track very well. For the last 10 years CCSM4 PIOMAS shows a steeper decline. Is this because of a deficiency in CCSM4 or maybe because natural variability gave us a particularly steep decline in sea ice over the last 10 years? A comparison of reality with the ensemble mean is not the measure by which to judge this. A comparison of observed sea ice decline with the model ensemble spread can tell us only how likely an observed trend is relative to that ensemble. See the Winton 2011 reference for an attempt to assess whether or not the observed sea ice time series fits with expected declines from the coupled models.
The real difficulty is how we assess whether or not a model represents the natural variability correctly at the relevant time scales. With only 30+ year time series of sea ice extent or volume, this is something difficult to do so we have to strive to construct longer time series that allow an assessment of natural variability at those times scales.
It takes a modeler to say something like that, but it was explained it to me may years ago like this: “Reality is only one realization of an ensemble”. It has worked for me. – axel]
This is–I belatedly add–an excellent article–informative, provocative and judicious.
I must admit to a gnawing feeling of unease, though. (Of course, “feelings,” whether of unease or anything else, have no standing in the court of scientific validity. But, as Hank likes to say of himself, “I’m just a guy on a blog.”) From the post, the decline in volume is real, and has been occurring over much longer than the 3-year ‘period of memory’ for sea-ice.
But record of volume is not just an abstract dataset, of course. Given the large energies associated with phase change, it’s also a proxy for the whole Arctic heat budget. Viewed in that way, the data says that the Arctic is warming even more in terms of heat content than we would think, based upon purely thermometric considerations.*
That in turn begs the question, what is driving this imbalance? I presume that we don’t know that in detail yet, since if we did we would have a model that would be highly consistent with the observations–a robust one, perhaps I should say. But it does make one wonder, why the apparent consistency despite the variability on short timescales? Could the “heat imbalance” reverse sign for more than a year or two? (Clearly it must have (virtually, of course) in Tietsche et al. (2011.))
Or is this imbalance more highly determined (perhaps I should say “tightly constrained?”)–in which case extrapolation won’t prove such a bad guide in the present case after all, (appropriate) cautions above notwithstanding.
*I should acknowledge that this isn’t my idea; I first encountered it as presented by Gareth Renowden, of “Hot Topic.” Even blog science can cite…
Chris Dudley: “It is virtually certain that the first ice-free July will occur some years later than the first ice-free September.”
Why do you say that? Anyone with any experience should recognize that the first ice-free conditions will arise due to a confluence of factors – just as the first ocean waves covering drowning Pacific islands will be due to a unique confluence of factors – tides + winds + global warming. Later on, the condition will become ‘normal’, as warming progresses throughout the end of this century (and we can be sure of that, just not the degree of warming).
So, it all depends on weather and ocean current conditions in the Arctic through the summer, and as all know, those are not very predictable from week to week, and Arctic subsurface ocean temps are poorly monitored at best. Hence, there’s no way of telling in advance if the first completely ice-free week will be in September or July – and it really doesn’t matter which. It will arrive, you can be sure of that.
Hi Ike (#15),
Good to hear from you. The change in volume between July and September is about 6000 km^3, about 2000 more than the recent difference between the September ice volume and ice-free http://psc.apl.washington.edu/wordpress/wp-content/uploads/schweiger/ice_volume/BPIOMASIceVolumeAnomalyCurrentV2_CY.png?%3C?php%20echo%20time%28%29?
The annual curve is pretty repeatable in shape so September does seem like the first month that will be ice-free.
I see another conceptual difficulty here. If one invokes low frequency natural variability to argue against a near term projection, one has to get the low frequency variation to operate at high frequency in order to act in time to counter the short term projection. But, since it had to be low frequency to escape detection in the data, it can’t really do that. It would be better to argue that high frequency variability is not well estimated than to invoke low frequency variability in this situation.
#12 Kevin McKinney
Re. #7 Dan H.
Kevin, Dan H. is suffering from an orificial conflation issue pertaining to his locution on climate issues that may be congenital, but most likely includes nurture influences. From which orifice one speaks from is relational to ones talent in manifesting the Dunning/Kruger effect. In this, my opinion is that Dan H. is quite an expert, though likely without cognition of his ability in this area. Orifice loquation origination issues should be a new field of social psychology study though, as quantification in this area may help us choose politicians and teachers better in the future.
Dan H’s perception of where the ice is piling up from seems to be analogous to other piles that do pile up when one speaks from a particular orifice, analogically speaking of course.
The kinder interpretation is he is ‘speaking out of his hat’.
“Ice free” is important symbolically, navigationally and biologically but from the point of view of energy doesn’t a residual volume of “fixed” ice which doesn’t melt come to much the same thing? If summer energy input is no longer going towards melting sea ice it’ll go elsewhere. Where? Melting land ice sheets or warming the water?
#18–Ah, I see. Speaking “ex galerus,” as one–the linguistically ingenious J.K Rowlings, perhaps?–might say.
“J.K Rowlings”–er, or her better-known alter ego, “J.K Rowling.”
Given the spectacular failure before ~2007 of the entire (relevant) scientific community to predict the very rapid decline in Arctic sea ice volume, there is indeed cause for humility in the expressing certainty in such predictions.
Even before I read the allusion to it above, the whole thing strikes me as if careful observers on the deck of the Titanic, having calculated carefully how soon the ship would hit the iceberg and subsequently sink, are suddenly surprised by the sudden jolt shuddering the whole ship. So now they are busily recalculating the range of possible moments at which the ship will actually sink, a calculation they want to get just right before presuming to prescribe any particular course of action to the ship’s policy makers.
I would humbly suggest that, while continued accurate measurements are always wonderful to have, the screamingly obvious main priority is loudly call for all to rapidly abandon ship–leave deadly fossil fuels behind and quickly climb into the lifeboats of efficiency, vastly reduced consumption, renewables, and population reduction.
But perhaps that’s just me.
Excellent article. Well reasoned and balanced. Quite a contrast to notable skeptics such as Joe Bastardi, who continues to suggest that the current downward trend in Arctic sea ice is simple cyclical thing and that there is no ice-free Arctic anywhere in our future whether it be 40 years or 240 years. I suggested to Joe that he really ought to stick with his weather forecasting and leave climate modeling and sea ice forecasts to others more suitably qualified.
On my blog I’ve been very critical of the extrapolation based claims of a rapid transition to a seasonally sea-ice free state. It’s good to read key issues being raised here in the main post. I’m still of the opinion that the extrapolation of data is useless.
However recently I’ve found myself wavering on the issue of how fast we’ll see a transition to a virtually sea ice free state (less than 1M km^2 off the Canadian Arctic Archipelago and the north of Greenland) and it’s because of the PIOMAS volume results. Rather than link to my blog posts, which were written as I worked on this issue so aren’t as succinct as they could be, I’ll summarise here.
The following is the PIOMAS volume series from 2000 to 2011.
http://farm8.staticflickr.com/7203/6801022094_7515a74805_o.jpg
This shows two step drops, one in 2007 being the result of the crash of that year, the other in 2010. These step drops are not exceptional in the full context of 1979 to 2011, however there are other facets that make 2010 worthy of note.
The 2010 and 2011 drops are due to a substantial volume loss in the Spring. The following graphic is of daily volume anomaly using the baseline of 1980 to 1999.
http://farm8.staticflickr.com/7069/6968923365_eb271a75ce_o.jpg
Prior to the 2000s the volume anomalies show drops at various times throughout the year. The coincident Spring volume losses of 2010 and 2011 stand out in the series from 1979. Using the naive calculation of thickness from the Cryosphere Today area index it can be seen that, if real, these volume losses imply a substantial loss of thickness.
http://farm6.staticflickr.com/5196/7057061699_b9858e2d07_o.jpg
The red line being around the date of area minima for 2010 & 2011. Such an impact should be apparent to those on the ground, as of now I can’t find anything to corroborate or disprove this.
Using PIOMAS and Cryosphere Today to calculate the thickness shows the impact of the last two years.
http://farm8.staticflickr.com/7184/6968947697_28a4be7b83_o.jpg
In the above figure you can ignore ExtentThickness as I’ve moved over to calculating AreaThickness, using area alone. Kevin O’Neill (a commenter at my blog) and I have been referring to the relatively flat area through the Summer as the ‘roof’. Its implication being that during the Summer volume loss has been largely accounted for by loss of area, hence thickness changes little. However in 2010 and 2011 this changed, with loss of thickness being ‘needed’ to account for the loss of volume. As the above graph shows this is unusual behaviour in the context of the full PIOMAS series.
Using NCEP/NCAR reanalysis the only weather that stands out as being anomalous is a high pressure system over the Arctic in 2010 presumably related in some way to high temperatures. However as the area was ice covered at that time increased insolation wouldn’t have caused high temperatures, although inflow of air or large leads/polnyas could. Spring 2011 was rather unremarkable from what I can see.
Temperature.
http://farm8.staticflickr.com/7036/6947128357_bf92588c05_o.png
Pressure.
http://farm8.staticflickr.com/7055/6801021974_319c834f2d_o.png
The reason I’ve found myself wavering on a fast transition is that I can’t find a prosaic explanation for these ‘observations’.
Can anyone suggest what is happening here?
I have heard that Dr. Maslanek projected that the Arctic would be ice free between 2013 and 2019. You did not refer to this projection in your article. Was this ever published? What do you think of this model?
How does PIOMAS account for changes in the amount of heat coming into the Arctic from ocean currents? Recent articles suggest that the heat content of the currents in the Fram strait have increased in recent years. Do these currents affect the ice significantly or is the heat content of the currents too small to affect the ice. Where does this heat go? Can you suggest a review article about heat contents of currents into the Arctic?
Excellent article. It is really good to see what real scientists think about the sea ice. Write a summary post for the sea ice blog.
Well, if it were real water cooler discussion, we would see more sea ice, wouldn’t we?
> Maslanek
This one?
Summer 2001: http://airbornescience.arc.nasa.gov/sites/default/files/documents/ASP_Smr11_nsltr_v1.pdf
“Dr Jim Maslanek of the University of Colorado, Boulder to observe
the “Spatial and Temporal Variability of Ocean and Ice Conditions In and Near the Marginal Ice Zone”
Possibly you mean Maslowski?
http://scholar.google.com/scholar?hl=en&q=naval+postgraduate+school+arctic+sea+ice&as_sdt=1%2C5&as_ylo=2012&as_vis=1
I’ve long suspected that anthropogenic black carbon (and possibly other dark aerosols) are responsible for some of the downward trend. Do the necessary albedo adjustments to PIOMAS show any time trend? If so, is it possible to estimate how much annual melting could be averted if black carbon emissions were curtailed? Are there other methods for estimating the magnitude of the effect?
[Response:There is little evidence that ‘black carbon’ is responsible see: http://www.atmos.washington.edu/~sgw/PAPERS/2010_Doherty_ACP.pdf. There are no time dependent adjustments in PIOMAS. Those adjustments are fixed for all time steps. – axel]
#25–Dr. Maslowski in 2008. Notice that this presentation–which is not a peer-reviewed paper–extrapolates the possibility (not a prediction!) of an ice-free Arctic as soon as 2013.
http://www.ees.hokudai.ac.jp/coe21/dc2008/DC/report/Maslowski.pdf
IIRC, the projection was refined to a sub-million km2 minimum in 2016, +/- 3 years.
Also:
http://meetings.copernicus.org/www.cosis.net/abstracts/EGU2008/06425/EGU2008-A-06425.pdf
This one just says “in the near future.”
More detail on this topic is given by this article from Joe Romm:
http://thinkprogress.org/climate/2011/05/19/208088/arctic-sea-ice-volume-death-spiral/
He traces this back to 2006.
TYPO! (mine): this is for Summer 2011, not 2001:
Maslanek http://airbornescience.arc.nasa.gov/sites/default/files/documents/ASP_Smr11_nsltr_v1.pdf
If we are to lend credence to Recovery mechanisms of Arctic summer sea ice, by Tietsche et al, shouldn’t the arctic have ‘recovered’ after 2007? While we saw a brief upward blip in September extent in 2008 -2009, volume losses continued. There was no recovery.
As Chris Reynolds points out in comment #24, there has been a significant change in the ‘average thickness’ graph (where average thickness is simply calculated by PIOMAS volume / CT area). It’s not just that the ice is thinner, but that the shape of the graph has changed. Prior to 2009 volume and area decreased at the same rate through most of the melt season, since then volume is decreasing at a faster rate than area during the summer months. The change is visually striking – where once there was a pulse waveform with discernible width there is now a sinusoidal waveform.
What Chris didn’t say (because neither of us has any idea of how to interpret it) is that if we take PIOMAS volume and divide it by EXTENT instead of area we get a different ‘thickness’ waveform. ‘Area thickness’ and’extent thickness’ each have their own characteristic waveshapes. These two totally different waveshapes have each morphed into the *same* waveshape today – essentially a sinusoid.
We may not be smart enough to know what it means – but we can definitely see that something has changed that no one is taking notice of or talking about.
[Response: That’s a misinterpretation of the word “recovery”. The paper simply demonstrates that if you remove the sea ice in July it will recover to the point where the current climate wants to have it. The earlier change in the 2010, 2011 thickness anomalies that Chris R. points out are very interesting. I would be careful though to attribute those to any “transition” of the system to some new state. We may have simply had a couple of warm springs as Chris R. shows.- axel]
This discussion indicates that we will have an ice free arctic in summer, no matter what human decisions are made ? Is that correct ?
ifso i am sad.
sidd
“In summary, we think that expressing concern about the future of the Arctic by highlighting only the earliest estimates of an ice-free Arctic is misdirected.”
I really don’t agree with this? Surely the precautionary principle argues that we ought to take the pessimistic estimates as a better planning basis than the model average? Given the probability that ice loss leads to existential threats by disrupting the weather patterns we rely on for agriculture – I don’t feel odds of 50/50 on being “right” are good enough in this case.
As I understand AMEGs statement they aren’t really making a forecast per se, more drawing attention to the fact that 1-2 years of above average melting could lead to loss of most of the ice and subsequent risk of both severe disruption to weather patterns and risk of a significant increase in methane emissions.
I remember only a few years ago people were talking about end of the century or later for ice loss – and as events unfold we seem to be rapidly reeling this estimate in closer – prudence would lead me to assume it best to take a pessimistic view in case we continue to shorten our estimates.
To be more clear – I appreciate the abstract scientific debate about this – but also believe we need to be planning effectively in the here and now, which means considering the worse end of the range to avoid being caught out!
[Response: Douglas, I have no issue with anyone providing a more “pessimistic” estimate. If anyone has one, they should explain their rationale, provide some assessment of the uncertainty, and subject their estimate to some review. That’s the scientific process. I don’t think we should bypass this process to achieve a particular political outcome. If someone can make a solid case for why the issues we mention are unimportant and that a skillful long-term estimate based on extrapolation of PIOMAS can be made, they should definitely go for it and let us know. We love to see our work put to good use. – axel]
I’m confused (again). Figure 1 shows ~4,000km3 in 2011 with a -3,100km3/decade trend. That leaves a linear trend to zero at ~2024. Figure 3 shows a PIOMAS trend hitting zero in 2015 (exponential) and 2023 (sigmoid)
Then, the last statement seems to toss PIOMAS in the dustbin by predicting 2040-2100. Are you guys saying PIOMAS is crap?
[Response: No. they are saying that extrapolation of complex non-linear systems using straight lines (or sigmoids etc.) are not reliable methods of prediction. – gavin]
Apologies if this has already been linked and I missed it. But Neven on his Arctic ice blog recently had post discussing the limits of curve fitting for making projections about Arctic ice volume that people might find interesting:
http://neven1.typepad.com/blog/2012/03/use-of-graphs.html
[Response: Yes, great post about the differences between blog posts and scientific testimony. – axel]
Hank:
You are correct, I meant Dr. Maslowski.
“If we are to lend credence to Recovery mechanisms of Arctic summer sea ice, by Tietsche et al, shouldn’t the arctic have ‘recovered’ after 2007?”
Not necessarily, no. As I recall the paper, it didn’t show that the ice would recover in some quasi-automatic fashion, it showed that it could recover from the ice-free state–that a seasonally ice-free Arctic is not a ‘tipping-point’ per se. (I believe earlier work reached the opposite conclusion; perhaps a moderator or knowledgeable commenter can elaborate?)
What the ice actually does in a particular year depends upon the ‘forcings’ (to misapply a term, perhaps) actually occurring–net ocean heat fluxes, net radiative fluxes, winds and currents (especially, but not exclusively, as they determine ice export to the North Atlantic.) As I recall Tietsche et al., the assumed post-ice-free ‘forcings’ were relatively conducive to recovery. (Again, I’d love to hear a better summation from those who know this topic better than me.)
Kevin,
I think you may have misunderstood the intent in my previous post. The sea ice does not originate in Greenland of any part of Canada. The references was to the landforms present in the Arctic which serve to shelter the ice from warmer ocean currents from the Atlantic. “piling up” occurs when the winds and currents push the ice landward, into cooler air and waters. Without the heat transport characteristics of the open Arctic, the sea ice cannot melt as readily as elseware. The NSIDC website has a nice visual on this:
http://nsidc.org/arcticseaicenews/category/analysis/
Excellent piece, thanks!
However, the final sentence, is somewhat unsatisfying. So sure, I get the argument that it’s not a particularly useful question to ask, but that won’t stop lots of people asking it, and there is some value in trying to answer it as honestly as possible.
So it seems you have a very conservative estimate from the CMIP ensembles, which are known to suffer from various weaknesses wrt sea ice, and which certainly don’t capture the trends over the last decade or so.
Then there’s models like PIOMAS, which, as you’ve argued, give us the best assessment over what has happened over the last couple of decades, but for which there are many problems with extrapolation.
You’ve argued that some extrapolations are more better than others, particularly those that take the physical properties of the ice into account; hence we should prefer a sigmoidal extrapolation rather than linear or polynomial.
But it really doesn’t then make sense, having weighed up all the strengths and weakness of each approach, to simply come to the conclusion that we should stick with the old CMIP projection of “between 2040 and 2100″. There is clearly enough evidence to at least add a caveat to say it *might* be much earlier. I think a more honest conclusion is projections based on PIOMAS are at odds with the CMIP projections, and at this point we don’t have enough evidence to prefer either.
[Response:Steve. Thank you. I think “might” has little useful scientific meaning. You’d have to assign some kind of probability threshold. Let’s say we define “might” as a 5% probability that the Arctic ocean is going to be ice free before 2040? How do you determine this probability? I can’t see a way other than looking at models. Coming up with this probability is a scientific problem that needs to be carefully pursued, will involve coupled models, and will take time. Dismissing the models as “biased” and extrapolating observations in our view is not a good alternative to this process (see also 13). – axel]
Gavin in #34,
But surely they have made at least one error here. The butterfly being wafted around by errant breezes and stirring up storms in Beijing with its wing flutters can still consider the usefulness of a liner extrapolation of the effect of the semitrailer 2 yards away and approaching at 80 mph. Invoking 30 year timescale variation to besmirch a 3 year projection is a little off base.
It also seems to me that insisting that the behavior of a demonstrably non-skillful model, CCSM4 AR4 runs, should be used as a guide is a little backwards. Why can’t the model get the volume right in hindcast rather than being off by 30% should be the first question. PIOMAS gets ground truthed by a large number of mechanisms. The free running models should be looking for unwarranted assumptions that may explain why they are off rather than insisting that the world should behave as they predict rather than as it does. They somewhat admit this but then proceed in that manner anyway.
Based on their choice of time-shift rather than volume shift to “correct” the models, I’d suspect that an assumption of lingering ice is built into the models. Perhaps it is assumed that piled ice always piles to the same thickness even if it comes from a thinner source, creating volume unphysically, or something of that sort. Surely we might be just as justified in subtracting 10000 km^3 from the model ensemble shown in fig 4. as a volume shift “correction” to match the 2011 volume minimum and get a number of realizations that are ice-free in short order, two even that would have been ice-free a couple years ago. Then, at least, the spread in the model runs could be put to some use.
It is the rare non-linear system that cannot be linearized usefully for at least the short term. That is why we use Taylor expansion so often.
[Response: Chris, See above in response to your 13. See also http://psc.apl.washington.edu/wordpress/wp-content/uploads/schweiger/ice_volume/validation/Fig13b.png for a comparison with the CCSM3 model for which no time shift was necessary. PIOMAS ice volume is reasonably within the ensemble spread of the CCSM3. The CCSM4 has a lot of natural variability which emphasizes our point: unless you can somehow quantify and separate the contributions of natural variability and forced variability to your observed time series, extrapolation will be problematic. This is of course less so for shorter projections than for longer ones. Why the CCSM4 is different than the CCSM3, whether or not models represent natural variability correctly, and whether the multi-model ensemble is a proper point of reference to measure the state of the art is a different debate. I think this debate needs to happen, it is happening. New predictions and improved models will come from it. I don’t think extrapolations are an adequate substitute for it.
If you think you can make a skillful long-term projection by extrapolation, I encourage you to show that you can. You’d probably have to go to the models to do so. If you come up with something, that would be a very interesting paper and I would be sure to cite it frequently. – axel]
#38–Yes, Dan, that’s a very different message than what you appeared to be saying in #7. Thank you for clarifying your point; I think that inclusion of the “glaciers” muddied the waters for me. (Surely the presence or absence of glacial ice doesn’t greatly affect the “piling up” of sea ice against the shore–or terminal ice shelf–by persistent wind and current out of the North?)
Anyway, what you apparently were trying to convey seems pretty consistent (as clarified) with both the post and with the NSIDC Arctic Analysis page you link to.
BTW, I don’t get why you characterize 2040 as “an extreme low end for estimates of an ice-free Arctic,” based upon Figure 4 of the present post; the earliest zero intercept looks to me to be about 2025. (That’s the sigmoid fit in yellow, and *everything* that hits zero in that figure is a sigmoid fit, if I’m reading correctly.)
Kevin,
I could see how my earlier post could be misinterpreted. Sorry about that.
True, the earliest intercept appears to be around 2025, but the highest is near the end of the century (using the 1979-2011 data). Estimates using the longer dataset are further into the future, due to the removal of natural fluctuations.
The simple curve fitting will treat all the sea ice as equal. However, as described in the article, that is not the case. Southern expansion into the North Atlantic and Bering Sea will encounter more heat exchange with the open ocean currents than the ice northward of Canada. Also, in mathematical terms, the volumetric loss will be tied to the amount of remaining ice. In order for the volumetric declines to keep pace with past calculations, the decline in sea ice area must accelerate. As the sea ice retreats, the volumetric losses must decrease, as shown in Figure 3. Hence the extrapolated fit to 2015, sigmoid fit to 2025, or other curves seem to be the outliers. I think is the main point of the article.
It is worth noting that in using a time-shift in fig. 3, 2040 in model years is shifted to 2020, the region of interest for early ice free conditions. However, Varvus et al. note that “CCSM4 simulates a hiatus in the secular Arctic climate trends during a decade-long stretch in the 2040s” http://www.cesm.ucar.edu/publications/jclim10/docs/vavrus.ccsm4.arctic_climatechange.pdf Thus, a time-shift of this model data set may be somewhat biased when applied to this particular question. However, having introduced the shift, allowing the 2070 estimate for ice-free conditions from CCSM4 to stand unaltered seems a little inconsistent. It should also be shifted to 2050.
One more thought on Varvus et al. While they report ice-free conditions occurring in 2070, examination of their fig. 2 reveals that this is for the model ensemble average. In particular realizations, ice-free conditions come an average of 7 years earlier (using their threshold). This is typical behavior of a descending trend with variability and eliminating the variability using the average introduces a bias. Thus, in consideration of comment #43 above, CCSM4 really predicts ice-free conditions in the early 2040s after the time-shift introduced in fig. 3 above.
In all, it would seem that models and extrapolations predict ice-free conditions between 2013 and 2045. The latter happens to agree well with a linear extrapolation of the 1979 to present PIOMAS data (though to zero and with no accounting of fluctuations; comment #5 above). Thus, extrapolation and modelling appear to agree after a few corrections to the model interpretation and perils were merely imagined.
In the spirit of the SEARCH Sea Ice Outlook, let me suggest that the Gompertz and other simple extrapolations be considered a class of black-box, naive models against which the predictions of more elaborate and theoretically better justified physical models can be compared. They’re null hypotheses that have not yet been rejected; hopefully (because they tend to look pessimistic) they will be rejected in time.
A second note: although extrapolations are often drawn as clean lines or curves that give the impression of an absolute cutoff at date X, they can be viewed probabilistically as well, with uncertainty also naively extrapolated from recent real-world behavior. See Figure 2 in this post (cited as the “blogosphere” link above) for an example applied to sea ice exten:
http://neven1.typepad.com/blog/2011/10/september-2011-sea-ice-extent-looking-ahead.html
Dan,
“The simple curve fitting will treat all the sea ice as equal.”
I like that comment because it throws into sharp relief how much information is disused if one simply takes one number–extent, area or volume–as description of the ice. A simplified picture, to say the least!
“Southern expansion into the North Atlantic and Bering Sea will encounter more heat exchange with the open ocean currents than the ice northward of Canada.”
‘Fraid you’re losing me again with this sentence. What southern expansion? If you just mean that there is greater potential for ice loss in the North Atlantic and Bering sectors than in some others, well, sure.
“Also, in mathematical terms, the volumetric loss will be tied to the amount of remaining ice. In order for the volumetric declines to keep pace with past calculations, the decline in sea ice area must accelerate.”
Logically, no–mathematically speaking, area could remain constant, and then volumetric decline would be exactly proportional to thinning.
On the other hand, if volumetric loss is a good proxy for Northward net heat fluxes, as discussed in my comment above, then we might expect the volumetric losses to remain relatively constant, in which case they would represent ever-greater proportions of the remaining ice. (I take it this expresses the relation between volume loss and total ice you are thinking about.)
But which variable–proportion of total ice, or volume loss–is really the independent one? I’ve just presented a physical rationale for considering the volume loss to be independent; do you have one for the opposite view?
“As the sea ice retreats, the volumetric losses must decrease, as shown in Figure 3.”
I don’t see that in Fig. 3, FWIW. The modeled loss trends do seem to decrease, possibly due to negative feedbacks, but if there’s a ‘must’ in there, it’s not self-evident to me.
#45,
That is a good point that you can simulate fluctuations in an extrapolation. And, it happens to illustrate why a sigmoid function is inappropriate in this situation. Fluctuations about the sigmoid would produce ice in September long after the source ice from April can’t survive past June. Fluctuations about a linear extrapolation, however, would not rise above zero in that case. Zero should not exercise any false tyranny here.
Kevin,
During this recent cold Alaskan/Kamchatkan winter, ice expanded further south into the Bering sea than in previous years. Once this starts to melt, we should see a larger drop in total sea ice.
http://kucb.org/news/article/bering-sea-ice-extent-breaks-records/
While in theoretical and mathematical terms, ice area could remain constant; in physical and practical terms, it will not. To visualize this, consider an ice cube in a glass of water. All dimensions are likely to melt at similar rates, such that the surface area and thickness will decrease proportionally. The volume, however, will decrease as a product of the area and thickness, such that a 10% decrease in both surface area and thickness, will result in a 19% decrease in volume. When 30% of the surface area and thickness have melted, 50% of the original volume is gone. The surface to volume area is increasing. The surface area is constantly exposed to the heat exchange processes, and independent of the starting value. Volume is dependent on the starting value. If surface area and thickness continue at a constant rate, then the volumetric loss must decrease, resulting in the sigmoidal curves. If volumetric losses remain constant, then surface area and thickness losses must accelerate. Does this make sense?
Since we have not measured accelerated sea ice area losses, the logical conclusion is that volumetric losses must be decreasing.
http://arctic.atmos.uiuc.edu/cryosphere/IMAGES/seaice.area.arctic.png
Dan H.,
As sea ice declines, we are left with some interesting competing effects. On the one hand, it will be colder,on average where we still have ice. Also, I’d expect the effects of black carbon to come into play less for more northern climes. On the other hand, the surface area to volume ratio will increase, as will the circumference to area ratio. The surface area to volume ratio means that an ever greater proportion of the ice is being irradiated, while the circumference to area ratio means more of the ice is being battered/warmed by the oceans areound it. This ought to be especially significant as ice withdraws and the oceans lower albedo leads to more absorption of sunlight earlier in the melt season.
Competing effects always lead to interesting dynamics–and it could be that we see a brief period of slowing followed by the ice disappearing rapidly like a water drop dancing on a hot skillet.
Guys I appreciate your work on this, but your scientific conservatism makes your conclusions seem unsatisfactory to me.
In terms of Shewart Control Chart Theory your system has “alarmed” three times in the last 33 years (Fig 1, using 2-sigma limits). (http://en.wikipedia.org/wiki/Control_chart) All three “alarms” have been in the downward direction. Although not definitive it would suggest the assumption of a linear trend is questionable. And if ensemble calculations are to be believed (Figs 3 & 4) the mean should be curving upwards rather than linear, which would make the most recent observations even more unusual. (What is you justificaton for not fitting an ensemble shaped trend?)
A minor issue is whether Fig 1 was constructed using the most recent data eg. 2011), which means it is not suitable for assessing whether that data is unusual. (i.e. To assess whether the record Sep 2011 minimum is unusual we would calculate the trend by excluding it.) Similarly the exponential and sigmoid fits are even more ad-hoc, being physically unrealistic and failing to fit the full time series. Finally the Fig 1 trends do show evidence of autocorrelation, so successive departures from trend are not as compelling as might first seem.
Getting back to the issue, yes it’s possible that this is still natural variability about a linear (or ensemble) mean, but it seems at least equally plausible that the modelling is simply WRONG. Such extreme short-term departures do not (to my eyes) appear in the models.
My conclusion is that you do not yet have sufficient understanding of the loss of Arctic Sea Ice and that it could be down below 1000 km^3 (i.e all gone with the exception of ice to the north of Greenland and a few other islands) as early as September 2014. True it may run it’s course and agree with ‘previous model-based predictions of somewhere between “2040 and 2100″’, but the evidence of MODEL FAILURE is becoming more compelling every year. Personally I’d be surprised if the Actic is NOT ice free by 2020, but that’s a guess! I would not be standing by the model predictions given the real world evidence.
If this continues, there is a point at which you must say, “The ice is disappearing faster than we can explain – all bets are off!”