There has been a lot of discussion related to the Hansen et al (2012, PNAS) paper and the accompanying op-ed in the Washington Post last week. But in this post, I’ll try and make the case that most of the discussion has not related to the actual analysis described in the paper, but rather to proxy arguments for what people think is ‘important’.
The basic analysis
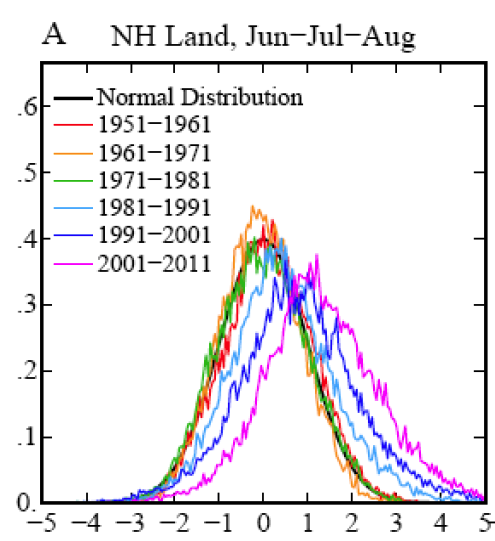
What Hansen et al have done is actually very simple. If you define a climatology (say 1951-1980, or 1931-1980), calculate the seasonal mean and standard deviation at each grid point for this period, and then normalise the departures from the mean, you will get something that looks very much like a Gaussian ‘bell-shaped’ distribution. If you then plot a histogram of the values from successive decades, you will get a sense for how much the climate of each decade departed from that of the initial baseline period.
The shift in the mean of the histogram is an indication of the global mean shift in temperature, and the change in spread gives an indication of how regional events would rank with respect to the baseline period. (Note that the change in spread shouldn’t be automatically equated with a change in climate variability, since a similar pattern would be seen as a result of regionally specific warming trends with constant local variability). This figure, combined with the change in areal extent of warm temperature extremes:
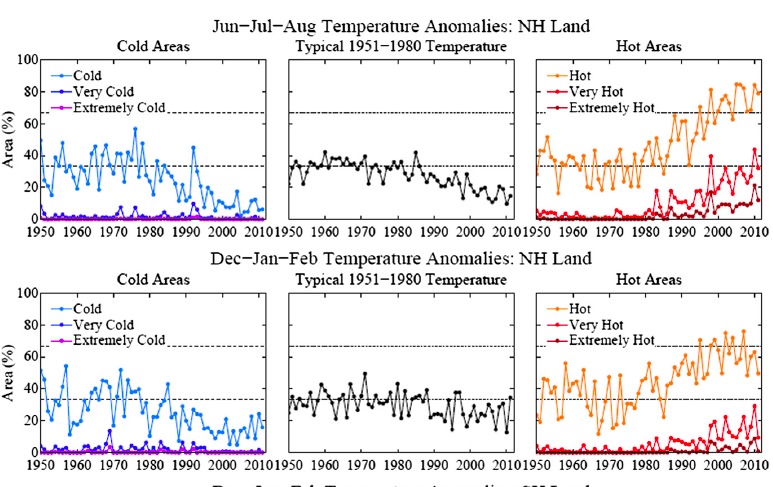
are the main results that lead to Hansen et al’s conclusion that:
“hot extreme[s], which covered much less than 1% of Earth’s surface during the base period, now typically [cover] about 10% of the land area. It follows that we can state, with a high degree of confidence, that extreme anomalies such as those in Texas and Oklahoma in 2011 and Moscow in 2010 were a consequence of global warming because their likelihood in the absence of global warming was exceedingly small.”
What this shows first of all is that extreme heat waves, like the ones mentioned, are not just “black swans” – i.e. extremely rare events that happened by “bad luck”. They might look like rare unexpected events when you just focus on one location, but looking at the whole globe, as Hansen et al. did, reveals an altogether different truth: such events show a large systematic increase over recent decades and are by no means rare any more. At any given time, they now cover about 10% of the planet. What follows is that the likelihood of 3 sigma+ temperature events (defined using the 1951-1980 baseline mean and sigma) has increased by such a striking amount that attribution to the general warming trend is practically assured. We have neither long enough nor good enough observational data to have a perfect knowledge of the extremes of heat waves given a steady climate, and so no claim along these lines can ever be for 100% causation, but the change is large enough to be classically ‘highly significant’.
The point I want to stress here is that the causation is for the metric “a seasonal monthly anomaly greater than 3 sigma above the mean”.
This metric comes follows on from work that Hansen did a decade ago exploring the question of what it would take for people to notice climate changing, since they only directly experience the weather (Hansen et al, 1998) (pdf), and is similar to metrics used by Pall et al and other recent papers on the attribution of extremes. It is closely connected to metrics related to return times (i.e. if areal extent of extremely hot anomalies in any one summer increases by a factor of 10, then the return time at an average location goes from 1 in 330 years to 1 in 33 years).
A similar conclusion to Hansen was reached by Rahmstorf and Coumou (2011) (pdf)) but for a related but different metric: the probability of record-breaking events rather than 3-sigma events. For the Moscow heat record of July 2010, they found that the probability of a record had increased five-fold due to the local climatic warming trend, as compared to a stationary climate (see our previous articles The Moscow warming hole and On record-breaking extremes for further discussion). An similarly concluded extension of this analysis to the whole globe is currently in review.
There have been been some critiques of Hansen et al. worth addressing – Marty Hoerling’s statements in the NY Times story referring to his work (Dole et al, 2010) and Hoerling et al, (submitted) on attribution of the Moscow and Texas heat-waves, and a blog post by Cliff Mass of the U. of Washington. *
*We can just skip right past the irrelevant critique from Pat Michaels – someone well-versed in misrepresenting Hansen’s work – since it consists of proving wrong a claim (that US drought is correlated to global mean temperature) that appears nowhere in the paper – even implicitly. This is like criticising a diagnosis of measles by showing that your fever is not correlated to the number of broken limbs.
The metrics that Hoerling and Mass use for their attribution calculations are the absolute anomaly above climatology. So if a heat wave is 7ºC above the average summer, and since global warming could have contributed 1 or 2ºC (depending on location, season etc.), the claim is that only 1/7th or 2/7th’s of the anomaly is associated with climate change, and that the bulk of the heat wave is driven by whatever natural variability has always been important (say, La Niña or a blocking high).
But this Hoerling-Mass ratio is a very different metric than the one used by Hansen, Pall, Rahmstorf & Coumou, Allen and others, so it isn’t fair for Hoerling and Mass to claim that the previous attributions are wrong – they are simply attributing a different thing. This only rarely seems to be acknowledged. We discussed the difference between those two types of metrics previously in Extremely hot. There we showed that the more extreme an event is, the more does the relative likelihood increase as a result of a warming trend.
So which metric ‘matters’ more? and are there other metrics that would be better or more useful?
A question of values
What people think is important varies enormously, and as the French say ‘Les goûts et les couleurs ne se discutent pas’ (Neither tastes nor colours are worth arguing about). But is the choice of metric really just a matter of opinion? I think not.
Why do people care about extreme weather events? Why for instance is a week of 1ºC above climatology uneventful, yet a day with a 7ºC anomaly is something to be discussed on the evening news? It is because the impacts of a heat wave are very non-linear. The marginal effect of an additional 1ºC on top of 6ºC on many aspects of a heat wave (on health, crops, power consumption etc.) is much more than the effect of the first 1ºC anomaly. There are also thresholds – temperatures above which systems will cease to work at all. One would think this would be uncontroversial. Of course, for some systems not near any thresholds and over a small enough range, effects can be approximated as linear, but at some point that will obviously break down – and the points at which it does are clearly associated with extremes that with the most important impacts.
Only if we assume that the all responses are linear, can there be a clear separation between the temperature increases caused by global warming and the internal variability over any season or period, and the attribution of effects scales like the Hoerling-Mass ratio. But even then the “fraction of the anomaly due to global warming” is somewhat arbitrary because it depends on the chosen baseline for defining the anomaly – is it the average July temperature, or typical previous summer heat waves (however defined), or the average summer temperature, or the average annual temperature? In the latter (admittedly somewhat unusual) choice of baseline, the fraction of last July’s temperature anomaly that is attributable to global warming is tiny, since most of the anomaly is perfectly natural and due to the seasonal cycle! So the fraction of an event that is due to global warming depends on what you compare it to. One could just as well choose a baseline of climatology, conditioned e.g. on the phase of ENSO, the PDO and the NAO, in which case the global warming signal would be much larger.
If however, the effects are significantly non-linear then this separation can’t be done so simply. If the effects are quadratic in the anomaly, a 1ºC extra on top of 6ºC, is responsible for 26% of the effect, not 14%. For cubic effects, it would be 37% etc. And if there was a threshold at 6.5ºC, it would be 100%.
Since we don’t however know exactly what the effect/temperature curve looks like in any specific situation, let alone globally (and in any case this would be very subjective), any kind of assumed effect function needs to be justified. However, we do know that in general that effects will be non-linear, and that there are thresholds. Given that, looking at changes in frequency of events (or return times, as is sometimes done), is more general and allows different sectors/people to assess the effects based on their prior experience. And choosing highly exceptional events to calculate return times – like 3-sigma+ events, or the record-breaking events – is sensible for focusing on the events that cause the most damage because society and ecosystems are least adapted to them.
Using the metric that Hoerling and Mass are proposing is equivalent to assuming that all effects of extremes are linear, which is very unlikely to be true. The ‘loaded dice’/’return time’/’frequency of extremes’ metrics being used by Hansen, Pall, Rahmstorf & Coumou, Allen etc. are going to be much more useful for anyone who cares about what effects these extremes are having.
References
- J. Hansen, M. Sato, and R. Ruedy, "Perception of climate change", Proceedings of the National Academy of Sciences, vol. 109, 2012. http://dx.doi.org/10.1073/pnas.1205276109
- J. Hansen, M. Sato, J. Glascoe, and R. Ruedy, "A common-sense climate index: Is climate changing noticeably?", Proceedings of the National Academy of Sciences, vol. 95, pp. 4113-4120, 1998. http://dx.doi.org/10.1073/pnas.95.8.4113
- S. Rahmstorf, and D. Coumou, "Increase of extreme events in a warming world", Proceedings of the National Academy of Sciences, vol. 108, pp. 17905-17909, 2011. http://dx.doi.org/10.1073/pnas.1101766108
- R. Dole, M. Hoerling, J. Perlwitz, J. Eischeid, P. Pegion, T. Zhang, X. Quan, T. Xu, and D. Murray, "Was there a basis for anticipating the 2010 Russian heat wave?", Geophysical Research Letters, vol. 38, pp. n/a-n/a, 2011. http://dx.doi.org/10.1029/2010GL046582
Apparently the answer to “…the question of what it would take for people to notice climate changing, since they only directly experience the weather…” depends on your ideological bent, at least in the USA. There is a nice piece on Ars Technica about the paper.
Great treatment of an important article.
It looks to me as if the Gaussian bells on your graph are breaking to the right at an accelerating rate decade by decade.
Do the measurements behind the graphs confirm this impression? If so, what does this suggest about what we might expect in the next couple of decades?
It seems to me that by failing to take a global perspective to assess a global phenomenon, Hoerling ends up telling just-so-stories rather than measuring anything.
If this is the NYT article you are thinking of http://www.nytimes.com/2012/08/07/science/earth/extreme-heat-is-covering-more-of-the-earth-a-study-says.html then Hoerling apparently has not read the paper he in commenting on since “Hoerling contended that Dr. Hansen’s new paper confuses drought, caused primarily by a lack of rainfall, with heat waves.” Yet, the paper barely mentions drought at all being about heat. Again, he appears to be making up stories.
Non-linearity in effects seems like a dispassionate term. But, the news today is sad. http://www.nytimes.com/2012/08/19/us/horses-fall-victim-to-hard-times-and-dry-times-on-the-range.html
Yes, values will become apparent when those non-linear effects start kicking like a mule. Like the 1 degree higher effect on corn growth, when the corn suddenly dies. GW is apparent when you see it on your plate.
I may have mentioned it earlier, but it is also worth noting that a lot of infrastructure, buildings and installations have been designed and dimensioned based on the climate in Hansens baseline period.
Building codes are typically based on 100-year events, or some analog improbability, for the local climate. During Hansens baseline period building codes were changed from rough overestimates to scientifically optimized requirements, in order to make buildings cheaper to build.
Analog observations can be made for how power transmission, drainage, bridges have been constructed in the last 50 years.
Five sigma can become very expensive for insurance companies.
Hansen’s analysis and its implications seem clear for anyone used to thinking about probability distributions. It’s also clear that extreme weather events cause disproportionate damage to human and ecological systems. The probability distributions published by Hansen are a logical extention of his “loaded dice” analogy.
Gavin,
It is very helpful to get an clear commentary from an informed scientist like you on this paper. Thank you for all your contributions.
Is this line correct:
“the causation is for the metric “a monthly anomaly greater than 3 sigma above the mean”.”?
I thought that the anomaly that Hansen calculates is the anomaly for the three month JJA period, not for single months. This is relevant in Hansen’s analysis of the 1930’s droughts, where July and August were extreme but the three month anomaly was not three sigma off the reference period. Extreme weather like this year’s “summer in March” also do not show up in Hansen’s analysis, since it was only about a month long. Rahmstorf and Coumou’s result addresses these short term records while Hansen addresses longer term change.
Keep up your great work, your work raises the web conversation on other blogs.
[Response: Thanks. You are correct – it should be the seasonal change. – gavin]
To whom it may concern:
Anthropogenic climate change will be a biatch.
Gavin,
You discuss the change in extremes by increasing the temperature 1C. Is there any reason to assume (as Hoerling and Mass do) that a 1C average increase in temperature would result in a 1C increase in extremes? It is well known that drought contributes to heat waves. If March, April and May were 1C warmer and evaporated a lot of water, wouldn’t that make it easier to have a 3C anomaly in summer since the ground is preconditioned for heat? Thus much more than 1C of the extreme heat could be due to global warming because of this local effect. There is data to show warming is greater in winter than summer. There is no a priori reason to suppose that a 1C increase in the annual temperature would lead to a 1C increase in extremes, the extremes might be greater or lesser. Hoerling and Mass have presented no reason to suppose that their basic premise is correct.
[Response: Indeed. I think there are certainly going to be non-linearities at the extremes – associated with soil moisture, fire, smog etc. – depending on where you are – and that makes the linear addition attribution metric even less satisfactory. But these issues are hard to quantify – both from the observations (since there are few occurrences) and models (which might not be complete/detailed enough to include these effects). – gavin]
Wouldn’t it make sense to parameterise the mean and the width of the gaussian distribution as a relatively smooth function of time (just a polynomial?), and then do an unbinned likelihood fit? That way you’d automatically take care of the effect of putting your data in bins of 10 years.
And then you could plot the resulting fitted functions versus time.
I’m genuinely curious if the gaussian is also getting wider, not just slowly shifting up.
Sorry for being a bit data-technical, and it would remain a bit of the problem to have nice convincing plots with data .. but doing an unbinned analysis does make sense, doesn’t it?
Excellent, as always. Thanks.
I recommend reading the “First Four Years” by Laura Ingalls Wilder. It was published posthumously in 1971 and might or might not be part of the Little House on the Prairie series (which was published in the 30’s and 40’s). In any event if you want to get a feeling for the effects of extreme weather it is a good one.
The incident from the book that I am thinking of is the following. Each year something happened to destroy their crops. One year everything was going perfect. They were finally going have a great harvest and pay off all their debt. Then, just before harvest time, a hot dry wind blew for three days and destroys their crops. If the change in wind had been averaged over the summer instead of occurring all in three days there’d have been no effect.
The Wilder book, “The Long Winter,” is another incredible portrayal of how weather effects life on the great plains.
You say the affects of a heat wave are very non-linear.
I can’t agree more. I work outside all summer. Sometimes doing work which requires wearing heavy clothing and carrying a lot of gear. I also exercise outside early in the morning when the daily temp is at it’s minimum. And I do this in Texas. The difference between 74f vs 77f, our climatological normal and what we’ve experienced these last two summers, is an incredible amount of distress.
Not everyone in the world runs from their house to the car to the office and can escape the increasing heat. When I think of the projections that show a 2C or 3.5F increase in average global temps in my lifetime it makes me feel hopeless. This will translate to 5 or 6 degrees F temperature increase experienced during my summer morning routine (expected increase in NH continental, summer, minimum temp) compared to the climatological norms my now retired coworkers used to deal with. I feel sorry for the poor folks next in line (my two kids).
Just curious, as the Thirties are held up by some as a natural time of heat events, what would Dr. Hansen’s method look like if the baseline was from 1921 to 1950? Would this in any way be able to tease out the natural from the anthropogenic?
[Response: While warm in the US, the 30s overall were not that warm, and so the percentage of 3 sigma + events globally was lower than the last decade. Hansen’s post-publication discussion has the data for 30s with respect to the 1951-1980 baseline, and the difference seen in using a 1931-1980 baseline (not much). – gavin]
Gavin,
An interesting analysis, but I can’t agree. Expressing climate change in terms of sigmas, and particularly exceedance of three sigmas, is less useful than other approaches, and potentially highly deceptive. In communicating with society and dealing with impacts, it is far more valuable to stay in true physical space. People understand temperature, not sigmas. The impacts are based on temperature and most official web sites, such as CPC, provide anomalies in C. Water freezes when temperature drops to 0C, pine beetles live if temperatures exceed a certain threshold. People can understand when you tell them 1 C of an anomaly is cased by global warming—it has meaning.
Using sigmas, and particularly a threshold of sigma, is quite deceiving. And examining a percent exceedance is worse. The truth is that many locations that exceeded 3 sigmas, would have been 2.8 sigma (or something like that!) without global warming–but no one says that. Hardly something that 99% of the folks would understand. Furthermore, 3 sigmas is entirely arbitrary and without physical meaning…unlike true temperature. But most serious of all, because of the highly non-linear shape of the gaussian, a relatively modest shift in temperature can cause a BIG change in percentage exceeding a threshold. A good way to scare people, but not a good way to communicate information. The implication given by many is that places that are exceeding 3 sigmas would have been normal without GW—this is simply not true.
Finally, the non-linearities in the impacts due to GW is an interesting issue, but it is not our place to juice our indices to be highly non-linear because we suspect such non-linearities exist. We need to give people the straight story….one they can understand…and that really needs to be in terms of physical temperature anomalies. …cliff
[Response: Before I get to the substance of your comment, I have to say that the use of terms like ‘deception’, ‘deceptive’, ‘deceiving’ and ‘juicing’, really are not appropriate for a scientific discussion. I think we can all agree that climate is complex, and there are multiple facets that can be communicated, but to say that someone who communicates a different view of the situation is deliberately out to deceive people is unfortunate at best, and offensive at worst. Given that there are people who regularly falsely accuse climate scientists of misconduct, fraud and deception for doing nothing more than reporting the facts, your use of these terms is inappropriate and not conducive to an improved public discourse.
Your first point seems to be that the public can’t deal with the concept of a distribution and so we shouldn’t talk about sigma’s because some people won’t understand. This is frankly bizarre. The public consist of many individuals who vary enormously in the attention they pay this discussion and in their background level of knowledge of statistics. Because someone might exist for whom this conversation is beyond them is no reason not to have it. But I even don’t agree with your basic assumption, most of the public have an intuitive grasp of distributions – look at the interest in playing poker, backgammon or craps. Statistical arguments given in terms that people can relate to, like dice throwing, are actually quite easily communicated.
Your second point is that absolute temperatures are more ‘real’ than sigmas, or presumably anomalies. I don’t really disagree, but it clearly isn’t the case the impact of 100ºF is the same everywhere – that is cool for a Phoenix summer day but almost unbelievable in Maine. Since climate is related to expectations – which differ enormously from place to place – anomalies allow you to look at similar levels of impacts and spatial coherence of the changes much more clearly. But obviously, anomalies aren’t ‘real’ in the sense you describe either, but are still very useful for scientists and lay people alike. Finally, dealing with distributions and deciles and sigmas is not that much of a leap – people understand the concepts of signal and noise with respect to the stock market, or tuning a radio and can grasp the idea with respect to climate and weather and extremes as well. There is nothing ‘deceitful’ in abstraction.
Your point about ice melting at 0ºC or temperature constraints on pine bark beetles actually reinforce my point and contradicts your second-to-last paragraph. Both of these effects are threshold events where any warming below the threshold is basically irrelevant, but the warming that crosses the threshold is responsible for all of the change. These are then classic cases where return time analysis and extremal exceedance are precisely the metrics that would be most tightly coupled to impacts. 3 sigma is of course arbitrary, but the same features are seen whatever threshold you pick, so that is hardly salient.
It might be obvious to you that shifts in the mean give rise to proportionately much greater numbers of warm extremes, but this isn’t necessarily true for anyone else. I don’t see how pointing this out, and showing that it is really occurring is ‘scaring’ people. Why is this fact something that should not be communicated? [For a very real example of the increasing impacts of small changes on the extremes, check out the graphs of Acqua Alta in Venice…]. And who has said that no heat waves would occur without GW? Or no El Niños or La Niñas? Not Hansen, Allen, Pall or Rahmstorf. If your beef is with distortions in the media or on headlines, then direct your criticisms to that, not to the scientists. – gavin]
[Response:I fully agree with Gavin, but here is an added simple point: if you prefer a temperature value rather than sigma, you could do the same analysis using the global mean of the sigma value (which is 0.6 degrees celsius). I.e., instead of plotting how often 3-sigma anomalies occur, you could plot how often anomalies exceeding 1.8 degrees occur. You’d get almost the same result as Hansen et al. Doing it that way would just be less sophisticated and informative, because in some places 1.8 degrees would just by nature of the local natural variability be exceeded much more easily than in some other places, so using that kind of threshold would not be as “fair” and even-handed as the 3-sigma threshold. -stefan]
Greetings,
It is so refreshing to read a logical, well reasoned interpretation of a paper without the hype and mis-interpretation [purposeful?] of the data and intent.
The Op-Ed in the WSJournal recently, is as bad an example of a comment I can imagine, that contributes nothing to a better understanding of this issue of climate change.
Ray
Gavin,
Thanks. Could you comment on the following in regards to whether Hansen’s type of analysis is relevant to daily extreme’s as well seasonal?
From Dr. Jeff Masters blog on the 15th of Aug the following data was provided.
Aug 13, 2012 Needles, CA, temp 118 F it started raining – a world record for hottest temp and rain
Jun 5, 2012 Mecca, SA, temp 109 F, rain, previous world record
July 10, 2010 Marrakech, Morocco, temp 109 F, rain, previous world record
Having world record daily weather events, such as the above, occur in such rapid sequence would seem to imply that Hansen’s type of analysis could be applied to daily events as well. The deviation between Jun 5 and Aug 13 (9 F) would seem to be very large. Is his research relevant or someone else’s?
Could you comment on the this. Thanks.
[Response: Hansen’s analysis was for seasonal anomalies – which are still averaging over a lot of weather. The shorter the time frame, and the more specific the extreme, the harder it is to detect a change, let alone attribute it. The most successful attempts to do this have used either global or continental statistics (as above), or thousands of model simulations of a local event (which use an initial condition ensemble to provide statistical power). It is certainly not the case that there is demonstrable link between every extreme and climate change (and indeed, some extremes – like bitter cold spells – are predicted to become less frequent). Looking at daily records can be insightful, but only when you have enough examples and a good metric to be comparing – the straight number of warm records is not good because even in a static climate you expect structure, but the ratio of warm to cool records is quite good because the expectation is that it should be 50:50 in the medium term (Meehl et al, 2010). Since the beginning of 2010, they are running ~4:1 in the continental US – though I am not sure about the rest of the world. – gavin]
Looking at specifics, Extremely Hot Summers (defined as a +3-sigma seasonal anomaly) increased from 0.1~0.2% of area in 1951-1981 base period to about 10% last decade (2001-2011). This is a factor of 50X~100x, or 5000% to 10,000% increase in 50 years. So now when a +3-sigma event happens, we know that the probability it was due to natural variation is 1/100 to 1/50 (1% to 2%) and the probability that it was due to global warming is 98~99%. That is for a single event. The probability that a string of such events are all due to natural variation is, as Dr. Hansen says, “minuscule, vanishingly small”.
In terms of return times, the Extremely Hot Summers used to occur every 500~1000 years at a particular location during the base period and they occurred about every 10 years during the last decade (and it is extremely likely that it will be more often this decade).
If this all wasn’t scary enough, +4-sigma events are now happening about 5% of the time and +5-sigma events, that formerly had a return time of about a million years , are now occurring about as often as 3-sigma events happened 50 years ago. With further warming, +4 and +5-sigma events will become “normal”.
but it is not our place to juice our indices to be highly non-linear because we suspect such non-linearities exist. We need to give people the straight story…
Cliff,
You say:
“but it is not our place to juice our indices to be highly non-linear because we suspect such non-linearities exist. We need to give people the straight story…”
In my comment #10 I point out that non-linearities can go both ways. Your suggestion that I discussed only raising temperatures is a deliberate deception. We know nonlinear effects exist but we do not know whether they make the temperature higher or lower. In your blog commentaries you claim absolute attribution and do not mention these uncertainties in your analysis. It is you who are deceiving your readers since you conceal your uncertainty. It is well known that hot weather breeds more hot weather. Please provide evidence to support your wild claims that the expected temperature increase in heat waves would be the same as the annual temperature increase.
You have made a large number of insulting comments accusing other scientists of deceiving readers without providing any specific examples or allowing comments to the contrary on your blog. You need to provide specific examples or stop insulting others. It appears to me that you are wrong and Hanson is right. If you think your argument has merit write up a paper and see if anyone will publish it. What you have put in your blog will never see publication, it has too many obvious errors.
Considering that Cliff rather insultingly dismissed authors of other remarks on his critique as ill-equipped to discuss this topic, I must say I find Cliff’s remarks here remarkably undistinguished in terms of revealing any special capabilities for illumination. Strictly garden-variety personal opinion.
A peek at textbook ranges associated with standard deviations and come up with these ranges:
Outside 2 sigmas: ~4.5/100
Outside 3 sigmas: ~3/1000
Outside 4 sigmas: ~7/50,000
(5 sigmas are so rare that putting them within such a variable background as climate that it seems to me to be meaningless.)
But weather events aren’t a once a year event so I have a hard time understanding the denominator
[Response: Hansen et al. look at seasonal anomalies, especially those for the average temperature of June-July-August. This anomaly can be computed (at each point of the globe) exactly one time for each year. An event of this type with a 1/100 probability thus would be expected to occur once in a hundred years. -stefan]
re: 20
“but it is not our place to juice our indices to be highly non-linear because we suspect such non-linearities exist. We need to give people the straight story…”
Whose place is it to accuse people of “juicing” indices?
Hansen is a great scientist, but group psychology is not his field.
Consider the 2010 Russia heat wave/ Pakistan flood. They were 3-sigma events, however NOAA promptly wrote an “attribution” calling the heat wave natural variation, and ignoring the related Pakistan flood.
And that was the professional weather community. Mostly, Americans ignored the event.
People will not take dramatic action on climate change until it bites them on their ass (e., g., a catastrophic, 9-sigma event). And, by then it may well be too late.
This summer we are seeing the 6th consecutive major Arctic sea ice melt event, and it has not even been mentioned in the presidential campaign. They have not tied this summer’s drought to AGW. They have not tied last winter’s South American drought to AGW. So look up and see what RC was saying, or equivocating and not saying about Arctic sea ice loss last April. What does RC say about five consecutive 4-sigma melt events in the same region?
As a certified “Alarmist” I must predict that we will see a substantially sea ice free Arctic — next summer. Will that prompt real action against AGW? Not unless it changes NH atmospheric circulation and we have another drought year, the crops fail, and the price of food goes up — a lot.
#16 Clifford Mass
There are many ways to convince oneself that one is right. Most of them are not scientific in nature.
I have found that of those that do not understand climate science well, extraordinarily few have the needed expertise regarding the relevant scope of the field… Even when they themselves are professors or scientists.
Sophist argumentation based in a distinct lack of knowledge is not a foundation upon which anyone, especially scientists or professors should base their arguments upon.
The Dunning/Kruger Effect illustrated by Isaac Asimov as a false premise:
“My ignorance is just as good as your knowledge”
It seems some still think this is a good argument and that argumentum ad ignorantiam should hold an equal place in any debate?
Though those of a thoughtful nature may still shake their heads and wonder why…
Don’t just make a claim:
http://cliffmass.blogspot.ch/2012/08/climate-distortion.html
File a comment for peer review. Writing to Anthony Watts so he can get ‘your word’ out to generally support a ‘belief’ that the scientists have it all wrong is not science, it’s practicing politics.
Oh yeah…
Watts Up With That?
http://wattsupwiththat.com/2012/08/09/cliff-mass-pans-hansens-pnas-paper/
In a nutshell, I think what people find most significant are the things they didn’t expect and were not prepared for.
And 5-sigma is probably the best way to capture that objectively.
I really don’t get what Cliff Mass’ problem is.
Can’t he see that the curve has become skewed?
Just like the probability of high and low temperature records being broken.
ReCaptcha: abstract icyband
Re- Gavin in his inline response in Comment by Clifford Mass — 19 Aug 2012 @ 10:37 AM:
I would like to add to your comment about the varying ability of the general public to understand climate science, that I also think that an even more important function is communication between scientists. A complicated problem is often dissected and studied in many different ways that are mostly understandable only by experts in the area. This is how most sciences proceed and to try to do teaching to the general public within research papers would require special sections in the journal, and external support for excess page charges and free public access to the journal articles.
It is easy to argue that the most important function of climate science to the general public is education for political purposes and I agree with this, but the best way to do this is to get the most accurate information from the scientists. Those who wish to spin scientific findings to favor their political or economic viewpoint do quite well twisting even the most straightforward data (e.g. surface temperature stations). Disseminating science to the public is a different specialty. Steve
It also depends on how you define extreme. Hot weather extremes may be more prevalent in some locations, but cold weather extremes which can be more injurious to agricultural interests seem to be decreasing. I was looking back at some historical Climatological Data reports for Ohio from the NCDC archives and you can certainly see the effects of climate change. Light frosts were reported to have occurred in July in many of the early years, with even a locally damaging frost in a couple of those years in outlying areas. This just simply doesn’t occur anymore. Frosts are very rare now even in June & August, when they used to be fairly common in the 19th Century.
Clifford Mass not only insults scientists as Gavin points out, but insults “society” by claiming we non-scientists must be spoon-fed the real world in simplistic terms that actually paint very fuzzy pictures, exactly as his blog post does – a bunch of hand waving that explains nothing while claiming to counter a reasoned and clear exposition of the true state of the climate. The paper in question and Gavins elaboration of it are waaay easier to follow and understand for this “average” layman.
Gavin in comment to to #18: “The shorter the time frame, and the more specific the extreme, the harder it is to detect a change, let alone attribute it.”
Yet that is exactly what the JASONs did back in 1992.
Their point was that the rate of new extreme values can be attributed and therefore their conclusion amounts to “Seing N new records…” (rather than “Seing this new record”) has odds of 1:1e5-1e6 of being climate change.
Extreme values (= weather records) are the inverse canary in the climate coal-mine: The more you see of them, the worse it is.
Re: Drought and high temp
Mueller and Seneviratne in PNAS address correlation between lo precip and subsequent hi T
sidd
Understanding statistical arguments is important for the general public to be able to do for all kinds of reasons, but especially to assess risks, costs, and policy. That they do not is unfortunate. That the media generally gets these wrong is worse, and does not help. We saw the same kind of thing with their treatment of evidence in favor of the Higgs Boson. This was widely discussed in the statistics community, and David Spiegelhalter, among others, addressed the matter. See http://understandinguncertainty.org/explaining-5-sigma-higgs-how-well-did-they-do. I learned a lot about how particle physicists (or should they be called “fundamental features physicists”?) think about this, including a great review by Lyons, available online at http://projecteuclid.org/DPubS/Repository/1.0/Disseminate?handle=euclid.aoas/1223908045&view=body&content-type=pdfview_1.
I think Clifford Mass is quite wrong. Life, civilization, and to some extent science is inextricably intertwined with statements of odds and chance, especially for complicated systems. Drs Leonard Smith and Nicholas Stern wrote poignantly about how policy is nearly always set in the context of uncertainty, and that even incomplete scientific assessments can be of great value (“Uncertainty in science and its role in climate policy”, http://www.lorentzcenter.nl/lc/web/2011/460/presentations/Smith.pdf). If anything we need more public erudition about these matters, and one way of encouraging that is putting more of this out there. Smith has (with Jarman) argued that (see http://eprints.lse.ac.uk/36330/1/Portrait_Jarman.pdf), and Spiegelhalter has applauded (via https://twitter.com/undunc/status/233483326508392448) the MET’s new probabilistic maps for weather forecasts (http://www.metoffice.gov.uk/weather/showcase/olympics_moguk_map_anim.html?wtype=precip&thres=rate60at30prob0000_2km#map). These are not only major statisticians, but people well-versed in communicating it.
The absence of such contributes to many social ills, whether failing to understand how health risks should be borne by a broad support to help curtail individual risk, the purpose of insurance, performance of social systems, or how reducing individual costs by allowing coastal construction in flood zones is based upon a lottery mindset. People think they can “get away with it”. Maybe that’s human, but it is also foolish. Jan
And this layperson too. Well said, flxible.
From the Financial Times (UK) of 15 August 2012:
“Scientists have long warned of more frequent floods and droughts as the world’s climate changes. But for Mr Mainord and many like him, global warming is bogus. “It’s more God and nature’s dictates, rather than a man-made event,” the Missouri farmer said this week as he harvested a corn crop one-quarter of its normal size.”
More of this article here:
http://www.ft.com/cms/s/2/be23cd60-e6d5-11e1-af33-00144feab49a.html#axzz241w1syog
Truly depressing.
From the Financial Times (UK) 15 August:
Scientists have long warned of more frequent floods and droughts as the world’s climate changes. But for Mr Mainord and many like him, global warming is bogus. “It’s more God and nature’s dictates, rather than a man-made event,” the Missouri farmer said this week as he harvested a corn crop one-quarter of its normal size.
http://www.ft.com/cms/s/2/be23cd60-e6d5-11e1-af33-00144feab49a.html#axzz241w1syog
Good presentation for scientists, of which the majority agree with AGW. Clifford Mass disagreement is incoherent, not at all in line with reality, he has to make a case when significant sigmas show warming when there is actually GT cooling, actually I am sure that there are contrarians out there who believe in the looming coming ice age, but strictly looking at data from the Arctic, there is a great warming happening. I am not sure if WUWT fans know that here are no urban heat islands over the arctic ocean?? However most people know what is going on. Mr Mass presumably included. There is a lot more heat showing in all seasons especially in the Northern Hemisphere exactly where it should happen. So the claim for dishonesty is rather a political ploy, a practice that they usually do, of course, practicing incorrect interpretations always gives no respectable prediction results, which by miracle from chance, if they would do one would be quantified as a high sigma anomaly not respecting any trends.
Re: 37 & 38
Ooooppps! I’ll blame it on CAPTCHA
Thank you, Gavin.
Hi Gavin, Great article. Very enlightening for someone with a Maths background and increasing understanding of climate change. I was interested in Chris Mass comment at #16. I would agree with him only in suggesting that most of the public have no clue about statistics of this level. Most people do not study Maths beyond standard deviation and mean, and rarely understand even that, so forget it very quickly after leaving school. So they would have no chance of following this article.
16 Clifford Mass wrote: “People can understand when you tell them 1 C of an anomaly is cased by global warming—it has meaning.”
I to only has meaning if you’ve done the analysis correctly and that is impossible to tell from your comment.
For the sake of discussion (FTSOD), assume we’ve had 1.5C change in mean temperature. Consider heat waves of some given magnitude, say 7.5C which FTSOD are once per century events without global warming and once per decade events with global warming. If I’ve understood you correctly you want to tell the people that the mean temperature increased by 1.5C and that it follows that 1.5C of the 7.5C heat wave is due to global warming and the rest is “natural”. It would be a reasonable to tell the people this only if there were 6C (7.5C-1.5C) heat waves every decade during the climatological period. This shouldn’t be difficult to check. Have you checked to see if your claim is correct? If you have I’d very much like to read it.
Gavin,
First, the definition of deceptive is:
“Giving an appearance or impression different from the true one”
Please don’t take the word further than I meant it. If you would prefer confusing, that is fine with me. You talk about using politic language as scientists…and then in the next paragraph you call my conclusions “bizarre.” I haven’t seen that word in many papers.
Regarding whether folks understand three sigmas, I give a lot of public talks and last week I asked a ground of roughly 150 highly educated folks how many understood what that meant—6 raised their hands. You can reach your own conclusions on this. I commend those laypersons comfortable with such stats…but most of the population and media don’t have a clue what it means.
You talk about anomalies being important…I agree…give them in degrees rather than sigmas to the general community if you want it understood.
And regarding transitions (like freezing)…there is no reason they would align on three sigmas or any other such basis. As noted in my original email, arbitrary lines in the sand like three sigma are inherent confusing and problematic. And the percentiles exceeding such 3 sigma thresholds increase rapidly with even moderate anomalies.
Folks…I know I am entering the lion’s den talking in this forum, but Hansen had no basis to say confidently that last summer’s heat wave was caused by global warming. …cliff
39 wayne davidson wrote “Clifford Mass disagreement is incoherent,”
I don’t agree that it is incoherent. Well, actually I re-read it and it isn’t exactly coherent, a bit of a rant I’d say, but he does have a legitimate point but it has to be checked. If global warming gave us dT of warming and we see extreme events with temperature dT_ext Clifford Mass claims that it is fair to say that of the extreme events dT is attributable to global warming and the rest is “natural”. This is a quantifiable claim. It isn’t a matter of opinion. If the frequency of dT_ext-dT events is the same before global warming as dT_ext events are after warming then Clifford is correct. If the frequency of dT_ext-dT events during the climatological period is much lower than the frequency of dT_ext events during the warm period then Clifford is incorrect.
The bell curve animated
NASA Climate Change Shifting Distribution of Summer Temperature Anomalies, 1951-2011 http://www.youtube.com/watch?v=-qFmVY4-G-Q&feature=plcp
” it is far more valuable to stay in true physical space. People understand temperature, not sigmas.”
Cliff, you managed to string a grand pair there! Made almost sorta reading your comment worthwhile.
The OP is about expectations and effects in the real world as it affects real people in local areas. If you want to know what a warmer world might be like for your town (ie, without surprises) then look to a period where that happened, as in the USA this year. Winter was grand, so the bugs didn’t die. Mosquitoes threatened. Fortunately, the rains failed and the skeeters died off. But the crops did too. And golly, the length of the hot events seemed longer than usual, and more than 2 degrees hotter, too…
It’s just anecdotal, but it’s probably pretty median. Of course, that’s just for an average year. Look at Hansen’s graphs and figure how wide the curve would be with the median at 3 sigma or so, and re-scale so the median is 0 sigma. Now visualize a 3 sigma event… better hope variability doesn’t keep increasing…
and don’t forget about those nasty surprises
John Pearson @13 The incident from the Laura Ingalls Wilder book about hot, dry winds killing crops in an (until then) good year in the 1930s was probably based on an actual occurrence. Just such an incident was related to me by my father-in-law, who farmed in northeast Nebraska in the 1930s. He mentioned that he thought the crop finally looked good in 1937, until a hot, windy day killed the corn outright. I saw a confirming notation of dead corn in an observation log book kept by the Weather Bureau in Norfolk, Nebraska for August 15, 1937. They recorded a high of 106 with a strong southwest wind. Wind from this direction usually has very low humidity on the Great Plains.
Re events that cause the most damage. Sea ice decline alters the pole pressure gradient, leads for instance to a higher amplitude Jet Stream and more ridges which create more stucky – persistent conditions. Explained here by Jennifer Francis, Rutgers University http://climatestate.com/pure-climate-science/item/lesson-arctic-sea-ice-decline.html
So this is not just temperature, it is a multitude of factors which affect the damage output. Another example would be ozone levels which become more unhealthy with high temperatures or the heat index.
Never mind the heat – feel the humidity
A look at the combined effect of heat and humidity
At the time of writing, the early morning temperature in Doha was 37C – not too bad you might think. But the relative humidity was 60%. The combination of the two gives a heat index of 51C – definitely unpleasant conditions.
The highest heat index ever recorded was in Dhahran on the Gulf coast of Saudi Arabia. On 8 July 2003 an air temperature of 42 degrees, combined with a dew point of 35 degrees resulted in a heat index 68.6C. http://www.aljazeera.com/weather/2012/08/201281891957105737.html
Now to contribute a single event to Global Warming, one has to look at the weather conditions, and if patterns are sighted which are tied to alteration of sea ice decline (our new atmosphere set up), we can connect the dots here too.
@Cliff Mass, re: comment 44
The meaning of the word “deceptive” depends on the context in which it is used, which you would know as well as anyone.
I think you demurred in a deceptive manner.
I do agree that most people, even the very educated, do not know the probabilities associated with sigmas and the bell curve. Far better to use the probabilities in percentages.