By raypierre , with the gratefully acknowledged assistance of Spencer Weart
In Part I the long struggle to get beyond the fallacious saturation argument was recounted in historical terms. In Part II, I will provide a more detailed analysis for the reader interested in the technical nitty-gritty of how the absorption of infrared really depends on CO2 concentration. At the end, I will discuss Herr Koch’s experiment in the light of modern observations.
The discussion here is based on CO2 absorption data found in the HITRAN spectroscopic archive. This is the main infrared database used by atmospheric radiation modellers. This database is a legacy of the military work on infrared described in Part I , and descends from a spectroscopic archive compiled by the Air Force Geophysics Laboratory at Hanscom Field, MA (referred to in some early editions of radiative transfer textbooks as the "AFGL Tape").
Suppose we were to sit at sea level and shine an infrared flashlight with an output of one Watt upward into the sky. If all the light from the beam were then collected by an orbiting astronaut with a sufficiently large lens, what fraction of a Watt would that be? The question of saturation amounts to the following question: How would that fraction change if we increased the amount of CO2 in the atmosphere? Saturation refers to the condition where increasing the amount of CO2 fails to increase the absorption, because the CO2 was already absorbing essentially all there is to absorb at the wavelengths where it absorbs at all. Think of a conveyor belt with red, blue and green M&M candies going past. You have one fussy child sitting at the belt who only eats red M&M’s, and he can eat them fast enough to eat half of the M&M’s going past him. Thus, he reduces the M&M flux by half. If you put another equally fussy kid next to him who can eat at the same rate, she’ll eat all the remaining red M&M’s. Then, if you put a third kid in the line, it won’t result in any further decrease in the M&M flux, because all the M&M’s that they like to eat are already gone. (It will probably result in howls of disappointment, though!) You’d need an eater of green or blue M&M’s to make further reductions in the flux.
Ångström and his followers believed that the situation with CO2 and infrared was like the situation with the red M&M’s. To understand how wrong they were, we need to look at modern measurements of the rate of absorption of infrared light by CO2 . The rate of absorption is a very intricately varying function of the wavelength of the light. At any given wavelength, the amount of light surviving goes down like the exponential of the number of molecules of CO2 encountered by the beam of light. The rate of exponential decay is the absorption factor.
When the product of the absorption factor times the amount of CO2 encountered equals one, then the amount of light is reduced by a factor of 1/e, i.e. 1/2.71282… . For this, or larger, amounts of CO2,the atmosphere is optically thick at the corresponding wavelength. If you double the amount of CO2, you reduce the proportion of surviving light by an additional factor of 1/e, reducing the proportion surviving to about a tenth; if you instead halve the amount of CO2, the proportion surviving is the reciprocal of the square root of e , or about 60% , and the atmosphere is optically thin. Precisely where we draw the line between "thick" and "thin" is somewhat arbitrary, given that the absorption shades smoothly from small values to large values as the product of absorption factor with amount of CO2 increases.
The units of absorption factor depend on the units we use to measure the amount of CO2 in the column of the atmosphere encountered by the beam of light. Let’s measure our units relative to the amount of CO2 in an atmospheric column of base one square meter, present when the concentration of CO2 is 300 parts per million (about the pre-industrial value). In such units, an atmosphere with the present amount of CO2 is optically thick where the absorption coefficient is one or greater, and optically thin where the absorption coefficient is less than one. If we double the amount of CO2 in the atmosphere, then the absorption coefficient only needs to be 1/2 or greater in order to make the atmosphere optically thick.
The absorption factor, so defined, is given in the following figure, based on the thousands of measurements in the HITRAN spectroscopic archive. The "fuzz" on this graph is because the absorption actually takes the form of thousands of closely spaced partially overlapping spikes. If one were to zoom in on a very small portion of the wavelength axis, one would see the fuzz resolve into discrete spikes, like the pickets on a fence. At the coarse resolution of the graph, one only sees a dark band marking out the maximum and minimum values swept out by the spike. These absorption results were computed for typical laboratory conditions, at sea level pressure and a temperature of 20 Celsius. At lower pressures, the peaks of the spikes get higher and the valleys between them get deeper, leading to a broader "fuzzy band" on absorption curves like that shown below.

We see that for the pre-industrial CO2 concentration, it is only the wavelength range between about 13.5 and 17 microns (millionths of a meter) that can be considered to be saturated. Within this range, it is indeed true that adding more CO2 would not significantly increase the amount of absorption. All the red M&M’s are already eaten. But waiting in the wings, outside this wavelength region, there’s more goodies to be had. In fact, noting that the graph is on a logarithmic axis, the atmosphere still wouldn’t be saturated even if we increased the CO2 to ten thousand times the present level. What happens to the absorption if we quadruple the amount of CO2? That story is told in the next graph:
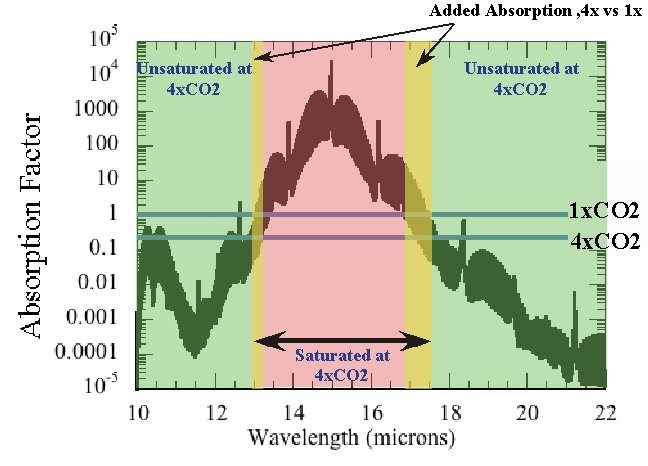
The horizontal blue lines give the threshold CO2 needed to make the atmosphere optically thick at 1x the preindustrial CO2 level and 4x that level. Quadrupling the CO2 makes the portions of the spectrum in the yellow bands optically thick, essentially adding new absorption there and reducing the transmission of infrared through the layer. One can relate this increase in the width of the optically thick region to the "thinning and cooling" argument determining infrared loss to space as follows. Roughly speaking, in the part of the spectrum where the atmosphere is optically thick, the radiation to space occurs at the temperature of the high, cold parts of the atmosphere. That’s practically zero compared to the radiation flux at temperatures comparable to the surface temperature; in the part of the spectrum which is optically thin, the planet radiates at near the surface temperature. Increasing CO2 then increases the width of the spectral region where the atmosphere is optically thick, which replaces more of the high-intensity surface radiation with low-intensity upper-atmosphere radiation, and thus reduces the rate of radiation loss to space.
Now let’s use the absorption properties described above to determine what we’d see in a typical laboratory experiment. Imagine that our experimenter fills a tube with pure CO2 at a pressure of one atmosphere and a temperature of 20C. She then shines a beam of infrared light in one end of the tube. To keep things simple, let’s assume that the beam of light has uniform intensity at all wavelengths shown in the absorption graph. She then measures the amount of light coming out the other end of the tube, and divides it by the amount of light being shone in. The ratio is the transmission. How does the transmission change as we make the tube longer?
To put the results in perspective, it is useful to keep in mind that at a CO2 concentration of 300ppm, the amount of CO2 in a column of the Earth’s atmosphere having cross section area equal to that of the tube is equal to the amount of CO2 in a tube of pure CO2 of length 2.5 meters, if the tube is at sea level pressure and a temperature of 20C. Thus a two and a half meter tube of pure CO2 in lab conditions is, loosely speaking, like "one atmosphere" of greenhouse effect. The following graph shows how the proportion of light transmitted through the tube goes down as the tube is made longer.
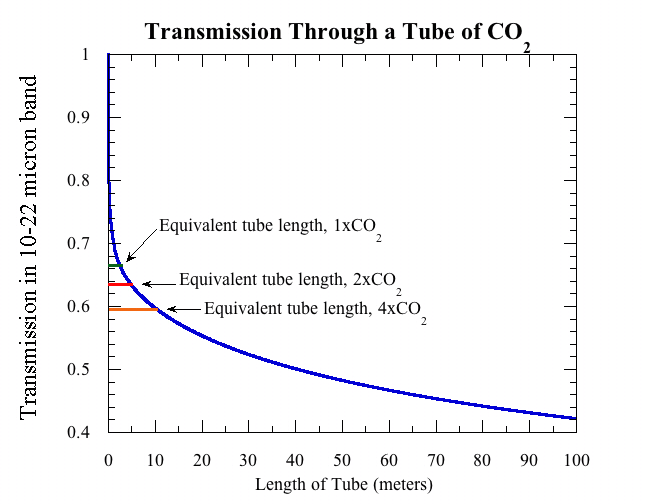
The transmission decays extremely rapidly for short tubes (under a centimeter or so), because when light first encounters CO2, it’s the easy pickings near the peak of the absorption spectrum that are eaten up first. At larger tube lengths, because of shape of the curve of absorption vs. wavelength, the transmission decreases rather slowly with the amount of CO2. And it’s a good thing it does. You can show that if the transmission decayed exponentially, as it would if the absorption factor were independent of wavelength, then doubling CO2 would warm the Earth by about 50 degrees C instead of 2 to 4 degrees (which is plenty bad enough, once you factor in that warming is greater over land vs. ocean and at high Northern latitudes).
There are a few finer points we need to take into account in order to relate this experiment to the absorption by CO2 in the actual atmosphere. The first is the effect of pressure broadening. Because absorption lines become narrower as pressure goes down, and because more of the spectrum is "between" lines rather than "on" line centers, the absorption coefficient on the whole tends to go down linearly with pressure. Therefore, by computing (or measuring) the absorption at sea level pressure, we are overestimating the absorption of the CO2 actually in place in the higher, lower-pressure parts of the atmosphere. It turns out that when this is properly taken into account, you have to reduce the column length at sea level pressure by a factor of 2 to have the equivalent absorption effect of the same amount of CO2 in the real atmosphere. Thus, you’d measure absorption in a 1.25 meter column in the laboratory to get something more representative of the real atmosphere. The second effect comes from the fact that CO2 colliding with itself in a tube of pure CO2 broadens the lines about 30% more than does CO2 colliding with N2 or O2 in air, which results in an additional slight overestimate of the absorption in the laboratory experiment. Neither of these effects would significantly affect the impression of saturation obtained in a laboratory experiment, though. CO2 is not much less saturated for a 1 meter column than it is for a 2.5 meter column.
So what went wrong in the experiment of poor Herr Koch? There are two changes that need to be made in order to bring our calculations in line with Herr Koch’s experimental setup. First, he used a blackbody at 100C (basically, a pot of boiling water) as the source for his infrared radiation, and measured the transmission relative to the full blackbody emission of the source. By suitably weighting the incoming radiation, it is a simple matter to recompute the transmission through a tube in a way compatible to Koch’s definition. The second difference is that Herr Koch didn’t actually perform his experiment by varying the length of the tube. He did the control case at a pressure of 1 atmosphere in a tube of length 30cm. His reduced-CO2 case was not done with a shorter tube, but rather by keeping the same tube and reducing the pressure to 2/3 atmosphere (666mb, or 520 mm of Mercury in his units). Rather than displaying the absorption as a function of pressure, we have used modern results on pressure scaling to rephrase Herr Koch’s measurement in terms of what he would have seen if he had done the experiment with a shortened tube instead. This allows us to plot his experiment on a graph of transmission vs. tube length similar to what was shown above. The result is shown here:
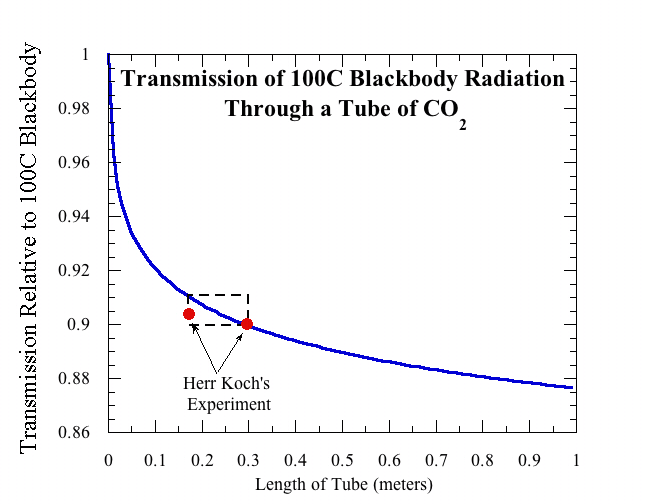
Over the range of CO2 amounts covered in the experiment, one doesn’t actually expect much variation in the absorption — only about a percent. Herr Koch’s measurements are very close to the correct absorption for the 30cm control case, but he told his boss that the radiation that got through at lower pressure increased by no more than 0.4%. Well, he wouldn’t be the only lab assistant who was over-optimistic in reporting his accuracy. Even if the experiment had been done accurately, it’s unclear whether the investigators would have considered the one percent change in transmission "significant," since they already regarded their measured half percent change as "insignificant."
It seems that Ångström was all too eager to conclude that CO2 absorption was saturated based on the "insignificance" of the change, whereas the real problem was that they were looking at changes over a far too small range of CO2 amounts. If Koch and Ångström had examined the changes over the range between a 10cm and 1 meter tube, they probably would have been able to determine the correct law for increase of absorption with amount, despite the primitive instruments available at the time.
It’s worth noting that Ångström’s erroneous conclusion regarding saturation did not arise from his failure to understand how pressure affects absorption lines. That would at least have been forgivable, since the phenomenon of pressure broadening was not to be discovered for many years to come. In reality, though Ångström would have come to the same erroneous conclusion even if the experiment had been done with the same amounts of CO2 at low pressure rather than at near-sea-level pressures. A calculation like that done above shows that, using the same amounts of CO2 in the high vs. low CO2 cases as in the original experiment, the magnitude of the absorption change the investigators were trying to measure is almost exactly the same — about 1 percent — regardless of whether the experiment is carried out at near 1000mb (sea level pressure) or near 100mb (the pressure about 16 km up in the atmosphere).
Re #100: Lawrence, if you read the posts just before yours (they may not have been there when you posted) you will see that while greenhouse gases absorb infrared radiation and warm the air, they also absorb kinetic energy from other molecules and radiate infrared. When this happens, there is less kinetic energy, thus local cooling. In fact, it appears there is more radiative cooling than warming.
You are right that the infrared radiation goes in all directions. This has little effect on the temperature structure of the atmosphere, which would be much the same without any greenhouse gases at all. It does warm the ground, which warms the air above by convection. Convection is how most energy moves through the atmosphere.
According to the radiation balance model, adding more greenhouse gas raises the average altitude at which they radiate into space. At higher altitude the atmosphere is cooler. A cooler greenhouse gas radiates less energy into space, so less energy is lost from the Earth system, so it gets warmer.
Blair, In the troposphere, convection is much more important than radiation for warming of the atmosphere. In the stratosphere, you can exchange energy, but warming by radiation is probably not all that significant. The main thing is that the CO2 in the stratosphere prevents IR from escaping and sends some of it back to the troposphere.
re 89, 90, 91: Well, blow me down. To prove Tamino and Ray wrong I dug out my Feynman lectures. Unfortunately Feynman beat hell out of me. It’s as you say — maybe even worse. It seems the more atoms in a molecule the more true kinetic energy is stored in the internal bonds, and at three atoms/molecule the internal KE is TWICE that of the whole molecule’s traveling through space. I could not have been more wrong! Worse than that — you might want to check my math on the following (I don’t want to show it here because it might be misleading to the unwary). I calculated (theoretically) the kinetic energy of one CO2 molecule at 250 degreesK to be 1.56×10-20 joules, 1/3 “external” and 2/3 internal (Damn, again!), with the whole molecule zipping around “externally” at 375m/sec. Then I gave it one photon at 14.7um, calculating its energy at 1.35×10-20 joules. Absorbed into the internal bonds, one photon raised the molecules temp to 469 degrees — almost double. Does that sound right to you all??? I must go regroup!!
re 93 (Hank): I’m a little gun shy, but I think you are wrong. A molecule of water vapor at 100 degreesC has more internal “heat” energy than a molecule of water at 100degreesC. Doesn’t it?? Or does it somehow immediately (??) dissipate?
>93, 94, thanks deWitt for the history; I was thinking of microwave pumping favored bond energy to increase a reaction product, thus: http://scholar.google.com/scholar?q=microwave+pump+reaction+path
and wondering if some microwave pumping could nudge molecules over the hump to emit an infrared photon—faster than a chemical reaction, but I guess you’re saying there’s no ‘tunable’ configuration that can be favored long enough to favor emitting an infrared photon?
Ray Ladbury (#99) wrote:
Well, I guess the best way for me to put it is that the greenhouse effect due to carbon dioxide in the stratosphere raises the temperature at ground level and sea level, resulting in more evaporation. This evaporation leads to increased water vapor, and water vapor results in moist air convection and an increase in the greenhouse effect. But the direct result of the greenhouse effect in the atmosphere in a cooling in which counterbalances the warming due to moist air convection. Finally, the cooling of the atmosphere due to the greenhouse effect involves the transformation of thermal/kinetic energy into long-wave infrared radiation, and while the direct trasformation of infrared radiation into thermal/kinetic energy in the atmosphere is certainly possible, within the atmosphere, the transformation of thermal/kinetic energy into infrared predominates.
Edit on #105
“The best way for me to put it…” got me to look at that last sentence. It should end:
“… and while the direct transformation of infrared radiation into thermal/kinetic energy in the atmosphere certainly occurs, within the atmosphere the transformation of thermal/kinetic energy into infrared is dominant.”
For this series, around 81 to 102, and Alastair in particular. What seems to me to need emphasis is the notion of a radiation field in which the molecules reside, and which is a consequence of being at a finite temperature. With molecules at temperature T and an isotropic field of thermal energy also at T, molecules are at equilibrium, joyfully emitting and absorbing at more or less the same rate. (For CO2 at the beach on a warm day, these radiations are relatively far up the chain of vibrational energy states.)
With flashlights or warm bodies like Earth, there may be additional fields of higher temperature, in which case there will be net absorption by the molecule in the direction of the gradient at the frequencies at which the molecule can exchange energy. Energy absorbed by the molecule will be subsequently re-radiated isotropically, thereby raising the temperature of its neighbors, but depleting the gradient at the same frequencies as were absorbed. So, yes, the atmosphere can be heated by absorption of energy emitted at the surface. It can also be cooled, depending.
Since the molecule can only come into equlibrium at the frequencies at which it emits and absorbs, it will usually be out of equlibrium at other frequencies. When the radiant field is of higher temperature than the molecule, the frequencies at which the molecule absorbs will appear less bright along the direction of the gradient. Some might call this a sort of saturation; some might not.
Caution�speculation begins here. Now, Alastair, do you buy that when the radiant field is of lower temperature than the molecule, as can happen when local thermal equilibrium begins to fail, the molecular frequencies can appear to be at a higher temperature than the general field? And perhaps when we see particular temperatures for certain molecules as you have observed, we are looking at the point where they crossed out of LTE?
Rod B (#103) wrote:
I admire your ambition and tenacity!
I have yet to break-out the calculator – although I used a spreadsheet a while ago.
[… he says, ending with an oh-so-charming and sheepish grin.]
I would be inclined to think that a water molecule which has just broken free of the liquid at the boiling point has more kinetic energy, but then again, the internal energy is quantized, and therefore the additional kinetic energy is probably due velocity, although there is probably an increased likelihood of excited internal states.
Rod wrote:
> A molecule of water vapor at 100 degreesC has more internal
> “heat” energy than a molecule of water at 100degreesC. Doesn’t it??
Nope. Unless “internal” is your point. Temperature is all the energy involved with the molecule; water vapor has its energy in the one molecule, motion, vibration, rotation between the atoms (it isn’t hydrogen bonded in a favorable position to other water vapor; when it does, it’s changing from water vapor to water, condensing into mist, energy going into the bonds that hold one molecule to the next).
Consider — you probably know the warning not to reheat a cup of water in a microwave, after you’ve brought it to a boil once. That’s because the first time you heat it to boiling, all the little gas bubbles in the cracks and crevices on the inside of the cup get dislodged. Those form points where the hot water easily turns to vapor, starting the boiling at a lot of little spots. You can see the same thing inside a glass kettle on a stove, strings of bubbles rising from particular points all over the inside surface as the water is just reaching the boiling point.
But if you bring a cup of water to a boil in a microwave, don’t open the door, let the water cool off, and do it again, and again — you are boiling off or physically removing all the little discontinuities.
What happens? It becomes possible to superheat the water because there aren’t those little points where the bubbles of vapor can easily form.
Result?
Kids, do NOT try this at home.
The caution is: If you’ve managed to reheat the water under these conditions, no banging on the countertop, no dirt falling into the cup from the top of the microwave chamber, clean cup, no nuclei to promote bubbles to form more easily at any point —- it’s possible the water will — all of it — be heated up to 100 degrees C, 212 fahrenheit, or even slightly higher.
And you open the door and the vibration or breeze causes a whole lot of that water to turn to vapor and you get a faceful of boiling water and steam.
Like I said, kids, do NOT try this at home. Look up “superheated” ….
Re #102 and #105: Ray and Timothy, I want to question the statement that carbon dioxide in the stratosphere is important to the greenhouse effect for two reasons: First, there is not much carbon dioxide there. Second, the temperature in the stratosphere rises with altitude, so the CO2 will radiate at a higher temperature, thus more heat will be lost compared to the upper troposphere.
I understood that greenhouse gases near the top of the troposphere were more significant.
Blair Dowden (#110) wrote:
Not a problem.
Temperature increase due to carbon dioxide is roughly proportional to the log of the concentration. While there isn’t much carbon dioxide in the stratosphere, this also implies that one doesn’t have to add much carbon dioxide to the atmosphere in order to double its concentration which directly results in an increase in temperature of approximately 1.2 degrees Kelvin and indirectly in an increase in temperature of approximately 2.9 degrees when one takes into account successive rounds of amplification due to increased water vapor in the troposphere.
When it radiates, roughly half of the radiation will be downwelling and half will be upwelling. Depending upon where the molecule is located, the photon will have a slight tendency to eventually reach either space or the ground as the result of a stochastic process of emission and re-absorption. However, upwelling radiation will tend to have slightly longer legs than downwelling radiation due to decreasing atmospheric density.
Blair, factor in the _time_ that has to elapse.
The temperature of the stratosphere is higher toward the top.
That doesn’t mean that when something causes it to LIFT UP slightly, it gets hotter. Quite the opposite — lift it up, it expands and gets cooler. That’s the prediction for when the planet warms up.
Surface warms.
Lower atmosphere warms (and because it’s warmed, it expands, and it can only expand upward not downward)
Upper atmosphere is being lifted higher from the surface
—- because it’s lifted, it expands and cools
A cool molecule emits its infrared photon at — a cooler temperature.
So the heat leaving the planet isn’t keeping up with the heat being held in the atmosphere/earth/ocean.
That takes a few hundred years — til the upper atmosphere, still out there a bit farther away, gets warmed up again and is emitting heat at the same rate as it originally was, the same rate as the incoming energy.
Meanwhile down in the lower atmosphere/earth/ocean system, it’s gotten hotter over those same several centuries and stayed hotter for quite a few centuries, until the CO2 gets captured in minerals and ocean sediments.
At the top you have the same number of CO2 molecules (or slightly more, over time). They’re the molecules
Blair, out of curiosity, where do you get your information that the stratosphere is depleted in CO2? The measurements I’ve been able to find suggest that the lower stratosphere (up to ~35 km) is only a few ppmv less than the troposphere, and that it is increasing at a rate that is not incomensurate with the increase in the troposphere. Most of the measurements I’ve seen date from the 70s and 80s. Do you have more recent measurements?
re 107: a quicky question/clarification: the radiated E-M field has no temperature…., does it??
Timothy, your statements in #111 are correct but do not address the issue of where most of greenhouse warming occurs. It may be worse than I said – carbon dioxide in the stratosphere radiates more energy than it absorbs, and thus causes the stratosphere to cool. This is independent of any effects from the troposphere. What I don’t know is whether or not this results in a (small) net cooling of the Earth.
I still think greenhouse warming take place mainly in the upper troposphere.
Hank, I am afraid you lost me with your comment. Photons move fast, so the greenhouse effect is almost instantaneous. Convection takes a little longer, maybe a few days.
a little public musing re my post 108 et al: It still doesn’t smell right. It says that E-M radiation is the direct primary and major cause of atmosphere temperature increases. Yet post after post here have implied otherwise, e.g. “a little bit….” Feynman’s equations also imply that any added energy to a molecule will get distributed between the internal kinetic energy and the overt kinetic energy with a definite ratio unique to each size (number of atoms) of molecule. Is this right?????
One other thought for mulling before I go try to find out. Is my contention of heat changing without changing the temperature only “valid” with averages ala Maxwell-Boltzman distribution? It sticks in my mind that the molecule that evaporates is the odd one out with much higher kinetic energy than the average speeding near the surface and luckily breaking free. It takes a much higher (but how much higher????) than average heat and temp with it, simultaneously adding temp and heat to the vapor and removing heat and temp from the liquid base. Any thoughts?
Still thinking aloud, fishing for responses: does that mean that evaporation from the sea surface cools the sea and warms the atmosphere? AND, possibly, the excited evaporated H2O molecule, with its kinetic energy distributed between its internal bonds and its overt velocity in a 2:1 ratio, can emit IR radiation, even if it had not absorbed any, with E-M energy taken from its bond energy???
I’m getting a headache!
An afterthought that’s driving be batty: Go anywhere on the web or to any standard physics textbook and 99 times out of 100 (I’m guessing) it will say that 1.5kT = kinetic energy = 0.5mv2 of the overt total molecule. Can anyone find where it says the total kinetic energy of a gas molecule = K.E. = 1.5(r-1)kT where r is the number of atoms in the molecule? Or am I just blind?????
> Photons move fast, so the greenhouse effect is almost instantaneous. Convection takes a little longer, maybe a few days
Blair, look up “mean free path” and the simulator Eli Rabett has been talking about. Photons move til the next interaction, which happens very fast in a gas. Yes, speed of light — but only til the next interaction. Else the heat would all rush off the planet every night. We had someone else here repeatiing basically these same beliefs a few weeks back, who finally left I guess. Where are you getting them, one of the other “climate science site” pages?
Blair Dowden (#115) wrote:
At the surface – moist air convection is what is primarily responsible for heating the troposphere.
Solar radiation includes UV rays which will heat the stratosphere as the result of ozone. This is the reason why a depleted ozone layer results in the cooling of the stratosphere over Antarctica, resulting in a higher temperature differential between it and the surface, increasing winds, results in an upwelling of nutrient-rich water from below, increasing the release of methane and carbon dioxide, intensifying the greenhouse effect and lofting moisture into the stratosphere which results in the slower replentishment of the ozone layer. Then there is terrestrial radiation. Then there are the aerosols.
Each plays a role.
But the important thing is actually fairly basic: if the system is in equilibrium, then all of the effects must cancel one another, at the surface, in the troposphere and in the stratosphere.
However, all of this assumes an equilibrium, and I see that Hank Roberts has done non-equilibrium in #112. Good thing too – since I have little doubt that he knows more about it than I do.
RE: #111 Carbon dioxide doesn’t emit any IR photons. All the IR energy that a carbon dioxide molecule absorbs is removed by collisions with nitrogen and oxygen molecules. Most of the greenhouse effect is due to water molecules near the surface of the earth and above and in fact, carbon dioxide plays little or no role in the greenhouse effect. At a concentration of 0.038% by volume there is too little molecular muscles to do anything except standby and watch water molecules, greedy little IR energy hogs, do all the work. The so-called feed back process is just a fantansy thought up by climatologists drinkin’ Thunderbird and smokin’ cheap Mexican pot on the patio at the Hotel California.
Air pressure is far more important than carbon dioxide on effecting the amount of water vapor in the air because the heat of vaporation of both solid and liquid water is primarily a function of pressure. For a non- associated liquid the heat of vaporation of solely a function pressure. Water is an associated liquid and the heat of vaporization also depends on a limited extent on temperature. This why high pressure cell are generally warm and dry in summer and cold and dry in winter. Low pressure have more moisture due to the lower atmosphere pressure.
Harold, for someone who doesn’t understand the science, you have awfully strong opinions.
[[You are right that the infrared radiation goes in all directions. This has little effect on the temperature structure of the atmosphere, which would be much the same without any greenhouse gases at all.]]
This is incorrect. Radiative transfer is a major process in the atmosphere. Layers of air are heated by the sunlight they absorb, and much more by the infrared they absorb both from the ground and from other layers of air.
[[Absorbed into the internal bonds, one photon raised the molecules temp to 469 degrees — almost double. Does that sound right to you all??? I must go regroup!!]]
Temperature isn’t a concept that applies to one molecule. You need a group of them.
[[RE: #111 Carbon dioxide doesn’t emit any IR photons.]]
Yes it does.
[[ All the IR energy that a carbon dioxide molecule absorbs is removed by collisions with nitrogen and oxygen molecules. Most of the greenhouse effect is due to water molecules near the surface of the earth and above and in fact, carbon dioxide plays little or no role in the greenhouse effect.]]
Wrong. Carbon dioxide provides about 26% of Earth’s greenhouse effect versus about 60% for water vapor.
[[ At a concentration of 0.038% by volume there is too little molecular muscles to do anything except standby and watch water molecules, greedy little IR energy hogs, do all the work.]]
It’s the absolute amount that matters, not the concentration. Most of the atmosphere, nitrogen, oxygen and argon, is not radiatively active. (Oxygen is a bit radiatively active in the UV). There are about 3 x 1015 kilograms of carbon dioxide in the air. That’s about 5.88 kilograms per square meter of Earth’s surface. That’s clearly enough to make a difference.
[[ The so-called feed back process is just a fantansy thought up by climatologists drinkin’ Thunderbird and smokin’ cheap Mexican pot on the patio at the Hotel California. ]]
You seem to have been indulging in a little of that yourself. I’d recommend reading up on some basic climatology instead. Try googling for “Clausius-Clapeyron law” and trying to understand why that implies a temperature feedback effect for carbon dioxide warming.
The Hadley Center of the British Met Office gives a clear graph of the emission of IR radiation at higher altitudes due to increasing levels of CO2 in the atmosphere.
http://www.metoffice.gov.uk/research/hadleycentre/pubs/brochures/2005/clim_green/slide07.pdf
The graph is followed by an explanation of present day conditions and from a hypothetical higher cooler level. The explanation is straightforward.The IR emission can’t emit as much at this cooler layer and the atomosphere must warm up until the rate of IR emission returns to the original rate. The surface, in the example will produce a warming of 10K over the present. day,meaning that increasing the present emissions from an average height of about 5.5 kilometers, to 7 kilometers raises the surface by this much- 10K or 10C
re 119 Chase: While the climate people may have their own definition of “equilibrium”, from the thermodynamic standpoint, if the atmosphere were at equilibrium with the radiation fields, then upwelling and downwelling radiation fields would be the same (definition of equilibrium, as distinct from steady state). We are at the bottom of distinctly non-equilibrium energy transport system, trying to explain it with equilibrium concepts.
My position is that the GHG effect is purely kinetic, not at all thermodynamic.
re 114, Rod B: Does a radiated field have a temperature? Sort of. It is common to compare measured intensity to that of a black body and produce a “brightness temperature”. Searching on this term and AIRS should get some spectra.
You have too many mixed questions to answer, but KE = 1/2 M V^2. period.
Rod, the total energy of a molecule in thermal equilibrium with its surroundings at temperature T is 3/2 nkT where N is the number of atoms (where did they get r from? The kinetic energy is 3/2 kT. That means that the internal energy is 3/2 (n-1) kT. Your formula was for internal energy, not kinetic.
RE #107 where Allan Ames wrote
“Now, Alastair, do you buy that when the radiant field is of lower temperature than the molecule, as can happen when local thermal equilibrium begins to fail, the molecular frequencies can appear to be at a higher temperature than the general field? And perhaps when we see particular temperatures for certain molecules as you have observed, we are looking at the point where they crossed out of LTE?”
I do buy that if you mean that when the brightness temperature (radiant field) is lower than the kinetic temperature of the air molecules, then the air is warmer than the radiant field produced by the surface of the Earth, and the system will no longer be in LTE. This happens every clear night when the surface cools and radiates less black body radiation towards the air than the air radiates towards it. The reverse process happens during the day. when the surface is warmed by solar radiation and the blackbody radiation field from it is warmer than the air containing the greenhouse gas molecules that are absorbing it. This means that the air next to the Earth’s surface is only in LTE twice per day, when the two temperatures cross.
And Re 114 where RodB wrote “the radiated E-M field has no temperature…., does it?”
It does have a temperature called the brightness temperature. This temperature is the Planckian temperature which is calculated by assuming that the radiator is a black body. When the Planckian (brightness) temperature and and the Maxwellian (kinetic) temperature correspond, then the gas is held to be in local thermodynamic equilibrium.
>Hank Roberts has done non-equilibrium in #112. …
Tim, I’m sure I don’t know more about it — I noticed Blair forgot that after a change in CO2, Earth’s heat takes time to reach equilibrium. I pointed it out and tried as usual for simple words. That took me a year to understand even as a notion!
Read me cautiously! At _best_ I’m useful here as a copy editor. Mostly I’m trying to find simpler, clearer words, knowing the explanations without the math are more poetry than physics. I long ago worked as a ranger=naturalist cave guide; that set my level. Someone asked, always, on every single cave tour: “How many miles of undiscovered cave are there here?”
Blair — this is helpful, it’s a new online simulator, try this one: http://www.seed.slb.com/en/scictr/watch/climate_change/challenge.htm
Eli, you might like this one too. It’s based on Tom Fiddaman’s work, link therewith.
Here’s one screenshot. http://farm2.static.flickr.com/1439/740529390_35e55d5dba.jpg?v=0
Gavin, I nominate this simulator for your ‘Start Here’ and links lists.
More people watch than read; this one ought to be in firmware in all the video-pods (grin).
re “Temperature isn’t a concept that applies to one molecule….”
While it may not be practical, I beg to differ. Theoretically (and really) you can have one molecule of a gas (or anything else) that has a mass of a few amu’s and is tooling around space at a velocity and therefore has kinetic energy (0.5mv2) and therefore has temperature ala 1.5kT.
re 127: “Does a radiated field have a temperature? Sort of. It is common to compare measured intensity to that of a black body and produce a “brightness temperature”.
I understand the concept, and maybe it’s a quibble, but the brightness temperature refers to the physical body that’s putting out the temperature-less E-M radiation.
“You have too many mixed questions to answer, but KE = 1/2 M V^2. period.”
Guilty; I’m trying to sort it out. I’m also trying to reconcile Feynman’s definition that K.E. = 3/2(r)kT where r is the #modes or degrees of freedom or (roughly) atoms/molecule. He doesn’t discount 1/2 m V^2, just says you have to include all masses and velocities of the molecule.
Re #132 RobB where you wrote:
I understand the concept, and maybe it’s a quibble, but the brightness temperature refers to the physical body that’s putting out the temperature-less E-M radiation.
It’s not a quibble if you are correct, so I used Google and found these:
http://en.wikipedia.org/wiki/Brightness_temperature
http://scienceworld.wolfram.com/physics/BrightnessTemperature.html
The brightness temperature is a value calculated using the wavelength and intensity of the E-M radiation from the body. For a blackbody, the temperature calculated at all frequencies will be the same, and will be equal to the body’s temperature found in the normal way.
For a solid or liquid the normal temperature is not due to the kinetic energy of the molecule. It is the energy of the molecular vibrations. IMHO, this makes it rather surprising that gases emit lines with the same intensity as the continuous radiation from a solid or liquid.
Thanks, Eli. Feynman’s use of “r” in the formula seemed odd to me too.
I think your distinction of “internal” and “kinetic” is easier to visually, though Feynman (and others) refer to it all as kinetic, by virtue of the actual kinetic energy from atom vibration and rotation internal to the molecule. In any case what I’m trying to verify is — does that internal energy affect the temperature? I.e. does absorption of E-M radiation per se, which I’m assuming goes into the “internal” energy, increase the temperature of said molecule? And by my calculations (but don’t bet the farm!), a BIG temp increase.
Alastair (134), et al: not sure if you agree or not. In any case to reassert, representing something with a “temperature” to maybe aid the comprehension is not the same as someting actually having temperature. Varying eneregy fields of Electrostatic and Magnetic flux do not have temperature. They come from things with temperature (and one can relate the things temperature with the peak intensity of the radiation accurately), and they can change the temperature of other things. But no temp for them….
re 132 Rod B: Google on specific heat of gases, and you find that the more modes of movement, the higher Cv and Cp. The numbers tells you more about the molecule than vice versa. Note Cp,Cv vary with T as more modes get activated at energies within the thermal continuum. Check out ammonia. There are several good expositions on the web on “heat capacity of gases.”
For the GH effect you need energy exchange at IR frequencies, not particularly Cp, but such exchange says there is a mode which would raise Cp so there is some connection.
Temperature is the difference from absolute zero. A molecule twitching and tapdancing after ingesting a photon is warmer than the same molecule beforehand, when it was sitting comatose and close to motionless.
re 133 Alsatair +1 Rod B: For me the part to get ones head around is “thermal equilibrium”, which is where (and only where) temperature is defined. At a finite temp. there will be a radiation field, modified by emissivity, through which matter exchanges energy with other matter on a continuing basis.
And yes, there will be local temperature fluctuations because quanta are lumps.
re 129 Alastair: As I said in 126, I think it is pretty clear that the system is mostly not in LTE. Have you explored the math of a non-LTE system?
Re #139
I got caught out by non-LTE, which is in the state of the thermosphere. It is not the same as not LTE. I have resorted to calling not LTE local thermal unequilibrium or LTU.
In non-LTE, the plasma becomes very excited because there are too few collisions to relax it. In LTU the radiation field is not isotropic. It exists at the base of the atmosphere where the absorption exceeds the emission, and at the top of the atmosphere the emission exceeds the absorption. The layer at the base of the atmosphere where this applies is only 30 m deep. The layer at the top of the atmosphere where this applies starts at a height of 6 km ie it includes half the the tropsophere, all the stratosphere and all the mesosphere.
A little thermodynamics. First, temperature is a macroscopic quantity. It does not apply to a single molecule. Look at the definition T=partial S/partial E. Now think of a single molecule–does it even have an entropy (apart from due to its chemical identity, I mean; remember we’re holding chemical potential, etc. constant). In point of fact the average kinetic energy will be 3/2 kT, so a temperature of a single molecule doesn’t make sense.
OK, now the question of the temperature of a radiation field. Well, the cosmic microwave background has a temperature (~3 Kelvins), and that is how we know anything about the Big Bang. That’s as real as anything.
Now on the question of the proportionality between energy and temperature. There’s nothing magical about 3kT/2. If you comfine your gas to 2 dimensions (as in an electron gas in a high-electron mobility transistor, or an adsorbed film on a surface, KE~kT). Likewise as the number of degrees of freedom of the molecule goes up, the proportionality constant (the specific heat) between energy and kT goes up. You can actually see this as you heat a gas up from a very low temperature. Initially, the temperature is too low to excite the quantized rotational and vibrational energy levels, so E~3kT/2. As T increases, you start to see more rotational and vibrational energy levels excited, and the specific heat actually increases. That is, you have to add more energy to get the same temperature rise. Now I’m sure this is review for most of you, but hopefully it refreshes memories of thermo or chemistry (at least if they are pleasant).
Ray (141): a quicky on part of your post — and I’m definitely not being argumentative over detail trivia, but I think this concept is important for understanding (at least by me!) the physics of absorption/emission and, getting really basic here, temperature. First, while maybe just inadvertant, I think S = Q/T (or E/T) (fill in the partials).
So while a single molecule will have a specific and precise kinetic energy greater than zero per Maxwell-Boltzman probability, it won’t have a temperature of its own??? Or when that single molecule bumps another or the wall it won’t impart some ot its KE (and in turn temperature)??? Makes no sense. The universal gas laws are derived starting with a sole lonely molecule — is that just convention???
My understanding is the 3 degreesK is specifically the temperature of the ubiquitous leftover soup of the Big Bang, not the common usage CMB radiation. Q: what is the temperature of the incoming solar radiation at, say, 1,000,000km from the earth???
I’ll respond to the last half of your post (and that of others) later; it served up good food for thought. Thanks.
Re #141 That does not affect the simple fact that the Earth system loses heat to space from the top of the atmosphere. Therefore the upper layers of the atmosphere must be losing heat, and are not in LTE. To compensate for the loss at the top of the atmosphere the air must be gaining heat somewhere, and basically the atmosphere gains heat at the Earth’s surface by absorbing radiation. This is the greenhouse effect shown by Horace de Saussure. The air at the base of the atmosphere is gaining heat, and so it is not in LTE either.
The current models see the whole of the troposphere as being in LTE and being homogeneous, ignoring the discontinuity at the top of the boundary layer. That is wrong.
Now that science has replaced religion as the custodian of the truth about how the world works, it is difficult for me to break down your belief that now it is the scientists who are preaching the word of God, and every thing they say is true.
The reason people are having trouble understanding the current theory is because it is wrong. The fact that we know that CO2 does cause climate change does not mean that the current theories are correct.
Ray, I would like to continue your thermodynamics lesson from “As T increases, you start to see more rotational and vibrational energy levels excited, and the specific heat actually increases. That is, you have to add more energy to get the same temperature rise.” If a greenhouse gas is present, vibrational energy levels can cause infrared radiation to be emitted, reducing the energy level of the gas. This means you need to add even more energy (eg. by IR absorption) to get the same temperature rise. Apparently, in the stratosphere carbon dioxide radiates out more energy than it absorbs, causing cooling.
I am trying to get back to my old question: does the greenhouse effect heat the air directly in the lower troposphere? When water vapor or CO2 absorb IR radiation, it is translated into kinetic energy, ie. heats the air. The increased temperature causes IR to be emitted, reducing the temperature. This cannot balance, or it would be impossible for air with greenhouse gas to warm up. So there must be some direct warming.
Air also warms via convection from the surface, so it might actually emit more IR than it gets from its greenhouse gases (as in the stratosphere), but this does not mean greenhouse gases cause a net loss.
If the lower troposphere is being warmed directly, how much of a role does the upper troposphere play, where radiation is escaping into space? I am having a hard time putting these two processes together.
Alastair, First the philosophical: I think there is sufficient truth in the Universe that both science and religion can be custodians should they choose–not to mention philosophy, literature, humor…
Now the science–if the energy in=energy out (or nearly so), you have LTE. And it is nowhere necessary for the models to assume homogeneity–although the troposphere is fairly homogeneous, and homogeneity is a reasonable local approximation throughout. The reason people are having difficulty with the science is because it is subtle.
Perhaps it would help both you and us if you would lay out all your problems with current theory in a systematic fashion. As I’ve been pointing out in the other thread–you have to know the likely effect of an error (even a systematic one) before you can gauge its significance.
Rod B. You are correct and thanks for the correction. It’s been a long time since stat mech. If you are looking at a single molecule in a macroscopic container, it will certainly interact with the walls. However, keep in mind that in a solid, motion is constrained (you no longer have the 3/2 kT for kinetic energy). The molecule can collide with the walls elastically (not losing energy) or inelastically (losing energy). If the collisions are elastic, we can approximate the walls as objects–and not worry about the molecular structure. For inelastic collisions, the molecule either excites an oscillation in the solid or it gains energy from the solid. However, the oscillations in the solid are quantized (as with any oscillator), so we have to describe this process quantum mechanically, and it’s easiest to do so in terms of phonons–quanta of vibration or sound. It doesn’t make sense to look at the molecules in the solid as individual molecules–their energetics within the solid is completely different than when they are on their own.
WRT solar radiation–it makes sense to use the Stefan-Boltzmann law. Solar energy density decreases as the square of the distance from the Sun. Temperature scales as the 4th root of the energy density, so temperature decreases roughly as the square root of distance.
Re 143 So do you suggest two regions, one where the Schwarzchild works, the other where we need formal field to mode coupling, or what? How close to what you want are the various LBL models?
Please wait.
Alastair is trying to get away to focus on writing his paper proving all climatologists are wrong. He’s said so repeatedly.
As long as we keep trolling for him here, baiting him to go on posting, distracting him from his work, he won’t ever get his work together in his own website and paper.
Going into his ideas off-topic in designated RC discussion threads does distract everyone from the topics at RC as well.
It’d be a kindness to everyone not to question Alastair further here, eh? Let him get his work together in one place so it’s coherent.
Asking questions in topics at RC just tempts him beyond the limit of his self control to repeat his ideas without writing them up in a scientific paper.
And until he does, they’re just frequently asserted beliefs, not science.
re 145: We are mostly in agreement. One minor continuing quibble (or maybe not…): it’s still the individual molecule vibrating within the solid or liquid that produces (or is the basis for), in part, the Planck radiation…., I think…
And — temperature of the emitting body, not of the actual radiation, scales to the fourth root of the radiated energy density. I don’t think the “temperature of the E-M radiation flux” halfway between the Sun and Earth is proportional (roughly) to 5000/(5.6×1021m2)…
Blair, As I said, it’s been a long time since stat mech, so I’m struggling with this as well. In part, we are falling victim to the limitations of language and visualization–necessary for understanding, but it only gives a piece of the story. For instance, we are talking about temperature AND about how an individual molecule will behave. However, temperature is a concept that only applies to fairly large aggregates of molecules. It is a concept that was developed when heat was still thought of as a substance (caloric), and that is why Boltzmann sought to make thermodynamics by deriving it from the physics of large numbers of molecules.
I think where we are getting confused is when we look at all “warming” as “temperature”. In reality what we are doing is adding energy to a system (or rather keeping it from escaping). Thermodynamics says when you do that the system has to heat up. But we’ve already seen there are other places the energy goes than kinetic energy–vibrational motion, rotational motion, even gravitational potential energy. Now when a molecule has a higher energy than surrounding molecules, there are a lot more ways for it to lose energy than to gain energy, so it will tend to thermalize–(that is move back to an energy close to 1/2 kt multiplied by the number of degrees of freedom). It can do this in a number of ways. It can fall from a great height, colliding with molecules to thermalize all the way down. It can lose vibrational energy via a collision or other interactions with surrounding molecules. It can emit a photon to relax back to its ground state. Some of these processes will heat the surrounding air. Some (e.g. photon emission) will not. However, half the photons emitted are now moving downward, so the molecules below, now have a flux of IR going downward and a flux going upward. More of them will absorb IR–and again, half the radiation goes down and half up. And so on, until IR photons are incident on the ground–or air near enough to the ground–we further warm the ground.
The key thing to remember is that you are adding energy to the system the system. That energy can warm things up. It can excite vibrational and rotational motion in molecules. It can melt ice or evaporate water. It can cause the atmospher to expand outward. It can warm water and land. However the important thing to remember is that you are increasing the energy of the system. Increasing the energy of a system always makes it less predictable. Does that help at all.
Re: #121 Absolutely. This “Fightin’ Illini” ( B.Sc.(Hon), 1967. U. of I, U-C) and Anteater (Ph.D., UC Irvine 1972) does indeed has strong opinions, and this ace organic chemist does not take cheap shots from anybody.