By raypierre , with the gratefully acknowledged assistance of Spencer Weart
In Part I the long struggle to get beyond the fallacious saturation argument was recounted in historical terms. In Part II, I will provide a more detailed analysis for the reader interested in the technical nitty-gritty of how the absorption of infrared really depends on CO2 concentration. At the end, I will discuss Herr Koch’s experiment in the light of modern observations.
The discussion here is based on CO2 absorption data found in the HITRAN spectroscopic archive. This is the main infrared database used by atmospheric radiation modellers. This database is a legacy of the military work on infrared described in Part I , and descends from a spectroscopic archive compiled by the Air Force Geophysics Laboratory at Hanscom Field, MA (referred to in some early editions of radiative transfer textbooks as the "AFGL Tape").
Suppose we were to sit at sea level and shine an infrared flashlight with an output of one Watt upward into the sky. If all the light from the beam were then collected by an orbiting astronaut with a sufficiently large lens, what fraction of a Watt would that be? The question of saturation amounts to the following question: How would that fraction change if we increased the amount of CO2 in the atmosphere? Saturation refers to the condition where increasing the amount of CO2 fails to increase the absorption, because the CO2 was already absorbing essentially all there is to absorb at the wavelengths where it absorbs at all. Think of a conveyor belt with red, blue and green M&M candies going past. You have one fussy child sitting at the belt who only eats red M&M’s, and he can eat them fast enough to eat half of the M&M’s going past him. Thus, he reduces the M&M flux by half. If you put another equally fussy kid next to him who can eat at the same rate, she’ll eat all the remaining red M&M’s. Then, if you put a third kid in the line, it won’t result in any further decrease in the M&M flux, because all the M&M’s that they like to eat are already gone. (It will probably result in howls of disappointment, though!) You’d need an eater of green or blue M&M’s to make further reductions in the flux.
Ångström and his followers believed that the situation with CO2 and infrared was like the situation with the red M&M’s. To understand how wrong they were, we need to look at modern measurements of the rate of absorption of infrared light by CO2 . The rate of absorption is a very intricately varying function of the wavelength of the light. At any given wavelength, the amount of light surviving goes down like the exponential of the number of molecules of CO2 encountered by the beam of light. The rate of exponential decay is the absorption factor.
When the product of the absorption factor times the amount of CO2 encountered equals one, then the amount of light is reduced by a factor of 1/e, i.e. 1/2.71282… . For this, or larger, amounts of CO2,the atmosphere is optically thick at the corresponding wavelength. If you double the amount of CO2, you reduce the proportion of surviving light by an additional factor of 1/e, reducing the proportion surviving to about a tenth; if you instead halve the amount of CO2, the proportion surviving is the reciprocal of the square root of e , or about 60% , and the atmosphere is optically thin. Precisely where we draw the line between "thick" and "thin" is somewhat arbitrary, given that the absorption shades smoothly from small values to large values as the product of absorption factor with amount of CO2 increases.
The units of absorption factor depend on the units we use to measure the amount of CO2 in the column of the atmosphere encountered by the beam of light. Let’s measure our units relative to the amount of CO2 in an atmospheric column of base one square meter, present when the concentration of CO2 is 300 parts per million (about the pre-industrial value). In such units, an atmosphere with the present amount of CO2 is optically thick where the absorption coefficient is one or greater, and optically thin where the absorption coefficient is less than one. If we double the amount of CO2 in the atmosphere, then the absorption coefficient only needs to be 1/2 or greater in order to make the atmosphere optically thick.
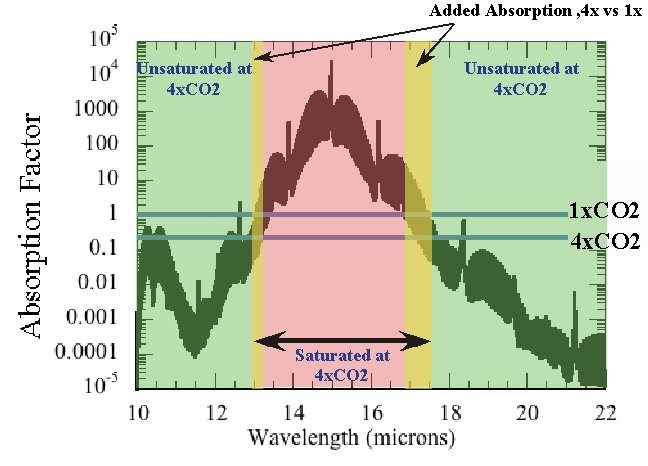
The absorption factor, so defined, is given in the following figure, based on the thousands of measurements in the HITRAN spectroscopic archive. The "fuzz" on this graph is because the absorption actually takes the form of thousands of closely spaced partially overlapping spikes. If one were to zoom in on a very small portion of the wavelength axis, one would see the fuzz resolve into discrete spikes, like the pickets on a fence. At the coarse resolution of the graph, one only sees a dark band marking out the maximum and minimum values swept out by the spike. These absorption results were computed for typical laboratory conditions, at sea level pressure and a temperature of 20 Celsius. At lower pressures, the peaks of the spikes get higher and the valleys between them get deeper, leading to a broader "fuzzy band" on absorption curves like that shown below.
We see that for the pre-industrial CO2 concentration, it is only the wavelength range between about 13.5 and 17 microns (millionths of a meter) that can be considered to be saturated. Within this range, it is indeed true that adding more CO2 would not significantly increase the amount of absorption. All the red M&M’s are already eaten. But waiting in the wings, outside this wavelength region, there’s more goodies to be had. In fact, noting that the graph is on a logarithmic axis, the atmosphere still wouldn’t be saturated even if we increased the CO2 to ten thousand times the present level. What happens to the absorption if we quadruple the amount of CO2? That story is told in the next graph:
The horizontal blue lines give the threshold CO2 needed to make the atmosphere optically thick at 1x the preindustrial CO2 level and 4x that level. Quadrupling the CO2 makes the portions of the spectrum in the yellow bands optically thick, essentially adding new absorption there and reducing the transmission of infrared through the layer. One can relate this increase in the width of the optically thick region to the "thinning and cooling" argument determining infrared loss to space as follows. Roughly speaking, in the part of the spectrum where the atmosphere is optically thick, the radiation to space occurs at the temperature of the high, cold parts of the atmosphere. That’s practically zero compared to the radiation flux at temperatures comparable to the surface temperature; in the part of the spectrum which is optically thin, the planet radiates at near the surface temperature. Increasing CO2 then increases the width of the spectral region where the atmosphere is optically thick, which replaces more of the high-intensity surface radiation with low-intensity upper-atmosphere radiation, and thus reduces the rate of radiation loss to space.
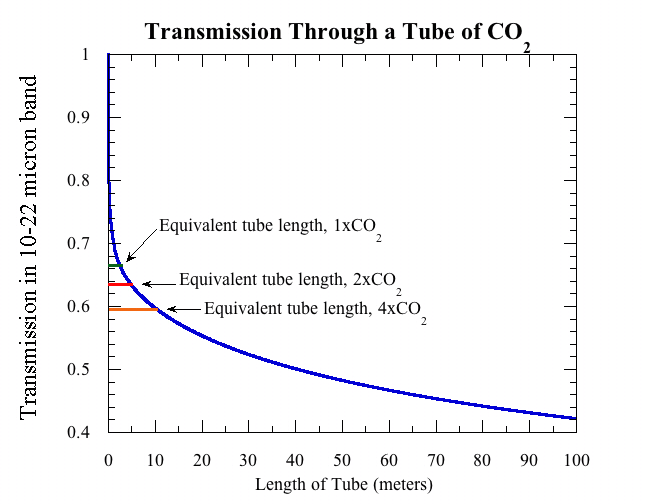
Now let’s use the absorption properties described above to determine what we’d see in a typical laboratory experiment. Imagine that our experimenter fills a tube with pure CO2 at a pressure of one atmosphere and a temperature of 20C. She then shines a beam of infrared light in one end of the tube. To keep things simple, let’s assume that the beam of light has uniform intensity at all wavelengths shown in the absorption graph. She then measures the amount of light coming out the other end of the tube, and divides it by the amount of light being shone in. The ratio is the transmission. How does the transmission change as we make the tube longer?
To put the results in perspective, it is useful to keep in mind that at a CO2 concentration of 300ppm, the amount of CO2 in a column of the Earth’s atmosphere having cross section area equal to that of the tube is equal to the amount of CO2 in a tube of pure CO2 of length 2.5 meters, if the tube is at sea level pressure and a temperature of 20C. Thus a two and a half meter tube of pure CO2 in lab conditions is, loosely speaking, like "one atmosphere" of greenhouse effect. The following graph shows how the proportion of light transmitted through the tube goes down as the tube is made longer.
The transmission decays extremely rapidly for short tubes (under a centimeter or so), because when light first encounters CO2, it’s the easy pickings near the peak of the absorption spectrum that are eaten up first. At larger tube lengths, because of shape of the curve of absorption vs. wavelength, the transmission decreases rather slowly with the amount of CO2. And it’s a good thing it does. You can show that if the transmission decayed exponentially, as it would if the absorption factor were independent of wavelength, then doubling CO2 would warm the Earth by about 50 degrees C instead of 2 to 4 degrees (which is plenty bad enough, once you factor in that warming is greater over land vs. ocean and at high Northern latitudes).
There are a few finer points we need to take into account in order to relate this experiment to the absorption by CO2 in the actual atmosphere. The first is the effect of pressure broadening. Because absorption lines become narrower as pressure goes down, and because more of the spectrum is "between" lines rather than "on" line centers, the absorption coefficient on the whole tends to go down linearly with pressure. Therefore, by computing (or measuring) the absorption at sea level pressure, we are overestimating the absorption of the CO2 actually in place in the higher, lower-pressure parts of the atmosphere. It turns out that when this is properly taken into account, you have to reduce the column length at sea level pressure by a factor of 2 to have the equivalent absorption effect of the same amount of CO2 in the real atmosphere. Thus, you’d measure absorption in a 1.25 meter column in the laboratory to get something more representative of the real atmosphere. The second effect comes from the fact that CO2 colliding with itself in a tube of pure CO2 broadens the lines about 30% more than does CO2 colliding with N2 or O2 in air, which results in an additional slight overestimate of the absorption in the laboratory experiment. Neither of these effects would significantly affect the impression of saturation obtained in a laboratory experiment, though. CO2 is not much less saturated for a 1 meter column than it is for a 2.5 meter column.
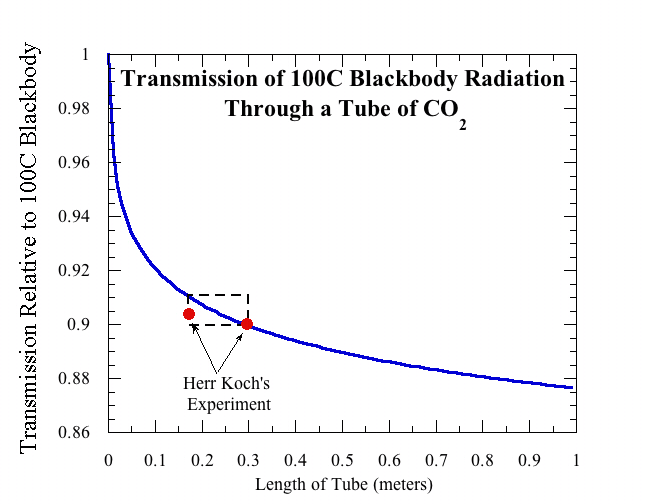
So what went wrong in the experiment of poor Herr Koch? There are two changes that need to be made in order to bring our calculations in line with Herr Koch’s experimental setup. First, he used a blackbody at 100C (basically, a pot of boiling water) as the source for his infrared radiation, and measured the transmission relative to the full blackbody emission of the source. By suitably weighting the incoming radiation, it is a simple matter to recompute the transmission through a tube in a way compatible to Koch’s definition. The second difference is that Herr Koch didn’t actually perform his experiment by varying the length of the tube. He did the control case at a pressure of 1 atmosphere in a tube of length 30cm. His reduced-CO2 case was not done with a shorter tube, but rather by keeping the same tube and reducing the pressure to 2/3 atmosphere (666mb, or 520 mm of Mercury in his units). Rather than displaying the absorption as a function of pressure, we have used modern results on pressure scaling to rephrase Herr Koch’s measurement in terms of what he would have seen if he had done the experiment with a shortened tube instead. This allows us to plot his experiment on a graph of transmission vs. tube length similar to what was shown above. The result is shown here:
Over the range of CO2 amounts covered in the experiment, one doesn’t actually expect much variation in the absorption — only about a percent. Herr Koch’s measurements are very close to the correct absorption for the 30cm control case, but he told his boss that the radiation that got through at lower pressure increased by no more than 0.4%. Well, he wouldn’t be the only lab assistant who was over-optimistic in reporting his accuracy. Even if the experiment had been done accurately, it’s unclear whether the investigators would have considered the one percent change in transmission "significant," since they already regarded their measured half percent change as "insignificant."
It seems that Ångström was all too eager to conclude that CO2 absorption was saturated based on the "insignificance" of the change, whereas the real problem was that they were looking at changes over a far too small range of CO2 amounts. If Koch and Ångström had examined the changes over the range between a 10cm and 1 meter tube, they probably would have been able to determine the correct law for increase of absorption with amount, despite the primitive instruments available at the time.
It’s worth noting that Ångström’s erroneous conclusion regarding saturation did not arise from his failure to understand how pressure affects absorption lines. That would at least have been forgivable, since the phenomenon of pressure broadening was not to be discovered for many years to come. In reality, though Ångström would have come to the same erroneous conclusion even if the experiment had been done with the same amounts of CO2 at low pressure rather than at near-sea-level pressures. A calculation like that done above shows that, using the same amounts of CO2 in the high vs. low CO2 cases as in the original experiment, the magnitude of the absorption change the investigators were trying to measure is almost exactly the same — about 1 percent — regardless of whether the experiment is carried out at near 1000mb (sea level pressure) or near 100mb (the pressure about 16 km up in the atmosphere).

Timothy (246) says “the bands and the lines broaden as the result of pressure and temperature. Likewise, there is lifetime broadening of a single line simply as the result of the uncertainty principle as it applies to energy and time.”
Do the lines actually broaden (increase their miniscule bandwidth) or become more available for absorption?
Why wouldn’t the uncertainty principle just as easily/often narrow the lines. (And I trust we’re not counting on Heisenberg for AGW validation [;-)….)
The lines are what’s observed in the instrument, photographed — the “line” is not the actual specific amount of energy transferred in any particular event.
It’s a sum over time of observations.
Same issue as with the question about specifying “the” altitude at which radiation escapes to space.
Rod B (#250) wrote:
Typically I don’t assume that someone is agreeing with me or disagreeing with me: I am simply trying to address the question that has been posed – to the extent that I understand the issues which are involved. Obviously there was a little more involved in 242, but in large part that was meant to be somewhat entertaining for you and others and perhaps even a little playful for those who wanted to examine it a little more closely.
But even when I disagree with people, while I might get annoyed, perhaps even strongly annoyed, I at least try not to take it personally. Afterall, whether we realize it or not, there is always more that binds us than separates us. As I look at the world, the “us vs them” which many view the world in terms of is at worse temporary and ultimately unnecessary. While I am not Buddhist, I would regard it as a “veil of maya,” an illusion which we should try and help one another escape from – if possible. But there are oftentimes other demands which for one reason or another must take precedence – at least for the time being.
Rod B (#239) wrote:
[Thinking for a moment…]
There will be typically be some difference between the two if the system is not in local thermodynamic equilibrium, and the more distant the system is from local thermodynamic equilibrium the greater the difference may be. As I understand it, a large part of the reason lies in the fact that radiation gets re-emitted before collisions can take place between the molecules which would otherwise equalize the two temperatures. Instead, the temperature of the re-emitted radiation will tend to reflect the temperature of the incident radiation.
Rod B (#240) wrote:
Well, regarding the photons “bearing labels,” as I understand it, the distribution of solar radiation will be a particular shape with a peak determined by the temperature of the sun and the same will be true of the blackbody radiation emitted by the earth’s atmosphere and surface. But in both cases, the distribution is probablistic, such that if you were to select a particular photon at random, some frequencies would be far more probable than others, but it could be at any given frequency. Likewise, no matter what direction a particular photon has, it could be a photon which has or has not be re-emitted from the surface or the atmosphere – simply because of the existence of scattering and the possibility (no matter how small it might be) that it has either been or not been absorbed by at least one molecule along its way.
You wrote,
“… but am bothered by its conclusive nature.
“While just an partially educated hunch, my basis for being a skeptic rests greatly on the molecular/atomic/sub-atomic very precise physics that goes on between radiation and gas molecules. A physics that I gather is still based a bunch on assumptions and reasonable scientific guesses.”
Well, in the final analysis, no knowledge is conclusive, at least not in any Cartesian sense.
At that level, one could argue that any given item of knowledge is merely a reasonable guess, scientific or otherwise. However, physics is capable of a degree of justification rarely encountered in everyday life – because of the many different lines of inquiry and wide body of evidence upon which a given scientific conclusion may be based. Granted, some of the tentative conclusions won’t achieve that level of justification – our discovery of the world is an ongoing process. But even the more tentative conclusions aren’t what we would ordinarily call “reasonable guesses” in as much as they are part of a systematic, scientific process.
Moreover, I would argue that much of our knowledge regarding the interaction of matter and electromagnetic fields is quite exacting and has achieved a great deal of justification. No doubt there are softer areas around the boundaries, but I suspect that such areas are far smaller than what many might suppose.
Re 248 Chase Not necessarily speaking for Alastair, I assert that, for all GHG (except some H2O spectra), we need to think in terms of lines, not bands, and we need to recognize that many of the interactions between the mechanical and radiative modes occur at the edge of, or out of, equilibrium, and that this failure is worst at the top and bottom of the atmosphere (and probably in violent storms). I have not found a LBL radiative transfer (RT) model that is self consistent in terms of temperature and the various coming and goings of quanta, but then I too have a lot to learn especially about all the historical work on RT.
RE 251 Rod B Lines represent the absorption or emission probabilities versus frequency of particular transitions, characterized by a functional form and frequency. As the function broadens through radiationless interactions it usually flattens so as to preserve its integral over frequency, the oscillator strength.
Allan Ames (#254) wrote:
I agree.
Personally I think that the material you brought up is fascinating and I hope that I will be able to give it the attention that will be required to understand it. Likewise, assuming the motivation, I believe that Alastair stands roughly the same chance as myself to understand it. I hope he will make the effort, in part because this acknowledges that he is right – to a degree.
At the same time, I believe that understanding things in terms of LTE is useful, much like Gavin’s “Simple Model,” although it obviously much more accurate. At the same time, taking into account the nonlocal equilibrium effects will be an improvement – to the extent that they are not already taken into account.
At the same time, it should be acknowledged that the author of the second paper admits that what he is doing is an approximation which does not take into account all of the effects (such as scattering). As such it is also an approximation. But some approximations are nevertheless better than others.
But it should also be acknowledged that any calculations which are performed will generally be at the expense of other calculations. There are always tradeoffs. For example, to the extent that the equations which he gives are more complicated than those assumed in an LTE model, when they are implimented, we may need to reduce the resolution of the model in order to perform the calculations within a reasonable amount of time. Or alternatively, we may need to keep certain other simplifying assumptions involving convection or humidity as we increase computer power – even though we know that they are only approximations. But what is most important is the net accuracy of the projections and the rate at which the calculations are performed. As such this should be the standard by which we judge the various tradeoffs.
re Timothy (253) It makes sense that equilibrium exists in order for Planck temperature to equal Maxwell’s temp. But, your explanation is of apples, not oranges. I equate Planck temp (actually radiation) with his black/graybody radiation with the temp calculating the total radiation and the peak wavelength. This has nothing to do with re-emission and relaxation of bond energy ala greenhouse gasses…. Do it??
My photon labeling was far too coarse, and you’re correct. Most photons you could classify with a pretty good probability, but no certainty. Others one could miss terribly.
I wasn’t meaning to be philosophical with “we don’t know for sure”. Quantum physics says I might not be in Texas the next minute. Though I may have come across as too flippant (I’m a flippant kinda guy!), one of my areas of skepticism rests in the old argument: does adding more CO2 really significantly increase the absorption of the Earth’s radiation. And while the physics and science is predominately good and accurate, I’m not convinced that some of the physics and modeling assumptions and averages are known well enough or are close enough. It sounds like minutia, but this process of line/band spreading and adjusting of the global averages from it seems a highly leveraged process to me. While most here would strongly refute my contention, I am not convinced we know exactly (are “more accurately”, if you will) how it works. Though the understanding and classification of molecular bonding energy levels (in the thousands) seems quite detailed (no way for me to know how accurate, but I have no reason to dispute it), the absorption physics is too fuzzy for me. It still is line absorption, not “band” absorption and some say that the granularity is very small, e.g. absorbtivity (??) going for near 1 to near 0 in less than 0.01um. It would be a massive undertaking and likely days of supercomputer time to determine absorption factors and numerically integrate the marginal absorption over the entire IR with varying pressures and temperatures… and then project that globally and annually for 100 years. Maybe the averages and assumptions ― “5.4ln[C/C0] is about right” ― are O.K. But I’m skeptical. Teeny-tiny tweaks could have a multiplied leveraged effect on the global situation — and warming.
Rod B (257) wrote:
I would say that a blackbody absorbs and re-emits radiation at all parts of the spectra – although the peak is determined by the temperature. Greenhouse gases are realistic bodies which absorb and re-emit only in certain parts of the spectra.
I am going off of a discussion in A Saturated Gassy Argument. Like you, I believed that the blackbody curve had little to do with absorption and re-emission by gases.
In response to something written by DeWitt Payne:
… I had stated:
DeWitt Payne had responded:
Bart Paul Levenson then corrected Payne:
However, a more extensive discussion of the same topic took place between Ray Ladbury and Ray Pierrehumbert in 154.
Anyway, I will respond to the rest of your post, but it probably helps to break things up.
PS to 258
I had cut off the bit by Bart Paul Levenson.
The full quote is from the discussion in A Saturated Gassy Arguement is:
Hopefully that will help my post make a little more sense.
In essence, the atmosphere is a realistic body which absorbs and re-emits radiation by means of greenhouse gases in the infrared where the radiation is “realistic body” radiation. As part of the atmosphere, all greenhouse gases have the same temperature, but different gases absorb and emit radiation in different parts of the spectra.
This is covered in more detail in the exchange between Ray Ladbury and Ray Pierrehumbert in the post #154 from the discussion following A Saturated Gassy Argument.
[[Why wouldn’t the uncertainty principle just as easily/often narrow the lines. ]]
Because the uncertainty is in the position of the lines, not their width. The broadening is a secondary effect, not a primary reality.
[[does adding more CO2 really significantly increase the absorption of the Earth’s radiation.]]
Yes.
Sources of Uncertainty
Rod B (#257) wrote:
Not a problem. But I try to be accurate, and I have the deepest respect for physics – although once you get to things like string theory I am not so sure. I guess I would have to say that the jury is still out.
[Quick Note: I am probably going to keep my response to just the quotes above – as it has already gotten rather long.]
Well, we know that it should – and by a little over a degree Celsius, directly. However, some of the calculations that would have to be performed to “derive” a number like climate sensitivity from well-established physics and the exact geometry of the land, oceans, etc. would obviously be far too complex. Not that they actually use this particular “constant” anyway, not for the models themselves, instead it is something which will fall out of the calculations of a given model. Likewise, the “adjustment” of global averages in terms of temperature isn’t something that one would plug into the models. But I don’t know enough to say how they handle the initial temperatures when they begin a given run.
What follows are some of the sources of uncertainty which I can see, but it should be kept in mind that this is coming from someone who is not an expert, but merely on the outside looking in.
There are numerous points at which they have to make “simplifying assumptions,” for example, in calculating fluid behavior, but these are no doubt fairly good approximations. But I believe that one of the bigger sources of uncertainty is the matter of resolution, that is, how coarse is the grid? How many layers do you divide the atmosphere into?
The stratosphere is divided into roughly a handful at this point – not that this will have that much of an effect upon the behavior of the system. The troposphere more like fifteen. How many layers do you divide the ocean into? This varies. And not all of the grid is spatial, either. For example, they no doubt have a grid of sorts for the treatment of spectra. I believe that is what the “radiation codes” are about.
To make the calculations “exact” one would have to have a continuous grid in space and time. But even then it wouldn’t be exact insofar as you wouldn’t know exactly how matter is layed out, for example, in terms of the atmospheric constituents. Then of course calculating the behavior of ice is not something that one would do in terms of the fundamental equations of quantum mechanics, not for some time to come. And something similar would no doubt come into play with the radiation codes as well. How do the various atmospheric constituents interact?
Well, the fundamental physics is known very exactly, but how molecules interact with one another even when they are molecules of the same exact makeup would be beyond our ability to solve exactly. Physicists have done something like this for standing water, analyzing its behavior reductionistically in terms of quantum mechanics such that the actual properties of water fall out of the equations, but even then there must be a grid of some sort and supercomputer power. Nevertheless, quite an accomplishment – and something which I find completely mind-boggling.
But the climate calculations involving ice doesn’t even begin to approach this in terms of its level of complexity. In fact, as the climate models have been done so far, all ice is the same. It melts uniformly – although Hansen has been doing calculations involving the effects of carbon pollution on the albedo of ice – and has found that in terms of current trends in the arctic this is as important as the increased levels of thermal radiation being absorbed by ice. But then you want to incorporate the nonlinear response of ice to its environment – and they are only beginning to work on this.
Likewise, Kirchoff’sLlaw is an approximation of sorts – a fair approximation, but an approximation nevertheless. In actuality climate modelers have already moved beyond Kirchoff’s Law in their calculations. Optics involving nonlocal thermodynamic equilibria. In fact, someone has been able to treate the problem in terms of exact integrals – but found it necessary to avoid dealing with certain phenomena such as scattering.
To look at a completely different level which we wouldn’t even begin to calculate in terms of physics, there is the behavior of organic matter (chum experiments in which one attempts to determine how much methane and carbon dioxide will be release with different degrees of mixing and at different temperatures. With this sort of thing they have to follow a well-defined recipe so that their experiments are reproducible..
But how about life? How many species of plants do you incorporate? On land? In the ocean? How many distinct levels of density do you assume? How do you model their responses? They are already dealing with these issues – and how one has to limit the calculations in terms of resolution. If I remember correctly, the number of species roughly a handful – although no doubt this will change. But then what about economies? Actually combined economy/climate model calculations are already being performed.
Given all this complexity, the calculations seem staggering. And currently we have computers capable of performing trillions of calculations per second, so this is doable at a certain level of approximation. Moreover, many of the “errors” with respect to one set of calculations will tend to be cancelled out by others – in the same way that the absolute level of error in predicting something which follows a bell distribution will grow as the square root of the population.
But more accuracy is always preferable. Nevertheless, anytime you try and improve upon a particular set of calculations, you have to keep in mind the fact that if the calculations are more intensive there, then certain other calculations will have to have some of their accuracy sacrificed, or the calculations will take longer or you will have to invest more in computers.
However, they do not tweak their calculations to make them fit the observed behavior of the climate system at a particular place or at a particular time. The equations are generalized. They may tweak global parameters – but their are very few of these to tweak. If they are to improve the modeling of climate behavior, the only thing they can do is improve the modeling in terms of the generalized equations, improve the initial data, or improve the resolution in one way or another.
As far as objectively judging the accuracy of their models in projecting future trends, there are a number of things they can do. They can compare their modeled behavior to actual empirical measurements and observations. They may perform multiple runs with slightly varied initial conditions to get a sense of how sensitive the system is to nonlinear behavior. They may improve the resolution for specific sets of runs. Or they can compare the trends projected by one model with those of another. In fact they do all of these.
But as for the accuracy of their calculations over a hundred years, Gavin and other climatologists with making calculations that far into the future – although we undoubtedly get a good sense of the trends which will be involved. Actually the biggest source of uncertainty lies in population, economies in terms of their behavior and response, and the extent to which we are able to control our emissions. These sources of uncertainty are in fact fairly negligible – for the next forty years. What we do today and for the next two or three decades will have very little impact upon what happens over this period of time.
But after that things begin to diverge – and more dramatically over time – largely due to what we do today and for the next several decades.
I’m almost getting there. There are still some details that seem poorly defined. First, I assume Planck radiation, commonly but technically incorrectly called “blackbody radiation”, is a function of wavelength and temperature of the radiating body with the emission by wavelength a smooth continuous curve (with the oddly skewed bell shape) over the entire spectrum but practically within a band with edges determined by the temperature. That same body will absorb the exact same radiation profile. Graybodies are those with emissivity less than one (and greater than zero) which means the total radiation (and absorption) is less than that of a blackbody, but such radiation curve is similar in shape, continuity and edges. For all practical purposes the emissivity does not vary by wavelength but is constant over the spectrum. This is commonly accepted for solids and liquids, but there is some uncertainty about gasses — I’ve seen many yesses and no’s. Gasses certainly absorb Planck-type radiation, like that emanating from the surface of the Earth in a smooth continuous function based on the temperature of the surface, which is derived from the 1/2mv2 kinetic energy of the ionized/charged molecules, atoms, and electron within the surface.
But gasses do not absorb radiation in a smooth continuous function, but rather in a highly discontinuous function strongly determined by the wavelength of a particular discrete extremely narrow band of this radiation. Secondly, it does not go into the 1/2mv2 kinetic energy of the gas molecule (and in turn increase its “pudding” which as I’ve said is “temperature” if it happens to a bunch of molecules — sorry!), but rather into the molecular bond energy (translation or bending oscillation) or the molecular rotational energy, or, in rare examples at shorter wavelengths, the electron energy level. Best guess for now is that this energy absorption does not increase the molecules’ temperature, though there have been conflicting opinions stated here. If it does not increase the temperature of the mole of molecules, it can’t be absorbed Planck-type radiation — though before it got absorbed and transferred it was. Does anybody accept or refute this? OTOH maybe it counts as Planck because it could later (soon though) turn into temperature with collisions and transferring bond energy from molecule #1 to kinetic energy in molecule #2. Does anybody know for sure??
Following the above thought then, if the molecule re-emits the earlier absorbed energy (again taking it from its bonds or rotation), the emission can’t (???) be Planck-type. Or is it? If not, I have no idea what type it is.
Going one further, assuming the above, can not the gasses still emit Planck-type radiation, separate from its bonding energy, by virtue of the gas’s kinetic energy from those molecules that have been ionized or have dipole moments (???? don’t know about that…) and based on the temperature of the atmosphere’s “surface”, wherever that might be? And this radiation will be a continuous function, not a pile of discontinuous discrete lines, and tend to cool the molecules.
I understand that some of the visible spectrum is absorbed by clouds (liquid) and that some of that is re-emitted toward Earth. Is this absorption wavelength specific or is it Planck-type coming and going??
Any thoughts?
ps one of the things that is confusing things is the generic and common use of “blackbody” to mean “Planck-type”, which comes in both blackbody (e = 1.0) and graybody (e not have the same temperature… do they???
A different quicky: Barton (260) says: “…the uncertainty [principle] is in the position of the lines, not their width…”
Got ya. Makes sense. I assume the uncertainty could move the line left or right, in any case having the effect of broadening the original line. Thanks.
repeating my ps paragraph from 263, which got clobbered by my attampt to say “e [less than sign] 1.0”
ps one of the things that is confusing things is the generic and common use of “blackbody” to mean “Planck-type”, which comes in both blackbody (e = 1.0) and graybody (e less than 1.0) forms. I suggest we adopt the popular but technically incorrect term of blackbody, and when we mean a true blackbody we call it a “blackbody with an e of 1.0”. But somethin’. I could buy Barton’s “realistic” term, though I don’t accept the e varying with wavelength part (with the possible exception of gasses ala the pontificating above.)
Rod B (#264) wrote:
I will have to look at the earlier post a little later – currently I have some laundry going and a big project of sorts which I am trying to get a bit done on during the weekends. (Last week was a little busy for me, too – several twelve hour days at work.)
However, as far as realistic bodies go, here is a somewhat oversimplified example, but consider a blue book…
The book absorbs all visible light except for the blue light that it scatters. Now its emissivity will be high in those other parts of the visible spectrum, so you might expect it to glow in those. Except of course it is room temperature, and the vast majority of light which it re-emits will be in the infrared part of the spectrum. The blackbody curve simply becomes too shallow by the time you reach the visible part of the spectrum. So it absorbs the other parts of the visible light without emitting in them.
However, if you have bodies which are good absorbers of infrared light in certain parts of the electromagnetic spectra, they should also be equally good emitters in the same parts of those spectra. And the same principle applies, more or less, to gases. Anyway, this is how I understand it. There will be more variation in the case of gases, for example, due to the effects of nonlocal thermodynamic equilibria, but this becomes important only at certain pressures and temperatures for various gases. So long as nonlocal thermodynamic equilibria are not an issue, one should be able to calculate an emissivity at each wavelength which will result from the mixture of gases, where all of the gases are at the same temperature, and thereby treate the atmosphere at a given temperature and pressure as a realistic body.
*
We live in a world that is stranger than we can see. The land glows brightly in the infrared, appearing white to eyes specially adapted to it. Above the land at somewhat longer wavelengths the atmosphere is like a glowing fog, strangely-colored, with more distant objects shading to different colors than those nearby due to their different colors being faded and washed out by the vapors inbetween.
[[But gasses do not absorb radiation in a smooth continuous function, but rather in a highly discontinuous function strongly determined by the wavelength of a particular discrete extremely narrow band of this radiation. Secondly, it does not go into the 1/2mv2 kinetic energy of the gas molecule (and in turn increase its “pudding” which as I’ve said is “temperature” if it happens to a bunch of molecules — sorry!), but rather into the molecular bond energy (translation or bending oscillation) or the molecular rotational energy, or, in rare examples at shorter wavelengths, the electron energy level. ]]
Almost all (> 99%) of increases in a molecule’s level of energy will be quickly collided out and distributed among neighboring molecules.
Re #266 Barton,
do you have a reference for “Almost all (> 99%) of increases in a molecule’s level of energy will be quickly collided out and distributed among neighboring molecules.”? I would very much like to see the calculations, or the theory behind that.
Cheers, Alastair.
re #265 (Timothy) You raise some interesting things to contemplate. Is it accurate to say a true blackbody (at least liquids and solids for now) will absorb exactly as it emits, but does not emit exactly as it absorbs, ala the blue book (black book??) which reflects/scatters visible blue but emits no visible wavelengths despite it absorption of them.
2) The blue book is clearly absorbing with an absorption coefficient dependent on wavelength — if its reflecting blue it can’t be absorbing it. Does this put a chink in my assertion that absorption coefficients are independent of wavelength (again talking of only liquids and gasses)? Would it also apply to emissivity (if we’re talking of something less than a pure blackbody where a = e)?
3) I would think a gas emission would be at exactly the same wavelength as its absorption (ignoring the “spreading for the sake of discussion): it absorbs discrete wavelengths based on its internal discrete energy levels, and can emit by relaxing those same energy levels — much like the light absorbed and emitted via electron level energy changes. delta Energy = hf, coming and going. Then I’m still contending (asking?) that this discrete emission for a gas is not Planck radiation, by definition, which emitted radiation is determined only by temperature stemming from a Maxwell distribution of kinetic energy. Also I would think the gas’ discrete specific radiation is independent of temperature, other than its potential goes away if the molecule loses the internal bonding energy through collisions — which might increase temperatures.
re #266 Barton says “Almost all (> 99%) of increases in a molecule’s level of energy will be quickly collided out and distributed among neighboring molecules.”
This would be in agreement with (one of) my contention. Though you are also saying that the molecule’s re-emission is theoretical and highly unlikely, as opposed to transferring its energy through molecular collisions, which can increase the atmospheric temperature. Do you concur with the last part — increasing temp?
Alistair, Re #219
I do not think the wings of the lines are irrelevant. The whole point of the original article was the soft saturation of the absorption in raypierres plot of absorption with distance. The wings of the lines cause this, mainly.
In #230 you say: *I am arguing that the emissions to space come from between the lines and from between the bands.*
Exactly, that is why the wings are important. As they creep in with concentration increase, it is like a set of blinds closing. The line centers are opaque. this forces the blackbody trying to radiate between them to adjust to higher temperature to maintain power balance.
The other contribution to the soft absorption satuation tail, in principle, are weaker lines, at the edge of the band, which come into prominence as the concentration (optical density) is increased. However, these do not contribute as much as the main center lines to increase in integrated absorption with concentration of CO2.
DO the following calculation. Assume two lines, 1 and 2 with identical lorentzian lineshapes, and cross-sections sigma1 and sigma2. sigma2 = R sigma1 with R
Re #270 seems like my post got cut off …
DO the following calculation. Assume two lines, 1 and 2 with identical lorentzian lineshapes, and cross-sections sigma1 and sigma2. sigma2 = R sigma1 with R
[Response: Don’t know what is going on here, but be careful with < signs (use & l t ; instead….) – gavin]
The “less than” followed by a “greater than” sign get interpreted as HTML and I think it just assumes you’re trying to code the end of a paragraph and truncates. Might check your /View/Character Encoding and see what’s being done to what you type by the too helpful software.
Try “view source” on this page — when I do that I see Gavin’s successful “less than” sign as code, and his explanation how to write it as different code.
I don’t know if I can even paste back what Gavin wrote, if there’s nothing following this line, try ‘view source’ for this as well:
be careful with < signs (use & l t ; instead…
Re #270 & 271. How about you showing the calculations? I doubt I could do them anyway.
Re #270 and #271 Sorry to crud up the thread. Hope this is better.
Do the following calculation: Assume two lines, 1 and 2 with identical lorentzian lineshapes, and cross-sections sigma1 and sigma2. sigma2 = R sigma1 with R less than 1.
We are interested in the derivative, with concentration (or OD at line center) of the integrated absorption for each line. Form the ratio and call it Q.
Plot Q vs. OD= sigma1*n*L for various values of R. I swept OD from 0.1 to 500 ( 10km/25m = 400) for R rangine from 1 to 1e-5.
For R=1, Q=1, of course. For OD very small ( say 0.1) then Q equals R. As the OD increases, Q increases, but never gets to 1. This means that a strong line alweays contributes more to the incremental absorption than a weak line at any concentration.
The exact amount depends on the details of the far wing shape of the lines ( about 10 to 20 times broadening parameter (HWHM)at the very large OD’s for main lines of CO2 at 15um. this is why knowing the wings is so important. Plot the function we are integrating. It is basically the lineshape with the center stomped out by the exp(-sigma*n*L* s(f)) factor (s(f) being the lineshape).
Because the weak lines at the edge of the branch( those at about 50% transmission since we are only concerned with ~doubling CO2) are fewer in number than the main lines in the center of the branch, their contribution will be further reduced.
I still think checking the exact lineshapes, rather than just assuming Lorentzian’s as HITRAN does, is important. We have this part of the problem under our control. It just takes time and spectrometers. Why introduce error right at the begining of the GW problem if we don’t have to. This directly impacts the Radiative forcing curves vs. CO2 concentration from the IPCC report which is important for deciding if there is any time left to do anything, and how high temps may go if we don’t.
There emay be a lot of lines, but the problem is surely much much smaller than the human genome project, and is maybe just as important.
Re #273
I wrote some short Matlab files. If anyone wants to check what I did, I can send them.
Here is psuesdo Mathematica language of what I’m talking about:
The integrated tranmisions up through atmosphere for each line. (Yes n is a function of L, not important here, just total OD=sigma*n*L).
n=CO2 concentration
L= thickness of gas slab we are looking through
sigma = absortption cross section for each line
T1(f) = Integral( df exp(- sigma1 * n* L *s(f)) )
T2(f) = Integral( df exp(- sigma2 * n* L *s(f)) )
Taking s(f) as lorentzian: s(f) = 1/( (f/G)^2 +1).
Take G=1 to normalize frequency to broadening parameter.
OK since we are only interested in ratio, below.
dT1/dn = Integral( df (-sigma1 * s(f)*L) exp(- sigma1 * n* L *s(f)) )
dT2/dn = Integral( df (-sigma2 * s(f)*L) exp(- R*sigma1 * n* L *s(f)) )
These integrals are just the lineshape with the center suppressed by the tranmission. Only the wings contribute when sigma*n*L is big.
A1(2) = 1-T1(2) for absorption.
Q = (dT2/dn) / (dT1/dn).
Plot Q vs. n or (OD =sigma*n*L in range 0.1 to 500),
for variuos R’s like R=1 (equal line strengths) down to R=1e-5 ( a very weak line).
Dave,
Thanks for letting us see those calculations. It helps in understanding your objections. However, they are not really valid. Let me explain why.
First, the Lorenzian line shape is only a first approximation. Calculation of the real wave shape is even more complicated than that. Secondly, the real wave shapes are being calculated and used in the models. The HITRAN data base only provides the line positions. When I criticise the radiation models I am told that I am wrong because of the care that is taken with these lines, but they are irrelvant to my objections.
On page 99 of Goody & Yung (the planetary radiation bible) they write:
If the composition is held constant, all of the ni [number density of the ith species] are proportional to the total pressure and (3.51) gives the important result, common to all impact theories, that the line width is proportional to the pressure [my emphasis]
Of course, doubling the CO2 concentration does not maintain a constant composition, but the change in pressure as a result of increasing CO2 from 280 ppm to 560 ppm is trivial. An increase in atmospheric pressure of 0.0280% is not going to cause the changes in global climate which are happening now. That is less than 1 mb!
The main greenhouse gas on Earth is water vapour. The way that CO2 influences the water vapour concentration and so the clouds (and the surface ice) is the answer to how CO2 affects the global climate. The venetian blind fine adjustment that you describe does happen, but it is trivial when compared with the velvet curtain effect produced by clouds.
The CO2 lines are saturated – optically thick – and this saturation happens within 30 m of the surface. Double the concentration and the saturation happens in the top 15 m. The air at the surface of the Earth gets warmer, there is more evaporation and less ice cover.
All that fancy maths with the Hamiltonians they use is irrelevant. It won’t stop the Arctic sea ice melting. The Arctic will become an ocean again with a maritime climate rather than the pseudo continental climate it has at present. The effects of that will spread to the Southern Hemisphere through the tele-connections that are only now being discovered.
The summer melt of the Arctic sea-ice is proceeding at an unprecedented rate. You have all been warned!
[[Re #266 Barton,
do you have a reference for “Almost all (> 99%) of increases in a molecule’s level of energy will be quickly collided out and distributed among neighboring molecules.”? I would very much like to see the calculations, or the theory behind that.]]
“Under atmospheric conditions of interest, the time between collisions [is] usually much shorter than the natural transition lifetime.”
Hanel, R.A. 2003. Exploration of the Solar System by Infrared Remote Sensing. Cambridge, UK: Cambridge Univ. Press. p. 100.
For the amount of energy dE transferred, we can calculate the probability:
P(dE) = exp(-dE / (k T))
where k is the Boltzmann constant and the T the “bath temperature.” Now note that there are approximately 2600 molecules of nitrogen and oxygen for every molecule of carbon dioxide, and you can conclude that thermalization will dominate over excitation — radiative as well as collisional.
[[re #266 Barton says “Almost all (> 99%) of increases in a molecule’s level of energy will be quickly collided out and distributed among neighboring molecules.”
This would be in agreement with (one of) my contention. Though you are also saying that the molecule’s re-emission is theoretical and highly unlikely, as opposed to transferring its energy through molecular collisions, which can increase the atmospheric temperature. Do you concur with the last part — increasing temp?]]
Certainly the infrared energy absorbed by the atmosphere results in raising its temperature. But radiative loss of that increased temperature mostly has to go through the greenhouse gases, since nitrogen and oxygen aren’t very radiatively active. A simple model would have a layer of atmosphere absoring infrared and then “reradiating it,” but in reality the process is a bit more complicated. The simple model gets the basic idea across, however, and for a sophisticated enough mathematical treatment can even get it quantitatively right.
Thanks, Barton (278), but I’m confused. First off I was talking about an excited (by IR radiation) molecule colliding with another (any kind) and transferring its delta energy to it as kinetic and thereby increasing the temperature of the local atmosphere. Does this happen? Secondly, I thought you said the relaxation by re-emission of the IR very seldom happens because the excited molecule will, by magnitudes, be likely to lose its energy via collision long before it re-emits. Is this accurate?
Third, you say “Certainly the infrared energy absorbed by the atmosphere results in raising its temperature. …” Does the absorption and transfer of IR energy to the bond and rotational internal energy of the molecule raise its temperature? (For discussion, ignore the silly “one molecule can’t have temperature” debate.) I’ve pursued that a number of times here to either no avail or varying answers. I think the crux (cruxes??) of the question is: 1) is it only 1/2mv2 kinetic energy that determines temperature (as opposed to internal potential, chemical, etc.)? 2) Do the vibrating bonds or rotating molecule (1/2Iw(omega)2???) constitute temperature affecting kinetic energy?
a ps to my #279 to Barton: an omitted (typo) but most important word: it should have read “Thanks, but I’m confused. …”
Re #279 Rod B
I have already given you the answer to your question about temperatures in #214. I will try to explain again without repeating myself.
Heat is a form of energy. For solids and liquids the energy is contained in the form of vibration of the atoms. If you pass an electric current through a solid it warms up by absorbing the energy and vibrating more. The increase in vibrations as a liquid heats up causes it to expand, and we measure temperature by seeing how much the liquid mercury has expanded, in a normal thermometer.
Electromagnetic radiation is also a form of energy, and when the sun shines on a surface, the surface gets warmer because because it is absorbing the solar energy. The solar electromagnetic radiation is absorbed by the surface and causes atomic vibrations.
When the heat is great enough the atoms will have enough energy to break away from the surface and form a gas. In other words the substance has evaporated. In that state the atoms are formed into molecules with kinetic energy. They are are moving about at random. When they hit other molecules they share their kinetic energy in the collisions. These molecules can be other gas molecules or the glass of a common thermometer. Thus the thermometer is registering the average kinetic energy of the gas molecules.
All the gas molecules are traveling at different speeds, and Maxwell worked out a mathematical function which describes the distribution of those speeds. So the temperature of a gas measured with a thermometer is called its Maxwellian temperature.
Kirchhoff found that the radiation entering a solid equals the radiation leaving it, provided its temperature is not changing. This is of course just a matter of the conservation of energy. The energy entering a body must equal that leaving if none is being stored. What Kirchhoff also realised was that if you have two plates facing each other, both at the same temperatures, then there must be a function which describes the radiation at each wavelength. This led to Planck’s function, quantum theory, and the measurement of temperature by matching it to Planck’s function. The temperature of a body measured using it radiation is called its blackbody, or Planckian temperature. For most solids the Maxwellian temperature and the Planckian temperature are equal.
The question then is, does the Maxwellian temperature of the Earth’s atmosphere equal its Planckian temperature? If so it is in local thermodynamic equilibrium (LTE.)
HTH,
Cheers, Alastair.
Re #276
This thread is almost dead, so no point is arguing much further.
The lorentzain expression is the only theorectical lineshape I am aware of. It arises from very simple assumptions about the statsitics ofthe collisions, and the collision duration compared to the center frequency of the line. Any thing else would have to be experimentally determined.
When I first got interested in AGW I *discovered* for myself the gray-body saturation problem. In simple gray-body calculations ( to get the 33-35K greenhouse effect) you can come to the conclusion that, having increased CO@ by 30%, we are more that halfway to saturation. That is, by adding just a bit more, we make the IR abosrption completely opaque, thus reaching maximum effect. If we measure 0.6C temp rise, maybe the max would be only double that.
I wrote as much to Gavin, and he sent me a reference to this paper, which set me straight on how things really work:
S. A. Clough, M. J. Iacono, Journal of Geographical Research, vol. 100, No D8, pg 16519-16535, 1995.
This is a line-by-line calculation of radiatve cooling rates. Right on page 2 of the paper, the authors say they are using data from HITRAN for line strengths and line widths. The mention they are doing clever numerical things to speed calculation, while only introdcuing 0.5% error which they say is small compare to the 5% error in the HITRAN data.
I am saying, possibly … maybe, the wings are not what HITRAN says, and therefore the error in the line-by-line calculation could be much bigger.
You are right about how strong the CO2 absorption is, but you can always detune from line center, between the lines, to a point where the transmission is much lower, and the aborption length is much much longer than 15 to 30m. The whole line does not saturate (in this sense) at the same time. In between is where the thermal blackbody radiation from the lower atmosphere and surface has to try leak out.
I bet that CO2 and H2O lines have never been measured accurate so far doen in the wings. Why would a chemist do it? The line positions are most important to them after all. Broadening is a *dirt* effect, unless you are interested in GW.
An experiment with broadband light would do all the integrals automatically, but you have to be able to measure the absolute transmission levels very carefully.
Measuring lineshapes is easier because it is a relative measurement (assuming the strnegth is already known). But there are so many lines to resolve, and you already have to do many air pressures, and CO2 concentrations to get the wings right.
I am not suggesting that the CO2 broadening is proportional to the CO2 concentration. CO2 is a trace gas. The broadening I use in independent of n(CO2) is my calculation, of course. It does say, however, that a strong line always dominates a weak line with the same linewidth at any pressure altitude.
I understand ( and believe from Manabe and Weatherall) the H2O feeedaback. I do agree that clouds are not accurately taken into account. Wasn’t there a bar graph in one of the IPCC reports which had about 10 different models that could’nt agree on the sign, much less the magnitude of the cloud feedback? Is there any prdiction on the change in dewpoint spread with increased CO2 ( with no cloud effects)?
I do agree that many times *experts* try to change the topic on you when you are trying to get a straight answer on a narrow, well-posed problem. This is because they really have’nt thought about the foundations on the field they work in. 99% chance you eventually get someone who finally knows the answer, and will tell you that your are wrong. But maybe there is something that was overlooked … Thats how I learn anyway.
Last, I don’t know what the conclusion would be if the wings were higher or lower (which I suspect) than Lorentzian. Would it be good or bad news for increasing temps? If saturation is slower, we may have more time to burn, but the final temp could be much higher and more dangerous. I don’t know.
> what HITRAN says
I looked it up. Here’s the reference I posted in the Part I thread on that question
https://www.realclimate.org/?comments_popup=455#comment-38413
re my 279 and Alastair’s 214 & 281: a quick clarification: I assume you mean molecular vibration of a solid/liquid. Or does the incoming solar radiation exite the intramolecular atomic bonds also. And if so do those vibrating intramolecular bonds also increase the temperature? Which is just like one of my questions re gasses, which your posts came close to answering, but didn’t quite make it (or I just couldn’t see it…if so , sorry).
I’ll be more simple and specific: Start with a mole of CO2 molecules, darting about and crashing into each other (ignore the walls) and distributing their kinetic energy according to Maxwell/Boltzman distribution, which in turn dictates the measurable temperature of the mole. Now blast it with a pile of infrared radiation, some of which will be absorbed by a bunch of the molecules and be seen as internal bond vibrational (lateral or bending) or molecular rotational energy only — no molecular kinetic or electron level energy changes (for now). The QUESTION is: does the temperature of the gas increase?
If so, do both types — internal vibrational and rotation — increase the temperature, or just one? Or, instead, might the temperature of the mole increase only after collisions when one molecule’s internal bond energy transfers to another (CO2) as molecular kinetic energy. Or can maybe the IR radiation transfer directly to molecular kinetic energy of CO2 molecules, which would increase the sample’s temperature?
Another aside clarification: I’m under the impression the excitation of electron energy levels does NOT increase the temperature of a gas. Right of wrong?? How about if the electron is blasted free ala ionization and now one has charged atoms/molecules and electrons speeding around…(and presumably giving off Planckian radiation)?
I think you’re back on the definition of temperature. The answer to your question just depends on which definition you’re using — and whether it’s applicable to a single atom or molecule and over what span of time.
“Temperature” isn’t a Platonic object. It’s how something behaves — on average, during some elapsed time.
Blast your imagined mole of CO2 with infrared photons, and some photons are absorbed.
Now — how would you _know_ the temperature of the CO2?
— Put a thermometer into it? Oops, the CO2 molecules have banged against the thermometer, violating your hypothetical requirement.
— Measure its infrared radiation? Oops, the CO2 molecules have emitted photons, violating your hypothetical requirement.
It will be warmer, when you measure it.
[[The lorentzain expression is the only theorectical lineshape I am aware of. It arises from very simple assumptions about the statsitics ofthe collisions, and the collision duration compared to the center frequency of the line. Any thing else would have to be experimentally determined.]]
There is also the “Doppler line shape,” which is important at high altitudes, and the “Voigt line shape,” which covers both Lorentz and Doppler broadening. See if you can find a copy of Goody and Yung’s “Atmospheric Radiation” (1989) in your local university physics library. They have an extensive discussion of line shapes.
Re #283 where Dave Dougherty Says:
This thread is almost dead, so no point is arguing much further.
Well, I am finding your perspective interesting, although it seems you are unwilling to consider these issues from mine :-(
In #277 Hank has found an interesting and relevant paper: Rothman et al. (2005) entitled History and future of the molecular spectroscopic databases. It makes several points which agree with things both of us have written. For instance on line shapes they write:
Historically, the line shape used by most of the line-by-line codes was either the Lorentz function (ignoring translational effects), the Doppler function (ignoring collisional effects), or the Voigt profile which is the convolution of the two.
I was not sure what you mean by the gray-body saturation problem. The gray-body concept was used as an approximation for the absorption of greenhouse gases by averaging the effect over the blackbody spectrum. This was abandoned for a band model, since averaging the absorption of a band which changes with height together with a window which has a fixed absorption of zero with height is invalid. Discovery that the bands were themselves composed of lines and gaps meant that the band models had to be abandoned and the LBL (line-by-line) approach is now used. However, although line broadening may remove the gaps, it will not remove the window. Therefore, and here I think I am agreeing with you, line broadening will not cause a major increase in the greenhouse effect.
However, you seem to be looking for reasons why the anthropogenic increase in greenhouse gas concentrations will not lead to severe changes in climate. I am looking to see what caused the dramatic climate changes in the geological past, and how it was that they seem to have been associated with changes in carbon dioxide (and methane.)
Returning to Rothman et al., they do agree with you again when they write:
3.3. The far wing problem
All the models discussed above have been developed within the sudden impact approximation. Consequently, they cannot
provide an accurate description of the far-wing absorption, where the effects of the collision durations are no longer negligible[20]. The importance of an accurate description of the far wings of the strong H2O rotational and vibrational bands for atmospheric modeling is a very well-known example.
And with my contention that this work has now advanced into the overlap of wings:
Here too, the databases have been vastly improved and for instance, the 2004 HITRAN compilation [12] provides flexible tools for taking into account line mixing in CO2 Q branches. However a number of effects remain unaccounted for and need to be included in the near future.
You wrote:
I bet that CO2 and H2O lines have never been measured accurate so far down in the wings. Why would a chemist do it? The line positions are most important to them after all. Broadening is a *dirt* effect, unless you are interested in GW.
But there is an interest in GW and I think Rothman et al. have shown that these issues are being addressed. OTOH, the big error is that the models all assume that the emissions match the absorptions for those lines (Kirchhoff’s Law.) In fact the re-emissions will be affected by collisions, but two chemistry books I have found which mentioned that problem did not discuss it writing that it was uninteresting!
The reason the modelers cannot get the clouds right is because their radiation model is wrong, but try telling the experts that and they will disagree, treating you as a poor fool, and explaining that the clouds are very complicated. The fact that their radiation model is very simple, radiation in equals radiation out at micro and macroscopic levels, seems to pass them by. The Manabe and Weatherall model you mention ignores feedbacks from latent heat and clouds and uses one column to describe a circular flowing system that requires a minimum to two columns. Worse, the lapse rate is effectively fixed at the value supplied as a parameter.
The odds of being right and the expert being wrong must be much lower than 1 in 100. I would rate it below one in a million. But that does not mean it cannot happen. People do get hit by lightening despite its improbability. Anyway, it is too late for me to get my ideas out. With levels of CO2 at their current values we are already getting floods, droughts and wildfires in America, Europe, Asia, and Australia. The scientists still do not know what causes abrupt climate change, but are too proud to listen to the thoughts of someone outside the box. We’re all doomed!
Re 287 and the final para: The odds of being right and the expert being wrong must be much lower than 1 in 100. I would rate it below one in a million. But that does not mean it cannot happen. People do get hit by lightening despite its improbability
The difference here is that while the chances of a particular individual being hit by lightening are extremely slim, given the population of the world i’m guessing (and guessing is right since have v limited knowledge of stats) it’s not too unlikely someone of the 6 billion plus will be struck sometime. Since Alistair is trying to prove the experts wrong in one aspect of science rather than all areas the comparison should be in nominating a particular person who wil struck beforehand which is surely a completely different magnitude of probability?
Re #284 where Rod B Says:
Re my 279 and Alastair’s 214 & 281: a quick clarification: I assume you mean molecular vibration of a solid/liquid.
Typically solids consist of crystal latices of atoms. Molecules are more a feature of gases. The heat energy of a solid is due to the vibrations between the positively charged nuclei of the atoms. It is their unconstrained movement which causes the continuum spectrum of blackbody radiation. Gases have fixed oscilations (vibrations and rotations) that their molecules can make and so it is a spectrum of lines. A solid, think of an iron bar, is just a mass of atoms vibrating in all directions.
Liquids fit somewhere in between solids and gases.
Your mole of gas will have a temperature. Put a thermometer in the gas and it will register a value that matches the average kinetic energy of the molecules. So it has a kinetic or Maxwellian temperature. Its Planckian temperature or brightness temperature is zero because we are assuming that it is not emitting any radadiation. Now blast it with a pile of infrared radiation … no molecular kinetic or electron level energy changes (for now) Its Maxwellian temperature is unchanged, and its Planckian temperature is unchanged because it is still not emitting any radiation. But it has aquired vibrational and rotational energy so now it has a vibrational temperature and a rotational temperature. Its electronic temperature is still zero.
But go back to the mole of gas before it was blasted. The molecules are colliding and that will cause them to vibrate and rotate. So in fact the gas will already have had a vibrational temperature and a rotational temperature. But those excited states are not permanent and will result in emissions, so the gas would have had a Planckian temperature. So if you take a mass of a greenhouse gas without any walls around it, it will slowly radiate away its heat (kinetic energy) via excitation of its vibrations and rotations and their emission of photons. This is what happens at the top of the atmosphere.
The blast of IR would have increased both the vibrational and the rotational temperatures, but as those excited states relax back to their equilibrium values by collisions then the gas kinetic temperature will rise. If they relax by re-emitting their energy, then the Planckian temperature will be temporarily raised.
So, as you wrote: the temperature of the mole increases only after collisions when one molecule’s internal bond energy transfers to another (CO2) as molecular kinetic energy. It can also transfer to other air molecules such as O2 and N2 in the Earth’s atrmosphere, and the kinetic energy will be shared by and with other CO2 molecules in the atmospheres of Mars and Venus..
The electronic excitation behaves just like the vibrational and rotational energies. The molecule/atom/ion will have an electronic temperature/energy which will be shared with its vibrational and then rotational states until it is degraded into thermal (kinetic) energy. I would imagine ions only give off photons when they collide, or are hit by electrons.
Finally, I would avoid the term Planckian radiation for blackbody or cavity radiation. Planck’s function describes the intensity for each wavelength of the continuous radiation from a blackbody emitting at a specificed temperature. If you then use the intensity and wavelength of an emission from a gas you can determine a Planckian or brightness temperature, but the gas is emitting line radiation not blackbody continuum radiation.
Although I have possibly raised more questions than I have answered I HTH,
Cheers, Alastair.
Alastair, rock, shale, dirt, etc are just “crystal latices of atoms”??? Not molecular?
Alastair, please.
http://www.madsci.org/posts/archives/2000-08/966273615.Es.r.html
“… One way to know if what you have is a crystal or not is to break it. Having a crystal form is what is known as a ‘physical property’.”
Re #290-1 A grain of sand is just a crystal of silica, and even dust or a speck of mud consists of millions of atoms in fixed proportions, not just one molecule. The kinetic theory of gases and Avagadro’s Hypothesis all depend on gaseous molecules. And of course,minerals break down into ions not molecules when dissolved in water.
However, I should have written: Inorganic solids consists of a crystal latices. Here is a picture of rock http://en.wikipedia.org/wiki/Image:Gabbro_pmg_ss_2006.jpg seen in a thin section 30 microns thick. It is just a load of crystals.
Wikipedia says “In general, the type of chemical bonds which hold matter together differ between the states of matter. For a gas, the chemical bonds are not strong enough to hold atoms or molecules together, and thus a gas is a collection of independent, unbonded molecules which interact mainly by collision. In a liquid, Van der Waals’ forces or ionic interactions between molecules are strong enough to keep molecules in contact, but not strong enough to fix a particular structure, and the molecules can continually move with respect to each other. In a solid, metallic, covalent or ionic bonds provide cohesion between molecules, and the positions of atoms are fixed relative to each other over long time ranges. This being said, however, there is a great variety in the types of intermolecular bonds in the different materials classes: ceramics, metals, semiconductors or polymers, and each material or compound may be different.” http://en.wikipedia.org/wiki/State_of_matter
So in a solid the position of the atoms are fixed relative to each other and it is the vibration of their nuclei which causes the blackbody radiation.
Well, no. Read it:
“In a solid the positions of the atoms are fixed relative to each other _over_long_time_ranges_ [by] … a great variety in the types of intermolecular bonds …” [Emphasis added]
Remember those bonds? Follow cites forward from the deep past, like this one: http://prola.aps.org/abstract/PRB/v4/i6/p2029_1
You don’t need to invoke “the vibration of their nuclei” (whatever that may mean).
OK I’ve read it. It talks about scattering phonons in a glass not emitting photons from an opaque solid. And it says “Such a mean free path can be quantitatively explained by approximating the glassy structure with that of a crystal in which every atom is displaced from its lattice site.”
What I am saying is that blackbody radiation can be quantitatively explained by approximating the opaque solid with that of a crystal in which every atomic nuclei is vibrating at random within its lattice site.
Or you can view it as that the molecules are held so rigidly they cannot rotate or vibrate and the blackbody radiation is a result of the internal vibrations of the atoms.
But if you have a better description of how blackbody type radiation (i.e. continuous radiation) is produced by solids then let us have it.
http://www.physicsforums.com/showthread.php?p=1383874
“Lightning,” people, “lightning,” not “lightening.” Lightening is what happens when something’s weight decreases.
Well if you are prepared to take the humble opinion of someone who signs him/herself “xez” then go ahead.
However xez writes: “The pressure and doppler broadening effects are why we see a basically continuous spectrum from the solar photosphere even though it’s mostly ionized Hydrogen/Helium plasma; the pressure and temperature are so high the lines are very broad, and basically it has become a blackbody radiation source at the equivalent temperature.” That is an explanation I have seen for the Sun’s radiation, but how come the Sun’s spectrum also has lines if the lines have been smeared into continuum radiation?
Moreover it does not explain the black body radiation emitted from the surface of the Earth, such as that emitted by snow, nor any other terrestrial thermal emissions. There is no high temperature to produce a Doppler effect here, or high pressure to produce collisional broadening.
You will have to show a bit more understanding of the science, to get any more responses out of me.
Alastair McDonald (#297) wrote:
Well, I happen to put a lota stock in what a certain waskely wabett has to say. Then again he generally speaks of himself in the third person. People who speak of themselves in the third person are usually very important. Xez doesn’t speak of himself in the third person, so he might not be as important.
xez sez:
xez sez:
Alastair wrote:
xez sez:
The operative word is like.
There are eight different types of local spectral broadening I can see:
http://en.wikipedia.org/wiki/Spectral_line#Broadening_due_to_local_effects
Maybe xez is talking about one or more of those things.
alistair:
tamino, simon donner and eli have been hashing some of this out on open mind, maribo and rabett run. I think you should see what you make of that.
1. Because there are other atoms in the sun besides hydrogen and helium
2. There is no Doppler shift from emissions from a solid if you are standing on the solid. OTOH, there is if someone is pegging it at you at a zillion km/h