Guest post by Tamino
In a paper, “Heat Capacity, Time Constant, and Sensitivity of Earth’s Climate System” soon to be published in the Journal of Geophysical Research (and discussed briefly at RealClimate a few weeks back), Stephen Schwartz of Brookhaven National Laboratory estimates climate sensitivity using observed 20th-century data on ocean heat content and global surface temperature. He arrives at the estimate 1.1±0.5 deg C for a doubling of CO2 concentration (0.3 deg C for every 1 W/m^2 of climate forcing), a figure far lower than most estimates, which fall generally in the range 2 to 4.5 deg C for doubling CO2. This paper has been heralded by global-warming denialists as the death-knell for global warming theory (as most such papers are).
Schwartz’s results would imply two important things. First, that the impact of adding greenhouse gases to the atmosphere will be much smaller than most estimates; second, that almost all of the warming due to the greenhouse gases we’ve put in the atmosphere so far has already been felt, so there’s almost no warming “in the pipeline” due to greenhouse gases already in the air. Both ideas contradict the consensus view of climate scientists, and both ideas give global-warming skeptics a warm fuzzy feeling (but not too warm).
Despite the celebratory reaction from the denialist blogosphere (and U.S. Senator James Inhofe), this is not a “denialist” paper. Schwartz is a highly respected researcher (deservedly so) in atmospheric physics, mainly working on aerosols. He doesn’t pretend to smite global-warming theories with a single blow, he simply explores one way to estimate climate sensitivity and reports his results. He seems quite aware of many of the caveats inherent in his method, and invites further study, saying in the “conclusions” section:
Finally, as the present analysis rests on a simple single-compartment energy balance model, the question must inevitably arise whether the rather obdurate climate system might be amenable to determination of its key properties through empirical analysis based on such a simple model. In response to that question it might have to be said that it remains to be seen. In this context it is hoped that the present study might stimulate further work along these lines with more complex models.
What is Schwartz’s method? First, assume that the climate system can be effectively modeled as a zero-dimensional energy balance model. This would mean that there would be a single effective heat capacity for the climate system, and a single effective time constant for the system as well. Climate sensitivity will then be
S=τ/C
where S is the climate sensitivity, τ is the time constant, and C is the heat capacity. Simple!
To estimate those parameters, Schwartz uses observed climate data. He assumes that the time series of global temperature can effectively be modeled as a linear trend, plus a one-dimensional, first-order “autoregressive” or “Markov” or simply “AR(1)” process [an AR(1) process is a random process with some ‘memory’ of its previous value; subsequent values y_t are statistically dependent on the immediately preceding value y_(t-1) through an equation of the form y_t = ρ y_(t-1) + ε, where ρ is typically required to be between 0 and 1, and ε is a series of random values conforming to a normal distribution. The AR(1) model is a special case of a more general class of linear time series models known as “Autoregressive moving average” models].
In such as case, the autocorrelation of the global temperature time series (its correlation with a time-delayed copy of itself) can be analyzed to determine the time constant τ. He further assumes that ocean heat content represents the bulk of the heat absorbed by the planet due to climate forces, and that its changes are roughly proportional to the observed surface temperature change; the constant of proportionality gives the heat capacity. The conclusion is that the time constant of the planet is 5±1 years and its heat capacity is 16.7±7 W • yr / (dec C • m^2), so climate sensitivity is 5/16.7 = 0.3 deg C/(W/m^2).
One of the biggest problems with this method is that it assumes that the climate system has only one “time scale,” and that time scale determines its long-term, equilibrium response to changes in climate forcing. But the global heat budget has many components, which respond faster or slower to heat input: the atmosphere, land, upper ocean, deep ocean, and cryosphere all act with their own time scales. The atmosphere responds quickly, the land not quite so fast, the deep ocean and cryosphere very slowly. In fact, it’s because it takes so long for heat to penetrate deep into the ocean that most climate scientists believe we have not yet experienced all the warming due from the greenhouse gases we’ve already emitted [Hansen et al. 2005].
Schwartz’s analysis depends on assuming that the global temperature time series has a single time scale, and modelling it as a linear trend plus an AR(1) process. There’s a straightforward way to test at least the possibility that it obeys the stated assumption. If the linearly detrended temperature data really do behave like an AR(1) process, then the autocorrelation at lag Δt which we can call r(Δt), will be related to the time constant τ by the simple formula
r(Δt)= exp{-Δt/τ}.
In that case,
τ = – Δt / ln(r),
for any and all lags Δt. This is the formula used to estimate the time constant τ.
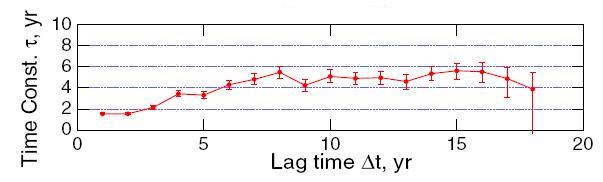
And what, you wonder, are the estimated values of the time constant from the temperature time series? Using annual average temperature anomaly from NASA GISS (one of the data sets Schwartz uses), after detrending by removing a linear fit, Schwartz arrives at his Figure 5g:
Using the monthly rather than annual averages gives Schwartz’s Figure 7:
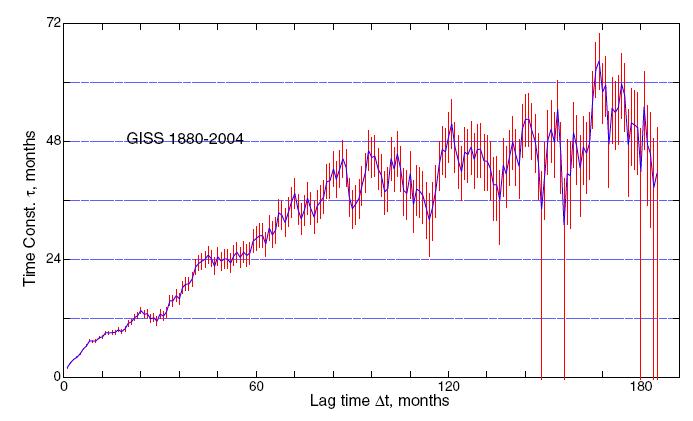
If the temperature follows the assumed model, then the estimated time constant should be the same for all lags, until the lag gets large enough that the probable error invalidates the result. But it’s clear from these figures that this is not the case. Rather, the estimated τ increases with increasing lag. Schwartz himself says:
As seen in Figure 5g, values of τ were found to increase with increasing lag time from about 2 years at lag time Δt = 1 yr, reaching an asymptotic value of about 5 years by about lag time Δt= 8 yr. As similar results were obtained with various subsets of the data (first and second halves of the time series; data for Northern and Southern Hemispheres, Figure 6) and for the de-seasonalized monthly data, Figure 7, this estimate of the time constant would appear to be robust.
If the time series of global temperature really did follow an AR(1) process, what would the graphs look like? We ran 5 simulations of an AR(1) process with a 5-year time scale, generating monthly data for 125 years, then estimated the time scale using Schwartz’s method. We also applied the method to GISTEMP monthly data (the results are slightly different from Schwartz’s because we used data through July 2007). Here’s how they compare:
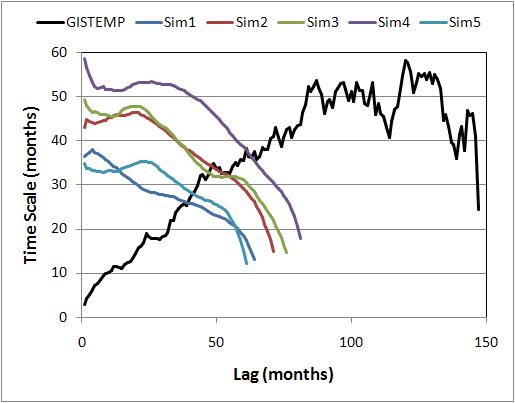
This makes it abundantly clear that if temperature did follow the stated assumption, it would not give the results reported by Schwartz. The conclusion is inescapable, that global temperature cannot be adequately modeled as a linear trend plus AR(1) process.
You probably also noticed that for the simulated AR(1) process, the estimated time scale is consistently less than the true value (which for the simulations, is known to be exactly 5 years, or 60 months), and that the estimate decreases as lag increases. This is because the usual estimate of autocorrelation coefficients is a biased estimate. The word “bias” is used in its statistical sense, that the expected result of the calculation is not the true value. As the lag gets higher, the impact of the bias increases and the estimated time scale decreases. When the time series is long and the time scale is short, the bias is negligible, but when the time scale is any significant fraction of the length of the time series, the bias can be quite large. In fact, both simulations and theoretical calculations demonstrate that for 125 years of a genuine AR(1) process, if the time scale were 30 years (not an unrealistic value for global climate), we would expect the estimate from autocorrelation values to be less than half the true value.
Earlier in the paper, the AR(1) assumption is justified by regressing each year’s average temperature anomaly against the previous year’s and studying the residuals from that fit:
Satisfaction of the assumption of a first-order Markov process was assessed by examination of the residuals of the lag-1 regression, which were found to exhibit no further significant autocorrelation.
The result for this test is graphed in his Figure 5f:
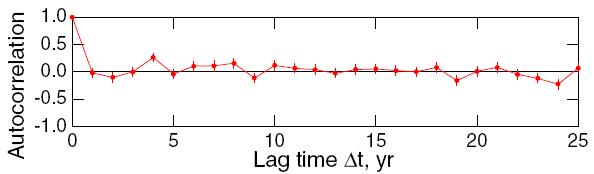
Alas, it seems this test was applied only to the annual averages. For that data, there are only 125 data points, so the uncertainty in an autocorrelation estimate is as big as ±0.2, much too large to reveal whatever autocorrelation might remain. Applying the test to the monthly data, the larger number of data points would have given this more precise result:
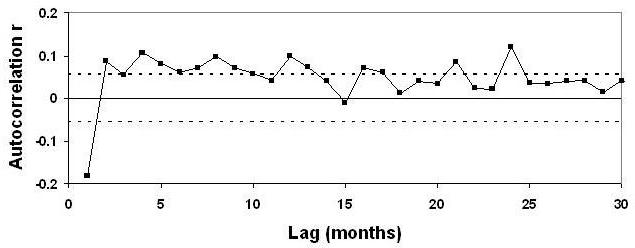
The very first value, at lag 1 month, is way outside the limit of “no further significant autocorrelation,” and in fact most of the low-lag values are outside the 95% confidence limits (indicated by the dashed lines).
In short, the global temperature time series clearly does not follow the model adopted in Schwartz’s analysis. It’s further clear that even if it did, the method is unable to diagnose the right time scale. Add to that the fact that assuming a single time scale for the global climate system contradicts what we know about the response time of the different components of the earth, and it adds up to only one conclusion: Schwartz’s estimate of climate sensitivity is unreliable. We see no evidence from this analysis to indicate that climate sensitivity is any different from the best estimates of sensible research, somewhere within the range of 2 to 4.5 deg C for a doubling of CO2.
A response to the paper, raising these (and other) issues, has already been submitted to the Journal of Geophysical Research, and another response (by a team in Switzerland) is in the works. It’s important to note that this is the way science works. An idea is proposed and explored, the results are reported, the methodology is probed and critiqued by others, and their results are reported; in the process, we hope to learn more about how the world really works.
That Schwartz’s result is heralded as the death-knell of global warming by denialist blogs and Sen. Inhofe, even before it has been officially published (let alone before the scientific community has responded) says more about the denialist movement than about the sensitivity of earth’s climate system. But, that’s how politics works.
ref 77 Timothy,
To a point I agree, there is a huge difference in thermal inertia between the poles. Polar trends would be at best similar. Still, I would expect to see at least some definable positive trend in both poles though the southern pole would be up to an order of magnitude (SWAG)lower.
RE 95 Vernon: “Jim, it would appear that a significant amount of the warming and melting in the Arctic is not due to global warming but pollution.”
Yes, we’ve discussed the McConnel paper on black carbon here before, but consider the following:
1) Any accumulated black carbon contained in the Arctic sea ice area that has melted is no longer in play, it went with the ice that melted.
2) Not only has Arctic sea ice area reduced each succeeding year, so has ice thickness, and therefore total mass, which accelerates the following year’s melt.
3) It takes 334 joules of heat energy to melt each gram of ice. That same amount of heat energy could raise a gram of liquid water by nearly 80ºC. As the total mass of Arctic sea ice is reduced in each succeeding year, more and more heat energy, whether from solar insolation or ocean current transport, is freed to heat liquid ocean water, permafrost, grounded ice and the atmosphere. Three of those impact directly on the Greeenland ice cap.
#100, That sounds like arctic haze. Visually speaking, it varies from year to year, of late on the Canadian side of the Arctic its been mainly on its way down, leaving in its wake “molecular air”
scenes of incredible beauty, ie Rayleigh scattering in its purest forms. Given that 2007 melt
largely occurred on the Canadian-Alaskan-Russian side of the Pole as opposed to the European side,
I take this “pollution” solution as an unlikely correct conclusion.
Re 100: I think there is more to it than just that. A fairly large number of factors contributed in a kind of perfect storm; the weekly reports of the icebreaker Polarstern: http://www.awi.de/en/infrastructure/ships/polarstern/weekly_reports/ contain a wealth of interesting info in a very readable format (they also have data). They found ice thickness to be in average half of what they measured in 2001. A lot of warm humid air reach high latitudes and there was apparently an unusual amount of rain this year in the Arctic.
As a layman trying to get a grip on the basics, I erred in the references in my post #66. The problem I’ve run into is interpreting the model predictions vs actual observations as presented in AR4. So, I made a temporary web page and extracted the relevant pictures from AR4 to make it easy to see what I’m asking.
See: http://webpages.charter.net/balplanman/GlobalWarming/GlobalWarming.html
Any help in improving my understanding would be appreciated.
dallas tisdale (101) wrote:
The trend around Antarctica is largely in the same direction albeit not the same magnitude as the Arctic.
Of course you will notice that the sea ice in the Southern Ocean is increasing over the past few years, but not by that much. We have nearly hit a new record in sea ice extent, but this is in the neighborhood of a percentage as opposed to the drastic reduction which has taken place in the Arctic. Likewise, there is a small segment of the Southern Ocean which has been cooling.
But beyond this, most of the Southern Ocean has been warming. The Larsen A Ice Shelf disintegrated in January of 1995 and the Larsen B Ice Shelf disintegrated in February of 2002. The West Antarctic Peninsula has been warming quite considerably. We have over a hundred glaciers which are picking up speed and heading to the ocean. The a large part of the continental interior of Antarctica experienced an unexpected melt only 310 miles from the South Pole back in 2005. Likewise the mass balance of Antarctica has been declining – this was detected by Grace in 2006. Snow is adding to the ice mass of Antarctica (not surprising given that it receives so little precipitation, and warming temperatures will actually increase this precipitation), but this increased precipitation is more than outweighed by the melting which is occuring.
So at this point both Greenland and Antarctica are losing mass and contributing to the rise in sea level. Granted, they are not yet contributing that much – most of the rise in sea level is due to thermal expansion of sea water, and the authors of one study seem to think that glaciers elsewhere will add more to sea level than either Greenland or Antarctica for the time being. But given the acceleration of melt in both Greenland and Antarctica (Greenland is experiencing three times as many ice quakes as it was a decade ago), this
may be premature on his part. In fact I strongly suspect it is – but I would prefer the opinion of an unbiased climatologist over my own in this area.
One other point: I wouldn’t be at all surprised if we see a great deal more sea ice at within a few years around Antarctica – but that won’t necessarily be a good sign. It depends upon where that sea ice is coming from. Glaciers? Another ice sheet? Of course, when this happens, we will know.
Anyway, I probably should have mentioned all this in comment #77, but I didn’t think about it until a few minutes afterwards.
Vernon stated:
“Maybe it is just me but we have the least sea ice in the Arctic coupled to Black Carbon and massive European pollution.”
It is just you.
In addition of warming in the Northern region, another reason is that the ocean currents play a role for loss of sea ice.
http://www.ametsoc.org/atmospolicy/documents/May032006_Dr.WieslawMaslowski.pdf
Why that is happening, no one knows, but perhaps global warming has an effect to the ocean currents too?
RE: 102 Jim, your post suggest that black carbon is a one time event. Since the mean circulation in winter is characterized by low-level transport from northern Eurasia across the Arctic toward North America. The pollution from Eurasia is replenished annually.
It was pointed out that while there is a definite impact on the Greenland ice cap, there is more the rest of the Arctic. The BC deposits cause melting which exposes both earth and water, not an issue on the ice cap, and acts a driver for further melting (warming).
Far be it for me to point out that the ice is the lease right after the pollution in the Arctic is the worst.
Since there is more sea ice and no warming in the Anarctic where there is no pollution, where is that pesky tipping point?
> Since there is …. no warming in the Anarctic
Cite please? This is a skeptic talking point, not a fact.
What are you relying on for your beliefs?
RE: 108 Vernon: “Jim, your post suggest that black carbon is a one time event.”
On the contrary, Vernon, I suggest that it is cumulative on permanent ice, such as Arctic sea ice that has not yet melted, but it is only annual on sea ice that has melted back. As for Greenland, BC in snow is cumulative, but BC in surface ice is at least partly carried away by surface melt s it drains into the interior of the ice cap.
“Since there is more sea ice and no warming in the Anarctic where there is no pollution, where is that pesky tipping point?”
I explained that previously, perhaps you missed it? First, as Timothy just pointed out, there most definitely is warming in the Antarctic, particularly on the West Antarctic Peninsula. The degree of Antarctic warming is simply not as great as that of the Arctic.
The sober fact is that permafrost contains more sequestered carbon than the entire atmosphere does. One tipping point is the point at which the warming induces sufficient thawing of permafrost and shallow methane calthrates to emit more CO2 and methane than humans currently do. At that point there will be nothing we can do to even slow the increase in greenhouse gases. We are already seeing an increase in permafrost melt and CO2 and methane off-gassing.
Another tipping point is that point when increasing fresh melt water begins to alter ocean circulation patterns. We are already seeing a change in influxes of warmer water into the Artcic.
Yet another tipping point is the point at which the Greenland ice cap begins to lose mass faster than it gains it each winter. It seems were are are also already at that point, as well. So, pick one. Any one will do.
Re: Pete’s #91
Do not worry about 3C, melting ice will keep us cool. Of course, there may be some change in level as a result.
Re Timothy Chase’s #94
When I did risk management at a large engineering firm, I kept a list of all the “bad things” that could happen, their probability, and how many people the event would effect. For a long time, that list was over 5 single spaced pages and included earthquakes (I live in the Bay Area), volcanoes, asteroids, killer bees, traffic accidents, bird flu, war, floods, hurricanes, tsunamis, cancers, and et cetera. Using my scoring system, it required that many possible events to accumulate 99 % of the possible risk. I decided that I was just not going to bother worrying about the last 1% of the risk.
Today that list is pretty much limited to global warming and its follow-on effects. I give GW a risk score of 6 billion. Nothing else score’s even 0.1% as high. Not that I think that the other events will not happen or that I think they will not affect large numbers of people. It is just the global warming is so much worse and coming so much faster, with so much more certainty, and global warming will affect so many more people, that I am not going to worry about anything else.
Here in the Bay Area, we will get an earthquake — soon. But Global warming is here! Look at the price and wheat and why it is so high. An asteroid would be bad, but so is an AGW driven drought in the American Southwest, and the drought is here now, and getting worse. (And with the warm water off-shore, we are more likely to get rain at intensities that will cause problems, rather than the snowpack that our infrasture is designed to acommodate.)
I am not that worried about a 3C temperature change in the atmosphere. I have lived in Saudi Arabia, and
California could learn to cope. I am worried about the temperature of the sea water at the ice-ocean interface below the WAIS. A fraction of a degree there makes a big difference.
A couple of years ago, an ice field that I had played on for decades slid out from under my feet. It gave me a new appreciation for non-linear processes in ice. There was a difference between understanding the physics of the situation and SUDDENLY hanging from my ice ax with a lot of air under my feet because a piece of ice the size of a football field slid down the valley. The take away lesson was “big ice can move very fast.” It was not something I could learn from doing numbers.
Re #100 [Vernon] I notice that the high levels of pollution from agricultural fires in Eastern Europe refer to 2006. Does anyone have information about such fires in 2007, and indeed about trends in them over time, and how, if at all, they correlate with Arctic ice summer melt?
Vernon doesn’t give an exact reference for Stohl 2006, but Google Scholar finds:
Characteristics of atmospheric transport into the Arctic troposphere
Stohl, A., Journal of Geophysical Research, Volume 111, Issue D11, CiteID D11306.
Was that your reference, Vernon?
This is from the abstract (I can’t access the full text):
“Sensitivities of Arctic air masses to emissions of air pollutants, based on transport alone, were calculated for times of up to 30 days before the air masses reached the Arctic. They were highest over Siberia and Europe in winter and over the oceans in summer. Using an inventory for anthropogenic black carbon (BC) emissions, it was found that near the surface and for transport timescales of 5 and 10 days, BC source contributions from south Asia are only 1.6% and 10%, respectively, of the corresponding European values, despite much higher emissions in south Asia. Using an inventory for BC emissions from forest fires, BC source contributions to the Arctic, particularly from fires in Siberia, were larger than anthropogenic BC source contributions in summer in years of average burning.”
The last sentence suggests to me that 2006 was exceptional, and normally Siberian forest fires (from the context, non-anthropogenic) are the main source of black carbon for the Arctic, but I admit it’s not that clear.
None of the above means it wouldn’t be a good idea to discourage agricultural fires in Eastern Europe, but without clearer evidence that they have greatly increased over recent years it seems quite a stretch to pin the blame for the melting Arctic sea-ice chiefly on them. We know CO2 levels have increased, and if this is not warming the planet, that’s in itself a huge scientific mystery.
JoeMA:
My take is roughly Timothy Chase’s. I only have 2 things to add:
1. Most of the time since the industrialization of the 19th c. a rise in GHGs was matched by a rise in particulate matter. We managed to curb the latter, but not the former. For a long time, our proportional net contribution to warming was less than it is now. On the other hand, we’ve become more efficient. We get much more GDP/GTon of C02 produced than the 19th and early 20th c. did.
2. Even if you quibble with 1888 as being a time when solar forcings fell behind human forcings, that’s beside the point. Even at a time when solar forcings produce more of a change in temperature, for the most part, they are cyclic, and in any event, natural. Any time you have any net contribution in the direction of warming by humans, even if it’s dwarfed by other forcings, you have anthropogenic global warming. As an analogy, if your uncle is sick in bed with malaria and you start feeding him arsenic, you don’t mark the time when the coroner says the cumulative arsenic was doing more damage to him than the malaria was as the time you began poisoning him. And no serious person quibbles with the statement that you cannot model climate change over the last 100 years without including the effects of human activity – the numbers don’t add up.
Re #111 Aaron,
That is what I was trying to say. All these numbers and arguments about whether global warming will give a 1.5 or 2.5 C is irrelevant when we know that the global temperature is already high enough to melt the Arctic ice, and that the Greenland ice is bound to follow.
When are the scientists going to stop pussyfooting about, and tell the politicians we have a crisis on our hands?
Quotes from the IPCC 4th Report, Antarctic issues.
Global sea ice extent:
“Satellite data indicate a continuation of the 2.7 ± 0.6% per decade decline in annual mean arctic sea ice extent since 1978. The decline for summer extent is larger than for winter, with the summer minimum declining at a rate of 7.4 ± 2.4% per decade since 1979. Other data indicate that the summer decline began around 1970. Similar observations in the Antarctic reveal larger interannual variability but no consistent trends.”
Antarctic surface temperatures:
“In the Southern Hemisphere, SAM (southern annular mode of atmospheric circulation) increases from the 1960s to the present are associated with strong warming over the Antarctic Peninsula and, to a lesser extent, cooling over parts of continental Antarctica…”
“Temperatures over mainland Antarctica (south of 65 S) have not warmed in recent decades (Turner et al., 2005), but it is virtually certain that there has been strong warming over the
last 50 years in the Antarctic Peninsula region.”
Complicating factors in Antarctic records: global ocean circulation and ozone depletion
“In the Southern Hemisphere, there has been a strengthening tropospheric antarctic vortex during summer in association with the ozone hole, which has led to a cooling of the stratospheric polar vortex in late spring and to a two- to three-week delay in vortex breakdown.”
“In the SH, SAM changes are related to contrasting trends of strong warming in the Antarctic Peninsula and a cooling over most of interior Antarctica. The increasing positive phase of the SAM has been linked to stratospheric ozone depletion and to greenhouse gas increases. Multi-decadal
variability is also evident in the Atlantic, and appears to be related to the THC (thermohaline circulation).”
The general concept predicted years ago was that global warming would result in increased polewards heat transport, which would cause temperatures in polar regions to increase at a faster rate than anywhere else. The Antarctic ice mass is a far stronger heat buffer than anything in the NH, so change there is at a slower pace.
Alastair McDonald (114) — I rather think that Dr. James Hansen has been saying that for some time now.
But politicians will be more likely to listen if all their constituents tell them that…
Hi, Smokeysmom (#82 & “Where ARE those people living”).
Unfortunately here on earth. I figure it this way, there’s this bell-shaped curve on the GW believer-denialist continuum, and the big glop in the center has been moving toward the believer side, with Katrina giving it an extra shove. However, that denialist tail goes out to infinity, so even when 99.9% of earth’s people believe GW is real and on the whole harmful, there will still be some that say it’s all fake.
But I have a better idea, I think the denialists should be in the forefront of getting us to mitigate GW, and slowly slowly destroy all that evidence that it is happening. Then they can be right (no GW), and I’ll be quite happy to be found wrong. In fact I’ll be ecstatic, and they can be ecstatic that they are right. So it’ll be a win-win situation. And when you figure in all the other environmental and non-environmental problems mitigating GW will solve, well, it’s a win-win-win-win-win situation!
Re #100
Vernon you are obviously clueless about the current climater changes in the arctic and subarctic. I live at the northern end of Sweden and here you do not need any indirect measurements to be able to tell that the climate is now warmer than it was 15 ears ago. We do not have a lot of glaciers here so any addition of black carbon does not make a big difference. Differences that we do notice is that the summer ends later, the growing season is longer and there are now plats growing here which you never saw 15 years ago.
When I was young we stored food outdoors for several months, it was colder than a frezzers outside. We can’t do this anymore since we now get temperatures above freezing regulary even in january.
These are not things that are some measurment problems or something related to snow melting a bit faster. These are real life everyday problems for us!
Alastair 114, I think the scientists are doing the right thing by keeping their heads down and churning out the numbers. Its for *we the people* to take the information and shove it in front of our politicians, explain what it means to us as people (most of my food is grown on alluvial coastal soils within 3m of high tide!) and get action.
These days, to keep the heat on our government, before I click the Submit Comment button here I make sure I send another email to someone on my Climate Email list who is in a position of influence.
Re 114
You tell them! You are as smart as most scientists, and smarter than most journalists. You, at least, did your homework.
I hope your letters to the Queen have more effect than my letters to POTUS. Still, I write to news media outlets and ask them why they are not devoting more coverage to AGW. I write to my elected represenatives.
I try to tell them the story in language that they understand, and provide them references where they can check the facts.
At this point, my real rage is against the quality of science education. I talk to computer programers and medical doctors,(and State Senators)that do not understand basic science.
[inappropriate language edited]
The fact is that there is little to no warming south of the Antarctic circle. The warming is taking place north of the Antarctic circle on the Antarctic Pen. The net change in Ice Map per Sheppard et al (2007) is +25 Gton for East and -50 Gton for the West Antarctic. Total Antarctic change is -25 Gton. Add that with what is happening to Greenland and it add 0.35 mm per year to the sea level. Based on this melting, only another 3000 years to get to a meter.
So while black carbon is leading to melting in the Arctic, there is not much melting in the Antarctic, actually, the Ice map away from the AP is increasing.
Added to the fact that sea ice in the Antarctic is raising the albedo which means less heat is absorbed by the ocean and it gets cooler. This is also documented.
If there is not warming at both poles (inside the Arctic and Antarctic circles) which is required for global warming, then why is that?
Vernon, are you getting your beliefs from CO2science?
Why don’t you try using Google Scholar, you can look up the articles for yourself, read the abstracts online and the actual articles at the library, and come to your own conclusions.
You’ll be more credible than if you post ideas that don’t have facts behind them that are traceable to the bogus sources like co2science.
Try this article for example:
http://adsabs.harvard.edu/abs/2007GeoRL..3414607Z
Or this one:
http://ams.allenpress.com/perlserv/?request=get-abstract&doi=10.1175%2FJCLI4236.1
Ah Arron 120! Tis true that:-
A man whose mind is made against his will
Is of the same opinion still!
I’m blowed if I know what carrot to dangle in front of their snouts to turn their silly heads around, but in the mean time I will keep hitting them with fact-sticks in the hope of at least attracting their attention for long enough for them to think that there may be something just a little odd going on with our world!
Well, Vernon has a history of reading articles, then claiming they conclude the direct opposite of what the authors say they conclude.
He’s a troll. Probably best not to feed him.
It’s funny that he’s posting here, given that over on Deltoid he insisted for a couple of weeks that he’d been banned here …
More for Vernon, as encouragement that you can look this stuff up for yourself instead of taking beliefs from the septic sites.
(on temperature change in the Antarctic):
http://scienceblogs.com/stoat/2007/02/revenge_of_the_killer_cosmic_r.php#comment-349908
and William there cites:
http://igloo.atmos.uiuc.edu/Antarctic.paper.chapwalsh.2005.pdf
Nigel Williams and many others — I recommend using visuals of arctic and Greenland ice melt, glaciers then and now in the Alps and elsewhere and also the following:
http://abcnews.go.com/Technology/TenWays/story?id=3602227&page=1
which shows various U.S. coastal cities with different amounts of sea stand rise. Then point out that during the Eemian, when the carbon dioxide concentration in the atmosphere rose to merely about 290 ppm, the temperature rose to a degree or two (Celcius) higher than today. The result was a sea stand about 5 meters higher than today. With just the current concentration of carbon dioxide in the atmosphere of 383 ppm, it does seem that the visuals in the link portend the near future. Unless we can somehow get the carbon back into the ground, that is.
Re 121 Vernon: “The fact is that there is little to no warming south of the Antarctic circle. The warming is taking place north of the Antarctic circle on the Antarctic Pen.”
Vernon, the fact is that well over three quarters of the West Antarctic Peninsula lies south of the Antarctic circle. Look it up.
“Add that with what is happening to Greenland and it add 0.35 mm per year to the sea level. Based on this melting, only another 3000 years to get to a meter.”
IF you assume that the rate of melting remains the same for the next 10-15 years, let alone for the next 3000. If you wish to wager that it will, I suspect that there are more than a few people far more knowledgeable than you about the stability of the Greenland ice cap and the West Antarctic ice shelf who would take that bet.
“So while black carbon is leading to melting in the Arctic, there is not much melting in the Antarctic, actually, the Ice map away from the AP is increasing.”
Again you assert that the primary cause of Arctic melting is BC without evidence to back up that statement, and you dismiss the significance of the destabilisation of the West Antarctic ice mass.
“If there is not warming at both poles (inside the Arctic and Antarctic circles) which is required for global warming, then why is that?”
The causes of the differential in the rate of warming of the Arctic and Antarctic have already been explained by several people here in this thread. You might try reading those explanations.
Vernon, according to McConnell et al in last week’s Science; (Vol. 317. no. 5843, pp. 1381 – 1384). Black Carbon levels in the artic are almost down to pre industrial levels after peaking the first part of the 20th cent.
Abstract: http://www.sciencemag.org/cgi/content/abstract/317/5843/1381
From the paper:
“… BC concentrations varied significantly during the past 215 years and were highly seasonal, particularly during the period before industrialization, beginning in the mid-1800s (Fig. 1A) (6). Average preindustrial annual BC concentration was 1.7 ng g–1, with generally consistent low winter (defined as December through May) concentrations averaging 1.3 ng g–1 and highly variable summer (defined as June through November) concentrations averaging 2.0 ng g–1. After 1850, annual BC concentrations began a gradual rise, followed by a rapid increase in 1888. Annual average concentrations reached a peak of >12.5 ng g–1 in 1908 before beginning a general, although erratic, decline through the late 1940s followed by a sharp drop in 1952. Maximum winter BC concentration peaked in 1908 at more than 20 ng g–1, with an average wintertime concentration of 13 ng g–1 during the highest 5-year period (1906 through 1910), which is about 10 times the mean winter concentration of 1.3 ng g–1 before 1850. During the period from 1851 to 1951, annual average concentrations were 4.0 ng g–1, with mean winter and summer concentrations of 4.1 and 3.9 ng g–1, respectively. From 1952 to 2002, average annual concentrations were 2.3 ng g–1 and were characterized by high year-to-year variability in summer and a gradual decline in winter BC concentrations through the end of the century (Fig. 1B)…”
So Vernon, why is the artic melting so much faster now than it was 100 years ago?
Arctic with a c.
#88 HITRAN is the hi res spectroscopic data base. MODTRAN is a program for calculating radiative transfer using spectra at moderate resolution
In a post by Joseph Romm on 21 August,titled “Are scientists overestimating — or underestimating — climate change? Part I” http://gristmill.grist.org/print/2007/8/21/102318/112?show_comments=no
He points out the following irony:”…the Deniers routinely attack the IPCC consensus for using elaborate computer models that they claim are still far too simplistic to model the real climate — claiming those models omit key variables and negative feedbacks that would reduce future climate change. But now they would have us embrace a self-acknowledged “simple model” — one far more simplistic than the climate models the Deniers repeatedly denounce as too simplistic. That’s chutzpah.”
Thank you Mr. Romm! It also answers the question of what planet many deniers occupy- Planet Hypocrisy. Chutzpah for anyone who doesn’t speak Yinglish, is unabashed audacity, and is sometimes illustrated by the tale of the boy who kills his parents and throws himself on the mercy of the court because he’s an orphan.
Eli (#131) wrote:
Sorry, Eli.
It was the “TRAN” that got me confused. Hi and Mod. Should be easy enough to remember.
I just want to point out that overexaggeration-based attacks on climate science (Alastair Macdonald’s comments) are just as misleading and detrimental as are deliberate efforts to understate the issue (Vernon’s comments).
In fact, such overexaggeration is a main theme that ‘denialists’ like to use. It provides easily demolished ‘straw man’ arguments, such as the supposed deep freeze of Europe due to a slowing Gulf Stream – a theme that the likes of Richard Lindzen always target as evidence that global warming isn’t a real phenomenon.
Statements like “As I see it, you are unwilling to accept that a catastrophe is possible. Once you do that, then you will see that a catastrophe is inevitable, unless there is a change of philosophy. -A.M.” really do more harm than good, and are incorrect as well. So do the endless attacks on the climate scientists who have spent decades carefully documenting the climate record, analyzing current data, and constructing and testing complex climate models. “Pussyfooting around” is a derogatory statement.
Perhaps this is not the place to discuss PR techniques – leave that to
http://www.desmogblog.com/slamming-the-climate-skeptic-scam
However, I will say this: it is not uncommon for clever and well-financed PR operations to set up straw man arguments for public tarring and feathering by sites such as http://climatehysteria.com/
I see no credentials behind Alastair McDonald’s name. I see no bio on her web site. I’ve made no secret of my background: UC Santa Cruz BS in biochemisty, MS in ocean sciences (2000), ongoing promoter of renewable energy R&D expansion.
Let me quote desmogblog:
“Few PR offences have been so obvious, so successful and so despicable as the attack on the scientific certainty of climate change. This is a triumph of disinformation. It is a living proof of the success of one of the boldest and most extensive PR campaigns in history, primarily financed by the energy industry and executed by some of the best PR talent in the world. As a public relations practitioner, it is a marvel – and a deep humiliation – and I want to see it stop…”
“…But few PR offences have been so obvious, so successful and so despicable as the attack on the scientific certainty of climate change. Few have been so coldly calculating and few have been so well documented.”
So, that’s my opinion of Alastair McDonald’s and Vernon’s posts. It may be a personal attack, but then those two have made quite a few personal attacks themselves.
The truth of the matter is that global warming is a serious problem, but it is one that also has obvious solutions – it is not a doomsday scenario. Those solutions require transition from a global fossil fuel-based economy to a renewable energy-based economy, an end to deforestation, and stabilization of global human population. The real barriers to change are strictly political and economic in nature, not technical or scientific. There you have it. Good night, and good luck.
Antarctica…
Vernon,
There is some cooling occuring in the interior Antarctica – and if you look really hard you might find a couple of tiny sections of the Southern Ocean which are cooling, but this isn’t entirely inexplicable. Part of it would appear to be related to ozone depletion in the stratosphere – which is far closer to the surface near the south pole than anywhere else.
This much was suggested back here:
The view that it is related to ozone depletion has received considerable support recently – and it appears that the ozone depletion is partly due to global warming and results in positive feedback resulting in more global warming.
**
Now that we have a better understanding of why some parts of Antarctica are cooling, lets look at your claim that all of the warming is taking place north of the Antarctic circle.
Its latitude is 66 degrees 33 Minutes, 39 Seconds – and I am seeing plenty of glaciers on the move south of that…
22 April 2005
Retreating Glacier Fronts on the Antarctic Peninsula over the Past Half-Century
https://www.realclimate.org/index.php?p=146
Image:
http://www.antarctica.ac.uk/met/wmc/summarymap2.png
Nearly the whole George VI Ice Shelf is south of 70 degrees – and its shrinking:
George VI Ice Shelf: past history, present behaviour and potential
mechanisms for future collapse
JAMES A. SMITH, et al.
Antarctic Science 19 (1), 131–142 (2007)
http://journals.cambridge.org/production/action/cjoGetFulltext?fulltextid=743656
Looks like nearly the whole ocean down there is heating up…
Climate of Antarctica
http://en.wikipedia.org/wiki/Climate_of_Antarctica
Image:
http://en.wikipedia.org/wiki/Image:Antarctic_temps.AVH1982-2004.jpg
Getting pretty warm at times as far south as 85 degrees – little more than 300 miles from the south pole…
Alastair, was that you at lunch at the EGU?
http://scienceblogs.com/stoat/2007/04/egu_thursday_1.php
John M (#105): You raise an important issue, one that has received a great deal of attention (you’re not the first to notice it!). The short answer is: the obs and models are different, and it’s not clear whether it’s the observations’ fault or the models’ fault, or both. For the long answer, see the Climate Change Science Program SAP 1.1.
If the idea promoted by Vernon has anything to it, it is rather easy to verify.
The pollution output from Europe diminished dramatically with the crash of East-European economies (including Russia) in the early 1990’s. Gradual growth since then has been based on improved, less wasteful processes.
Western European output of particulate pollutants has declined radically since the 1950’s. Very few smokestacks remain, almost all of them equipped with filters.
As to the melting on snow and ice, it is quite obvious from everyday experience that there is an impact of short duration. Dirty snow melts easily, and melting concentrates the soot in the surface layer. When meltwater pools form, the situation changes. Dirty water is not more efficient in absorbing solar energy than clear water.
Agricultural burning is just grasping some straws in this context …
I believe he was refering to the rise in the global average temperature due to anthropogenic carbon dioxide.
There is no way he can know what that is since 1. He doesn’t know what the solar contribution is (but would appear to be at least 50%) and 2. He has no idea what the aerosol contribution is.
NASA Goddard Institute of Space Studies (2007) would suggest that well-mixed anthropogenic greenhouse gases have had a forcing which exceeded that of solar variation relative to 1880 for every year since but 1881.
Please see the chart on page 26 of the following…
As I say no-one has any idea what the aerosol effect is and it’s becoming increasingly obvious that the 20th century solar effect has been underestimated.
I see this site is back to not posting comments that has studies to support them. What, am I banned again?
RE: 122 Hank, you make this too easy. Yes you are good at tossing ad homs, but no I am not a regular reader of the CO2science site. What I am is a reader of papers on topics which interest me.
Shepherd et al (2007) Recent Sea-Level Contributions of the Antarctic and Greenland Ice Sheets can be found at:
http://www.sciencemag.org/cgi/content/abstract/sci;315/5818/1529
First, why GRACE does not agree:
I left the references in the quote so if you read the paper you can look them up.
Hank, I would rather read the real works at AAAS’s site.
Now as to what was found:
That is a ~41 percent increase in warming due to BC on average.
Ike (134), you say “The real barriers to change are strictly political and economic in nature” (with which I totally agree). That to me sounds consistent with Alastair’s statement that “a change of philosophy” is needed. Alastair didn’t say that there is no solution to the problem, only that when we do not chose to work towards such a solution, that the problems will become very large. Perhaps your disagreement is with the term “catastrophic”, but besides that I don’t see why you find the quoted text incorrect and harmful. I think the two of you agree to a large extent.
Re #135, http://www.nature.com/news/2007/070917/full/070917-3.html
This article seems to be stating that Antartic sea ice is at record levels as opposed to the Arctic which is at record lows.
The sea ice issue is complex and people are not even totally sure that the loss of sea ice in 2007 is due to climate change because for some reason the Arctic has been unusually cloud free this year and Russia was unusally warm at the start of the year.
Hi all
Good post.
Just want to know who Tamino is and what qualifications he has. Never too sure when someone puts a post/paper out there that they are genuine. I beleive the forcing affect of CO2 is 4 deg C, doubling from 1980 levels.
Peter
RE # 130
Dan, you are correct. What the Arctic needs more than anything is some a.c.
Vernon, I think we have to distinguish two trends. First, the climate is warming globally. All of the sources you have cited support that. Second, the ice is melting much more rapidly than anticipated based on the considerations of climate models. As the climate models do a pretty good job or reproducing temperatures (note, I said pretty good, not perfect), it is reasonable to assume we are missing some physics in our understanding of the dynamics of melting ice sheets. Black carbon may well be a part of that, but if it is, it is a feedback that would likely not be as important if the climate near the poles were not warming. Moreover, it is unlikely to be the sole explanation. We don’t understand the dynamics of melting ice, nor of its flow. What is certain, is that as ice continues to melt, this, too is a feedback that will further exacerbate warming near the poles, and the magnitude of this feedback is also not included in the models. Likewise, the effects of bubbling methane from thawing permafrost, etc.
So, while I think Alastair’s alarmism and deliberate and unprovoked attack may not have been the best strategy, it is probably a safe assumption that the situation is substantially more serious than we thought it was even 5 years ago. It may be an exaggeration to say that we are at a tipping point. However, societally, we are at a turning point.
RE: 139 Vernon: “Jim, I do not want to see postings that ‘explain’ things from anonymous sources. I want to see published, peer reviewed papers.”
Fair enough, Vernon. Others have provided several such references and sources, so here my published reference:
To explain just the geographical reasons why the current warming is much less in the Antarctic than in the Arctic all I needed to consult was a lowly atlas, namely a very old copy of the Reader’s Digest Great World Atlas, which shows both the Arctic and Antarctic poles at the same scale.
Go ahead, laugh if you will, but the differences in the geography of the poles easily explains much of the difference in their rate of warming. It is quite plain for anyone to see that the ocean and land mass distribution of the two poles is vastly different. That the area, and therefore the mass, of the Antarctic ice cap is at least eight times as large as that of Greenland, and thus has at least eight times the thermal inertia of Greenland. That the Southern Ocean allows clear, virtually unhindered circulation of both circumpolar ocean currents and air masses around the perimeter of Antarctica, while Greenland and the continental land masses of North America and Eurasia do exactly the opposite for the Arctic. That the typical depth of the Southern Ocean is 4000 to 5000 meters, while the much smaller Arctic Ocean averages a little over 1000 meters with two basins of 4000 to 4500 meters, again yielding a very large difference in thermal inertia. All other factors aside, geography alone clearly explains much of the warming difference.
Vernon: “So while there is a lot of melting in the Arctic, both the UC Irvine (2006) study and Sheppard et al (2007) show that a major agent of that warming is BC.”
Good to see that you are now saying that black carbon is a major agent of warming rather than the primary cause. That is progress. What say you about Pekka J. Kostamo’s post pointing out that:
“the pollution output from Europe diminished dramatically with the crash of East-European economies (including Russia) in the early 1990’s. Gradual growth since then has been based on improved, less wasteful processes. Western European output of particulate pollutants has declined radically since the 1950’s.”
Vernon: “So, getting back on topic, the CO2 level has gone up from 280 to 390 which is a 40 percent increase. The temperature in the same period has gone up 0.6 degree C. Now if you take that out to doubling, there is only going to be ~1.3 degree C increase based on the current trend.”
You are ignoring inertia. You are also ignoring feedbacks from known carbon sinks that are already observed to be coming into play.
#140
Vernon, I know perfectly well that climate is the average of weather over a long time period, rather than just weather a particular year. With regard to where I am living I am talking about a long term trend of more than 15 years. That is a change in a long term average, not just the weather of one year. If I had wanted to talk about weather during single years I could have brought up that the northern coast her did not get proper snow until Christmas last year. That’s about two months too late, and that similar things have happened several times over the last few years now, but never before during my whole life. But that jut the last few years so than not a change in a long term average, yet!
With regards to being just a local change that can be dismissed you are completely wrong. On Greenland they have the same problem as we do here, but even more. Their ice season has become too short to support their tradition hunting, they can not longer make transports over the ice as they used too. In Alaska and northern Canada whole communities now have to move since the permafrost is melting thereby causing land erosion. The same kind of metling is happening in Siberia. And permafrost peat bogs are dark by nature and do not thaw in the summer because of soot pollution.
So if by “local” you mean all areas around the arctic you are correct. If you meant “just the north of sweden” you are indeed clueless.
As I said before, unlike you some of us already live with the very real effects of climate change visible in everyday life.
Tamino
Please could you define your variables in your simple equation
S = (time constant)/C
and give the appropriate units for each variable?
Re: #148 (AEBanner)
C is the heat capacity; choice of units is up to the user, but a decent choice is Watt-years per square meter per Kelvin = W yr/m^2/K.
Time constant in years.
S is the sensitivity, units Kelvins per (Watt per square meter) = K m^2 / W.
No warming since 1998 Vernon? This site has discussed it at length, Tamino has an excellent numerical analysis with all the graphs you could need and it has been shown again and again to be nonsense.
What should we think about where one stands by respect to “facts” and “science” when we hear the no-warming-since-1998 tune?