Over the last couple of months there has been much blog-viating about what the models used in the IPCC 4th Assessment Report (AR4) do and do not predict about natural variability in the presence of a long-term greenhouse gas related trend. Unfortunately, much of the discussion has been based on graphics, energy-balance models and descriptions of what the forced component is, rather than the full ensemble from the coupled models. That has lead to some rather excitable but ill-informed buzz about very short time scale tendencies. We have already discussed how short term analysis of the data can be misleading, and we have previously commented on the use of the uncertainty in the ensemble mean being confused with the envelope of possible trajectories (here). The actual model outputs have been available for a long time, and it is somewhat surprising that no-one has looked specifically at it given the attention the subject has garnered. So in this post we will examine directly what the individual model simulations actually show.
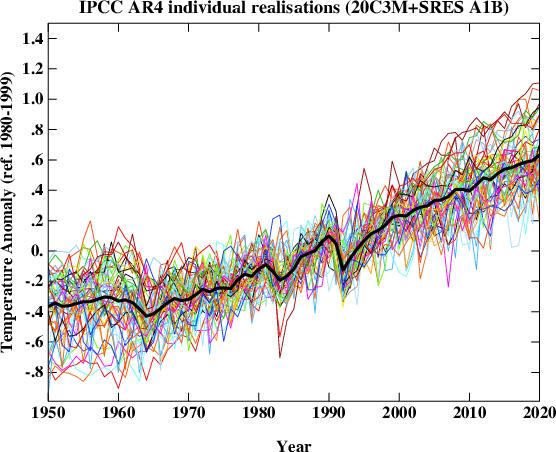
First, what does the spread of simulations look like? The following figure plots the global mean temperature anomaly for 55 individual realizations of the 20th Century and their continuation for the 21st Century following the SRES A1B scenario. For our purposes this scenario is close enough to the actual forcings over recent years for it to be a valid approximation to the simulations up to the present and probable future. The equal weighted ensemble mean is plotted on top. This isn’t quite what IPCC plots (since they average over single model ensembles before averaging across models) but in this case the difference is minor.
It should be clear from the above the plot that the long term trend (the global warming signal) is robust, but it is equally obvious that the short term behaviour of any individual realisation is not. This is the impact of the uncorrelated stochastic variability (weather!) in the models that is associated with interannual and interdecadal modes in the models – these can be associated with tropical Pacific variability or fluctuations in the ocean circulation for instance. Different models have different magnitudes of this variability that spans what can be inferred from the observations and in a more sophisticated analysis you would want to adjust for that. For this post however, it suffices to just use them ‘as is’.
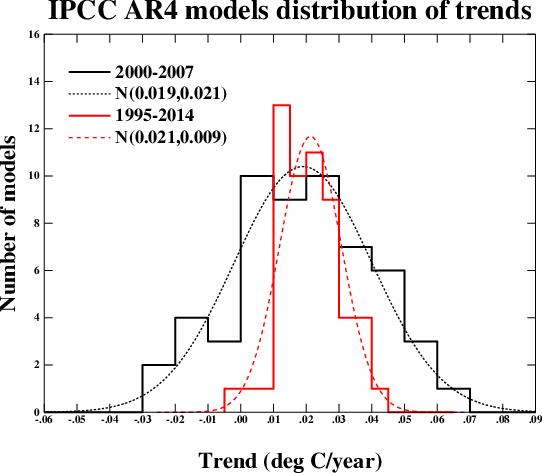
We can characterise the variability very easily by looking at the range of regressions (linear least squares) over various time segments and plotting the distribution. This figure shows the results for the period 2000 to 2007 and for 1995 to 2014 (inclusive) along with a Gaussian fit to the distributions. These two periods were chosen since they correspond with some previous analyses. The mean trend (and mode) in both cases is around 0.2ºC/decade (as has been widely discussed) and there is no significant difference between the trends over the two periods. There is of course a big difference in the standard deviation – which depends strongly on the length of the segment.
Over the short 8 year period, the regressions range from -0.23ºC/dec to 0.61ºC/dec. Note that this is over a period with no volcanoes, and so the variation is predominantly internal (some models have solar cycle variability included which will make a small difference). The model with the largest trend has a range of -0.21 to 0.61ºC/dec in 4 different realisations, confirming the role of internal variability. 9 simulations out of 55 have negative trends over the period.
Over the longer period, the distribution becomes tighter, and the range is reduced to -0.04 to 0.42ºC/dec. Note that even for a 20 year period, there is one realisation that has a negative trend. For that model, the 5 different realisations give a range of trends of -0.04 to 0.19ºC/dec.
Therefore:
- Claims that GCMs project monotonic rises in temperature with increasing greenhouse gases are not valid. Natural variability does not disappear because there is a long term trend. The ensemble mean is monotonically increasing in the absence of large volcanoes, but this is the forced component of climate change, not a single realisation or anything that could happen in the real world.
- Claims that a negative observed trend over the last 8 years would be inconsistent with the models cannot be supported. Similar claims that the IPCC projection of about 0.2ºC/dec over the next few decades would be falsified with such an observation are equally bogus.
- Over a twenty year period, you would be on stronger ground in arguing that a negative trend would be outside the 95% confidence limits of the expected trend (the one model run in the above ensemble suggests that would only happen ~2% of the time).
A related question that comes up is how often we should expect a global mean temperature record to be broken. This too is a function of the natural variability (the smaller it is, the sooner you expect a new record). We can examine the individual model runs to look at the distribution. There is one wrinkle here though which relates to the uncertainty in the observations. For instance, while the GISTEMP series has 2005 being slightly warmer than 1998, that is not the case in the HadCRU data. So what we are really interested in is the waiting time to the next unambiguous record i.e. a record that is at least 0.1ºC warmer than the previous one (so that it would be clear in all observational datasets). That is obviously going to take a longer time.
This figure shows the cumulative distribution of waiting times for new records in the models starting from 1990 and going to 2030. The curves should be read as the percentage of new records that you would see if you waited X years. The two curves are for a new record of any size (black) and for an unambiguous record (> 0.1ºC above the previous, red). The main result is that 95% of the time, a new record will be seen within 8 years, but that for an unambiguous record, you need to wait for 18 years to have a similar confidence. As I mentioned above, this result is dependent on the magnitude of natural variability which varies over the different models. Thus the real world expectation would not be exactly what is seen here, but this is probably reasonably indicative.
We can also look at how the Keenlyside et al results compare to the natural variability in the standard (un-initiallised) simulations. In their experiments, the decadal mean of the period 2001-2010 and 2006-2015 are cooler than 1995-2004 (using the closest approximation to their results with only annual data). In the IPCC runs, this only happens in one simulation, and then only for the first decadal mean, not the second. This implies that there may be more going on than just the tapping into the internal variability in their model. We can specifically look at the same model in the un-initiallised runs. There, the differences between first decadal means spans the range 0.09 to 0.19ºC – significantly above zero. For the second period, the range is 0.16 to 0.32 ºC. One could speculate that there is actually a cooling that is implicit to their initialisation process itself. It would be instructive to try some similar ‘perfect model’ experiments (where you try and replicate another model run rather than the real world) to investigate this further though.
Finally, I would just like to emphasize that for many of these examples, claims have circulated about the spectrum of the IPCC model responses without anyone actually looking at what those responses are. Given that the archive of these models exists and is publicly available, there is no longer any excuse for this. Therefore, if you want to make a claim about the IPCC model results, download them first!
Much thanks to Sonya Miller for producing these means from the IPCC archive.

Your thesis has collapsed, Gavin. Right from the start, you claimed the Skeptic equation was deceptively fitted to the GCM outputs, that I had chosen the value of “base forcing” to deliberately manufacture a congruence, and finally that I behaved dishonestly. None of that has borne out for you.
You are now reduced to claiming that the equation itself is meaningless. But that’s wrong. It has internal and expository meanings.
[Response: Ah…. you will find that I am not ‘reduced’ to claiming your equation is meaningless, it meaninglessness was apparent from the get-go. You will also find that I accused you of none of the things you appear to be exercised over. Your personal qualities are not in the least bit interesting to me. I said your equation was a fit, and that remains the case (more below). – gavin]
The internal meaning is given by the expressed internal relations themselves, by which the equation estimates a value for an initial fractional average global temperature induced by water vapor enhanced greenhouse gas forcing, and scales that value with the fraction of increased forcing due to a positive trend in those same gases to derive the change in temperature they induce. Whatever one may think about the validity of the approach or the results, that internal meaning remains.
[Response: This is simply nonsense. Any old random grouping of quantities has internal meaning by that definition – and just about the same relevance to climate (i.e. zero). – gavin]
The expository meaning is given by the results stemming from use of the equation in comparison with GCM outputs showing their projected global average surface air temperature increase due to a positive trend in greenhouse gases. The congruent result that so upsets you establishes an expository meaning to the equation, in that the striking co-linearity with the GCM outputs demands an explanation. This is true no matter the direction taken by the ultimate explanation. You may here apply your standard of scornful dismissal. Others, some equally qualified, will have a different interpretation.
[Response: The ‘striking’ co-linearity comes from convincing yourself that you have found a algebraic formula for a low climate sensitivity (which is inconsistent both internally and with reference to the real models), an unfounded assumption of no internal heat capacity and an artificially enhanced forcing to match the model trends. I’d be very interested to read of someone ‘equally qualified’ who has come to a different interpretation. – gavin]
The rest of your response is variations on a theme of empty baiting, taking the forms of specious vacuities about changing the equation or attempts to revivify the corpse of fitted results. I began a point-by-point reply, but pretty quickly realized that you had nothing left of substance.
[Response: How convenient for you. For reference, I’ll re-iterate my points in a summary below. – gavin]
Now that the spoon-feeding necessitated by your quest for coup has left the method entirely in view for easy replication, anyone with an algebra background can test the Skeptic Figure 2 results and see for themselves whether the congruence with the GCM outputs comes directly from application of the equation, or not, using only physical and calculated quantities, and with no fitted or subjective inputs. That test itself makes the result objective. When the result passes the test, that makes your argument void. None of my values were chosen. All of them are physically reasonable and stem from published equations and sources, and are completely relevant to the intent of the initial audit.
[Response: Hmm…. the ‘spoon feeding’ would not have been necessary had you given the base forcing number in your text, explained ahead of time that you used inapplicable logarithmic functions to estimate the total GHE from CO2, made clear that you don’t know how to calculate logarithms and not kept changing the definition of what your equation meant to fix the inconsistencies. But I agree, readers are in a much better position to evaluate your work now. My initial estimate of what forcings you used was too high since I incorrectly thought it was a 100 year trend in the figure instead of 80, and that lead me to the mystery of your base forcing, which lead to your peculiar definition of what zero means, and so on. The summary below gives my current opinion. – gavin]
You wrote, “Your description of where it came from was vague (and in the end arbitrary)…”
Let’s see what you think is arbitrary. To estimate the water vapor enhanced greenhouse temperature due to a positive trend in GHGs, the net greenhouse temperature of Earth (33 K) is first scaled to reflect the fraction due to water vapor enhanced GHGs (0.36), at the trend origin. Temperature increases are found by scaling the original w.v.e. GHG temperature by the fractional increased forcing due to the GHG trend. All the equations and values are from appropriate peer-reviewed sources, and are completely independent of any interests or opinions I (or anyone else) may have.
[Response: Of what you discussed, only the total greenhouse effect is an objectively chosen number. The form of your equation is subjective (why is the heat capacity of the system zero? why is it a different equation for 1900 to 1960 than it is for the future simulation?), the 0.36 is subjective (this corresponds to an assumption about the feedbacks in the system which actually corresponds to close to zero feedback). Given that there are many papers including the one you choose to cite that have feedbacks which are substantially larger than this, this is subjective (but again, see the summary below). Your base forcing number is based on a subjective choice of C0 as 1 ppm. Any other number would be as justifiable (ie. not) and would have given a different answer. And finally, since you use a forcing in your equation which is larger than the one used in the models for no apparent reason, I can only conclude that this is subjective as well. To paraphrase Elaine from Seinfeld: ‘Subjective. Subjective. Subjective.’ – gavin]
This, you call arbitrary. [edit – do please calm down]
Regarding your last paragraph, you came rather late to the wisdom of avoiding character assassination as your default tactic in debate. Your apology, if that’s what it was, is grudging and rises not even to equivocation. And as for, “series of errors and misunderstandings…” — recrudescent pap, Gavin, meant to gull non-scientists and provide grist to the partisans.
Once again, no cogent argument refuting the study has been offered. There is no obvious reason to continue the debate.
[Response: I agree. I think we have got to the bottom of things, and your refusal to address the forcings issue or acknowledge your errors in dealing with logarithms in particular is telling. For the record, this is a concise summary of what is wrong with your approach (informed, without question, by your interactions here):
Summary: too low sensitivity + no heat capacity + exaggerated forcings = no match to the GCMs
As I stated above, I have little interest in how this state of affairs came about – whether by malice aforethought or by the multiplication of serial errors, a sincere belief in what you were doing and a little luck. The bottom line is the same. Your equation is a nonsense and it’s application to anything related to climate is pointless. – gavin]
“You may here apply your standard of scornful dismissal. Others, some equally qualified, will have a different interpretation.” — Pat
“I’d be very interested to read of someone ‘equally qualified’ who has come to a different interpretation.” -– Gavin
Well, I’d also be interested in the evaluation of someone qualified in climatology. Are there any climate scientists or other *qualified* people out there who might weigh in on this debate so that we lay people would be better informed?
Re-captcha caption: fighters ladles. We have two people ladling out differing perspectives. Who is ladling out the real goods?
[Response: Who do you think? Seriously, I’m interested in how these things play out for the audience. I thought that pointing out that Frank has a different interpretation of what taking the logarithm means than anyone else would have been a clincher. – gavin]
Re #452
Well, I’m a PhD Geophysicist somewhat involved in reconstruction of the paleo-geomagnetic field, and I’ve learned this valuable lesson:
In future, when I present a manuscript for peer-review, any reviewer who calls me to account for trivial math errors is clearly engaging in polemical grandstanding.
It’s a bright new world!
Dear Pat Frank,
stimulated by the discussion, I read through your article: “ A climate of Belief – supporting information”.
You used 3 data points from the paper (S. Manabe and R. T. Wetherald (1967) Thermal Equilibrium of the Atmosphere with a given Distribution of Relative Humidity in the Journal of the Atmospheric Sciences 24, 241-259) in order to fit a logarithmic relationship between equilibrium surface temperature T and the concentration of CO2. I read through the paper as well.
Your fitting equations have the general structure a*log(c)+b, so it is clear that they should fit 3 data points.
It is certainly possible to use the equations in an interpolation. However using them in an extrapolation, as you do, seems to be highly questionable, since other equations with 3 free parameters will also provide an excellent fit.
Especially, since the asymptotic behavior of the Log function towards zero means approaching a singularity.
Gavin, as long as you are soliciting audience reviews on the Pat Frank correspondence, I’ll comply. Some years ago there was a television commercial in which a professional basketball player who also played the piano challenged 80-year-old pianist Rudolf Firkusny to a combined basketball/piano one-on-one competition. The basketball portion went as one would expect, but after Firkusny led off the piano portion with a brief virtuosic flourish, the basketball player grinned sheepishly and offered to call the whole thing a draw. Without the last bit, which both made the commercial cute and illustrated the folly of challenging a professional on his own turf, it would have been merely a display of cruelty. I’m waiting for the piano competition.
[Response: I’d be game. – gavin]
Pat Frank, short of it is: why is it a log that fits the system? Not the figures. The system.
After all, saying “Ovals fit the orbitals of planets” really does fit. But you can get that and STILL have no idea why. All you did was some very accurate reading. That rule, though “true”, doesn’t tell you why planets go faster than they do when they are near the foci the sun is on than the foci the sun is not on.
Saying that the laws of gravity (GmM/r2) when applied to the system will cause a planet to describe an oval with the sun at one focus and, because the force is greater when closer to the sun (r^-2) it will therefore go faster.
In fact that law of gravity tells you that they will sweep out equal areas in equal times. Getting it the other way round requires you be REALLY SMART.
So you’ve matched the temperature to the logarithmic curve you’ve set. So explain to us the physical process that, when you do all the sums, makes it describe a logarithmic of that shape.
spilgard:
In my experience, reviewers who point out “trivial errors” might be “grandstanding.” But this is also how authors talk when feeling defensive about their own sloppiness.
For Frank’s log error, it’s not trivial – closer to a fatal flaw.
From the get go, Frank´s stuff seemed pretty strange. I mean anyone that has boiled water knows that water has quite a heat capacity. Given that there is a lot of water present on the earth, claims that one can ´audit’ GCM by some fitting procedure that explicitly assumes no heat capacity must be viewed with skepticism. It is well known that within GCMs (like in the real world) water takes some time to heat up. Franck´s efforts to justify his position have also been instructive. I agree with Ian (number 457), that the business with the logs, for example, is fatal for Frank.
Re 457:
Ian,
I agree completely, and your observation expresses my original intent. Sloppy choice of words on my part. After I hit the “post” button I realized that my use of “trivial errors” was ambiguous… “bone-headed errors” or “highschool-level errors” would have been more appropriate. Sorry for the confusion.
I note that nobody has refuted Miklós Zágoni’s work.
I would also note that there were no sunspots in August. Looks more like cooling than warming.
[Response: It’s not Zagoni’s work, and many people have. – gavin]
Thank-you for making your case explicitly, Gavin. Point-by-point follows:
1. Your equation, “Delta T = 0.35*Delta F” is wrong on its face because the equated dimensions are incommensurate. T does not equal W/m^2. When tracking the dimensions, the equation reduces to Delta T = [(0.36 C)/Wm^2]*Delta F (W/m^2); i.e., C=C. I’ve already pointed out that the 33.302 W/m^2 base forcing includes the forcing of aboriginal N2O and CH4. If you want to strictly calculate the temperature change due to CO2 doubling alone, you need to put in the forcing for aboriginal CO2 alone. That value calculates to 30.47 W/m^2. Using that value, the doubling sensitivity of CO2 alone is 1.44 C, not 1.32 C.
Your point that the Skeptic equation does not reflect the full 2.6 C sensitivity of Manabe’s model has already been answered (see again below). Your complaint in any case can be equally applied to the 10 GCMs displayed in Skeptic Figure 2, in that during the time of CO2 doubling they, too, do not reflect anywhere near an included doubling sensitivity of 3 C (the IPCC average). In fact, they show a large range of sensitivity over CO2 doubling — 1.3-2.2 C — amounting to a variation across 50% while modeling the identical change in CO2. That’s not very reassuring, is it.
Under the same circumstances of CO2 doubling and historically increasing N2O and CH4, the Skeptic equation shows a doubling sensitivity of 1.6 C, which is almost smack in the middle of the GCM range (1.8 C).
I’ve already pointed out that the 33 C greenhouse temperature reflects the quasi-equilibrated global temperature response to aboriginal GHG forcing, not the instantaneous response of the atmosphere to increased forcing. It’s not surprising in retrospect, therefore, that the Skeptic equation displays a lesser sensitivity than calculated for an increase in GH gases absent the long term re-equilibration of initial forcing energy among the various climate modes. I.e., the longer term moderating effects from the heat capacity adjustments of the rest of the climate is already reflected in the 33 C.
2a. I did not “assume” that 11.9 C of the greenhouse effect is caused by base forcing. That 11.9 C is calculated directly from the fraction of greenhouse warming due to water vapor enhanced GHG’s obtained from Manabe’s data (0.36) times the greenhouse temperature unperturbed by human-produced GH gases (33 K). Neither of those quantities is assumed, and the evidence and rationale are provided for both (Figure S1, and references SI 1 and article 19. See also below.).
2b. There is no assumption that the role of forcing is linear from 0 ppm. Figure S1 shows a log relationship between forcing and CO2, and therefore between induced temperature and CO2. You have criticized me earlier for extrapolating Manabe’s log relationship to low CO2, and so it’s ironic that you now criticize me for assuming a purported linear relationship.
The base forcing reflects the direct non-water-vapor-enhanced forcing of the GH gases present in the base year (e.g., 1900) and was verified by two independent means, as demonstrated already in post #450. In that event, the end-point scaling of 297.7 ppm (not 2100) is rendered empirically valid (see further below). Zero ppm CO2 has zero relevance in any of that.
2c. The water vapor feedback is indeed in the Skeptic equation. As assumed by GCMs, the 33 K unperturbed greenhouse temperature is taken to reflect constant relative humidity. The 11.88 C following from the Manabe extrapolation approximates the proportion (36%) of the w.v.e. GHG temperature in the baseline greenhouse 33 K. The linear extrapolation of this 11.88 C with fractional increased forcing approximates continuation of constant relative humidity, SI Figure S2. This is discussed explicitly in SI page 3.
You wrote, “the effects of water vapour and clouds provide roughly 80% of the GHE today…,” but “water vapour” includes the intrinsic water vapor plus the enhanced water vapor induced by GHG warming. So, your 80% excludes only the pure dry forcing due to GH gases. That value, using your percent, is 0.2*155 W/m^2=31 W/m^2, (or 0.2*179 W/m^2=35.8 W/m^2, using Raval’s value) which is again virtually identical to the base forcing value (= dry GHG forcing) used in the Skeptic equation. The argument about what would be left behind in a colder 0 ppm CO2 world followed from extrapolation of Manabe’s calculation. My intent was always to determine the case for GCMs, not for Earth. See the continuation of this point, below.
3a. You wrote, “… which is an obvious nonsense (since In(0) is undefined), you must have used CO2=1 ppm instead (again!).”
Log plots are asymptotic to zero. The zero intercept is at infinity mathematically, but is physically meaningful. I.e., an extrapolation can be carried out arbitrarily close to zero until the residual is smaller than any uncertainty. You have no case here. It’s very peculiar that your quote from the SI explicitly included my reference to “asymptotic intercepts,” while you went on to wax indignant about the meaninglessness of “ln(0).” How is “ln(0)” implied by “asymptotic”?
The plot in SI Figure S1 is ppm CO2 vs. temperature (K), fitted with a natural log function. Let’s see if extrapolation to an asymptotic zero ppm CO2 intercept of that function is physically reasonable. CO2 forcing is linearly related to absorbance. For our readers, radiation absorption is given by Beer’s Law, and is transmitted intensity = I = Io*e^-ax, where “a” is molar absorptivity, and “x” is path length (in cm for convenience). Beer’s Law can be expressed in terms of number of molecules by defining a’ = a/rho, where rho is density (gm/cc). Then I=Io*e^-a’d, and absorbance = A = log(Io/I)= a’d, and “d” has units of gm/cm^2.
But Beer’s Law absorbance is itself linear only when the radiation is monochromatic and absorption occurs at constant molar absorptivity (e.g., at a band maximum). Neither of those conditions is satisfied in the absorbance of OLR by atmospheric CO2. OLR is polychromatic, and absorption occurs simultaneously across the entire 15 micron CO2 absorption band, over which molar absorptivity varies sharply. Each of these two conditions produces non-linearity. When both of these conditions apply, A = log[(sum of multiple I’s)/(sum of multiple Io’s)] = log(sum of multiple e^-a’d)’s, and absorbance is a non-linear function of CO2 number density over every range of concentration, including arbitrarily close to 0 ppm CO2.
This means as soon as CO2 reaches a concentration where forcing becomes non-zero, the induced temperature increase is immediately a non-linear function of increasing CO2 concentration. There is no linear absorption range of atmospheric CO2 concentration. Below, I show that the log relation between temperature and CO2 concentration, as in Figure S1, is itself justifiable to low concentrations of CO2. The only question remaining here is whether the Figure S1 coefficients are reasonably constant over the entire range of [CO2]. A shift in the slopes during propagation toward 0 ppm will change the asymptotic intercepts and may ultimately affect the fraction of G due w.v.e. GH gases.
An accessible way to approach this latter question is to ask whether the 0.36 of G represented by the extrapolation of Manabe’s data is a reasonable fraction. Luckily for us, you provided one means for testing this, Gavin, by letting us know that the direct contribution of GHG forcing to G is 35 W/m^2, +/-10%, courtesy of the GISS GCM. The w.v.e. enhanced GHG contribution is then about 68 W/m^2. The fraction of w.v.e. GHG forcing in G is then ~(68/155)=0.44(+/-)4.
A second test comes from the publication of Kiehl and Trenberth, 1997,* who gave CO2 forcing as 32(+/-)5 W/m^2, so the w.v.e. CO2 fraction can be estimated as (32*1.932/155)= 0.40(+/-)6. These results show the 0.36 w.v.e. fraction derived from the log extrapolation of Manabe’s data is of very reasonable magnitude (more on this below).
In addition, when testing the 0.36 result from the extrapolation of Manabe’s work, I calculated the lines for 1% compounded CO2 plus trace gases, substituting in w.v.e. GHG fractional contributions of 0.3, 0.4, 0.5, and 0.6 instead of 0.36. Fractions 0.3 through 0.5 did a good job of tracking the GCM outputs shown in Skeptic Figure 2, with the 0.4 line the best fit with respect to the envelope of GCM lines. So, the Skeptic analysis survives intact with a w.v.e. GHG fraction of 0.40 or 0.44. Nothing important changes.
*J. T. Kiehl & K. E. Trenberth (1997) “Earth’s Annual Global Mean Energy Budget” BAMS 78, 197-208.
3b. My use of Myhre’s equation merely assumed that forcing is negligible at 1 ppm CO2, and so the forcing of any current or projected high [CO2] is equal to 5.35*ln(CO2). This is exactly what Myhre’s equation implies with Delta Forcing = 5.35*(lnC – lnCo), i.e., both ln(C) and ln(Co) have independent meaning. This assumption was verified twice, as noted in post #450. Your point about 0.1 ppm, etc., is irrelevant because, while trivially true, it ignores the _1 ppm CO2 = zero forcing_ assumption, and is leveraged only by a specious retention of dimensionality that allows you to produce nonsense numbers.
So, let’s see if CO2 forcing is negligible at 1 ppmv. The absorption coefficient of CO2 at 15 microns (the main GW band) for low concentrations of gas is about 2.5 cm^-1 atm^-1.* For 1 ppmv of CO2, the 1/e decrease in transmitted intensity (where self-absorption begins) occurs at about 11 km, requiring virtually the entire troposphere. The CO2 absorption maximum is at 15 microns, and less at the wings, so at 1 ppmv CO2, absorbed OLR is pretty much freely re-radiated into space and the forcing of CO2 is approximately zero.
*C.W. Schneider, et al. (1989) “Carbon dioxide absorption of He-Ne laser radiation at 4.2 [micrometers]: characteristics of self and nitrogen broadened cases” Applied Optics 28, 959-966, and the NIST spectrum of CO2 at http://webbook.nist.gov/chemistry.
With respect to the extrapolated log fit to Manabe’s data, the 1 ppm ‘no-forcing’ calculation immediately above assumes monochromatic radiation and is restricted to the 15 micron band maximum. However, it allows the rough estimate that band saturation probably begins somewhere between 2 ppm and 3 ppm CO2 (the 1/e length is 5.4 km and 3.6 km, resp.). So even under ideal spectroscopic conditions the log relationship between CO2 concentration and forcing (and thus temperature) probably begins about there; showing that a log relationship between forcing and [CO2] is good to low ppm CO2.
3c. You wrote, “and do not correspond to any real calculation with a radiative-convective model.”
They correspond to the results from the radiation-convection model of Manabe extrapolated to an asymptotic 0 ppm CO2.
You wrote, “…you must have used CO2=1 ppm instead (again!)”
I begin to wonder if you understand the meaning of asymptotic to zero.
You wrote, “Had you chosen CO2=0.1 ppm, the ‘zero CO2 GHE’ would have reduced to 12 deg C, or with 0.01 ppm, it would be down to 3.8 deg C.”
This comment just shows you neglected the obvious meaning of ln(1)=0, which is that forcing is assumed to be negligible at 1 ppm CO2. This is the only way to rationally understand the subsequent use of Myhre’s equations to calculate base forcing at elevated CO2. Your assertion that it reflects some naive error only displays the result of a tendentious analysis. The carping on this non-issue led me to make the atmospheric absorption estimate of 1 ppm CO2, above, which pretty much validates the assumption of negligible forcing at 1 ppm CO2 as very reasonable.
You wrote, “Thus by subjectively choosing ‘zero’ ppm CO2 to be really 1 ppm…”
Rather, the intercepts were obtained by reasonably taking as physically meaningful, the asymptotic approach to 0 ppm CO2 of the log fit.
You wrote, “and incidentally, even using CO2=1, you get 0.37, not 0.36 as your fraction.”
Round-off error. Good catch, Gavin.
4. You wrote, “You made the same error using logarithms in defining you (sic) base forcing.”
I’ve made no error anywhere using logarithms. You have merely overlooked a reasonable assumption (1 ppm CO2 = ~0 forcing), displayed a lack of perception concerning asymptotes, then manufactured a false case and waved it about.
5. This, your last point, is a recapitulation of what you wrote above, ending with, “I should have spotted that earlier! Thus, not only is your sensitivity way too low, you used a higher forcing to get a better match! (emphasis added)”
An enduring trait of your argument has been a default impulse to character assassination by an invited inference to dishonesty. Another has been a careless disregard for what I actually did. Both are in evidence there. From the SI: “When the temperature increase due to a yearly 1 % CO2 increase was calculated, the increasing CO2 forcing was adjusted to include the higher atmospheric concentration of this gas, but the increasing forcings due to methane and nitrous oxide were left unchanged at their Figure S4 values.”
That is, the forcing in Skeptic Figure 2 is larger than for CO2 alone because the trace gases CH4 and N2O were allowed to increase across their 1960-2040 measured or extrapolated values. All of those choices were made a priori. None were made after the fact, “[in order] to get a better match!” Your unfailing innuendoes are inappropriate and tedious.
The GCMs themselves were not uniformly conditioned to atmospheric chemistry. Some included trace gases (CERFACS1, GISS, HadCM3, DOE PCM), others did not. Some included aerosols (CERFACS1, GISS, ECHAM3), others did not. I included the trace gases CH4 and N2O because it seemed reasonable that if CO2 were to increase from industrial outputs, so would CH4 and N2O.
However, I later calculated the effect of doubling CO2 alone with no added CH4 or N2O at all (again from the CMIP 1960 origin), using the Skeptic equation. The slope of the resulting line was lower than the published line, but was still well within the 10-GCM envelope. In fact, the Skeptic equation CO2-alone line coincided very nicely with the Figure 2 GISS and NCAR projections.
On the other hand, following your GISS model estimate for the direct forcing produced by GH gases (35 W/m^2), and the resultant 0.44 of G fraction it produces for w.v.e. GHG forcing, I tested that value by substituting it for the Manabe fraction (0.36) in the Skeptic equation under the CO2-alone conditions. The resulting line went beautifully through the middle of the 10-GCM envelope. Even including N2O and CH4, the 0.44 line showed a 1.9 C trending increase at double CO2, putting it in the upper range of GCM projections.
Ancillary points:
Where you wrote, “This is simply nonsense. Any old random grouping of quantities…”
‘_Artichokes garble boot laces_’ is grammatically correct but transmits no coherent internal meaning, in analogy with “any old random grouping…” However, the Skeptic equation has an internal meaning, which is, _scale the w.v.e. temperature component of the total greenhouse temperature by the fractional increase in forcing_. This is a coherent internal meaning, regardless of your liking for it.
Where you wrote, “too low sensitivity:” In your response to #450, you wrote, “[the total greenhouse forcing without feedbacks is] about 35 W/m2 (+/- 10%) (calculated using the GISS radiative transfer model). The no-feedback response to this would be about 11 deg C consistent with the Manabe calculation. This implies that your formula is only giving the no-feedback response of course.”
I should have paid attention to this earlier. You are on record as giving the climate sensitivity as 0.75 C/Wm^-2, here: http://tinyurl.com/5vdg2r as well as in published work, where you wrote, for example, that, ““The eventual equilibrium global temperature change is roughly proportional to the forcing, with the climate sensitivity as the constant of proportionality.,” where that sensitivity/constant of proportionality is again given as 0.75 C/Wm^-2.*
This 0.75 C/Wm^-2 is an interesting number. We can take the 235 W/m^2 of deposited solar energy and add the greenhouse G of 155 W/m^2 to find that over-all climate sensitivity is (288 C)/(235+155)W/m^2 = 0.74 C/Wm^-2. What a coincidence.
But really, solar forcing alone is what raises Earth atmospheric temperature from a normative minimum to the 255 C that obtains without any greenhouse from water vapor or other GH gases. The forcing responsible for the last 33 C is the greenhouse G, and so for Earth climate as it is now, with water vapor and GH gases, a better estimate of over-all sensitivity is 33 C/155 W/m^2=0.21 C/Wm^-2, which includes the w.v.e. feedback response and the energy redistribution through climate heat capacity. This empirical estimate seems rather closer to the 0.36 C/Wm^-2 implied by the Skeptic equation than the 0.75 C/Wm^-2 of the GISS GCM, doesn’t it.
*G. A. Schmidt, et al. (2004) “General circulation modeling of Holocene climate variability” Quaternary Science Reviews 23, 2167–2181.
However, with respect to our debate, the sensitivity of the Skeptic equation with respect to Earth climate is not an issue. The issue is whether with reasonably valued inputs, the Skeptic equation is able to reproduce the trend projected by GCMs during a rise in GH gases. This it does, merely by an extrapolation of the w.v.e. greenhouse component of 33 C, linearly scaled by fractional increased forcing. We can here note again that the sensitivity over CO2 doubling shown by the Skeptic equation matches well the sensitivity shown by all 10 GCMs during the course of the same trend in rising CO2. Auditing the GCM trend was the point, of course, not the actual climate sensitivity of Earth.
There is no sensitivity built into the forcing fraction calculated from Myhre’s equation. Nor is there a sensitivity built into the very reasonable w.v.e. greenhouse fraction extracted from Manabe’s data. We know this latter point is true because a comparable temperature trend is obtained from the Skeptic equation using the 0.40 or 0.44 w.v.e. GHG fractions extracted or calculated from other independent estimates of GHG forcing as noted above. So, the sensitivity comes from the only remaining part of the Skeptic equation, which is the 33 C of greenhouse temperature increase. This 33 C must reflect the quasi-equilibrated climatological response to 155 W/m^2 of greenhouse forcing and so implicitly includes the sensitivity of global average temperature to GHG forcing.
So, your “too low sensitivity” isn’t too low at all. It’s the same sensitivity shown in aggregate by GCMs while they are projecting the temperature response from a rising trend in CO2, which projection the Skeptic equation was meant to test.
Likewise, your “no heat capacity” ignores the climatological heat capacity reflected by the magnitude of the quasi-equilibrated net greenhouse 33 C.
And your “exaggerated forcings” is just you not noticing the mentioned inclusion of CH4 and N2O. I.e., it merely reflects your own careless reading of the Skeptic SI, as shown in detail above. And whether or not these gases are included, the Skeptic equation nevertheless tracks the GCM projections. You case here has zero content.
Indeed, your entire case has zero substantive content.
[Response: Oh, I thought we were done? Obviously not. My last post said pretty much all I have to say, but since you are in complete denial about the meaning of an asymptote or what happens to logarithms near zero, I’ll give you a basic mathematics lesson instead. The asymptote of a function f(x) at a point x0 where f(x0) is undefined is lim(f(x)) as x->x0. Sometimes this exists, sometimes this is undefined. For the function f(x)=sin(x)/x, f(0)=0/0 is nominally undefined, but by taking limits and using l’Hopitals rule, you get that lim(f(x)/g(x))=lim(f'(x)/g'(x))= lim(cos(x)/1)=1 as x-> 0. sin(x)/x is then said to asymptote to 1 as x->0. If f(x)=x log(x), then you would have lim((1/x)/(-1/x^2))=lim(-x)= 0, again a finite asymptote. But for either log(x) or 1/x there is just a singularity i.e. lim(log(x)) or lim(1/x) are infinite. You can see the same thing using Taylor expansions, or just drawing a graph or by putting in ever smaller numbers into your calculator. Your insistence to the contrary is an embarrassment to any educational establishment of higher learning you have ever attended. Please, for your own sake, do not continue to insist that log(0) asymptotes to a finite number. (To other readers: If you are a friend or correspondent with Frank, please email him and tell him to desist. Perhaps you can have an intervention?). Compared to this basic mathematical error, all of your misunderstandings about climate pale into utter insignificance. – gavin]
#453 — and if the claimed error is both insistent and invented?
#454 — but the log-form fit is the only one physically justified. See also my discussion of an asymptotic zero intercept in post #460.
#456 — forcing is linear with absorption at higher [CO2], and absorbance follows the log of concentration when on an absorption tail due to band saturation.
[Response: Please stop – it’s too much! i) it’s neither, ii) over a particular range only (roughly 200 to 1000 ppmv), iii) forcing is linear only at very low concentrations, not high ones. – gavin]
[Intervention]
I didn’t bother reading Pat’s paper, but I know the pattern. Please Pat, stop it. Stop taking punches like a palooka. Go to Steve Mosher and have him salve your bloody face. I’ll hold off Gavin with a Bessel function, so he doesn’t hit you any more.
P.s. Ever notice how Steve McI doesn’t comment on this sort of thing. Just lets the carnage go on. It’s so obvious (as with Loehle) that he’s not going to back up nincompoops. But doesn’t want to call them out, either. Since they’re “on his side”.
Just a postscript to the Frank discussion. He has claimed at another place that I “was reduced to the scientifically spurious criticism that the asymptotic intercept of a log plot is physically meaningless”. Hmmm…. whether anyone actually points out to him there that the log function asymptote is in fact the y-axis (x=0) and so there is no finite intercept will be telling.
Based on reading alot of what is over my head, I understand that CO2 only has a “greenhouse effect” (reflecting and keeping the heat in?) at certain wavelengths of frequencies. Based on what I have read CO2 shares these frequencies with other greenhouse gases and water vapor share. What study can you point me to that proves that a specified increase in CO2 level in PPM will actually cause the retention of more heat on the planet? Could it be possible that the effect CO2 has in contributing to warming on planet earth was at a maximum based on it being one of several contributors to global warming (and not even the greatest contributor)and that the temperatures we are experiencing are just normal variations over a long term climate record that we have no certainty of given the short period of time we’ve been able to measure it?
Ed 465.
Do you think you’ve just had a blinding flash of inspiration that has not hit anyone before?
Here’s proof for you.
Put one thin jumper on and go outside at night (day if it’s cold outside).
Cold.
Now put on another one.
Warmer.
Another.
Getting hot.
Another.
Sweating now.
Even though each jumper is blocking the same thing as each other, they accumulate.
Ed, welcome to RealClimate; it is a good place to get answers to such questions. There has been a lot of discussion of these points on this forum. I’m an amateur on the site, but I will try to answer quickly, then give a pointer for more information.
Basically, it is not true that the CO2 absorption bands are completely shared; increased CO2 has been shown to cause increased IR absorption. Furthermore, at higher altitudes there is very little water vapor, so CO2 becomes more and more significant as altitude increases. See the post on “Saturated Gassy Argument” on the sidebar of topics to the right hand side of the window for more on your initial concern.
Regarding your concern about attribution of theobserved warming, no-one has been able satisfactorily to explain that warming without resorting to the idea of the “greenhouse effect”–and that warming is apparently unprecedented in recent geological history. Additionally, we observe stratospheric *cooling* in conjunction with the warming we see on land, sea, and in the lower atmosphere–this a real fingerprint that the greenhouse effect is responsible. (You wouldn’t see that, for example, if the warming was driven by the sun.)
Ed, you’ve posted FAQs, let me point you to answers so you have primary sources instead of opinions as answers.
> what study
Try the Start Here link at top of page, and the History link (first one under Science) at right side
> Could it be possible
Hypothetically yes; it’s been checked, and it isn’t.
See the same links above.
Great postscript, Gavin.
Further to the statement in #467 “Additionally, we observe stratospheric *cooling*”
Think of your thin single jumper. How warm IS that jumper? Fairly warm.
How about the outermost of your fourth jumper? Pretty cold.
It is an experiment you can do yourself without letting them other people blind you with maths.
Nice of me, eh?
[Response: Actually strat cooling is a tad more complicated than this, and relies on the fact that the IR radiation is spectrally varying. – gavin]
Jeez, guys.
That took four goes with changing words until you didn’t think it spam.
And what the clicking bell is wrong with
a
m
b
i
e
n
t
?
What spam does that turn up in?
[Response: “ambien” is a drug name. This is flagged in the spam response page as a possible issue, no? – gavin]
I encountered this problem several months ago, it took me several iterations to discover that the hidden word was the problem.
To Gavin’s response:
I’ve never heard of it.
However, I’ve heard of “a.m.b.i.e.n.t temperature”. I suspect many astronomers, physicists and meteoroligists have too.
Never get a program to do a man’s work.
Hey, one way to close this site down would be to make a drug called “AGW” “Climate” and “CO2”! Nobody would ever be able to post here again!!!
NOTE: If it highlighted the bad words then we wouldn’t have to guess what it was whinging about. I took out science and scientist in case something was wrong with them.
Also, putting spaces (which is darn common now with spam filters being so widespread) stops it being spam.
Uh, not too effective.
Nothing’s very effective, Mark. Publishing the list would enable the spammers to work around it. We just have to try to be smarter than the spammers. Check your own spam bucket for likely keywords — that helps figure out what’s popular with the crap merchants but caught by filters.
Ask anyone with a website how much spam gets past their best filters that they have to remove by hand.
Sturgeon’s Law meets Tragedy of the Unmanaged Commons.
[Response: Actually, ours is now down to one or two spam comments a day. – gavin]