

 The British tabloid Daily Mirror recently headlined that “Sea will rise ‘to levels of last Ice Age’”. No doubt many of our readers will appreciate just how scary this prospect is: sea level during the last Ice Age was up to 120 meters lower than today. Our favourite swimming beaches – be it Coogee in Sydney or the Darß on the German Baltic coast – would then all be high and dry, and ports like Rotterdam or Tokyo would be far from the sea. Imagine it.
The British tabloid Daily Mirror recently headlined that “Sea will rise ‘to levels of last Ice Age’”. No doubt many of our readers will appreciate just how scary this prospect is: sea level during the last Ice Age was up to 120 meters lower than today. Our favourite swimming beaches – be it Coogee in Sydney or the Darß on the German Baltic coast – would then all be high and dry, and ports like Rotterdam or Tokyo would be far from the sea. Imagine it.
But looking beyond the silly headline (another routine case of careless science reporting), what was the real story behind it? The Mirror article (like many others) was referring to a new paper by Grinsted, Moore and Jevrejeva published in Climate Dynamics (see paper and media materials). The authors conclude there that by 2100, global sea level could rise between 0.7 and 1.1 meters for the B1 emission scenario, or 1.1 to 1.6 meters for the A1FI scenario.
The method by which they derive these estimates is based on a semi-empirical formula connecting global sea level to global temperature, fitted to observed data. It assumes that after a change in global temperature, sea level will exponentially approach a new equilibrium level with a time scale τ. This extends the semi-empirical method I proposed in Science in 2007. I assumed that past data will tell us the initial rate of rise (and this initial rate is useful for projections if the time scale τ is long compared to the time horizon one is interested in). The new paper tries to obtain both the time scale τ and the final equilibrium sea level change by fitting to past data.
Therefore, my approach is a special case of Grinsted’s more general model, as you can see by inserting their Eq. (1) into (2): namely the special case for long response times (τ >> 100 years or so). Hence it is reassuring and a nice confirmation that they get the same result as me for their “Historical” case (where they get τ=1200 years) as well as their τ=infinite calculations, despite using a different sea level data set (going back to 1850, where I used the Church&White 2006 data that start in 1880) and a more elaborate statistical analysis.
However, I find their determination of τ is on rather shaky ground since the data sets used are too short to determine such a long time scale with any confidence. That their statistics suggest otherwise cannot be right – you can tell by the fact that they get contradictory results for different data sets (e.g., 1200 +/- 500 years for the “Historical” case and 210 +/- 70 years for the “Moberg” case). Both can’t be correct, so the narrow uncertainty ranges are likely an underestimate of the uncertainty.
The problem gets even more apparent when looking at the equilibrium sea level resulting from their data fit. From paleoclimatic data (see Figure) we expect that per degree of temperature change, the final equilibrium sea level change is somewhere between 10 and 30 meters (as I argue in my Science paper – this was my basis for assuming τ must be very long). Grinsted et al. find from their data fit that this is only 1.3 +/- 0.4 meters (for the Moberg case, which they call the most likely) – see Figure. This means that getting the sea level lowering of ~120 meters that is well-established for the Last Glacial Maximum would have required a global cooling of about 90 ºC according to their model. And for the future, the model would predict that melting all ice in Greenland and Antarctica (resulting in 65 meters of sea level rise) would require about 50 ºC of global warming. This lack of realism matters, since it is directly linked to the short τ: the observed sea level rise of the past century or so can either be fitted by a short τ and a small equilibrium rise, or by a long τ and a large equlibrium rise (per degree). I consider the latter case the realistic one.
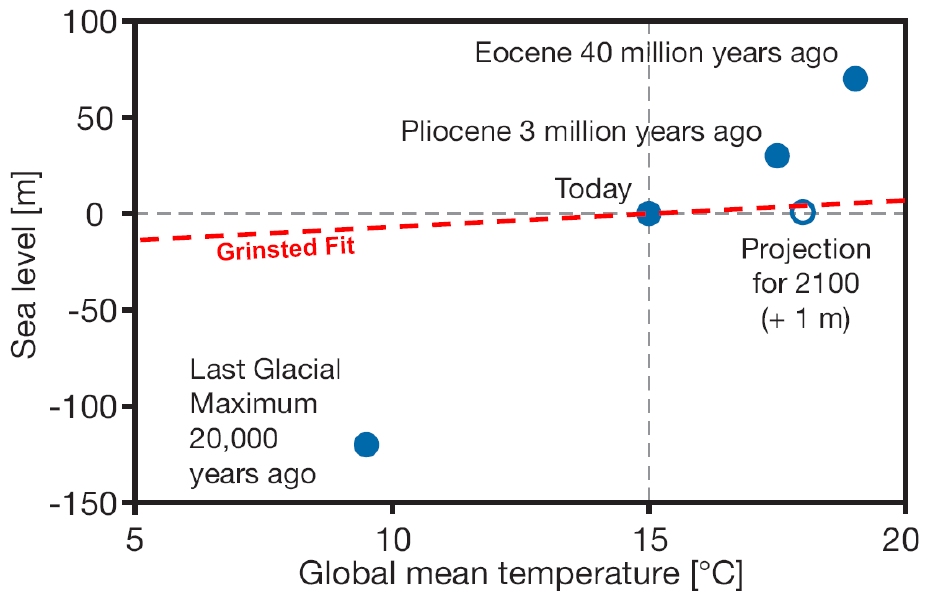
Global mean temperature and sea level (relative to today’s) at different times in Earth’s history, together with the projection for the year 2100 (which is not an equilibrium change!). The red line shows the “most likely” equilibrium response according to Grinsted et al. [Modified after Archer (2006) and WBGU 2006; see p. 33 there for references and discussion.]
Grinsted et al. did apply some paleoclimatic data constraints, but they are based on a misunderstanding of these data. They assume (their constraint 3) that the last interglacial was globally 3-5 ºC warmer than present – however the reference cited in support (the IPCC paleoclimate chapter, of which I am a co-author) explains that these are Arctic summer temperatures. This Arctic summer warming is due to orbital changes which cause cooling elsewhere on the planet, resulting in global mean changes that are very small (see e.g. Kubatzki et al. 2000). Grinsted et al make the same mistake for glacial climate (their constraint 4), where they assume glacial maximum temperatures were globally 17 ºC below present – the reference cited states already in the abstract that this only applies to the latitude band 40-80ºN. Glacial cooling was highly non-uniform, with global mean cooling estimated as 4-7ºC (see Schneider et al. 2006, “How cold was the Last Glacial Maximum?”) These misguided paleo-constraints lead Grinsted et al. to limit equilibrium sea level rise to a fraction of what the data points show in the Figure above, and this rules out a good data fit for long time scales τ.
For these reasons I am unconvinced by the short τ found (or assumed) by Grinsted et al. which is the key difference to my earlier study, and I would still maintain that assuming the equilibration time to be very long is a more robust assumption. Note that (unlike Grinsted et al.) this does not assume that the approach to equilibrium is exponential with a single time scale, which in itself is doubtful given the different processes involved. It only assumes that the initial rate of rise scales with temperature and is relevant on time scales of interest. On the positive side, Grinsted et al. have shown that the data fit and projected sea level rise for the case of large τ is robust with respect to the chosen statistical method and data set.
Refinements of the semi-empirical approach are welcome – I had hoped that my paper would stimulate further work in this direction. While empirical approaches will not give us definitive answers about future sea level since the past can never be a perfect analogue of the future, these analyses can still be useful to give us a better feeling for how the sea level responded in the past and what that might imply for what lies ahead. But one thing is certain: I’m not too worried that sea level might drop to glacial levels during this century.
I am very happy that our paper is discussed here in realclimate (one of my favorite blogs).
Before I start discussing the points raised in this blog entry, I want to emphasize the agreement between our projections. We both project sea level in the order of a meter or more by the end of this century. That is considerably more than the IPCC AR4. The point to take home is that if you make a semi-empirical model linking temperature to sea level, then you will get these kinds of numbers. In our Grinsted et al. (2009) paper we state “We find that projected 21st century sea level is virtually independent of response time (Fig. 6 and table 3) and that IPCC model projections are much too low even for millennia scale response times (Table 2)”.
The difference between our model and that from Rahmstorf (2007) can be summarized as follows: We derive a “short response time (~250yrs) / small long-term response” whereas Rahmstorf assumes a “long response time (~5000yrs) / large long-term response”. We show that if you make the response time longer then you will need to compensate with a smaller response in order to keep the good fit to observations. The consequence is that for near term predictions (100 year predictions) these two effects largely cancel out.
In his comment Rahmstorf extrapolates our semi-empirical model to a 65 m rise in sea level and finds unrealistic results. This is, however, to be expected as our model is clearly only valid for small perturbations from equilibrium (and we never make any such careless extrapolations).
[Response: Dear Aslak, first of all thanks for this good discussion. My point here is that your estimate even for small perturbations is based on fitting an equilibrium response and a time scale. If this equilibrium response is unrealistic, then so is your fitted time scale. Hence my conclusion that the short time scales you obtain are not realistic.]
Rahmstorf correctly points out that our model only has a single effective response time. It is clear that each contributor to sea level rise has a different response time. The thermal expansion and ice sheet decay probably has quite long response times, whereas small glaciers have a relatively fast response time. This is another reason it is wrong to make the extrapolation far away from equilibrium. With respect to medium term predictions (i.e. 1000 years) it is, however, interesting to test the models. I have made hind-casts of sea level applying the Rahmstorf (2007) model to various paleo-temperature reconstructions. It shows a large rising trend in sea level for the past two millennia inconsistent with observations. It is clear that the model lacks realism even in the medium term. The argument and figure is presented on my website.
[Response: The misfit you find in your “hindcast” has nothing to do with the assumption of a long time scale tau. It is to do with the best fit for T0, which determines any long-term drift in my simple model. The best fit found for T0 for the 20th Century data is not necessarily good for all paleo-reconstructions, but if you consider the uncertainty ranges then there is no inconsistency. For example, the uncertainty range stated in the Mann and Jones (2003) reconstruction, which gives the largest sea level drift in your graph, is such that it includes -0.5 ºC (wrt to the 1951-1980 mean), which is my temperature level for zero sea level rise (i.e., T0). So within the uncertainty range of the data, a zero drift in sea level is just as possible as the large drift you show.
Looked at another way: for the Moberg case, the sea level drift for the preindustrial time of 0.45 mm/year you show in your hindcast vanishes completely if you assume T0=-0.35 ºC instead of -0.5 ºC in my model, which hardly changes my other results. So – despite the simple model definitely not being designed to perform for such circumstances, it is not inconsistent with paleodata as you claim.]
Rahmstorf is also critical of our a priori constraints: a) sea level will not rise more than 5 m if we hold temperatures at the 1980-2000 average. b) the sea level sensitivity is less than 10 m/ºC . First I want to emphasize that constraint a) is the stronger constraint and this effectively already rules out the part of the parameter space that constraint b) affects. Thus it is only important to discuss constraint a) and I acknowledge that the support for this constraint may be argued. Through my communication with Stefan and others I have found that models of the Last Interglacial (LIG) generally have a relatively cold LIG. E.g. Otto-Bliesner et al. (science 2006) gets -0.7 ºC relative to present (personal communication) and yet sea level was several metres higher. On the other hand SST proxies seem generally to be several degrees warmer – I have not found any global scale estimates of the LIG temperature maximum. I also want to point out that at least for the ‘Moberg’ experiment then this constraint does not significantly alter the found response time.
I would really welcome comments concerning LIG temperatures. Is there a global proxy based estimate out there somewhere?
[Response: Global mean temperature during the Last Interglacial is not going to be very useful to constrain the response to global warming, since sea level rise during that time was caused mainly by strong summer insolation right over Greenland due to orbital changes. The Last Interglacial is a great example of a time where you do not expect sea level and global temperature to be connected.]
Finally I want to note that our confidence intervals (also on tau) show the likelihood distribution assuming a given temperature history. The reason they do not necessarily overlap is that the different temperature reconstructions cannot all be true. This source of uncertainty does not go into the clearly defined likelihood function.
[Response: Still my question remains – can you really conclude from 150 years of noisy data, as you do in your “Historical” case, that the response time of the system is 1200 +/- 500 years? – Stefan]
A quick look at the figure from WBGU above suggests that we could be in for a 50 m equilibrium response if you connect the solid dots (linear) and then trace the projected temperature response (open circle) up to that line. I’m still unconvinced, even with these papers and those by Pfeffer et al., that we are not going to see a larger response if temperatures do rise as predicted. But perhaps I am just an alarmist…
Stefan asks “can you really conclude from 150 years of noisy data, as you do in your “Historical” case, that the response time of the system is 1200 +/- 500 years?”
The answer is yes, but only because of the a priori constraint (b<5 m). The uncertainties are standard errors and the upper limit of ~2000 years comes from the this constraint. This leads me to conclude that the historical case is under-determined and that there is a need to include the longer paleo-reconstructions.
[Response: I can see that your paleo-constraint rules out long time scales – that’s my criticism of it. But how would it rule out that the time scale is shorter than 700 years? That was my question, since it is the very point where it contradicts your other cases, as I noted in my post. -Stefan]
I would be careful using the nice figure in the blog post for making near-term predictions. They presumably concern the equilibrium response on very different time-scales than the period we are most interested in (2100). Further, there are no uncertainties in the figure – can we really be sure that there is a linear relationship spanning such different climates?
Rahmstorf questions the constraint we put on the sensitivity ‘a’. We note that this is somewhat irrelevant as it does not affect our results.
* For the LGM we argue that: a~=7m/ºC. (Rahmstorf says it must be 10-30m/ºC – Mark Siddal has been estimating 8m/ºC)
* For the LIG we get: a<2m/ºC. (Rahmstorf argues that this is wrong because it was really not that much warmer).
[Response: Aslak, I double-checked this with Mark Siddall, and your statement is not correct. He does not estimate 8m/K for the LGM, but for interglacials (where you get <2m/K). -stefan]
The appropriate value for the present must be somewhere in between. Probably alot closer to the LIG values than the LGM values. To me it seems intuitive that the value of ‘a’ must depend on global ice volume. We use a constraint that a<10m/ºC.
Sorry my incapabilities in stats and projections, but does this represent now the worst-case long-term scenario (up by 50m/2000 years) and the near best-case short-term scenario (up by 1m /100 years? I admit the response of ecosystems that are reported are not very promising, but I have some faith in the adaptation capabilities of ecosystems (human assisted (better) or not (a bit worse)). Whether we can have all the ecosystems currently present is another matter that I don’t much like to think about.
Re Captcha says “time entirely”.
Curious to know how much of historical changes in sea level were due to changes in land based ice masses and to thermal expansion/contraction of oceans.
It would probably make sense to seperately model each contributor with their own response times.
Hansen’s paper last year found much quicker response times and much larger sea level rises in the geological record. Few scientists seem to agree with his estimates and yet the geological record he draws his conclusions from is the same everyone uses. I presume that the difference lies in a constraint found in current conditions that makes a significant difference. Without going into too much detail, what are the differences in the current conditions that would inhibit the sea level rises that Hansen predicts?
reCaptcha: eruption simply
Thanks to the researchers, I hope the topic can focus on your papers for a while. (Perhaps tangential and derivative questions can be acknowledged but then addressed later, or elsewhere?)
It’s wonderful to see scientists doing this kind of work in public. I hope we amateurs sit back and read.
ReCaptcha says:
————-
“SIGMAS sis-“
So then, what is the likely hood of a larger sea level rise by the end of the century? Or what is the likely hood of a 5ft rise by 2050ish?
What will happen to the Great Lakes (US-CAN)? There are geographical records that show periods where lake levels were much lower than today, so much so that Lake Erie became three seperate “ponds”. There are also ancient shorelines much higher than today that indicate that Lake Michigan cities such as Milawaukee, Chicago and others would be at risk of being flooded.
william, I wouldn’t think that sea level rise would affect the Great Lakes directly at all. They are currently not glacier-fed, so further melting won’t affect their “H2O input levels.”
Precipitation levels *do* affect the Lakes, but just off the top of my head, I doubt we are yet able to predict future lake levels with any confidence. There is still a lot of investigation to do in modeling precipitation in a warmer world, from what I read.
How a non scientist sees it.
1) Linear modeling in a non linear world.
2) This time we have an (I think) unprecedented mixture of negative and positive radiative forcing. Would not, the pan evaporation paradox be exaggerated in the highly reflective polar environments thus giving more meltponding rather than evaporation and sublimation. Therefore more melt-water lubrication and a greater disintegration of the ice.
Glad your are the ones doing the science and not me. It would appear whatever answer you come up with, it will be criticised.
#3 – Reply to Stefan: I get a response time of 1200+/-500. If it was normally distributed then the 2 sigma confidence interval would be 200 to 2400 years. So, it is not significantly different from the 200 years from the Moberg experiment (which also has an uncertainty). Also from the definition of the likelihood function these uncertainties do not include the uncertainty in the reconstructed temperatures – which would make the difference even less significant.
#6: Andrew. It is a good idea to separate the response from each contributor but very difficult to do in practice given the short sea level record with highly serially correlated errors. Also, if two contributors have the same response time then they would be near impossible to separate. That said it would help a lot if you know some parameters in advance. E.g. what the response time of the thermal expansion is.
By the way, that should be “Coogee”, not “Cogee”.
A new Lovelock book is here now:
http://www.rushprnews.com/2009/01/26/the-vanishing-face-of-gaia-brings-hope-to-global-warming/
and my letter to future class of 2099:
http://tufts2099.blogspot.com
I have just posted over at Climate Audit and basically told Steve what he should do with his hockey stick. Here, in the halls of many good Scientists I am humbled. Since Barack Obama used the Internet to get his message across, why shouldn’t you. If all the energy spent is only for each of you to learn, shouldn’t some of that energy be better spent elsewhere. Denier sites are growing at an alarming rate, and public opinion does matter.If each one of you spent fifteen minutes to blog at denier sites, than Real Science would lead the debate on the Internet.David B.Benson has, and Paulm,Andrew,Chris Colose,Dennis Hlinka,and David Bloom.So please,go to Accuweather, IceCap, Climate Audit, and other dumb sites, and teach them a little about AGW. There is this big debate about the cooling of the Antarctic(this week). Your grandchildren should not carry a burden, that you could shoulder now. You are neither weak nor undereducated. You are strong, and the world will thank you for it. Yes, people are already suffering too much. How would you like to be taken off of your sacred land, to be moved next to Walmart. Thanks,Kipp
Thanks much for the pdf of your paper from “Science.” Please other people at RC, put pdfs of your papers into your RC articles, and please stick to the oldest version of Acrobat you can find. I cannot use any Acrobat reader newer than Version 3 for Mac. My computer told me that there were some things it couldn’t interpret, but they must have been in adjacent articles. Both equations and graphics came through OK. I am glad to know that where I am at 600 feet above sea level will remain dry for the foreseeable future.
Somebody once asked me if “Ocean World” is possible. I told him that I think the ocean would boil by the time sea level rise got to 800 feet. Was I right?
16 Kipp Alpert: Denialist propaganda is like Soviet propaganda. They spew out “soldier words” that are meant to “die” or not be believed. Everybody knows that they are lying, but we use up our emotional energy and our time responding to them or fighting them off psychologically. That leaves us no time to attack the source and the money behind the source. To make a revolution, you have to concentrate on attacking the system, which is the fossil fuel [especially coal] industry. It is like using a robot or a TOW missile. If the enemy shoots at the TOW missile or the robot, he accomplishes nothing. If the enemy soldier shoots at the person who is controlling the TOW missile or the robot, you have to duck and loose control. When you duck, the TOW missile hits the ground. The coal industry is firing a TOW missile at you and you are still shooting at the missile. It is a valiant effort, but doomed to failure. Attack the coal and oil industries instead.
Kipp Alpert said: “If all the energy spent is only for each of you to learn, shouldn’t some of that energy be better spent elsewhere.”
What you perhaps are not appreciating is that RealClimate already is both a means of communication to the public as well as a pro-bono service of the scientists involved.
You are also assuming that sites like IceCap don’t already know about the discussions here, and that people over there really care what the RealClimate scientists have to say.
As someone who attempts to keep up on climatology news yet doesn’t work in the field I can tell you that the internet is full of useful sites (on which to spend all my free time if I so desire) as well as junk science sites.
The issue is not that there are not enough scientists discussing with the public the issues, but rather than the public has at most a marginal taste for the subject (as science.)
It is also interesting to consider the policy implications of our projections. For simplicity let us not consider any other impacts than sea level rise. For that purpose it is useful to consider the response to an optimistic scenario compared to a pessimistic scenario. We project ~80 cm rise for B1 and ~135 cm rise for A1FI. The conclusion is that mitigation does pay off, but adaptation is unavoidable. Rahmstorf get ~70 cm for B1 and ~100 cm A1FI. So it may seem that there is less incentive for mitigation. However, in the long term he foresees a 20-90 m rise for these two scenarios (using 20 m/degC). If we imagine an even more optimistic scenario where temperatures do not rise at all, then we will still be committed to a ~10 m rise. Consider how we would adapt to that – extreme mitigation measures (geo-engineering) start to sound attractive.
While I think that Rahmstorfs long-term estimates are too high, then our study does not exclude such a possibility. My model uses an effective response time which is intimately linked to the estimates of the equilibrium sea level. Therefore, our estimates of equilibrium sea level should be used with care on very long-timescales (as pointed out by Rahmstorf above). It is not wise to extrapolate our model to the far future in a warm climate (this is too far from the calibration interval).
Guys, I know this is a bit off topic but I’m having an argument with several denialists, and I really want to make a bet with them, ie ‘I bet you than in 10 years the XXX yearly measure of world average temperature’ will be more than now. The problem is what do I name as the correct measure….? Any feedback gratefully received.
#11 Kevin
I don’t understand your comment. The great lakes levels have experienced cycles in the past. 20 years ago Lake Michigan was at a high and washing away the shoreline and 20 years before that it set record lows. From the studies I’ve seen cited in the news there are predictions of future record droughts all over the world because of the coming global warming. Wouldn’t the great lakes be impacted by that?
william, sorry if I confused you. Since the thread is about sea level rise, I first related your comment to that issue, hence the first part of my response.
As to your recent comment, sure future precipitation trends will affect the Lakes. The problem is that, AFAIK, no-one yet knows specifically how. Regional climate forecasting is a high research priority, but I haven’t read any huge success stories yet. So the Lakes may get more, less, or about the same precipitation in the future warming world.
Stay tuned, though. When researchers do know more about that, you’ll probably read it here first.
#21
I’m not a scientist, but my understanding is that GW will actually increase precipitation in the Great Lakes Basin – most of Canada and the Midwest – while significantly decreasing precipitation in the American southwest, and areas of the southeast. If this were the only factor, then maybe the Great Lake level would rise; however rising temperatures, and increasing lack of ice-cover in the winter are likely to cause higher rates of evaporation. Thus I think there is some uncertainty about the future lake levels, but there seems to be a prevailing thought that their level will drop somewhat. You might want to check reports released from the US Geological survey, available online at http://water.usgs.gov/wateravailability/greatlakes/.
#20:
The *rate* of warming, even decade over decade, will not necessarily increase. But it’s pretty safe bet that it will remain significantly positive.
Why not simplify things? Just bet on warming vs cooling. One simple way is to take the average temperature for the decade 1999-2008 and compare it to 2009-2018. If the difference between the later and earlier decades is .1 deg. or more you win and if it is -.1 deg. or less, they win. Anything in between is a sawoff.
As to which temperature set to use, it should be one of the recognized global surface sets (or perhaps an average): GISS, Hadley or NCDC/NOAA.
The important point is to bet on decadal averages not individual years.
Dave, are you looking for a quantity or a source? A quantity is going to be tough – it’s a pretty safe bet that the average global temperature will have increased, but 10 years is a short period to say by how much. If that’s what you’re after, I would say maybe look at the various projections (IPCC, Hansen, etc.) and find the most likely range.
If you’re looking for sources, you could cite NASA GISS/GISTEMP, HadCRU, NCDC … I warn you, though, your denialist will probably argue with you that the data sets are wrong for some reason.
A factor missing from discussions on water level is longer terrestial growing seasons, with greater annual transpiration and less inflow to the Great Lakes and other fresh water bodies. It seems that increases in the duration of growing seasons, and annual transpiration, would have minimal global effect on sea levels.
Aslak, Stefan — I hope you all can keep control of this topic (Contributors? throttle or move the digressions, oh please?).
To Aslak and Stefan — another thankyou for doing this in public. Can you agree on what you disagree on, for us amateur watchers? Is it how the statistical analysis is done, and can you spell that out? Or is it something else? Or is it different conclusions from the same information (if so can you poke at what difference you see in this, for us, a little more?)
I realize asking for introspection about process is a lot to ask! But we learn much from what you show about this.
[Response: I think it is quite clear what we disagree on: whether the response time scale of sea level rise is long (millennia says Stefan) or short (centuries says Aslak). The answer to this question determines whether the new projections of Grinsted et al. for 2100 – which are significantly higher than those of my 2007 Science paper – are well-founded. I think not – Aslak thinks yes. The discussion of methodology in the post above – the use of paleo constraints etc – gives the reasons why I have serious doubts about this. Aslak – is this a fair summary? -Stefan]
SamWeiss.EdwardGreis: Your both right, concerning what your function is, and who is the real enemy. There are still people on the internet that you can turn and I have done that. At Boston University,we marched to Cambridge, which got national coverage.We didn’t stop the war, but I’ll take one percent. This stuff does add up. Thanks,Kipp
Dave:I think you should read the IPCC Ar4 report.You should learn this for yourself.It is important.Kipp
Dave (20) — Annual average global surface temperature as determined by the XXX temperature product. The usual choices for XXX are compared here:
http://tamino.wordpress.com/2008/01/24/giss-ncdc-hadcru/
I suggest you structure the wager to depend upon 10 year averages:
http://tamino.wordpress.com/2009/01/15/what-if/
Could either of you do an evaluation on Hansen’s peer-reviewed Climate Change writings vis a vis your own research?
Hansen’s suggestions on paleoclimate evidence suggesting a shorter response time scale of sea level rise?
“This planetary energy imbalance is itself now sufficient to melt ice corresponding to one meter of sea level rise per decade, if the energy were used entirely for that purpose.”
(Hansen et al 2005). Hansen J 2005 A slippery slope: how much global warming constitutes dangerous anthropogenic interference? Clim.
Change 68 269–79
Hansen J, Johnson D, Lacis
“Indeed, the palaeoclimate record contains numerous examples of ice sheets yielding sea level rises of several metres per century when forcings were smaller than that of the business-as-usual scenario. For example, about 14,000 years ago, sea level rose approximately 20 metres in 400 years, or about 1 metre every 20 years.”
“Potential implications of the human-made planetary energy imbalance for the response time of ice sheets are not yet fully appreciated, I believe. No known
paleoclimate analogue exists.”
Thanks,
Thanks Stefan (and thanks in advance to Aslak).
I realize I’m asking you to ‘dumb it down’ considerably.
Thinking of my high-school-age relatives, wanting them to be able to follow this.
How is it that such an important public policy issue has such a weak literature? The IPCC basically ducks the question.
The authors of both papers are very competent. If they really wanted to address the public policy issues, they would have synthesized the state of the art in ice physics, geology, engineering, climate, and weather into a risk based projection of sea level rise that could be presented to policy makers. Instead they produce fine academic papers. It seems like people want to make a career out of STUDYING climate change. I do not think we really have time for that. We need decide if we are going to mitigate or adapt or both or something else.
Sometimes public policy needs to serve science, and sometimes science needs to serve public policy. Now is a time for the latter. Somebody needs to tell our science organizations here are the dollars, now, bring us good, honest, risk based numbers for sea level rise.
jeez, Aaron.
The IPCC said ‘don’t know yet’ last time.
The 5th IPCC synthesis comes next; it’ll be put together from papers, published since the 4th one.
Papers like these go to informing the synthesis.
“Don’t let the best be the enemy of the good.”
The new information on Antarctic warming calls for new information on 21st century sea level projection, from the public’s point of view.
… “But a new analysis of satellite and weather station data has shown that Antarctica has warmed at a rate of about 0.12 degrees Celsius (0.22 degrees F) per decade since 1957, for a total average temperature rise of 0.5 degrees Celsius (1 degree F).”
http://earthobservatory.nasa.gov/IOTD/view.php?id=36736
So if I understand, … under a scenario of eventual 2.5 deg. C rise from end of 19th century, Stefan is projecting eventual equilibrium sea level rise of 25-75m with a “best” estimate of 50m (a few millenia from now).
And Aslak would project
Fascinating post, and discussion, apart from some really strange diversionary comments. From this medical person, with a good “scientific” training, but no particular expertise elsewhere, seeing a really interesting scientific argument (in the nicest, professional way) is very enlightening. One becomes an interested spectator in scientific history and as such, also a participator. Mind you, I am not claiming I understand most of what you are arguing, so your reply to Hank Roberts’ question is very pertinent to me.
This argument is a very good example of the sort of scientific uncertainty that can be mis-used by global warming denialists to obfuscate the simple fact that the vast majority of scientists who are in this field agree about global warming, that increasingly they are getting more concerned about their own projections, and probably increasingly concerned on a personal level with the lack of action to deal with the problem in the world at large. It still seems to be the case that prognostications about the rate of sea level rise are one of the most difficult parts of the global warming crisis to be certain about. But in my book, as a cautious sort of person, to be uncertain about something, is not the same as to be unconcerned about something, it depends on the severity of the threat and the likelihood or not of being able to deal with it if it is neglected. On that basis, it is difficult to understand how any sentient person would refuse to take this problem other than with the utmost seriousness, indeed terror might be an appropriate noun. But history is not really on our side, history strongly suggests that humanity, as a collective, will never act for its own future interest if it means a perceived present sacrifice of wealth, of deferring gratification, or of a resented interference to our sense of entitlement – we would rather our civilisation would fail than act otherwise. I suspect that this is what is happening, in a rather more trivial way, in regard to our present economic straits.
and, when I say being concerned about your projections, I mean CLIMATE projections!!
6&7 have some interesting questions. I think a simple model, with a single time constant is unrealistic. We could propose one time constant for seawater expansion, another for large ice sheets, and perhaps yet another for mountain/piedmont glacier response. But, then given to poor quality of the data, you could not pin down multiple sensitivities and time scales.
My takehome from Hanson’s argument that the melting timescale might be a lot faster than previously assumed. He refers to an icesurface albedo flip, whereby once a surface becomes wet the albedo drops. If my concerns, that an abalting ice surface might accumulate dirt and soot, and thus drastically lose albedo are correct, then it could be that the deglaciation timescale is much shorter than the glaciation timescale. But, again you run into the problem of not having a dataset good enough to determine multiple parameters.
” Just bet on warming vs cooling.”
A bet on a sea level rise vs sea level drop would also be quite safe…
If sea level rises more than an inch the coming decade…i win..
If it drops more than an inch…they win…
anybody?
bets are elsewhere, try clicking this link for a start:
http://scienceblogs.com/stoat/2008/05/betting_on_climae_change_again.php
Just to flag it, because inline comments sometimes get missed:
Aslak, Stefan answered “inline” above a question I asked for both of you, timestamp 27 January 2009 at 1:06 PM, waiting to see if you agree.
2nd try:
So if I understand, under a scenario of eventual 2.5 deg. C rise from end of 19th century, Stefan is projecting eventual equilibrium sea level rise of 25-75m with a “best” estimate of 50m (a few millenia from now).
And Aslak would project less than 25m? What is the lower bound? Best estimate?
P.S. to Hank: Sorry for digression – won’t happen again.
This question is more in line with the bet proposed by Dave in #20.
From previous discussions here on this site, it seemed that temp rise up till app. 1975 is strongly correlated to solar activity ref. However, for the temp rise from 1975 to 2000 we have no alternative explanation than antropogenic CO2.
Do you agree with this statement?? Gavin??
[Response: No. Up until the 70s no one forcing dominated, but since then anthropogenic forcings have become the most important. – gavin]
@Hank (27, 42): I agree with Stefan that we are disagreeing about the response time. However, I do not reject the possibility that some components of the system have a millennia scale response time. So, in my eyes, the disagreement is actually not that great. My point is that, for near-term projections then it is important to take the fast reacting contributors into account. The fast contributors are also the most important for the relatively small variations in temperature around the equilibrium for the last 2000 years. From this point of view I find that a short effective response time is useful, even if it is does not model the long-term response well.
Some more detail: There are several contributors to sea rise, each with its own response time. Thermal expansion and ice sheets react slower than smaller glaciers and ice caps. It is therefore clear that my simple model, with a single effective response time, can only be an approximation. Stefan is right that the effective response time is intimately connected to the equilibrium response. Therefore you cannot extrapolate our model very far from the calibration interval. However, our primary interest is the sea level projections for the 21st century (not the equilibrium response) and therefore it is good to take the fast reacting components into account. Stefan’s model implicitly assumes that the response time of all significant contributors is very long compared to the combined length of the observation and projection periods. This is not a good approximation for the small glacier contribution, and there is growing concern that the ice sheets may have a rapid dynamical response to warming. However, in my study I find an effective response time of ~250 years and even for so short response times then Rahmstorf’s approximation can be justified.
@Deep Climate (43): Stefan is arguing on the basis of the plot in the blog post (am I right, Stefan) that the eventual rise for a 2.5 degC warming will be 25-75m. So note this is not a result of his model. From my model I do get an equilibrium sea level which is much lower. But you should not interpret the equilibrium response literally (see the explanation to Hank above, or my website). I agree with Stefan’s opinion that it will take much less than a 50 degC warming to get sea levels to rise 65m.
@45 Aslak: “Therefore you cannot extrapolate our model very far from the calibration interval.”
I think the idea that this is an “extrapolation” is incorrect, because your model is based on the very concept of fitting the eventual equilibrium sea level rise. Why else would you attempt to constrain this parameter with paleo data e.g. from the Last Glacial Maximum, which lasted for enough millennia to assume that sea level was close to equilibrium? This equilibrium level you obtain directly affects the time scale you obtain and hence your 21st Century projection. Thus it is not an extrapolation but simply the key question about your method: how realistic is this equilibrium level you assume?
For the 21st Century you are projecting the response to about 3 or 4 ºC warming – and this is based on what your model assumes to be the equilibrium rise to this warming. In your model, it is about 4 to 5 meters. It is central to your 21st Century projection to ask whether this is realistic – and the paleoclimatic data I show above suggest it is too low by a factor of 10.
Again – it is not a question of extrapolation. This is the basis of your 21st Century projection, and the reason why it is higher than mine. If you use a larger equilibrium level you get a longer response time, and then you get the same result as me (as your paper also shows).
I’m surprised that you now argue your response time is representing the “fast reacting components”. That’s directly opposed to what you say in the paper, where this response time is the approach to the final equilibrium, as constrained by paleoclimatic data.
It seems to me (layperson) these estimations of ca. 1m in 2100 are more an academic exercise (yet of scientific value, for sure).
Hansen’s horror picture is more credible for me:
The system is receiveing a very hard and non-natural blow, so we can forget about “typical” response times derived from infinitesimal system perturbations. E.g. Greenland could well melt away exponentially, and if the rate continues to double every decade it would be gone ca. 2100, and voila: 7m SLR. A daring hypothesis perhaps, but there is many another nonlinear weirdness to be expected – so I won’t be surprised about, say, 4m in 2100.
[Response: I would be very surprised. 1 meter would already be a disaster, but the need now is for better quantifications of the possibilities using as much of the physics and observations as possible. Back of the envelope calculations are not going to be satisfactory anymore. – gavin]
Gavin, you described at least part of the Pfeffer calculations as being “back of the envelope”.
Does that mean all current assessments of likely SLR by 2100 are “back of the envelope”?
What has Hansen said? To me he’s saying SLR by 2100 is likely to be measured in meters (the 5 meter thing, he himself says cannot be proven to be accurate, so how can people seriously say that is his claim), which is anything over one meter, and that is within the bounds being discussed. Since Pfeffer did a calculation for what Greenland and West Antarctica are actually likely to contribute to SLR by 2100, isn’t the best range to cite 80 cm to 2 meters?
Would you be surprised if SLR by 2100 is measured in meters?
[Response: Well, yes – because it would imply some large amount of lifespan-extension between now and then! However, looking at the estimates out there, and the limited modelling that has been done, 1m is within the bounds of possibility under business-as-usual. The Pfeffer limits are I think a reasonable guide for the time being. – gavin]
“Greenland could well melt away exponentially, and if the rate continues to double every decade it would be gone ca. 2100, and voila: 7m SLR.”
As Gavin notes, this is not supported by currently accepted theory or observations. Unfortunately Hansen’s unrealistic projections on SLR have permitted an opening for “skeptics” to attack his tremendous contributions and insights in climate modelling and evaluation of global temperature trends.
Aslak # 45: “I agree with Stefan’s opinion that it will take much less than a 50 degC warming to get sea levels to rise 65m.”
How much less? In other words, I’m still not clear on what equilibrium SLR you consider realistic for temp rise on the order of 2.5-4 deg. C (perhaps best expressed as m/deg. C as Stefan has done).
All I know is it’s under 10 m/deg apparently.
But anyway … we have two radically different approaches here and both are showing SLR by 2100 significantly greater than IPCC AR4.
So here’s my response to Aaron Lewis (#33): “We need decide if we are going to mitigate or adapt or both or something else.”
Clearly we need to both mitigate and adapt. And not “decide if we are going” do it – but actually do it.