Is the number 2.14159 (here rounded off to 5 decimal points) a fundamentally meaningful one? Add one, and you get
π = 3.14159 = 2.14159 + 1.
Of course, π is a fundamentally meaningful number, but you can split up this number in infinite ways, as in the example above, and most of the different terms have no fundamental meaning. They are just numbers.
But what does this have to do with climate? My interpretation of Daniel Bedford’s paper in Journal of Geography, is that such demonstrations may provide a useful teaching tool for climate science. He uses the phrase ‘agnotology’, which is “the study of how and why we do not know things”.
Furthermore, many descriptions of our climate are presented in terms of series of numbers (referred to as ‘time series‘), and when shown graphically, they are known as curves. It is possible to split curves into pieces in an analogous way to how π may be split into random numbers.
All curves (finite time series) can be represented as a sum of sine and cosine curves (sinusoids), describing cycles with different frequency. This is demonstrated in the figure below (source code for the figure):
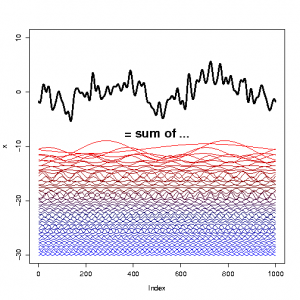
The random time series, here represented as the bold curve on the top, may be physically meaningful, but the components made up of cosine and sine may not all have a physical interpretation (especially if the time series is from a chaotic or complex system).
However, cosine and sine curves represent only one special case, and there may be other curves that equally well can make up a time series. A technique called ‘singular spectrum analysis‘ (SSA), for instance, is designed to find curves with other shapes than sinusoids.
The process of representing a series of numbers as a sum of sinusoids (cycles) with different frequencies (or wave lengths) is known as a Fourier transform (FT). It is also possible to go the other way, from the information about the frequencies, and reconstruct the original curve – this is known as the inverse Fourier transform.
Fourier transforms are closely related to spectral analysis, but these concepts are not exactly the same. The reason is that all measurements hold a finite number of observations, and provide just a taste – a sample – of the process. The FT makes the assumption that the curve that is analysed repeats itself exactly for infinity, something which clearly is not the case for real noisy or chaotic data.
One of the gravest mistakes in the attribution of cycles is trying to fit sinusoids with long time scales to short time series. We will see some examples of this below.
In the meanwhile, it may be useful to note that spectral analysis tries to account for mathematical artifacts, such as ‘spectral leakage‘, probabilities that some frequencies are spurious, and the significance of the results. Anyway, there is a number of different spectral analysis techniques, and some are more suitable for certain types of data. Sometimes, one can also use regression to find the best-fit combination of sinusoids for a time series.
A recent paper by Loehle & Scafetta (L&S2011) in a journal known as the ‘Bentham Open Atmospheric Science Journal‘ (also discussed at Skeptical Science) presents some analysis using regression to describe cycles in the global mean temperature, showing us many strange tricks one can do with curves and sinusoids, in something they call “empirical decomposition” (whatever that means).
They fit 20-year and 60-year sinusoids to the early part (1850-1950) of the global mean temperature from the Hadley Centre/Climate Research Unit. I have reproduced their analysis below, although I do not recommend using this for any meaningful purposes than just having fun (source code)
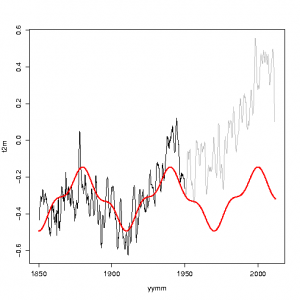
It’s typical, however, that geophysical time series, such as the global mean temperature, are not characterised by one or two frequencies. In fact, if we try to fit sinusoids with other frequencies (here only one was used rather than two), we get the following picture (source code):
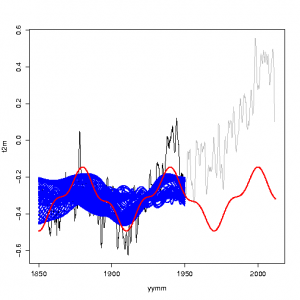
In fact, we can compare the amplitudes of these different fits, and we see that the frequencies of 20 and 60 years are not the most dominant ones (source code):
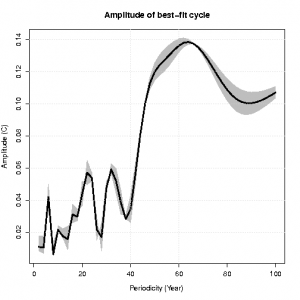
Fitting sinusoids with long time scales compared to the time series is dangerous, which can be illustrated through constructing a synthetic time series that is much longer than the one we just looked at. This time series is shown below (source code):
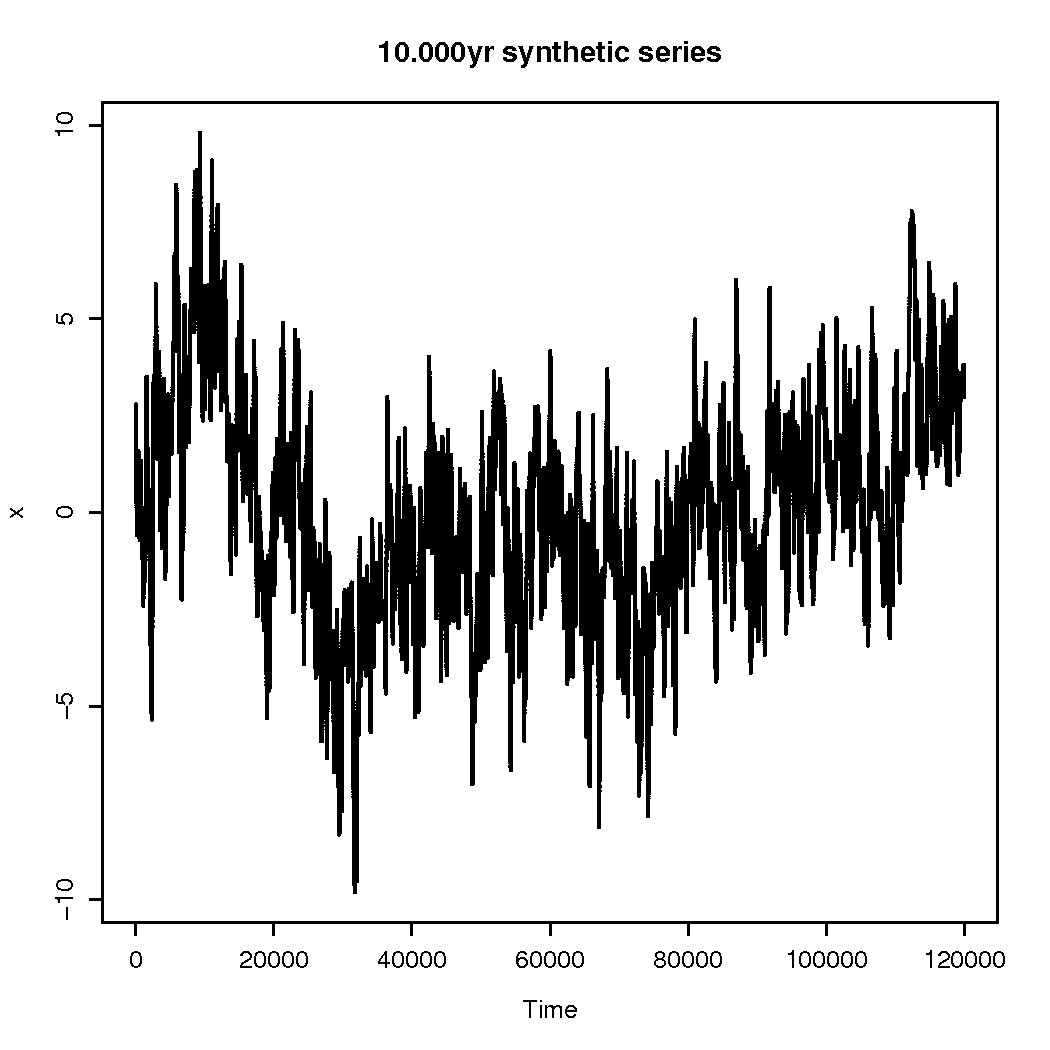
We can divide the above time series into sequences with the same length as that L&S2001 used to fit their model, and we can then do a similar fit to these sequences (source code):
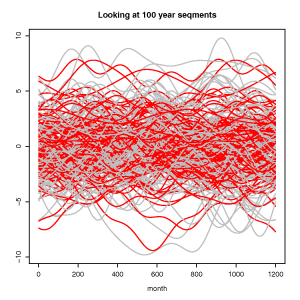
The red curves, representing the best-fit are all over the place, and they differ from one sequence to the next, although they are all part of the same original time series. But the point here is that we could get similar results for other frequencies, and the amplitude for the fits to the shorter sequences would typically be 4 times greater than a similar fit would give for the original 10,000 years long series (source code). This is because there is a band of frequencies present in random, noisy and chaotic data, which brings us back to our initial point: any number or curve can be split into a multitude of different components, most of which will not have any physical meaning.
Loehle & Scafetta also assume that the net forcing of the earth’s climate is a linear combination of solar and anthropogenic. The fact that our climate system involves a series of non-linear processes, as well as non-linear feedback mechanisms that may be influenced by both, suggest that this position may be a bit simplistic – it ignores internal, natural variability for instance.
Some of the basis of L&L2011’s analysis can be traced back to a 2010 paper that Scafetta wrote on the influence of the great planets on Earth’s climate. I’m not kidding – despite the April 1st joke and the resemblance to astrology – Scafetta claims that there is a 60-year cycle in the climate variations that is caused by the alignment of the great gas giants Jupiter and Saturn. This conclusion is reached only 3 years after he in 2007 argued that up to 50% of the warming since 1900 could be explained by 11 and 22-year cycles (a claim which Gavin and I contested in our 2009 paper in JGR).
The Scafetta (2010; S2010) paper presents spectral analysis for two curves which are fundamentally different in character – to quote Scafetta himself:
Spectral decomposition of the Hadley climate data showed spectra similar to the astronomical record, with a spectral coherence test being highly significant with a 96% confidence level.
The problem is immediately visible in the figure below:
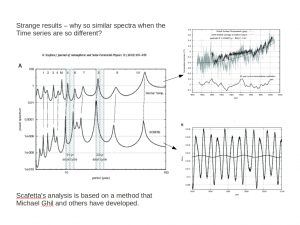
For any spectral analysis, it should in principle be possible to carry out the reverse operation to get the original curve. S2010 presented a figure showing the alleged spectra for the terrestrial global mean temperature and the rate of motion of the solar systems centre of mass. It is conspicuous when spectra of two very different looking curves appear to produce similar peaks.
So how was the spectral analysis in Scafetta carried out? He used the Maximum Entropy (MEM) method, keeping 1000 poles. The tool he used was developed by Michael Ghil and others, and the method is described in one of the chapters of a text book by Anderson and Willebrand (1996).
As the number of peaks increases with M [number of poles], regardless of spectral content of the time series, an upper bound for M is generally taken as N/2.
If X not stationary or close to auto-regressive, great care must be taken in applying MEM
So the choice of number (1000) of poles cannot be justified, as this will more likely lead to spurious results, and one of the time series is not stationary (temperature) while the other is far from being auto-regressive (astronomical record). It is worth pointing out that if an Akaike Information Criteria (AIC) is applied to this series (which balances the number of parameters used with the gain in goodness of fit), the number of poles is 32.
L&S2011 also claim that a 60-year must be the effect from Jupiter and Saturn. What is the implications of such an assertion? Does it mean that the broad frequency band, seen in the global mean temperature record, can be taken as evidence for many new unknown celestial objects affecting the solar system mass, and hence the solar activity? No, I don’t think so.
The solar activity shows a clear 11-year cycle, and no trend during the last 50 years, and no clear 60-year periodicity.
In my humble opinion, Loehle and Scafetta (2011) is a silly paper, making many claims with no support from science (about planets, the sun, GHGs, urban heat island, aerosols, GCMs, significance levels, and weird coherence results). I would not be surprised if rumours about the journals lacking rigour are true. But, on the other hand, Daniel Bedford may cherish the opportunity to learn from such mistakes.
References:
Anderson, DLT. and J. Willebrand, J.(1996) ‘Decadal Variability’, Springer, NATO ASI series, volume 44; chapter: ‘Spectral Methods: What they Can and Cannot Do for Climate Times Series’ by M. Ghil and P. Yiou
OT, Fukushima radioactive tracers might be used to measure the true lenghts of oceanic cycles, I guess there are enough longlived isotopes released to find them on random measurements around the globe. No need for carefully balanced messages in the bottles.
On topic, thanks for the good presentation of this powerful method. Can one use the FT method to estimate the period of outliers as in ‘100-year flood’?
Valentine’s Day is also known as π-1 Day among nerds and geeks.
jyyh,
100-year floods are not periodic events. They are, broadly speaking, random events that have a 1% chance of occurring in any given year. You can’t use FT analysis to identify them.
It appears that Ghil, and others specifically warn against the use of MEM and temperature data:
“Instrumental temperature data over the last few centuries do not seem,
for instance, to determine sufficiently well the behavior of global or local
temperatures to permit a reliable climate forecast on the decadal timescale
by this SSA-MEM method.” Ghil, et al., Reviews of Geophysics 40(1),2002.
Thanks, an interesting post.
A couple of minor typos, if you care:
“The tool he used was developed my Michael Ghil” and “the other if far from being auto-regressive.”
Excellent post, and discussion of meaningful numbers reminds me of intresting numbers paradox. of course, that applies to integers, not reals.
Of course, Scafetta in particular has a long history of trying numerous mathematical techniques to avoid CO2 and find cycles. I really, really recommend lecture and slides @ EPA.
1) Watch a bit of the lecture for context.
2) Then, flip through the slides, get to Rhodes Fairbridge. (Hmm, RF an expert on climate change? That seems to come from J Coastal Research.
3) Once again, I sure with John Tukey were still around.
Fourier transforms applied to a time series of bounded length, say the interval [0,t], assumes that all prior and subsequent intervals, [nt,(n+1)t], for all integers n, are identical to the values in the given interval [0,t].
For geophysical time series this assumption is astoundingly naive. Fourier transforms can be used to identify potentialy (nearly) periodic behavior which must be be justified via the physics. The best example I know tis the ~3.75 year Rossby/Kelvin wave in the North Pacific, for which that ocean basin is resonant at that period.
However, an attempt to find periodicities in ENSO fails, for me, on the grounds that insufficient (quasi-)cycles have been observed:
Variability of El Niño/Southern Oscillation activity at millennial timescales during the Holocene epoch
http://www.nature.com/nature/journal/v420/n6912/full/nature01194.html
It’s pretty obvious that Loehle and Scafetta chose MEM because other (appropriate) methods didn’t give them what they wanted. They further pumped up the number of poles to a ridiculous value because a realistic choice didn’t give them what they wanted.
Thanks for an insightful glimpse of their “mathturbation.”
John Mashey,
I had a bit of an argy with a poster on SepticalScience about Fairbridge (who seemed a decent sort) a few year ago, and had a good look at Mackey’s silly paper on Fairbridge in J. Coastal Research. Here’s my comments.
Just shows that there’s a limited amount of this nonsense out there – it just goes round and round…
I am not a mathematician or scientist (actually, I’m a lawyer), but I think I understand the point this piece makes. But from a layperson’s perspective, it seems to be too indirect. If I understand the argument, fourier transforms allow you to arbitrarily decompose any time series into a sum of sine waves. This is surely fun, but absent some reason to believe the sine waves represent actual physical processes, it’s simply an exercise in curve fitting (akin to curve fitting using higher order polynomials – increasing the power of x increases the R^2 but doesn’t tell you anything useful about whether your equation makes any sense). In fact, where a process has substantial noise (i.e., internal variability) you are probably just fitting your curves to the noise.
So, couldn’t you take the instrumental record for global mean temperature, subdivide it into chunks (say 10 or 20 years at a time), then analyze each chunk separately using a fourier transform? Assuming that the internal variability dominates over the signal (which I am sure I have read on RC before multiple times), wouldn’t one expect the “cycles” you identify in each chunk of data to be different from every other chunk? Wouldn’t this be a much more direct disproof of using fourier transforms to identify climate trends than what is actually done in this article? (At least, it seems more direct to me. If the process says that each 10 year chunk is dominated by a completely different set of “cycles,” that seems to put the nail in the coffin of the idea that climate is really driven by as yet undiscovered natural cycles and clearly shows that such attempts are just exercises in curve fitting)
Cheers,
Re 9 chris – I remember that. I tried to follow that whole sun wobbling concept and it seemed to lead to an idea that (as I recall) the planets stir the sun by making it move around. But it’s just in a state of free fall, so how could that stir it? I pointed out that if the planets did anything to stir the sun, it would (so far as I know**) be by tides on the sun, which are incredibly tiny. (**I tried to considered the idea of planets tugging on the solar wind which would tug on the magetic field, or directly wobbling the magnetic field, which would tug on the sun, but the amount of mass involved and the small distortions considering the dimensions… well I don’t know, doesn’t seem likely (it would just be tidal disortion of a much larger object?, so the strain should still be small?).)
(and tides on the sun are dominated by somewhat different planets than the center of mass wobbling; okay, done with that.)
You all, IPCC, sceptics, shroudwavers and riders on the gravytrain
alike, are all nitpicking around the periphery of this issue. The only
people who see it in perspective are the geologists.
I put the issue in perspective a few days ago without any response.
The Pleistocene Period, in which the ice ages and much of human
evolution took place, lasted some 2.5 million years.
That 2.5 million years is a tiny fraction of the 4,500 million year
history of this planet.
Compare this 2.5 million year period with the distance between the floor
and the ceiling of the room you are sitting in. The stud height is
probably around 2.5 metres. In NZ it is almost certainly 2.4 metres.
That is 1 mm for each 1,000 years. Modern man entered Europe about
40,000 years ago; 40 mm or less than 2 inches below your ceiling.
10,000 years ago the last ice age ended; 10 mm or less than half an inch
below your ceiling. About 4,000 years ago man started using metals.
The Abrahamic religions started about 2,500 years ago or less. Most of
our properly recorded history commenced about 1,000 years ago, 1 mm
below your ceiling. We have been measuring temperature and the like for
about 150 years. That is little more than one tenth part of a
millimetre on the scale we are considering, about the thickness of a
hair. Our irrelevant lives are measurable on that scale only with a
microscope.
All the ranting, raving and political posturing considers only events
within that miniscule period. It is simply and utterly absurd.
[Response: And commenting on a blog is even more so. Really, why do you even get out of bed in the morning if everything is so trivial? – gavin]
A few notes on the FT, or as we coastal engineers usually analyze ocean wave data call it, the FFT (2^N).
You have dt and N, multiply N*dt, and you get the timebase, or the lowest frequency possible (1/(N*dt)) from your analysis (zero frequency is just the mean of the time series, if you first haven’t taken out the mean).
The Nyquist frequency has to be half the sampling frequency, N equations = N unknowns (complex numbers for each frequency represent phase and amplitude).
The time series must be stationary (or is assumed to be stationary), which is often true for ocean wave climates, same for assuming an ergodic process (spatial vs temporal equivalence).
Now any time series with a trend, linear or otherwise, must be detrended first, before doing any sort of linear spectral analysis.
So, for example, take a purely linear trend, run it through an FFT, and what does one get?
A log-log power spectra that displays 1/f^2 (red) trend at the lowest frequency limit, through to (and pass) 1/f^1 (pink), and ending up as 1/f^0 = 1/1 (white), or white noise at the upper (Nyquist) frequency limit.
There are tidal cycles, there are water wave period cycles, there are harbor resonance cycles, there are harmonics.
However, there are no well defined climate cycles at exactly 20 (or even approximately) or exactly 60 (or even approximately) years, meaning having a physical (or physics) basis in reality.
Most certainly, there is no interaction between Jupiter/Saturn and Earth’s climate, at any periodicities, L&S is quite simply a POS.
13, Roger Dewhurst: You all, IPCC, sceptics, shroudwavers and riders on the gravytrain
alike, are all nitpicking around the periphery of this issue. The only people who see it in perspective are the geologists.
Really? How does that perspective help the rest of us to decide whether, and how much, to spend $$$$$$ and labor rapidly replacing our CO2-intensive energy sector with something that will stabilize or reduce atmospheric CO2?
Gavin’s reply to Mr. Dewhurst @13 should be in the internet hall of fame.
Well, this explains the crank that was obsessively spamming over at theconversation.edu.au about planetary cycles. His explanation was (I kid you not) that it’s all down to tidal heating of the Earth by the big planets.
[Response: And commenting on a blog is even more so. Really, why do you even get out of bed in the morning if everything is so trivial? – gavin]
It is the debate around AGW that would be so trivial if it is not so dangerous. It is all a bit like the EU, corrupt individuals and and a bunch of ostriches with their heads in the sand.
[Response: So everything is trivial compared to the 4.5 billion year perspective except corruption in the EU and your commenting on blogs. Got it. But are you trying to make some kind of coherent point here? – gavin]
Fourier analysis is a rich and intensely complicated subject.
In general, the FT (Fourier Transform) is not the same as the FFT (Fast Fourier Transform). They give the same result for a finite time series with all the observations equally spaced in time (“evenly sampled”). But for an unevenly sampled time series, the FFT doesn’t give the correct result — one is advised to use the DFT (Discrete Fourier Transform), and even that benefits from modification for best results. That’s one of the reasons there are so many variants (like the Lomb-Scargle modified periodogram or the Date-Compensated Discrete Fourier Transform), many of which have been reinvented multiple times under different names in different disciplines. With irregular time sampling a raw DFT can give misleading results, and these variants are especially popular (and useful!) in disciplines like astronomy for which the time sampling is rarely (if ever) even.
Also, it is possible to compute the FT for frequencies lower than the “fundamental” frequency (1/”timebase”). Its meaning can be ambiguous, and in most circumstances it’s not recommended, but it’s possible and can sometimes be informative.
It’s not really necessary to detrend a time series before Fourier analysis, but it usually helps by removing the spectrum of the trend itself, allowing closer inspection of the non-trend spectrum. On the other hand, if you’re really interested in the spectrum of the trend itself then you’d want to leave it in. It’s certainly not necessary for a time series to be stationary, in fact when searching for genuine periodic behavior we expect that the time series is *not* stationary, rather that it might be periodic.
It’s also possible to compute the FT for frequencies which don’t fall on the “grid” of frequencies usually computed for a DFT. This is “oversampling” the FT, and is extremely useful in some circumstances (especially for period estimation) but is another thing that for which the FFT is inappropriate.
There are profound issues regarding the use of an observed time series. The straightforward DFT computes the spectrum of a time series which is repeated periodically for all time, but that rarely (if ever!) represents reality. If the time series is inherently discrete, what you really want is the DTFT (Discrete-Time Fourier Transform) but to compute that you’d need an infinite number of data points, obviously an impossibility. The DFT is only an approximation of it, and is no good beyond the Nyquist frequency. Furthermore, the discrete time window creates significant differences between the computed DFT and the DTFT (it’s the origin of the problem of “spectral leakage”), especially since the “window” has such sharp edges. There are various methods to compensate, including a variety of “windows” that can be applied which can reduce spectral leakage but at the cost of a degradation of spectral resolution. In fact there’s a whole field concering window design, sometimes called “window carpentry.”
Methods like MEM (Maximum Entropy Method) are designed to get a better picture of the FT of the entire signal rather than just the window of observations. However, there are considerable risks involved (as this post makes clear), and they are vulnerable to abuse if certain parameters (like the number of poles) are ill-chosen.
If the time series is *not* inherently discrete, instead the observations are a discrete sampling of a continuous function, then we really want “the” FT, but again the DFT is only an approximation. Interestingly, in this case there can be distinct advantage to sampling at times which are *not* evenly spaced — a random time sampling may be best of all, because then you are not limited by a “Nyquist frequency,” you can in fact explore the behavior at frequencies far higher than the sampling rate.
I’ve tried to encourage colleagues in astronomy to randomize the time sampling, not only to allow exploring high-frequency space, but also to ameliorate the problem of “aliasing.” This occurs when two different frequencies give signals which look identical, or very similar, when restricted to the times of observation. When the time sampling itself exhibits periodicity, aliasing can be a severe problem — this often happens in astronomy because the availability of observations is governed by cycles such as day/night and the yearly progress of earth in its orbit.
One must also be aware of what one wants from a Fourier analysis. A common goal is simply to transform from the “time domain” to the “frequency domain,” often extremely useful, but this may have little or nothing to do with the problem of “period search,” another ubiquitous application of Fourier analysis. Period search exists apart from Fourier analysis (although Fourier is the most common method), and there are a host of non-Fourier methods like PDM (Phase Dispersion Minimization) or minimum-string-length based on “folding” the data with a trial period. In fact, there’s a wonderful variant of PDM based on the analysis of variance, developed for astronomy, which not only gives excellent results, it’s also optimized for statistical efficiency and minimum computational workload (which really helps when analyzing terabyte databases such as come from modern satellite missions). Some of these non-Fourier methods are far better than Fourier analysis when the waveform is distinctly non-sinusoidal, and some astronomical objects (like eclipsing binary stars) exhibit such behavior.
Fourier analysis is one of the most useful and common methods of analysis, and one of the most beautiful mathematical creations of the human mind. As the post makes clear, it’s also, at times, subject to abuse.
tamino @18 — Thank you.
Just a bit of inspiration for EFS_Junior in @14 and others who are (legitimately) using FFT: You should spend a moment looking into “(Modified) Allan Variance” and try it on your data, it very often reveals interesting and otherwise unavailable details about the noise processes affecting a time-series.
The global mean temperature data shows a 60-years cycle as shown in the following graph.
http://bit.ly/emAwAu
Assuming the data is valid, should we stop believing what it says?
No doubt the Sun indeed runs ‘60 year cycle’, (pi/3 = 60 ; pi/…), as this NASA’s record confirms: http://sohowww.nascom.nasa.gov//data/REPROCESSING/Completed/2009/mdimag/20090330/20090330_0628_mdimag_1024.jpg
“π is a fundamentally meaningful number”
But it’s not a rational one and therefore it’s not countable.
Maybe it would be better to desribe it as a Function, with an output consisting of an infinite real number series.
I analyzed the Scafetta paper from an astronomical/physical perspective (I am an astronomer) in http://giannicomoretto.blogspot.com/2010/03/sole-e-clima.html, unfortunately in Italian, but also the mathematics is flawed, as shown here.
A MEM analysis, as performed by Scafetta, is meaningful when you already know that your series is composed by a limited number of sinusoidal (or quasi-sinusoidal) components. Moreover, it is not meaningful to find “correspondences” between components that have distinctly different frequencies, as shown by OBLIQUE lines in Scafetta figure: if they don’t match, don’t match, is like saying you “almost win” the lottery because the winning number is “almost” yours.
Summarizing my considerations, the velocity of the Sun (or its acceleration) with respect to the Solar System barycenter has no physical meaning. General Relativity Equivalence Principle tells us that a free falling body (as the Sun pulled around by the planets gravity) is exactly equivalent to an undisturbed body at rest, for any physical phenomenon. Only mareal forces (differences in the gravity as seen by different parts of the Sun) are important.
Computing gravitational tides due to planets on the Sun is straightforward, and it spectrum is obviously composed of a limited number of sinusoids (at the planets orbital periods). But the spectrum is completely different from the one shown by Scafetta, the outer planets contribute very little, the 20 year component is weaker than that due to Jupiter, and the 60 year one still weaker. The strongest components are at short periods (around one year), and filtering anything shorter than a few years leave basically just the Jovian component, that is close (but not identical) to the solar 11 year period. Just to give the right proportions, these tides correspond to MILLIMETERS on the surface of the Sun.
The 11 year period can be seen in the climate record, with an amplitude of a few hundredths of a degree, so a near-correspondence can be found. The correspondence goes out of phase in about a century, at the point that a resonance of 14/15 (physically VERY unlikely) has been proposed. But on a shorter timescale (as in Scafetta’s paper) it could be quite impressive.
Girma, got tired of spouting the same thing over and over again at Open Mind? Do you think your climastrology is going to make more sense the more blogs you post it on? Your imaginary “cycles” (based on far too short of a time series) have no physical basis. Until you can provide one, one that explains why the known forcings over the same period of time had no affect on temperature, they are meaningless. As has been pointed out to you (over and over), if your cycles had really been happening that would mean temperatures were far colder over the last 1,000 years than we know they were. When did your magic cycle begin? When will it end, and why? Mystical gibberish.
Please borehole Girma. Not only has he hijacked and largely wasted one thread over at open mind, as ointed out by Robert Murphy, but he has an entire 2200+ post thread devoted to his nonsense over at Deltoid. Plus top billing at WUWT.
Surely that’s enough exposure for this particular Galileo, at least until he publishes and wins his Nobel?
#25 A careful reading of the Scafetta papers (2010; L&S 2011 etc.) shows that the ‘astronomical’ rationale is completely post-hoc. That is, the timescales are chosen based on what was already diagnosed from the temperature time-series, not selected objectively on the basis of any real theory. In 2010, the 9.1 period is added completely arbitrarily because it popped up in the temperature record. The multi-decadal peaks in CMSS are never discussed, the other peaks in SCMSS are ignored. The superficially impressive split-period validation uses periods defined from the full temperature series, not just what would be available from the split periods themselves. All in all, these are classic examples of how not to analyse data.
Tamino’s comments are always substantive. Sometimes I can even understand them. Not this time though. I wish I understood more math.
@14, “Most certainly, there is no interaction between Jupiter/Saturn and Earth’s climate, at any periodicities….” is wrong. Earth’s orbital variations are driven partly by gravitational interactions with the gas giants, and those variations drive the Milankovich forcing.
#30
That paper does mention Milankovitch, but AFAIK, Milankovitch cycles can’t even explain the change in ice age cycles from ~41Kyr to ~100kyr.
http://en.wikipedia.org/wiki/100,000-year_problem
So,in other words, the Solar System is not deterministic over long periods of time, that much we do know.
Now, if you were to believe this “theoretical” paper, you would be able to tell me the exact position of all the planets, like 20Mya even, relative to what exactly?
I stand by my original statement “no interaction between Jupiter/Saturn and Earth’s climate” until such a time when direct incontrovertable empirical evidence is presented. Sound familiar?
“Long periods of time” being the key phrase.
Laskar’s most recent paper says; “it will never be possible to recover the precise evolution of the Earth’s eccentricity beyond 60 Myr.”
I don’t think anything he’s done would explain the 100k year cycles.
See “Strong chaos induced by close encounters with Ceres and Vesta”
J. Laskar1, M. Gastineau, J.-B. Delisle, A. Farrés and A. Fienga1.
http://www.aanda.org/articles/aa/pdf/2011/08/aa17504-11.pdf
While I agree that is extremely easy, not to mention tempting, to produce spurious results by tuning the parameters using the MEM method, I would not dismiss the possibility of finding a periodic signal related to the orbital periods of the giant planets out of hand. The reason is that the earth orbits around the barycentre of the solar system, which is slightly displaced from the centre of the sun. Depending on the alignment of the planets, the displacement is less than 1% of an AU, but the effect might be detectable.
Of course, none of this has any significance for the current warming.
@31: In addition to #32, “direct incontrovertible empirical evidence” is an overly strict criterion for accepting a scientific theory. While Milankovich theory has problems, it’s the best explanation thus far for glacial cycles. On the 100,000-year problem, Ashkenazy & Gildor 2008 speculatively suggest that orbital variations cause equatorial insolation changes that may (along with feedbacks) explain the 100,000 year cycles. Raypierre also mentions an interesting idea (p.467 of his textbook) about variations in precession and eccentricity largely cancelling due to Kepler’s law, leaving variations in obliquity (~40kyr) as the largest effective forcing, with some nonlinearity (CO2?) causing “skipping” of obliquity cycles and thus the appearance of ~100kyr cycles.
While I don’t currently know enough (yet!) to rigorously evaluate these ideas, Milankovich is far from dead. In any case, thank you for motivating me to look into this topic more deeply.
What do you suggest causes glacial cycles?
CAPTCHA: the ntiplik
@31: Also suggestive (but hardly conclusive) on Milankovich, Jochum et al 2011 (draft paper) got glacial inception in a CCSM4 model by subjecting it to orbital forcings from 115 kya.
Re 33 Tom P – not an expert in celestial mechanics, but given the inverse square law, the Earth is ‘disportionately affected’ by closer masses than farther masses. It is considerably closer to the sun than Jupiter, so while the Earth-moon system won’t exactly orbit the barycenter of the Earth-moon-sun system (in part because the Earth-moon system is not spherically symmetric?), it won’t orbit the barycenter of the whole solar system.
(I tried to educate myself on the details of how orbital cycles arise and from what I can tell thus far, I wouldn’t expect the cycles to be perfectly smooth on the microscale – precession and obliquity for example should change more rapidly at some times of the year/month/18-year/whatever than others (solar or lunar-driven precession itself can’t (approximately) happen at those times when the sun or moon cross the equatorial plane)- I imagine little jumps in obliquity accumulating over time in a way that can easily be approximated as a smooth cycle (well, not a perfect cycle, but anyway). I can imagine little jumps being associate with eccentricity, which maybe would mean that the Earth sometimes is just a little closer or farther away from the sun on shorter timescales than it would be if the cycle were truly smooth over time. But how big would these jumps be and could they have a multidecadal average effect – even if only through alignment with seasons? I’m guessing it wouldn’t be signficant, but as for the celestial mechanics – is there a website which explains this in more detail?)
My nitpicky side also thought of Milankovitch cycles when the post mentioned that the other planet’s don’t cause changes in Earth’s climate, but I don’t think that is what Scafetta had in mind.
See my post that goes into more detail on the influence of the other planetary bodies (or even theoretical Milankovitch cycles on other planets) than most other sources that deal with just Earth’s glacial-interglacial applications (which is not dead at all, but I agree with others that a fully coherent theory for how various orbital parameters conspire to pace the ice ages is not yet established with high confidence…but I don’t think anyone argues that Milankovitch plays a large role).
It’s one thing to say thay our Solar System does a certain dance.
So, for instance, the Sun-Earth-Moon would be the dominant dancers (assuming we are all are from the same planet called Earth).
So, for instance, we know that the moon is “locked” to the Earth, simply because we ever only see the side facing Earth.
The Earth-Moon are synchronized;
http://en.wikipedia.org/wiki/Moon#Appearance_from_Earth
Then there is the planet Mercury;
http://en.wikipedia.org/wiki/Mercury_(planet)#Orbit_and_rotation
It’s a whole other thing to say that Jupiter/Saturn are phased locked with the Earth at specific periodicities or even quasi-periodicities (e. g. pertubations about a set of mean periodicities).
So, for example, a spectral plot of all contributions to Earth’s motions is a prerequisite for any meaningful discussion about the dynamics of these celestial drivers upon Earth’s motions alone, without even bringing Earth’s climate into the discussion.
But, I would hazard a guess, that the dominant drivers, by many orders of magnitude, would be the three body problem of the Sun-Earth-Moon system itself.
To carry this further, say we do find (quasi-)periodicities between the Earth-Jupiter-Saturn system in the geologic record (which AFAIK hasn’t been shown conclusively (or even at all) to date).
We then need a physical basis (i. e. a physics based explanation) to relate these arbitrarily small (by several orders of magnitude) net perturbations to Earth’s climate system, you know cause AND effect, or causality;
http://en.wikipedia.org/wiki/Causality_(physics)
And you just can’t wave your hands and say Milankovich cycles, as these, as of today, are not a complete causal answer to the current ice age cysles we see in the geologic record.
So far, all I’ve seen are rather outlandish conjectures with respect to the the Solar System’s gas giants and there purported impacts on Earth’s climate system, no hypotheses, no theories, just guesswork.
@37: I don’t know what the blazes Scafetta had in mind, but it wasn’t Milankovich cycles. BTW, given the contents of the SS article you cited, shouldn’t “but I don’t think anyone argues that Milankovitch plays a large role” read “but I don’t think anyone argues that Milankovitch doesn’t play a large role”?
%34 & $35
Are Jupiter/Saturn themselves modeled in any of those papers that you just throwed up?
Remember this discussion in now aboot Jupiter/Saturn and any direct linkage with Earth’s climate, such that, for instance, Jupiter/Saturn are the causative agent of Earth’s 41kyr and 100kyr ice age cycles.
Also, with respect to L&S2011 and the probative nature of Jupiter/Saturn and Earth’s climate over the past ~150 years, if Jupiter/Saturn are the major drivers of today’s recent climate history, then where were thes two gas giants prior to aboot 150 years ago? Surely, the climate changes seen over these past 150 year would have been there and quite noticable before ~1850AD, correct?
:-(
Re my: (solar or lunar-driven precession itself can’t (approximately) happen at those times when the sun or moon cross the equatorial plane) … refering specifically to the component of precession that is wobbling of the Earth’s angular momentum vector in an inertial reference frame; another component comes from shifting of the semimajor axis.
ReCAPTCHA: “pollutees ontrals”
@40: I never said that the gas giants are “the causative agent of Earth’s 41kyr and 100kyr ice age cycles”. They are one driver of earth’s orbital variations, which probably drive glacial cycles via ice-albedo and other feedbacks. Please see Laskar 1999 (esp. p.1752) for some discussion of the gas giants’ effects on earth’s orbit, along with Laskar et al 2004. I have not attempted to calculate the gas giants’ contribution relative to that of the other bodies, though Jupiter is ~1/1047th the sun’s mass and Saturn 1/3498th, so the solar system’s center of mass is (sometimes) outside the sun itself.
Also I’m not arguing for L&S at all, nor for the preposterous idea that “Jupiter/Saturn are the major drivers of today’s recent [~150 yr] climate history”. I’m sorry if I gave that impression.
Meow,
Yes you are right. Sorry for the typo.
He uses the phrase ‘agnotology’, which is “the study of how and why we do not know things”.
This makes agnatology the shadow of science. People have an innate propensity to believing propositions, sometimes whole collections of propositions, for which there is little or no evidence: “God gave this land to us”; “[insert name here] was a prophet of God”; astrology, phrenology, psychoanalysis; phlebotomy is an effective treatment; aspartame is dangerous; apricot pit extract can cure cancer.
Science is unique among systems of knowledge in elevating skepticism and critical evaluation to norms to be followed. To assert that disbelief requires explanation overturns this great advantage of scientific methods.
#42
Here’s an acronym for you: NALPOS (Not Another Lasker Piece Of Ship)
From p. 1752 and I quote;
” ,,, COULD be obtained by passage through an ice age … ”
COULD? Not according to the very next paragraph!
“With these new values, the passage into the resonance s6 − g6 + g5 could NO LONGER BE OBTAINED during an ice age. Nevertheless, the proximity of the resonance SHOULD still have a singular effect on the obliquity solution, and it SHOULD be noted that, due to the tidal evolution of the Earth-Moon system, we will SURELY enter into this resonance in the NEAR FUTURE.”
SURELY? SHOULD? NO LONGER BE OBTAINED? NEAR FUTURE?
Hmm, I’dah be wantin’ to see some cited references in those two sentences, but there are NONE. On NOLPOS’s timescale “near future” probably means within 60Myr.
I COULD go on, but why bother, when a pure theoretician, assumes the Solar Systen is made up out of constants, and there are no empirical data (the one paper he does cite seems to be all over the place with time scaling issues though) to support the multitude of his various claims.
It’s like assuming no two bodies in our Solar System have ever collided 250Myr into the past through to 250Myr into the future. Now that’s rich.
However, he does finish up that page by mentioning the Earth Tide;
http://en.wikipedia.org/wiki/Earth_tide
What’s missing from that webpage? Why Jupiter AND Saturn, OMFG!
From the last sentence of the NALPON 2004 paper;
“For the calibration of the Mesozoic time scale (about 65 to 250 Myr), we PROPOSE to use the term of largest amplitude in the eccentricity, related to g2 − g5, with a fixed frequency of 3.200 ”/yr, corresponding to a period of 405000 yr. The uncertainty of this time scale over 100 Myr should be about 0.1%, and 0.2% over the full Mesozoic era.”
PROPOSE? This guy is obviously a moving target, he’s definitely not a constant, that much we do know for sure.
Here’s another acronyn: OPNAC (Oh Please Not Another Constant)
Oops, I spotted an error on p. 4, b = 0.00339677504820860133, should be;
b = 0.00339677504820860133 insert random number generator after the last digit, because we need more digits!
Does NALPOS ever present any type of empirical data in any of his plots, he kind of reminds me of Pielke Sr. at WTFUWT always self referential.
So, in closing, I’m still waiting for some skill or predictions of periodicities between the Earth and Jupiter/Saturn, known and confirmed periodicities, because, by golly, I don’t believe everything in our Solar System is actually made up out of literally hundreds and hundreds of constants.
I need an amplitude and a phase and a period, just one will do, for the Earth and Jupiter/Saturn connection. Then we can go aboot how this is somehow, somewhere, somewho, somewhat, somewhen, somewhy connected to Earth’s climate.
S. Matthew #44,
I don’t think you’ve got that right. First, agnotology professes to study “ignorance”, not “disbelief” as such. In fact, Proctor, in his introduction to the term he coined, explicitly lists “faith” and not “disbelief” as a phenomenon overlapping with ignorance or generating ignorance (along with phenomena such as secrecy, stupidity, apathy, censorship, disinformation, and forgetfulness).
You might argue that e.g. global-warming deniers are not ignorant, as they are typically well aware of the body of scientific knowledge that they choose to actively disbelieve, so they are not a proper subject of agnotology as I understand it. I’d object that public ignorance that there is a scientific consensus on many aspects of global warming is a proper subject of agnotology, and that no theory of this ignorance can ignore the active efforts of those sort-of-knowledgeable deniers. Besides, doesn’t selective disbelief in mounting evidence qualify as a form of ignorance? Certainly it’s the opposite of skepticism as a scientific virtue.
Second, the form of ignorant belief you describe perhaps falls under what Proctor calls “ignorance as a native state.” In his brief taxonomy of ignorance, he distinguishes two more forms of ignorance, “ignorance as lost realm (or selective choice)” and “ignorance as a deliberately engineered and strategic ploy (or active construct).” Benson’s concern, in the article Rasmus referenced, is with the latter. We are not discussing people to whom the basic knowledge about global warming have not yet filtered down, but people whose knowledge is distorted by a political campaign of doubt and disinformation; not ignorance as a passive state, but as something actively produced.
Reference: Robert N. Proctor, “Agnotology: A Missing Term to Describe the Cultural Production of Ignorance (and Its Study),” in Agnotology: The Making and Unmaking of Ignorance, ed. Robert N. Proctor and Londa Schiebinger (Stanford, California: Stanford University Press, 2008).
Typo: In my reply to Matthew above I meant to refer to Daniel Bedford, an author mentioned in the OP. Dunno where “Benson” came from. Apologies.
Septic Matthew: “Science is unique among systems of knowledge in elevating skepticism and critical evaluation to norms to be followed. To assert that disbelief requires explanation overturns this great advantage of scientific methods.”
Uh,… no. Do not conflate skepticism with disbelief. Skepticism is the requirement of evidence to underly belief, and of belief to be only as strong as the evidence. Disbelief need be based on evidence no more than belief need be. Disbelief in anthropogenic climate change requires dismissing literal and figurative mountains of evidence. That requires tremendous credulity–the opposite of skepticism.
To: vukcevic #23
“vukcevic says:
1 Sep 2011 at 6:14 AM
No doubt the Sun indeed runs ‘60 year cycle’, (pi/3 = 60 ; pi/…), as this NASA’s record confirms: http://sohowww.nascom.nasa.gov//data/REPROCESSING/Completed/2009/mdimag/20090330/20090330_0628_mdimag_1024.jpg”
Vukcevic: Your link just shows a photo of the sun. It doesn’t confirm anything about cycles (or much of anything else). Kindly post the correct link if you please.
To GIRMA #22:
“Girma says:
1 Sep 2011 at 2:48 AM
The global mean temperature data shows a 60-years cycle as shown in the following graph. http://bit.ly/emAwAu Assuming the data is valid, should we stop believing what it says?”
Girma I looked at your graph and it does show two apparent minima about 60 yrs apart. But this isn’t a “cycle.” Just 2 not-necessarily-related data points.
The chart you refer to is generated using parameters chosen within a plotting application at your link. The chart that people see when they first open your link shows global temperatures remaining roughly constant from 1880 to 2010, but varying within a wide range.
I experimented with the parameters of this plotting application: When I set the “detrend” parameter for series 1 (“GIS Temp Land-Ocean Global Mean” which shows the 2 minima) from 0.75 to 0 and click the “Plot Graph” button, I see a chart of steadily increasing temperature from 1880 to 2010. NOW there is not even the remotest suggestion of a “cycle.” Just relentlessly increasing temperature.
Based on this, your comment appears to be, let us say, incorrect.
Or not: Can you help me understand what, if anything, I am misunderstanding?