Are the rising atmospheric CO2-levels a result of oceans warming up? And does that mean that CO2 has little role in the global warming? Moreover, are the rising levels of CO2 at all related to human activity?
These are claims made in a fresh publication by Humlum et al. (2012). However, when seeing them in the context of their analysis, they seem to be on par with the misguided notion that the rain from clouds cannot come from the oceans because the clouds are intermittent and highly variable whereas the oceans are just there all the time. I think that the analysis presented in Humlum et al. (2012) is weak on four important accounts: the analysis, the physics, reviewing past literature, and logic.
This time Humlum et al. did not directly remove part of the data which didn’t fit their conclusions, however, they chose to use a short record of global mean CO2 from NOAA Earth System Research Laboratory (ESRL), starting from 1980, rather than the longer Keeling curve from Mauna Loa starting in 1958.
The two CO2 records, however, are almost identical over 1980-2012 (green curves in Fig. 1), and hence it would be more appropriate to use the longer record because CO2 is expected to play a role for long timescales. Hence, the Humlum et al. paper highlights the need for sorting out some classic misunderstandings, namely the mix-up between time scales. We have already discussed the absurdly misguided claims of a “halted global warming” based on a brief period after 1998 (here and here and ….)
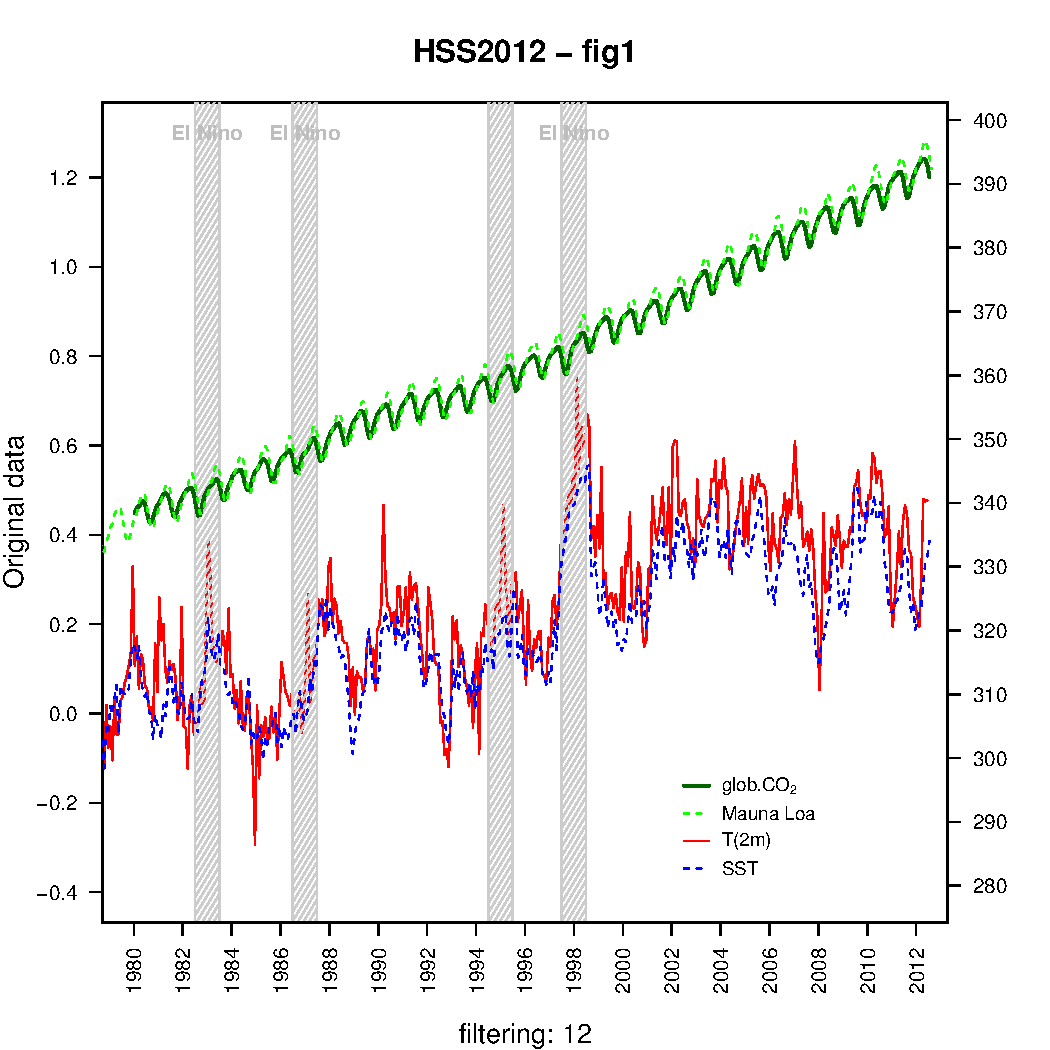
In order to assess the claims made in Humlum et al. (2012) (in italics above), I have repeated part of their analysis and got very similar results (all reproduced with the on-line R-script). Fig 1 here is a replication of figure 1 in Humlum et al. (2012) and I got almost identical results using the Keeling curve from Mauna Loa starting in 1958 rather than the global curve starting in 1980.
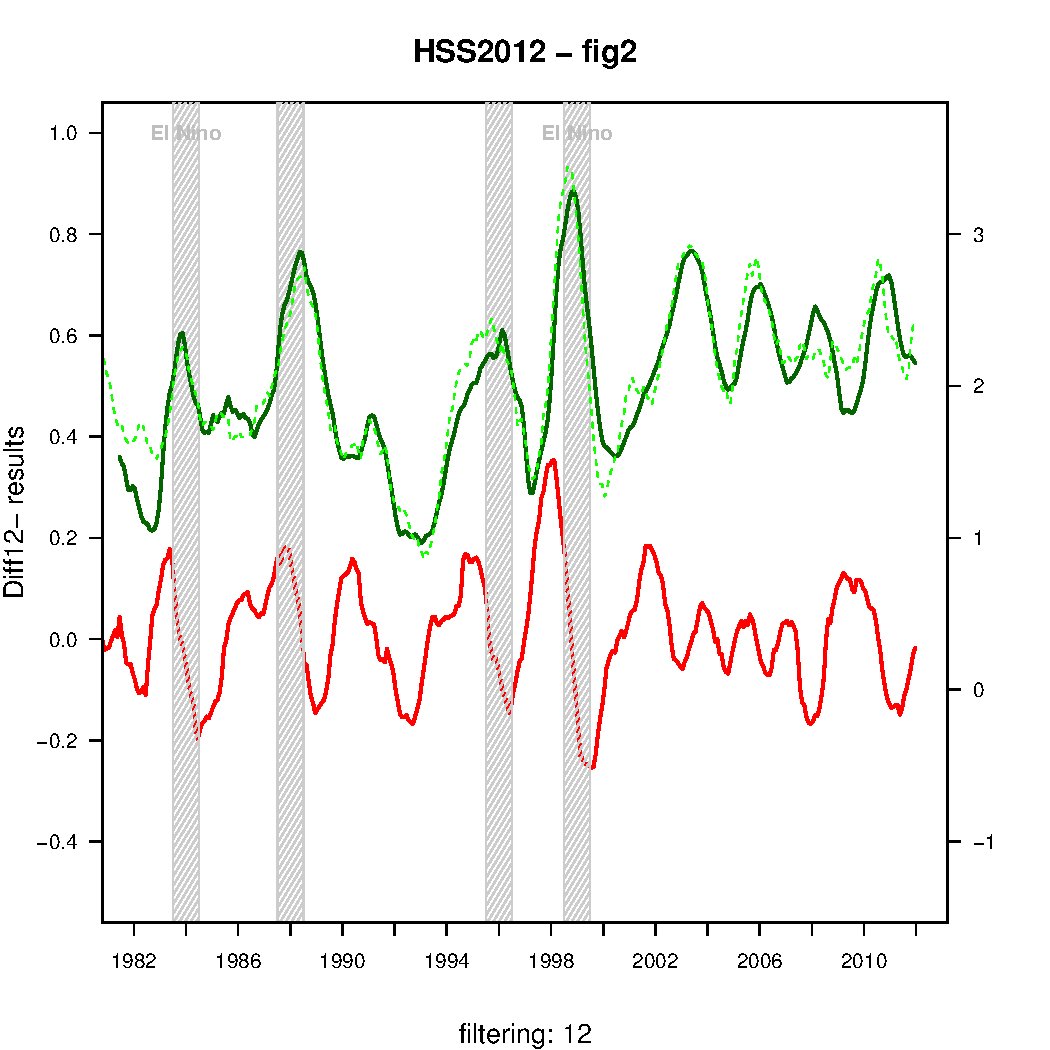
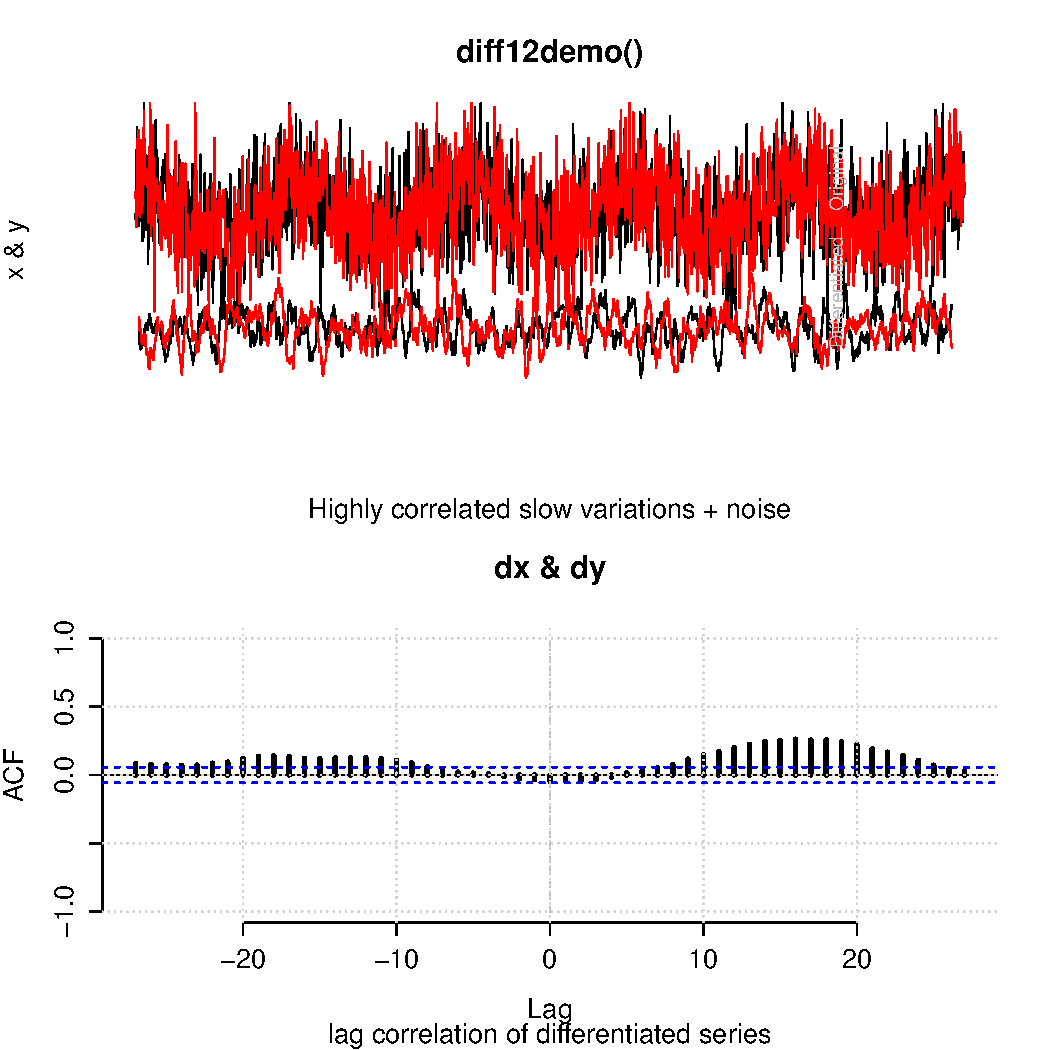
Fig. 2 corresponds to the lower panel in their figure 2, and shows the results of my attempt to reproduce the quantities making up the basis for their claims: their ‘DIFF12’ quantities (a type of differentiation operator) which really is meant to describe the rate of changes in the original curves.
Their main argument about causality between temperature and CO2, however, was based on a lagged correlation analysis between ‘DIFF12’ series from temperature and CO2. Fig. 3 corresponds to figure 4b in Humlum et al. (2012):
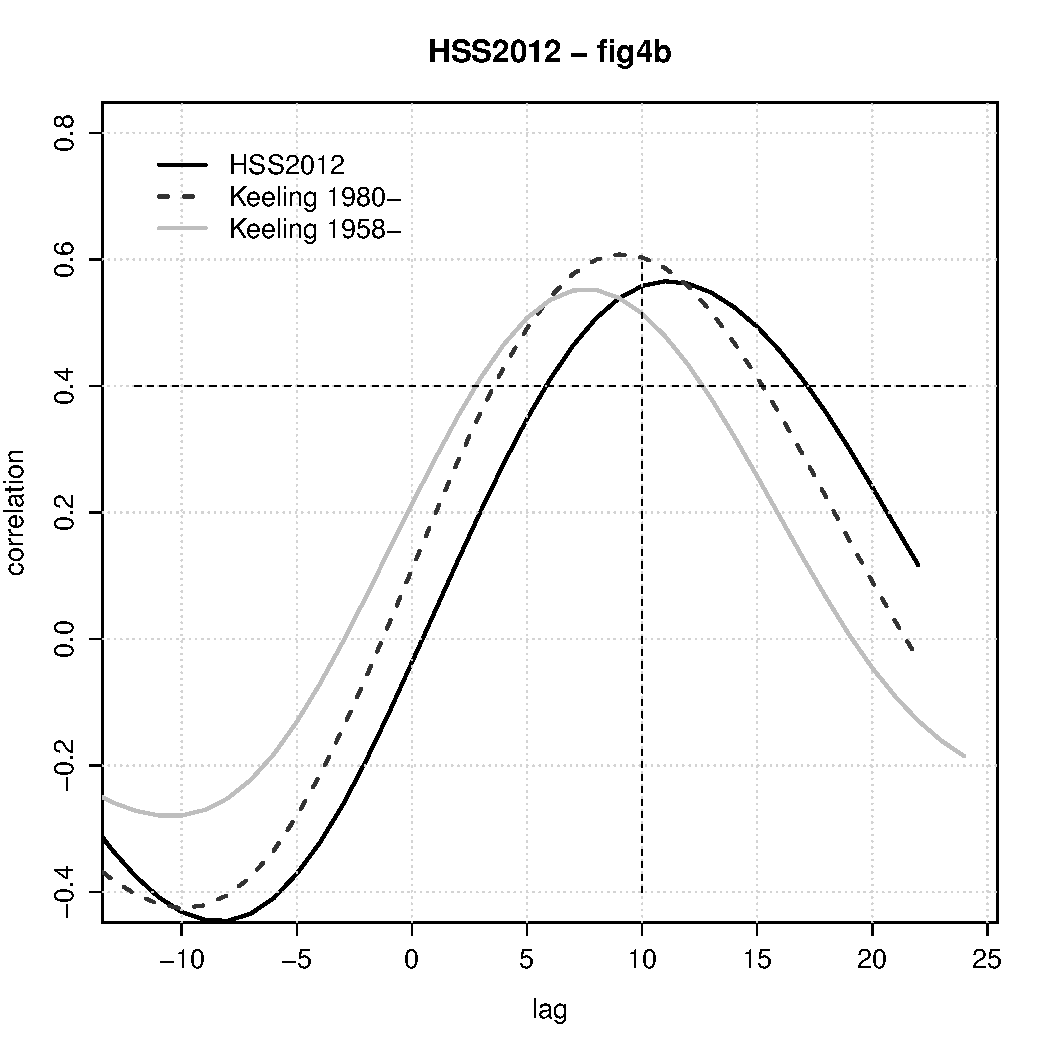
The correlation that I get is similar but not identical to theirs. Using a longer record did affect the lag correlation analysis as seen in Fig. 3. Nevertheless, the analysis still indicated that CO2 lagged the temperature. Big surprise?
No! Applying correlation to the results from the ‘DIFF12’ quantities cannot detect any trends – it’s just a simple mathematical fact. These results merely confirm already well-known facts, which ironically, they themselves hinted to in their paper (but they obviously did not make the connection):
changes in atmospheric CO2 appears to be initiated near or a short distance south of the Equator, and from there spreads towards the two Poles within a year or so.
The answer is of course: El Nino! A google scholar search with ‘”El Nino” AND CO2’ gives more than 20,000 hits, and Humlum et al. have rediscovered well-known facts which Keeling and Revelle discussed already in 1985.
El Ninos affect the CO2 concentrations for a brief time interval, through their effect on temperature and marine biology. But unlike Keeling and Revelle, this discovery caused quite some confusion, as evident in the following citation:
…showing that changes in the emission of anthropogene CO2 are not causing changes in atmospheric CO2.
So how did they get to this conclusion? The answer is in their analytical set-up, and for this they have quite an unusual record (here and here).
It’s well-known that taking differences also picks up short-term rather than long-term variations where mean trends are represented by a constant value. Hence, a correlation analysis is bound to give mean trends zero weight. This is demonstrated in Fig. 4:
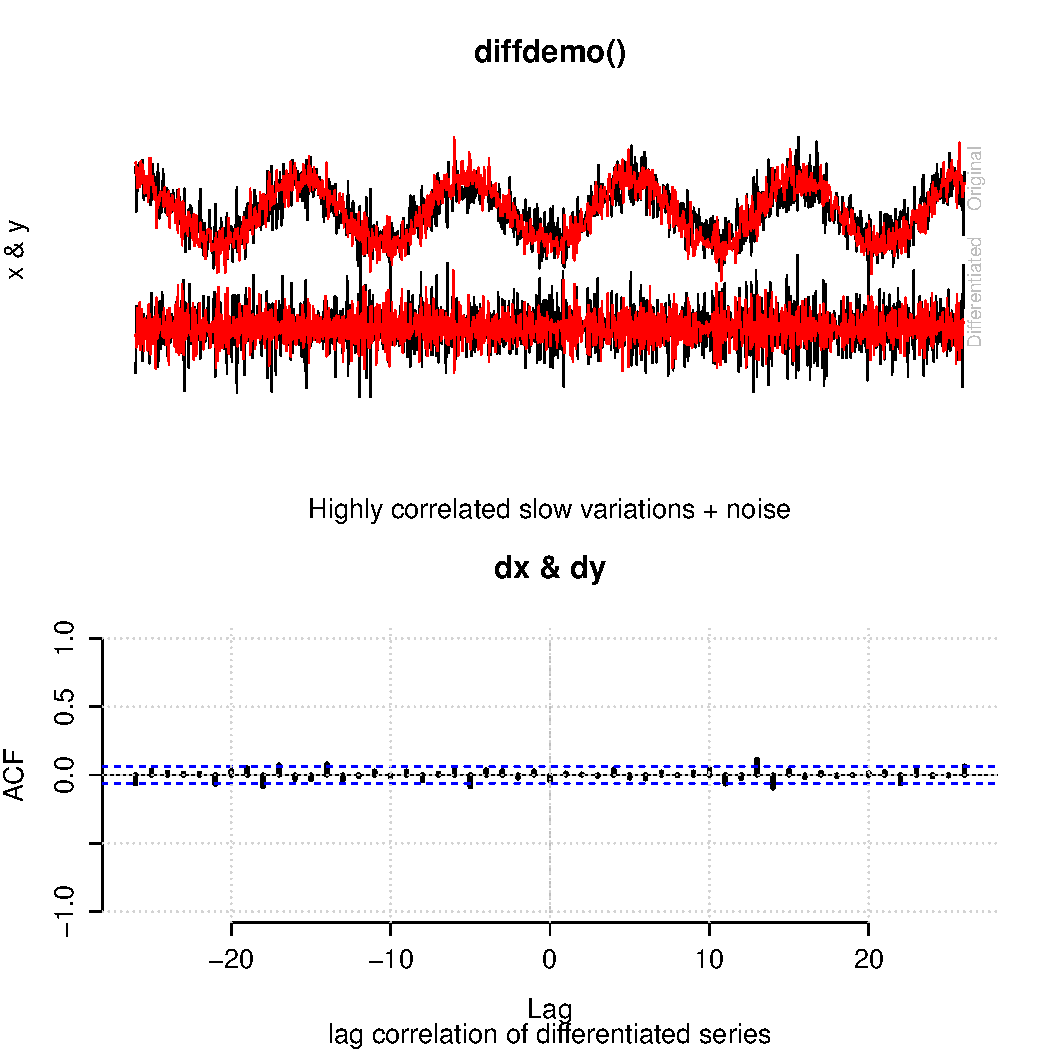
Simply by choosing a method that ignores trends associated with human activity, they argue that atmospheric CO2 is ‘largely independent of humans‘. This logic is circular reasoning, but since they did not specify time scales, their argument gets a bit fuzzy (the argument is true on short time scales but not on decadal time scales – just see the trends in the figure).
The set-up with ‘DIFF12’ also does a strange mix to the data and gives weird results as already noted on Troy’s scratchpad. It is indeed easy to show that the ‘DIFF12’ methods fail to pick up long-term co-variations, as done in Fig. 5:
Contrast these results with the claim made by Humlum et al. (2012):
the association between periods of maximum DIFF12 CO2 increase and no or negative ocean surface temperature change … is difficult to reconcile with the notion of atmospheric CO2 changes controlling changes in ocean surface temperature.
Choosing a method discarding the trends may get one into trouble, however, one would also expect a consistent picture in terms of physics. Here is another glitch, and the weak-on-physics aspect is due to the failure to appreciate what implications their claims would have for the climate sensitivity.
They implicitly expected that minute and almost invisible similarities between the inter-annual variations in CO2 would have a visible effect on inter-annual variation in the global mean temperature (this is their hidden “strawman” argument; see curves in Fig. 1). Yet they ignored the CO2‘s steady march upwards.
Furthermore, they failed to note that the forcing is proportional to the natural logarithm of CO2 – ln(conventration in volume). Such are omissions expected from novices (my speculation: this is somehow related to the composition of the author team consisting of a professor in geology, a statistician from a telephone company, and an astrophysicist).
The extraordinary claims about the relationship between temperature, CO2, and human activity made in Humlum et al. (2012) also makes me think of a Carl Sagan citation: “Extraordinary claims require extraordinary evidence”. I must say I’m disappointed by the reviewing process of Global Planetary Change and this is the second (Humlum et al., 2011) unpersuasive paper in that journal making such bold claims.
Earth shattering claims should meet rigorous evaluations. It would be useful for reviewers to google the authors of the papers, as some do have quite a track record of well-established mistakes (here and here and here and here).
In addition to failing the analytical set-up and the physics (which should have been picked up), they also provided some unusual citations, missed important works, and referred to questionable publications.
Furthermore, using the NOAA ESRL CO2 data, Humlum et al. could have sought advice with the data providers before submitting their paper (the ESRL is not mentioned in their acknowledgement, and I wonder if they would have a view on this analysis). Indeed, the ESRL encourages such quality checks according to the heading of the data file:
If the data are obtained for potential use in a publication or presentation, ESRL should be informed at the outset of the nature of this work. If the ESRL data are essential to the work, or if an important result or conclusion depends on the ESRL data, co-authorship may be appropriate. This should be discussed at an early stage in the work. Manuscripts using the ESRL data should be sent to ESRL for review before they are submitted for publication so we can insure that the quality and limitations of the data are accurately represented.
I also wonder what the affiliated universities think about Humlum et al.s work and their past record, and I think misguided work, as presented here, is not exactly good advertisement. Furthermore, they are also involved with an organisation called “klimarealistene” (with collaborations with the Heartland Institute), which claims that the IPCC has ‘cheated‘ in terms of the temperature data (which ironically, they themselves rely on in Humlum et al. (2012)) and produced the ‘famous hockey stick’ (The people thanked in the acknowledgement reads like who-is-who within “klimarealistene”).
A good thing is that Humlum et al. now have obliged themselves to share their data, results and methods by using the CO2 data from NOAA:
RECIPROCITY – Use of these data implies an agreement to reciprocate. Laboratories making similar measurements agree to make their own data available to the general public and to the scientific community in an equally complete and easily accessible form. Modelers are encouraged to make available to the community, upon request, their own tools used in the interpretation of the ESRL data, namely well documented model code, transport fields, and additional information necessary for other scientists to repeat the work and to run modified versions. Model availability includes collaborative support for new users of the models.
I’ve asked them to share their results, data and methods before, but so far with little success. My job as a climate scientist is to replicate results. Further progress may take place if we can go through the analysis together, test methods and data, and agree on which give robust answers and which don’t.
References
- O. Humlum, K. Stordahl, and J. Solheim, "The phase relation between atmospheric carbon dioxide and global temperature", Global and Planetary Change, vol. 100, pp. 51-69, 2013. http://dx.doi.org/10.1016/j.gloplacha.2012.08.008
- O. Humlum, J. Solheim, and K. Stordahl, "Identifying natural contributions to late Holocene climate change", Global and Planetary Change, vol. 79, pp. 145-156, 2011. http://dx.doi.org/10.1016/j.gloplacha.2011.09.005
Their results are robust, it is just their conclusions, the inferences they draw from these results, which are flawed. Implied in what they are saying is that because a warm ocean surface produces more atmospheric CO2 then the rise in CO2 must be due to global warming and not to the burning of fossil fuels.
It is well known that the solubility of carbon dioxide in water decreases with temperature so it should be no surprise that CO2 levels rise when SST’s rise. What they are missing is that this is a positive feedback loop. More CO2 produces more warming. This leads to higher SST’s and more CO2. The same thing seems to have happened during the Termination of the last glaciation. Solar flux over the South Pacific increased as a result of Milankovitch cycles. CO2 increased, which amplified the warming and, as a result of the positive feedback loop, the ice age ended abruptly. That is why CO2 lags the temperature rise shown in the Antarctic ice cores. But of course other positive feedbacks were also active including the ice albedo feedback.
So there is nothing new in Humlun et al.’s paper. They are just another bunch of sceptics that don’t understand system science.
Cheers, Alastair.
One has to wonder why people like Humlum never seems to notice a peculiarity in figures like Fig 2 (rate of change for CO2 and T). The CO2 rate of change curve is always positive, whereas the T rate of change curve is sometimes positive and sometimes negative. To express it as simply as possible: when temperature goes up, CO2 goes up. When temperature goes down, CO2 still goes up.
That should at least be a hint that changes in temperature are not sufficient for explaining changes in CO2.
Nice article,
However, it begins:
“Are the rising atmospheric CO2-levels a result of oceans warming up? And does that mean that CO2 has little role in the global warming? Moreover, are the rising levels of CO2 at all related to human activity?
These are claims made in a fresh publication by Humlum et al. (2012). ”
Those aren’t claims, they’re questions. I know that’s a bit pedantic but it’s an important distinction. If they make the claims that the questions allude to you should cite them.
Warwick
Another key flaw in the paper is that they suggest there should be a correlation between DIFF12 of atmospheric CO2 and DIFF12 of annual anthropogenic emissions. However one would expect atmospheric CO2 to rise in proportion (i.e. the airborne fraction) with *cumulative* anthropogenic emissions. So the expected relationship should be between DIFF12 atmospheric CO2 and annual anthropogenic emissions itself. Essentialy they are expecting a correlation between the gradient of atmospheric CO2 and the *curvature* of anthropogenic emissions. Hardly surprising then that there isn’t much of a correlation!
I wrote a pre-bunking of Murry Salby’s yet to appear article for Skeptical Science (http://www.skepticalscience.com/salby_correlation_conundrum.html), and Humlum et al. have made exactly the same error.
Furthermore high frequency carbon dioxide fluctuation occurs mainly because of changes in the terrestrial biosphere fluxes, during el nino the ocean actually is a sink of carbon dioxide because of the reduced upwelling of carbon rich waters, the opposite occurs during la nina.
http://www.met.rdg.ac.uk/~mat/hadcm3lc/paper.pdf
The authors have also done some interesting hand-waving regarding volcanic activity and climate impacts. They write,
“Perhaps eruptions larger than VEI=6 are required to affect the global
atmospheric composition and climate significantly, but there has been no eruptions of this
magnitude during the study period.”
VEI: Volcanic Explosivity Index See, http://www.volcano.si.edu/world/largeeruptions.cfm
According to the listing there has not been a single eruption during the Holocene with a VEI > 6.
“On the time scale investigated here,
the dominant effect of volcanic eruptions appears to be increased removal of CO2 from the
atmosphere by the oceans, presumably caused by volcanic eruptions affecting the global cloud
cover, and thereby resulting in lower ocean surface temperature.”
How convenient.
Of course academic decorum dictates that this trio are handled here with kid gloves. You describe them as “misguided” but these are also recidivists. The poor level of their scientific judgement can be assessed courtesy of the Heatlandesque “Klimarealistene” who provide the PDF of Humlum et al 2011.
The highlight of this 2011 paper is perhaps the high frequency end of their 4,000 year analysis (which had a resolution of a couple of decades). Tabular lists of cycles include those at 79 and 58 years without a word of mention in the text. Do bear in mind the ampitude of the biggest cycle in this 4,000 year analysis couldn’t manage even half a degree celsius. The unmentioned 79 & 58 year cycles are presumedly miniscule in comparison.
So I wonder how it is that the 4,000 year analysis didn’t identify the same powerful cycles found in the shorter 1912-2010 analysis, cycles of frequency 60 – 90 year with ampitude of possibly 1.2 degrees celsius, “dominant” cycles, “stable with regard to both magnitude and frequency” that “characterise the entire record” from 1912 to 2010. Were these powerful cycles absent over a millenial scale, unseen before 1855? The analysis is silent so their absence appears a safe conclusion. Could it be their recent appearance is due to some recent phenomenon, rising CO2 for instance? Is this yet more evidence of a ‘hockeystick-type’ change in Earth’s climate?
Apparently not. According to the Misguided Trio they are all explainable as beat frequencies of an 8.8 year cycle and guess what, the Lunar orbit has just such a frequency. So it is all pure lunacy!!
Of course any reviewer worthy of his hire would have pounced on the following quote with a vengence – “The difference in record length and time resolution between the (4,000 year) GISP2 record and the (1912-2010) SvalbardMAAT series explains why many of the periodic variations found in the Svalbard series are not apparent in the GISP2 series, and vice versa. “Many?” You mean ‘none’ and your explanation is complete pants!!!”
“Klimarealistene” have yet to post the Trio’s latest paper in full but it will be worth waiting for. I do enjoy a good laugh!!
BillS,
According to the listing there has not been a single eruption during the Holocene with a VEI > 6.
Try Tambora, 1815.
From the quote: “…presumably caused by volcanic eruptions affecting the global cloud cover, and thereby resulting in lower ocean surface temperature.”
Could be a matter of terminology but the main cooling effect of large volcanic eruptions comes from the injection and formation of sulphate aerosols in the stratosphere, where clouds don’t (usually) form. The proliferation of these aerosols is adequate to explain the drop in insolation and subsequent reduction in SSTs. Of course, there could well be subsequent positive feedbacks whereby cloud changes caused by lower SSTs impart a further cooling but that assertion would probably require more than ‘presumably’.
Searching the literature some papers do refer to ‘stratospheric aerosol clouds’ as opposed to water vapour clouds in the troposphere so it’s possible their sentence is simply ambiguously worded.
The errors in the paper are so obvious that I’m not sure they even deserve this much discussion. It almost lends the conclusions credibility. I would reduce the critique to a few simple points,such as…
1. If increasing CO2 is due solely to a warming ocean, why is the annual rate of change in CO2 always positive while the annual change in SST is often negative (see Figs 2 and 3)?
2. It is the consistently positive mean annual change of atmospheric CO2 that creates the long term trend, for the most part. A correlation that explains variations in annual change in CO2 does nothing to explain this positive mean rate of change.
3. How could pH be decreasing and aqueous pCO2 in the ocean be increasing if the ocean is a net source of CO2 to the atmosphere?
4. Where do Humlum et al. think all the anthro CO2 has gone?
The real question is why didn’t the peer reviewers require answers to these (and other) obvious questions? Is it too much to ask for logical consistency, appropriate interpretation of statistical analyses and adherence to principles like conservation of mass?
It may be useful to know that the authors are known “contrarians” in Norway, who have argued in various non-peer-reviewed periodicals (in Norwegian) in recent time that observed warming is due to naturals cycles. It is therefore a fair assumption IMHO that they set out with the conclusion in mind and worked diligently until they created the “evidence” they needed.
The source of the ‘new’ carbon in the atmosphere, beyond the natural fluxes, is revealed by isotopic geochemistry. This is ‘old’ carbon depleted in 14C and from photosynthetic fractionation (read ‘fossil fuels’). The BEST group ‘discovered’ the link between CO2 levels and warming, perhaps some day klimarealistene will also.
There is bad science that needs ignoring, and bad science that needs retracting. Which is this?
(I know what I think, but I doubt the editors would listen to me.)
Thank you for this analysis. I knew this paper would be slaughtered sooner or later, given its premises and its mere repetition of rather well aged skeptical arguments. Wonderful job though, so thanks again. RC rocks!
The influence of an El-Nino on CO2 fluxes from oceans and land is no surprise at all. There is a paragraph in the IPCC AR4 report where this issue is mentioned:
http://www.ipcc.ch/publications_and_data/ar4/wg1/en/ch7s7-3-2-4.html
Despite what one might intuitively assume it is not the warming of the oceans that influences the CO2 flux during/after an El-Nino, but several processes on land, e.g. see figure 4 and 5 in:
http://eas8803.eas.gatech.edu/Reading_Materials/Bakeretal2006-IAV.pdf
Some information of the CO2-rich water being replaced by water with less CO2 induced by El-Nino can be found in:
http://climate.columbia.edu/sitefiles/file/2006Feely.pdf
It is visualized on the following NOAA website:
http://www.pmel.noaa.gov/co2/elnino.html
If a lay person can find this rather quickly on the internet, Humlum et al should have mentioned all this. In my opinion they should be ashamed of themselves.
This analysis is not complete without reference to Troy’s work, which shows that even his own model, which has CO2 forcing temperature, gives an apparent *lag* of CO2 versus temperature in the Humlum methodology.
Link here:
https://troyca.wordpress.com/2012/08/31/comment-on-the-phase-relation-between-atmospheric-carbon-dioxide-and-global-temperature/
Oh, and Rasmus, Troy is looking for a co-author willing to do the hard work…
@gp (#5): Thanks for the information. The Jones et al. 2001 article you link to is a serious analysis, and by comparison, a good reminder of the crankness of this debated article as well as other tries (M. Salby, L. Hocker, W. Spencer,…the skepticalscience site is a mine of information on this topic) which amount to just attempts at rediscovering tepid water, followed by wild conclusions.
Bseides, the interesting part of the analysis of the ENSO effect on CO2 variations is that the land (biosphere, pedosphere), not the ocean, is the main source of CO2 during ENSO events.
If the contrarian view (anthro CO2 excess rapidly homogeneised into the entire 38000 GtC ocean and recent CO2 rise mainly due to ocean outgassing) had any validity, then dCO2/dt should be maximal during the La Nina events, or at least compensate for the land sink.
Oops… R.Spencer, of course
RE: #8 Paul S.
Ahhh…right you are! I missed it, thanks.
If they are going to state as one of their conclusions (#7) that
“On the time scale investigated, the overriding effect of large volcanic eruptions appears to be a reduction of atmospheric CO2, presumably due to the dominance of associated cooling effects from clouds associated with volcanic gases/aerosols and volcanic debris.”
wouldn’t it be helpful to be a bit more definitive about the causes of such a reduction? Just a thought.
I thought this linked plot that I have constructed would add some grist for the mill in the discussion of short term (on a monthly scale) CO2 concentration and LT temperature relationship.
http://i161.photobucket.com/albums/t231/Occam_bucket/CO2TempCorr.gif
The plot shows a comparison between the deviation of monthly global LT temperature from its linear trend line and the deviation of the rate of CO2 change from its exponential trend curve. Or in other words it shows a deviation from the expected temperature vs. a deviation from the derivative of expected CO2 curve.
You can see a highly significant correlation which appears to be close to coincident. The R^2 value is 30%, but if you lag the temperature data by 2 months you would get a 33% value – which I doubt is significantly different but there might be something to that fact. Lagging the CO2 values on the other hand causes R^2 to drop off quickly.
I am not an expert so I won’t offer opinions on the meaning of it all as there are many complicating considerations that might explain the time relationship between CO2 and temperature changes and/or the measurements themselves. However it seems clear to me that the short term CO2 fluctuations are caused by the short term temperature changes. It is easy to see from a physical perspective that a change in absolute temperature could impact the rate of change in CO2, but the converse does not seem physical, i.e. acceleration of CO2 concentration (regardless of absolute concentration)causing temperature changes.
This plot says nothing about long the term relationship.
I am sure this is not news to the climate scientists, but I found it interesting to see graphically.
(Basically the same message as gp’s and Jos Hagelaars’, but some more information.)
Relationship bewteen El Nino and CO2 budgets is also shown by Japan Meteorological Agency here http://www.data.kishou.go.jp/obs-env/cdrom/report/html/exesum_e.html (Executive Summary of the Annual Report on Atmospheric and Marine Environment Monitoring, No. 11), in the figure titled “Time series of the NINO.3 deviation and estimated monthly CO2 fluxes from land and ocean areas estimated by inversion analysis”. This is an estimate of global CO2 budget (though the rest of the report discusses more local features). El Nino events (peaks in the yellow curve which shows Eastern Equatorial Pacific sea surface temperature) tends to coincide with peaks of the net land-to-atmosphere CO2 flux (the green curve. Note that a certain reference value has been subtracted). Their full report (in Japanese) http://www.data.kishou.go.jp/obs-env/cdrom/report/html/2_1_2.html says that net loss of carbon from terrestrial biosphere by drought condition in Southeast Asia is responsible at least in the 1997/1998 El Nino event(Watanabe et al., 2000; Patra et al., 2005. Their list of references is here http://www.data.kishou.go.jp/obs-env/cdrom/report/html/2_1ter.html .
Thanks for this article because there is no doubt that Humlum will be quoted as proof by the denialists for the next 5 years. Those problems with the statistical tools are things that should have been learned in school.
All these helpful graphs appearing on this thread are clouding the main point to take away from the discussion. I had hoped the graphs of Dikran Marsupial that he linked to @8 would be the things to demonstrate clearly and conclusively the arrant nonsense in Humlum et al 2012, but they are perhaps too numerous and use synthetic data.
So using GISS & MLO data and ripping away the smoke and mirrors, this appears to be the full substance of Humlum et al 2012. (Usually two clicks to ‘download your attachment’) I would suggest that calling it “arrant nonsense” is perhaps being too generous!
Seems to me if the paper is a poorly done as the article and comments here indicate, more pointed questions should be directed to the journal that published it– http://www.journals.elsevier.com/global-and-planetary-change/#description. Is it a credible journal? I do not have the time or expertise to evaluate the matter (although the top “popular download,” “Thermal pollution causes global warming”, by B. Nordell [Global Planet. Change 38 (2003), 305–312] doesn’t sound too promising).
Toby: Thank you for pointing me to a great oeuvre I had previously overlooked: Bo Nordell not only published his 2003 GPC paper, but a 2009 paper in the International Journal of Global Warming (http://www.zo.utexas.edu/courses/THOC/Nordell-Gervet2009ijgw.pdf). Sadly, some scientists who think that understanding atmospheric physics is necessary for publishing climate papers published rebuttals (http://www.ltu.se/cms_fs/1.5035!/covey%20et-al%20gpc%20vol%2047%20p72-73.pdf and http://www.ltu.se/cms_fs/1.5035!/gumbel-rodhe%20gpc%20vol%2047%20p75-76.pdf). Fortunately, the great Nordell was unperturbed, as can be seen in his two replies to said comments (http://www.ltu.se/cms_fs/1.5035!/nordell%20gpc%20vol%2047%20issue%201-%20p74.pdf, http://www.ltu.se/cms_fs/1.5035!/nordell%20gpc%20vol%2047%20issue%201-%20p77-78.pdf).
Actually, really sadly is that my first first-author climate paper was in fact published in Global Planetary Change, and every dumb skeptic paper that appears there makes my paper feel that much less worthy…
Toby,
That Bo Nordell paper is a hoot. He’s claiming in that article that the warming we’ve seen since 1880 was mostly caused by heat released from burning fossil fuels, and not at all from GHG’s. The journal sounds very fishy.
PS: The same Bo Nordell wrote this ditty in 1988 in support of dowsing:
http://www.ltu.se/cms_fs/1.5014!/dowsing.pdf
Because confusion is a human trait that might not be easily or directly caused by El Nino and CO2, I might suggest a title revision to “Confused researchers bothered by El Nino’s effect … ”
On the other hand, I wonder, perhaps hypoxia actually did cause the confusion.
Have a lot of crazy stuff from Nordell wrote one article to discredit his nonsense cure for all kinds of pain… the “Crystal Plaster” basicly a plaster with rocks in it… but all my debunks are in Swedish.
This paper could become a classic for postgraduate courses in the carbon cycle, with students asked to come up with at least two reasons why it does not stand up to scrutiny. Back in the 1950s, Rafter had considered the idea that increases in CO2 might come from a warming ocean but his very early (pre-bomb) work on radiocarbon measurements showed that the difference between the surface ocean and atmosphere was not large enough to be consistent with that. Then Keeling’s work at Scripps deliberately included 13C measurements and provided stronger evidence again that the ocean could not be a source.
As already mentioned, for the Humlum et al paper to do an analysis like this without treating the ENSO variability quite explicitly is just trying to fit it to a subjective opinion rather than doing an objective analysis.
I tried to understand some of the relationships between CO2 fluctuations and temperature fluctuations, and got plenty of evidence confirming the ENSO relationship. If you try to correlate various global temperature time series with the CO2 fluctuations on interannual time scales, the cleanest coherences with the most-interpretable phase relationships come from the time series that include SST data (e.g., not the satellite-based tropospheric time series). The interesting feature was that the phase between CO2 and global-average temps changed in the late 1970s. This change is best seen in the frequency domain, not the time domain, because the change went from a simple time lag in the early part of the data series to a 90-degree phase lag (i.e. CO2 varies with the first integral of global temps).
see
http://earth.geology.yale.edu/~jjpark/Park_2011_CO2coherence.pdf
Park, J., Evidence for oceanic control of interannual carbon cycle feedbacks, American Journal of Science, 311, 485–516, DOI 10.2475/06.2011.01, 2011.
For SVD-lovers, there are a few cases where I reconstructed phase delays at all the GLOBALVIEW CO2 recording stations with 30 years of data, suggesting that, although the pacing of the ENSO-scale CO2 variations in the far northern hemisphere is tied to tropical SST variations, the signal probably originates from terrestrial plants via rainfall variations (and not the continental temperatures themselves).
People the world over readily accept the scientific fact that changing a patch of South Pacific from warm to cool by only a couple of degrees C, and the resulting comparatively narrow El Nino/La Nina current across the Equatorial Pacific to South America, can have a profound effect on the weather. Not only here in the United States, but to a lesser degree Europe and Africa. On the other hand, transforming a much closer, (boarders in many cases), highly reflective patch of earth from significantly bellow freezing to dark open water above freezing, a difference of 10′s of degrees C and couple that with an area that is larger than India and it is just going to be no problem! Get real. I am telling you, Science is telling you, and the on the ground reality is telling you we have trouble here. Of course vested interests are spending big bucks trotting out “red herrings” as fast as they can. Perhaps that must be factored into the attitudes of the masses, you think?
Time to toast the deniers, not the Kidders…
There’s an interesting take on Humlum et al here:
http://troyca.wordpress.com/2012/08/31/comment-on-the-phase-relation-between-atmospheric-carbon-dioxide-and-global-temperature/
Where the ‘Diff12’ approach is tested against the ‘one-box energy balance’ model and shows the same kind of results the paper does. Looks like a nice refutation to me. The author freely offers the technique to be used by anyone who would like to get it peer-review published as a refutation to the paper.
You can see Humlum (Sadly invited på the Swedish royal acadamy, why? Feel free to ask them.) having a really bad debate here here: http://kva.screen9.tv/#6xOBFturYGoDFhodx5SU6Q
http://kva.screen9.tv/#iEH5CzCOHF9oylk1Dh-ViQ
Thankfully Scott Denning also where there.
As usual, you do a very nice job of taking down the specific “analyses” and assumptions in Humlum´s “paper”, Rasmus.
However, as a terrestrial ecologist, the part I find most troubling about their main claim about non-anthropogenic CO2 rise is that nobody apparently challeged them on the isotopic data C13/C12 ratio and the decline in C14 (as briefly mentioned by #11 and #27), or pointed them to e.g. Sabine et al. (1994) or just any research demonstrating that oceanic carbon content has increased steadily along with atmospheric CO2. Even ignoring all problems with their short timescale and the ENSO link, this alone should dispel with the old idea of oceans being a source for atmospheric CO2.
Humlum & co. even have the audacity to quote a 1997 JGR paper by Nakazawa et al. (http://www.agu.org/pubs/crossref/1997/96JD02720.shtml) which makes the ENSO link, the C13 decline in atmospheric CO2 and the necessary link to fossil fuel combustion unambiguously clear in the abstract:
“Values of δ13C decreased secularly at a rate of about −0.03‰/year, owing mainly to increased amounts of isotopically light CO2 produced in fossil fuel combustion and deforestation. Interannual variations of the long-term trend of δ13C in association with the El Niño–Southern Oscillation (ENSO) event and other factors were clearly observed, which were almost opposite in phase with those of the CO2 concentration”.
– which is, of course, simply ignored by Humlum et al., who just quote this as a useful “continuous in situ measurement” of SH CO2.
Thus, it sure seems like these authors have gone through quite some trouble to remain “unaware” of the wide body of decade-old research already having debunked their hypothesis. And as you well know, it has been pointed out to Humlum several times that his oceanic CO2 idea is ridiculous, but he just simply keeps repeating the old points.
Humlum is also well known for fiddling with nonphysical curve-fitting:
http://uppsalainitiativet.blogspot.dk/2011/12/vadan-med-polynomanpassningar.html?showComment=1323850074427
– and we had a healthy debate on Ole Humlum´s contradicting himself several times on the page klimadebat.dk (in Danish) recently. http://www.klimadebat.dk/forum/part-4-opdaterede-sol-is-temp-hav-data-d12-e2045-s160.php
On his climate4you page, he first states that “global warming stopped in 1998”, just judging by eyeballing. Next, he produces a curve with global warming “stopping in 2002”, but with another completely random choice of a break point in 2002. On yet another place on his same page, he suddenly produces this graph with a linear increase in temperatures:
http://www.climate4you.com/images/GlobalTemp%20HadCRUT3%20since1850%20LinearFit1908-2008%20C4Y.gif
where he now claims that “The whole warming period since 1908 may therefore bee seen as representing one single development, not showing a new trend corresponding to the rising atmospheric levels of carbon dioxide and other greenhouse gases after the mid-1970s”. Of course, all this is just “blog science”, which would likely have trouble getting past even the sleepy reviewers of this paper.
I would like to hear the opinion from Rasmus or anyone else taking a look at Humlum´s record: Does anybody seriously think that Humlum honestly believes all this internally contradictory stuff himself? Or that he, being a geology professor, really is legitimately unaware of the basics of the last 3-5 decades of carbon cycle research – which is something that most biology/geology undergraduates would readily know?
Personally, I think it is time for competent scientists in the field to publicly call Humlum by his appropriate name: a liar.
Christoffer Bugge Harder: Personally, I think it is time for competent scientists in the field to publicly call Humlum by his appropriate name: a liar.
More charitably, “crank.”
Leif at #30 wrote:
“People the world over readily accept the scientific fact that changing a patch of South Pacific from warm to cool by only a couple of degrees C, and the resulting comparatively narrow El Nino/La Nina current across the Equatorial Pacific to South America, can have a profound effect on the weather. Not only here in the United States, but to a lesser degree Europe and Africa.
On the other hand, transforming a much closer, (boarders in many cases), highly reflective patch of earth from significantly bellow freezing to dark open water above freezing, a difference of 10′s of degrees C and couple that with an area that is larger than India and it is just going to be no problem! Get real.”
Nice comparison, one I hadn’t thought of.
Doug Bostrom: It is perhaps not really that important, but to my mind, a crank is someone who has lost (or never possessed) contact to reality, typically either an overconfident Dunning-Krügerish amateur sometimes clearly suffering from a mental disorder like e.g Christopher Monckton, or an once-respected scientist like Nils-Axel Mörner, who strolled into dowsing and “Erdstrahlung” at some point nearing retirement – i.e, somebody whom you would recommend never to leave home without being properly equipped with a high-quality tinfoil hat.
In contrast, Humlum is a well respected (and, indeed, rightly so) scientist within his field, geomorphology, not nearing retirement, with no inclination towards conspiracy theories, and there is no indication that he has any special political or economic interests. He has published extensively about mineral sequestration and mountain formation which shows no lack of understanding of biogeochemical cycles.
I have occasionally heard, read and seen him in Denmark or Norway talking about different subjects, and I must say that when talking about his favourite canard of an oceanic source for the CO2 increase, he leaves a quite distinct impression that he does not really believe what he says. In many other aspects, he is reasonable and keen on acknowledging weaknesses and errors, and quotes peer-reviewed research. But when confronted with the obvious (but friendly posed) questions about how to reconcile his “CO2 increase driven by the oceans”-meme with the facts on isotopes and the oceans being a major net carbon sink, he suddenly turns to strange “common-sense” arguments. First, he just says that his “temperature drives CO2” argument did not necessarily have anything to do with the ocean being the source. When then asked about what the source for his temperature-driven CO2 increase might be if it were not the oceans, he then states something like “well, the oceans are the main carbon deposit, while the atmosphere is only an “intermediate deposit” – now wouldn´t you expect the main deposit to control the overall distribution”? When finally confronted with the basic fact that the oceans have, in fact, long been shown to actually have a net influx from the supposedly “intermediate deposit” in the atmosphere, he then just delves into sanctimonious rubbish about nature being so big and mankind so small and how there were many things we still did not know and how it was important to keep an open mind and maintain a nuanced debate etc. etc.
He is a perfect example of the kettle defense “I never borrowed it, I delivered it back in perfect condition, and by the way it was already broken when I first borrowed it”. Everybody rational realises that when one argues like this, one is out on a limb. Most of us have used this kind of defense occasionally when we suddenly find ourselves in a hole, but most people then quietly bow out and try to avoid broaching the subject again later. Humlum just repeats the same nonsense over again, year after year, apparently figuring that he will not be called in the next audience. I have no idea what his motivation might be, but he is neither an amateur, nor an obvious ideologue or a nutter. He speaks to an often numerate audience and he still has a reputation to think of. Therefore, I think that it would be appropriate to officially suggest – politely, calmly and clearly – that Ole Humlums arguments can be taken apart by simple textbooks on the carbon cycle (and often have been), that a skilled researcher of his class surely is aware of such basic facts, and that he thus most likely does not believe what he says himself. I might be naive, but it might just force him out of the hole to publicly show that he has no clothes, and make the media interested in looking beyond the annoying “brave heretic”-framing.
I would be very interested in hearing other views/experiences on this.
This comes from a non-scientist who appreciates your site’s focus on facts.
I’m in California and we watch the ENSO report closely. There’s been a nice correlation between the existence of El Nino conditions and wet winters for our area. Much of California is semi-desert and this is a big deal for us.
As you know El Nino arises when a relatively small patch of the Pacific is warmer that usual. Apparently it works to direct the jetstream farther south than usual.
My question for you folks is this: with AGW acting on the oceans, are we likely to see El Nino conditions more often in the future (i.e., generalized warming translating into localized warming)? Is this why the long-term climate models show less future aridity for California than for the rest of the U.S. Southwest?
Science and geography is great combination to explain this issue.
The Humlun paper came up at Taminos, and I commented there re “…changes in atmospheric CO2 are not tracking changes in human emissions.” I downloaded Mauna Loa CO2 from http://www.woodfortrees.org/data/esrl-co2/mean:12/from:1959.7/every:12 and anthropogenic CO2 emissions from http://co2now.org/images/stories/graphics/carbon-budget/global-carbon-budget-2009-data-co2now.pdf, and found that the correlation between Mauna Loa CO2 and 315 + 0.21 * CO2E is 0.99948496, with a 95% confidence interval of 0.9991 to 0.9997 – whadda they want, 6 nines?
This paper is waste of energy. The same result it is enough to look at Keeling curve. During NH Summer the CO2 levels are going down while emissions continue so it is obvious that ” changes in atmospheric CO2 are not tracking changes in human emissions”. It is the same logic of using small perturbation to understand the main phenomena.
37 sbripman asked, “with AGW acting on the oceans, are we likely to see El Nino conditions more often in the future”
I’m also a layman, but I’ll note that you’re looking at a specific result of El Nino which applies when the arctic sea ice is intact and temps are as they are today. Change those two things, and I’m not sure the link between El Nino and your precipitation will remain. Scientists here and elsewhere have stressed that regional results are wicked hard to predict. Other than that, I’ll join you in awaiting more expert opinion.
Cant believe it… how could have this article go through review process? I almost tend to think about a kind of conspiracy theory… lets give an analogy.
Let’s suggest I have a cancer. As a result of it I fall down more often than before, and this falling causes increasing blood pressure. When I get up, blood pressure goes down. However, with increasing frequency of falling, my blood pressure goes through the roof after several years, until I die. However, doctor would conclude, that cancer has nothing to do with long-lerm increasing blood pressure, since I was falling before, and blood pressure went up too!
That is crazy…. right?
#36 Christoffer Bugge Harder:
I think I came across some “lukewarmish” site of Humlum some years ago…. thank You for this insightful elucidation of some skandinavian insider knowlege.
All the best,
Marcus
Hi Rasmus: if they don’t agree to share their data, you can always try an FOI request.
I think you are nitpicking. You only identify weakness in 4 aspects of the paper, “the analysis, the physics, reviewing past literature, and logic”. You should give them credit for things they did right, like spelling their own names.
I am amazed that this nonsense was published in an otherwise reputable peer-reviewed journal. Is it worth writing a “Comments on…” for submission, or is this a case where the less attention paid the better?
#41 Jim Larsen says: “you’re looking at a specific result of El Nino which applies when the arctic sea ice is intact and temps are as they are today. Change those two things, and I’m not sure the link between El Nino and your precipitation will remain.”
Thank you for helping me to a broader perspective.
It seems to me that the simplist challange to this paper is the math of the C02 going in and out of the atmosphere as shown at:
http://www.globalcarbonproject.org
2009
“Fuel sources contributed 30.8 gtons CO2
Land use changes contributed4.0 gtons CO2
Land and ocean sinks removed 57%
Humans added 3.7ppm to the atmosphere
Land and ocean sinks removed 2.1ppm
Atmospheric CO2 increased 1.6ppm
2010
Emissions from fossil fuel and cement
Fossil fuel CO2 emissions increased by 5.9% in 2010, with a total of 9.1±0.5 PgC emitted to the atmosphere (33.4 Pg of CO2; 1 Pg = 1 billion tons or 1000 x million tons). These emissions were the highest in human history and 49% higher than in 1990 (the Kyoto reference year). Coal burning was responsible for 52% of the fossil fuel emissions growth in 2010 (gas 23% and liquid 18%). Read
CO2 removal by natural sinks
Natural land and ocean CO2 sinks removed 56% of all CO2 emitted from human activities during the 1958-2010, each sink in roughly equal proportion. During this period, the size of the natural sinks has grown almost at the same pace as the growth in emissions, although year-to-year variability is large. There is the possibility, however, that the fraction of all emissions remaining in the atmosphere has a positive trend due to changes in emissions growth rate and decline in the efficiency of natural sinks.”
There is variability in the ocean uptake of C02, but this should not be confused with the ocean being the source of C02.
This explains it all.
http://www.youtube.com/watch?v=ARJK0MWAITM&feature=related
We are talking about a super short period of monitoring at the 1000hPa level, correct?
It may behoove us to determine the levels up to 10hPa, wouldn’t it?
Several sensors dropped to the bottom of the ocean systems, measuring temperature and constituent levels wouldn’t be a bad idea either.
“We are talking about a super short period of monitoring at the 1000hPa level, correct?”
No, Not correct.