Absolute temperatures and relative anomalies

Most of the images showing the transient changes in global mean temperatures (GMT) over the 20th Century and projections out to the 21st C, show temperature anomalies. An anomaly is the change in temperature relative to a baseline which usually the pre-industrial period, or a more recent climatology (1951-1980, or 1980-1999 etc.). With very few exceptions the changes are almost never shown in terms of absolute temperatures. So why is that?

There are two main reasons. First of all, the observed changes in global mean temperatures are more easily calculated in terms of anomalies (since anomalies have much greater spatial correlation than absolute temperatures). The details are described in the previous link, but the basic issue is that temperature anomalies have a much greater correlation scale (100’s of miles) than absolute temperatures – i.e. if the monthly anomaly in upstate New York is a 2ºC, that is a good estimate for the anomaly from Ohio to Maine, and from Quebec to Maryland, while the absolute temperature would vary far more. That means you need fewer data points to make a good estimate of the global value. The 2 uncertainty in the global mean anomaly on a yearly basis are (with the current network of stations) is around 0.1ºC in contrast that to the estimated uncertainty in the absolute temperature of about 0.5ºC (Jones et al, 1999).

As an aside, people are often confused by the ‘baseline period’ for the anomalies. In general, the baseline is irrelevant to the long-term trends in the temperatures since it just moves the zero line up and down, without changing the shape of the curve. Because of recent warming, baselines closer to the present will have smaller anomalies (i.e. an anomaly based on the 1981-2010 climatology period will have more negative values than the same data aligned to the 1951-1980 period which will have smaller values than those aligned to 1851-1880 etc.). While the baselines must be coherent if you are comparing values from different datasets, the trends are unchanged by the baseline.

Second, the absolute value of the global mean temperature in a free-running coupled climate model is an emergent property of the simulation. It therefore has a spread of values across the multi-model ensemble. Showing the models’ anomalies then makes the coherence of the transient responses clearer. However, the variations in the averages of the model GMT values are quite wide, and indeed, are larger than the changes seen over the last century, and so whether this matters needs to be assessed.

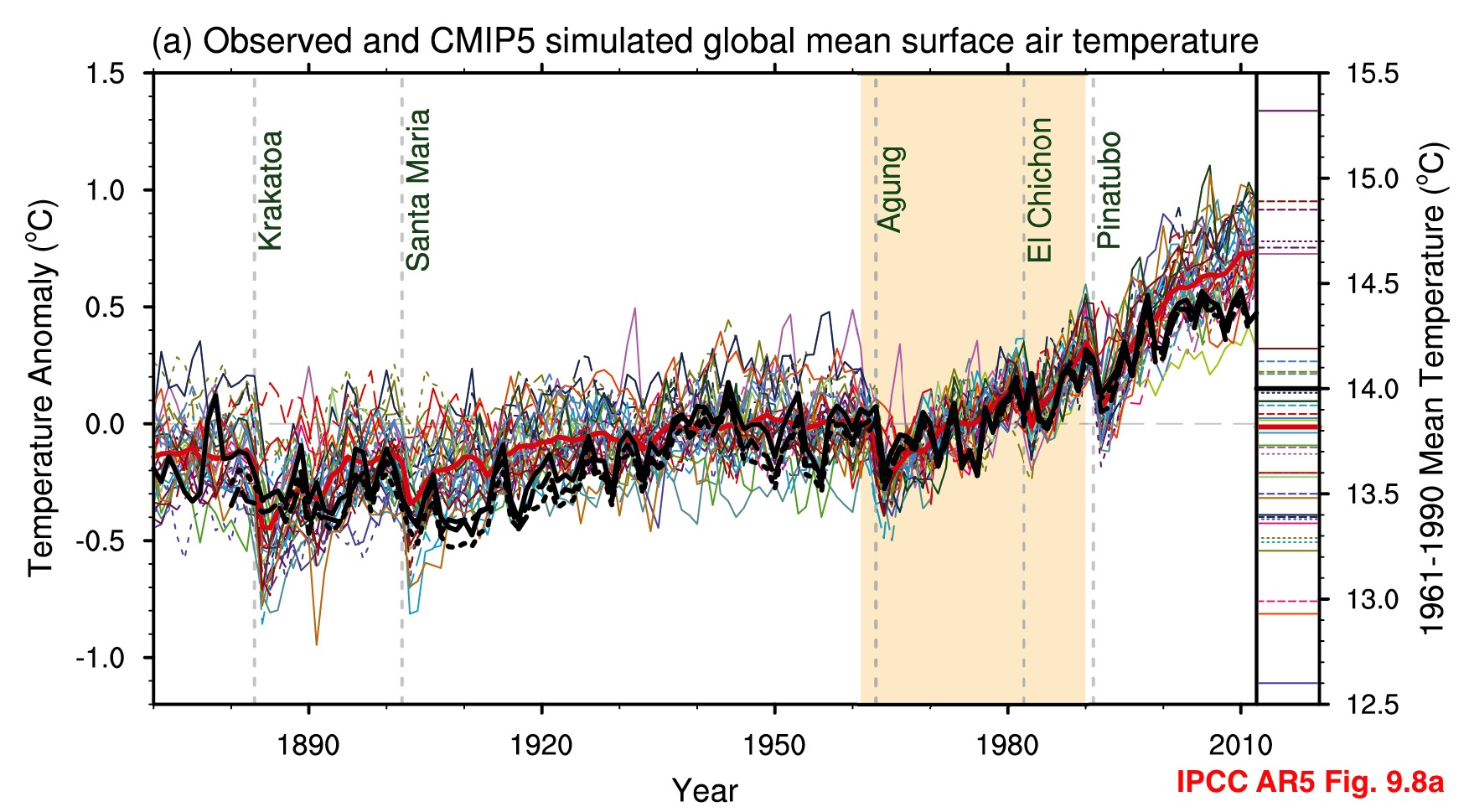
IPCC figure showing both anomalies as a function of time (left) and the absolute temperature in each model for the baseline (right)

Most scientific discussions implicitly assume that these differences aren’t important i.e. the changes in temperature are robust to errors in the base GMT value, which is true, and perhaps more importantly, are focussed on the change of temperature anyway, since that is what impacts will be tied to. To be clear, no particular absolute global temperature provides a risk to society, it is the change in temperature compared to what we’ve been used to that matters.

To get an idea of why this is, we can start with the simplest 1D energy balance equilibrium climate model:

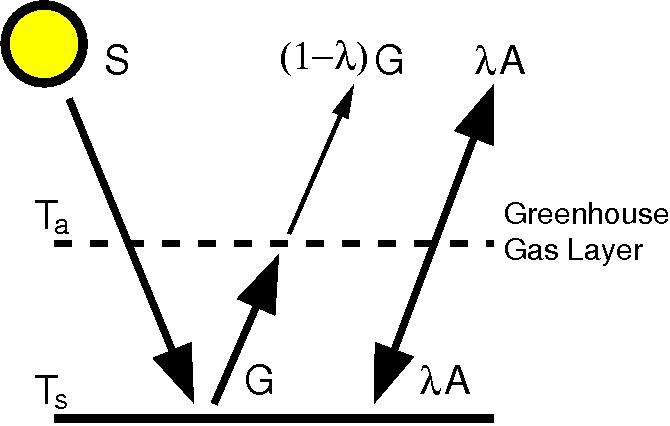
In the illustrated example, with S=240 W/m² and =0.769, you get a ground temperature () of 288 K (~15ºC). For the sake of argument, let’s assume that is the ‘truth’. If you (inaccurately) estimate that = 0.73, you get =286K – an offset (error) of about 2K. What does that imply for the temperature sensitivity to a forcing? For a forcing of 4 W/m2 (roughly equivalent to doubling CO₂), the change in in the two cases (assuming no feedbacks) is an almost identical 1.2 K. So in this case, the sensitivity of the system is clearly not significantly dependent to small changes in GMT. Including a temperature feedback on would change the climate sensitivity, but doesn’t much change the impact of a small offset in . [Actually, I think this result can be derived quite generally based just on the idea that climate responses are dominated by the Planck response while errors in feedbacks have linear impacts on ].

Full climate models also include large regional variations in absolute temperature (e.g. ranging from -50 to 30ºC at any one time), and so small offsets in the global mean are almost imperceptible. Here is a zonally averaged mean temperature plot for six model configurations using GISS-E2 that have a range of about 1ºC in their global mean temperature. Note that the difference in the mean is not predictive of the difference in all regions, and while the differences do have noticeable fingerprints in clouds, ice cover etc. the net impact on sensitivity is small (2.6 to 2.7ºC).

We can also broaden this out over the whole CMIP5 ensemble. The next figure shows that the long term trends in temperature under the same scenario (in this case RCP45) are not simply correlated to the mean global temperature, and so, unsurprisingly, looking at the future trends from only the models that do well on the absolute mean doesn’t change very much:

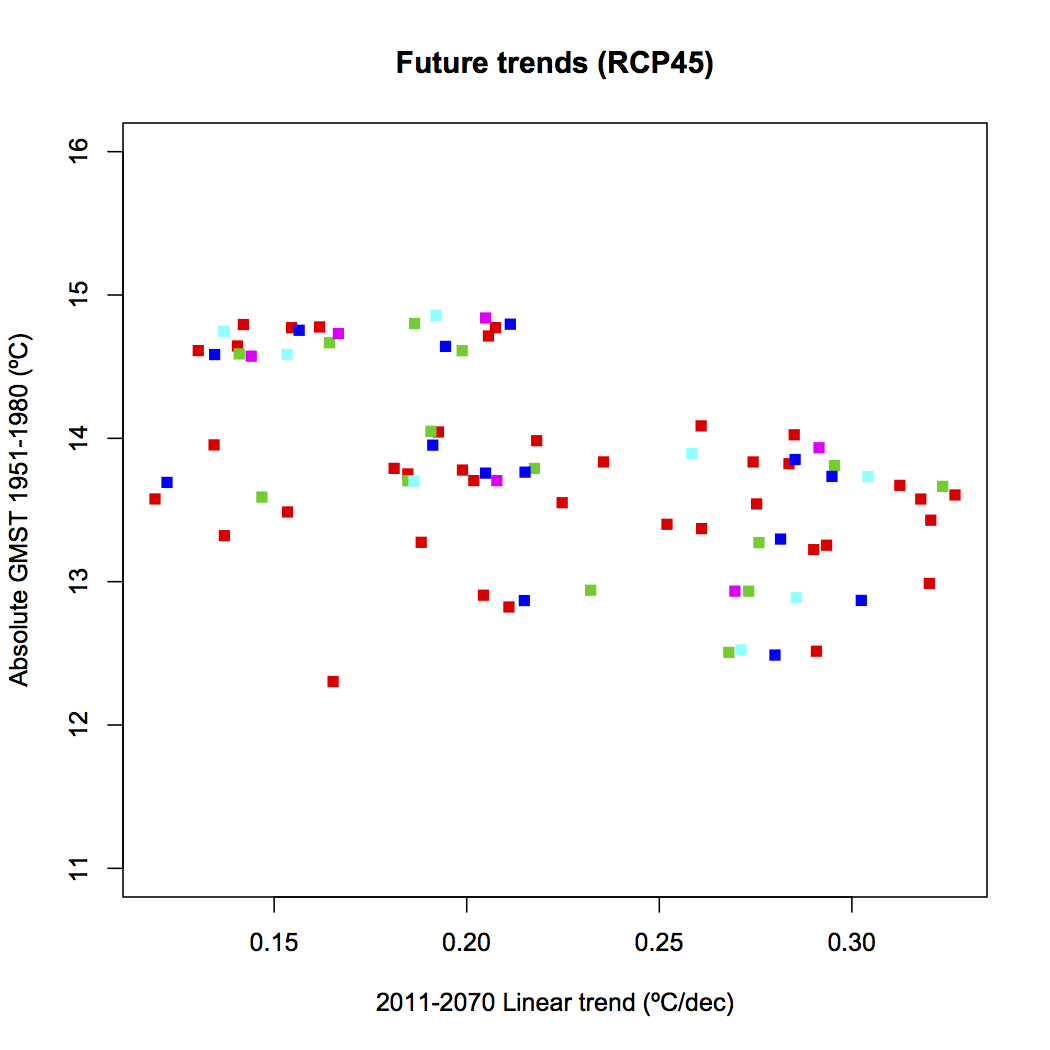
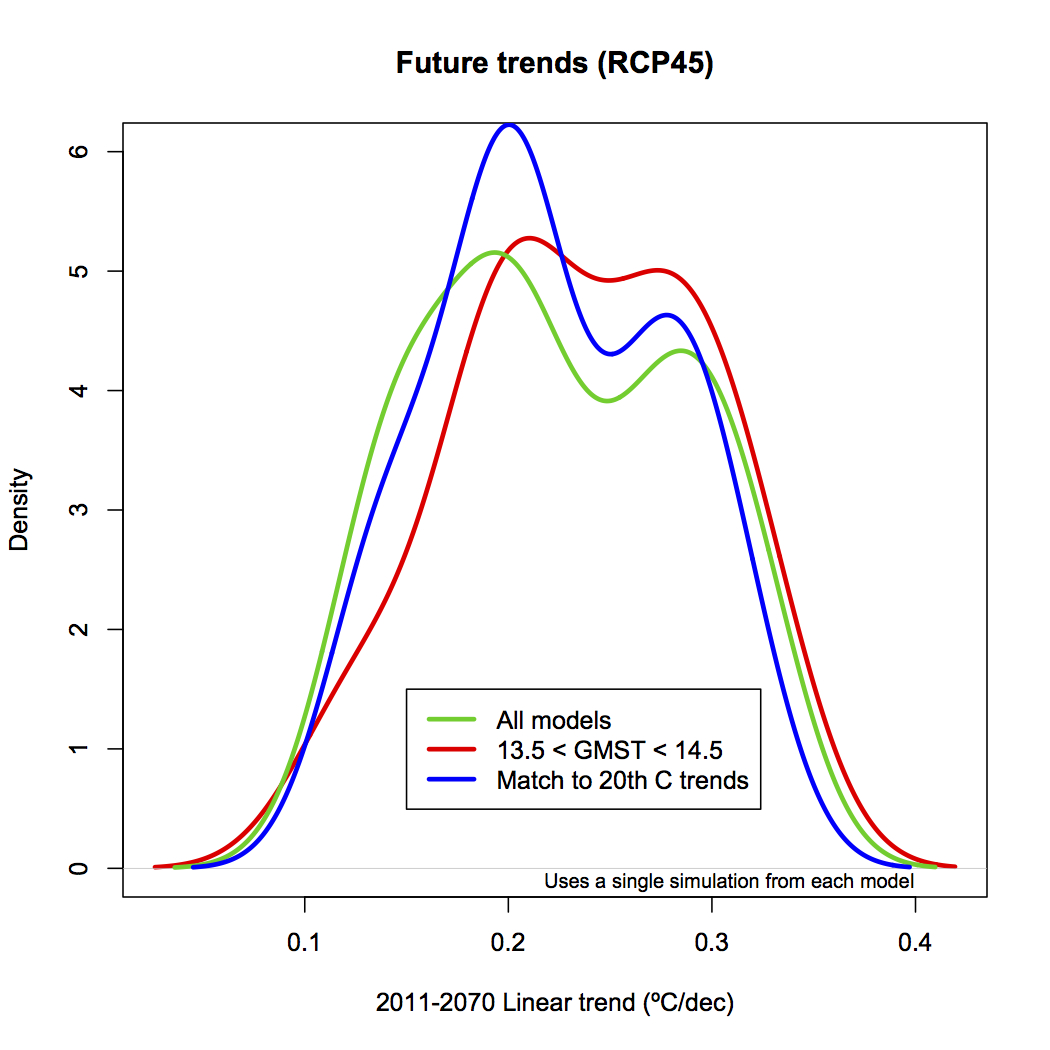
A) Correlation of absolute temperatures with trends in the future across the CMIP5 ensemble. Different colors are for different ensemble members (red is #1, blue is #2, etc.). B) Distribution of trends to 2070 based on different subsets of the models segregated by absolute temperatures or 20th Century trends.

So, small (a degree or so) variations in the global mean don’t impact the global sensitivity in either toy models, single GCMs or the multi-model ensemble. But since there are reasonable estimates of the real world GMT, it is a fair enough question to ask why the models have more spread than the observational uncertainty.

As mentioned above, the main problem is that the global mean temperature is very much an emergent property. That means that it is a function of almost all the different aspects of the model (radiation, fluxes, ocean physics, clouds etc.), and any specific discrepancy is not obviously tied to any one cause. Indeed, since there are many feedbacks in the system, a small error somewhere can produce large effects somewhere else. When developing a model then, it is far more useful to focus on errors in more specific sub-systems where further analysis might lead to improvements in that specific process (which might also have a knock on effect on temperatures). There is also an issue of practicality – knowing what the equilibrium temperature of a coupled model will be takes hundreds of simulated years of “spin-up”, which can take months of real time to compute. Looking at errors in cloud physics, or boundary layer mixing or ice albedo can be done using atmosphere-only simulations which take less than a day to run. It is therefore perhaps inevitable that the bounds of ‘acceptable’ mean temperatures in models is broader than the observational accuracy.

However, while we can conclude that using anomalies in global mean temperature is reasonable, that conclusion does not necessarily follow for more regional temperature diagnostics or for different variables. For instance, working in anomalies is not as useful for metrics that are bounded, like rainfall. Imagine that models on average overestimate rainfall in an arid part of the world. Perhaps they have 0.5 mm/day on average where the real world has 0.3 mm/day. In the projections, the models suggest that the the rainfall decreases by 0.4 mm/day – but if that anomaly was naively applied to the real world, you’d end up with an (obviously wrong) prediction of negative rainfall. Similar problems can arise with sea ice extent changes.

Another problem arises if people try and combine the (uncertain) absolute values with the (less uncertain) anomalies to create a seemingly precise absolute temperature time series. Recently a WMO press release seemed to suggest that the 2014 temperatures were 14.00ºC plus the 0.57ºC anomaly. Given the different uncertainties though, adding these two numbers is misleading – since the errors on 14.57ºC would be ±0.5ºC as well, making a bit of a mockery of the last couple of significant figures.

So to conclude, it is not a priori obvious that looking at anomalies in general is sensible. But the evidence across a range of models shows that this is reasonable for the global mean temperatures and their projections. For different metrics, more care may need to be taken.

References

1. P.D. Jones, M. New, D.E. Parker, S. Martin, and I.G. Rigor, "Surface air temperature and its changes over the past 150 years", Reviews of Geophysics, vol. 37, pp. 173-199, 1999. http://dx.doi.org/10.1029/1999RG900002