What is the uncertainty in the Earth’s temperature rise?

Guest commentary by Shaun Lovejoy (McGill University)

Below I summarize the key points of a new Climate Dynamics (CD) paper that I think opens up new perspectives on understanding and estimating the relevant uncertainties. The main message is that the primary sources of error and bias are not those that have been the subject of the most attention – they are not human in origin. The community seems to have done such a good job of handling the “heat island”, “cold park”, and diverse human induced glitches that in the end these make only a minor contribution to the final uncertainty. The reason of course, is the huge amount of averaging that is done to obtain global temperature estimates, this averaging essentially averages out most of the human induced noise.

Two tough sources of uncertainty remain: missing data and a poor definition of the space-time resolution; the latter leads to the key scale reduction factor. In spite of these large low frequency uncertainties, at centennial scales, they are still only about 13% of the IPCC estimated anthropogenic increase (with 90% certainty).

This paper is based on 6 monthly globally averaged temperature series over the common period 1880-2012 using data that were publically available in May 2015. These were NOAA NCEI, NASA GISTEMP, HadCRUT4, Cowtan and Way, Berkeley Earth and the 20th Century Reanalysis. In the first part on relative uncertainties, the series are systematically compared with each other over scales ranging from months to 133 years. In the second part on absolute uncertainties, a stochastic model is developed with two parts. The first simulates the true temperatures, the second treats the measurement errors that would arise from this series from three different sources of uncertainty: i) usual auto-regressive (AR)-type short range errors, ii) missing data, iii) the “scale reduction factor”.

The model parameters are fit by treating each of the six series as a stochastic realization of the stochastic measurement process. This yields an estimate of the uncertainty (spread) of the means of each series about the true temperature – an absolute uncertainty – not simply the spread of the series means about their common mean value (the relative uncertainty). This represents the absolute uncertainty of the series means about a (still unknown) absolute reference point (which is another problem for another post).

Key science

1. The usual uncertainties have short-range auto-regressive correlations, so that when averaged over long enough periods, the differences between series will eventually be close to white noise. This is presumably the main type of error that we could expect if there were the usual human glitches caused by changing station locations, technologies and the like; the usual sources of human bias. The corresponding fluctuations fall off relatively rapidly with time interval t: as t^-1/2. This type of behaviour is never observed even at scales of a century (see figs. 1, 2; Haar fluctuations were used, see the note at the bottom). If this type of error were indeed dominant, then the centennial scale differences between the series would be about ±0.005^oC, which is about ten times smaller than those we calculate.


Fig. 1: The Root Mean Square (RMS) Haar fluctuations (structure functions S(t)) averaged over the six series (top), averaged over all the 15 pairs of differences (second from top), averaged over the differences of each with respect with the overall mean of the six series (third from top), and the standard deviation of the S(t) curves evaluated for each of the series separately (bottom). Also shown for reference (dashed) is the line that data with independent Gaussian noise would follow (Adapted from fig. 2).


Fig. 2: The top set of curves (solid) are S(t) for each of the different series, the bottom set (dashed) are the differences of each with respect to the mean of all the others: NOAA dark purple, NASA (brown), HadCRUT4 (green), Cow (blue), 20CR (orange), Berkeley Earth (red) (indicated at the left in the order of the curves). Adapted from fig. 3 of CD.

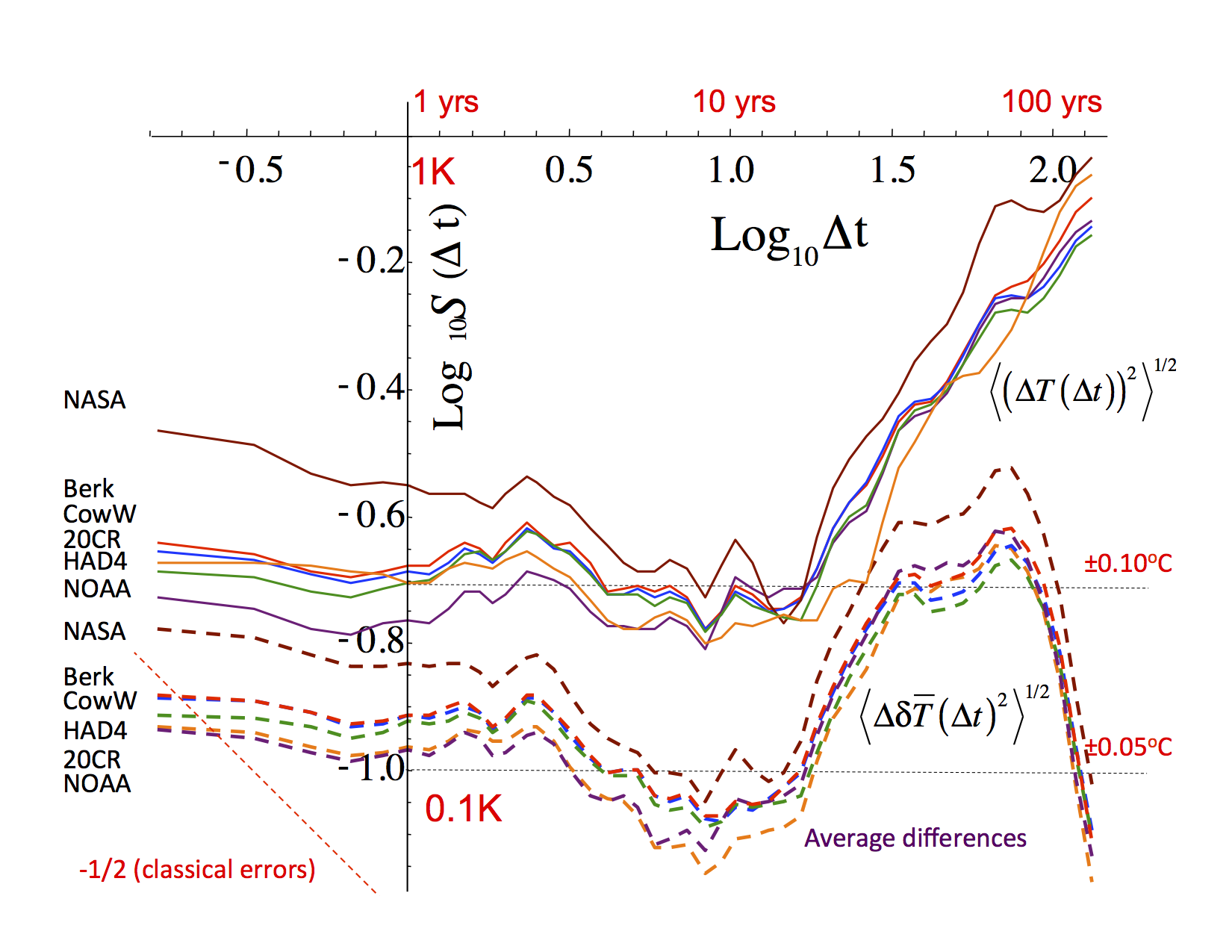
2. All the series seemed to be both statistically very similar to each other and each was pretty much equally distant from the mean of all the others (i.e. equally similar or dissimilar to each other, depending on your view). Significantly, this included the 20th Century Reanalysis (20CR) that didn’t use any land temperature station data whatsoever (fig. 2) and even turned out to be the closest (with NOAA) to the mean of all the others!
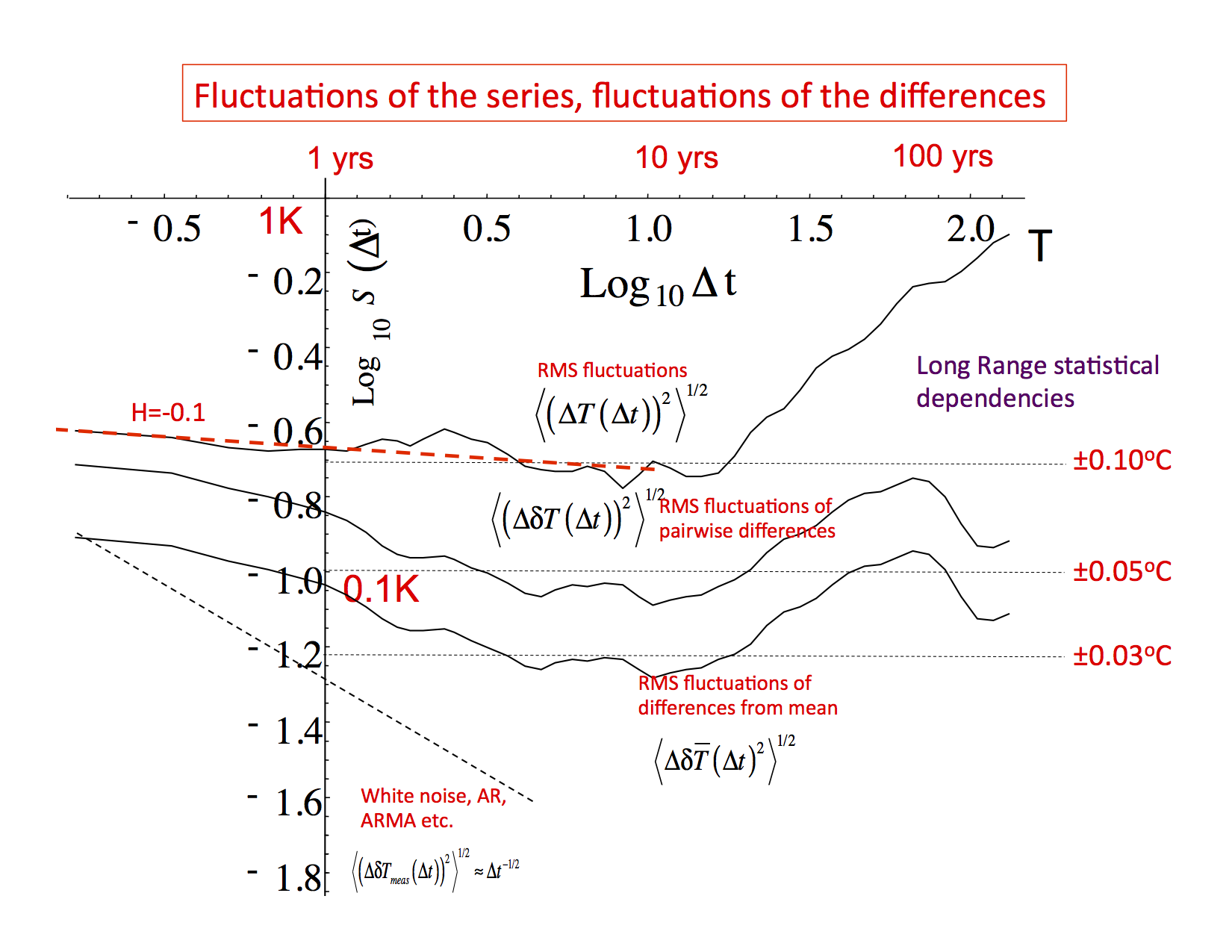
3. Up until a scale of about 10 years (the “macroweather” regime), the fluctuations in the series and in the differences between the series have different amplitudes (the ratio is between 2 and 3), but both are scaling with roughly the same fluctuation exponent H ≈ -0.1 (fig. 1, 2).   This implies strong long-range statistical dependencies (long range memories) in both the series themselves and in their differences. The obvious interpretation is that over this range of scales that each of the series are missing data (typically about 50% of pixels have no data), but each series misses somewhat different data.
4. For scales longer than about 10 years, the global temperature fluctuations begin to increase with time scale: the internal macroweather variability is increasingly dominated by low frequency changes due to anthropogenic warming: this is the beginning of the climate regime. At the same time, the fluctuations in the differences between the series stops following the fluctuations in the series themselves, leveling off at about ±0.05^oC (fairly independently of the time scale). This is a kind or irreducible uncertainty (figs. 1, 2).
5. These differences below about (10 yrs)^-1, can be explained by poorly defined space-time data resolutions. Fig. 4 in CD shows that the amplitudes of the fluctuations are quite sensitive to the amount of space-time averaging and they systematically decrease with the averaging scale according to somewhat different exponents in both space and in time.

   Let’s say that the basic data were gridded at 5^o resolution in space and at one month in time.  In that case, there is a typical amplitude of 5^o x 5^o x 1 month space-time temperature fluctuation, but since there are generally insufficient data in each 5^o x 5^o x 1 month “space-time box” they are not perfectly estimated, there is not enough data to sufficiently average it over the nominal space-time scales. Because the fluctuation exponents in fig. 3 (in both and in time) are negative, this implies that the amplitudes of the fluctuations are spuriously large by a multiplicative factor that depends on the difference between the actual “effective” resolution and the nominal resolution (5^o x 5^o x 1 month). This is the origin of the scale reduction factor and it has the particularity of being multiplicative: it affects all scales. This is the dominant source of error at scales beyond a decade. It gives the dominant contribution to errors in estimating anthropogenic warming.

   This effect is actually familiar to long-range forecasters who routinely “rescale” model outputs so that the amplitude of the model internal variability is realistic when compared to empirical temperatures. The scale reduction factor is simply the same mechanism but applied to the empirical series themselves.

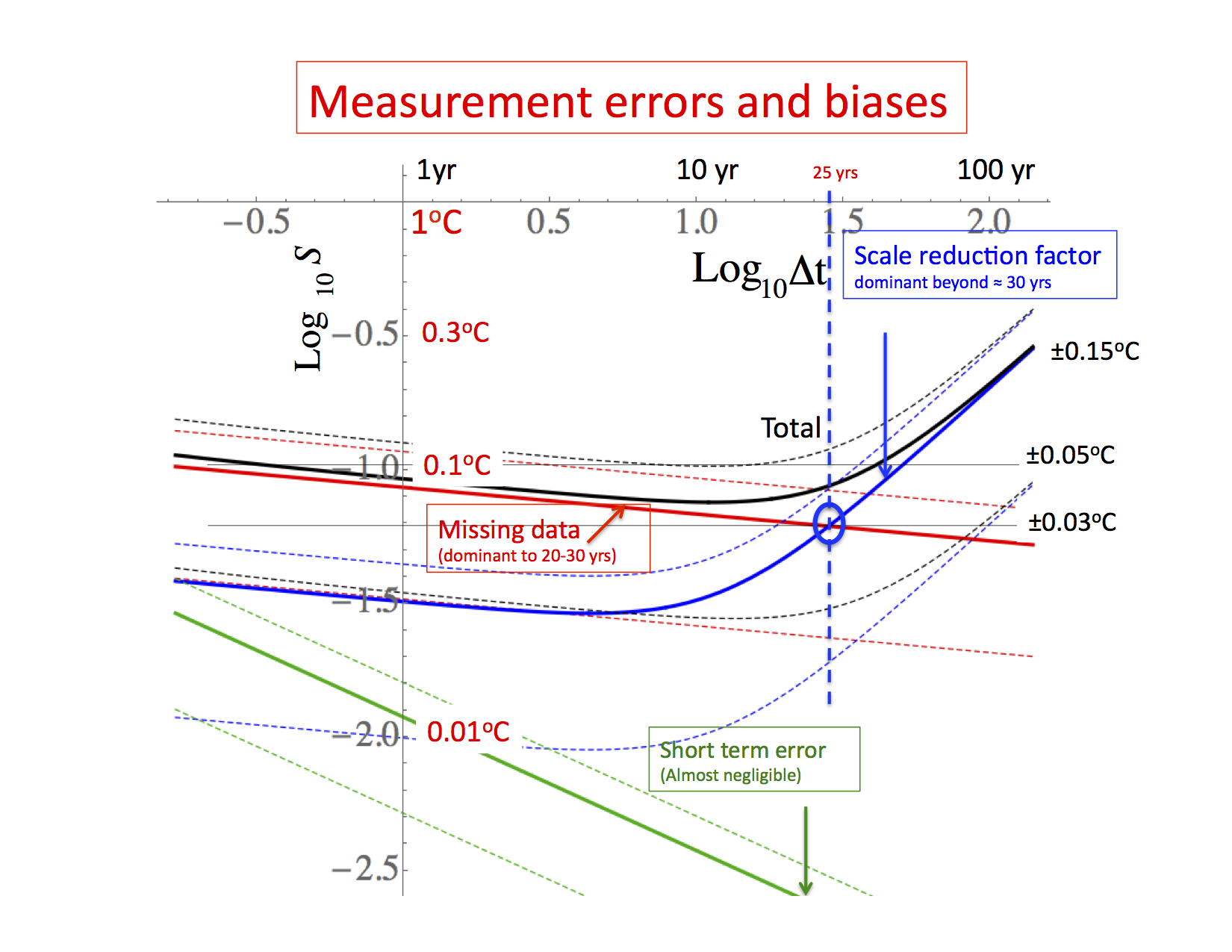
6. In order to go beyond relative errors estimated via the series to series differences, to obtain the absolute errors, we constructed a simple stochastic model (fig. 4) of both the actual temperature and the three sources of error: the classical short range error, the missing data term and the scale reduction factor. Using statistical analysis of the fluctuations of the series to series differences, we estimated the statistics of the amplitudes from each contribution (fig. 5). The key results of the paper follow, notably:
   • Up to 10 years, missing data was the main source of error: 15±10% of the temperature variance. The ±10% about the 15% refers to series to series variation in the amount of missing data (these are one standard deviation limits).
   • After ten years, the scale reduction factor was dominant giving an error of 11%±8% error. This is the main source of centennial scale error.
   • Overall, with 90% confidence it was found that the true temperature lies in the range -0.11^oC to 0.13^oC of the reported monthly values (90% confidence).
   • Overall: the change since the 19^th century can be estimated with nearly the same uncertainty as for the monthly value: ±0.11^oC (90% confidence).
   • This uncertainty is much higher than conventional (AR type) approaches predict, (about ±0.005^oC).
   • All of these numbers are much smaller than the roughly 1^oC of warming that has occurred since the 19^th century, so that we can be quite confident of the magnitude of the warming.

   
   Fig. 3: The RMS fluctuations (structure functions, S) of the various measurement errors with one standard deviation limits shown as dashed lines (corresponding the variation from one measurement series to another). The blue curve is the contribution of the scale reduction factor, the red is from missing data (slope = H = -0.1) and the green is the short-range measurement error (slope -1/2). The black curve is the sum of all the contributions. Notice that most of the contributions to the errors are from the scaling parts. These Haar structure functions have been multiplied by a canonical factor of 2 so that the fluctuations will be closer to the anomalies (when decreasing) or differences (when increasing). Note that these show essentially the difference between the true earth temperature and the measurements; the difference between two different measured series will have double the variances, the difference structure function should thus be increased by a further factor 21/2 before comparison with fig. 2, 3 or the figures below. Adapted from fig. 6 of CD.

7. The stochastic model was able to closely reproduce not only the temperature statistics but also the differences between series, and this at all scales from one month of > 100 yrs. This is a strong validation (see figs. 9, 10, 11 of CD).
8. The 20CR series is not based on anomalies but absolute temperatures, yet it was statistically just as close to the others as if it had been based on anomalies. We can therefore use it to determine the absolute temperature of the earth; the error estimates in the above paragraph will hold.