Many of you will have seen the obituaries (MIT, NYT) for Ed Lorenz, who died a short time ago. Lorenz is most famous scientifically for discovering the exquisite sensitivity to initial conditions (i.e. chaos) in a simple model of fluid convection, which serves as an archetype for the weather prediction problem. He is most famous outside science for the ‘The Butterfly Effect’ described in his 1972 paper “Predictability: Does the Flap of a Butterfly’s Wings in Brazil Set Off a Tornado in Texas?”. Lorenz’s contributions to both atmospheric science and the mathematics of dynamical systems were wide ranging and seminal. He also directly touched the lives of many of us here at RealClimate, and both his wisdom, and quiet personal charm will be sorely missed.
Ed Lorenz had a reputation of being shy and quiet, and this was indeed the impression he gave on first meeting. Indeed raypierre was interviewed by Ed at MIT in 1979 for his first faculty job — and remembers having to ask most of the questions as well as answer them. But he also remembers a lot of timely support from Ed that helped smooth over the somewhat rocky transition from basic turbulence theory to atmospheric science. The longer you were around Ed, the more you came to appreciate his warmth and sense of humor. He was an avid hiker, and many in the community (our own Mike Mann included) have recollections of time on the trail with him around the hills of Boulder and elsewhere.
Lorenz launched the modern era of the study of chaotic systems, which has profound implications both within and beyond atmospheric science. We’ll say more about that in a bit, but the monumental work on chaos should not leave Lorenz’s other contributions to atmospheric science completely in its shadow. For example, in a 1956 MIT technical report, Ed introduced the notion of “empirical orthogonal functions” to atmospheric science, and this technique now plays a central role in diagnostic studies of the atmosphere-ocean system. He also pioneered the study of angular momentum transport in the atmosphere, and of atmospheric energetics. Among other things, he introduced the important notion of “available potential energy,” which quantifies the fact that not all of the potential energy can be tapped by allowable rearrangements of the atmosphere. Later, he pioneered the concept of resonant triad instability of atmospheric waves, an idea that has repercussions for the sources of atmospheric low frequency variability. As if that weren’t enough Ed also introduced the concept of the “slow manifold” — a special subset of solutions to a nonlinear system which evolve more slowly than most solutions. The atmospheric equations support a lot of very quickly changing solutions, like sound waves and gravity waves, but on the whole what we think of as “weather” or “climate” involves more ponderous motions evolving on time scales of days to years. Ed’s work on this subject launched the study of how such slowly evolving solutions can exist, and how to initialize a numerical model so as to minimize the generation of the fast transients. This is now part and parcel of the whole apparatus of data assimilation and numerical weather forecasting.
Ed was not a user of general circulation models. His essential approach was to crystallize profound phenomena into very small sets of equations for how a handful of variables change with time. He left behind him a dozen or so such models, each of which would repay many lifetimes of study. He was indeed a master of “seeing the world in a grain of sand.” You can read about some of these models in the talk raypierre gave at the 1987 Lorenz ‘retirement’ symposium — not that this slowed him down!
Now let’s take a closer look at that butterfly effect. Despite the fact that there are no butterflies or tornadoes in climate models, Lorenz’s discoveries and their implications played a central role in climate modelling efforts and in the most recent IPCC report.
The notion of the butterfly effect itself was drawn from a simple but astute observation of the way the solutions of certain nonlinear equations behave when they are solved using a computer. Start with a greatly simplified representation of thermal convection, first formulated by Barry Saltzman using a technique called “low order modelling.” If you run a simulation using these equations and then try and replicate it using starting values that only differ in the last decimal place, you will find that the simulations quickly diverge from one another – and by quickly, it means that the differences grow exponentially fast. Lorenz found this phenomenon by accident, but quickly recognised the profound implications. If the real weather system displayed the same behaviour, it meant that since however well one knew the initial conditions of the atmosphere, there would always be some uncertainty, that uncertainty would be quickly magnified, rendering weather forecasts useless after a few exponential doubling times. The practical implication is that – even if you had a perfect model – for every halving of the error in the initial conditions you only get one extra time period of useful forecast. Given this time period is only a few hours in many cases, the practicality of true weather forecasts for periods longer than two weeks or so, is vanishingly small.
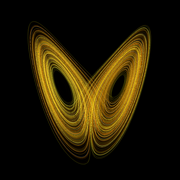
The mathematically inclined reader who takes a look at Ed’s early papers on what is now called the “Lorenz Attractor” will be astonished at the depth and modernity of his ideas about chaos. This line of work was no mere remark on a numerical exercise. Lorenz actually teased out the geometry of chaos — the many-leaved structure of the attractor — realizing that it was no simple geometric entity like a sphere or a folded sheet of paper. It was indeed “strange” in a sense which he made geometrically precise. This is why the work had such lasting impact on the area of pure mathematics known as dynamical systems theory. He went beyond that to develop or apply many fundamental concepts in chaotic systems, quantitatively formulating various measures of predictability and connecting the Lyapunov exponent — a certain precise mathematical characterization of chaos — with the structure of strange attractors. But that’s for the mathematicians. What makes Lorenz’s work interesting to the entity on the Clapham omnibus is the notion of sensitive dependence on initial conditions. Some have even seen in this deterministic chaos the resolution to the problem of free will!
The idea that small causes can have large and disproportionate effects is not at all new of course. The poem: “For the want of a nail, the battle was lost” (medieval in origin) encapsulates that well, and popular culture is full of such examples, “It’s a wonderful life” (1946) and Ray Bradbury’s “A Sound of Thunder” (1952) for instance. Curiously, Bradbury’s story also involves a butterfly, and since it predates Lorenz’s coining of the phrase by a decade or so, people have speculated that there was a connection to Lorenz’s choice of metaphor (he started off with a seagull in his 1963 Trans. N.Y. Ac. Sci. paper). But that doesn’t appear to be the case (see here for a history). It’s worth adding that all of Lorenz’s papers were exceptional in their clarity and are well worth tracking down as an example of science writing at its best.
However, the difference between the long-standing popular conception and Lorenz’s work is that he demonstrated this effect in a completely deterministic system with no random component. That is, even in a perfect model situation, useful predictability can be strongly limited. Strictly speaking, Poincaré first described this effect in the classic three-body problem in the early 1900s, but it was only with the onset of electronic computers, as used by Lorenz, that this became more widely recognised. To throw in another popular culture reference, Tom Stoppard’s Arcadia has a character, Septimus, who drives himself mad trying to calculate chaotic solutions to the logistic map by hand.
So what does this have to do with the IPCC?
Even though the model used by Lorenz was very simple (just three variables and three equations), the same sensitivity to initial conditions is seen in all weather and climate models and is a ubiquitous phenomenon in many complex non-linear flows. It is therefore usually assumed that the real atmosphere also has this property. However, as Lorenz himself acknowledged in 1972, this is not directly provable (and indeed, at least one meteorologist doesn’t think it does even though most everyone else does). Its existence in climate models is nonetheless easily demonstratable.
But how can climate be predictable if weather is chaotic? The trick lies in the statistics. In those same models that demonstrate the extreme sensitivity to initial conditions, it turns out that the long term means and other moments are stable. This is equivalent to the ‘butterfly’ pattern seen in the figure above being statistically independent of how you started the calculation. The lobes and their relative position don’t change if you run the model long enough. Climate change then is equivalent seeing how the structure changes, while not being too concerned about the specific trajectory you are on.
Another way of saying it is that for the climate problem, the weather (or the individual trajectory) is the noise. If you are trying to find the common signal that is a signature of a particular forcing then averaging over a number of simulations with different weather works rather well. (There is a long standing quote in science – “one person’s noise is another person’s signal” which is certainly apropos here. Climate modellers don’t average over ensemble members because they think that weather isn’t important, they do it because it gives robust estimates of the signal they are usually looking for.)
The ensemble approach, and indeed the multi-model ensemble approach, used in IPCC then derives directly from Lorenz’s insights into his serendipitous numerical problem.
Re: #101 As a matter of fact if you search on PubMed http://www.ncbi.nlm.nih.gov/pubmed/ there are four articles with my name. In two of them I appear as first author. And no, they are not first-rated earth-shattering Science or Nature articles about climate science.
But as we all agree now, that’s beside the point.
Let’s me start again from a simple question. Hansen et al did compare model results to observations.
“Climate simulations for 1880–2003 with GISS modelE”, Clim Dyn (2007) 29:661–696 – DOI 10.1007/s00382-007-0255-8
For example, consider fig. 9 (the PDF of the article is on the internet, apologies but I do not have time to search for it right now):
“Fig. 9 Global maps of temperature change in observations (top row)
and in the model runs of Fig. 8, for 1880–2003 and several
subperiods. […]”
Observations there are shown in periods respectively of 124 years (1880-2003), 54 years, 61 years, 40 years and finally 25 years (1979-2003).
Presumably, this provides a first approximation of what time spans are needed to talk about climate (around 25 years). The actual shortest period may be 40 years or longer, as 1979-2003 has been chosen primarily as “the era of extensive satellite observations”. Please correct me if am wrong.
Let’s take now a clear-cut example. The authors write “All forcings together yield a global mean warming ~0.1C less than observed for the full period 1880–2003.”. And that’s a remarkable result.
But…may I ask this rather elementary question: say, if the global mean warming yielded by all forcings together had been much less, or much more than observed, what would have been the (absolute) threshold above which the climate simulations would have been declared a failure?
Or has this question no meaning either? If not, why not?
Once again, I am consciously simplifying things here but this is a blog…more a brainstorming session than a week-long workshop.
> this rather elementary question: say, if the global mean warming
> yielded by all forcings together had been [grossly different]
Well, you can’t go back earlier than Arrhenius’s work and he wasn’t far off the current numbers. So you’re into fantasy there.
http://www.aip.org/history/climate/co2.htm
You’re saying that in some universe, the original work would have been so far from fact that
> the climate simulations would have been declared a failure
About all we can say is, the first estimate in the field was already close enough that people found it interesting to investigate.
People will investigate blind alleys — cold fusion, perhaps; Bode’s Law, perhaps; epicycles, certainly. But you’ve got to be “not even wrong” to get people to swear off thinking about an idea.
It does happen.
Maurizio Morabito (103) — It is necessary to move beyond notions of ‘falsifiability’, a la Karl Popper. Here some form of informal and formal Bayesian reasoning is required.
http://en.wikipedia.org/wiki/Bayes_factor
is one place to begin exploring the concepts.
Maurizio, Since we are talking climate here, the longer the period, the greater the signal to noise ratio. However, one can model the noise as well as the signal and look at how often fluctuations produce the given result–or how often noise alone would be expected to produce the signal.
This is purely a swag, but I suspect that if predictions were consistently off by more than half a degree, the models would be judged incomplete. Note that this is not really Popperian falsification–that really doesn’t apply here. It is pretty certain that the basic physical processes are correct. Climate science is really pretty mature. Yes there is much still to learn, but that does not diminish the importance or the confidence in what is already known (e.g. CO2 sensitivity).
#86 Gavin There should be a post dedicated to Hit and Run journalism. They take a swipe at AGW theory, run for cover, and then reappear again at the next cold spell. Here are a few stellar examples:
Forget global warming: Welcome to the new Ice Age
http://www.nationalpost.com/opinion/ columnists/story.html?id=332289
Is Winter 2008 Making Climate Alarmists Question Global Warming …
newsbusters.org/blogs/noel-sheppard/2008/ 03/02/winter-2008-making-climate-alarmists-question-global-warming
Prepare for the Next Ice Age «
michaelscomments.wordpress.com/ 2008/04/25/prepare-for-the-next-ice-age/
Now that 2008 is turning hot, we should be glad to have a moment of respite from contrarian propaganda…..
Re: 106
Thank you Ray. I can see some progress there (“incomplete” models rather than “wrong”). Perhaps some esteemed epistemologist will write a post on RC one day on how climate modelling does differ, say, from cosmology. Or doesn’t: still there’d be something to learn.
Thoughts spring to mind about classical physics being “really pretty mature” at the end of the XIX century apart from the “noise” called “black-body radiation”…only, for quantum physics to be discovered.
Maruizio, your reference to classical physics shows that you have an incomplete understanding–of the transition between classical and quantum/relativistic physics and of how science works. The failures of classical physics came when scientists tried to apply it to realms well outside those in which it developed–the very small for the quantum revolution and near-light-speed for relativity. Nothing like that is happening here. What is more, you will note that classical physics did not go away. Nobody solves the Schroedinger equation for a plane or looks at foreshortening for a rock falling. In fact, the successes of classical physics required that the new theories look very much like the old–a requirement Niels Bohr formalized in the Correspondence Principle.
So, even if you were to see a “new theory” of climate, it would look very much like the old–and since the old has been very successful and is not failing, I rather doubt you’ll see a new theory of climate.
re: #87
Yes, the momentum equations are based on a viscous fluid. I did not say that they were not.
The energy equation, however, does not contain the term that accounts for dissipation of fluid motions into thermal energy. See Equation (4) as I noted in my comment.
That is, I did not say the model was based on the Euler equations. My original statement is correct as it stands. If it is not, kindly point to the specific term in the energy equation model that accounts for the dissipation into thermal energy.
[Response: There are other forms of dissipation besides that one dissipative term, and the Saltzmann equations include dissipation. This is a pointless argument. Systems like Lorentz/Saltzmann are without question and obviously dissipative in the sense used in dynamical systems. Otherwise they wouldn’t have attractors! A Hamiltonian system conserves volume in phase space, which means you can’t contract down onto an attractor. This is the whole difference between Hamiltonian chaos (treatable for many degrees of freedom by standard thermodynamic principles) and dissipative chaos, which is orders of magnitude harder to get a grip on by statistical methods. –raypierre]
Maurizio, your website claims you’re being silenced here, calls the site ‘Goebbelist’ and throws tantrum after tantrum about your being mistreated. You may want to check your perspective on life a bit.
[Response: Seconded. I would like to firmly underline that the use of inappropriate Nazi analogies is deeply offensive and will at no times be tolerated here. I don’t care who does it, it is out of order. Get a grip. – gavin]
re: 110
I did not say the systems are not dissipative. And of course the systems are dissipative as that term is used in dynamical systems analyses.
I said, for the third time, that the energy equation model does not contain accounting of dissipation of fluid motions to thermal energy. The usual/standard positive-definite term on the RHS of the temperature form of the energy equation model is not present in the Saltzman system.
I said this based on Eq. 4 in the Saltzman paper.
If no one can point to that equation and show the error of my statement, the statement stands as correct as stated.
I hope RC will kindly allow this comment to be posted. I am only trying to make clear the term that I am pointing to.
[Response: But what in the world is your point in making such a fuss about that one term? It’s not relevant to anything we’ve been discussing. –raypierre]
As a matter of fact, Morabito accused ME of using goebbelite fashion (whathever that means) since I could not reply to his arguments (not true, of course. I have my own blog, which he knows, with a post on the very same topic; http://leucophaea.blogspot.com/2008/05/caldo-o-freddo-o-tutti-e-due.html – in italian). As far as I understand, according to Morabito, asking Realclimate to counter his arguments with data, and calling him a negationist, means trying to silence him with phisical threats. Tell me, Gavin, what have you done to scares the beejezus out of Morabito?
Gibbertarian?
Hi all,
I have been reading this writeup on Ed Lorenz and the subsequent discussions and comments with very great interest. It is very nice to be privy to the unfolding of profound new areas of knowledge such as chaos theory, and applications such as climate science. In the process I’ve started to also sense (and enjoy) a little of the personal aspects of those who work in the area – for example, gavin’s mature and knowledgeable responses to various queries, the subtle philosophical background to raypierre’s way of putting things across (I’ve read your rebuttal to Dawkin’s The God Delusion) and so on. I was reminded of Hermann Haken, whose name I came across in a book by Giuseppe Caglioti titled “The dynamics of ambiguity”. This book deals with the dynamics of human perception and I personally found many parts of it to be thought provoking, for example this bit in the preface:
“Caglioti proposes a return to the image of the scientist-philosopher, that is, of the man of science who doesn’t limit himself to the role of ‘Lord of Technology’, but who emerges as a thinker whose purpose is to investigate, albeit in technical-scientific terms, even those problems inherent to man’s psychic-cognoscitive equilibrium”
Cheers,
Madhu
Re #107
I am preparing a relatively long commentary on what I am learning from this blog and its comments. For now let me clarify that I do not think that current climate models are based on incorrect physics.
The black-body radiation equivalence still holds though, as what looked like a relatively minor nuisance (“noise”?) to your average XIX century physicist, was the basis for a whole new understanding of the whole science of physics.
Think of genetics: yesterday’s “junk DNA” is (in part) today’s “gene switches”. Who knows what tomorrow will bring.
As for the comments policy, in the past I have seen some thoughts of mine not published, for whatever reason. I am pleasantly surprised that nothing of the sort is happening this time around, and hopefully the situation won’t change.
Another clarification
Re #109
I have never categorized RealClimate as “goebbelite”.
As a matter of fact, in order to mantain a proper perspective on life and climate and everything, I suggest that on Real Climate we all stick to what is written in Real Climate. No website can become the repository of all discussions entertained and comments made somewhere else.
=======
I have posted a simple question in #101 but only received an answer so far, by Ray Ladbury in #104 where he says he “suspect[s] that if predictions were consistently off by more than half a degree, the models would be judged incomplete”.
Does anybody else think along the same lines?
And am I right in assuming, based on Hansen et al’s cited in #101, that to talk of “climate” we must consider a period of time of 25 years or longer?
It surely would be nice to know
Maurizio, Just where do you think the incorrect physics lies, and how do you think you can figure that out without a thorough understanding of the physics?
I should elaborate on my previous answer–it may be as important HOW the models are off as it is to know the magnitude. Is the problem in the “noise” in the system? In this case, there may be some source of variability not in the models. Are the predictions consistently high or low? That’s something else altogether.
I would say that 22 years (a full solar cycle) is an absolute minimum for a climatic trend to be truly climatic. However, depending on the noise one is willing to accept, the required period could be longer or shorter.
I used to have a calculus professor who said “What is epsilon? Give me a delta, and I’ll give you an epsilon.”
Maurizio, you have a very incomplete idea of science. It goes way beyond Popper or Kuhn. I’d recommend reading Fischer and von Neumann and Bohr. But if you are going to criticize climate science, then for the life of me, I can’t understand why you wouldn’t want to study it systematically first.
Maurizio Morabito (115) — Real Climate has a funky spam filter. I’ve been hit by it a few times. Also remember that the internet is ‘best effort’ only, no guarantees. As traffic grows by leaps and bounds, more messages may end up in the bit bucket.
Yes, for ‘climate’, longer time periods are better. A standard of sorts is 30 years. I suppose that is the standard because it is what the National Weather Service uses. Better still would be 140 years, about 2 quasi-cycles of the PDO. But of course it depends upon what one is attempting to understand.
Re # 114 Maurizio Morabito
“Think of genetics: yesterday’s “junk DNA” is (in part) today’s “gene switches”. Who knows what tomorrow will bring.”
Good question. But, the realization that some of the so-called junk DNA codes for gene switches did not, in my humble estimation, bring about a whole new understanding of genetics. As far as I know, most genes still code for proteins (some code for RNA), and proteins still pretty much run the show inside cells. There is plenty to learn about these things,of course, but I doubt the basic concepts will be overturned.
I understand that GCMs account for the effects of CO2 on radiative forcing. What about the convective and conductive components which would be greatly affected by turbulence? Is it justifiable to describe these effects simply as noise and hence affecting weather as opposed to climate? These perturbations would be non-linear and on different spatial scales. After all the average global temperature should depend on the difference between the energy coming in (from the sun) and energy going out and this should depend on all heat transfer phenomena. Would someone care to comment on the last paragraph in the attached essay by Prof. Tennekes? http://www.sepp.org/Archive/NewSEPP/Climate%20models-Tennekes.htm
[Response: Turbulence is indeed a huge problem. But given that we will never have a full understanding or capacity to model it in the atmosphere or oceans at all the relevant scales, Tennekes position would seem to be there is no point in doing any modelling at all. This ‘a priori’ dismissal of climate models completely ignores the fact that they work for many aspects of the problem. His attitude presupposes that there are no predictable aspects of the problem that are robust to errors in the small scale turbulence. However, he is simply wrong. The large scale temperature and circulation variability is usefully predictable – look at the cooling following large volcanoes or at the LGM or the ocean circulation during the 8.2kyr event or the tele-connections to El Nino events or the rainfall patterns in the mid-Holocene etc. All of these observed changes are a function of large scale changes to the basic energy and mass fluxes and are robust to uncertainty in the details of the turbulence. – gavin]
Re: #116
Ray:
(1) You ask “Just where do you think the incorrect physics lies?”. Actually, I have written: “I do not think that current climate models are based on incorrect physics”
(2) Of course, science is not just about falsification. But there is no science without falsification (in the sense of, the possibility to falsify). And of course that should not be treated simplistically: I can forecast a temperature tomorrow for London between -40 and +50C. Such a forecast is falsifiable, and it may turn up to be false if something very very strange is going to happen…still, with such a huge range given, none would call it a “scientific forecast”. It’s just a very, very safe guess.
Re: #118
Chuck: in truth, epigenetics is “overturning” some very basic concepts of old genetics, including the relationship between nature and nurture. You may think of it as if in the past, “nature” and “nurture” were considered separate “forcings” on the organism, whilst now we know of ways for “nurture” to significantly influence “nature”. Separated-twin studies are likely to have to undergo a major rethink, apart of course from those based around “pure” mendelian inheritance.
May 2008’s SciAm has a great article on “gene switches”. But of course we’re getting far from climatology…
Ray, it is nice to talk with you in HGS building. I read your article again tonight and enjoy it very much.
In a interview by Dr. Taba of WMO bulletin, Lorenz himself desribed how he found chaos. I think it approriate to paste his words here, though the sotry is well-known, and I believe
he will be always a legend to young scientists.
——————————-
WMO Bulletin,1996,Vol 45, No2
Some statistical forecasters claimed there was mathematical proof that linear regression was inherently capable of performing as well as any other procedure, including numerical weather prediction. I was sceptical and proposed to test the idea by using a model to generate an artificial set of weather data, after which I would determine whether a linear formula could produce the data. if the artificial sequences turned out to be periodic, repeating their previous values at regulars intervals, linear regression would produce perfect forecasts. For the test, therefore, I needed a model whose solutions would vary irregularly from one time to the next,just as the atmosphere appears to do. I started testing one model after another and finally arrived at one that consisted of 12 equations. The 12 variables represented gross features of the weather, such as the speed of the global westerly winds. After being given 12 numbers to represent the weather pattern at the starting time, the computer would advance the weather in six hour time-steps, each step requiring 10 seconds of computation. After every fourth step- or every simulated day- the computer would print out the new values of the 12 variables, requiring a further 10 seconds. After a few hours, a large array of numbers would be produced and I would look at one of the 12 columns and see how the numbers were varying. Ther was no sign of periodicity. At times, I would print out more solutions, sometimes with new starting conditions. It became evident that the general behavior was non periodic. When I applied the linear regression method to the simulated weather, i found that it produced only mediocre results.
At one point, I wanted to examine a solution in greater detail, so I stopped the computer and typed in the 12 numbers from a row that the computer had printed earlier. I started the computer again and went out for a cup of coffee. When I returned, about an hour later, the computer had generated about two months of data and I found the new solutions did not agree with hte original one. At first, I suspected trouble with the computer but, when I compared with the new solution, step by step, with the older one, I found that the solutions were the same at first and then differed by one unit in the last decimal place; the difference became larger and larger, doubling in magnitude in about four simulated days until, after 60 days, the solutions were unrecognizable different.
The computer was carrying its numbers to about six decimal places but,in order to have 12 numbers together on one line, I had instructed it to round off the printed values to three places. The numbers I typed in were therefore not the original numbers but rounded off approximations. The model evidently had the property that small differences between solutions would proceed to amplify until they became as large as differences between randomly selected solutions.
This was exciting: if the real atmosphere behaved in the same manner as the model, long-range weather prediction would be impossible, since most real weather elements are certainly not measured acculately to three decimal places. Over the following months, I became convinced that the lack of periodicity and the growth of the small differences were somehow related and I was eventually able to prove that, under fairly general conditions, either type of behavior implied the other. Phenomena that behave in this manner are now collectively refered to as chaos. That discovery was the most exciting event in my career.
——————————-