
by Gavin Schmidt and Caspar Amman
Due to popular demand, we have put together a ‘dummies guide’ which tries to describe what the actual issues are in the latest controversy, in language even our parents might understand. A pdf version is also available. More technical descriptions of the issues can be seen here and here.
This guide is in two parts, the first deals with the background to the technical issues raised by McIntyre and McKitrick (2005) (MM05), while the second part discusses the application of this to the original Mann, Bradley and Hughes (1998) (MBH98) reconstruction. The wider climate science context is discussed here, and the relationship to other recent reconstructions (the ‘Hockey Team’) can be seen here.
NB. All the data that were used in MBH98 are freely available for download at ftp://holocene.evsc.virginia.edu/pub/sdr/temp/nature/MANNETAL98/ (and also as supplementary data at Nature) along with a thorough description of the algorithm.
Part I: Technical issues:
1) What is principal component analysis (PCA)?
This is a mathematical technique that is used (among other things) to summarize the data found in a large number of noisy records so that the essential aspects can more easily seen. The most common patterns in the data are captured in a number of ‘principal components’ which describe some percentage of the variation in the original records. Usually only a limited number of components (‘PC’s) have any statistical significance, and these can be used instead of the larger data set to give basically the same description.
2) What do these individual components represent?
Often the first few components represent something recognisable and physical meaningful (at least in climate data applications). If a large part of the data set has a trend, than the mean trend may show up as one of the most important PCs. Similarly, if there is a seasonal cycle in the data, that will generally be represented by a PC. However, remember that PCs are just mathematical constructs. By themselves they say nothing about the physics of the situation. Thus, in many circumstances, physically meaningful timeseries are ‘distributed’ over a number of PCs, each of which individually does not appear to mean much. Different methodologies or conventions can make a big difference in which pattern comes up tops. If the aim of the PCA analysis is to determine the most important pattern, then it is important to know how robust that pattern is to the methodology. However, if the idea is to more simply summarize the larger data set, the individual ordering of the PCs is less important, and it is more crucial to make sure that as many significant PCs are included as possible.
3) How do you know whether a PC has significant information?
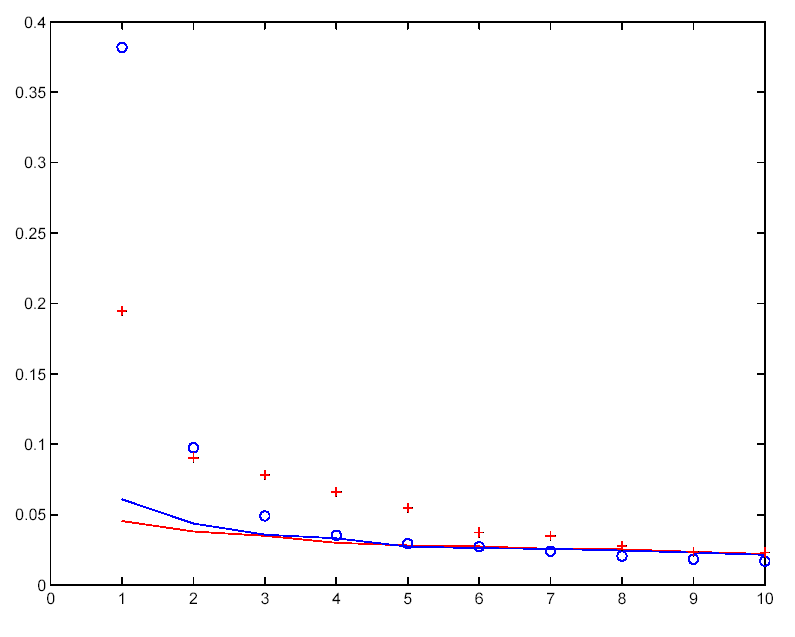 This determination is usually based on a ‘Monte Carlo’ simulation (so-called because of the random nature of the calculations). For instance, if you take 1000 sets of random data (that have the same statistical properties as the data set in question), and you perform the PCA analysis 1000 times, there will be 1000 examples of the first PC. Each of these will explain a different amount of the variation (or variance) in the original data. When ranked in order of explained variance, the tenth one down then defines the 99% confidence level: i.e. if your real PC explains more of the variance than 99% of the random PCs, then you can say that this is significant at the 99% level. This can be done for each PC in turn. (This technique was introduced by Preisendorfer et al. (1981), and is called the Preisendorfer N-rule).
This determination is usually based on a ‘Monte Carlo’ simulation (so-called because of the random nature of the calculations). For instance, if you take 1000 sets of random data (that have the same statistical properties as the data set in question), and you perform the PCA analysis 1000 times, there will be 1000 examples of the first PC. Each of these will explain a different amount of the variation (or variance) in the original data. When ranked in order of explained variance, the tenth one down then defines the 99% confidence level: i.e. if your real PC explains more of the variance than 99% of the random PCs, then you can say that this is significant at the 99% level. This can be done for each PC in turn. (This technique was introduced by Preisendorfer et al. (1981), and is called the Preisendorfer N-rule).
The figure to the right gives two examples of this. Here each PC is plotted against the amount of fractional variance it explains. The blue line is the result from the random data, while the blue dots are the PC results for the real data. It is clear that at least the first two are significantly separated from the random noise line. In the other case, there are 5 (maybe 6) red crosses that appear to be distinguishable from the red line random noise. Note also that the first (‘most important’) PC does not always explain the same amount of the original data.
4) What do different conventions for PC analysis represent?
Some different conventions exist regarding how the original data should be normalized. For instance, the data can be normalized to have an average of zero over the whole record, or over a selected sub-interval. The variance of the data is associated with departures from the whatever mean was selected. So the pattern of data that shows the biggest departure from the mean will dominate the calculated PCs. If there is an a priori reason to be interested in departures from a particular mean, then this is a way to make sure that those patterns move up in the PC ordering. Changing conventions means that the explained variance of each PC can be different, the ordering can be different, and the number of significant PCs can be different.
5) How can you tell whether you have included enough PCs?
This is rather easy to tell. If your answer depends on the number of PCs included, then you haven’t included enough. Put another way, if the answer you get is the same as if you had used all the data without doing any PC analysis at all, then you are probably ok. However, the reason why the PC summaries are used in the first place in paleo-reconstructions is that using the full proxy set often runs into the danger of ‘overfitting’ during the calibration period (the time period when the proxy data are trained to match the instrumental record). This can lead to a decrease in predictive skill outside of that window, which is the actual target of the reconstruction. So in summary, PC selection is a trade off: on one hand, the goal is to capture as much variability of the data as represented by the different PCs as possible (particularly if the explained variance is small), while on the other hand, you don’t want to include PCs that are not really contributing any more significant information.
Part II: Application to the MBH98 ‘Hockey Stick’
1) Where is PCA used in the MBH methodology?
When incorporating many tree ring networks into the multi-proxy framework, it is easier to use a few leading PCs rather than 70 or so individual tree ring chronologies from a particular region. The trees are often very closely located and so it makes sense to summarize the general information they all contain in relation to the large-scale patterns of variability. The relevant signal for the climate reconstruction is the signal that the trees have in common, not each individual series. In MBH98, the North American tree ring series were treated like this. There are a number of other places in the overall methodology where some form of PCA was used, but they are not relevant to this particular controversy.
2) What is the point of contention in MM05?
MM05 contend that the particular PC convention used in MBH98 in dealing with the N. American tree rings selects for the ‘hockey stick’ shape and that the final reconstruction result is simply an artifact of this convention.
3) What convention was used in MBH98?
MBH98 were particularly interested in whether the tree ring data showed significant differences from the 20th century calibration period, and therefore normalized the data so that the mean over this period was zero. As discussed above, this will emphasize records that have the biggest differences from that period (either positive of negative). Since the underlying data have a ‘hockey stick’-like shape, it is therefore not surprising that the most important PC found using this convention resembles the ‘hockey stick’. There are actual two significant PCs found using this convention, and both were incorporated into the full reconstruction.
4) Does using a different convention change the answer?
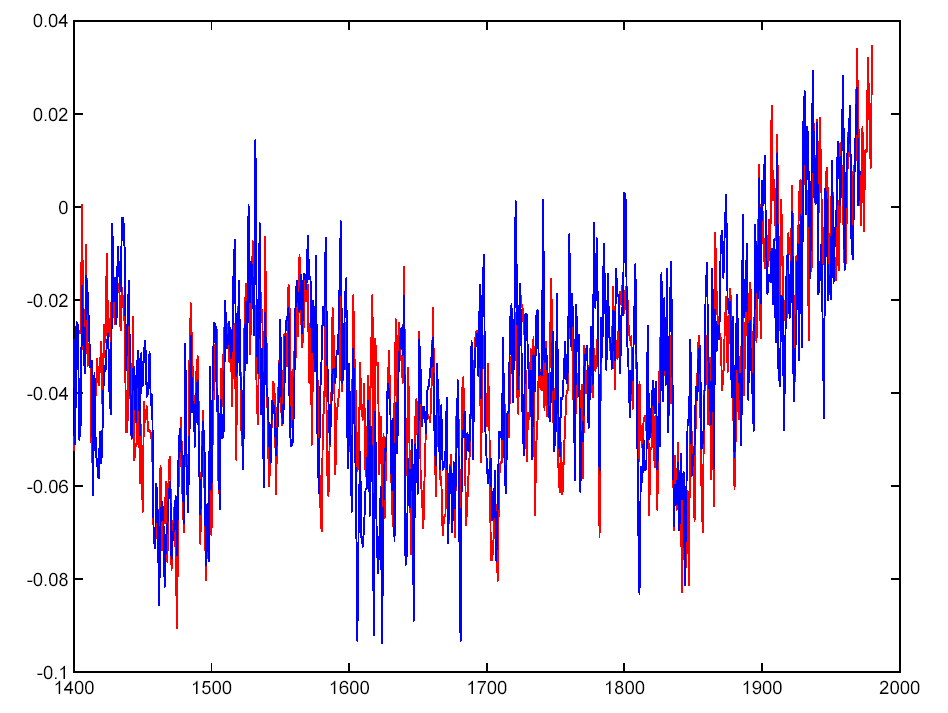
As discussed above, a different convention (MM05 suggest one that has zero mean over the whole record) will change the ordering, significance and number of important PCs. In this case, the number of significant PCs increases to 5 (maybe 6) from 2 originally. This is the difference between the blue points (MBH98 convention) and the red crosses (MM05 convention) in the first figure. Also PC1 in the MBH98 convention moves down to PC4 in the MM05 convention. This is illustrated in the figure on the right, the red curve is the original PC1 and the blue curve is MM05 PC4 (adjusted to have same variance and mean). But as we stated above, the underlying data has a hockey stick structure, and so in either case the ‘hockey stick’-like PC explains a significant part of the variance. Therefore, using the MM05 convention, more PCs need to be included to capture the significant information contained in the tree ring network.
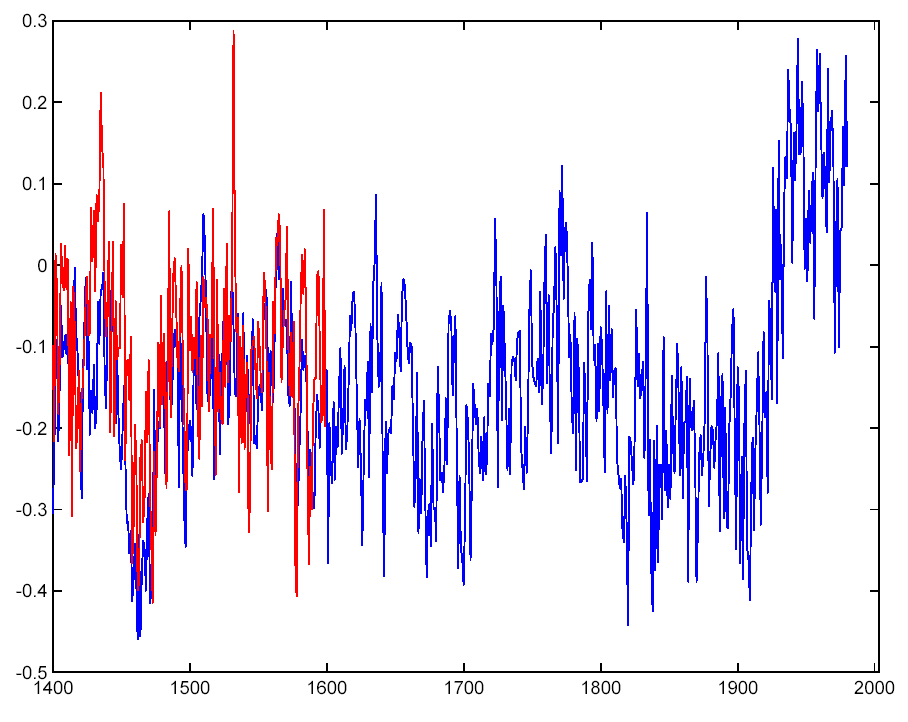
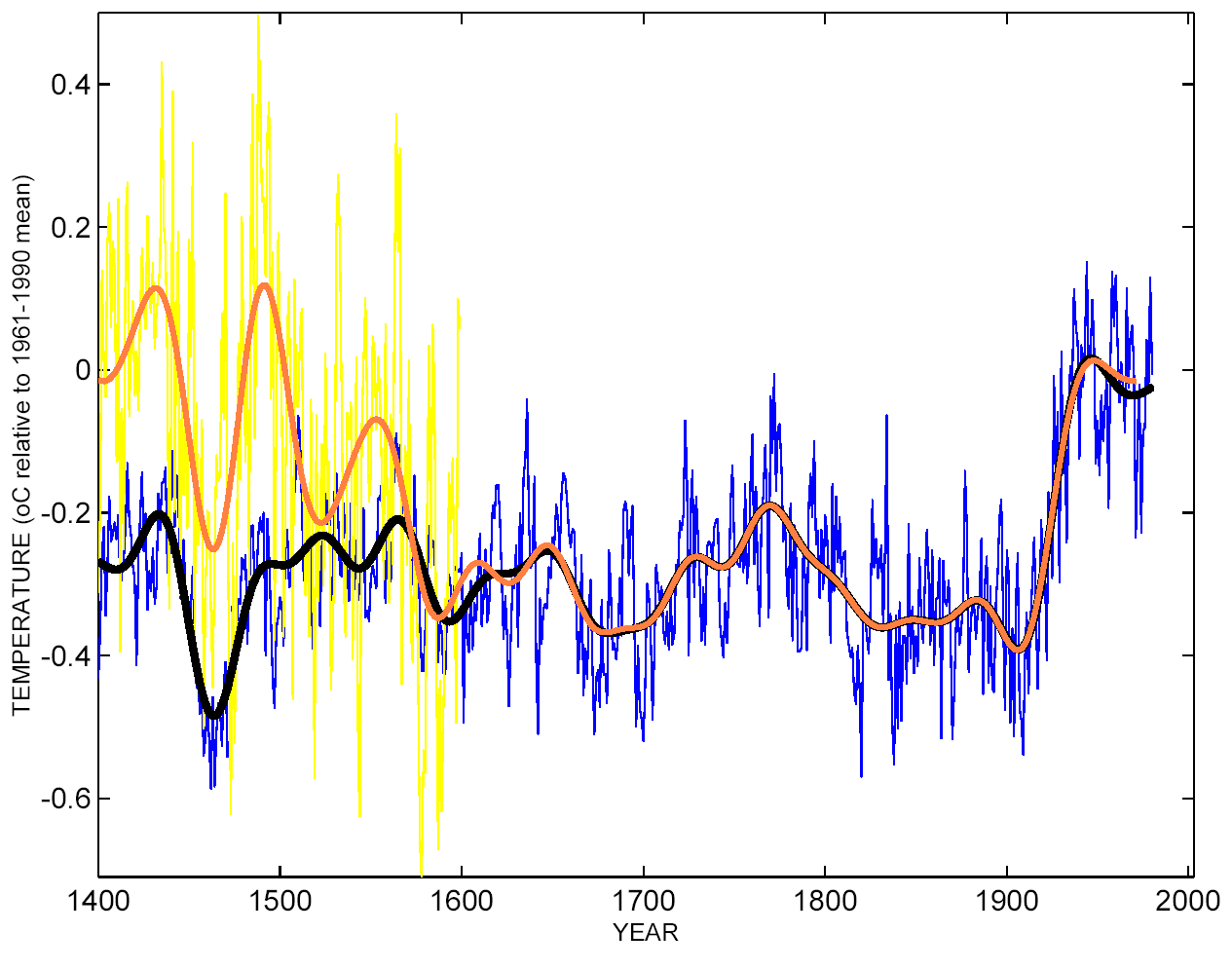
This figure shows the difference in the final result whether you use the original convention and 2 PCs (blue) and the MM05 convention with 5 PCs (red). The MM05-based reconstruction is slightly less skilful when judged over the 19th century validation period but is otherwise very similar. In fact any calibration convention will lead to approximately the same answer as long as the PC decomposition is done properly and one determines how many PCs are needed to retain the primary information in the original data.
5) What happens if you just use all the data and skip the whole PCA step?
This is a key point. If the PCs being used were inadequate in characterizing the underlying data, then the answer you get using all of the data will be significantly different. If, on the other hand, enough PCs were used, the answer should be essentially unchanged. This is shown in the figure below. The reconstruction using all the data is in yellow (the green line is the same thing but with the ‘St-Anne River’ tree ring chronology taken out). The blue line is the original reconstruction, and as you can see the correspondence between them is high. The validation is slightly worse, illustrating the trade-off mentioned above i.e. when using all of the data, over-fitting during the calibration period (due to the increase number of degrees of freedom) leads to a slight loss of predictability in the validation step.
6) So how do MM05 conclude that this small detail changes the answer?
MM05 claim that the reconstruction using only the first 2 PCs with their convention is significantly different to MBH98. Since PC 3,4 and 5 (at least) are also significant they are leaving out good data. It is mathematically wrong to retain the same number of PCs if the convention of standardization is changed. In this case, it causes a loss of information that is very easily demonstrated. Firstly, by showing that any such results do not resemble the results from using all data, and by checking the validation of the reconstruction for the 19th century. The MM version of the reconstruction can be matched by simply removing the N. American tree ring data along with the ‘St Anne River’ Northern treeline series from the reconstruction (shown in yellow below). Compare this curve with the ones shown above.
As you might expect, throwing out data also worsens the validation statistics, as can be seen by eye when comparing the reconstructions over the 19th century validation interval. Compare the green line in the figure below to the instrumental data in red. To their credit, MM05 acknowledge that their alternate 15th century reconstruction has no skill.
7) Basically then the MM05 criticism is simply about whether selected N. American tree rings should have been included, not that there was a mathematical flaw?
Yes. Their argument since the beginning has essentially not been about methodological issues at all, but about ‘source data’ issues. Particular concerns with the “bristlecone pine” data were addressed in the followup paper MBH99 but the fact remains that including these data improves the statistical validation over the 19th Century period and they therefore should be included.
8) So does this all matter?
No. If you use the MM05 convention and include all the significant PCs, you get the same answer. If you don’t use any PCA at all, you get the same answer. If you use a completely different methodology (i.e. Rutherford et al, 2005), you get basically the same answer. Only if you remove significant portions of the data do you get a different (and worse) answer.
9) Was MBH98 the final word on the climate of last millennium?
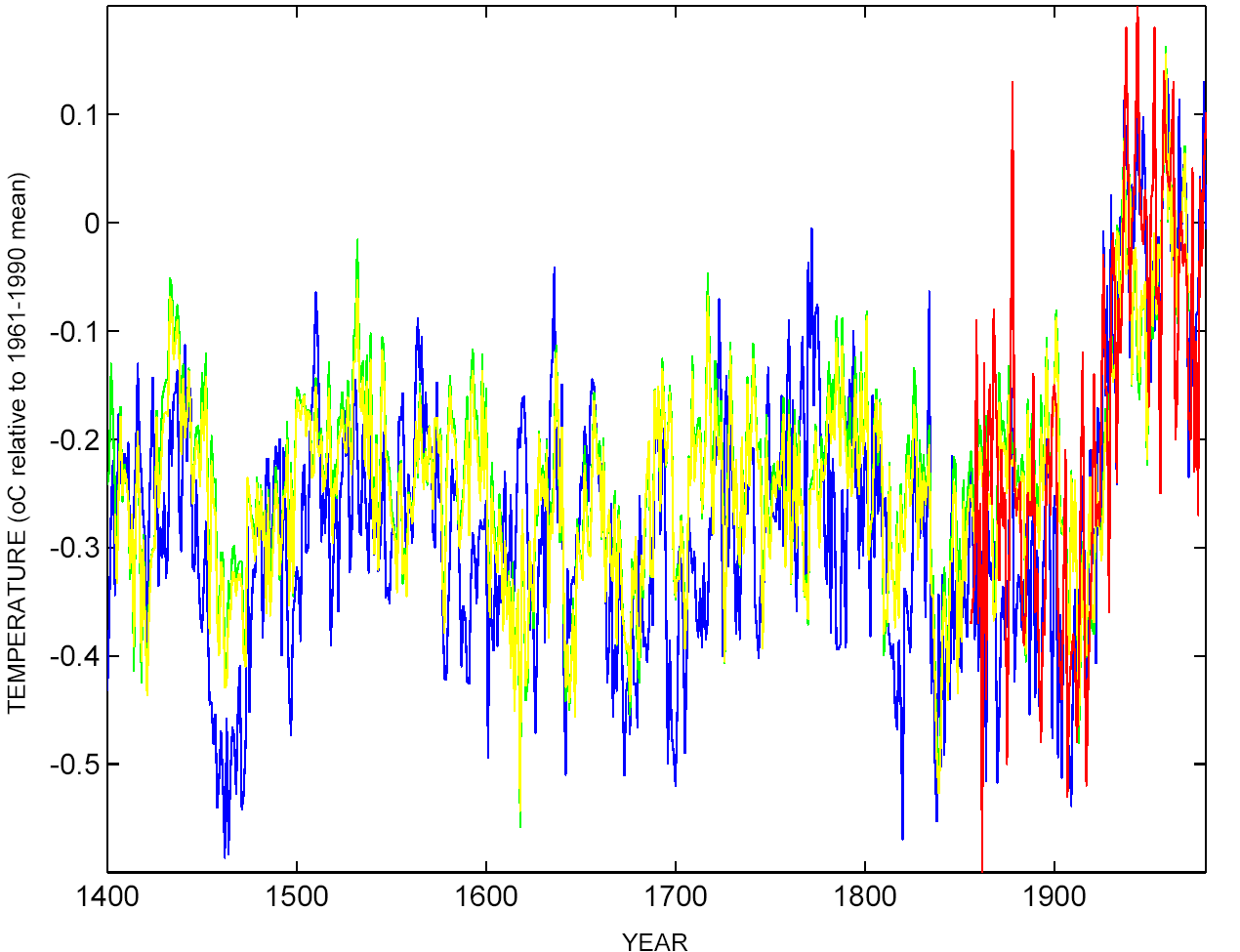
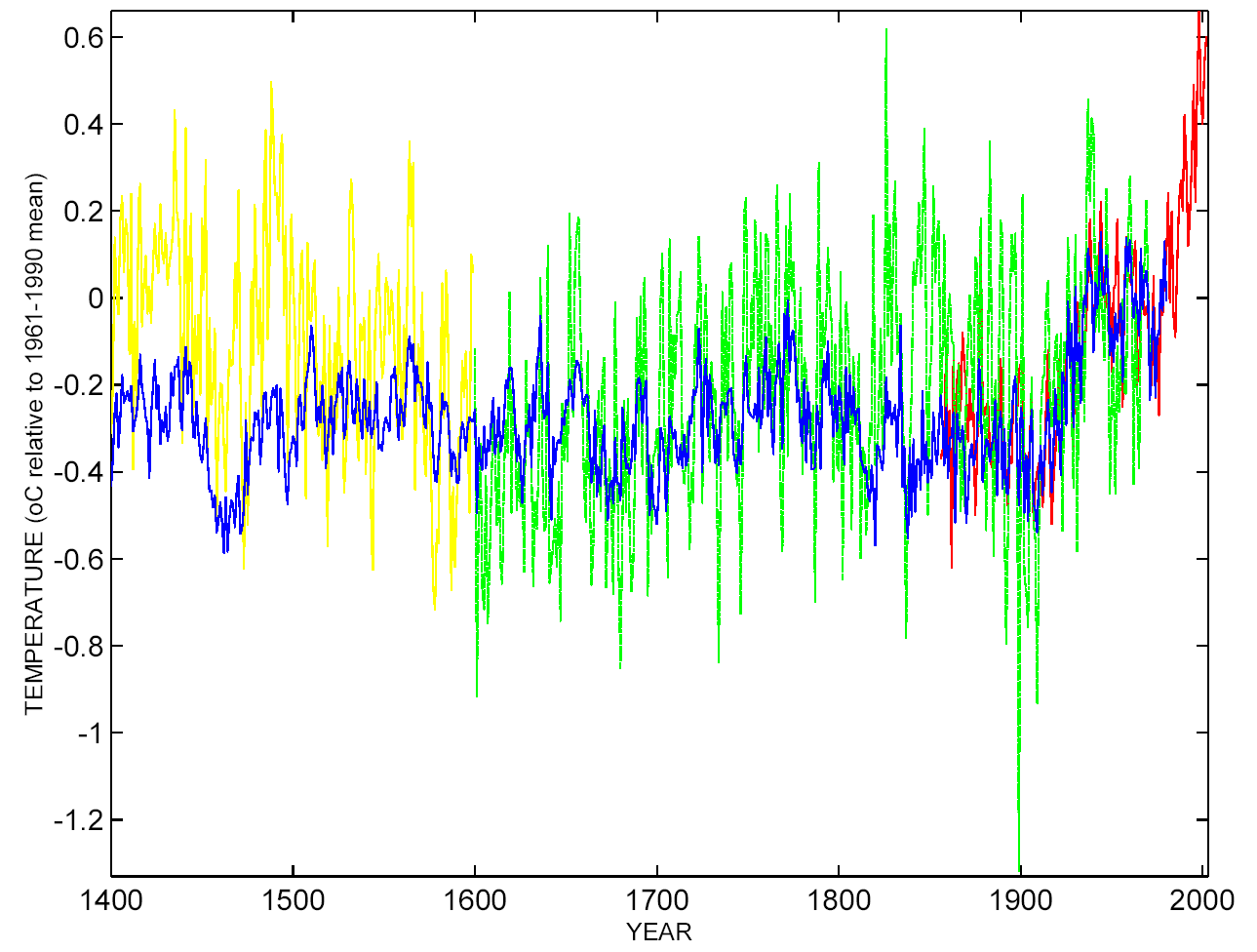
Not at all. There has been significant progress on many aspects of climate reconstructions since MBH98. Firstly, there are more and better quality proxy data available. There are new methodologies such as described in Rutherford et al (2005) or Moberg et al (2005) that address recognised problems with incomplete data series and the challenge of incorporating lower resolution data into the mix. Progress is likely to continue on all these fronts. As of now, all of the ‘Hockey Team’ reconstructions (shown left) agree that the late 20th century is anomalous in the context of last millennium, and possibly the last two millennia.

Thanks for this effort, as you say at the top, “to describe what the actual issues are in the latest controversy, in language even our parents might understand.” At least part of that controversy is today’s Wall Street Journal editorial “Hockey Stick on Ice: Politicizing the science of global warming.” (It’s available on the free-access part of the WSJ’s heavily access-restricted site at http://www.opinionjournal.com/editorial/feature.html?id=110006314 .) I don’t blame the RealClimate scientists for their often-stated preference simply to report scientific facts and to leave actual political debating to others. And I too use my mom as a calibration for keeping technical readability at the right level. But I have to say, it would heavily stretch my mom’s and my capacities to apply this dummies’ guide to what’s been asserted this morning in what may be the world’s most influential newspaper for denying RealClimate’s scientific facts. So I hope the RealClimate scientists will consider responding in some direct, plain way on this specific issue of politics that is also an issue of science. (Maybe they’re working on it and I’m just rushing them.) Thanks.
[Response: We considered responding directly to the WSJ article, but felt that a point-by-point rebuttal wasn’t warranted. Although there were a variety of overstatements and mistatements, this was by no means an example of the worst reporting we’ve seen. Perhaps more to the point, there was not much in the article that we hadn’t already addressed (though we did respond to the insinsuation that we were part of some “environmental group” (see here) –eric]
[Response: I think the reference is actually to the WSJ editorial, rather than the column a few days back. However, there is nothing new scientifically in the Op-ed piece, and so this post and others previously would still appear sufficient. – gavin]
I probably need the Complete Idiot’s Guide, but what I get out of this is, using the mean of the whole data set (if it does have an actual hocky stick shape) as zero creates a higher horizontal line from which all the data vary in various amounts & it tends to “pull up” the negative differences & makes the positive differences look not so big (or it makes all the data look on average equally large in distance from the mean, both in pos & neg directions), making the whole thing look like nothing much is happening, aside from cyclical changes. Whereas, using the past (lower) data to establish a mean gives us a lower horizontal line from which data vary — making the past data look fairly cyclical (except for that mini-ice age), and the recent data look like it’s going into new and higher territory.
Congratulations. Now you can break out a bottle of the good stuff.You are actually beginning to sound like Tim Lambert, the Australian math and computer science guy who can count and explain in a very basic way.
Of course, it is still a little on the high end, but I can see it is very difficult to condense and digest to such a point that material can be thrown up in sports page language. But this piece really is a big jump forward in expository style and content.
Lambert also knows what to do with a hockey puck, and you do not have to shout at him to “shoot, shoot the dam thing” You are reaching that level.
May I offer some material for practice shots? Please take a look at what Mcintyre does to Malcolm Hughes in Climate Audit, Feb.13, “Better for our purposes”. This is a guy that wants to advance science? That is how you do it, with a hit-and-run-attack?
Like I say, shoot the damm thing.
I must congratulate you on a much clearer presentation of the current issues than has previously been set out.
I would also like to encourage the more dispassionate presentation of the discussion. The lack of invective makes this a much more accessable article than a number of others on this site. I must admit that, regardless of the issues involved, when one party to a debate uses invective I find it very difficult to evaluate them on their merits. I suspect that others who are not invested in the debate would feel similarly.
I agree that this presentation is quite a good read, even for someone who has no prior knowledge of PCA; I doubt if my mother would understand it however ;-)
[Response: Probably mine wouldn’t either, but at least I tried. – gavin]
I doubt that Mr. McIntyre is particularly interested in “advancing science” (# 3); if you look at his musings (here) on the difficulties that a hard-working sceptic has in bringing climate scientists to book, it becomes evident that what he’s really interesting in doing is making the normative standards of the business world those of the environmental sciences as well. Which would make the environmental sciences more tractable, from a business perspective – probably the ultimate point – but they would no longer be recognizable as sciences, in the sense that they are today.
The WSJ editorial referred to in #1, among its many serious flaws, contains the following:
Yet there were doubts about Mr. Mann’s methods and analysis from the start. In 1998, Willie Soon and Sallie Baliunas of the Harvard-Smithsonian Center for Astrophysics published a paper in the journal Climate Research, arguing that there really had been a Medieval warm period. The result: Messrs. Soon and Baliunas were treated as heretics and six editors at Climate Research were made to resign.
“Made to resign” does not match well with the events as described at http://w3g.gkss.de/staff/storch/CR-problem/cr.2003.htm .
Is it too much to expect a publication as influential as the WSJ to refrain from twisting history like this?
From the “Dummies guide” I have understood what PCA does, but I’m always curious and like to know the technicalities; could anyone refer me to a – preferably free and online – source that explains how PCA works (in general or specific case)?
I’m trained in advanced math (physics engineer) so don’t hold back on that front ’cause I’ll sort that out for myself.
[Response: Something that’ll help a bit is to recognize that the basis of PCA is simply an eigenvalue/eigenvector decomposition. I’ll also try to track down a good on line reference to the essentials — there definitely are some out there. -eric]
Michael Tobis, Soon et al. was published in 2003, not 1998, so the op-ed is even more mendacious and obfuscatory than you state, notwithstanding the op-ed not explaining why the Eds. resigned.
D
A PCA reference that I like is: I. T. Jolliffe, Principal Component Analysis, Springer-Verlag, New York, 1986. It’s in its 2nd edition, which I haven’t seen, but is available via amazon.com.
Thanks for making the PDF version available. The graphs don’t show up well in my web browser.
The Wall Street Journal accusing Dr Mann of trying to “shut down the debate” is a case of do as I say, not as I do.
This is also a rhetoric technique. You cover up your mistake or wrong-doing by accusing the other side of it first. In the blame game the first one to act has an advantage even if the accusation is inaccurate or dishonest. The goal is to clear yourself of any wrong-doing and to make the other side look bad. This will strengthen your position in a debate or even stop it completely.
The WSJ has apparently joined the opponents of climate change laws and regulations. The opponents want to prevent climate change laws and regulations from being made for political, philosophical or economic reasons. If they prevent or stop the climate change regulation debate no laws will be enacted and they will achieve their goal (see my comments in “Strange Bedfellows” #6, 27, 34, 35 40 42 45 and “A Disclaimer” #15). The opponents of climate change regulation question the basic science to keep the debate from moving on to the next step, the possible effects of human-caused climate change and what laws and regulations should be made to address it.
I wonder if the WSJ will report the results of the study just announced by the Scripps Institute of Oceanography. It is at http://Scrippsnews.ucsd.edu/article_detail.cfm?article_num=666.
In the study scientists at Scripps and their colleagues “have produced the first clear evidence of human-produced warming in the world’s oceans, a finding they say removes much of the uncertainty associated with debates about global warming”. I’m guessing no.
The “hockey stick” controversy reminds me of a quote by Jared Diamond about the Maori people and the extinction of the moa in New Zealand. “I wonder what the Maori who killed the last moa said. Perhaps the polynesian equivalent of ‘Your ecological models are untested, so conservation measures would be premature’? No, he probably just said ‘Jobs not birds’ as he delivered the last blow.”
Well, finally I understand. It is another case of confusing radians and degrees on the part of McKitrick. It would be interesting to look at the package he used for his analysis to see what the warnings are for use of the algorithm.
In comment to #12 by Joseph O’Sullivan: I would say that your statement that “the WSJ has apparently joined the opponents of climate change laws and regulations” is an understatement. The WSJ editorial page has been at this for a long time…They are more of a founding member than a joiner!
In fact, what surprised me about this WSJ editorial (particularly their last paragraph) in relation to past editorials is the shift a little bit from their previous position that I’d characterize as “Global warming is a bunch of hooey” to a more nuisanced position of “Aren’t there still some uncertainties in the science that we need to consider before starting to take serious action?” My guess is that this change in tone is being driven by the fact that, even within the business community, there is building pressure for some real regulatory action, if for no other reason that it is seen to be inevitable and it will provide more certainty than the current situation.
Who knows, maybe in another 10 years or so, the WSJ editorial page will be claiming that they were never really against actions to deal with climate change but they just felt the science needed to be more certain first. Or maybe I’m just being an optimist.
Although you say
> [Response: We considered responding directly to the WSJ article,
> but felt that a point-by-point rebuttal wasn’t warranted.
Folks, this is what hypertext is supposed to make easy.
Copy the text of the WSJ piece
Break it up into individual statements
Put an ellipsis _every_ place you remove something
For each chunk of text you quote,
Add a link that takes the reader to the existing information rebutting it.
Don’t retype, don’t rewrite, don’t just add more words.
Show what they said, with a link to information relevant to it.
Your mom is _way_ too sophisticated to serve as a validator for this information. The average reading level now is, what, 7th grade? And we’re not talking 1950s literate 7th grade, we’re talking a thumb-typing modern 7th grader with loud music in the earphones who’s not paying attention. Those are the voters you need to reach.
I know you had an earlier post re “what if the hockey stick were wrong.” This is what my limited climate science knowledge tell me, if the hockey stick were wrong. Let me know is my ideas are off or on the mark.
If the hockey stick is wrong, and there is more climate variability in the past, then we might be in for more trouble (than if it were correct). If human emitted GHGs do contribute to GW, even in a little, then this could trigger a much larger climate response (since the climate varies so wildly from natural causes).
The implication then would be that we should redouble our efforts and do all we can to reduce our part of the GHG contribution, because we wouldn’t want to trigger wildly fluctuating nature into much greater global warming. I think it is well established that natural GHGs have an impact on climate, and increasing these through human activities would very likely also have an impact. So if the hockey stick is incorrect & climate varies wildly from natural causes, then even a “small” (as skeptics view it) input of human GHGs, would then have a much larger impact by virtue of triggering a more sensitive and wild nature.
That’s what I come up with, given my limited understanding. Is it wrong?
Re: Climate In Medieval Time
In so far as M&M are trying to distort the climate data over the last 1000 years to show that the so-called “Medieval Warm Period” replicates or exceeds the current warming – and so natural variability could possibly account for that warming – I thought it worthwhile to put out some information about Medieval climate.
Here’s an abstract for Bradley et. al. Climate in Medieval Time, Science 2003 302: 404-405. (The original appears to be on-line, but I couldn’t access it). Here’s a Science Daily summary Medieval Climate Not So Hot of the Science article. Here’s a paper by Bradley called Climate of the Last Millenium covering the same material.
Re: Addendum to #18
The Bradley et. al. Science paper is indeed on-line here.
I also want to emphasize the truth of a statement from a recent post What If … the ‘Hockey Stick’ Were Wrong?.
So I guess I need to ask what this “hockey team” storm is all about. What we have here is a situation in which MM05 attempts to make a point to discredit climate warming which – even if they were correct – would not affect the indicated existence of human forcing of climate via GHG emissions/land use changes occurring now.
I can understand the need, especially at realclimate, to make the “hockey team” science clear and debunk the distortions. But from a somewhat larger perspective, this scientific result is just one piece of a host of results all indicating where the current warming comes from. As the IPCC says, “the bulk of the evidence shows….” So my suggestion for realclimate.org is to focus more on the forest and not the trees. Granted, the “hockey team” is a big tree in the forest, but it’s not the only one.
I would urge a more varied approach to climate science topics on this site. For example, climate models seem to indicate more pronounced warming in the Arctic and sub-Arctic happening prior to warming effects seen at lower latitudes. And this is indeed occurring. This would make a good subject for a posting. Another example would be the data showing some expected warming in the surface/mid layers of the oceans as reported by Levitus et. al. here a few years back in 2000 (with no follow-up since that I know of), from which I quote:
I’m sure there are a number of subjects I haven’t thought of off the top of my head.
I’m not criticizing, only making a suggestion, though I’m a bit weary of the “hockey stick controvery” which, at this point is akin in my mind to beating a dead horse.
[Response: You are not alone in thinking this….Hopefully we can get back on track soon! – gavin]
In response to #17 by Linn,
If there was more natural variability in the past as shown in MBH98/99, e.g. as the Moberg reconstruction shows, that doesn’t necessary lead to the conclusion that climate is more responsive to greenhouse gases (GHGs).
That would only be true, if the climate response was the same for the amount of energy retained by GHGs, as for the incoming energy from sunlight reaching the earth. But part of the sun’s influence is in the stratosphere, where CO2 (unlike some other GHGs) doesn’t play an important role. This leads to changes in Jet Stream position and in general (and specific low) cloud cover, fortifying the solar signal. No matter what (unknown) physical process causes the changes in cloud cover, these changes are observed during a sun cycle. See: http://folk.uio.no/jegill/papers/2002GL015646.pdf
If there was more natural variation in the past millenia, specifically due to solar changes, then that goes at the cost of the GHG/aerosol combination, as both are near impossible to distinguish from each other in the warming of the last halve century… Solar activity has never been as high, and for an as long period, as current in the past millenium (and even the past 8,000 years). See: http://cc.oulu.fi/~usoskin/personal/Sola2-PRL_published.pdf
[Response: The thinking here is essentially correct. If the influence of solar variability has been greatly underestimated, and the greater century-scale climate variability shown in some reconstructions is a) correct and b) due to that solar variability, then the climate sensitivity could be the same (or less) then indicated by other reconstructions. However, the data do not in fact suggest much evidence for (b): estimates of past solar forcing do not match up very well with the low frequency reconstructions — for example, if you try to explain the warming of the 20th century with solar forcing, then you wind up unable to explain the warm temperatures of the so-called Medieval warm period. Put another way, the “shape” of those reconstructions (e.g. Moberg et al.) which show greater century-scale variability are pretty much the same as the shape of the other reconstructions, so the correlation with solar variations doesn’t change. This leaves us with the explanation suggested by comment #17 above, which basically says that if the climate is more variable, then the climate system is more sensitive. See also the comments following our discussion of the Moberg et al. article –eric
[Response: Following up on what Eric has stated, we have to be very careful in drawing inferences regarding climate sensitivity from eyeballing these reconstructions. Such determinations require careful, quantitative analyses involving forcings estimates and reconstructions, and are fraught with limitations owing to uncertainties in both the forcing estimates and reconstructions–an excellent discussion is provided in this manuscript by Waple et al and references therein. A relevant cautionary tale involves the paper by Esper et al (2002) discussed elsewhere (here and here) on this site. Much was made of the possibility that this reconstruction might indicate greater sensitivity than other previously published reconstrucitons, because of the greater century-scale variability. A quantitative analysis by Crowley, however (AGU presentation, Spring 2002, Baltimore MD) indicated that this reconstruction actually implied a negative sensitivity to solar irradiance variations–something that is clearly unphysical. Its turns out that this is probably an artificial consequence of the simple fact that this reconstruction emphasises continental summer temperature variations, which exhibit a very large response to volcanic radiative forcing. The large volcanic forcing signal basically obliterates the far smaller solar forcing signal, which cannot be isolated in the presence of noise and other forcings from this reconstruction, yielding the spurious apparent negative response to solar irradiance. Another excellent discussion of these considerations is provided by: Hegerl, G.C., T.J. Crowley, S.K. Baum, K-Y. Kim, and W. T. Hyde, Detection of volcanic, solar and greenhouse gas signals in paleo-reconstructions of Northern Hemispheric temperature, Geophys. Res. Lett., 30, 1242, doi: 10.1029/2002GL016635, 2003. Suffice it to say, it is premature to speculate what implications the Moberg et al reconstruction might have for climate sensitivity, until a careful analysis such as that done previously by Hegerl et al, has been performed. –mike]
Maybe a dumb question BUT since the “hockey stick” shows up in the sunspot curves in 20 above, in the Solanski 2002 Jeffreys lecture solar irradiance curves, in Be-10 curves etc etc, indicating a driving solar forcing for the hockey stick, then why doesn’t it show up in the GCM models for natural only (see Is modelling science https://www.realclimate.org/index.php?p=100) Surely the volcanic forcings from one 1991 volcano can’t dominate the sun?
[Response: The forcings from the various components can be seen here. The variations in solar are indeed small over the last 50 years (basically just the 11 yr solar cycle), while there have been a number of important volcanoes dating from the 1960s (not just Pinatubo). And the volcanoes are undoubtedly a bigger effect. There is some uncertainty in the long term solar component, but not enough to change the balance over this time period at least. – gavin]
I think the essential point here is that the models, with some exceptions, only use direct insolation (the amount of heat from the sun reaching the surface) for the sun’s influence, the same way that other influences like from GHGs are covered. But there are essential differences. Most of the variation of the sun’s output is in the (far) UV, which has it’s largest influence in the stratosphere, while most GHGs have their influence in the lower troposphere.
The variation in the stratosphere leads to changes in jet stream position, rain patterns and especially cloud cover. The latter shows a variation of ~2% over a sun cycle. See Kristjánsson et al. The variation in sun cycle thus is reinforced, although the exact mechanism is not known. While there is less variation in solar strength in the past decades, the activity still is high and the oceans may not be (yet) in equilibrium with the extra heat inflow…
It is true that, as evidence that global warming is underway in accord with basic physics,
the hockey stick is just one item of evidence among many, and not even the most important one. However, there is a legitimate reason for putting so much energy into defending it. The “hockey stick” is an excellent educational tool. Much of the evidence and theory is complex and hard to explain. We are short on scientifically respectable arguments that can be immediately grasped by the public. I know from my own use of Mann et al when it first came out that it was a very good aid to public education about the nature of the problem. This is what it means to be an “icon.” The downside of an icon is that if it turns out to be wrong, or vulnerable, then skeptics can just try to pull down your icon and imply that everything else comes down with it. The Kilimanjaro glacier is also an icon of sorts, and Crichton’s disinformation on tropical mountain glaciers has similarly started working its way into the press.
(Note in passing: Skeptics have their icon’s too. Remember the satellite data that was supposed to show there was no warming? Why is it that there was not as much press attention paid to how wrong skeptics were about this? It’s as if they’re coated with teflon; they look bad to us, but I don’t think they look as bad as they ought to to other folks.)
Raymond Pierrehumbert has provided some crucial information. I wondered why the “hockey stick” was being singled out, and his comment explains alot. This removes much of the uncertainty about the attacks on the hockey stick. The attacks are political hits on the science. This is like the “swift boat veterans” ads from the right and “Fahrenheit 9/11” from the left in the past presidential election. All three played with the facts to score political points.
There is a current struggle for the support of the U.S. public. Simply put, if there is a great deal of public support climate change laws will be made. Those who oppose climate change regulation want to win the public relations game because without public support no climate change laws will be made.
The first step, but definitely not the only step, is to go after the science. Ideally bring down the science that is seen as the strongest science by the general public. As Raymond Pierrehumbert very aptly notes if you can take down the public icons you can cast doubt on all the science. If the public does not support the science they will not support the enactment of climate change regulation, and the climate change opponents will achieve their goal.
I think that “MM” are Canadians is also very important. They can be seen as outsiders and so not connected to the political debate in the U.S.. “MM” might not be seen as biased so will be seen as more believable by the U.S. public. Also since they are not scientists they are more likely to go to extremes that most scientists would not go.
The climate change science opponents take very deliberate and calculated steps. Things that seem like convenient coincidences probably are not and are more likely to have been planned out. I must admit, as much as I dislike their tactics, that the climate change opponents are very, very good at what they do in a very machiavellian way.
Raymond Pierrehumbert, you are thinking like a lawyer. This can be fairly easy to do. Just think, “If I wanted to stick it to someone what should I do?” Morals and ethics can be ignored for the purpose of this question.
Re #24. I agree that upon analysis it seems that M&M are operating in a Machiavellian way to score political points. But on the surface, they seem to truly believe that they are honest people trying to have a positive influence on climate science and public policy. I suspect that this has much more to do with complex psychology rather than deliberate deceit. Many people will jump through pyschological hoops rather than admit to themselves and others that their views on a particular matter might be incorrect. Political and philosophical worldviews will often cause people to selectively retain only certain facts, while discarding or overlooking ones that conflict with their worldview. This is often an unconscious process rather than deliberately planned.
Now consider this: to deal with greenhouse gas emissions, international agreements and national government policies and regulations are being proposed and enacted(at least in Europe and Canada). Some people automatically find such an approach repugnant, because they believe that centralized ‘bureaucrats’ are interfering with free market principles. This tends to colour their thinking and attitude towards the problem, including the scientific aspects. To give an example, a political science professor that I’ve communicated with believes that a good analogy for climate science and the ‘Kyoto clique’ is what happened in totalitarian communist Russia when they accepted the theory of ‘Lysenkoism’. Lysenkoism was a pseudo-Lamarckian biological theory that meshed with socialist philosophy, and was accepted as scientific truth for many years in Russia, but actually was total nonsense. So by analogy he implies that scientists working within the ‘global warming establishment’ are not really scientists, but actually are subversive manipulators and twisters of truth who hate capitalism!!(reminds me a bit of Chrichton’s book) There seemed to be no reasoning with him to change this view-it is so entrenched psychologically that he will do anything to convince himself that global warming is a non-science.
I’d also like to comment on the idea that that M&M being Canadian may have been designed purposefully to influence US policy. I find this is a bit of a speculative conspiracy theory. I think M&M are primarily concerned with the billions of dollars being spent by the Canadian federal government to meet Kyoto commitments, and that they truly have convinced themselves that this is a waste of taxpayer dollars (including their own). They have tried to loudly voice these concerns in forums such as ‘The National Post’, to try to spread the word among the Canadian public and scare policymakers away from the issue.(incidentally, much money was allocated towards a Kyoto strategy in the recent federal budget, but of course, it remains to be seen whether the strategy will work).
I think it might help to understand these psychological aspects of loud skeptics a bit more, rather than assume that they are simply the mouthpiece of “special interests”.
Sorry that this thread is getting a bit political, but ….
Thank you George (posting 25) — this is considerably more insightful than the old chestnut “all the contrarians are in the pay of the fossil fuel industry”. Your view coincides well with the impression I have gained from communicating with the contrarians over the past few years. A somewhat hyperbolical summary is that they are “mad not bad”. Which doesn’t mean to say that companies and organisations with something to gain from ignoring the “global warming story” do not make very good use of the resultant contrarian information!
I thank George Roman and John Hunter for their comments. Some constructive criticism is a good thing. When I try to keep my comments brief sometimes the message does not come out the way I intended.
My comment was not about M&M as individuals but really about how the hockey stick controversy and M&M’s arguments fit into the bigger picture of the climate change debate. M&M could definitely be acting on their own beliefs and were not originally connected to anyone else in the climate change debate.
In the U.S. there is an organized public relations campaign to dispute climate change science. What is notable about it is the sophistication and the negative tactics used. This can explain why the contrarians seem to be “coated with teflon” as Raymond Pierrehumbert notes. Maybe I will make another comment on that later. My earlier comment (#24) was really about this public relations campaign generally. When I said that the opponents of climate change science were very good but very machiavellian I meant the people involved in the public relations campaign, and not M&M specifically. I have commented against the negative tactics many times.
I think Raymond Pierrehumbert very lucidly explains why the hockey stick is being singled out. The way I brought up the fact that M&M are Canadian is conspiracy theory-ish. I will try again. I think it was possibly a political rhetoric tactic. Why the climate change contrarians in the U.S. latched onto M&M could be related to the fact that since M&M are not from the U.S. they could be perceived by the U.S. public as disinterested third parties and not politically partisan. It would be like getting a second opinion from a neutral observer. The goal is to be seen by the general public as unbiased and therefore more credible and more likely to be believed.
M&M are now involved in the U.S. climate change debate. They testified to the U.S. Congress after being invited by the very influential Senator Inhofe. The prestigious and widely read Wall Street Journal reported on their work and printed editorials favorable to them.
The issue of M&M not being scientists is something else I would like to address. In a purely scientific debate the question generally is if a study is valid. M&M’s (as an economist and mining executive) concerns are more politically, philosophically and economically motivated. They are more concerned with the economic and other effects of policy based on the science. This is not necessarily a bad thing, but it does influence the types of arguments used. M&M’s criticisms of the hockey stick are not very scientifically rigorous and sometimes venture into personal criticism. This is more of a legal type of argument that would be more common in the business world. Legal arguments are more about disparaging someone or something while scientific arguments focus on disproving an idea.
On a lighthearted note, maybe we should understand the psychological aspects of each other a bit more. We could have a more sensitive debate about climate change science. Maybe M&M and Dr Mann should get together and openly and honestly discuss their feelings and emotions.
Good post Mr Roman.
D
Your “dummies guide has confused me in an exponential sense even before I achieved a satisfactory base understanding of your theorem.
In the first section, You use the ambiguous term ‘noisy records’. Can you define ‘noisy records’ for my mom?
[Response: A data record that has a signal (that you are interested in), and ‘noise’ that you aren’t. Like listening to a static-filled radio station.]
From the second section please explain the following: Please explain in a geo-metaphysical sense, the relationship between ‘climate data applications’ and ‘the physics’ of a given algorithmic situation. Please explain this so my mother could understand it.
[Response: Think of a swing in a kid’s playground. It can move in a number of ways (or modes) (back and forwards, twisting, side to side) that can be predicted based on the physics (the length of the ropes, how far apart they are, the weight of the seat etc.). Now take a time series of the motion of a random swing. Numerically I can try and see what the most important patterns of movement are by doing a PC analysis. It’s likely (but not certain) that the first few individual PCs will resemble the modes I would have predicted based on the physics. But sometimes they won’t (if for instance someone was pushing the swing in a particular way). Thus the answers from the PC analysis may have a distinct physical meaning, but they don’t necessarily. When looking at climate data, the PCs may each have a distinct physical meaning, but not necessarily.]
From Section 3: Explain the ‘Monte Carlo’ simulation for us “dummies” before you apply it to your empirical position. Please do it in a way that my mom could understand.
[Response: Monte Carlo is famous for it’s casinos. There, many games of chance are played that depend on random numbers (i.e. the sequence of roulette plays). Many methods in mathematics or statistics that use large amounts of randon numbers to estimate whether something is coincidental or significant are therefore called Monte Carlo methods. For example, from many, many Monte Carlo simulations we know that rolling a normal die gives a 6 about 1/6th of the time. If instead, a die gave you a 6 a third of the time (over a long enough period) you would judge that significant and might therefore suspect it was loaded. ]
From Section 4: If your methods are objectively scientific, explain your ‘a priori’ parameters so my mom could understand them.
[Response: The question really is ‘do any ‘a priori’ assumptions affect the final result?’ The answer is no.]
This should keep your plate full. I will wait with baited breath for your response that will, no doubt, assimilate nicely with invective for the truth, and the scientific method.
[Response: Let me know how your mom gets on. -gavin]
Here’s an introductory chapter on-line about PCA as used in some astronomical applications:
http://adsbit.harvard.edu/cgi-bin/nph-iarticle_query?1999ASPC..162..363F
I tried to post a comment here on 28 February but perhaps it did not reach you by my mistake. It was a question about the second figure in the Section 4 of Part 2. I thought that it did not correspond with the text
“The MM05-based reconstruction is slightly less skillful when judged over the 19th century validation period but is otherwise very similar.”
Later I found that the figure is identical with as the Figure 2 of your previous posting (https://www.realclimate.org/index.php?p=8), and that it is clearly documented there. Thus I understand that the values of the MM05-based reconstruction over the 19th century was simply not shown. I still wish you to add some clarification for the readers of this page.
K. Masuda
In Yokohama (sometimes in Fujisawa), Japan
Ugh. This is so horribly written as to require a dummies guide to your dummies guide.
I’m speaking as someone who was somewhat well-read as to the state of the science circa 1993, who’s trying to brush back up on the subject.
[Response: Feel free to write it. -gavin]
Gavin: That would require my first understand finding out what the hockey stick is.
[Response: Ah. I see the problem…. Try this introductory post. – gavin]