A lot of what gets discussed here in relation to the greenhouse effect is relatively simple, and yet can be confusing to the lay reader. A useful way of demonstrating that simplicity is to use a stripped down mathematical model that is complex enough to include some interesting physics, but simple enough so that you can just write down the answer. This is the staple of most textbooks on the subject, but there are questions that arise in discussions here that don’t ever get addressed in most textbooks. Yet simple models can be useful there too.
I’ll try and cover a few ‘greenhouse’ issues that come up in multiple contexts in the climate debate. Why does ‘radiative forcing’ work as method for comparing different physical impacts on the climate, and why you can’t calculate climate sensitivity just by looking at the surface energy budget. There will be mathematics, but hopefully it won’t be too painful.
So how simple can you make a model that contains the basic greenhouse physics? Pretty simple actually. You need to account for the solar radiation coming in (including the impact of albedo), the longwave radiation coming from the surface (which depends on the temperature) and some absorption/radiation (the ’emissivity’) of longwave radiation in the atmosphere (the basic greenhouse effect). Optionally, you can increase the realism by adding feedbacks (allowing the absorption or albedo to depend on temperature), and other processes – like convection – that link the surface and atmosphere more closely than radiation does. You can skip directly to the bottom-line points if you don’t want to see the gory details.
The Greenhouse Effect
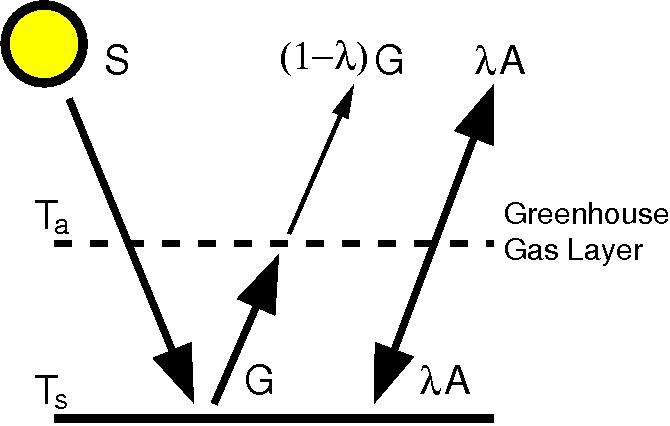 The basic case is set up like so: Solar radiation coming in is
The basic case is set up like so: Solar radiation coming in is ![]() , where
, where ![]() is the albedo, TSI the solar ‘constant’ and the factor 4 deals with the geometry (the ratio of the area of the disk to the area of the sphere). The surface emission is
is the albedo, TSI the solar ‘constant’ and the factor 4 deals with the geometry (the ratio of the area of the disk to the area of the sphere). The surface emission is ![]() where
where ![]() is the Stefan-Boltzmann constant, and
is the Stefan-Boltzmann constant, and ![]() is the surface temperature and the atmospheric radiative flux is written
is the surface temperature and the atmospheric radiative flux is written ![]() , where
, where ![]() is the emissivity – effectively the strength of the greenhouse effect. Note that this is just going to be a qualitative description and can’t be used to quantitatively estimate the real world values.
is the emissivity – effectively the strength of the greenhouse effect. Note that this is just going to be a qualitative description and can’t be used to quantitatively estimate the real world values.
There are three equations that define this system – the energy balance at the surface, in the atmosphere and for the planet as a whole (only two of which are independent). We can write the equations in terms of the energy fluxes (instead of the temperatures) since it makes the algebra a little clearer.
Atmosphere:
Planet:
The factor of two for A (the radiation emitted from the atmosphere) comes in because the atmosphere radiates both up and down. From those equations you can derive the surface temperature as a function of the incoming solar and the atmospheric emissivity as:
If you want to put some vaguely realistic numbers to it, then with S=240 W/m2 and ![]() =0.769, you get a ground temperature of 288 K – roughly corresponding to Earth. So far, so good.
=0.769, you get a ground temperature of 288 K – roughly corresponding to Earth. So far, so good.
Point 1: It’s easy to see that the G (and hence ![]() ) increases from S to 2S as the emissivity goes from 0 (no greenhouse effect) to 1 (maximum greenhouse effect) i.e. increasing the greenhouse effect warms the surface.
) increases from S to 2S as the emissivity goes from 0 (no greenhouse effect) to 1 (maximum greenhouse effect) i.e. increasing the greenhouse effect warms the surface.
This is an extremely robust result, and indeed has been known for over a century. One little subtlety, note that the atmospheric temperature is cooler than the surface – this is fundamental to there being a greenhouse effect at all. In this example it’s cooler because of the radiative balance, while in the real world it’s cooler because of adiabatic expansion (air cools as it expands under lower pressure) modified by convection.
Radiative Forcing
Now what happens if something changes – say the solar input increases, or the emissivity changes? It’s easy enough to put in the new values and see what happens – and this will define the sensitivity of system. We can also calculate the instantaneous change in the energy balance at the top of the atmosphere as ![]() or
or ![]() changes while keeping the temperatures the same. This is the famed ‘radiative forcing’ you’ve heard so much about. That change (+ve going down) is:
changes while keeping the temperatures the same. This is the famed ‘radiative forcing’ you’ve heard so much about. That change (+ve going down) is:
where ![]() are the small changes in solar and change in emissivity respectively. The subscripts indicate the previous equilibrium values We can calculate the resulting change in G as:
are the small changes in solar and change in emissivity respectively. The subscripts indicate the previous equilibrium values We can calculate the resulting change in G as:
so there is a direct linear connection between the radiative forcing and the resulting temperature change. In more complex systems the radiative forcing is a more tightly defined concept (the stratosphere or presence of convection make it a little more complex), but the principle remains the same:
Point 2: Radiative forcing – whether from the sun or from greenhouse gases – has pretty much the same effect regardless of how it comes about.
Climate Sensitivity
The ratio of ![]() is the sensitivity of
is the sensitivity of ![]() to the forcing for this (simplified) system. To get the sensitivity of the temperature (which is the more usual definition of climate sensitivity,
to the forcing for this (simplified) system. To get the sensitivity of the temperature (which is the more usual definition of climate sensitivity, ![]() ), you need to multiply by
), you need to multiply by ![]() i.e.
i.e. ![]() . For the numbers given above, it would be about 0.3 C/(W/m2). Again, I should stress that this is not an estimate for the real Earth!
. For the numbers given above, it would be about 0.3 C/(W/m2). Again, I should stress that this is not an estimate for the real Earth!
As an aside, there have been a few claims (notably from Steve Milloy or Sherwood Idso) that you can estimate climate sensitivity by dividing the change in temperature due to the greenhouse effect by the downwelling longwave radiation. This is not even close, as you can see by working it through here. The effect on ![]() due to the greenhouse effect (i.e. the difference between having
due to the greenhouse effect (i.e. the difference between having ![]() and its actual value) is
and its actual value) is ![]() , and the downward longwave radiation is just
, and the downward longwave radiation is just ![]() , and dividing one by the other simply gives
, and dividing one by the other simply gives ![]() – which is not the same as the correct expression above – in this case implying around 0.2 C/(W/m2) – and indeed is always smaller. That might explain it’s appeal of course (and we haven’t even thought about feedbacks yet…).
– which is not the same as the correct expression above – in this case implying around 0.2 C/(W/m2) – and indeed is always smaller. That might explain it’s appeal of course (and we haven’t even thought about feedbacks yet…).
Point 3: Climate sensitivity is a precisely defined quantity – you can’t get it just by dividing an energy flux by any old temperature.
Feedbacks
Now we can make the model a little more realistic by adding in ‘feedbacks’ or amplifying factors. In this simple system, there are two possible mechanism – a feedback on the emissivity or on the albedo. For instance, making the emissivity a function of temperature is analogous to the water vapour feedback in the real world and making the albedo a function of temperature could be analogous to the ice-albedo or cloud-cover feedbacks. We can incorporate the first kind of physics by making ![]() dependent on the temperature (or
dependent on the temperature (or ![]() for arithmetical convenience). Indeed, if we take a special linear form for the temperature dependence and write:
for arithmetical convenience). Indeed, if we take a special linear form for the temperature dependence and write:
then the result we had before is still a solution (i.e. ![]() ). However, the sensitivity to changes (whether in the greenhouse effect or solar input) will be different and will depend on
). However, the sensitivity to changes (whether in the greenhouse effect or solar input) will be different and will depend on ![]() . The new sensitivity will be given by
. The new sensitivity will be given by
So if ![]() is positive, there will be an amplification of any particular change, if it’s negative, a dampening i.e. if water vapour increases with temperature that that will increase the greenhouse effect and cause additional warming. For instance,
is positive, there will be an amplification of any particular change, if it’s negative, a dampening i.e. if water vapour increases with temperature that that will increase the greenhouse effect and cause additional warming. For instance, ![]() , then the sensitivity increases to 0.33 C/(W/m2). We could do a similar analysis with a feedback on albedo and get larger sensitivities if we wanted. However, regardless of the value of the feedbacks, the fluxes before any change will be the same and that leads to another important point:
, then the sensitivity increases to 0.33 C/(W/m2). We could do a similar analysis with a feedback on albedo and get larger sensitivities if we wanted. However, regardless of the value of the feedbacks, the fluxes before any change will be the same and that leads to another important point:
Point 4: Climate sensitivity can only be determined from changes to the system, not from the climatological fluxes.
Summary
While this is just a simple model that is not really very Earth-like (no convection, no clouds, only a single layer etc.), it does illustrate some relevant points which are just as qualitatively true for GCMs and the real world. You should think of these kinds of exercises as simple flim-flam detectors – if someone tries to convince you that they can do a simple calculation and prove everyone else wrong, think about what the same calculation would be in this more straightforward system and see whether the idea holds up. If it does, it might work in the real world (no guarantee though) – but if it doesn’t, then it’s most probably garbage.
N.B. This is a more pedagogical and math-heavy article than most of the ones we post, and we aren’t likely to switch over exclusively to this sort of thing. But let us know if you like it (or not) and we’ll think about doing similar pieces on other key topics.
I enjoy the challenge of obtaining a more robust understanding. Most people some to this site for more in depth analysis so I expected some math earlier. I support similar posts – but not to many. I suggest that you have a section on your site for a mathematical analysis. In addition you should have some links to “atmospheric math/science for dummies” so a lay person such as myself could get an even deeper understanding. In time there would be interest for sporadic intermediate or higher level postings that could be heavily linked for a newbie to obtain the necessary knowledge to follow the argument. Keep up the great work.
I would like to see one article in the future.
It is clear that different factors affect the climate.
For example, solar, C02, …
Given the data it is possible to build a model that shows the contribution of each of the factors to global temperature in a statistical way. This shows how important in each factor was in the historical climate record.
The factors of which I’m aware are solar, atmosphere constituents, volcanos, orbital mechanics.
They all contribute and in somes cases with lags.
The statistical model then shows which are significant and which aren’t.
Now you move forward to the industrial era and you can now show what man’s contribution is, and whether or not it is statistically significant.
You can also take the models, and see if they predict the historical record, and if they are statistically different.
Nick
[Response: Try: https://www.realclimate.org/index.php/archives/2005/05/planetary-energy-imbalance/ -gavin]
Bring on the math. As the lucky father of a mathematically gifted 12 year old I’ll have him explain it to me.
Seriously though, unfortunately, most people think like the infamous jornalist Richard Cohen who wrote the piece entitled “What Is the Value of Algebra?”
http://www.washingtonpost.com/wp-dyn/content/blog/2006/02/15/BL2006021501989.html
I’m not good at maths but the way to get better can’t be no maths.
Gavin,
I know this is already a simple model, but I think it would be a great addition to post the diagram that always gets drawn with it. I can try to dig one up at work, but I believe that just sketching a couple of arrows and scanning the figure would really help to make this actually “simple.”
[Response: You are absolutely correct. A figure has now been added. – gavin]
Re #55 It seems that this is a well known model. Does it have a name, or is there another way to cite it?
[[I’m not sure I picked up the distinction between atmospheric absorption and atmospheric emission (not an engineer). How do these two relate? ]]
For an object in “local thermal equilibrium,” the emissivity equals the absorptivity (Kirchhoff’s Law). In English:
Assuming no chemical or nuclear change, light can only interact with a material object in one of three ways —
* absorption — the object can absorb the light, usually heating up.
* reflection — the object can bounce back or scatter the light.
* transmission — the object can let the light go right through it.
Expressed as decimal fractions, these three have to sum to 1:
A + R + T = 1
To pick an example, the Earth’s surface absorbs about 95% of incoming light in the visual range, reflects about 5%, and transmits none at all (it’s opaque).
Now, every object not at absolute zero radiates photons. The power (energy per unit time per unit surface area) radiated by an object is:
F = ε σ T4
where F is the output per unit area (F for “flux”), σ is the Stefan-Boltzmann constant (5.6704 x 10-8 in the appropriate units in the SI), and T is the temperature (degrees Kelvin in the SI).
The quantity ε is the “emissivity.” This can range from 0 to 1 for any real object. A perfect radiator with ε = 1 is a “black body” or “black body radiator.” But in practice very few objects are perfect blackbodies, most have an emissivity between 0 and 1.
Under “local thermal equilibrium,” ε = A (Kirchhoff’s Law again).
Engineer’s know just enough to get in to trouble? I think the engineer’s have a better handle on it than the scientists who never took the really hard classes. We actually have to design things that work. This article should have contained some info. on the stefan boltzmann equation forcing more cooling with increase in surface temp. but didn’t. “cooler because of adiabatic expansion (air cools as it expands under lower pressure)” Please check the def. of adiabatic. You may have meant the right thing but said it in the wrong way.
Re: #58 (KS)
The solution to engineer-bashing is not scientist-bashing. Let’s judge each argument on its merits, regardless of its origin.
As for “cooler because of adiabatic expansion (air cools as it expands under lower pressure) Please check the def. of adiabatic,” a parcel of air does indeed cool as it expands adiabatically. Adiabatic does not mean isothermal.
One has to wonder what kind of engineer is being talked about here with “just enough math to get in trouble”. Obviously not engineers who have taken thermodynamics, and have been talking about convection on this subject for a long time. Maybe software “engineers”? “Hot air rises” is not a new concept…
P.S. you’re letting your prejudice show:
“Now we can make the model a little more realistic by adding in ‘feedbacks’ or amplifying factors”
Feedbacks are also damping factors.
[Response: Hmmm. Who is lettering their prejudices show? Who ever said that an ‘amplifying factor’ cannot be a ‘negative feedback’ (i.e., a ‘damping factor’ depending on precisely which variables you are talking about). Consider the radiation of outgoing longwave radiation (OLR) to space. As you increase the surface temperature, you tend to increase the OLR, in proportion to the 4th power of the temperature in fact. Seems like an ‘amplifying factor’ to me. Of course, its obviously a ‘negative feedback’ as well (warmer surface temperatures leading to greater heat loss from the surface), in fact the key negative feedback that prevents runaway warming of the Earth’s surface over time. In other words, it is an ‘amplifying factor’ with respect to OLR, but a ‘damping factor’ with respect to surface warmth. – mike]
re: 60. ??? Nothing in the original statement said ‘feedbacks’ could not be damping factors. It was “‘feedbacks’ OR amplifying factors” (emphasis added). To assume otherwise is showing your prejudice.
Adding up the A1B scenario greenhouse gas forcings for 2100 taken from the IPCC TAR I get about 4.1 Watts/m^2, most of which (3.48) comes from CO2.
The calculation above gives a temperature rise of 1C relative to 2000, but the models (in the 4th assessment report SPM) give a range of about 1.8-4.2C rise for the A1B scenario which require upto 8-9 Watts more forcing.
So what are the other processes in the models that are causing the additional warming? Section 7.2.1.1 suggests that water vapour doubles (or more) the warming. Is this it? Or are there other major effects.
Steve —
Doubling CO2 increases the Earth’s temperature 1.2 K by itself (Houghton 2004) but 2-4 K with all the feedbacks (IPCC 2001, 2007).
Thanks for this introduction to climate modeling.
A quantitative model is a quantitative hypothesis. We have observed historical climate data over the last 150 years which we can test against climate models/hypotheses. A climate model which ‘simulates’ (fits) past observations better than another is more likely to be true. There are too many variables so some approximation is inevitable.
The climate debate is about whether there is a significant human cause of current global warming.
– Climate skeptics no longer doubt that the earth is warming, they claim the causes are purely natural eg sunspots and volcanoes.
– The IPCC does not doubt that there are natural causes of recent global warming but they claim 90% certainty that this warming has a significant human cause.
These competing hypotheses can be tested by quantitative models see UK Met Office Climate Change Myths.
http://www.metoffice.gov.uk/corporate/pressoffice/myths/index.html
The two graphs next to Myth 2 show that natural causes alone cannot explain the increase in earths temperature since about 1975. But If human factors are added to natural causes we get a much better fit to the observed data.
AFIK climate skeptics have not been able to provide a quantitative model of natural-only causes which fit the observed data so well. Please correct me if I’m wrong.
This is the key data the climate skeptics ignore, instead they attack the straw man that ALL climate change is man-made.
So, climate models do simply explain it all?
(Yes, I am a denialist, an skeptical, or whatever thing you call those people who does not trust the global warming as a matter of faith)
#62, The context is feedbacks (aka) amplifying factors, as RC typifies feedbacks as generally positive. This statement just entirely negates the potential for damping feedbacks – RE#64. Of course #64 discounts the fact we know next to nothing about cloud feedbacks – even the sign.
#65, don’t confuse CO2 forcings with all anthropogenic forcings, including land use changes, black carbon and other dust on ice, etc. Re those other changes, could not we tell the magnitude of the difference in CO2 forcing compared to some of the other anthropogenic forcings by looking at the temperature trend of the Arctic vs. Antarctica?
#63 and #64 I know that water vapour is a feedback, not a forcing, but since water vapour seems to be so important I’m really looking for an addition to the simple model that says X amount of warming results in Y increase in water vapour, and barring clouds etc. this water vapour adds an additional “radiative forcing” of Z – such that a few iterative calculations can provide an estimate of the temperature rise.
If such a simple extension is not helpful, then why not?
re: the parentheses in 66. Of course it is not a matter of faith. No one shoud accept it as that. It is a matter of science. Data, experiments, hypotheses, conclusions, peer review…the scientific method. It works. And the science behind global warming is quite strong.
Feedbacks come in two very different types. 1) Negative feedbacks which, despite their name, are good and stabilise the system by damping any changes. 2) Positive feedbacks which, unlike their name, are bad and amplify changes. Once they get over 40% they cause oscillations or strange attractors. If they get over 100% they produce a runaway effect – just like what happened in the rapid climate change at the end of the Younger Dryas stadial.
So you can have negative feedbacks and amplifying factors, or damping effects and positive feedbacks, but not feedbacks and amplifying factors. “Amplifying factors” is redundant when used that way.
HTH,
Cheers, Alastair.
re: 67. No, not at all. RC does not typify feedbacks as generally positive. To assume so is a quite clear prejudice. As a simple example, a quick search on “negative feedback” at the top of the page yields, among other things, https://www.realclimate.org/index.php/archives/2006/08/climate-feedbacks/
Both positive and negative feedbacks are discussed in that one specific example. Now particular feedbacks may be discussed as positive, such as CO2 or water vapor, simply because they are.
Ian Plimer is again getting some mileage here in Australia. This ran as a lead story on news.com.au and has already been the subject of a couple of op-ed pieces here. Lots of tired old stuff that have been covered countless times before, yet for some reason, this fellow seems to attract more media than he deserves.
http://www.news.com.au/story/0,23599,21542564-2,00.html
I just wanted to say that I’m very glad to see this sort of article on your site. RealClimate is one of the most popular climate sites on the net so I think that you do your readership a great service by bringing them up to speed on the basics of climate science. The people who honestly want to learn about climate science understand that they need to learn the basic mathematics of the science.
I’d go even further and say that I think you should long running series of articles based on this simple model that eventually build up to as close of a model to the ones found in IPCC report as possible. Given the collective will of reasonable people to not kill life on earth, using your site to raise the cognitive models of how people view climate should help raise the level of debate due to people with good models being able to trash the arguments of people with bad models. You do that a lot here in your comment section, so I think by putting a series of articles together that can help others learn to trash similarly poor arguments they encounter in their own lives you give the truth a weapon.
In short, kudos and I hope this is not the last of the “more technical” articles. This site is your bully pulpit and I think your readership will appreciate any help in lifting their cognitive models.
Thanks…now if these types of articles were just available as PDFs (or even PS files)….quibble, guibble…More of the same would be fine with me.
re: #72:
As I recall, news.com.au belongs to Rupert Murdoch, i.e., like Fox News.
I conjecture that’s adequate reason for this to appear there.
I’ve been in Oz about dozen times, and unless it’s changed recently:
a) You have a *lot* of coastline, and most Australians live near it.
b) Most of the big cities aren’t very far above sea level. I’d be a little nervous for places like the Whitsundays, Freemantle, the Gold Coast, Cairns, even with 1-2-foot rise. Canberra seems safe.
c) You could use more water.
d) Like here in CA, you have trouble with forest fires, especially when it’s hot.
At least the article was a nice checklist of bad ideas :-)
Re: #73 (EntropyFails)
I’d love to see such a work. But it would involve much more complicated mathematics (vector calculus), and much more complicated physics (the Clausius-Clapeyron equation is not for everybody). So I don’t think it would be appropriate as a series of blog posts.
It would make an appropriate textbook. So if any of you RC guys have such a work, at that level, available as pdf, then … bring it on!
because I’m not sure where else to post this, is there any resource that I might use to explain climate anomalies such as the cold snap we are having in April, within the global warming debate?
Gavin
You made mention of being careful about cold events in relation to climate change.
Strikes me with more energy in the system – gradients are steeper and boundary conditions between high and low pressure systems may vary from the longer term geographic norms…..ie stronger Pacific storms might force cold continental systems further south and east at times just as a for instance.
More energy retained I would think would produce more chaotic boundaries with higher energies, – an abnormal incursion of warm or cold air masses might push farther and run into geophysical regions ( ie Great Lakes or mountain funnels not reached in a less energetic atmosphere. )
Seems to me that gradients might build higher before releasing as well in an energetic/chaotic climate so while cold events might occur outside the norms from time to time as air masses collide with more energy.
I would also think the jetstreams would show increased energy levels which again might mean unusual cold intrusions.
I’d be happy to be set straight but seems to me that “outside the norm” excursions of cold air or water could be expected in some locales in an overall more energetic system.
Jaime, someone (maybe you? I forget) asked that elsewhere recently. Weather isn’t climate, so this is the wrong website; have you tried NOAA?
http://www.cpc.ncep.noaa.gov/products/tanal/montoday/mon2day.gif
One more for Jamie, this might be helpful (just found with a quick Google search, not something I can evaluate, you might find reading up on this a challenge worth taking on):
http://weatherclimatelink.blogspot.com/2007/01/no-fooling-around-possibly-severe-cold.html
Could not we tell the magnitude of the difference in CO2 forcing compared to some of the other anthropogenic forcings by looking at the temperature trend of the Arctic vs. Antarctica?
[Response: No. The impact of any forcings depends on a number of issues – local heat capacity (much higher in the Southern Hemisphere due to the greater extent of oceans), difference in dynamics and impacts of other factors (like the ozone hole). It’s therefore not as straightforward as one might hope. – gavin]
Re #77 (Jamie): The question is whether the cold snap that we are having here in the Eastern U.S. is really that unusual. Sure, it has been colder than average for several days…maybe even a couple standard deviations colder than average for a few of them. But, I didn’t get the impression it was record-setting cold. (A few places may have broken DAILY records…that is the record for a particular day…but those are relatively easy to break.)
The point is that in the absence of crunching through the statistics, one can’t really determine how anomalous this cold is. And, frankly, I don’t get the impression that it is that anomalous. It takes a lot of work to actually pull out a trend from a system with large fluctuations.
Reference #57
First off, thanks for responding.
This “local thermal equilibrium” concept appears important.
I can understand the idea of solid objects radiating at each, and having the same radiation field if they are at the same T and are made of the same material. I think I have a reasonable grasp of black body radiation coming from objects based on the temperature of the object.
It makes sense that bodies of gases in the same state should have the same radiation properties.
In either case, the net radiation should be zero.
Black body to balck body, gas to gas.
You are losing me at the gas/solid interface. Does this concept of “local thermal equilibrium” apply to the gas/solid interface? Are there other concepts that are necessary to consider in this case?
If a gas is in contact with a black body, and they are both at the same temperature, does the concept imply that they will have similar radiation characteristics? I am not clear on this point.
These kind of posts are very valuable and much appreciated, even if they take much longer to read through. :)
Regarding “Point 1: It’s easy to see that the G (and hence T(s) ) increases from S to 2S as the emissivity goes from 0 (no greenhouse effect) to 1 (maximum greenhouse effect) i.e. increasing the greenhouse effect warms the surface.”, I’d suggest including a graphical representation of the equation, with lambda on the x-axis and both G and T(s) on the y-axis. A picture of an equation is a lot easier for the layperson to understand than an algebraic expression and helps remove the equation fear factor (and is also easier to see).
Also, simple terms like emissivity can be confusing, but wikipedia and other sites have good descriptions: http://en.wikipedia.org/wiki/Emissivity
As to how engineers can get into trouble with math, this is not really a dig at engineers – cross-field misunderstandings are many. Comments on positive and negative feedbacks by engineers whose experience is with electronics are a good example and have appeared on RC. Understanding feedback in an electronic circuit doesn’t mean that you understand the multi-variable and competing positive/negative feedbacks that affect climate, from albedo to water vapor to carbon cycle effects (once I spent five minutes talking to a history teacher about positive and negative feedbacks and climate before I realized he thought I was saying ‘good’ and ‘bad’ – whoops!)
Anyway, this kind of thing is very useful. A simple box model of the carbon cycle could be treated similarly.
Interesting. thanks for your responses. The type of people I am in conversation with at times use this as “evidence” of the “myth” of global warming.
I think this post is great!
It clearly breaks down the basic “voodoo-witchery” mystery of how climate models work for the public.
This is something they can see, feel and manipulate…and dare I say relate to better now because of this post. Outstanding! Great topic!
As a friendly note to those who suggested Mr. Schmidt et al. should do “this” or “that” on this site. Do it yourself or give these folks a $100 or more donation.
I do find it funny about those who demand extreme levels of scientific proof that high amounts of CO2 can heat up a planet, given … hmmm … Venus.
It’s that neon-argon Venusian atmosphere, I guess.
#77 This Southern cold snap was one month in the making in the North American Arctic (during March), studied it with great fascination before it went to your location, it simply slowly moved South since early April. I would rather look at the rest of the world, as a sure sign of the summer weather to come, In its wake, Arctic temperatures made an about face, total rebound in temperatures, from record cold to record warm in a few days. I’ll have an optical breakdown of this March cold air mass on my website at the end of April, Density weighted temperature reached 231 Kelvin at its coldest point, it was like being in the reverse eye of an hurricane, no wind, extremely low tropopause and very little heat.
I appreciate this post, as there is not enough equations…. Examples about practical use of these equations would be greatly appreciated.
RE #22:
In addition to good points made by Steve in post #31, I would add the following.
Some of the solar energy turns liquid water and soil moisture into water vapor instead of “heating” the surface and near-surface air. Instead of raising the temperature of the soil, it induces the phase change. The resulting water vapor is lofted upward (lower density than the “air”). The total heat in this case is the same – its just distributed differently making the effective air temperature at the surface cooler. In the desert, the heat is concentrated at the surface of the absorbing/reflecting object.
At night, in the desert, a significant fraction of the heat absorbed is quickly radiated away. In the wet environment, the additional water vapor created during the day absorbs the long wave radiation emitted at night (greenhouse effect) and then as the night wears on and the air cools, the water vapor condenses back to the surface warming the surface and near-surface air by giving “back” the heat required to become vapor. Of course, some of the water vapor lofts high into the atmosphere and flows away from the source redistributing that heat elsewhere (stupid complexity issues…)
The net effect being the desert is really hot during the day – but fairly cool at night. Over areas of high moisture (ocean, jungle, etc). The day is very warm (but typically under 40C) and humid, but the night is warm and humid. If the albedo effects are a “wash” and the convection doesn’t carry off too much vapor, the “average” temperature (24 hour day) is going to be higher in the wet climate than the desert climate at the same latitude. But you can die from heat stroke in both places.
I aint a scientist but id like to know what HAARP contributes to global warning if any?
Being a simpleton, and not having been forced to endure mathematics for a couple of decades, it would be helpful if you better explained all math symbols (particularly the subscripts and superscripts, Kelvin scale, the tilda, etc.) used (even if that bores you and all of the engineers), to plug in real figures, and to provide more explanation of the involved factors. I followed some of the equations but eventually gave up.
Don’t underestimate the ignorance of the lay person…
Here is Gavin’s model (without feedbacks) in the Just Basic programming language. Sorry for the way it appears in HTML, e.g. the apparent lack of indents. < pre > wasn’t much of an improvement. For anyone who wants to use it, just cut and paste into your own Basic interpreter or compiler, or translate to C or Fortran or whatever.
‘******
‘—–
‘ Gavin.bas implements a simple greenhouse model.
‘—–
sigma = 5.6704e-08 ‘ Stefan-Boltzmann constant.
answer$ = “Y” ‘ Response from user.
while answer$ = “Y”
input “Solar constant? Observed is 1367.6: =>”; S
input “Bond albedo? Observed is 0.306: =>”; A
input “Emissivity? Observed is 0.769: =>”; lambda
Ftop = (S / 4.0) * (1.0 – A) ‘ Find absorbed flux.
G = Ftop / (1.0 – 0.5 * lambda) ‘ Find ground emission.
Ts = (G / sigma) ^ 0.25 ‘ Find ground temperature.
Print
Print “Ftop =”, Ftop ‘ Display results.
Print “G =”, G
Print “Ts =”, Ts
Print
input “Again [Y/N]? =>”; answer$ ‘ Repeat if user wishes.
answer$ = upper$(answer$)
Print
wend
end
RE “factor 4 deals with the geometry (the ratio of the area of the disk to the area of the sphere)”
I like to visualize things. Does this 1/4 have to do with the sun hitting a flat (if made small enough thru calculus) area on earth, as opposed to a spherical area. Or does it have to do with a flat area (if made small enough thru calculus) of the sun aimed at us, as opposed to the radiation from its entire spherical surface (i.e., we don’t get the whole of the sun’s radiation, only 1/4 — which seems a bit large, since we are so small)?
What is the Stefan-Boltzmann constant? Is that the temp of the earth, if you go down, say, 6 feet? I know there is a some constant of about 55 degrees F (assuming there isn’t a extreme deep freeze that bursts the pipes).
If so, I believe that’s the principle behind geothermal heating/cooling systems. If it’s 10 below zero F outside, you pump 55 degree air through the underground pipe system, then warm it a bit more to comfort level. I think it may also work as an AC as well.
What is “emissivity”? Is that like reflection of warmth, or reflection plus existing warmth (the earth’s constant being maintained in the process)? Or infrared waves?
Hi chaps,
How about sending this article to that Viscount Monckton? Not that I’m implying anything of course of someone who’s not afraid of sending in the lawyers…
http://environment.guardian.co.uk/climatechange/story/0,,2053520,00.html
Here are some links, some of which have to do with models underestimating the rate of world-glacier/ice shelf disintigration.
The models don’t include yet (or weakly model) alot of the ice physics, such as positive feedbacks such as melt ponds, crevasse propagation, thermal ice diffusion, buttressing/ keystone effects, moulin, water lubrication effects ..remember Gavin’s feedback equations above!!!)…
and some mention of Gavin’s work too. Fascinating and understandable.
http://portland.indymedia.org/en/2007/04/357344.shtml
Re: #94 (Lynn Vincentnathan)
It has to do with the fact that the earth intercepts sunlight proportional to its cross-sectional area (pi * R^2), but that energy gets spread over the earth’s surface area (4 * pi * R^2). So the 1366 W/m^2 for a square meter directly facing the sun, is diluted by (p * R^2) / (4 * pi * R^2) = 1/4 of that, or about 341.5 W/m^2.
No, the Stefan-Boltzmann constant relates the energy emitted by a radiating object to its temperature. Warm objects (“warm” meaning above absolute zero) radiate away some of their energy as electromagnetic waves (light). The amount they radiate depends on temperature. Since energy is measured in one set of units (Joules, ergs, watt-hours, whatever) and temperature in another (deg.K), there has to be a conversion factor: the Stefan-Boltzman constant is it.
The Stefan-Boltzman constant is unrelated to geothermal heating. But the earth, below its surface, is indeed hotter than the surface, and we can use that temperature difference to drive a heat engine, extracting the energy for useful work. Also, the earth’s subsurface temperature doesn’t follow the same annual cycle (seasons) that surface temperature does. And, the deeper you go into the earth, the hotter it is.
No, it’s the radiation of energy. The energy is already there, as heat (or other forms), but objects naturally tend to give that energy away as electromagnetic waves (light) — that’s emissivity.
[[I like to visualize things. Does this 1/4 have to do with the sun hitting a flat (if made small enough thru calculus) area on earth, as opposed to a spherical area. Or does it have to do with a flat area (if made small enough thru calculus) of the sun aimed at us, as opposed to the radiation from its entire spherical surface (i.e., we don’t get the whole of the sun’s radiation, only 1/4 — which seems a bit large, since we are so small)?]]
The Earth intercepts sunlight on its cross-sectional area, which is pi R^2, where R is the Earth’s radius. But its actual surface area is that of a sphere, 4 pi R^2. So the Solar constant has to be divided by four to see how much sunlight hits an average square meter of the Earth.
[[What is the Stefan-Boltzmann constant?]]
It’s the proportionality constant in the Stefan-Boltzmann radiation law:
F =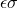 T4
T4
F is the flux the object radiates, power per unit area (watts per square meter in the SI). is the object’s emissivity (discussed below);
is the object’s emissivity (discussed below); 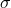 is the Stefan-Boltzmann constant, T is the temperature (degrees Kelvin in the SI).
is the Stefan-Boltzmann constant, T is the temperature (degrees Kelvin in the SI).
The value of the Stefan-Boltzmann constant is about 5.6704 x 10-8 W m-2 K-4 in the SI. In the English system it would have a different value and the units would be something like BTUs per second per square foot per Rankine degree to the fourth power.
[[What is “emissivity”?]]
It’s µ from the above equation, and it describes an object’s efficiency as a radiator. An emissivity of 0 means the object radiates nothing at all (it’s surrounded by some kind of perfect insulator). An emissivity of 1 means the object is a perfect or “black body” radiator. Most real objects have an emissivity somewhere in between.
Re 93 (Lynn’s comments)
One way to visualize the factor of four difference due to the geometry of a disk versus a sphere is to imagine a colander, which one might use to strain spaghetti, for example. The top surface, which is open, is shaped like a disk, while the bottom screened surface is shaped like a hemisphere. The same quantity (heat, light, electric field, etc.) that passes through the curved surface must pass through the disk-like surface, as long as no heat, light, or charge is generated in the colander itself. In other words, the flux passing through the curved surface must be the same as the flux passing through the disk. This is the essence of Gauss’s Law. When you calculate a flux, you have to take into account the angle between the field line and the normal to your surface. If the sun’s rays come in at a glancing angle, your flux is smaller. The flux is zero at the edges of the sunlit side of Earth, and it is a maximum at the center of the sunlit surface. Now you could systematically integrate across the hemispherical surface of Earth, taking into account the angle of the sun’s rays, or you could remember that the flux is the same for a disk or a hemisphere. The reason for this is because the sun’s rays are perpendicular to the disk everywhere.
As for your question about Stefan-Boltzmann’s constant, it might help to consult a reference such as Wikipedia to get a feel for what the relationship is. I have my students investigate the Stefan-Boltzmann law by using a light bulb connected to a variac, which is used to systematically change voltage. They have to connect an ammeter and a voltmeter, so that they can calculate the resistance of the tungsten filament as the bulb gets brighter and brighter. By examining published tables for resistivity of tungsten as a function of temperature, students can estimate the filament temperature at each voltage step. By plotting power (current times voltage) against temperature on a log-log plot, they get an exponent of about 3.9. My hope is that by using commonplace objects, students will realize that many objects obey Stefan-Boltzmann’s equation, not just distant stars like our Sun.
Re #93: [If so, I believe that’s the principle behind geothermal heating/cooling systems. If it’s 10 below zero F outside, you pump 55 degree air through the underground pipe system, then warm it a bit more to comfort level. I think it may also work as an AC as well.]
Err… Not exactly. What you’re describing is ground source heating/cooling, though it’s often miscalled geothermal in ads. A true geothermal heating system uses heat from a hot spring or similar. A ground source system uses a heat pump to take advantage of the fact that the ground below the frost line stays at a fairly constant 55F or so year round. Thus in the winter, the system can actually move heat from the relatively warm ground to the house using less energy than it would to heat the cold outside air, while in summer the reverse is true.
If this seems like magic to you, well, it does to me too :-)
Re:
The basic case is set up like so: Solar radiation coming in is S=(1-a) mbox{TSI}/4, where a is the albedo, TSI the solar ‘constant’ and the factor 4 deals with the geometry (the ratio of the area of the disk to the area of the sphere). The surface emission is G=sigma T_{s}^{4} where sigma is the Stefan-Boltzmann constant, and T_s is the surface temperature and the atmospheric radiative flux is written lambda A=lambda sigma T_{a}^{4}, where lambda is the emissivity – effectively the strength of the greenhouse effect. Note that this is just going to be a qualitative description and can’t be used to quantitatively estimate the real world value
It isn’t the math that gets me, when I was taught pi=C/D I was also told what circumference and a diameter was.
What is albedo, what is the disk(area of sunlight?) (is the sphere is earth?) , and Stefan-Boltzmann constant, and surface temperature and the atmospheric radiative flux