Guest post by Tamino
In a paper, “Heat Capacity, Time Constant, and Sensitivity of Earth’s Climate System” soon to be published in the Journal of Geophysical Research (and discussed briefly at RealClimate a few weeks back), Stephen Schwartz of Brookhaven National Laboratory estimates climate sensitivity using observed 20th-century data on ocean heat content and global surface temperature. He arrives at the estimate 1.1±0.5 deg C for a doubling of CO2 concentration (0.3 deg C for every 1 W/m^2 of climate forcing), a figure far lower than most estimates, which fall generally in the range 2 to 4.5 deg C for doubling CO2. This paper has been heralded by global-warming denialists as the death-knell for global warming theory (as most such papers are).
Schwartz’s results would imply two important things. First, that the impact of adding greenhouse gases to the atmosphere will be much smaller than most estimates; second, that almost all of the warming due to the greenhouse gases we’ve put in the atmosphere so far has already been felt, so there’s almost no warming “in the pipeline” due to greenhouse gases already in the air. Both ideas contradict the consensus view of climate scientists, and both ideas give global-warming skeptics a warm fuzzy feeling (but not too warm).
Despite the celebratory reaction from the denialist blogosphere (and U.S. Senator James Inhofe), this is not a “denialist” paper. Schwartz is a highly respected researcher (deservedly so) in atmospheric physics, mainly working on aerosols. He doesn’t pretend to smite global-warming theories with a single blow, he simply explores one way to estimate climate sensitivity and reports his results. He seems quite aware of many of the caveats inherent in his method, and invites further study, saying in the “conclusions” section:
Finally, as the present analysis rests on a simple single-compartment energy balance model, the question must inevitably arise whether the rather obdurate climate system might be amenable to determination of its key properties through empirical analysis based on such a simple model. In response to that question it might have to be said that it remains to be seen. In this context it is hoped that the present study might stimulate further work along these lines with more complex models.
What is Schwartz’s method? First, assume that the climate system can be effectively modeled as a zero-dimensional energy balance model. This would mean that there would be a single effective heat capacity for the climate system, and a single effective time constant for the system as well. Climate sensitivity will then be
S=τ/C
where S is the climate sensitivity, τ is the time constant, and C is the heat capacity. Simple!
To estimate those parameters, Schwartz uses observed climate data. He assumes that the time series of global temperature can effectively be modeled as a linear trend, plus a one-dimensional, first-order “autoregressive” or “Markov” or simply “AR(1)” process [an AR(1) process is a random process with some ‘memory’ of its previous value; subsequent values y_t are statistically dependent on the immediately preceding value y_(t-1) through an equation of the form y_t = ρ y_(t-1) + ε, where ρ is typically required to be between 0 and 1, and ε is a series of random values conforming to a normal distribution. The AR(1) model is a special case of a more general class of linear time series models known as “Autoregressive moving average” models].
In such as case, the autocorrelation of the global temperature time series (its correlation with a time-delayed copy of itself) can be analyzed to determine the time constant τ. He further assumes that ocean heat content represents the bulk of the heat absorbed by the planet due to climate forces, and that its changes are roughly proportional to the observed surface temperature change; the constant of proportionality gives the heat capacity. The conclusion is that the time constant of the planet is 5±1 years and its heat capacity is 16.7±7 W • yr / (dec C • m^2), so climate sensitivity is 5/16.7 = 0.3 deg C/(W/m^2).
One of the biggest problems with this method is that it assumes that the climate system has only one “time scale,” and that time scale determines its long-term, equilibrium response to changes in climate forcing. But the global heat budget has many components, which respond faster or slower to heat input: the atmosphere, land, upper ocean, deep ocean, and cryosphere all act with their own time scales. The atmosphere responds quickly, the land not quite so fast, the deep ocean and cryosphere very slowly. In fact, it’s because it takes so long for heat to penetrate deep into the ocean that most climate scientists believe we have not yet experienced all the warming due from the greenhouse gases we’ve already emitted [Hansen et al. 2005].
Schwartz’s analysis depends on assuming that the global temperature time series has a single time scale, and modelling it as a linear trend plus an AR(1) process. There’s a straightforward way to test at least the possibility that it obeys the stated assumption. If the linearly detrended temperature data really do behave like an AR(1) process, then the autocorrelation at lag Δt which we can call r(Δt), will be related to the time constant τ by the simple formula
r(Δt)= exp{-Δt/τ}.
In that case,
τ = – Δt / ln(r),
for any and all lags Δt. This is the formula used to estimate the time constant τ.
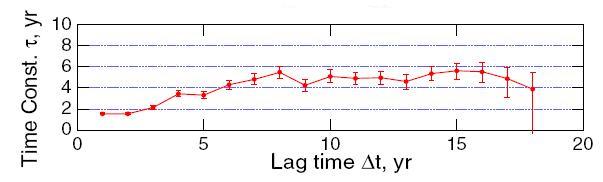
And what, you wonder, are the estimated values of the time constant from the temperature time series? Using annual average temperature anomaly from NASA GISS (one of the data sets Schwartz uses), after detrending by removing a linear fit, Schwartz arrives at his Figure 5g:
Using the monthly rather than annual averages gives Schwartz’s Figure 7:
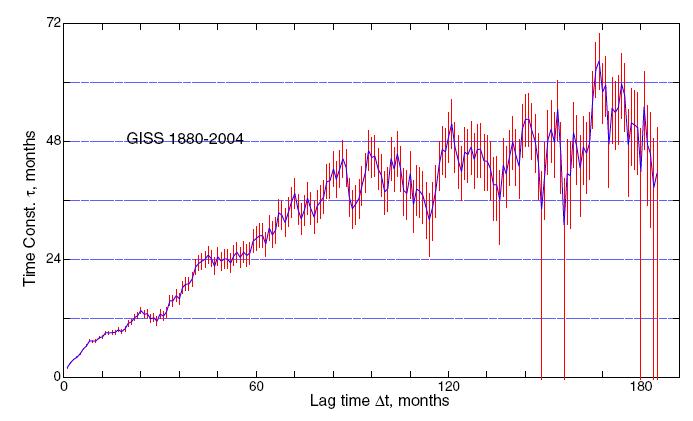
If the temperature follows the assumed model, then the estimated time constant should be the same for all lags, until the lag gets large enough that the probable error invalidates the result. But it’s clear from these figures that this is not the case. Rather, the estimated τ increases with increasing lag. Schwartz himself says:
As seen in Figure 5g, values of τ were found to increase with increasing lag time from about 2 years at lag time Δt = 1 yr, reaching an asymptotic value of about 5 years by about lag time Δt= 8 yr. As similar results were obtained with various subsets of the data (first and second halves of the time series; data for Northern and Southern Hemispheres, Figure 6) and for the de-seasonalized monthly data, Figure 7, this estimate of the time constant would appear to be robust.
If the time series of global temperature really did follow an AR(1) process, what would the graphs look like? We ran 5 simulations of an AR(1) process with a 5-year time scale, generating monthly data for 125 years, then estimated the time scale using Schwartz’s method. We also applied the method to GISTEMP monthly data (the results are slightly different from Schwartz’s because we used data through July 2007). Here’s how they compare:
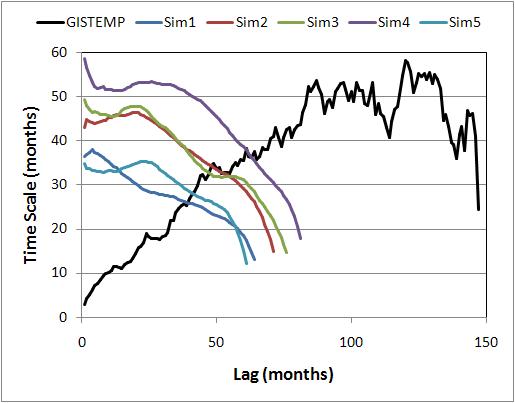
This makes it abundantly clear that if temperature did follow the stated assumption, it would not give the results reported by Schwartz. The conclusion is inescapable, that global temperature cannot be adequately modeled as a linear trend plus AR(1) process.
You probably also noticed that for the simulated AR(1) process, the estimated time scale is consistently less than the true value (which for the simulations, is known to be exactly 5 years, or 60 months), and that the estimate decreases as lag increases. This is because the usual estimate of autocorrelation coefficients is a biased estimate. The word “bias” is used in its statistical sense, that the expected result of the calculation is not the true value. As the lag gets higher, the impact of the bias increases and the estimated time scale decreases. When the time series is long and the time scale is short, the bias is negligible, but when the time scale is any significant fraction of the length of the time series, the bias can be quite large. In fact, both simulations and theoretical calculations demonstrate that for 125 years of a genuine AR(1) process, if the time scale were 30 years (not an unrealistic value for global climate), we would expect the estimate from autocorrelation values to be less than half the true value.
Earlier in the paper, the AR(1) assumption is justified by regressing each year’s average temperature anomaly against the previous year’s and studying the residuals from that fit:
Satisfaction of the assumption of a first-order Markov process was assessed by examination of the residuals of the lag-1 regression, which were found to exhibit no further significant autocorrelation.
The result for this test is graphed in his Figure 5f:
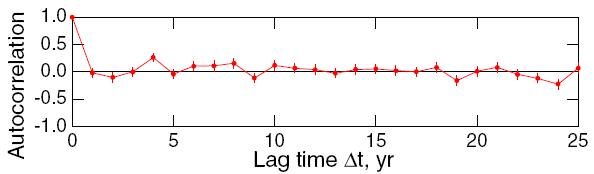
Alas, it seems this test was applied only to the annual averages. For that data, there are only 125 data points, so the uncertainty in an autocorrelation estimate is as big as ±0.2, much too large to reveal whatever autocorrelation might remain. Applying the test to the monthly data, the larger number of data points would have given this more precise result:
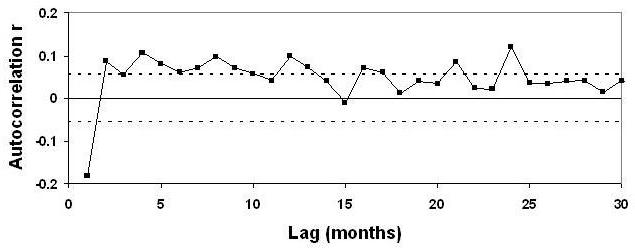
The very first value, at lag 1 month, is way outside the limit of “no further significant autocorrelation,” and in fact most of the low-lag values are outside the 95% confidence limits (indicated by the dashed lines).
In short, the global temperature time series clearly does not follow the model adopted in Schwartz’s analysis. It’s further clear that even if it did, the method is unable to diagnose the right time scale. Add to that the fact that assuming a single time scale for the global climate system contradicts what we know about the response time of the different components of the earth, and it adds up to only one conclusion: Schwartz’s estimate of climate sensitivity is unreliable. We see no evidence from this analysis to indicate that climate sensitivity is any different from the best estimates of sensible research, somewhere within the range of 2 to 4.5 deg C for a doubling of CO2.
A response to the paper, raising these (and other) issues, has already been submitted to the Journal of Geophysical Research, and another response (by a team in Switzerland) is in the works. It’s important to note that this is the way science works. An idea is proposed and explored, the results are reported, the methodology is probed and critiqued by others, and their results are reported; in the process, we hope to learn more about how the world really works.
That Schwartz’s result is heralded as the death-knell of global warming by denialist blogs and Sen. Inhofe, even before it has been officially published (let alone before the scientific community has responded) says more about the denialist movement than about the sensitivity of earth’s climate system. But, that’s how politics works.
Hi!
It looks like the graphs aren’t showing. I suspect it’s because the link to them has an extraneous “.” at the end of the url.
[fixed, sorry–had to do w/ the different ways images are referenced in preview and publish mode w/ the updated wordpress software. -mike]
It takes two to tango but I wonder how many of the readers of this blog genuinely understand the two contrasting arguments and are able to say anything at all about it that is meaningful. I, for one, cannot. Pretty soon, it seems, the “denialists” will be saying high CO2 levels are actually good for us. If human body lice studies are confirmed as indicating that not a single human wore clothing, not even animal skins, as recently as 169,000 years ago, then the average temperature globally must have been considerably warmer than it is now in African latitudes where most of us may have been located in those days. Humanity survived those high temperatures without technology of any kind, and without clothing. To that extent, surely we can adapt even better today if those high temperatures reoccur. Thus, though I do not fall into the denialist camp, nonetheless I would tend to be among those who are somewhat reassuring if the worst temperature rises do occur. But this is not an argument to do nothing. We do need clean energy. What we require is government to reward those who are willing to experiment with wind, solar, geothermal etc.so that those guys with hummers and their ilk actually pay much more to those of us willing to make the green enrgy investments. It’s time for government to get heavily involved in the process and not leave it up to the privatizers at all.
A sidebar: cherry-picking bits and pieces and declaring an “AHA! I TOLD YOU SO!” moment is not monopolized by the AGW antagonists; protagonists do their share.
None-the-less, and coming from a skeptic (different from antagonist), while my initial gut response is dubious (though not yet backed up with any cogent analysis), it is a well-done admirable post. Much to think about.
Thanks for posting this rebuttal!
Perhaps Mr. Schwartz should have passed this by such a rigorous test as above before he let go with his findings.
Seems to me the empirical evidence puts ALL the climate modeling into catch-up mode. IPCC rainfall projections are questionable. Now this.
What’a really worrisome is that the CO2 induced temperature rise we have now has been sufficient to trigger enough climate feedbacks and rapid ice melting as to make AGHG plus aerosols forcing just a component of impending changes.
With China’s rapid industrialization adding to the CO2/aerosol triggers I don’t think dangerous climate change can be stopped.
The Schwartz paper refers to Levitus 2005, Warming of the world ocean, 1955–2003. It also seems to rely on a certain value for the ‘effective heat capacity of the oceans’:
“The present analysis indicates that the effective heat capacity of the world ocean pertinent to climate change on this multidecadal scale may be taken as 14 +/- 6 W yr m-2 K-1. The effective heat capacity determined in this way is equivalent to the heat capacity of 106 m of ocean water or, for ocean fractional area 0.71, the top 150 m of the world ocean. This effective heat capacity is thus comparable to the heat capacity of the ocean mixed layer.” Other literature values are 35 +/- 16 W yr m-2 K-1 (Andrea 2005) and (3.2 – 65) W yr m-2 K-1, (Fram 2005).
However, Levitus 2005 has much more to say on this matter:
“There are three reasons one does not expect uniform heating of the ocean from the observed increase in atmospheric greenhouse gases. The first is that internal variability of the earth system (e.g., El Nino) may affect regional ocean heating rates in a non-uniform manner.”
“The second is that the natural and anthropogenic aerosols are not well-mixed geographically and can have a substantial effect on regional warming rates. This has been documented for the northern Indian Ocean by Ramanathan et al. (2001a,b) who estimate a decrease of absorbed surface solar radiation exceeding 10Wm-2 over much of the Indian Ocean due to the presence of aerosols. The IPCC (2001) report also documents the geographical variability of various aerosols, ozone, black carbon, etc. that affect the amount of radiation available to enter the world ocean.”
“The third reason is that any change in the earth’s radiative balance may induce global and regional changes in the circulation of the atmosphere and ocean which could in turn affect the net flux of heat across the air-sea interface on a regional basis.”
What’s very unfortunate in the Schwartz paper is the following, however: “However in a subsequent publication a year later Lyman et al. [2006] reported a rapid net loss of ocean heat for 2003-2005 that led those investigators to estimate. . . a value much more consistent with the long-term record in the Levitus et al. [2005] data set.”
That’s just sloppy. That estimate was based on an error in the measurement system (floats) and was retracted. Either the author or the referees should have known that. Thus, there seem to be a lot of assumptions about ocean heat uptake which lead to the unsupported conclusion that there is ‘rapid equilibration of the climate system to applied forcings’.
To the non scientific eye it might appear, without further examination or considerations, this paper by Stephen Schwartz is a handy way to look at the science of global warming.
Myself, not being an expert but of reasonably sound mind and body (sort of) looking at it with what might be considered common sense, see something else. So at the risk of oversimplifying this, I thought I would take a stab at it.
Cause and effect relationships are hardly simple in complex systems with extensive dynamics that compile and interact with each other. Examining a simple view to return a simple result may have advantages for understanding aspects of a system, but hardly the overarching implications or affects in a system that has systems from which it derives energy and interactions, and subsystems that reach from macro to micro systems all interacting, at all levels, with ramifications extending in influence in relation to the magnitude and reach of their influence. These systems react upward into parent systems, and downward into sub-systems, as well as interacting with collateral systems. Climate is anything but simple.
The old adage comes up: “You know why they call them weather men… they don’t know whether it’ll rain or not”.
That in mind, reasonable conclusions in cause and effect, inertia and logic can give one a modicum of insight into possibility or even probability. So let’s take a look at what it looks like this study seems to represent within the scope of its limits and extent.
If I were to roll a ball down a hill 10 feet and measure with precision the distance, speed direction and behavior of the ball in that span of time and distance, I could describe the observations fairly accurately. But if I don’t take into account that the hill is 10,000 feet long and steepens along the way, and has varying slopes and a multitude of obstacles; predictability on exact behavior dissipates into probabilities (so it is reasonably hard to see into the future) based on the complexity of ones understanding of the physics involved and any other predictable or potential factors, one might figure out that precise outcomes are hard to predict. However, one can reasonably predict the ball with go down hill, and likely speed up as it goes. Depending on the complexity or number of things it can bump into along the way one might see that it could cause an avalanche or some other cascade effect. The inertia of the ball will likely increase and there may even be some lag effects, like it bumps a little rock that might roll down another way and hit some other rocks that may or may not cause some really big rocks to go bump something else (and there are lots of opportunities for it to bump into things along the way).
You might assume that the ball hits a tree or gets stuck between two rocks 20 feet down the hill… But then, it really depends on the size of the ball and any obstacles that might get in its way, doesn’t it? The thing you know though, is that it’s a hill, and it goes down from the top. You don’t have to me a rocket scientist to figure this out.
So while I have drawn no conclusions, maybe I painted a picture that helps us understand the limited scope of a particular study, in this case, a ball rolling 10 feet down a 10,000 foot hill.
P.S. It seems more that reasonable to believe that the global climate ball has been given some added weight in the form of added greenhouse gases. To assume that this is a little ball with little effect over time seems to be more neurotic than realistic in consideration of the preponderance of the evidence as understood in the aggregate earth system, and known influencing factors.
Thanks for a very clear post.
At the last fall AGU meeting I saw the last few minutes of a presentation on this (OS11: Empirical Determination of the Time Constant, Heat Capacity, and Sensitivity of Earth’s Climate System, by Stephen E Schwartz). In the question period the presenter was asked why climate models showed different results. His response was that this was the responsibility of modellers, not his. – And now we know why.. – great post!
Umm, this isn’t right:
heat capacity is 16.7±7 deg C / (W/m^2), so climate sensitivity is 5/16.7 = 0.3 deg C/(W/m^2).
[Response: thanks, yes we’ve fixed. -mike]
Tamino,
I suspect you got the units wrong on the heat capacity:
16.7±7 deg C / (W/m^2)
Shouldn’t that be
16.7 +/- 7 Wa/(m^2 deg C)
(i.e., energy content change per temperature change, for one square metre)?
(So to be pedantic, this is “heat capacity surface density”)
[Response: Correct, see above. -mike]
Funny how much authority denialists give to models when they cast doubt on the scientific consensus.
No, I suppose it’s not funny at all…
Actually I see something good in this too: even if you over-simplify the
modelling to the point of cruelty to animals, the data will
still give you a sensitivity result that’s in the right ballpark…
meaning that this sensitivity is a pretty robust property of the climate
system.
Good article.
There’s a typo: “In such as case” should be “In such a case”.
Also, it would be nice to know who Tamino really is.
Dave
Vern Johnson(2) — The paleoclimate 169,000 years ago was glacial, in the previous galcial maximum period. So it is extremely unlikely that Africa was anything but, on average, a few degrees cooler than now.
During the previous intergacial, the Eemian, around 125,000 years ago, the sea stand rose to about 5 meters above today’s, suggesting that Africa might have been slightly warmer than now.
Re. #2, I don’t follow your argument. The issue is not whether the human body can cope with higher temperatures, but whether today’s human civilisation (and ecosystems) can cope with the (probably unprecedently) rapid changes that are likely in the next 100 years. For instance, 169,000 years ago, correct me if I’m wrong, but I don’t believe there were millions of people living in huge built-up coastal cities. Many of these cities will be submerged ice melt continues at its current rate (which is already greatly outstripping the highest-end IPCC projections – e.g. see
here.
Is there a possibility we could get Schwartz’s comments on this on this site?
Thanks for the review. Now any insights on how Schwartz came publish such a paper, and how it passed peer review? For example, did someone in a funding agency request this study?
It shows more about the stupidity of the scientific community and RealClimate scientists in particular, that they are more concerned about a paper containing the ramblings of an idiot who cannot see global warming is happening, than they are by the melting of the Arctic ice cap.
The loss of the Arctic sea ice is bound to cause a warming of the whole Arctic region, and lead to the melting of the Greenland ice cap, and a 7 m rise in sea level.
But the scientists are tying themselves in knots, because they are locked into a search for a mythical holy grail – climate sensitivity. Sensitivity is a meaningless average, because global warming will not be spread over the planet in an even fashion, any more that it will rise each year by a small increment.
The temperature rise that matters is in the continental regions where we live. Not in the 7/10ths of the surface (majority) which is covered in ocean.
Re #12: Tamino leads a humdrum existence doing non-climate-related time series analysis in his day job. I know who he is and can confirm his expertise. I’m sure Mike does and can as well.
There is at least one other climate blogger in Tamino’s situation, i.e. not a climate scientist but with a substantial degree of relevant expertise, who maintains anonymity for the same reason: In this age of easy googling, they don’t want someone (e.g. an NSF grant manager) checking up on their professional activities only to find mostly just climate blog material, none of which is strictly relevant to their career and often gets a little, um, unprofessional in tone if not content. So please leave those masked persons to their anonymity.
Re #15: To be fair to Schwartz, he threw in a huge caveat at the end of the paper, basically saying that his work amounts to an interesting idea that he would like the modelers to have a look at, but not expressing confidence that it would hold up under that examination. Be aware that journals do sometimes publish papers that are novel, provocative or otherwise amount to scientific outliers, which is a perfectly reasonable practice albeit a little confusing for us amateurs.
Off-topic, but James Hansen was interviewed by the BBC World Service today in “The Interview” series; it lasts just under half an hour. You can download it as a 12MB mp3 file here; or for the next six days you can listen to it on streaming audio here.
I seem to be the only person who read both of Schwartz’s pieces and thought he was setting up the argument others have tried to make incoherently or politically — seeing if he could give it a fair expression that a refereed journal would pass. Kind of fleshing it out, standing it up against the wall and asking if anyone saw a target there worth shooting at.
But I didn’t find anything in what he wrote that suggested he wanted to believe in his numbers.
#17 Allastair, its rather academic infighting which seems to fuel contrarian smiles, it was part of their original cigarette denial mode, confusion is bliss, yet more than 30% of the ice cap has melted already. Refuting such a paper is necessary nevertheless, I must add that the CO2 X2 sensitivity is about to pass the +1 C mark. In light of present situation I agree that that there is incredible apathy though, notice no film showing this wide open Arctic Ocean body yet, by any media source, but lots of cameras on silly things which need not be mentionned…
#2: “It takes two to tango but I wonder how many of the readers of this blog genuinely understand the two contrasting arguments and are able to say anything at all about it that is meaningful”
I can’t say I read this blog all the time, but I can say quite a bit about time series, and many years ago, was closely associated with climate scientists.
A: Even 20 years ago there was work on time series modeling of recent and paleoclimate temperatures (Ghil and Vautard, etc.) The tools of (then current) large scale Kalman filtering were well understood by climate scientists from the dynamic meteorology side of the game (I think Eugene Isaacson brokered some of that deal). The multitaper spectral analysis was already in the toolkit (the Thomson style multitaper stuff was brought in to the fistfight over whether Milankovic was the explanation of ice ages). If the answer were a univariate AR(1) model we would not have had to wait until 2007 to find that out; tools quite capable of indicating that have been carefully applied to these problems for decades. It’s frankly astonishing that Schwartz considers such a model at all. I’m sort of stunned that JGR had no referees poke him on that.
B: Playing around with low dimensional time series and getting “no evidence of further autocorrelation” happens all the time, but is not probative. It is an unfortunate gap in understanding even in many people who actually consider themselves well informed on time series that they misuse standard tests for coefficient significance as if they indicate validity of inference using a reduced model. That is completely untrue, as simple examples can readily demonstrate. (And in this case, the comment here in realclimate indeed exposes the lack of faithfulness of the AR(1) model so I won’t have to give these examples).
If Hank is right (#20) Schwartz seems to be naive at best about the fodder he is giving to denialists, who are marketing both pieces very effectively and disingenuously. See also William’s blog post here and Inel’s response.
Dave
Thank you Tamino for the work you have put in to examining Shwartz’s paper. All of the science and maths was way above my head, but at the end of the day, I have been convinced that the Schwartz paper doesn’t yet overturn the consensus on climate change and sensitivity.
It would appear that Schwartz has put out an article for discussion and thought, nothing wrong with this, but perhaps, knowing how such a paper would be seized on by global warming sceptics, deniers and contrarians, the caveats should have come at the beginning and in large print?
But it all goes to prove that if you want to keep up to date with the latest information and arguments about global warming, this is the place to come.
Thank you team and commentators for your insight and efforts.
Perhaps this topic should have been titled: Schwartzs Insensitivity.
For so astute a scientist to even to begin to offer the undecided vote the hope of a trivially simple zero-dimensioned climate model and to settle on a process that comes up with a climate sensitivity that is so far out of whack with recent more sound calculations shows a truly naive insensitivity to the critical state of the climate-change dialogue. Totally unhelpful. Poor show old chap.
“…knowing how such a paper would be seized on by global warming sceptics, deniers and contrarians, the caveats should have come at the beginning and in large print?…”
Just musing: why should skeptic caveats be any different than protagonists’ caveats?
Re # 17 Alistair McDonald: “It shows more about the stupidity of the scientific community and RealClimate scientists in particular, that they are more concerned about a paper containing the ramblings of an idiot … than they are by the melting of the Arctic ice cap.”
On what basis can you conclude that the scientists in question are more concerned about the former than the latter? The RC moderators have stated time and time again (and a glance at their bios will confirm this) that they have day jobs, and run this site in their spare time. I’m sure most people think about hundreds, if not thousands, of different subjects during an average day. There is no reason climate scientists can’t interrupt their thinking about the melting of the Arctic ice cap (or whatever area their research focuses on) and start thinking about a peer-reviewed paper in a mainstream scientific journal by a well-established scientist dealing with global warming.
Re #2: [If human body lice studies are confirmed as indicating that not a single human wore clothing, not even animal skins, as recently as 169,000 years ago, then the average temperature globally must have been considerably warmer…]
This does not follow. The human body is quite capable of adapting to, and even being fairly comfortable in, a much wider range of temperatures than the average “civilized” person might believe. See for instance Darwin’s accounts of the naked inhabitants of Tierra del Fuego…
Re 20. Whether Schwartz “believes” in his numbers or not – why should that be relevant? But strangely there seem to be many who think science is about belief and not about whose evidence is better.
In a way, keeping Tamino’s identity secret may be good, so that his person may be kept out of the debate. Turning the whole scientific discourse into an anonymous or pseudonymous exchange could well be recommended: no more ad homs.
Ref #21 “…In light of present situation I agree that that there is incredible apathy though, notice no film showing this wide open Arctic Ocean body yet, by any media source….”
See: http://www.esa.int/esaCP/SEMYTC13J6F_index_0.html
I’m curious about the effect it has on researchers that their papers can be sized and used for political propaganda in ways that totally misrepresent them or make a certainty out of a deliberately speculative result. Do you manage to ignore that background noise and only publish for other scientists as in most other fields, or are potentially interesting papers canceled because they may be abused? In normal science you are usually remembered for your good papers while the bad ones are quickly forgotten, but in climate science you risk having your worst paper become the most widely known.
I too would be eager to hear a response from Schwartz both on the science and what he thinks about the way his paper is being used.
Re #2 Vern Johnson suggests that leck of clothing is evidence of warmer temperatures. Darwin give a great description of his encounter with the folk of Tierra del Fuego. The were completely naked, the sleet melting on a womans bosom as she suckled her infant.
No, the weather hasn’t got colder, it’s we who have grown soft :)
Yes, yes, all well and good, but is the recent Artic data the first “tipping point”? – Sorry just listened to the Hansen audio link above and to be honest even though I have a BSc this story is not worth the effort of trying to understand, from my point of view the paper in question is just one amoungst many and will be shot down in a hail of negative cites, OTOH it would be fine for a “Friday roundup”.
Anyway, looking forward to RC’s take on all the N.W Passage stories that are quoting some trully “alarming” data for ice coverage (if you read carefully and do some naive math).
Thanks for doing this debunking. I also have a three part series on this subject at ClimateProgress that begins here: http://climateprogress.org/2007/08/21/are-scientists-overestimating-or-underestimating-climate-change-part-i/
[Response: thanks for the heads up Joe, very nice piece. Can you link parts 2 and 3 for our readers too? thanks! -mike]
Would it not be a good idea to apply Schwartz’s method to GCM results, for which we already know the climate sensitivity? I wonder if the method gives consistent results with the model climate sensitivities.
[Response: Rasmus, indeed! James Annan has already taken a stab at this. And there is more in the pipeline (submitted to JGR), as Tamino alludes to in his piece. -mike]
Re #34 James Annan did such a check against climate models:
http://julesandjames.blogspot.com/2007/08/schwartz-sensitivity-estimate.html
This was helpful. Thank you. It raises the question why a reputable researcher would make simplified assumptions such a single heat capacity and a single time scale for all of Earth’s sphere’s when there are such large differences for land surface, atmosphere and ocean, and expect it to fly.
We were alerted in a paper by Gavin “Learning From a Simple Model” https://www.realclimate.org/index.php/archives/2007/04/learning-from-a-simple-model/
on April 10, about flim flam detectors – that when someone does a simplified calculation to prove everyone wrong we should subject it to more critical scrutiny. which Tamino has done.
This is indeed the way science should work.
re #2
Pretty soon, it seems, the “denialists” will be saying high CO2 levels are actually good for us.
================
They’ve been doing this for a while, actually.
Schwartz claims that their model is able to work with a time-varying changing in forcing. My understanding is that with an exponentially growing forcing, one cannot figure out the time constant from the temperature data alone, as there are an infinite number of valid solutions, some with longer time constants and higher heat capacities, and some with shorter time constants and lower heat capacities.
Only once the forcing leaves the exponential track (which it has roughly followed for over a century) will one have any hope of getting the time constant from just the temperature series alone. Even then the model of the Earth as a giant capacitor is oversimplified and unlikely to be very accurate.
A third alternative approach to looking at this. GHG forcing is a signal and the climate system is a filter. The fundamental question remains, what is the nature of the filter? We have some clues about it, but as yet, do not fully understand all of its characteristics. So called “denialists” are arguing that the characteristics of the filter are such that the GHG forcing transient is eithter being filtered out, or, is being overcome by negative feedback. So called “alarmists” are arguing that the transient has overexited the system into a state where it is out of the safe operating area. What is most likely? Probably an intermediate case. My own educated guess is that there is measurable sensitivity to GHG forcing. I also guess that had we continued on a global development path that followed to paradigm of say, the Western countries 100 years ago, we’d already be in seriously deep doo doo, right now – in a hellish world. As it turned out, we became more refined in our approach and have managed thus far to avoid such a horrid outcome. If the current sociolpolitical trends hold, there will be an ever tightening screw of reduced energy consumption in advanced Western democracies. My guess is, partial pressure CO2 will top out 50 – 150 years from now and will enter into a steep decline. Global cooling may actually be incited, assuming that other forcings have not already begun it. A lot can change between now and then, and, the world may go through a hellish phase along the way. Or not …
I read the James Annan criticism linked to above in and it pointed out that at the 2stdev level the calculated sensitivity from the Schwartz study was around 4.5C.
In fact, the 16%-84% probability interval (the standard central 68% probability interval corresponding to +- 1sd of a gaussian, and the IPPC “likely”) of this quotient distribution is really 0.18-0.52K/W/m^2 (0.7-1.9C per doubling) and the 2sd limit of 2.5% to 97.5% is 0.12-1.3K/W/m^2 (0.4-4.8C per doubling). While this range still focuses mostly on lower values than most analyses support, it also reaches the upper range that I (and perhaps increasingly many others) consider credible anyway. His 68% estimate of 0.6-1.6C per doubling is wrong to start with, and doubly misleading in the way that it conceals the long tail that naturally arises from his analysis.
That doesn’t sound like earthshaking heresy.
We are dealing with a nonlinear problem which keeps changing as ice melts and greater area of water is exposed, raising the solar absorption. Also glaciers sliding on under-ice rivers and lakes don’t lend themselves to single time constants for the whole Earth.
Tamino, just for grins try 72 to 84 months with your models and see how things move around.
Re #17
This type of post is uncalled for.
Jerry(43) — I agree. Tamino has performed a clear, useful, volunteer service.
E.g. #16 – the question of whether it was right that Schwartz’s paper be published. Surely the important question now is how he responds to the criticisms? If he engages in a serious debate, he’ll almost certainly arrive at a position a long way from the one set out in the paper. That will cut the ground from under the feet of the sceptics – though we all know by now that they’ll just keep blathering on anyway.
39 CO2 forcing is a LN function not exponential function, that is why this subject is being debated. If both poles were showing similar temperature trends, there would not be a debate. There is a debate, however misguided you feel the other side may be, because some parts of the complex system being modeled are behaving in a manner that is somewhat confusing.
Many “skeptics” do not deny warming, only question the rate and impact of the various potential causes. A lot depends on your frame of reference.
In # 17 Alistair says in part “The temperature rise that matters is in the continental regions where we live. Not in the 7/10ths of the surface (majority) which is covered in ocean.”
Have you forgotten that the warming of the oceans causes more water to evaporate into the atmosphere causing further warming? Or that the warming of the surface waters in the tropical Atlantic is suspected of giving us future hurricanes of greater intensity? The warming of the oceans past a certain threshold also has a detrimental effect on coral reefs and the biota that live in and around them.
All of the Earth’s components are interrelated in one way or another.Think of it this way. None of us live on the ice in Greenland.So what do we care if it melts?
Re 18: “To be fair to Schwartz, he threw in a huge caveat at the end of the paper, basically saying that his work amounts to an interesting idea that he would like the modelers to have a look at, but not expressing confidence that it would hold up under that examination. Be aware that journals do sometimes publish papers that are novel, provocative or otherwise amount to scientific outliers, which is a perfectly reasonable practice albeit a little confusing for us amateurs.”
What you say is true,Steve,yet some public figures,like Senator Imhofe, a modern day Lysenko,for all of me, glom on to these hypotheticals like a drowning man grabs for a rope. It’s important that short cuts that don’t simulate true values be thoroughly analyzed and if they don’t fit, nipped in the bud, mainly for this reason.
Mike — thanks for the kind words at #34. In response to your request, I’ll give all three posts here. They examine
(1) the evidence scientists are NOT overestimating climate sensitivity
http://climateprogress.org/2007/08/21/are-scientists-overestimating-or-underestimating-climate-change-part-i/
(2) the evidence scientists are seriously UNDERestimating climate sensitivity (because of unmodeled carbon cycle amplifying feedbacks)
http://climateprogress.org/2007/08/22/are-scientists-overestimating-or-underestimating-climate-change-part-ii/
(3) how these omissions suggest the climate has a “point of no return” that severely constrains the safe level of human-generated emissions.
http://climateprogress.org/2007/08/23/are-scientists-overestimating-or-underestimating-climate-change-part-iii/