Many readers will remember our critique of a paper by Douglass et al on tropical tropospheric temperature trends late last year, and the discussion of the ongoing revisions to the observational datasets. Some will recall that the Douglass et al paper was trumpeted around the blogosphere as the definitive proof that models had it all wrong.
At the time, our criticism was itself criticised because our counterpoints had not been submitted to a peer-reviewed journal. However, this was a little unfair (and possibly a little disingenuous) because a group of us had in fact submitted a much better argued paper making the same principal points. Of course, the peer-review process takes much longer than writing a blog post and so it has taken until today to appear on the journal website.
The new 17-author paper (accessible pdf) (lead by Ben Santer), does a much better job of comparing the various trends in atmospheric datasets with the models and is very careful to take account of systematic uncertainties in all aspects of that comparison (unlike Douglass et al). The bottom line is that while there is remaining uncertainty in the tropical trends over the last 30 years, there is no clear discrepancy between what the models expect and the observations. There is a fact sheet available which explains the result in relatively simple terms.
Additionally, the paper explores the statistical properties of the test used by Douglass et al and finds some very odd results. Namely, that their test should nominally inadvertently reject a match 1 time out 20 (i.e. for a 5% significance), actually rejects valid comparisons 16 times out of 20! And curiously, the more data you have, the worse the test performs (figure 5 in the paper). The other aspect discussed in the paper is the importance of dealing with systematic errors in the data sets. These are essentially the same points that were made in our original blog post, but are now much more comprehensively shown. The data sources are now completely up-to-date and a much wider range of sources is addressed – not only the different satellite products, but also the different analyses of the radiosonde data.
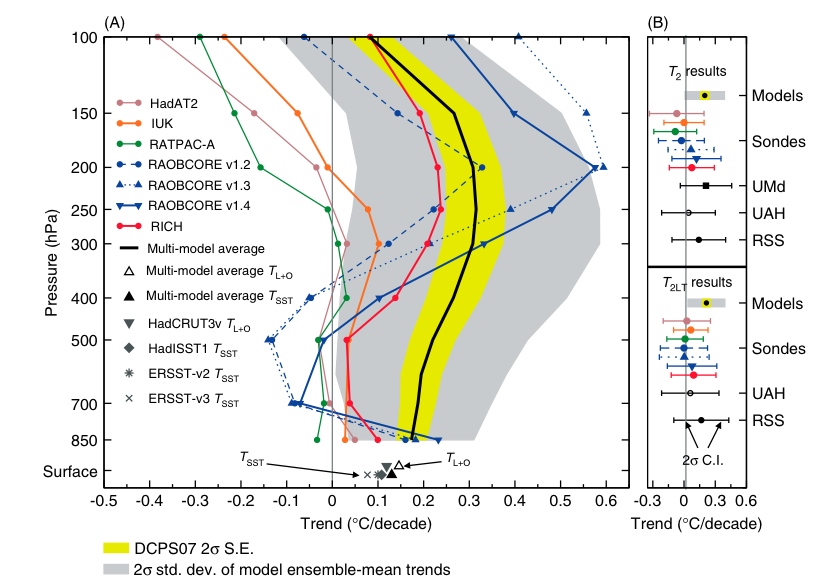
The bottom line is best encapsulated by the summary figure 6 from the paper:
The grey band is the real 2-sigma spread of the models (while the yellow band is the spread allowed for in the flawed Douglass et al test). The other lines are the different estimates from the data. The uncertainties in both preclude any claim of some obvious discrepancy – a result you can only get by cherry-picking what data to use and erroneously downplaying the expected spread in the simulations.
Taking a slightly larger view, I think this example shows quite effectively how blogs can play a constructive role in moving science forward (something that we discussed a while ago). Given the egregiousness of the error in this particular paper (which was obvious to many people at the time), having the initial blog posting up very quickly alerted the community to the problems even if it wasn’t a comprehensive analysis. The time in-between the original paper coming out and this new analysis was almost 10 months. The resulting paper is of course much better than any blog post could have been and in fact moves significantly beyond a simple rebuttal. This clearly demonstrates that there is no conflict between the peer-review process and the blogosphere. A proper paper definitely takes more time and gives generally a better result than a blog post, but the latter can get the essential points out very quickly and can save other people from wasting their time.
Let me correct that — there would also be some albedo from Rayleigh scattering in the cloudless atmosphere. About 6%, so the Earth’s albedo would be perhaps 0.2 and the temperature of surface and atmosphere would be 264 K.
RE:Steve Carson (#248)
“can anyone recommend 2 or 3 good introductory climatology books.”
For start, the links an this page
https://www.realclimate.org/index.php/archives/2007/05/start-here/
For the history of climate science
http://www.aip.org/history/climate/index.html
You said you have an engineering degree. Depending on your previous knowledge in physics and mathematics, I suggest Ray Pierrehumbert’s Climate Book
http://geosci.uchicago.edu/~rtp1/
Steve Carson says: “Even if you can see clearly into the hearts and minds of others, keep it to yourselves and just explain climate theories as clearly as you can.”
Steve, I agree that this is good advice and would adhere to it if I had superhuman patience. However, when the same denialists continue to post the same discredited arguments day after day, ignoring all reasoned replies, it is difficult not to draw some conclusions about either their intelligence or their honesty. Even Jesus suggested forgiving our brethren “seventy times seven” times–many of these guys would be pressing their luck even with him!
Re: #250: Barton, wouldn’t you still have a lapse rate even in a pure O2/N2 atmosphere? Drop in pressure == drop in temperature and all that? As I understand it, GHGs don’t change the lapse rate (well, with the exception of water) but one way of explaining their effect is that GHGs change the optical thickness of the atmosphere and therefore to change the effective radiation height, right? And with zero GHGs, the effective radiation height would be zero.
Re: #254: Me: Sigh. Lapse rates are hard, let’s go shopping (or maybe I should retake my atmospheric chemistry and dynamics course). Clearly GHGs _can_ have an impact on lapse rates: see, for example, ozone which causes a positive lapse rate in the stratosphere. Also, I found at least one website that claims that increasing GHGs may decrease the lapse rate somewhat (a negative feedback) though I would prefer a more trusted source on that. Having said that, I still hold that an O2/N2 atmosphere would likely have something near to the dry-adiabat lapse rate.
Tamino has a nice description of lapse rate – thanks Tamino! http://tamino.wordpress.com/2007/07/16/lapse-rate/
At least I’m not the only one to have confusion in this area – even Gavin can make mistakes:
https://www.realclimate.org/index.php/archives/2004/12/why-does-the-stratosphere-cool-when-the-troposphere-warms/
[Response: Why do people keep bringing that up? I’m fully reformed now… ;) gavin]
MArcus, #255. The problem is how do you get a lowered lapse rate. Increased uplift of air is about the only global atmosphere effect that could managed that. Or increased water content (so that energy is more efficiently transported by ferrying vapour up to condense, release the energy and rain out). But that would require more water or more temperature first…
Barton’s effect is correct, near enough: IR finds a pure O2/N2 atmosphere transparent. Therefore the IR radiation goes straight out. Then you have conduction into the lowest level of the boundary layer. And air is pretty good as an insulator.
Nearly removing all the conduction that allows the atmosphere to have a lapse rate. The lapse rate is then all that is required to get the pressure equal to the mass of atmosphere above.
Gavin, FWIW, you have my vote to no longer sit on the Group W bench.
Interesting. One consequence of the increasing lapse rate should then be increased turbulence–or should I say, instability–around the tropopause, right? (And I think I recently saw something about observations of this phenomenon, too.) What in turn follows from this?
Does it matter, Kevin?
We have what we do know.
We have what we know we don’t know.
What we know looks bad if we don’t change our ways, what we know we don’t know isn’t going to help things and everything else isn’t going to know how to magically help things, so is as likely to make it worse as better, so best not rely on anything other than “bad” from them.
Remember, a pessimist is only ever pleasantly suprised.
(note: one reason I think so many do NOT believe AGW is because they really do believe that the universe won’t let anything bad. God, in other words, wouldn’t let that happen. I say, why would god not try the same thing with the apple of knowledge and see if we’ve learned now whether to use that knowledge to *respect* the creation or whether we’re no better than mindless automata, demanding our ephemeral needs be succored).
Mark, interesting sidebar. If you take the entire Bible at its word God allowed a ton of really bad things to happen — even purposefully caused some.
[Response: No more theology please. – gavin]
Matter? In terms of the need to “change our ways,” no–or probably no, at least. In terms of understanding the larger picture, yes of course.
I’m reading between the lines that you may think I’m one of the brigade that is forever seeking a reason to do nothing now.
That is somebody else!
But I am curious, and do believe that there is a good chance somebody on this forum may have a piece of the answer and may be kind enough to share it.
(Captcha: “cities sincere.” Make of that what you will.)
Uh, re Levenson (250): if there is no radiative coupling whatsoever of the earth to the atmosphere or of the atmosphere to itself, then outside of convective instability (which would lead to an adiabatic lapse rate), the only transport mechanism is conduction. That would seem to support the notion the atmosphere would be isothermal, unless there’s some weird effect of gravity I’m forgetting.
Anyway it’s a pretty academic exercise since you’d be hard pressed to find a real planetary atmosphere in which either radiative or convective transport didn’t completely and totally dominate conductive transport.
So as for (242): I am looking at the same graph as everybody else, at the top of this page. This shows sondes and models, among other things. The sondes (colored data) *clearly* show the lapse rate is changing, becoming more unstable between surface and 500 hPa and less unstable btw 500 and 250. So for all this discussion of changing lapse rates, the data’s right in front of our noses, isn’t it? :)
Ps re 243 (Fred): Sorry, man, but you’re really out of your depth. It’s good to try to understand this stuff, but even you admit that you “do not know how much the radiative effect will add to the surface temperature” (to use your words).
Houghton is an OK book, but it’s pretty basic. I’m an astrophysicist, but I wouldn’t pretend to understand how to model the atmosphere without some serious technical reading that goes waaay beyond his book.
And please, anybody serious about thermal transport understands how a duvet works.
Kevin, I poked around and didn’t find anything specific about more turbulence at the tropopause; maybe you’re thinking of hurricane strength increasing with increasing lapse rate? Certainly the strength of thunderstorms and thermal columns increases with a higher lapse rate — a nice post-frontal day with a very cold air mass moving in over warm moist air on the ground makes for great hang glider flying and, yes, much more turbulent air.
That would not necessarily go up to the tropopause — by definition the tropopause is where the lapse rate goes to zero (and it varies and moves around). What scale are you thinking of? More aircraft bumps? better lift for gliders? Higher wind shear at cloud tops? You might mean a lot of things.
We have a tropopause because of the ozone layer, the air gets colder up to that point; above that, there’s an inversion, warmer air, where the ozone is significantly contributing to the temperature as oxygen, absorbing ultraviolet, gets heated, splits, and recombines as ozone, I gather. Ray Pierrehumbert or any other atmospheric expert can say far more than my vague understanding (have you read his “Science Fiction Atmospheres” and other work at his website? Link is in the sidebar).
________________
“he Educational”
I appreciate that, Hank. I’m afraid I don’t recall very specifically what I think I saw, or I’d have dpne more searching myself. I was trying to reason from the general point toward something more specific, motivated purely by curiosity. Thanks, too, for the suggestion on the sidebar item.
Kevin, there were two reasons for #259.
1) Stop someone using that message inappropriately (“See! You could be wrong!”)
2) It really doesn’t make much difference and there are more impactful unknowns (made up word) that deserve attention
As to the note, it was more an idea to consider in explaining why someone really isn’t listening. I find it quite frustrating to think that someone who seems intelligent really isn’t thinking. That idea in the note was more to help reduce the frustration.
Ray Ladburys’ comment (143 ‘Greenspan, Einstein, and Reich’) does suggest that he has looked at Tamino’s composite chart (29, first “this”).
He can see that it would be absurd to claim that the rise in temperature, 0.6 degrees, from 2000 to 2002 is “climate”, and the fall, 0.6 degrees, from 2005 to date is mere “weather”.
We could reasonably call the increase and the decrease “weather”, ignore them both, and accept that current temperatures are back to their seventies level (take out 1998/99 El Nino peak also, stop at 1997, and the upward trend from the seventies virtually disappears).
The fall from the Medieval Warm period into the Little Ice Age had nothing to do with additional CO2. Can we really claim that the rise to the peak in the forties was not equally natural? The acceleration in CO2 concentrations came later, and was accompanied by a fall in temperature down to the trough in the seventies.
Are there not grounds for reasonable AGW doubt from this data.
Mr Wexler (157’Greenspan, Einstein, and Reich’) suggests that it is nonsense to treat heat energy as electro-magnetic waves, because it is not possible to construct a theory of molecular absorption without photons. In fact, Grant W Petty, University of Wisconsin Madison, derives the resonant absorption equations on page 252 of his book First Course in Atmospheric Radiation. He writes:
“We see, to our amazement, that the photon frequency associated with the transition is just an integer multiple of the classical resonant frequency of the harmonic oscillator”
Not, I have to say, to my amazement. Neutrons in reactors behave like particles, random walking across the moderator, slowing by collision, until they are absorbed by fissile material. You can calculate their wave-length equivalent (as you can for a billiard ball) but it adds nothing to the model of physical reality.
Heat waves in the atmosphere behave like waves. Resonant absorption will convert heat energy to kinetic energy in the molecule (water vapour, CO2 et al) and be transferred by collision to the general atmosphere, from where it will be radiated into space.
I introduced the duvet, Mark, 249, to demonstrate basic insulation. You have to establish a temperature differential across an insulating barrier for heat to transfer. Think about your loft insulation, double gazing, and the clothes you wear (string vests are very effective – it is the air, not the string). Part of the temperature differential across the atmosphere, from earth to space, is due to the same effect.
Fred, neutrons and billiard balls _are_ particles.
If the double-slit experiment worked with billiard balls, pool tables would be different and the whole game would be more interesting.
Also you left a few words out of your explanation, these:
> … be transferred by collision to the general
> atmosphere, from where it will be
transferred back by collision to other molecules that are greenhouse gases, lather rinse repeat, until heat radiated from a greenhouse gas molecule eventually fails to interact before it is
> radiated into space.
Mind the gaps.
Re Mark, 266: “As to the note, it was more an idea to consider in explaining why someone really isn’t listening.”
I don’t want to generate another demarche into theology, but I suspect that the ideo- or theo-logy you describe is an important psychological factor for some–Spencer and Christy come to mind.
Fred, your attempt to equate current temps to the 70’s just doesn’t fly. (In fact, I can’t imagine what you were thinking of.) (“. . .accept that current temperatures are back to their seventies level. . .”)
Per the HadCrut data, as rank-ordered on the Hadley site, only five of the years from the seventies–73, 77, 79, 78, and 72–crack the top fifty warmest years. Of these, 73 is the warmest at 26th warmest, followed immediately in rank by 77 and 79; 78 and 72 are the 47th and 48th warmest. (Indeed, for the last two, their anomaly is actually below that of the reference period (61-90.))
By contrast, *every year* of the current decade except 2000 makes the top ten. (2000 was “merely” the 13th warmest.) Eyeballing the data gives a mean around .3 degrees higher for the 2000s vs. the 70s.
Kevin, Fred wasn’t thinking.
Or, rather, he was thinking of talking a load of bull to flim flam anyone who comes on here to hear what’s going on.
At least RodB sometimes asks a good question.
Fred, never.
I don’t think there’s even the faintest possibility that mankind’s dominating forces (which are in more totalitarian control than ever) will do anything to the climate problem before it’s far too late. They’re crushing the climate science under a mountain range of oil- and carindustry propaganda. The mediatorship has by now completely buried the climate crisis deep below the “financial crisis” even as the climate crisis completely dwarfs the “financial” (which not one economic theory is able to explain or was able to foresee, but those “theories” are met with enormous respect in the same media industry which ridicules overwhelmingly consensual climate science).
“I used to believe that collective denial was peculiar to climate change. Now I know that it’s the first response to every impending dislocation.”
http://www.monbiot.com/archives/2008/10/14/this-is-what-denial-does/
So, Mark and Hank, we believe with 90% certainty that the AGW effect, which began about 250 years ago with the Industrial Revolution (near here at Ironbridge, Shropshire, plentiful wood and water) has waited 250 years to manifest itself as a 0.3 degree increase in the average temperature in the lower atmosphere/surface. This after a 40% increase in atmospheric CO2.
You could not measure average temperature to that degree of accuracy over 10 years in a garden shed, and if you attempted it you would need quality control procedures which are manifestly lacking across the US (probably the best available apart from the UK) – see Watts Up with That.
If you think you know the sea surface (more than 70% of the total) temperatures sufficiently accurately look at this post:
http://earthobservatory.nasa.gov/Features/OceanCooling/page2.php
I object to the unjustified certainty, and the absence of laboratory based experimental evidence (Angstroms demonstration of Saturation is dismissed as “botched” and Woods greenhouses’ as irrelevant). Nothing is offered in their place.
It would be absurd if it were not so dangerous. The US economy will suffer even more if the automobile industry fails. In the UK power supplies will fail in about seven years from now unless now invest in new coal-fired stations – it is too late for nuclear power. We are now converting corn to Ethanol (when I wrote professional papers on this subject, light years ago, I raised that possibility as a joke)
Meanwhile the chances of China and India foregoing their Industrial Revolutions are vanishingly small, so CO2 we will continue to increase and the temperatures will obstinately fail to respond (I am 90% certain).
Hmm…so let me see if I’ve got this straight.
Even using your 2-sigma levels, 4 of the 7 radiosonde data sets
have trend averages that lie outside the 95% confidence interval
for the models. In addition, the average of all radiosonde trends
also lies outside the 95% confidence level. And this is evidence
of NO discrepancy between the models and data?
[Response: No. It is evidence that there is no obvious discrepancy with the models. On it’s own this data is not a very strong constraint on anything much, but what you can’t say is that it proves that there is a discrepancy. – gavin]
You do understand, I hope, that the likelihood of even one data-set
average falling outside the lower end of the interval by random chance
is only 2.3%. The likelihood of 4 out of 7 doing so is less than 35*(p)^4,
or 1 part in 100,000. This implies a real and obvious discrepancy between
the data and models, with systematic errors existing for the data or models,
or both. Your own reworking of the statistics still supports the conclusion
of Douglass et al.
I would add that ALL data sets (radiosonde and satellite) except for UMd
agree with NO WARMING TREND at the 1-sigma level. Unless large systematic
errors can be identified for all data sets, one must conclude that no warming
is occurring in the troposphere at tropical latitudes.
My final point is that the statistical approach of Douglass et al. is correct.
When looking for SYSTEMATIC deviations between data and model simulations,
one calculates the mean and the standard deviation of the mean for each
and compares. One wants to know, after all, how uncertain the plotted mean value
is.
[Response: The observation is not the expected mean, and so the test they performed makes no sense at all. – gavin]
“[Response: No. It is evidence that there is no obvious discrepancy with the models. On it’s own this data is not a very strong constraint on anything much, but what you can’t say is that it proves that there is a discrepancy. – gavin]”
Gavin,
Thanks for your response. No, the data don’t “prove” there’s a discrepancy. As a scientist, I think you know better than to use such loaded language. But the data do strongly suggest that a discrepancy exists. The discrepancy is obvious to me.
But let’s be more precise in our language. As I interpret it, the observed data have less than a 2.3% chance of occurring if the models are correct. For a 30-year trend, this would amount to a once-in-a-millenium fluctuation, assuming no systematic error. I would therefore consider the “no obvious discrepancy” hypothesis unlikely. If you disagree, then you should say at what confidence level you would consider the discrepancy obvious.
[Response: But you have ignored the uncertainty in the data – which is much larger than this. If the data were perfect (which it isn’t – look at the spread in the different estimates of it), then you could make that kind of calculation (but I have no idea what you are comparing here – what field? which version of the data and which distribution of model simulations?). – gavin]
The approach of Douglass et al. makes sense to me, but I can be convinced otherwise. Unfortunately, I don’t understand what you mean by “the observation is not the expected mean.” The T2 and T2LT data points are averaged over altitude and (for the theory) the various models. Why wouldn’t one then calculate the standard deviation of the mean to compare the two?
[Response: There are two issues here – one is the forced signal defined as the average of what you would get with the same (transient) external conditions over an infinite number of multiple Earths. Second is what any one realisation of the weather would give. The difference between knowing the 3.5 is mean after throwing a dice an infinite number of times, and seeing a 2 on an individual throw. The particular sequence of dice throws is a random realisation of an underlying stochastic process with a well defined mean and distribution. The same is true for the MSU trend. If you ran the planet over, you wouldn’t get the same thing. Therefore, you can’t assume that the observed MSU trend defines the underlying ‘forced’ trend – instead it has a component of random noise. This would become smaller with a longer time-series, but in the comparison period selected by Douglass (1979-1999), it is still a big term. – gavin]
Gavin,
Thank you for your substantive response. I agree with your point about the uncertainty on the model mean. The sigma you provide gives the range of possible outcomes and the data are one particular realization of those weather conditions over the 30-year period. I
therefore accept your criticism of Douglass et al. on this point, though with some caveats stated below.
I also agree that my calculations above have ignored the large uncertainty in the data. But this is easy to account for. When comparing two means, each with an associated uncertainty, the distribution of the means has a width given by adding the individual widths in quadrature. That is, (sigma-means)^2 = (sigma-data)^2 + (sigma-model)^2. In general, sigma-means can never be bigger than 1.4 times the larger of the two sigmas. As an example, we can compare the radiosonde averages for both T2LT and T2 to the model means. For simplicity, I will use the data mean and the average sigma of the data sets to represent a “typical” radiosonde data set. Using the broad uncertainty you provide for the models (weather noise, etc.), I calculate that the T2LT and T2 means deviate from the model means at the level of 1.25 and 1.26 (sigma-means), respectively. This implies that a typical radiosonde data set has only a 10.4 – 10.6% chance of being that far below the model predictions, in the absence of systematic deviations.
[Response: But that is a big term also (see our previous discussion). – gavin]
Using the language of the IPCC, I would say there’s a “likely” chance of a real discrepancy between the data and theory. This hardly agrees with your claim of “no obvious discrepancy.”
But your position deteriorates further when considering an important refinement of this analysis. All of the radiosonde data are measuring the tropospheric temperature trend under the same noisy (i.e., weather) conditions, so we can usefully calculate the overall mean AND standard deviation of the means. The latter is calculated directly from the seven data sets, but it should be close to (sigma-data)/sqrt(7), which it is. This greatly reduces the uncertainty in the overall radiosonde mean, and implies that the model uncertainty dominates in the calculation of (sigma-means).
[Response: But that assumes they are all independent estimates, and they certainly aren’t since they use the same raw data. – gavin]
Consequently, the overall data means for T2LT and T2 deviate from the model means at the level of 1.82 and 1.63 (sigma-means), respectively. This implies that the aggregate radiosonde data have only a 3.5 and 5.2% chance of being that far below the model predictions without systematic deviations. I would conclude that a real discrepancy between the radiosonde data and the models is “highly likely.”
Now, the above analysis assumes the model uncertainties given in Santer et al. My two caveats are as follows. First, doesn’t the model uncertainty include both model noise (i.e., weather fluctuations) and systematic differences among the models? It’s not valid to calculate (sigma-model) based on both. This makes the noise seem larger than it is.
[Response: Over short periods the size of the weather noise is significantly larger than the structural differences in the models. – gavin]
Second, it is not valid to treat the model noise as if it is unconstrained by observation. Specifically, any weather noise over the last 30 years in the troposphere must hold for the surface as well. If we have indeed experienced 1-chance-in-20 low trend for the last 30 years, it should be evident in the surface data.
Alternatively, weather fluctuations in the models that are not consistent with the surface data should be eliminated altogether.
Doing so, I think, would reduce the model uncertainty.
[Response: If you screen the models to have surface trends similar to that observed, you do reduce the tropospheric range of responses, but error bars still overlap with the uncertainty in the obs. (I did this calculation back in the first comment on this subject). – gavin]
Re: #276 (Brian B)
This suggests you’re using a one-sided test. A two-sided test will double that chance; I see no justification whatever for a one-sided test.
> So, Mark and Hank, we believe …
Ah, Fred’s back, again attributing his ideas to other people.
Using wattsface for his science facts, and belief tanks for his political fundamental assumptions.
Boring, Fred.
tamino,
I am not using any kind of “test.” I am making a straightforward
and precise statement based on the numbers. There’s only a 10% chance
of any data point falling in the range 1.25 sigma or more below the
model mean. Note that ALL the data points fall in the lower range.
The data themselves are one-sided, precisely because there is a discrepancy.
This is also why averaging them together gives an even tighter condition,
making the discrepancy all but certain.
[Response: But that assumes they are all independent estimates, and they certainly aren’t since they use the same raw data. – gavin]
Gavin,
Averaging together the data points does not assume they are independent
estimates. Quite the opposite, it assumes they are estimates of the same
underlying data. This is no different from your averaging together the models,
or averaging the radiosonde data over altitude. In this case, the variation
is due to differences in how each group analyzes the data. Since we have
no way of determining who is right and who is wrong, this variation can be
treated as random error. Any wrong assumptions held in common are, of course,
systematic error.
“[Response: If you screen the models to have surface trends similar to that observed, you do reduce the tropospheric range of responses, but error bars still overlap with the uncertainty in the obs. (I did this calculation back in the first comment on this subject). – gavin]”
Overlapping error bars are irrelevant. You have to CALCULATE the probability
of such an arrangement, as I’ve done above. If the model error bars reduce,
then the probability of getting the data we see becomes even less than
the 3 – 5% chances I’ve quoted above. For the 30-year radiosonde data, this
requires once-in-more-than-a-millenium noise for there to be no discrepancy.
Highly unlikely.
[Response: Sorry, but you have completely misunderstood the nature of the uncertainty here. The errors in the radiosonde data are systematic, not random. Averaging together differently systematically biased numbers does not remove the bias, however many times you do it. Neither are the different methods used to treat the data random, they are structurally different, and can’t be averaged together to improve the estimate. As for ‘overlapping error bars’, this is a reasonable heuristic for this level of conversation – better CALCULATIONS can be found in Santer et al, 2008 (see how annoying that is?).
Let me give you an example. Someone has a scale that has a non-linear error (because the spring is worn out or something) – this has the effect of progressively under-predicting the weight as the weight gets larger. Say the true calibration is W=M*(1+M/0.81), with M is the measured weight, and W the true weight. Thus the error at 1kg is 10% (measure would be 0.9kg), and the error at 2kg is 16% (measure would be 1.66 kg) etc. Now someone takes a weight of makes a measurement and gets 1.52kg. Someone else comes along and calibrates the scale at 1kg, and estimates a correction of 10% and estimates the true weight is 1.69 kg (which is better but still off). Now you come along and suggest the two estimates are independent random estimates of the same value and suggest that the actual value is (1.52+1.69)/2=1.61 kg with some improved accuracy. Isn’t it obvious that this isn’t appropriate? (the real answer in this constructed case is 18kg). – gavin]
Re: #279 (Brian B)
Obfuscation. [edit] On the basis of this “precise statement” you concluded
Discrepancies can be high or low, so one must account for that when making statements such as this. All your “probabilities” are only half as large as they should be.
You finish with the truly ludicrous:
Not only do you fail to understand the nature of systematic bias and autocorrelation, this statement reveals that you assumed your hypothesis was true even before you applied any analysis.
You made up your mind that you’re right, then fudged the numbers to make it seem objective. [edit]
Gavin,
I haven’t misunderstood anything. I understood from the beginning that
each radiosonde data set involves systematic differences in the way the
data is processed. There may also be systematic errors that are common
to all data sets. Averaging together the various data sets is useful for
identifying these latter errors. The same is true of the models. They also
contain systematic errors that differ from model to model, in addition to
systematic errors that are common to all. Averaging them together, as you
did in Santer, et al., allows these latter errors to be identified.
Comparison of data and model means is not helpful for identifying
systematic errors that are unique to each model/data set. At this level
of comparison, such systematic errors look like random error and simply
increase the apparent noise level. Is this distinction difficult to understand?
In your example, the distinction I’m making is adequately demonstrated
(though your formula seems not to work–W = M*(1+M/0.81) gives 90% error
at M = 0.9 kg., doesn’t it?). Averaging the two results together does not
give a more accurate estimate–I never claimed that it did. But comparison
to the actual weight would point to a systematic error present in both analysis
methods.
Your overlapping error bars heuristic is not adequate at any level of discussion.
Suppose the theory and data have the same error bars and the means are separated
by 3 sigma. The 2-sigma error bars will overlap substantially. Does this imply
“no significant discrepancy?” No. The distribution for the means will have error
bars bigger by sqrt(2) = 1.4, so that the means differ by 3/1.4 = 2.1 sigma, clearly
a statistically significant discrepancy.
Your claim of a better calculation in Santer, et al. is not annoying to me at all.
I’ve read the paper multiple times but couldn’t find the number I was looking for.
Perhaps I simply missed it. In that case, you should have no trouble quoting the
confidence level calculated in Santer, et al. That’s really what I’ve asked for
from the beginning. A lot of typing on both sides could have been saved by simply
supplying the number.
tamino,
Hmmm…you accuse me of obfuscation, ludicrousness, and fudging.
This is not exactly a substantive reply on your part. I think you
can do better than that. Just because you don’t like my conclusions
doesn’t mean I’ve made a mistake or that I have a prearranged conclusion.
Discrepancies can indeed go both ways. With random error they always do.
The fact that the data points are all consistently low seems to point
to a systematic error. This suspicion is supported by my calculation.
If I fail to understand the “nature of systematic bias and
autocorrelation,” then perhaps you can point out how. I am
always happy to learn new things and am quick to acknowledge
errors on my part when they become clear to me. :)
Re: #283 (Brian B)
You claim to understand that deviations can go both ways. But you persist in defending the use of a one-sided statistic for a deviation that can go either way.
This isn’t esoteric — it’s as basic as it gets, and is an error on your part. Let us know when it becomes clear to you.