
This is Hansen et al’s end of year summary for 2009 (with a couple of minor edits). Update: A final version of this text is available here.
If It’s That Warm, How Come It’s So Damned Cold?
by James Hansen, Reto Ruedy, Makiko Sato, and Ken Lo
The past year, 2009, tied as the second warmest year in the 130 years of global instrumental temperature records, in the surface temperature analysis of the NASA Goddard Institute for Space Studies (GISS). The Southern Hemisphere set a record as the warmest year for that half of the world. Global mean temperature, as shown in Figure 1a, was 0.57°C (1.0°F) warmer than climatology (the 1951-1980 base period). Southern Hemisphere mean temperature, as shown in Figure 1b, was 0.49°C (0.88°F) warmer than in the period of climatology.
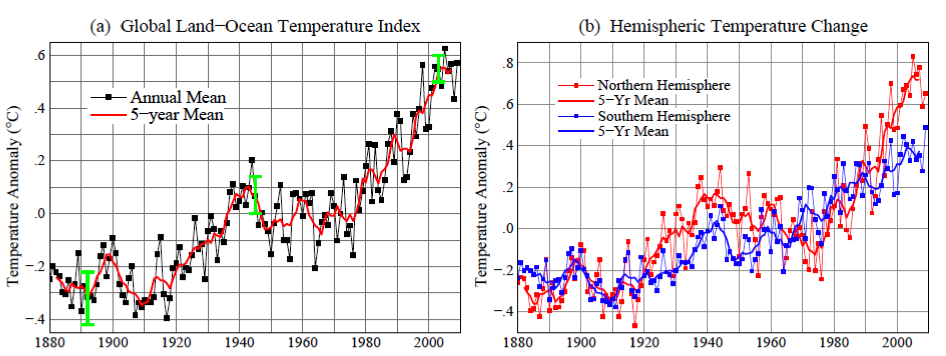
Figure 1. (a) GISS analysis of global surface temperature change. Green vertical bar is estimated 95 percent confidence range (two standard deviations) for annual temperature change. (b) Hemispheric temperature change in GISS analysis. (Base period is 1951-1980. This base period is fixed consistently in GISS temperature analysis papers – see References. Base period 1961-1990 is used for comparison with published HadCRUT analyses in Figures 3 and 4.)
The global record warm year, in the period of near-global instrumental measurements (since the late 1800s), was 2005. Sometimes it is asserted that 1998 was the warmest year. The origin of this confusion is discussed below. There is a high degree of interannual (year‐to‐year) and decadal variability in both global and hemispheric temperatures. Underlying this variability, however, is a long‐term warming trend that has become strong and persistent over the past three decades. The long‐term trends are more apparent when temperature is averaged over several years. The 60‐month (5‐year) and 132 month (11‐year) running mean temperatures are shown in Figure 2 for the globe and the hemispheres. The 5‐year mean is sufficient to reduce the effect of the El Niño – La Niña cycles of tropical climate. The 11‐year mean minimizes the effect of solar variability – the brightness of the sun varies by a measurable amount over the sunspot cycle, which is typically of 10‐12 year duration.
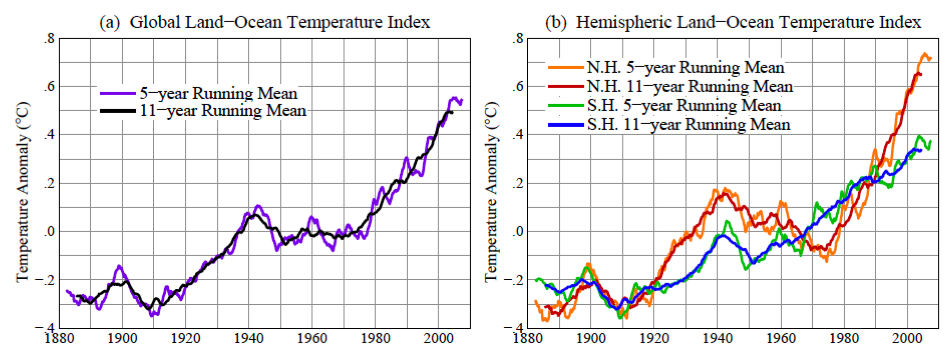
Figure 2. 60‐month (5‐year) and 132 month (11‐year) running mean temperatures in the GISS analysis of (a) global and (b) hemispheric surface temperature change. (Base period is 1951‐1980.)
There is a contradiction between the observed continued warming trend and popular perceptions about climate trends. Frequent statements include: “There has been global cooling over the past decade.” “Global warming stopped in 1998.” “1998 is the warmest year in the record.” Such statements have been repeated so often that most of the public seems to accept them as being true. However, based on our data, such statements are not correct. The origin of this contradiction probably lies in part in differences between the GISS and HadCRUT temperature analyses (HadCRUT is the joint Hadley Centre/University of East Anglia Climatic Research Unit temperature analysis). Indeed, HadCRUT finds 1998 to be the warmest year in their record. In addition, popular belief that the world is cooling is reinforced by cold weather anomalies in the United States in the summer of 2009 and cold anomalies in much of the Northern Hemisphere in December 2009. Here we first show the main reason for the difference between the GISS and HadCRUT analyses. Then we examine the 2009 regional temperature anomalies in the context of global temperatures.
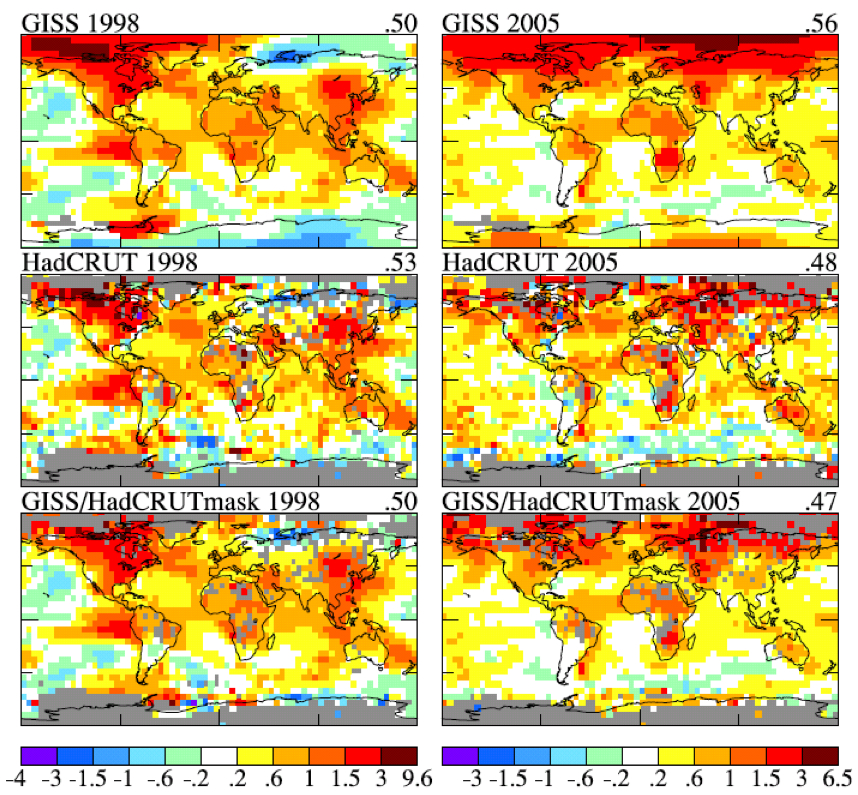
Figure 3. Temperature anomalies in 1998 (left column) and 2005 (right column). Top row is GISS analysis, middle row is HadCRUT analysis, and bottom row is the GISS analysis masked to the same area and resolution as the HadCRUT analysis. [Base period is 1961‐1990.]
Figure 3 shows maps of GISS and HadCRUT 1998 and 2005 temperature anomalies relative to base period 1961‐1990 (the base period used by HadCRUT). The temperature anomalies are at a 5 degree‐by‐5 degree resolution for the GISS data to match that in the HadCRUT analysis. In the lower two maps we display the GISS data masked to the same area and resolution as the HadCRUT analysis. The “masked” GISS data let us quantify the extent to which the difference between the GISS and HadCRUT analyses is due to the data interpolation and extrapolation that occurs in the GISS analysis. The GISS analysis assigns a temperature anomaly to many gridboxes that do not contain measurement data, specifically all gridboxes located within 1200 km of one or more stations that do have defined temperature anomalies.
The rationale for this aspect of the GISS analysis is based on the fact that temperature anomaly patterns tend to be large scale. For example, if it is an unusually cold winter in New York, it is probably unusually cold in Philadelphia too. This fact suggests that it may be better to assign a temperature anomaly based on the nearest stations for a gridbox that contains no observing stations, rather than excluding that gridbox from the global analysis. Tests of this assumption are described in our papers referenced below.
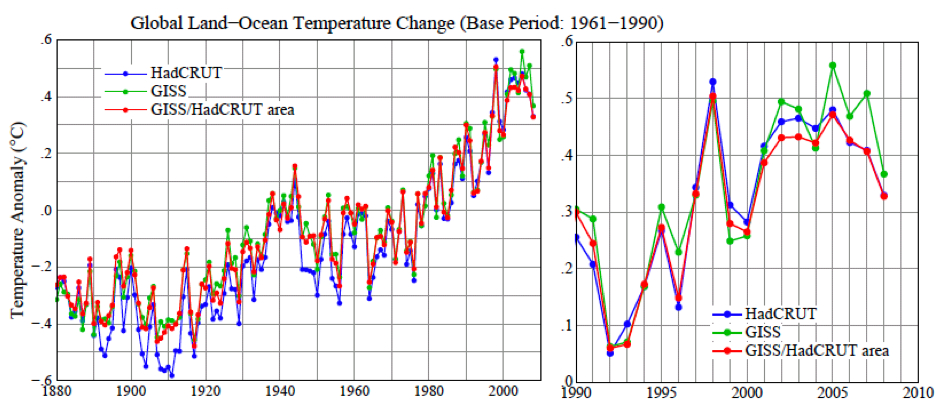
Figure 4. Global surface temperature anomalies relative to 1961‐1990 base period for three cases: HadCRUT, GISS, and GISS anomalies limited to the HadCRUT area. [To obtain consistent time series for the HadCRUT and GISS global means, monthly results were averaged over regions with defined temperature anomalies within four latitude zones (90N‐25N, 25N‐Equator, Equator‐25S, 25S‐90S); the global average then weights these zones by the true area of the full zones, and the annual means are based on those monthly global means.]
Figure 4 shows time series of global temperature for the GISS and HadCRUT analyses, as well as for the GISS analysis masked to the HadCRUT data region. This figure reveals that the differences that have developed between the GISS and HadCRUT global temperatures during the past few decades are due primarily to the extension of the GISS analysis into regions that are excluded from the HadCRUT analysis. The GISS and HadCRUT results are similar during this period, when the analyses are limited to exactly the same area. The GISS analysis also finds 1998 as the warmest year, if analysis is limited to the masked area. The question then becomes: how valid are the extrapolations and interpolation in the GISS analysis? If the temperature anomaly scale is adjusted such that the global mean anomaly is zero, the patterns of warm and cool regions have realistic‐looking meteorological patterns, providing qualitative support for the data extensions. However, we would like a quantitative measure of the uncertainty in our estimate of the global temperature anomaly caused by the fact that the spatial distribution of measurements is incomplete. One way to estimate that uncertainty, or possible error, can be obtained via use of the complete time series of global surface temperature data generated by a global climate model that has been demonstrated to have realistic spatial and temporal variability of surface temperature. We can sample this data set at only the locations where measurement stations exist, use this sub‐sample of data to estimate global temperature change with the GISS analysis method, and compare the result with the “perfect” knowledge of global temperature provided by the data at all gridpoints.
| 1880‐1900 | 1900‐1950 | 1960‐2008 | |
|---|---|---|---|
| Meteorological Stations | 0.2 | 0.15 | 0.08 |
| Land‐Ocean Index | 0.08 | 0.05 | 0.05 |
Table 1. Two‐sigma error estimate versus period for meteorological stations and land‐ocean index.
Table 1 shows the derived error due to incomplete coverage of stations. As expected, the error was larger at early dates when station coverage was poorer. Also the error is much larger when data are available only from meteorological stations, without ship or satellite measurements for ocean areas. In recent decades the 2‐sigma uncertainty (95 percent confidence of being within that range, ~2‐3 percent chance of being outside that range in a specific direction) has been about 0.05°C. The incomplete coverage of stations is the primary cause of uncertainty in comparing nearby years, for which the effect of more systematic errors such as urban warming is small.
Additional sources of error become important when comparing temperature anomalies separated by longer periods. The most well‐known source of long‐term error is “urban warming”, human‐made local warming caused by energy use and alterations of the natural environment. Various other errors affecting the estimates of long‐term temperature change are described comprehensively in a large number of papers by Tom Karl and his associates at the NOAA National Climate Data Center. The GISS temperature analysis corrects for urban effects by adjusting the long‐term trends of urban stations to be consistent with the trends at nearby rural stations, with urban locations identified either by population or satellite‐observed night lights. In a paper in preparation we demonstrate that the population and night light approaches yield similar results on global average. The additional error caused by factors other than incomplete spatial coverage is estimated to be of the order of 0.1°C on time scales of several decades to a century, this estimate necessarily being partly subjective. The estimated total uncertainty in global mean temperature anomaly with land and ocean data included thus is similar to the error estimate in the first line of Table 1, i.e., the error due to limited spatial coverage when only meteorological stations are included.
Now let’s consider whether we can specify a rank among the recent global annual temperatures, i.e., which year is warmest, second warmest, etc. Figure 1a shows 2009 as the second warmest year, but it is so close to 1998, 2002, 2003, 2006, and 2007 that we must declare these years as being in a virtual tie as the second warmest year. The maximum difference among these in the GISS analysis is ~0.03°C (2009 being the warmest among those years and 2006 the coolest). This range is approximately equal to our 1‐sigma uncertainty of ~0.025°C, which is the reason for stating that these five years are tied for second warmest.
The year 2005 is 0.061°C warmer than 1998 in our analysis. So how certain are we that 2005 was warmer than 1998? Given the standard deviation of ~0.025°C for the estimated error, we can estimate the probability that 1998 was warmer than 2005 as follows. The chance that 1998 is 0.025°C warmer than our estimated value is about (1 – 0.68)/2 = 0.16. The chance that 2005 is 0.025°C cooler than our estimate is also 0.16. The probability of both of these is ~0.03 (3 percent). Integrating over the tail of the distribution and accounting for the 2005‐1998 temperature difference being 0.61°C alters the estimate in opposite directions. For the moment let us just say that the chance that 1998 is warmer than 2005, given our temperature analysis, is at most no more than about 10 percent. Therefore, we can say with a reasonable degree of confidence that 2005 is the warmest year in the period of instrumental data.
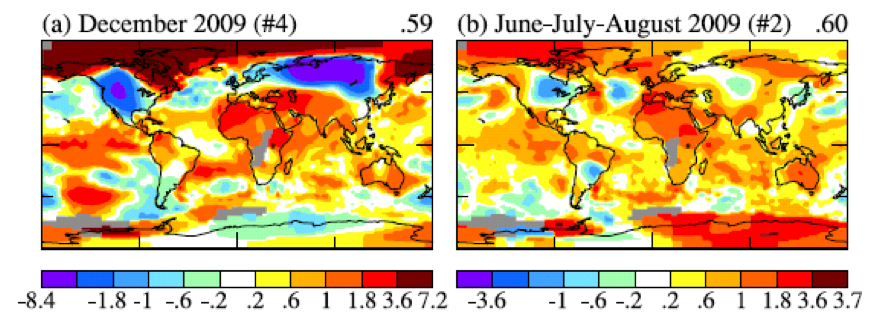
Figure 5. (a) global map of December 2009 anomaly, (b) global map of Jun‐Jul‐Aug 2009 anomaly. #4 and #2 indicate that December 2009 and JJA are the 4th and 2nd warmest globally for those periods.
What about the claim that the Earth’s surface has been cooling over the past decade? That issue can be addressed with a far higher degree of confidence, because the error due to incomplete spatial coverage of measurements becomes much smaller when averaged over several years. The 2‐sigma error in the 5‐year running‐mean temperature anomaly shown in Figure 2, is about a factor of two smaller than the annual mean uncertainty, thus 0.02‐0.03°C. Given that the change of 5‐year‐mean global temperature anomaly is about 0.2°C over the past decade, we can conclude that the world has become warmer over the past decade, not cooler.
Why are some people so readily convinced of a false conclusion, that the world is really experiencing a cooling trend? That gullibility probably has a lot to do with regional short‐term temperature fluctuations, which are an order of magnitude larger than global average annual anomalies. Yet many lay people do understand the distinction between regional short‐term anomalies and global trends. For example, here is comment posted by “frogbandit” at 8:38p.m. 1/6/2010 on City Bright blog:
“I wonder about the people who use cold weather to say that the globe is cooling. It forgets that global warming has a global component and that its a trend, not an everyday thing. I hear people down in the lower 48 say its really cold this winter. That ain’t true so far up here in Alaska. Bethel, Alaska, had a brown Christmas. Here in Anchorage, the temperature today is 31[ºF]. I can’t say based on the fact Anchorage and Bethel are warm so far this winter that we have global warming. That would be a really dumb argument to think my weather pattern is being experienced even in the rest of the United States, much less globally.”
What frogbandit is saying is illustrated by the global map of temperature anomalies in December 2009 (Figure 5a). There were strong negative temperature anomalies at middle latitudes in the Northern Hemisphere, as great as ‐8°C in Siberia, averaged over the month. But the temperature anomaly in the Arctic was as great as +7°C. The cold December perhaps reaffirmed an impression gained by Americans from the unusually cool 2009 summer. There was a large region in the United States and Canada in June‐July‐August with a negative temperature anomaly greater than 1°C, the largest negative anomaly on the planet.
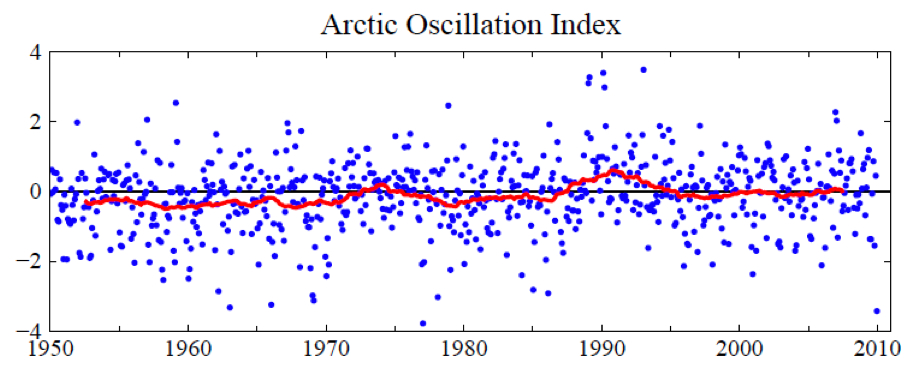
Figure 6. Arctic Oscillation (AO) Index. Positive values of the AO index indicate high low pressure in the polar region and thus a tendency for strong zonal winds that minimize cold air outbreaks to middle latitudes. Blue dots are monthly means and the red curve is the 60‐month (5‐year) running mean.
How do these large regional temperature anomalies stack up against an expectation of, and the reality of, global warming? How unusual are these regional negative fluctuations? Do they have any relationship to global warming? Do they contradict global warming?
It is obvious that in December 2009 there was an unusual exchange of polar and mid‐latitude air in the Northern Hemisphere. Arctic air rushed into both North America and Eurasia, and, of course, it was replaced in the polar region by air from middle latitudes. The degree to which Arctic air penetrates into middle latitudes is related to the Arctic Oscillation (AO) index, which is defined by surface atmospheric pressure patterns and is plotted in Figure 6. When the AO index is positive surface pressure is high low in the polar region. This helps the middle latitude jet stream to blow strongly and consistently from west to east, thus keeping cold Arctic air locked in the polar region. When the AO index is negative there tends to be low high pressure in the polar region, weaker zonal winds, and greater movement of frigid polar air into middle latitudes.
Figure 6 shows that December 2009 was the most extreme negative Arctic Oscillation since the 1970s. Although there were ten cases between the early 1960s and mid 1980s with an AO index more extreme than ‐2.5, there were no such extreme cases since then until last month. It is no wonder that the public has become accustomed to the absence of extreme blasts of cold air.

Figure 7. Temperature anomaly from GISS analysis and AO index from NOAA National Weather Service Climate Prediction Center. United States mean refers to the 48 contiguous states.
Figure 7 shows the AO index with greater temporal resolution for two 5‐year periods. It is obvious that there is a high degree of correlation of the AO index with temperature in the United States, with any possible lag between index and temperature anomaly less than the monthly temporal resolution. Large negative anomalies, when they occur, are usually in a winter month. Note that the January 1977 temperature anomaly, mainly located in the Eastern United States, was considerably stronger than the December 2009 anomaly. [There is nothing magic about a 31 day window that coincides with a calendar month, and it could be misleading. It may be more informative to look at a 30‐day running mean and at the Dec‐Jan‐Feb means for the AO index and temperature anomalies.]
The AO index is not so much an explanation for climate anomaly patterns as it is a simple statement of the situation. However, John (Mike) Wallace and colleagues have been able to use the AO description to aid consideration of how the patterns may change as greenhouse gases increase. A number of papers, by Wallace, David Thompson, and others, as well as by Drew Shindell and others at GISS, have pointed out that increasing carbon dioxide causes the stratosphere to cool, in turn causing on average a stronger jet stream and thus a tendency for a more positive Arctic Oscillation. Overall, Figure 6 shows a tendency in the expected sense. The AO is not the only factor that might alter the frequency of Arctic cold air outbreaks. For example, what is the effect of reduced Arctic sea ice on weather patterns? There is not enough empirical evidence since the rapid ice melt of 2007. We conclude only that December 2009 was a highly anomalous month and that its unusual AO can be described as the “cause” of the extreme December weather.
We do not find a basis for expecting frequent repeat occurrences. On the contrary. Figure 6 does show that month‐to‐month fluctuations of the AO are much larger than its long term trend. But temperature change can be caused by greenhouse gases and global warming independent of Arctic Oscillation dynamical effects.

Figure 8. Global maps 4 season temperature anomalies for ~2009. (Note that Dec is December 2008. Base period is 1951‐1980.)
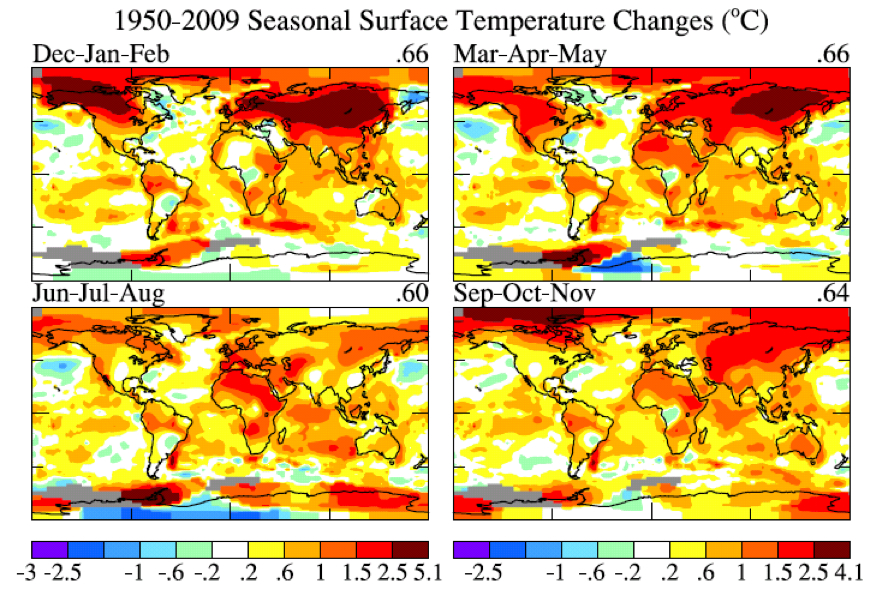
Figure 9. Global maps 4 season temperature anomaly trends for period 1950‐2009.
So let’s look at recent regional temperature anomalies and temperature trends. Figure 8 shows seasonal temperature anomalies for the past year and Figure 9 shows seasonal temperature change since 1950 based on local linear trends. The temperature scales are identical in Figures 8 and 9. The outstanding characteristic in comparing these two figures is that the magnitude of the 60 year change is similar to the magnitude of seasonal anomalies. What this is telling us is that the climate dice are already strongly loaded. The perceptive person who has been around since the 1950s should be able to notice that seasonal mean temperatures are usually greater than they were in the 1950s, although there are still occasional cold seasons.
The magnitude of monthly temperature anomalies is typically 1.5 to 2 times greater than the magnitude of seasonal anomalies. So it is not yet quite so easy to see global warming if one’s figure of merit is monthly mean temperature. And, of course, daily weather fluctuations are much larger than the impact of the global warming trend. The bottom line is this: there is no global cooling trend. For the time being, until humanity brings its greenhouse gas emissions under control, we can expect each decade to be warmer than the preceding one. Weather fluctuations certainly exceed local temperature changes over the past half century. But the perceptive person should be able to see that climate is warming on decadal time scales.
This information needs to be combined with the conclusion that global warming of 1‐2°C has enormous implications for humanity. But that discussion is beyond the scope of this note.
References:
Hansen, J.E., and S. Lebedeff, 1987: Global trends of measured surface air temperature. J. Geophys. Res., 92, 13345‐13372.
Hansen, J., R. Ruedy, J. Glascoe, and Mki. Sato, 1999: GISS analysis of surface temperature change. J. Geophys. Res., 104, 30997‐31022.
Hansen, J.E., R. Ruedy, Mki. Sato, M. Imhoff, W. Lawrence, D. Easterling, T. Peterson, and T. Karl, 2001: A closer look at United States and global surface temperature change. J. Geophys. Res., 106, 23947‐23963.
Hansen, J., Mki. Sato, R. Ruedy, K. Lo, D.W. Lea, and M. Medina‐Elizade, 2006: Global temperature change. Proc. Natl. Acad. Sci., 103, 14288‐14293.
Bbbbbuttt…. it’s all those temperature gauges sitting right next to air-conditioning exhaust vents!
Oh, wait… this time of year, most of those “air conditioners” are either off or are running in “heat-pump” mode. Never mind….
The big question is — will we get freezing temps again in Edinburg, TX, in the lower Rio Grande Valley this season (latitude 26.3 N)? My husband wants to know if he can plant his vegetable garden. The one he planted earlier froze (which hardly ever happen here).
Mr Hansen you have demonstrated at Fossil Fuel powered electrical generating facilities, and testified for greenpeace activists whom have demonstrated at Fossil Fuel powered electrical generating facilities!
yet to the best of my knowledge neither you or greenpeace support replacement technolgies, why is that ?
[Response: Knowledge about Jim Hansen’s view are best found by reading what he has written on the subject. Try his book, or his plentiful popular science pieces. I can’t speak for Greenpeace, but you are definitely wrong about Hansen. – gavin]
> heat-pump mode
Yeah, see, they’re sucking the heat right out of the thermometers, making it seem colder than it really is. Oh, wait ….
The debate used to be about whether to call it “Global Climate Destabilization” – a much more descriptive term.
From what I read and what I experience, one can say that our climate is destabilized, with more to come. This means extreme, erratic weather events of all kinds – not just heat. Expect stronger storms, wetter rains, dryer droughts, colder cold snaps, and plenty of heat waves.
[Response: This is not something that emerges from the IPCC consensus. You can see from the AO index how hard it is to discern a trend in the mean and to validate that against model expectations, trying to do the same with the variability is much harder and has not been done. Given the link between cold air outbreaks and the AO, one would anticipate fewer cold extremes as a function of the expected positive trend in the AO. The blanket claim that more variability in every index is expected because of ‘climate destabilisation’ is wrong. Statements about extremes of any kind are very specific to exactly what is being discussed and the extent to which any changes are expected needs to be properly sourced. – gavin]
December was .59 degrees C warmer than average. Really? That’s ..well…curious.
It’s nice to see time-linear data presented (at least on occasion) as “running means”. Figure 2 demonstrates their utility in making order out of chaos. As long as the author doesn’t opt for 100-year applications!
Lynn, if you’re serious about that question, you’re a bit muddled, and you’re probably asking the wrong people: you’re asking about the weather, not the climate. If you want an answer, it’s ‘maybe’– if the AO drops through the floor again, arctic air could flow down to your neighborhood again. But the frost you’ve had might just be a one-off; after all, as you said, it’s a pretty rare event.
Can you address this story, in a way that Joe Public can understand?
http://blogs.telegraph.co.uk/news/jamesdelingpole/100022474/climategate-goes-american-noaa-giss-and-the-mystery-of-the-vanishing-weather-stations/
[Response: It’s nonsense born of ignorance of what these analyses do and prejudice against the results. The basic claim is apparently that a coastal station absolute temperature is being used to estimate the current absolute temperature in the mountains and that the anomaly there is warm because the coast is warmer than the mountain. Well, if anyone was doing that, the temperature anomalies would be a lot larger than a few tenths of a degree! What is actually done is that temperature anomalies are calculated locally from local baselines, and these anomalies can be interpolated over quite large distances. This is perfectly fine and checkable by looking at the pairwise correlations at the monthly stations between different stations (London-Paris or New York-Cleveland or LA-San Francisco). The second thread in their ‘accusation’ is that the agencies are deleting records – this just underscores their lack of understanding of where the GHCN data set actually comes from. They could just try reading Peterson and Vose (1997) which indicates where the data came from, and which data streams give real time updates. The principle one is the CLIMAT updates from WMO GCOS. These are distributed by the Nat. Met. Services who have decided which stations they choose to produce monthly mean data for (and how it is calculated) and is absolutely nothing to do with NODC or NASA. – gavin]
Those charts show less than a one degree rise in 130 years. That would seem consistent with pre-industrial centuries preceding this chart.
Ok, disclaimer: I’m a layman, I have a decent amount of general math and science knowledge. BTW, I have just gotten through some very unseasonably cold weather here in South Florida…So I’ve heard the Oh, sooo much for global warming, eh?, cliche so much recently, that I just want to punch people out at this point!
I just took the time to carefully read What Hanson et al have written in this short paper. I’m willing to bet a considerable amount of money that your typical climate change denialist will not even take the time to read a single paper such as this and even if they did they probably don’t have a clue what something as basic as:
means.
Let alone grasp something as basic as the difference between weather and climate.
So you guys must be doing a lousy job getting the true story out to Joe public! ;-)
Just kidding, frustated in Florida!
[Response: Understood, but you need to see that the information conduit is a process. Scientists do their job and produce technically correct statements, and hopefully some context, and then the various levels of popularisers take that information and make pithier and more palatable (though less informative statements) that are nonetheless consistent with the scientific statements. So here, soundbites like ‘it’s weather not climate’, or ‘look globally, not locally’, can follow knowing that there is some factual basis for that. Scientists can of course be popularisers as well, but we can’t neglect the technical stuff that stands behind it. – gavin]
People believe those lies because public relations professionals got those lies placed in front of the public over and over. Even if people doubt a statement, if it is repeated over and over to them from different sources, people will come to accept it.
For such acceptance, the lie must be simple and repeated often. It does not have to be self consistent or consistent with any other knowledge framework.
Scientists are different from public relations professionals because scientists get tired of saying the same thing over and over and over. (RC may say the same thing a few times. Real PR guys would get those things said thousands of times. Folks have to find, and come to RC. Real PR guys would “push it out”, whether people wanted to read it or not.)
Face it, (climate) science just does not “get” the concepts of public relations and mass communications. Science does not market itself or its products. For one thing, science does not have a marketing budget. Imagine writing a grant proposal to do atmospheric research and putting in a line item that was 30% of the total request to “market” the results.
In contrast, the oil companies and car companies really do understand the fine points of marketing. Each of their products has a fully funded marketing budget.
Our marketing program is called “public education”, and it has been under resourced for a long time.
I just came across — and mentioned over at Tamino’s — this year-old story; it looks at the same Arctic weather and ice conditions and at an ocean circulation hiccup. http://www.whoi.edu/page.do?pid=12455&tid=282&cid=54347
Followup there http://tamino.wordpress.com/2010/01/13/models-2/#comment-38598 about modeling generally; just curious if the wind change discussed there is related to this winter’s weather changes.
A useful antidote to the “my drive has more snow than I’ve ever seen” school of climate science.
A future piece on oscillations would be of interest. My understanding is that they explain a lot but cannot themselves be explained.
Regarding Gavin’s response to #5 (extreme weather events), would it be accurate to narrow down and say that more and/or worse droughts and heat waves can be inferred from high-probability IPCC conclusions (though of course not in all locations)?
[Response: Yes. But the regionality of the droughts (in particular) is still poorly defined. – gavin]
What is the diference between the rankings from GISS and NOAA?
http://www.ncdc.noaa.gov/sotc/
[Response: Different treatment for urban heat effects and different procedure for extrapolation to data poor areas. The correlation is pretty high though. – gavin]
“Underlying this variability, however, is a long‐term warming trend that has become strong and persistent over the past three decades.”
Figure 4 undercuts the use of the term “strong” for the last decade of that three-decade period. Unfortunately, this is the sort of imprecise language that causes problems.
Typo Fig. 3 “Temperature anomalies in 1988 (left column)” should be 1998.
[Response: Fixed. Thanks. – gavin]
Looking at GISS hemispheric data, the SH busted all prior 130 years on their record and not by that silly 5th decimal BS “oh 1934 was warmer than 1998, for the United [below Canada] States” margin… 0.489C+ anomaly for 2009, with in second place 2002’s 0.443C+ anomaly. Oceanic heat content starting to come back at us with a vengeance.
I need help in interpreting the statement in the main article: “The AO index is not so much an explanation for climate anomaly patterns as it is a simple statement of the situation. However, John (Mike) Wallace and colleagues have been able to use the AO description to aid consideration of how the patterns may change as greenhouse gases increase. A number of papers, by Wallace, David Thompson, and others, as well as by Drew Shindell and others at GISS, have pointed out that increasing carbon dioxide causes the stratosphere to cool, in turn causing on average a stronger jet stream and thus a tendency for a more positive Arctic Oscillation.”
What I get out of it is that greenhouse gases warm the planet overall, but can also cause artic oscillations that change the pattern of the jet stream and therefore cool portions of the planet affected by the change in the jet stream. Is there an inconsistency in saying that CO2 causes the stratosphere to cool while causing the earth to warm?
“Is there an inconsistency in saying that CO2 causes the stratosphere to cool while causing the earth to warm?”
No, because they do different things.
If you sleep under a thin blanket, the top of the blanket will be warm because of your body and your body cold because of the heat it is letting through.
If you sleep under a thick blanket, the top of the blanket will be cooler because it’s stopping more heat loss and your body warmer because your body is still generating the same heat.
Dr. Hansen: “This information needs to be combined with the conclusion that global warming of 1‐2°C has enormous implications for humanity. But that discussion is beyond the scope of this note.”
That is the reason why the average person isn’t listening. What is an enormous implication? A 1% drop in the stock market? The ONLY thing the average person cares about is the implication for himself. Quit writing “this note” and write about the implications for humanity. The other reasons are the financial clout of the fossil fuel companies, the extreme length of the article and that people want to see blood. Shorten it to a sound byte.
What are people watching almost continuously now? The disaster in Haiti. They get to see dead bodies in Haiti. They like to see dead bodies and flowing blood. Seeing what they want to see it makes them feel guilty, so they “contribute”. Make climate change graphic and gory. Make it bleed. If it doesn’t bleed, it doesn’t lead. Make sure you outdo the story from the earthquake in Haiti. Include lots of pictures of mountains of dead people. Tell them that, if AGW isn’t stopped, THEY will personally be at the bottom of the pile of dead bodies.
Figure 4b will be interpreted by the denialists to mean that AGW stopped in 2000.
realist, did you pick the same conditions at the start of that 130 years as at the end?
1) Solar minimum
2) ENSO minimum, picking up to a warm phase
3) Similar PDO phase
?
If not, you’re comparing apples to oranges. Solar state can make a .2C difference, either end, straight off the top, there, for example. We know we’re at a minimum of solar. What was 1870?
Fred Magyar says: 17 January 2010 at 12:23 PM
Your comment seems consistent with others I’ve read elsewhere.
I’m an enthusiast for this sort of stuff right now, and I still did not take time to wade through the details. Perhaps that’s because I’m fairly confident about my ability to discern weather versus climate, but all the same, it’s a pretty dense essay.
All the same, if anything is left out or is treated ambiguously, doubters will exploit that. So, a bit of a dilemma.
A succinct distillation for consumption by journalists accompanied by a full appendix would be an excellent move.
Russ, I think you got that mixed up. The idea is that a strengthening of the northern jet stream will tend to keep arctic air in the arctic, instead of having it break out into temperate zones. Key phrase there is “tend to”. There will still be cold air outbreaks since there is a natural variation in the AO, and as mentioned, there are other possible influences as well (e.g. arctic ice conditiions).
Here’s another, possibly more user-friendly explanation, in TV form:
http://www.youtube.com/v/sAvqabAPIr4
More great stuff here:
http://www.youtube.com/view_play_list?p=029130BFDC78FA33&search_query=Climate+Crock
Don Shor says:
Figure 4 undercuts the use of the term “strong” for the last decade of that three-decade period. Unfortunately, this is the sort of imprecise language that causes problems.
The “problem”, I would say, is in how you fail to recognize that the statement in the article is referring to a 30 year period, not to any individual 10 year period. Seems pretty clear to me.
According to NOAA, the AO reached a record low since 1950:
“The phase of the AO is described in terms of an index value. In December 2009 the AO index value was -3.41, the most negative value since at least 1950, according to data from the NOAA Climate Prediction Center.”
http://nsidc.org/arcticseaicenews/
However, Figure 6 of this Article indicates a blue dot around 1977 or so that is just about the same as the most recent blue dot. The AO during the 1950’s doesn’t look very negative.
Which one is correct?
Thanks!
Hi there. Thanks for the great post. Informative as always. I just thought I’d point out an excellent blog post I read just yesterday, pointing out in very simple, layman friendly terms, just how difficult it is to identify trends over statistically small samples with such “noisy” data i.e. where local (spatial/temporal) anomalies swamp the trend line.
http://blogs.crikey.com.au/pollytics/2010/01/17/nerdy-sunday-when-trends-go-bad/
Keep up the good work.
Jim Bouldin says: 17 January 2010 at 3:11 PM
“The “problem”, I would say, is in how you fail to recognize that the statement in the article is referring to a 30 year period…”
Jim, remember, the default in a situation of “failure to communicate” is that the communicator failed, not the listener. If an average reader is susceptible to misunderstanding the message, the message could probably use some additional tuning.
Perhaps it would be better if the phrase was “summarizing all of the available data, we see a long‐term warming trend that has become strong and persistent over the past three decades” or something to that effect.
I think some of the problem with the perception among us lay people is the way the charts are drawn. The chart is a rectangle with roughly 3:2 aspect ratio. Using the constraints of the data as the max and min for each axis you have to use extreme compression of the horizontal axis to accommodate 139 years whereas the whole vertical axis is just 1.4 degrees.
I understand that these are the constraints of the data – but it does give the impression of a precipitous rise in temperatures when it actually is only around +0.9 deg C in 129 years. I often think that people look at the chart and think “no, the temperature is not rising that fast!” without actually realising that the global warming signal is just around 0.02c a year hidden within a huge annual variability, such as between -5c and +30c in the UK. I think the statement:
“But the perceptive person should be able to see that climate is warming on decadal time scales.”
is presuming people have some quite miraculous memory for temperatures!
As for myself, my abiding impression of my childhood was that it was much warmer than it is today. Clearly it wasn’t but I think “the perceptive person” is no good judge at all over decadal timescales!
I am not sure what to use as an alternative range for the vertical axis. Perhaps the average variance of temperatures between night and day? The average human being could at least relate to that.
The 11 year running mean does show a very clear linear upward trend – so how does this compare with the predictions of +3 to +6 degrees between 2000 and 2100?
Looking at the chart the current upward trend in temperatures seems to start in the early 1970s. I have taken the data and calculated 11 year running means from 1965 to 2009. This produces the first data point in 1975 which is -0.030c. The last data point, 2009, is +0.608c with an almost straight line between the two points. Using the 11 year running mean as a proxy for the actual data (not sure how valid this is) the difference is 0.638c over 34 annual data points.
That gives an annual rise of 0.01876c a year. Extrapolated over the next 100 years that would give a change of just 1.876c.
Now I am sure the argument is that the models show accelleration in warming as the century progresses. But there is little sign of it yet, and of course that also presumes that the current linear trend continues and that we won’t see any more periods of flat temperature like we saw between 1940 and 1970 at any point in the next 90 years.
Just a few random thoughts…
Re: Cardin #6
The NCDC climate report breaks down December into different areas that Dr. Hansen does. They report that the weather in the US WAS below average. It actually was cold in the USA in December. Dr. Hansen’s data above discusses the GLOBAL average anomaly. The NCDC global anomaly is similar to Dr. Hansen within the limits of the errors Dr. Hansen describes. If you look at figure 5, the anomaly in December for the USA is substantially cold (it is also cold in Siberia). Keep in mind it is Global climate change and you expect there to be regional variations on a monthly basis.
In the post here at RC at:
https://www.realclimate.org/index.php/archives/2009/12/updates-to-model-data-comparisons/comment-page-9/#comment-152359
we see that 10×10^23 Joules went into the oceans from 1985 to 2005. If that had not happened the world atmosphere would be about 7.5 degrees C warmer than it is now.
That would have been easy to see in the data.
“Jim, remember, the default in a situation of “failure to communicate” is that the communicator failed, not the listener.”
True, but you can’t see the lack of lividity over the internet: we can’t tell who are zombies.
And when they’re on the line, the communicator isn’t the problem: zombie ears don’t hear too good.
Using red ink for the loss. If you’ve ever wondered why people don’t trust these graphs, perhaps you should consider using colors that do not make it look like the planet is being parbroiled. This is a bad trick sufficient for inclusion in Lies, Damned Lies, and Statistics.
[Response: Riiiight…. People don’t trust climate scientists because of the colour scheme. Got it. – gavin]
“Now I am sure the argument is that the models show accelleration in warming as the century progresses. But there is little sign of it yet,”
But how many 11 year periods do we have as the century progresses? What is the normal figure for working out non-linear line fitting and therefore seeing an accelleration? 8? 12 periods?
But 11 years isn’t really long enough to show climate, since there’s still plenty of variation by non-persistent causes in those values.
So instead of taking 11 year means and using the fewer plots, check to see what the best-fit accelerating curve fitting that line would be, with all the points used.
That should give you the exponent and therefore how much accelleration you would expect to see.
Roll that back into how many 11-year periods you would have to sample and see if there’s signal appearing above the noise.
If you have enough, but there’s no such acceleration, then the hypothesis is not borne out by your analysis.
If you have enough, and that acceleration is seen, then the hypothesis is seen.
If you haven’t enough, then you can’t say one way or the other. If you do or don’t see that acceleration, then it could easily be a mathematical ghost brought from the analysis.
If you really want to see and there’s not enough time, then you need to get clever with the analysis.
Which requires you think of a physical cause and then model its emergent result on the data.
If you’re going that way, might as well try and get a grant…
Why the obsessive need to explain and justify the GISS readings? It is like an orchestrated campaign of persuasion. If your temperatures are correct then we are in serious trouble should the trend persist. If you are not right and the satellites have the right trend then we have nothing to worry about.
I don’t want to give away my own personal position, suffice it to say that I am NOT worried at all.
Keep up the good work though James. Your people need you.
[Response: Suffice to say your personal position is very clear. However, the satellites also show warming – I fail to see how that means you have nothing to worry about. – gavin]
re: #22 (but for all)
I continue to recommend (for USA), Global Climate Change Impacts in the United States from the USGCRP. It is well-written and illustrated, and in particular, it has a 5-10-page section per region, which is really, really important, given the regional differences in effects.
I think for most people, this is way more impactful than average global temperature changes.
Like: will there be more or less water than I Like?
A: yes, and which depends on where you are…
Foobear:
http://www.fark.com/cgi/comments.pl?IDLink=1092301&hl=Teachers-switch-to-purple-pens-to-correct-papers-since-red-is-too-harsh-Here-comes-pseudo-science
35 Comp.F.U.
What Jim are you talking to?
(comment numbers would help a lot)
“If that had not happened the world atmosphere would be about 7.5 degrees C warmer than it is now.”
Jim, please prove that. If you can point to a couple of papers that show that, this is sufficient, but all I’ve heard is you saying that.
Remember: include all the changes and explain where you may have forgotten something or where your assumptions make a difference.
Sorry, post 35 was to Doug posting about Jim Bullis. Your post from me was (currently) 42.
David Harington says: 17 January 2010 at 3:59 PM
“Why the obsessive need to explain and justify the GISS readings? It is like an orchestrated campaign of persuasion.”
Out of the whole document the one thing that compels a comment from you is a between-the-lines extraction of meaning confirming some kind of conspiracy to mislead the public. Same deal as the TomskTwaddle email dust sieving. It’s amazing how oblivious some folks are to the impression they make; don’t you find yourself a little embarrassed from time to time, blurting out such nonsense?
Completely Fed Up says: 17 January 2010 at 4:26 PM
CFU, I -think- Jim’s point is that there’s a lot of additional energy trapped on the planet that’s hidden from us air breathers. He’s not calling the essay into question.
This is all very nice RC and once again scientifically exact but it won’t wash with a lot of the public regardless of what science says. There is a lot at stake here, out entire way of life to be fair and hence you cant really expect to be listened to all that much. 100,000 people potentially lie dead in Haiti – how did AGW effect them?
It didn’t and hence our cultural way of life is not going to change for a meer 0.8C of global average warmin now is it.
42 Compfu
Ok, there are 10 million meters from equator to pole so area of earth is 5.1×10^14 m^2, volume of a roughly 200 km thick atmosphere is 1.02×10^20 m^3, weight of that atmosphere is 1.33×10^23 grams. Specific heat of air, const. vol., is .24 cal/gm, and 4.186 Joules/calorie. From this, it turns out that it takes about 1.34×10^23 Joules to change the atmosphere 1 degree C. The 10×10^23 Joules that went into the ocean from 1985 to 2005 would raise the air temp by 7.46 degrees C if that energy had gone into the atmosphere instead.
Some of my numbers are rough estimates. As far as explaining where I may have forgotten something, you are joking of course. Maybe I should just say, “The only time I was ever wrong was once when I thought I was wrong.” And I am joking.
But let me put it back on you. Where is there a discussion of how climate models explain how the massive amount of energy got into the oceans as shown in the NOAA chart here at:
https://www.realclimate.org/index.php/archives/2009/12/updates-to-model-data-comparisons/comment-page-9/#comment-152359 ????
David Harrington, do you have any comprehension of how involved an analysis you must perform on the satellite data to get a meaningful lower tropospheric temperature? So what is your basis for preferring these datasets–particularly given their shorter span?
Also, add GISTEMP and it’s trend–how divergent are the slopes of the 3 trends? What does that tell you?
On Harrington nr.38 and the in-line by Gavin… hmmm not worried about what the stats indicate… well eventually the sheep Dolly had to be put out of it’s misery too. Go http://discover.itsc.uah.edu/amsutemps/execute.csh?amsutemps , select near surface, ch04, redraw, tick the 1998, 2002, 2005, 2007, 2009 and 2010 boxes then see what Jan.2010 is looking like :P
Expect Dr.WATTS to studiously comment “As expected …”
What is the scientifically accepted reason for the lack of warming during the 50s and 60s?
“The magnitude of monthly temperature anomalies is typically 1.5 to 2 times greater than the magnitude of seasonal anomalies.”
I don’t understand this statement. The magnitudes of the seasonal anomalies are on the same order as the monthly anomalies; you average the monthlies to get the seasonal.
I’ll accept that the annual means are more noisy than the seasonal means, which are in turn more noisy than the monthly means. Is that what this sentence is trying to say?