A couple of months ago, we discussed a short paper by Matthews and Weaver on the ‘climate change commitment’ – how much change are we going to see purely because of previous emissions. In my write up, I contrasted the results in M&W (assuming zero CO2 emissions from now on) with a constant concentration scenario (roughly equivalent to an immediate cut of 70% in CO2 emissions), however, as a few people pointed out in the comments, this exclusive focus on CO2 is a little artificial.
I have elsewhere been a big advocate of paying attention to the multi-faceted nature of the anthropogenic emissions (including aerosols and radiatively and chemically active short-lived species), both because that gives a more useful assessment of what it is that we are doing that drives climate change, and also because it is vital information for judging the effectiveness of any proposed policy for a suite of public issues (climate, air pollution, public health etc.). Thus, I shouldn’t have neglected to include these other factors in discussions of the climate change commitment.
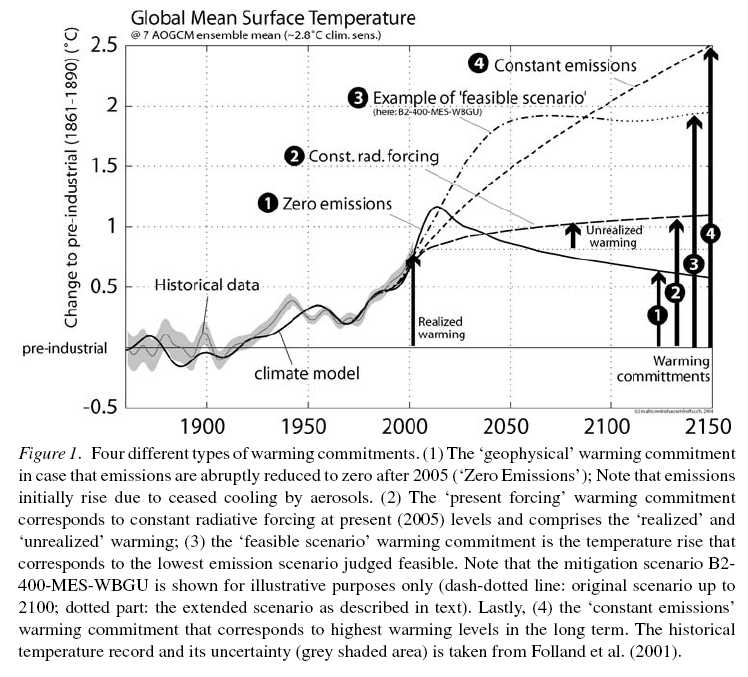
Luckily, some estimates do exist in the literature of what happens if we ceased all human emissions of climatically important factors. One such estimate is from Hare and Meinshausen (2006), whose results are illustrated here:
The curve (1) is the result for zero emissions of all of the anthropogenic inputs (in this case, CO2, CH4, N2O, CFCs, SO2, CO, VOCs and NOx). The conclusion is that, in the absence of any human emissions, the expectation would be for quite a sharp warming with elevated temperatures lasting almost until 2050. The reason is that the reflective aerosols (sulphates) decrease in abundance very quickly and so their cooling effect is removed faster than the warming impact of the well-mixed GHGs disappears.
This calculation is done with a somewhat simplified model, and so it might be a little different with a more state-of-the-art ESM (for instance, including more aerosol species like black carbon and a more complete interaction between the chemistry and aerosol species), but the basic result is likely to be robust.
Obviously, this is not a realistic scenario for anything that could really happen, but it does illustrate a couple of points that are relevant for policy. Firstly, the full emissions profile of any particular activity or sector needs to be considered – exclusively focusing on CO2 might give a misleading picture of the climate impact. Secondly, timescales are important. The shorter the time horizon, the larger the impact of short-lived species (aerosols, ozone, etc.). However, the short-lived species provide both warming and cooling effects and the balance between them will vary depending on the activity. Good initial targets for policy measures to reduce emissions might therefore be those where both the short and long-lived components increase warming.
… okay, m^2 = r^2 itself only means m = + or – r, so I didn’t completely solve that…
… But if m = -r, then m would be imaginary. So for real m, m = r.
…(that’s for real r, etc, of course)
Geoff,
I’m not sure what portion of my rather short, vague musing you are taking issue with. In describing a population inversion, I’m merely pointing out that when you take a theory developed to describe equilibrium systems and apply it to a system far from equilibrium (and therefore unstable or metastable), you get some odd results (like negative temperatures being higher than positive infinite temperatures). It’s not that you can’t gain some insight from thermo applied to such systems.
Nonequilibrium statistical mechanics remains one of the frontiers of physics–particularly the path through phase space a system far from equilibrium takes as it relaxes. LTE is one of the approaches for dealing with it. The atmosphere is in LTE because only a tiny minority of molecules will be excited by outgoing IR at any given time.
Bob (Sphaerica) (697), you raise valid and natural questions. My interest here is that global warming (and in my specific area of skepticism, not warming per se but its differential — commonly referred to as saturation and/or broadening) is strongly related to molecular level energy transfers in their most precise and exact (within the bounds of quantum mechanics) fashion. I find a ton of disagreement and some uncertainty on what is actually going on at the molecular level in things like energy transfer, temperature change and equilibrium, internal energy level modification, spontaneous radiation, etc. When someone tells me that if a mole (say) of gas is not in LTE and the its molecular energy doesn’t satisfy (completely) equipartition, that you not only can’t measure its temperature, it doesn’t even have a temperature, then something is amiss.
I tenaciously wish to resolve these questions though I can understand how it gets tiresome after a while here in RC. We’ve been done this debate before. I’m glad you at least find it interesting (amusing? ;-) ). BTW we’re dangerously close to resurrecting the old chestnut about a single molecule having temperature; you’ll probably find that a hoot (though I try to keep that buried for about a year at a time!)
As I’ve said (as did Ray, almost) LTE is a convenient construct that allows one to plow ahead with an analysis that is clearly “close enough” even though not perfect. As you imply, technically and theoretically there is no volume of gas beyond a single molecule (2 or 3 by chance at the outside) that is in perfect thermal equilibrium. That comes straight out of the M-B distribution of molecular kinetic energies. And none that satisfies 100.000% equipartition. This from Boltzmann equation. But this has not stopped tremendously accurate analyses. We can even take the temperature! Hell, I did just this morning off my deck!
Ray
I’ll try and say the same things in a slightly different way.
Yes
No! negative temperatures are a perfectly respectable phenomonon in equilbrium thermodynamics.
But the converse is false, or highly misleading. Metastable does not imply far from equilibrium; at least not unless you wait for a time so long that it has no effect on the system under discussion which has had plenty of time to reach internal equilibrium (maximum entropy).
No ; this is not odd. It is a consequence of Kelvin’s choice of the temperature scale which itself was caused by lack of knowledge in the 19th century. Many books use beta = 1/T which as I mentioned last time is a good measure of coldness. This time lets try -beta =-1/T as a measure of hotness.
Benefits.
1. Gone: that inaccessible T=0. That has got thrown off to infinity which is a better representation of something inaccessible.
2.Gone: that topological monstrosity at T= 0 previously the bogus boundary between positive and negative temperatures.
3. -beta=0 now appears to be accessible , at least mathematically. At first this looks bad, because it implies you can reach infinite Kelvin temperature. But thats just what we want! Infinite Kelvin temperatures are accessible if the energy levels have a maximum. So this is a benefit.
4. The discontinuity between positive and negative temperatures at T =0 has now been replaced by smooth behaviour at -beta =0.
5. There is no odd haviour.
“T=-50K is hotter than T= +30K”
that looks odd. But it now reads
” -beta = 1/50 is hotter than -beta=-1/30″
“T= -70K is hotter than T=-100K”
odd? but it also reads
-beta=1/70 is hotter than -beta = 1/100
and just to make sure
“T=70K is hotter than T=40K”
Becomes
-beta =-1/70 is hotter than -beta=-1/40
Odd behaviour fixed i.e.
as -beta increases so does the hotness
Energy travels from a hot body to a less hot one one still valid.
Irrelevant.
Correction to my last post:
Please replace the second line in
“T= -70K is hotter than T=-100K”
odd? but it also reads
with the word
becomes
“that you not only can’t measure its temperature, it doesn’t even have a temperature, then something is amiss.”
For some purposes a temperature could be assigned, based on the temperature that the parcel of material would have if adiabatically allowed to achieve LTE.
Rod B. says, “When someone tells me that if a mole (say) of gas is not in LTE and the its molecular energy doesn’t satisfy (completely) equipartition, that you not only can’t measure its temperature, it doesn’t even have a temperature, then something is amiss.”
Rod, what is amiss is your understanding that models are always approximate. Their purpose is to yield understanding, not “answers”. The value of the understanding will diminish as the model veers away from the reality, but it need not necessarily go to zero.
Thermodynamics is really the study of systems at or very near equilibrium. As such, classical stat mech deals with similar systems. When you seek to extend the applicability of thermo/stat mech, it’s natural to start with a system at equilibrium and push it slightly away. Then you see what you can still use from the classical theory and what you have to modify and how. LTE is just such an extension. This model is more than adequate to tell us how the energy flows.
705 (Rod B),
Actually, I was saying the opposite, that for all intents and purposes, in the real world, every discrete chunk of atmosphere is effectively in LTE at all times. The time it takes to “equalize” under the relatively small scale (in relation to the shear number of molecules involved) but constant bombardment of IR makes the need to use a concept like LTE immaterial. I’m not sure why things are so hung up on that.
I think you’re overreacting. First, for all intents and purposes, in science, if you can’t measure something (i.e. it’s imperceptible) then it effectively isn’t there (a la Schrodinger’s cat). This is the point I believe he was making (was it CFU?).
And temperature is a concept, not an actual thing. Temperature in a gas is measure of the kinetic energy of the molecules, which, assuming equipartition of energy, is a proxy for the total energy of the system. Temperature in a solid is a measure of the vibrational energy of the molecules, which, again, assuming equipartition of energy (with fewer degrees of freedom) is a proxy for the total energy of the system.
So temperature is nothing but a convenient and easy way of measuring the energy of a batch of molecules. When you can’t measure it, it’s not a meaningful concept.
But in everything we’re discussing, you can measure temperature, because equipartition of energy for all intents and purposes re-balances instantaneously in the situations we’re describing.
What’s the temperature of a bullet travelling at mach?
706 & 707 Geoff said about -beta .
Interesting post. I need to think about your post more but I’m not convinced that
-beta=0 isn’t still a pretty special place to be. How much energy is required to heat a gram of H2O from -beta=-10^(-google) to -beta = +10(-google) ?
#712 John Pearson.
You are right, except that your question refers to a property of the energy level spectrum rather than to the scale of temperature which should be universal and independent of it.
-beta =0 is a very hot place. If, as in water, there is no finite upper limit to the energy spectrum it will also be inaccessible i.e. it will require an infinite energy to reach. Since I introduced inaccessibility as a criticism of T=0K, I should have mentioned that.
But the best way to think about the -beta scale is to consider a mixture of weakly interacting systems with positive and negative T (or beta). You will then be forced to have a common scale for all of them and -beta will be the sensible choice for avoidance of anomalies.
Bob (Sphaerica), Ray Ladbury, I think we are still getting wrapped around the esoteric philosophical axle. Ray, I think I agree with your #709 with one diversion and while it implies a rebuttal, I can’t see how. Of course models are an approximation. Taken to the extreme everything is an approximation. You say models provide “understanding”, not “answers.” What does this mean? Is the actual final output of GCMs after entering all of the inputs a simple printout that says “something very bad might happen sometime”? That would certainly be understanding. Or does it provide answers with numbers and dates and stuff? And why wouldn’t that also be understanding?
This is all very simple. It was asserted that a system not in thermal equilibrium (local if you like), including equipartition, does not have temperature and/or one at least can not measure it. I say that is wrong. One side is simply incorrect and it doesn’t have to morph into a silly dog chasing tail discussion like the old GW-GDP-negative correlation morass.
In one part I’m guilty of what I accuse you folks of, being too esoteric. The “no LTE beyond 2-3 molecules” is physically correct but of no worth. If you have a mole of a gas, while molecules have a wide range of velocity and maybe mass and only a few would be in strict LTE, those molecules follow the M-B distribution and that mole is in LTE at a precise temperature almost by definition. So that was not helpful and I withdraw it.
If you can’t measure something then it effectively isn’t there, says Bob. Might be true though effectively is the operative word. In many cases stuff can exist even though you can’t measure it — esoteric quantum cats aside. None-the-less I most certainly and quite accurately can measure the temperature of a mole of gas that is most probably not in thermal equilibrium. Equipartition of energy DOES NOT re-balance instantaneously. Most gases at atmospheric temperatures are predominately out of equipartition.
“And temperature is a concept, not an actual thing.” ??? What does that mean? Where does velocity, acceleration, radiation, etc. fall in that division? But you are 100% correct that “Temperature in a gas is measure of the kinetic energy of the molecules.” If you add average to that you have the definition of temperature of a gas. And assuming equipartition of energy, temperature (or kinetic energy) is a proxy for the total energy of the system. At the same time however the average translation kinetic energy and so the temperature will be what it is, without change, with or without equipartition.
My head is starting to hurt! ;-)
Re my 700
https://www.realclimate.org/index.php/archives/2010/06/climate-change-commitment-ii/comment-page-14/#comment-178289
So the temperature cycle amplitude, for a given flux cycle amplitude at z=0, is smaller for larger m (for same k), larger C*ω, larger z, but it is larger for larger k at (if I did the derivatives correctly) z > 1/m, and smaller for larger k at z < 1/m. (Somewhat analogous to the change in a weighting function as optical thickness per unit distance is changed). This makes sense – greater thermal conductivity increases the temperature cycling deep within a thermal mass but decreases it at the exterior where the cycling is forced, by increasing the 'access' to the heat capacity deeper inside.
———-
PS Re quasi-equilibrium of semiconductors:
Following the physics of photovoltaic energy conversion, it occurs to me that a semiconductor absorbing nearly monochromatic radiation with photon energy not too much larger than the band gap could cool the semiconductor (absorption produces charge carriers that are relatively cold within each band, crystal lattice loses heat to the charge carriers, recombination emits photons with more energy, but over a larger range of wavelengths (lower brightness temperature than the input radiation) – it would be a heat pump. I wonder if that would be practical?
Patrick at end of #715
If you really believe in your invention, then I suggest you start with an analysis of a complete heat pump with source and sink and repeat it for your semiconductor version. Please look out for sign errors.
Now I must apologise but I won’t have more time to spend on this (off-topic) question, but since this is your invention perhaps you could complete or correct the following:
1. Put the semi-conductor in contact with a heat bath.
2. The temperatures of s.c. and heat bath equalise. There is just one temperature for heat bath, phonons, electrons and holes.
3. Plot the number of electrons and holes as a function of this temperature.
4. Take a few more electrons and excite them into the conduction band.
5. Now you could have done this by raising the common temperature of sc and heat bath. The results can be predicted from step 3.
6. But you are on an economy drive and claim to be able to get the same population increase with rather less energy, by using photons instead of phonons.
7. Which is warmer now the heat bath or the sc? Preferably do the calculation for your own sake.
If the moderator puts a stop to this discussion , you could try a more relevant forum.
690: Completely Fed Up said, qutoing someone:
“there is absolutely no place where collisions are required to derive ideal gas law”
and then
“Go on, derive those laws without them.”
Collisions with what? To derive the ideal gas law you need only consider particle-wall collisions but not particle-particle collisions. The standard derivation from statistical mechanics is to write down the hamiltonian for a bunch of identical noninteracting particles: H = m/2 sum_i v_i^2 and use that to evaluate the partition function and from there to the equation of state. I believe that if you confine an ideal gas between two walls at z=0 and z=L (and infinite in the x and y directions) with T(0)=T1 and T(L)=T2 that you will not see it approach a linear temperature gradient. Precisely what happens will depend on what you assume for the distributions that a particle obeys after colliding with the wall. If you make what I think is the most natural assumption, that after collision with the wall at T1 the particle velocity is drawn from a Boltzmann distribution with temperature T1 and similarly for the other wall you will always have two populations of particles. If you give the particles a finite size hard core repulsion they will no longer obey the idea gas law. I guess you could do a numerical experiment in which you start with zero particles and begin adding finite size particles. You should see the behavior transition from this weird very non-equilibirum state in which the particles are all in one of these two distributions to a non-equilibrium state that obeys the heat equation once the density is large enough that particle-particle collisions are about as common as particle-wall collisions.
The simple kinetic theory arguments that lead to heat transfer in an ideal gas are based on the mean free path which will be infinite for a gas that is truly ideal.
Re 716 – actually I half expected someone might tell me that it’s been known awhile and has a name like the ‘[scientist’s name here] effect’, but yes it was OT (but at least it’s not the same old OT), although it did follow from discussing LTE … so I’ll just ‘Google it’ or something.
But just for the record here:
5. Now you could have done this by raising the common temperature of sc and heat bath. The results can be predicted from step 3.
6. But you are on an economy drive and claim to be able to get the same population increase with rather less energy, by using photons instead of phonons.
Actually the key thing is that I don’t claim to expect the same change – I expect a different change. The absorbed photons (with high brightness temperature for their frequencies) would increase the populations of exited charge carriers, but if the incident photons are concentrated into a range of energies that are all only a little more than the band gap energy (relative to the temperature of the semiconductor crystal lattice) then the resulting excited charge carriers could be more concentrated towards the band edges than in a Fermi-Dirac distribution for the temperature of the semiconductor; they will tend to spread away from the band edges by aquiring energy from the lattice (a process that is considerably more rapid than recombination, at least if the band gap is big enough). In steady state, the same number of photons are emitted as are absorbed (in an ideal case – no other avenues for recombination are used) but the emitted photons have more energy on average – but also carry more entropy because they are spread out more over the spectrum (they have lower brightness temperatures then the absorbed photons).
http://en.wikipedia.org/wiki/Quasi_Fermi_level
I won’t say anything more about it here, I promise.
Re: #719 Patrick
It all depends on the calculations. According to Gunnar Moller * , the electron phonon relaxation time may turn out to be greater than the recombination time. This is because of the selection rules. Also the band gaps would provide a practical limit.
——–
* Cavendish Lab.
Re 720 – okay, thanks.
“The simple kinetic theory arguments that lead to heat transfer in an ideal gas are based on the mean free path which will be infinite for a gas that is truly ideal.”
Simple kinetic theory postulates that there is a finite MFP and short enough that there are many collisions, so your assertion there is false.
Collisions with what?”
With other molecules that constitute the gas under consideration.
“To derive the ideal gas law you need only consider particle-wall collisions but not particle-particle collisions.”
No, because you then need inelastic collisions with the container wall. This is not then a simple theory.
“The standard derivation from statistical mechanics is to write down the hamiltonian for a bunch of identical noninteracting particles: H = m/2 sum_i v_i^2 and use that to evaluate the partition function and from there to the equation of state.”
See what I mean? And isn’t this pre-supposing a statistical spread of energies? This is rather a post-hoc justification of the theory of thermodynamics. “We have a spread of energies among the particles and this causes a spread of energies among the particles”.
“If you make what I think is the most natural assumption, that after collision with the wall at T1 the particle velocity is drawn from a Boltzmann distribution with temperature T1”
See what I mean? You’re assuming a Boltzmann distribution after collision with the stationary wall. Are you surprised at getting a Boltzmann distribution of the gas from that? I’m not.
But in any case, you need to prove why that assumption exists. WHY are the molecules leaving one bouncing wall given a Boltzmann distribution? You fail to show therefore you have given no proof.
CFU, John is correct. Even if you do not assume a Boltzmann distribution, the gas will move toward said distribution as it interacts with the walls. This is precisely how one derives the blackbody distribution–although there the distribution is BE. Photons are noninteracting, but are assumed to either reflect from or be absorbed and re-emitted by the walls.
[Response: This discussion is extremely tedious. No more please. – gavin]
The equation of state for a hard sphere gas is:
P = nRT/(V-n v)
where V is the volume of the container and v is the excluded volume for a mol of the spheres. It is not ideal.
717 I totally agree with John and last Ray’s post. Van der Waals corrective terms are due to long range interaction potential (a/V^2) and finite volume (V-b) of molecules. This means that ideal law is valid only in the limit of zero range potential and zero volume molecule, in which case the scattering cross section is… zero. Collisions are useful indeed to insure the energy transfer between various degrees of freedom. They help establishing the local thermal equilibrium, but they’re by no ways a necessary ingredient of the ideal law- actually they cause departure from the ideal law. There is a confusion here between the establishment of thermodynamical equilibrium, which can occur with any system (and is helped by collisions) and ideal law , which describes a gas of non interacting particles.
“WHY are the molecules leaving one bouncing wall given a Boltzmann distribution? You fail to show therefore you have given no proof.”
Because of microreversibility; If the wall have a non-zero temperature, the molecules of the wall are themselves vibrating, and collisions with moving molecules will transfer energy in such a way that their distribution moves towards maximum entropy (H-theorem). Collisions between gas particles themselves are not required per se to establish equilibrium, any process insuring a transfer of energy can do it.
And to answer an old question of CFU : not only I’ve got my first degree in physics a long time ago, but I’m actually teaching it now – and even higher. [edit]
[edit – the one-a-day rule does not trump the basic rules on comment etiquette. Please calm down, or we’ll move to the ‘none-a-day’ rule]
Correction: earlier I breezed through the concept of an emission weighting function and the distribution of absorption for radiation in the opposite direction. One can construct an emission weighting function for the flux per unit area, but the equivalence between emission weighting function and absorption is only strictly true for radiant intensity for one direction (emission toward and absorption from that direction), along with the other qualifications (a particular frequency, polarization if that matters, location of course, and with conditions held constant over the travel time of photons (easily approximated as true for photons in the Earth’s atmosphere), and with LTE, … and setting aside (so far as I know) any doppler shifting during scattering, or Raman or Compton scattering and maybe some other things (stimulated emission?)). For the two distributions to be idential for opposing fluxes per unit area, the intensity must be isotropic within each hemisphere of directions – though the two distributions can/may be similar even with some anisotropy; they can/may be similarly compressed or expanded by changes in optical properties.