One might assume that people would be happy that the latest version of the Hadley Centre and CRU combined temperature index is now being updated on a monthly basis. The improvements over the previous version in terms of coverage and error estimates is substantial. One might think that these advances – albeit incremental – would at least get mentioned in a story that used the new data set. Of course, one would not be taking into account the monumental capacity for some journalists and the outlets they work for to make up stories whenever it suits them. But all of the kerfuffle over the Mail story and the endless discussions over short and long term temperature trends hides what people are actually arguing about – what is likely to happen in the future, rather than what has happened in the past.
The fundamental point I will try and make here is that, given a noisy temperature record, many different statements can be true at the same time, but very few of them are informative about future trends. Thus vehemence of arguments about the past trends is in large part an unacknowledged proxy argument about the future.
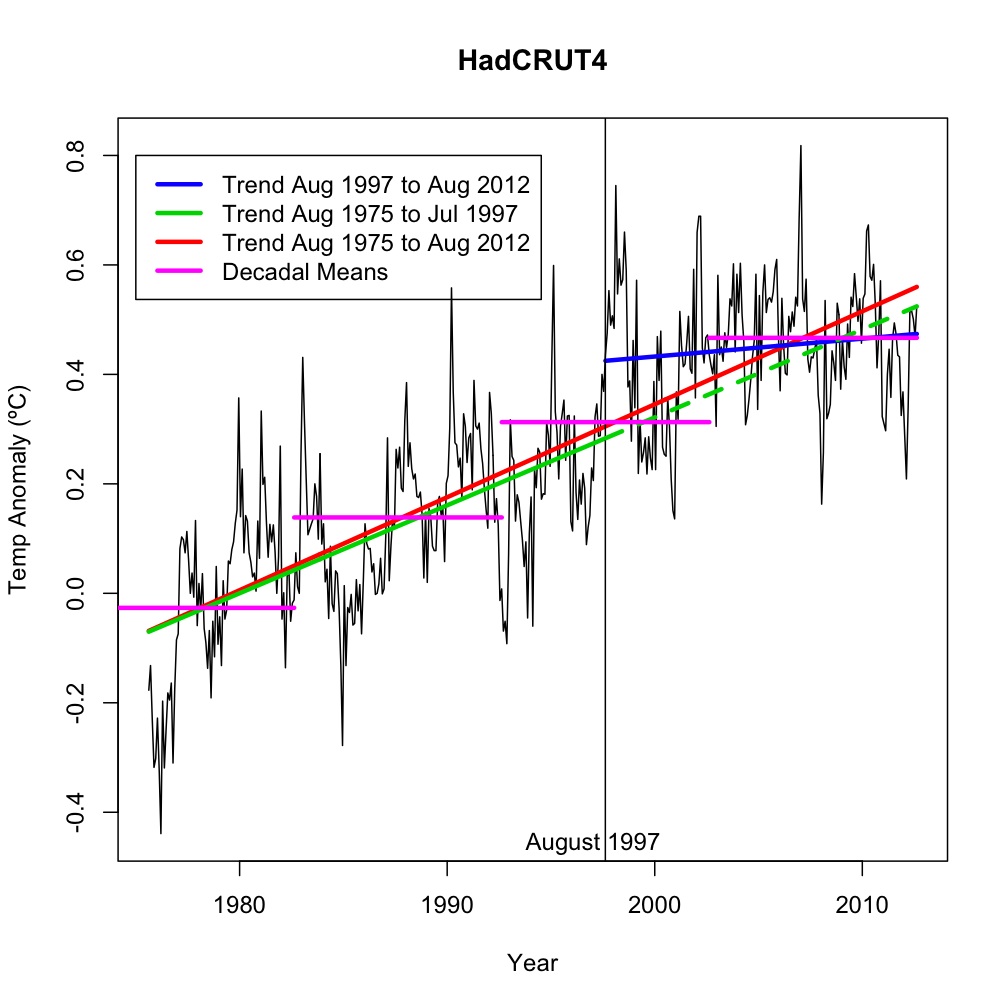
So here are a few things that are all equally true, conveniently plotted for your amusement:
- The linear trend in HadCRUT4 from August 1997 to August 2012 (181 months) is 0.03ºC/decade (blue) (In GISTEMP it is 0.08ºC/decade, not shown).
- The trend from August 1975 to July 1997 is 0.16ºC/dec (green), and the trend to August 2012 is 0.17ºC/dec (red).
- The ten years to August 2012 were warmer than the previous 10 years by 0.15ºC, which were warmer than the 10 years before that by 0.17ºC, which were warmer than the 10 years before that by 0.17ºC, and which were warmer than the 10 years before that by 0.17ºC (purple).
- The continuation of the linear trend from August 1975 to July 1997 (green dashed), would have predicted a temperature anomaly in August 2012 of 0.524ºC. The actual temperature anomaly in August 2012 was 0.525ºC.
The first point might suggest to someone that the tendency of planet to warm as a function of increases in greenhouse gases has been interrupted. The second point might suggest that warming since 1997 has actually accelerated, the third point suggests that trends are quite stable, and the last point is actually quite astonishing, though fortuitous. Since all of these things (and many others) are equally true (in that their derivation from the underlying dataset is simply a mechanical application of standard routines), it is clear that our expectation for the future shouldn’t be simply based on an extrapolation of any one or two of them – the situation is too complex for that.
There are two main responses to complexity in science. One is to give up studying that subject and retreat to simpler systems that are more tractable (the ‘imagine a spherical cow’ approach), and the second is to try and peel away the layers of complexity slowly to see if, nonetheless, robust conclusions can be drawn. Both techniques have their advantages, and often it is the synthesis of the two approaches that in the end provides the most enlightenment. For some topics, the two paths have not yet met in the middle (neuroscience for instance), while for others they almost have (molecular spectrometry). The climate system as a whole is one of those topics where complexity is intrinsic, and while the behaviour of simpler systems or subsystems is fascinating, one can’t avoid looking directly at the emergent properties of the whole system – of which the actual temperature changes from month to month are but one.
We have found some ways to peel back the curtain though. For instance, we know that the shifts in equatorial conditions associated with El Niño/Southern Oscillation (ENSO) in the Pacific have a large impact on year-to-year temperature anomalies. So do volcanoes. Accounting for these factors can remove some of the year-to-year noise and make it easier to see the underlying trends. This is what Foster and Rahmstorf (2011) did, and the result shows that the underlying trends (once the effects of ENSO are subtracted) are remarkably constant:

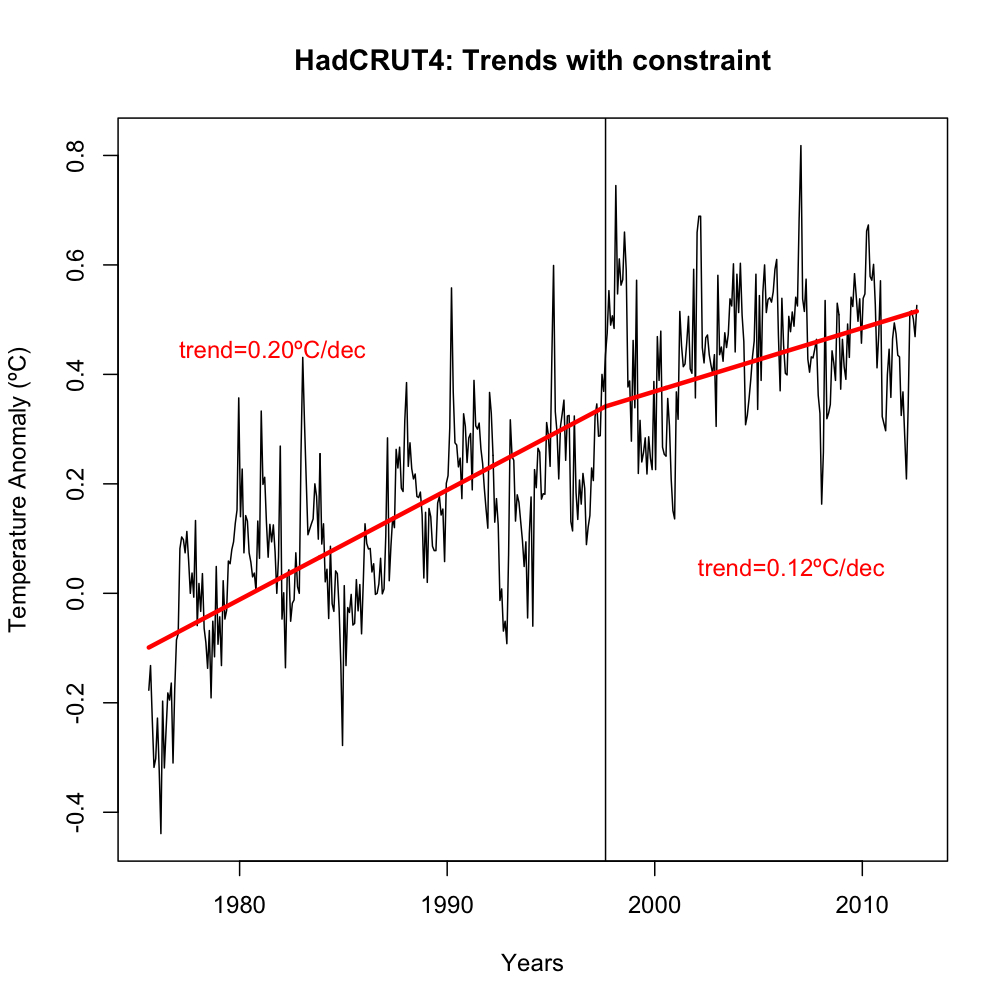
Another way one might deal with the seemingly contradictory tangle of linear trends is to impose a constraint that any linear fits must be piecewise continuous i.e. every trend segment has to start from the end of the last trend segment. Many of you will have seen the SkepticalScience ‘Down the up escalator’ figure (a version of which featured in the PBS documentary last month) – which indicates that in a noisy series you can almost always find a series of negative trends regardless of the long term rise in temperatures. You will have noted that the negative trends always start at a warmer point than where the previous trend ended. This is designed to make the warming periods disappear (and sometimes this is done quite consciously in some ‘skeptic’ analyses). The model they are actually imposing is a linear trend, followed by an instantaneous jump and then another linear trend – a model rather lacking in physical basis!
However, if one imposes the piecewise continuous constraint, there are no hidden either warming or cooling jumps, and it is often a reasonable way to characterise the temperature evolution. If you looked for a single breakpoint in the whole timeseries i.e. places where the piecewise linear trend actually improves the fit the most, you would pick Apr 1910, or Feb 1976. There are no reasons either statistically or physically to think that the climate system response to greenhouse gases actually changed in August 1997. But despite the fact that August 1997 was shamelessly cherry-picked by David Rose because it gives the lowest warming trend to the present of any point before 2000, we can still see what would happen if we imposed the constraint that any fit needs to be continuous:
A different view, no?
But let’s go back to the fundamental issue – what do all these statistical measures suggest for future trends?
If we assume for a moment that the ENSO variability and volcanoes are independent of any change in greenhouse gases or solar variability (reasonable for volcanoes, debatable for ENSO), then the work by Foster and Rahmstorf, or Thompson et al (2009) to remove those signals will reveal the underlying trends that will be easier to attribute to the forcings. This is not to say that ENSO is the only diagnostic of internal variability that is important, but it is the dominant factor in the global mean unforced interannual variability. Given as well that we don’t have skillful predictions of ENSO years in advance, future trends are best thought of as being composed of an underlying trend driven by external drivers, with a wide range of ENSO (and other internal modes) imposed on top.
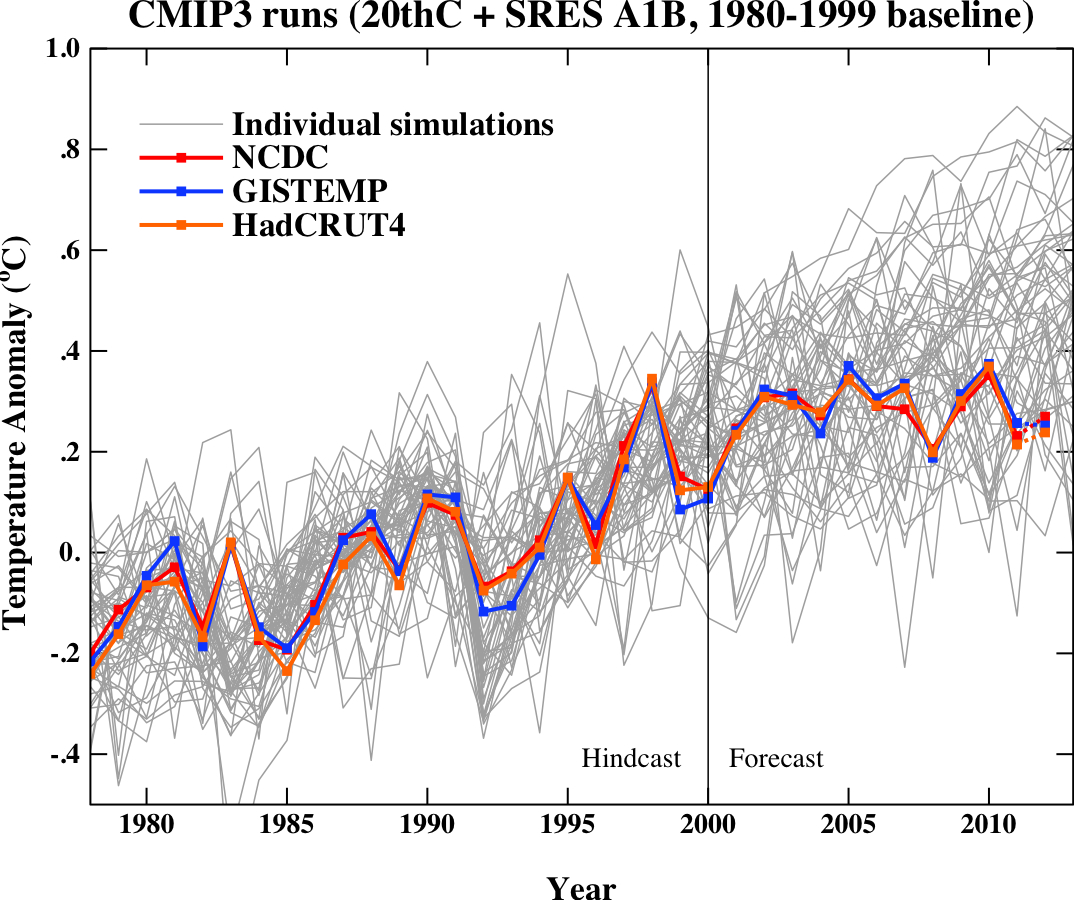
We can derive the underlying trend related to external forcings from the GCMs – for each model, the underlying trend can be derived from the ensemble mean (averaging over the different phases of ENSO in each simulation), and looking at the spread in the ensemble mean trend across models gives information about the uncertainties in the model response (the ‘structural’ uncertainty) and also about the forcing uncertainty – since models will (in practice) have slightly different realisations of the (uncertain) net forcing (principally related to aerosols). Importantly, the ensemble mean trend is often closely related to the long term trend in any one specific realisation, while the short term trends in single realisations are not.
In any specific model, the range of short term trends in the ensemble is quite closely related to their simulation of ENSO-like behaviour. I say “ENSO-like”, rather than “ENSO” since the mechanisms resolved in the models vary widely in their realism. Consequently, some models have tropical Pacific variability that is smaller than observed, while for some it is larger than observed (this is mostly a function of the ocean model resolution and climatological depth of the equatorial thermocline – but a full description is beyond the scope of a blog post). Additionally, the spectra of ENSO-like behaviour can be quite different across models, or even for century scale periods in the same simulation (see this presentation on the GFDL model by Andrew Wittenberg for examples). Thus it is an open question whether the CMIP3 or CMIP5 models completely span the range of potential ENSO behaviour in the future – and that is assuming that there is no impact of climate change on the ENSO statistics. Though if there is an effect in the real world, the century-scale variance seen in the GFDL model for instance, would mean that it will take a long time to reliably detect in the observations.
We saw above that the ENSO-corrected underlying trends are very consistent with the models’ underlying trends and we can also see that the actual temperatures are still within the model envelope (2012 data included to date). This is not a very strong statement though, and more work could perhaps be done to construct a better forecast using the underlying trends in the models and statistical models for the ENSO and internal variability components inferred from observations, rather than purely from model realisations. It is also worth pointing out that the CMIP5 estimates of ENSO variance might be significantly improved over what was seen in CMIP3.
So, to conclude, if you think that future ‘global warming’ is tied to the underlying long term trend in surface temperatures, there is no evidence from HadCRUT4 to warrant changing expectations (and no physical reasons to either). However, if you think that the best estimate of the future comes from extrapolating the minimum trend that you can find over short time periods in single estimates of surface temperatures, then you are probably going to be wrong.
References
- G. Foster, and S. Rahmstorf, "Global temperature evolution 1979–2010", Environmental Research Letters, vol. 6, pp. 044022, 2011. http://dx.doi.org/10.1088/1748-9326/6/4/044022
- D.W.J. Thompson, J.M. Wallace, P.D. Jones, and J.J. Kennedy, "Identifying Signatures of Natural Climate Variability in Time Series of Global-Mean Surface Temperature: Methodology and Insights", Journal of Climate, vol. 22, pp. 6120-6141, 2009. http://dx.doi.org/10.1175/2009JCLI3089.1
I like the piecewise linear with constraint graph. I suspect that if you move the breakpoint about you will find that the 1997.7 date is a pretty good choice to maximise the difference between the two trends.
Given that the long term trend increases if we include the post-1997 data, what we are actually seeing is a bump around 1998. In my HadCRUT4 analysis post I attempted to analyse the effect of coverage bias by latitude band using a couple of methods.
The most notable result is that the poor Arctic and Antarctic coverage both contribute to a peak in warm bias around 1998, declining to a cool bias today. It’s not up to peer review standards and it would be interesting for someone who knows more about reanalysis to have a look at it from that perspective, but the results are at least suggestive.
One interesting question is how this squares with Foster and Rahmstorf. They get a linear result without correcting for coverage bias. If I’m right about the coverage bias, then they must be mopping up the coverage bias in the other three terms.
Good stuff as usual. If you just look at your first graph, the decadal means look pretty convincing to me on their own.Just by eye, they seem to fit the Aug 1975-Aug 2012 line pretty well.
As usual, a very nice presentation of the issue.
One minor request, could you attach a number to each of the figures for ease of reference for the posters here?
On larger question–aren’t all attempts to predict the future based merely on lines on graphs from the past what is called ‘curve fitting’–generally not considered a very reliable method?
Shouldn’t the emphasis always be on the underlying physics and dynamics that might explain both historical trends and possible future developments?
[Response:Extrapolation into the future, based on past trends, is in fact highly reliable if you have strong reason to believe that the underlying physical drivers of the system under study are not going to change. With climate change of course, we have no such confidence, because of the enormous and rapid increase in GHGs, whose physical basis as a radiative forcing agent is well understand, and quantified. Thus the importance of GCMs, which incorporate this understanding, and also attempt to integrate it with other possible forcings as well as shorter term variations.–Jim]
Thanks again for a clear and compelling piece.
Very useful! A slight typo, 1st para below the 1st graph: “…in that there derivation…”
[Response:Fixed. Thanks – gavin]
Response to Willi @ 3: “[A]ren’t all attempts to predict the future based merely on lines on graphs from the past what is called ‘curve fitting’…?” No. The emphasis is on the underlying physics and dynamics that explain both historical trends and possible future developments. Get yourself a copy of “Challenges of climate modeling” by Inez Fung in the Journal of theAmericanInstitute of Mathematical Sciences. It’s a good concise description of climate modeling.
Thanks for pointing out the fact that different statements about the same data can be true at the same time, and that there is a disconnect between a graph and reality when that graph shows a discontinuity in energy state. Apart from microscopic quantum effects, it simply isn’t physically possible for the earth to transition between two disparate energy states with no states in between. That puts such graphs firmly in the realm of mathturbation.
I’m not sure how you imposed the connected constraint. I assume that the line segments must be calculated using time periods that overlap the preceding one by half the length of one being created. That would be not that different from a running average. Illustration:
http://www.woodfortrees.org/plot/hadcrut4gl/mean:12/plot/hadcrut4gl/mean:180/plot/hadcrut4gl/from:1997.75/trend/plot/esrl-co2/mean:12/normalise
I assert that recently, more of the heat in the atmosphere has gone into warming the oceans and warming/melting ice. Thus, today, we have warmer ice, warmer oceans, and relatively cooler air. Further, air temperatures do not capture the latent heat in the atmosphere, and the latent heat in the atmosphere has increased.
My point is that for periods as short as a decade, air temperatures are not a precise measure of the heat in the climate system. And, it is the total heat in the system that drives weather.
The curves above are for educational purposes only and should not be used for engineering or policy making. If the above are the best data available (and they may be), then safety factors should be applied. The above are not a basis for engineering design.
Thank you. Calm and clear. And simple enough even for me.
(The solid green line seems to stick out well past July 1997 before it turns into a dotted line? Is it plotted correctly?)
These kinds of issues are routinely faced by many other disciplines, which climate scientists should draw upon – economics, demographics, sociology, etc. Whenever you get a time series, especially one that involves human action, there are a wide range of complex statistical issues and complex attempts to address them. These have been explored in millions of studies. With a few exceptions, climate scientists ignore this expertise and analyze trends in a simplistic manner.
[Response:There is no basis for this last statement. In general, physics (upon which climate science is very largely based) has done as good, or better, of a job at tying underlying physical drivers to observed phenomena, as has any other branch of science, right up there with chemists and molecular biologists. And there are good reasons for why this is so.–Jim]
Roddy at 8…Looks to me like the dotted line begins at the solid black vertical line denoting August ’97, creating the illusion that it’s a continuation of the solid line from the prior period.
[Response: yes. – gavin]
Walter at 10 (and Gavin’s confirmation) – I thought of that and zoomed in on that section of the graph – the gaps between the dotted sections are quite big, too big to get lost in that particular junction I think?
Using HadCRUT4 and a nice set of cherry picked years in combination with the logic of Rose et al, you could proof with trends that the world hasn’t warmed at all since 1957. Trends correctly rounded down in °C/decade:
1957 – 1986 : 0.02
1987 – 1996 : 0.02
1997 – now : 0.04
According to Rose global warming has stopped in this last period of 16 years and the two preceding periods have trends that are almost close to zero. So three periods of no global warming since 1957 and the overall conclusion, using the correct skeptic logic + statistics, is that the world of 2012 is as warm is the world in the 1950’s.
Using the catchphrase of the great philosopher Obelix: “These skeptics are crazy!”.
http://www.woodfortrees.org/plot/hadcrut4gl/from:1957/to:1987/plot/hadcrut4gl/from:1957/to:1987/trend
http://www.woodfortrees.org/plot/hadcrut4gl/from:1987/to:1997/plot/hadcrut4gl/from:1987/to:1997/trend
http://www.woodfortrees.org/plot/hadcrut4gl/from:1997/to:2012.6/plot/hadcrut4gl/from:1997/to:2012.6/trend
http://en.wikipedia.org/wiki/Obelix
Response:Extrapolation into the future, based on past trends, is in fact highly reliable if you have strong reason to believe that the underlying physical drivers of the system under study are not going to change (Jim)
Here is an extrapolation into the future based on the 3 CET constituent harmonic components + the existing linear trend:
http://www.vukcevic.talktalk.net/CET-NV.htm
As it happens the multi-decadal trends closely follow the geological non-climatic based records (North Atlantic Precursor) confirming the primacy of the natural variability.
Good article overall. A couple comments.
1. Picking a starting point in the graphs at 1980 is just asking for a beating from skeptics for obvious reasons. I will refrain here as we have all been down this well worn path.
2. “we can also see that the actual temperatures are still within the model envelope (2012 data included to date)”. Although you qualify this in the next sentence, this is indeed misleading IMO. When a very large percentage of the simulations are over estimating temperature versus observations, this should require one to question the validity of these simulations *** out loud ***.
3. And the big picture. The simulations leading to possible dangerous climate change are contingent upon an accelerating temperature profile in response to BAU carbon output. When the temperature profile is decelerating, this warrants real discussion on the bigger picture, particularly whether climate sensitivities are too high in the models. This seems to be the “theory that shall not be named”. One has to consider the opposite condition, if all the simulations were under-estimating temperatures, would there not be rampant speculation that climate sensitivities were too low?
[Response: Probably, but that would not be justified either. There is no question that the current situation is the lower part of the model distribution in temperature, but it is not yet inconsistent, and given that the ENSO corrected trends are still very much within the fold, my forecast is that it won’t prove to be. Remember that sensitivity is not defined from the models, but from the paleo-climate observations, and so you would need some radical departure from expected behaviour to challenge that. We are nowhere close. – gavin]
Apparently, in the last decade or so, surface and lower troposphere temperature has risen more slowly than the long term trend, but ocean heat content to 2km has risen faster than the previous two decades. What could the physical reason be for that?
[Response: A decadal variation in the rate of deep ocean heat uptake. This uptake is related to advective effects in the North Atlantic and Southern oceans, as well as through diffusion, and we know that the circulations have decadal and multi-decadal variability, thus one can imagine a situation where the advection to depth increases for a short time (due to internal variability, or driven by surface wind anomalies), which would take heat to depth, create a negative SST anomaly (relative to what would have been expected), drawing more heat into the ocean, and slightly cooling the atmosphere (again relatively speaking). If this was true, one would expect the anomalous OHT to have increased faster in downwelling regions. I haven’t checked though. – gavin]
Thought provoking..
Why not take some data that is one thousand years old and perform a similar analysis with regards to the escalator trends….
And if you don’t have good enough resolution, simply add enso-like variability to the underlying trend of the proxy data.
I’m sure you could work backwards from a detailed core from the indo pacific, compare it to data from the same area and the global as a whole today, and deduced a very crude global mean temperature estimate from one thousands years ago.
It doesn’t have to be accurate. Or use some hockey stick data, whatever.
My guess is that (shock horror) you will find a “trend”. Hey, you never know, if you look hard enough you might end up going up the down escalator.
Jos Hagelaars (#12),
Put another way, I prefer to ask, “Using the same logic and math that you are using now, you would have been 0 for N in the historical record; what makes you think you are right this time?”
” One has to consider the opposite condition, if all the simulations were under-estimating temperatures, would there not be rampant speculation that climate sensitivities were too low?”
It would depend on what ENSO and the sun and volcanoes were doing. If ENSO trends were driving faster warmth, the sun was hot, and volcanoes dormant, then it would not be appropriate to think that simulations running cold was indicative of a high sensitivity. If ENSO, solar, and volcanic activity were as observed currently, and simulations were running cold, I think that high sensitivity would definitely be a useful speculation. (oceanic temperature trends would be an important partner to surface air temperature trends, too)
Few nitpicks:
– improvements are*
– The magenta decadal trends drawn should date back to ’62 as you include five in the description, yet only four on the graph
[Response: No. The graph starts in 1975, so only four decades are included. – gavin]
– tendency of the* planet to warm
– The UAH data is v5.4, v5.5 limits the recent deviance
– “no hidden either warming or cooling jumps” reads awkwardly
– “But despite the fact that August 1997 was shamelessly cherry-picked by David Rose because it gives the lowest warming trend to the present of any point before 2000” – It was picked to show 15 years, not the lowest trend. If he were to have desired the lowest trend (or better yet a negative one) he could have done so beginning with other dates prior to 2000.
[Response: Actually no. Aug 1997 gives the lowest trend of any point prior to 2000. – gavin]
Also, why is trending from August of 1975 itself not considered an arbitrary beginning point?
[Response: You can show that there is significant break in the trend around 1975, but feel free to do your own analysis starting whereever you want. The whole point of the post is that one should not draw conclusions about the future from short term trends. – gavin]
Upon glancing over all the data of HadCRUT4 it seems a rather cold spot to start from, although perhaps you were simply trying to start a trend line from around the 0.0 point (albeit a bit under)? However, this is quite arbitrary as well because 0.0 points are also assigned based upon subjective time-frame selections. If, for example, we were to create a piece-wise continuous trend keeping your own trend, we’d find the 0.17 C decadal warming trend from your starting point preceded by an estimated warming of equal magnitude in the combined 125 prior years (beginning at a time where only 1/4 of the present day coverage existed, thus placing the entire 125 year warming more or less within the margin of statistical insignificance). From there we’d have to enter that abhorrent mess that is proxy data, which one could use to pick out a plethora of enormous warming trends if pulling from the LIA, or again less so (possibly no trend, possibly negative) if starting from the MWP, etc. but I’d rather not even…
[Response:I have no idea what point you are making here. There are statistical tests that one can use to determine whether a break in the trend is significant so it doesn’t have to be arbitrary. – gavin]
Furthermore, the whole “If we assume for a moment that the ENSO variability and volcanoes are independent of any change in greenhouse gases or solar variability” doesn’t sit very well with me on multiple levels, thus using it to set up an argument seems spurious.
[Response: If you want to claim that ENSO has been noticeably affected by climate change, I’d like to see the evidence. The complexity of the ENSO timeseries, with uncertain amounts of multi-decadal power and poor model simulations makes detection of a change very difficult. If you can’t show an influence, the best thing is to assume independence – at least as a working hypothesis. – gavin]
This is my first post (hopefully of many, if you’ll tolerate me) on RealClimate and in case you hadn’t noticed (you have) I’m not exactly super confident in current modelling projections or ability to accurately account for past variability. That being said, yes, much of the nonsense you’ll find on WUWT and in the Daily Mail article in question is just that, nonsense.
Thanks for taking the time to run this site.
What do we know about complex systems?
Well, ask those who’ve built them:
BEGIN QUOTE
________
“His biggest contribution is to stress the ‘systems’ nature of the security and reliability problems,”….”That is, trouble occurs not because of one failure, but because of the way many different pieces interact.”
… “complex systems break in complex ways” — … complexity … has made it virtually impossible to identify the flaws and vulnerabilities …..
_________
END QUOTE
http://www.brisbanetimes.com.au/technology/technology-news/killing-the-computer-to-save-it-20121031-28jze.html
“There are two main responses to complexity in science. One is to give up studying that subject and retreat to simpler systems that are more tractable (the ‘imagine a spherical cow’ approach), and the second is to try and peel away the layers of complexity slowly to see if, nonetheless, robust conclusions can be drawn. Both techniques have their advantages, and often it is the synthesis of the two approaches that in the end provides the most enlightenment. ”
Beautiful. I am stealing this to use the next time that I get the “science is reductionist and therefore flawed/unreliable/useless” response to some evidence-based point I am making.
Thank you. Prof. Neumann, who has “built them,” is an advocate (as per the linked article) of learning lessons about them from biology–systems yet-more-complex.
The level of complexity of climate systems is right up there. This post bears out the advice that if you want to talk to a real sceptic, skip the imposters and talk to a practicing climate scientist.
How much would observations have to deviate from the models (and over what time period) to justify questioning their validity? Could some aspect of our situation, e.g. the extreme rapidity of the forcing change, be sufficiently novel to make Earth’s climate respond differently than it has in the past, and could this cause divergence from models based on paleoclimate sensitivity estimates? And finally, what’s the connection if any to Hansen et al.’s “Earth’s energy imbalance and implications”? They argue that climate models respond too slowly, but doesn’t that increase the burden of explanation?
Aaron Lewis @ 7 – That’s not how the oceans are warmed by greenhouse gases. See this Real Climate post for explanation.
Once more a piece of contrariness – in fact devoted to several points.
First, I always wander with the obsession with linear trends. Especially when the system is as complex as the global climate. Piece-wise joined or step-like constructs of linear trends (figs 1 and 3) would always suffer from the arbitrariness of the breakpoints. But why assume that the trend is linear? Simple fit to the 1975-2012 HADCRUT monthly data with quadratic and cubic polynomials gives significantly better R^2 over the whole range. And shows decrease in the warming ratio. Very significant decrease in the case of the cubic fit. Now, one may ask: why cubic? why quadratic? To which I reply: why linear? Because GHG increase roughly linearly (supra-linearly)?
[Response: Linear is pretty close to what one would expect given the the anthropogenic drivers for the underlying forced response, so it isn’t such a stretch. There is no expectation that the climate will follow a cubic trend – and the results once the impact of ENSO and volcanoes are taken into account support that. – gavin]
The data is noisy and tied with many unknowns, so only time will tell…
[Response: So throw out physics because the future is uncertain? – gavin]
The second point is with the simulations. To quote: “We saw above that the ENSO-corrected underlying trends are very consistent with the models’ underlying trends and we can also see that the actual temperatures are still within the model envelope”. Well, being within the envelope – if the envelope is as large as it seems, is no bragging point.
[Response: Agreed. It is not a particularly powerful test. But that is because even simulations from the same model but different initial conditions show a large divergence in short term trends – which underscores the main point above that short term trends are not predictive of long term changes. – gavin]
The question is: what would be the predicted value of today’s temperature anomaly that the model authors would give without knowing the 2000-2012 measurements? By visual inspection of the density of simulations I think that one would expect something like 0.5C. Significantly away from the measurements.
[Response: Whether it is significant or not depends on the uncertainties (which you neglect to mention). In fact the 2012 annual values (with the same baseline as in the figure) are 0.49 +/- 0.35 (95% spread), so the current values of the 2012-to-date anomaly (0.24-0.26) are not actually significantly different. – gavin]
As for the Foster/Rahmstorf paper: adjustment of data to remove specific effects in a NONLINEAR, coupled system is always risky. Climatic cause and effect may be independent in the case of volcanoes, but for MEI such decoupling needs long term studies. As the saying goes: if you massage the data enough, you can get anything.
[Response: Don’t be silly. We know that ENSO has an influence on global mean temperatures and is the largest interannual signal in the surface temperature field. It is completely natural to examine what happens when that is corrected for – particularly since that is the main reason in models why the trends are not linear. Complaining about the procedure because it does actually clarify what the underlying trends look like is post-hoc justification. And no, it doesn’t give you ‘anything’. – gavin]
Lastly, with respects to the statements that we know the physics “pretty well”. A recent paper by Graeme L. Stephens, Juilin Li, Martin Wild, Carol Anne Clayson, Norman Loeb, Seiji Kato, Tristan L’Ecuyer, Paul W. Stackhouse Jr, Matthew Lebsock & Timothy Andrews An update on Earth’s energy balance in light of the latest global observations, Nature Geoscience, 5, 691–696 (2012), which indicates significant adjustments to the energy balance MEASURED data shows how far we are from certainty.
[Response: Again the use of ‘significance’ without understanding what is being done. The Stephens et al paper is a very incremental change from previous estimates of the global energy balances – chiefly an improvement in latent heat fluxes because of undercounts in the satellite precipitation products and an increase in downward longwave radiation. Neither are large changes in the bigger scheme of things, though you will no doubt be happy to hear the shifts bring the data closer to the model estimates. But really, are you really going to try and pull the ‘there is uncertainty, therefore we know nothing’ line? That isn’t going to fly. – gavin]
You may think me a “denier” or “sceptic” – but my motivation is different: being a physicist from material science field I am reasonably far removed from political pressures and conflicts. And mu goal is simple: to ask for a focus on data and analyses with an open mind. DO NOT FOLLOW COVEY’S RULE OF “BEGIN WITH THE END IN MIND”.
[Response: Advice I would proffer to you in return. – gavin]
[ Response:… The complexity of the ENSO time series, with uncertain amounts of multi-decadal power and poor model simulations makes detection of a change very difficult. If you can’t show an influence, the best thing is to assume independence – at least as a working hypothesis. – gavin]
Geological records of the Equatorial Pacific would suggest that the frequency and possibly the amplitude of the ENSO oscillations are indeed independent of the climate change.
http://www.vukcevic.talktalk.net/ENSO.htm
T Marvell “With a few exceptions, climate scientists ignore this [statistical] expertise and analyze trends in a simplistic manner.”
The criticism would be better directed at the press and those making claims of “no warming since [insert cherry picked start date here]”. The usual error is to assume that a lack of a statistically significant warming trend implies that there has been a pause in global warming. However that is a statistical non-sequitur, based on a poor understanding of frequentist hypothesis testing, unless the test can be shown to have adequate statistical power (which seems never to be mentioned by those claiming a pause in warming). It is clear from the Telegraph article that Phil Jones understands this point perfectly well, but that David Rose clearly doesn’t.
PAber,
I am surprised that you do not understand the purpose and significance of linear trends, particularly when you emphasize the noisiness of the data. It is simply that in a noisy system, the linear term will likely be the first to emerge from the noise. Higher terms will emerge as we gain more information.
And again, your criticism of Foster and Rahmstorf seems bizarre. If you have a system with lots of noise, cancelling known components of that noise is a well tested method for bringing out signal. If nonlinearities are important, as you suggest, one would expect the result to be…well, crap, not the emergence of a linear trend, and certainly not a linear trend with magnitude equal throughout the observation period.
And if you are not desperate, then why are you grasping at straws that will not support you–e.g. the Stephens et al. paper?
re inline comment on 24,
What I noted was that the ocean skin equilibrium referenced in RC 5 Sept 06 could be influenced by variations in ocean currents and the cryosphere to affect atmospheric temperature on the scale of decades.
When warm air blows across cold water, the air cools and the water warms. Even in a time of global warming, an increase in ice sheet melting or deep water upwelling can cool the atmosphere relative to the long term trend. The heat of the system continues to increase at the rate of global warming, however, the partitioning of the heat into the various phases of the system changes. It takes a long time for the various phases of the system to come into equilibrium. And, as long as the system is being forced, the system is by definition, not in equilibrium. It the system is not in equilibrium, then air temperature may not be a good measure of heat in the system.
Re 25 I have to concur climate change deals with processes related to the melting/decomposition of ice /clathrates. Vapor processes are a important in the system. All of these curves are discontinuous in the region of these materials’ melting points. The curves are kinked. I would say that the failure of the climate models failure to predict Arctic Sea Ice behaviour are partially due to this issue.
Take a unit of air at temperature of -10 (100% RH) and a unit of air at 10 (100% RH) and mix them together. You do not get 2 units of air at 0 degrees.
And yet, when you do trends of global data you are averaging air temperatures over intervals where the heat content is not continuous, and thus the trend that is the average temperature does not show the actual trend of the heat content.
While anomalies are the darling of staticians, where the base line environmental temperatures cross the freezing point/melt point of water, the anomalies from those temperature data sets are just the average of nonsense.
The solution is to work with the standard deviation of the system’s Gibbs Energy on a period after period basis. That will tell you if the system is gaining or losing energy in a meaningful way and avoids all arguments.
“No. The graph starts in 1975, so only four decades are included.”
– Correct, which is why I find the fifth added in the description to be unnecessary.
“Actually no. Aug 1997 gives the lowest trend of any point prior to 2000.”
– Is not the August ’97 HadCRUT4 temp anomaly 0.436? If so that would mean there are 14 months (by my count) he could have used between that date and 2000 which would have given lesser or negative trends. February of 1998, for one. That’d then go from 0.745–>0.524 (September 2012 anomaly), so he could claim a negative slope, as many idiots actually have bothered to do by selecting from the Niño peak. Perhaps I’m looking at the wrong data set, if so my mistake, but I thought he chose that date just to go from month to month over 15 years because the Mail’s audience could better “connect” with it in that format, or something along those lines. No doubt he intended to mislead, though that wasn’t a point I was contending.
[Response: Trend is the ordinary least squares fit to the data – not just the anomaly this month minus the anomaly in 1997. And the trend from august 1997 is 0.033ºC/dec, which is the lowest you can get from any point prior to 2000. From Feb 1998, it is 0.042ºC/dec (95% conf is about +/-0.04ºC/dec). There is no doubt that he picked that start date for that reason. – gavin]
“You can show that there is significant break in the trend around 1975, but feel free to do your own analysis starting whereever (sic) you want. The whole point of the post is that one should not draw conclusions about the future from short term trends.”
– I’m not quite sure why you think I’m debating the validity (or lack thereof) of short term linear trends, as I’m clearly not. As per your choosing of August 1975 “There are no reasons either statistically or physically to think that the climate system response to greenhouse gases actually changed in August 1975.” We were at, about, 330 ppm then, correct? If you are suggesting natural variability was chiefly responsible prior to 1975, that would ignore an 18% rise from the baseline 280 ppm. Considering 395 ppm now, shouldn’t the earlier 50 ppm increase have affected temperature almost as much as the later 65 ppm additional increase due to the logarithmic nature of impact?
[Response: This is the fallacy of the single determinant of climate. CO2 is not the only thing that matters! There are however statistical reasons why 1975 is a break point – breaking the trend there provides a substantially better fit over the whole record (not true for Aug 1997), and if you look at when anthropogenic effects came out of the ‘noise’ of global temperatures, it is about the same time (fig 9.5 WG1 AR4). But if you want to look at longer datasets, go ahead. -gavin]
“I have no idea what point you are making here. There are statistical tests that one can use to determine whether a break in the trend is significant so it doesn’t have to be arbitrary.”
– Basically if you piece-wise your own starting point with the entire HadCRUT4 data set you are left with nothing more than perhaps a couple of tenths, still within the range of noise, for the remaining 125 years, thus making it seem as if you believe GHG forcing only mattered after August of 1975.
[Response: Not sure how any of that follows. GHG forcing has been important since about 1800, but only substantially larger than everything else since the mid-1970s. If you put in a break point in the whole series (from 1850) in Aug 1975, you get a trend of 0.03ºC/dec before, and 0.16ºC/dec after. – gavin]
“If you want to claim that ENSO has been noticeably affected by climate change, I’d like to see the evidence. The complexity of the ENSO timeseries, with uncertain amounts of multi-decadal power and poor model simulations makes detection of a change very difficult. If you can’t show an influence, the best thing is to assume independence – at least as a working hypothesis.”
– But I don’t want to claim that, I want to state the fact that it is impossible to determine at this point in time. Such a tenuous working hypothesis needn’t even be brought into the discussion.
[Response: Then why are you objecting to a explicit removal of ENSO effects in the time series? – gavin]
Icarus,
If you just compare the recent data to the long term trend, then yes, it is rising more slowly. However, if you compare the data from the two decades prior, then it is rising much faster than the long term trend. The question is whether this is just noise in the long term trend, or meaningful variations that require more research.
For all those who thought the Skeptical Science “Up the Down Escalator” post was satire:
http://www.skepticalscience.com/going-down-the-up-escalator-part-1.html
I give you Jefe:
“Basically if you piece-wise your own starting point with the entire HadCRUT4 data set you are left with nothing more than perhaps a couple of tenths, still within the range of noise, for the remaining 125 years, thus making it seem as if you believe GHG forcing only mattered after August of 1975.”
Jefe apparently does not realize that clean air legislation and the development of catalytic converters (which require low-sulfur fuel) diminished the effects of aerosols around 1975 and in subsequent years.
Jefe is proof that Poe’s law applies to climate science.
Using the Core BJ8-03-31MCA, Makassar Strait, Indonesia (Oppo et al. 2009 Nature 460:1113),
There is a 30% relationship between gistemp (3 year res.) and Indo -pacific temps with a 40 -50 year lag. The series is only 42 data points long (equating to 126 years), so is hardly robust, however, it may be a useful predictor of future temps since it is gistemp that lags the SST.
The correlation is centered on the rapid warming which occurred between 1980 – 1998 in gistemp and the rapid warming which (apparently) occurred between 1936 -1960 in Indo SST.
The significant lag time and short length could mean the relationship is simply due to chance, if however the relationship holds true, it would be a remarkable superposition and extremely unlikely due to humans.
http://www.ncdc.noaa.gov/paleo/recons.html
Thus is the danger of interpreting short trends…anyone can do it…
Seasonal-to-Decadal Predictions of Arctic Sea Ice: Challenges and Strategies (pre-publication)
by
Committee on the Future of Arctic Sea Ice Research in Support of Seasonal-to-Decadal Predictions; Polar Research Board; Division on Earth and Life Studies; National Research Council
available at
National Academies Press online
(On topic because a theme is lack of observation data.)
Just to add as an after thought, you could also add 6 month lag El Nino data to the Indo proxy, which could increase the correlation with gistemp, given that it would be a far cry to expect anything higher from something that occurred half a century ago, but there it is.
Aaron Lewis @ 24 – “What I noted was that the ocean skin equilibrium referenced in RC 5 Sept 06 could be influenced by variations in ocean currents and the cryosphere to affect atmospheric temperature on the scale of decades”
This is what you wrote @ 7:
I assert that recently, more of the heat in the atmosphere has gone into warming the oceans and warming/melting ice. Thus, today, we have warmer ice, warmer oceans, and relatively cooler air.
That is wrong. That’s not how the physical world operates, in climate models perhaps, but not Earth. The transport of energy into the ocean is via shortwave radiation (sunlight), whereas the longwave radiation (heat) forcing, from the atmosphere, governs how much energy is retained in the ocean. That is the fundamental background that you have misinterpreted.
Even if longwave fluxes into the ocean proper were physically possible, the huge disparity in heat capacity between the ocean and atmosphere would barely register in ocean heat content uptake. I think you need to read the post by Professor Minnett again, and perhaps look at the 2011 paper by John Church & colleagues.
There’s a very simple reason why global surface temperatures have been cool of late – the La Nina-dominant trend of the last 6 years has buried more heat in the subsurface ocean, and the sea-air flux of heat exerts a large influence on global surface temperature. This will not last. Even an apparent global dimming trend in the last decade has been unable to slow the inexorable warming of the global oceans.
Want to back up this smear against physics-based models with some hard evidence?
Re 36
My point is not about how the ocean warms/cools as a result of radiation/GHG, but the more neglected area of the stability of the heat partition between the phases.
I think the heat partition between phases is much less stable than has been assumed, and the implications for AGW have not been thought though. In particular, the implications for the detection and monitoring of AGW as the system warms have not been fully considered.
I do not think atmospheric temperatures are a consistent and precise proxy for the total heat content of the global system. Tiny changes in heat transfer between the atmosphere and the oceans affect the temperature of the atmosphere. One real world example of this was offered in the last paragraph of comment 36.
La Nina/ PDO is a perfect example where changes in ocean currents/ocean upwelling affect heat transfer between the phases of the system (and cool the air) – on a human time scale. In La Nino, global air temperatures cool, and that heat goes where? Well, some of it goes into the ocean.
In the real world, sometimes air does heat water, and sometimes water does transfer heat to air. Air-water heat flux may not significantly affect the temperature of the ocean, but it does affect the temperature of the atmosphere – as in the air over Europe is warmed by the North Atlantic Drift.
Water- air heat flux also affects the latent heat content of the atmosphere as moist air contains more heat than dry air of the same temperature. Thus, we cannot do arithmetic on air temperatures and assume that the result reflects the total heat in the air. That kind of stuff is ok as an educational exercise, but if we are going to do engineering and public policy planning we need to either insert safety factors or work with the Gibbs energy. If we are going to work with Gibbs energy, we need to be careful to bound and define the systems, and to ensure that we understand the nature of the equations of state, e.g., kinked curves.
One simply cannot do arithmetic (least squares trends) on the temperature of environmental air and expect the result to reflect the changes in heat content. As AGW moves forward, the latent heat content of the air changes, so that air of the same temperature has more heat in it, and warmer air has even more heat in it. HadCRUT4 does not reflect the latent heat in the atmosphere! Thus, plots of HadCRUT4 data do not reflect the full amount of atmospheric warming.
Recently documented changes in atmospheric circulation patterns mean that ocean currents are changing. If La Nina/El Nino can affect global air temperatures in a period of a few years, than other changes in ocean currents (driven by AGW) can affect global atmospheric heat content in a few years.
We can no longer assume that it takes generations and generations for a change in ocean currents to have a real impact on humans. We have that lesson in El Nino.
My comment on Church (2011) is that they do not account for heat that has gone into warming ice, which does not get warm enough to melt. In a time of moulin formation on the GIS, this is a non-trivial.
” “That’s not how the physical world operates, in climate models perhaps, but not Earth.”
Want to back up this smear against physics-based models with some hard evidence?”
sigh… the old “cold can’t transmit” whine. Totally ridiculous. Convert from English to Science-speak instead of trashing English, and avoid pointless arguments about nothing.
I sure would be very grateful if someone could shed some light on the questions I asked @23. Gavin? Jim? Anyone? Or if they’re poorly formulated please tell me so I can improve them. I’m not being contrary or anything like that, I’m just trying to understand.
[Response:On your 2nd question, I don’t know about the speed of the radiative forcing creating novel situations, but there is good reason to be concerned that the speed of the temperature increase itself could indeed cause states that modern society has not encountered. That’s a slightly different issue of course–Jim]
What does the hindcast of the models and temperature look like from 1880-2012?
Rob Painting @ 36:
Global dimming has changed trends. The earth is now presently approx 4% brighter than in 1990.
Recent reversal
In 2005 Wild et al. and Pinker et al. found that the “dimming” trend had reversed since about 1990 [8]. It is likely that at least some of this change, particularly over Europe, is due to decreases in pollution; most governments have done more to reduce aerosols released into the atmosphere that help global dimming instead of reducing CO2 emissions.
The Baseline Surface Radiation Network (BSRN) has been collecting surface measurements. BSRN didn’t get started until the early 1990s and updated the archives. Analysis of recent data reveals the planet’s surface has brightened by about 4 % the past decade. The brightening trend is corroborated by other data, including satellite analyses
It seems to me (a rank amateur) that the most reasonable way to estimate temperature trends due to CO2 increase is to find the statistical correlation between the CO2 and the temperature anomaly time series. Using NASA’s CO2 series for 1850 -2011 (http://data.giss.nasa.gov/modelforce/ghgases/Fig1A.ext.txt) and NASA’s temperature anomaly series http://data.giss.nasa.gov/gistemp/graphs_v3/Fig.A2.txt) I find that for the period 1880-2011 the two series correlate with R-sq~.86. Using the natural log of the CO2 may be more appropriate, but it makes little difference for the specified time period since the CO2 level increases by “only” 35%. The logarithmic relationship is Anom =0.17+3.12ln(CO2/341) deg K, where CO2 is the annual level ppm, and 341ppm is the average of the beginning and end point levels. NASA gives a “2 deg K” CO2 scenario for the time period 2012- 2099. It ends with a CO2 level of 560 ppm. With this scenario the above statistical model projects the expected 2. deg K for the 1880-2099 temperature change (a simple linear model would give 2.5 deg K).
The “random” fluctuations about this trend due to El Nino’s etc have a standard deviation of 0.1 deg K. Only two data points deviate from the model predictions by more than 2 standard deviations. For the years 2001-2011 inclusive, the actual anomaly was above the model prediction 8 times, below 3 times. All the data points for this period are within 2 standard deviations of the statistical model.
Short term trend estimates seem to be an exercise in futility. For example, based on the temperature data, the average 10 year trend (using moving 10 year intervals) is 0.07 deg K/decade. The standard deviation of the trend is double this, 0 .14 deg K/decade. Roughly speaking, the frequency spectrum of the noise (El Nino etc) has components at higher frequencies than those of the signal (CO2), so differentiation (finding the trend) worsens the signal to noise ratio.
Based on this, I suggest that the best way to monitor trends would be to use a statistical correlation model (such as the above)and check if new data points fall within 2 standard deviations of the model predictions.
Jim Larsen @ 39 – It’s evident you don’t comprehend the post by Professor Minnett. Try reading it again, and see if it is any clearer to you. I think he’s done a sterling job of explaining the fundamentals of an incredibly complex, and counter-intuitive, issue.
If you can’t parse that, I doubt you are going to follow the primary peer-reviewed literature itself. And your comment about “cold can’t transmit” demonstrates you have no understanding of the topic under discussion. Until you do, further discussion will prove fruitless.
Camburn @ 41 – Skeptical Science seems to be down at the moment, but I’ve written a recent post on Hatzianastassiou (2011). It is the 2nd such peer-reviewed study to find a dimming trend in the noughties. Note that the surface station networks show a good agreement (in a statistical sense) with the modelled tendencies from the satellite-derived data.
Time will tell how well this holds up, but there are other global datasets that might give some insight.
Dhogaza @ 37 – That seems to be a kneejerk reaction. “Slur” is highly emotive. Perhaps you can explain to me how a micro-physical effect, such as the reduced thermal gradient in the cool skin layer, is simulated in the ocean models?
And just for the record; unless one want to resort to goat entrails, and reading tea leaves – as contrarians might have us do, there is no alternative but to use climate models. But wouldn’t it be great if the model spread was greatly reduced, and they exhibited greater accuracy?
Mr. Aaron Lewis writes on the 3rd of November, 2012 at 2:37 PM:
“…work with the Gibbs energy…”
while i agree about the partitioning of heat flux into phase change, which particular gibbs free energy are you referring to ? both phase change of ice to water and water to vapour are involved. and more.
melting ice seems to be around 1e21J, so far. erosion of cold content as Prof. Jason Box puts it is …?
sidd
PAber (25) suggests that a linear model of temperature growth might not be appropriate. In support of that I note that CO2 appears to be growing expodentially. Also physics models of AGW contain feedbacks, which suggest non-linear growth.
[Response:But the radiative forcing is the natural logarithm of the [CO2] ratio at two time points.–Jim]
He also says that one must watch out for research that starts at the end, or what I call “result-oriented research”. Both AGW advocates and skeptics accuse each other of this. In practice it’s hard to tell whether one is quilty, so it makes charges easy. I can suggest several tests: whether the researcher uses SOP, whether the researcher uses the best data, whether there is thorough robustness analysis (concerning methods and data alternatives), whether the discussion seems balanced, whether the data and programs are made available to other researchers, and whether the researcher is associated with an advocacy organization.
If one spots odd procedures in a paper, one can ask the author to explain them. If the author doesn’t, the paper can be dismissed.
I disagree with the suggestion that short-term climate trends have little meaning, but their usefulness occurs only in relation to longer trends. They are important when testing time series models. Researchers routinely model long time series based on theories of what affects the variable in question A good way to test the model is to see whether events in future periods conform with what the original model pedicted. It’s a difficult procedure, but commonly done. Of course, the subjects of this post wouldn’t think of doing that. Their failure do so is a good argument against them – e.g. “what model of AGW climate change are you using when you say that recent trends do not support AGW?”
> cool skin layer is simulated ….
LMGSTFY or this blog post may help
In his inline responses to my quick post (#25) gavin set out several remarks that actually more than anything else validate my points. Let me answer in return.
// on using linear trends //
[Response: Linear is pretty close to what one would expect given the the anthropogenic drivers for the underlying forced response, so it isn’t such a stretch. There is no expectation that the climate will follow a cubic trend – and the results once the impact of ENSO and volcanoes are taken into account support that. – gavin]
To limit ourselves to phenomena with a fixed rate of change would be fine – if we would not observe significant changes in these rates, bot in the long time view (where climate changes are definitely NOT linear) or even in the short time range (where one could use the linear/ first derivative approximations). But at the very moment when one considers joined piecewise linear approximations [fig 4], without giving the reasons why the system would change its characteristics at that very time, perhaps it is more sensible to look for mechanisms (or effects, if we are unsure of the mechanisms) that describe the changing rate of change (leading to quadratic description) or perhaps even other functional forms: periodic, logistic, cubic. Sure the antrhopogenic GHG do increase linearly, but the system they are “inserted” into is not linear – this is my core point. Linearizing nonlinear system is computationally risky. More on this in later comment.
I wrote”
“The data is noisy and tied with many unknowns, so only time will tell…”
[Response: So throw out physics because the future is uncertain? – gavin]
No, definitely. I do not advocate throwing out physics. But with the very sparse data that we have available and with the complexity of the system: are we sure we know all the physics to put in?
Let me answer by a simpler example. Suppose one is to describe the behavior of a transistor (let alone a coupled system of transistors such as an integrated circuit), using Ohm and Kirchoff laws. The switching, nonlinear behavior of the transistor might be very difficult to explain using these linear laws, without the knowledge of the internal structure of the transistor. Moreover, perhaps one would lack the idea to measure the gate voltage, in which case the results would be truly bizarre: the same source/drain characteristics would produce different results in separate measurements. Would throwing doubt on such measurements and attempts to “linearize” the transistor amount to throwing out the Ohm and Kirchoff laws?
Now, to validate the analogy: the climate system is a system of interacting components. Worse, the basic hydrodynamical equations are themselves nonlinear, which makes the description of their interactions and influences even more difficult. I do not advise throwing out radiation physics, N-S equations, absorption/emission curves and any of the physics already involved. I question if we, indeed, use all the necessary knowledge and if we are not missing key couplings between the systems.
On simulations accuracy
[Response: Agreed. It is not a particularly powerful test. But that is because even simulations from the same model but different initial conditions show a large divergence in short term trends – which underscores the main point above that short term trends are not predictive of long term changes. – gavin]
[Response: Whether it is significant or not depends on the uncertainties (which you neglect to mention). In fact the 2012 annual values (with the same baseline as in the figure) are 0.49 +/- 0.35 (95% spread), so the current values of the 2012-to-date anomaly (0.24-0.26) are not actually significantly different. – gavin]
What worries me – to the point of actually rising the issue – is not only the spread of the results – but the fact that they depend so much on the models and the starting data. The spread for the hindcast phase is almost as significant as for the forecasting phase. To me this is as close to a proof as I may have that the points I made above, about our lack of a good model, are valid. If I tried to come out with similar “theoretical model” in solid state physics, my papers would be summarily rejected. Yet, in climate science we keep them – because we (at least for the moment) do not have anything better. Gavin: are you truly satisfied with the quality of the model results (especially hindcast)?
[Response: Don’t be silly. We know that ENSO has an influence on global mean temperatures and is the largest interannual signal in the surface temperature field. It is completely natural to examine what happens when that is corrected for – particularly since that is the main reason in models why the trends are not linear. Complaining about the procedure because it does actually clarify what the underlying trends look like is post-hoc justification. And no, it doesn’t give you ‘anything’. – gavin]
Why should I be silly to assume that not only ENSO drives the climate changes on a global scale (I do) but also that ENSO depends on these changes (probably to an unknown degree)? This is what I meant by dividing the volcanic/sun/possible meteor impact and other “climate independent” events. I complain to the process of decoupling ENSO because it separates this signal without proving that it is indeed separable on a cause/effect level.
On the global energy flux issue.
[Response: Again the use of ‘significance’ without understanding what is being done. The Stephens et al paper is a very incremental change from previous estimates of the global energy balances – chiefly an improvement in latent heat fluxes because of undercounts in the satellite precipitation products and an increase in downward longwave radiation. Neither are large changes in the bigger scheme of things, though you will no doubt be happy to hear the shifts bring the data closer to the model estimates. But really, are you really going to try and pull the ‘there is uncertainty, therefore we know nothing’ line? That isn’t going to fly. – gavin]
Yes and no: Yes I am claiming that we do not know the system well enough. No, I do not claim we know nothing.
Let me answer firs with respect to the new flux balance. Some of the changes – es they are corrections – touch the “small” but important areas, such as cloud effects. Important because – to my knowledge – a lot of model uncertainty is tied with them. So, I agree with Gavin’s optimism: if new models/or even old models with the new data would reproduce observations better – I would be more willing to trust them.
But my whole point is: I think we are still too far away from a model that would allow quantifiable predictions. Thus the focus should be on: gathering the data – more varied, better quality, better resolution. In parallel, on developing the models with an open mind. Not to search for proof of AGHG influence or to scare the public, but to understand what is happening. I track the political efforts on both sides, the “majority” and the “sceptics” (or if one prefers another type of language, the “alarmists” and the “deniers”) and I see that too much of the discussion has changed into nonscientific grounds. Too many scientists have become politicians, ready to support their camp anyway they can.
And that is a true problem for me.