The recent warming has been more pronounced in the Arctic Eurasia than in many other regions on our planet, but Franzke (2012) argues that only one out of 109 temperature records from this region exhibits a significant warming trend. I think that his conclusions were based on misguided analyses.
The analysis did not sufficiently distinguish between signal and noise, and mistaking noise for signal will give misguided conclusions.
We must know how random year-to-year variations compare to the long-term warming in order to determine whether a trend is statistically significant. The year-to-year variations are often referred to as noise, whereas the trend is the signal.
Franzke examined several models for describing the noise. These are referred to as null models. One involved the well-known lag-one autocorrelation (AR(1)). Another null model was an ARFIMA model, similar to Cohn and Lines. The third null model involved phase scrambling surrogate model (see below for details).
He examined the autocorrelation functions (ACF) of fitted noise models with the autocorrelation of the temperature records, and found that the ACF for phase scrambling was the same as for the original data. This similarity is expected, however, due to the fact that the phase scrambling preserves the spectral power.
The fact that the ACFs were similar for the data and the null model is also a clue for why the analysis is wrong. The ACF for the temperature data included both signal and noise, whereas the null models are only supposed to describe the noise. Moreover, the null models in this case derived the long-term persistence from a combination of the signal and noise.
The mixing-up between signal and noise is illustrated in the example below, where the variable y was constructed from a signal component and a noise component. The lagged correlation coefficients of the grey ACF estimated from y were substantially higher than those for the AR(1) noise (red), due to the fact that the signal contained a high degree of persistence.
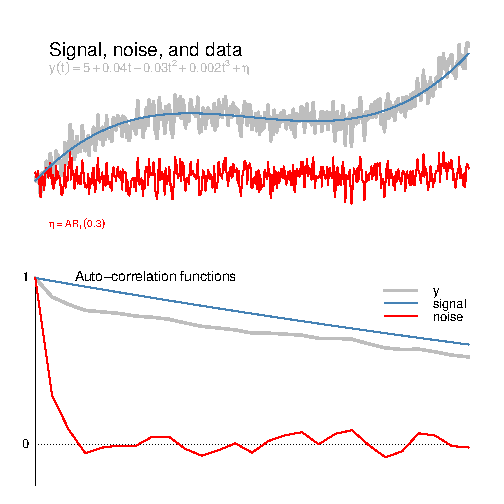
The phase scrambling will give invalid estimates for the confidence interval if the low frequencies represent both the signal and noise. Even the ARFIMA model is invalidated by the presence of a signal if it is used to describe confidence intervals. The problem is similar to the weakness in the analysis of Cohn and Lins discussed in the ‘Naturally Trendy?‘ post. Hence, both these null models over-estimate the amplitude of the noise. Alternatively, it may be a question about definition: if one defines the trend itself as noise, then it will not be statistically significant (circular reasoning).
Update:Christian Franzke, the author of the article that I discuss here, presents his views on my post in comment #10 below.
Details
The third null model involved a Fourier transform, followed by changing the Fourier coefficients while ensuring that the spectral power stays the same, and then by an inverse Transform.
References
- C. Franzke, "On the statistical significance of surface air temperature trends in the Eurasian Arctic region", Geophysical Research Letters, vol. 39, 2012. http://dx.doi.org/10.1029/2012GL054244
I am not sure that this caveat also applies to the phase-scrambling method: if the Fourier decomposition is properly restricted to periods between 2 years and 2N years, all Fourier components are trend-less. The surrogate series are thus extracted from a mean-stationary population.
I think the other two null-models are indeed contaminated by the signal if their parameters are estimated from observations
If the raw timeseries are phase-scrambled the surrogates will have the exact same frequency-spectra (and autocorrelation-spectra) as the original timeseries. The surrogates will therefore also include the same trends and secular variations as the original timeseries.
If you want to test if a trend can be due to a chance occurrence you will need to remove the trend from the original timeseries before the phase-scrambling.
In a paper submitted to J. Clim. (get a preprint here http://web.dmi.dk/solar-terrestrial/staff/boc/records.pdf) I introduce a phase-scrambling approach that takes both spatial and temporal correlations into account.
Interesting.
Is it possible to do the same exercise and make the same point with Franzke’s data?
“but Franzke (2012) argues that only one out of 109 temperature records from this region exhibits a significant warming trend.”
sounds much different than:
“All stations show a warming trend but only 17 out of the 109 considered stations have trends which cannot be explained as arising from intrinsic climate fluctuations when tested against any of the three null models. Out of those 17, only one station exhibits a warming trend which is significant against all three null models. The stations with significant warming trends are located mainly in Scandinavia and Iceland.”
And how far off was Franzke? Is it that a few more sites got over the “magic” significant minimum or that all sites show significant warming? Or is Franzke correct that 17 out of 109 were robustly warming, and we’re just talking scientific quibbles? (Quibbles are very important scientifically, but policy pretty much ignores them)
Rasmus–
I made a similar observation discussing Cohn and Lin’s paper here: http://rankexploits.com/musings/2011/un-naturally-trendy/
I’m unfamiliar with the phase scrambling though. It seems eduardo and bo think that might be immune to this effect. Have you done monte carlo on that?
Rasmus– Sorry for the quick double post especially as I asked you something and now I’m speculating what my own answer is!
eduardo
My first thought is the difficulty is not related to whether or not the elements of the Fourier decomposition are trendless. The potential difficulty lies in the possibility that even if you remove a linear trend, the non-linearities in the signal will be treated as low frequency noise. When this occurs, the estimated spectrum of the detrended realization will contain too much energy at low frequencies. So, for example, if we create a series from a cubic + AR1 noise, the true spectrum of the AR1 noise looks like this:
But the spectrum you get by removing the best estimate of the linear trend and treating this detrended series as noise looks like this:
It’s true that all fourier components are trendless. The difficulty is that the estimated spectrum (a) has too much power and (b) much of the excess is at very low frequencies.
I suspect no matter what one does with the analysis these two elements will tend to result in too many “fail to reject” a null hypothesis that the data are trendless.
Lucia: In the power-spectrum of a timeseries of finite length a linear trend is most often represented mainly by the lowest frequencies.
Using the phase-scrambling method we can estimate the probability for that the high frequencies (the noise) have conspired to give a variability that looks like a trend or a change (the climate signal). This can happen for some configurations of the Fourier-phases which are not conserved with the phase-scrambling method.
Using only the data it is not obvious how to separate the signal from the noise. We can remove a linear fit or a polynomial fit from the original data before the phase-scrambling and investigate the probability that the remaining variability can give surrogate timeseries with trends or changes comparable to those found in the original data.
I am not sure how Franzke makes his surrogates so I can not judge if Rasmus is right when he thinks that Franzke makes a mistake.
markx: Yes, the spatio-temporal phase-scrambling can also be performed on irregularly positioned station data if the different timeseries cover the same period.
Bo–
Thanks.
Using only the data it is not obvious how to separate the signal from the noise. We can remove a linear fit or a polynomial fit from the original data before the phase-scrambling and investigate the probability that the remaining variability can give surrogate timeseries with trends or changes comparable to those found in the original data.
The text of his paper seems to suggest he (she?) did at least try to separate signal from noise. Specifically, I read the text to convey that they treated the signal as a cubic. The noise would then be whatever remains after the best estimate for the signal– assumed as a cubic is.
Of course, as you note, it’s not easy to separate signal from noise based on data alone. Still, based on my reading of the text, Franzke’s method attempts to separate the two. It appears he went certainly went to more trouble than merely treating signal as a linear trend. So, unless someone gets the code or teases out more detail, it at least appears Franzke’s autocorrelations apply to an estimate of the noise with an estimate of the signal removed.
I don’t use Fourier Transforms in my work but I always enjoy seeing his name show up in posts…after all; Joseph Fourier: 1824 Annales de chimie et de physique and 1827 Mémoire sur la température du globe terrestre et des espaces planétaires are generally considered the original work on the “Greenhouse Effect”. Smart man.
Hi,
as the author of the paper I would like to make the following points to defend my approach.
The starting point of my investigation was that intrinsic climate variability is able to create apparent trends over rather long time periods without any external forcing. Those apparent trends will be superposed on external forced trends. Thus we can write that
Trend_{Effective} = Trend_{External} + Trend_{Internal}
where Trend_{Effective} is the trend we can observed (say our least
square estimate from a given time series), Trend_{External} is the trend component due to say CO2 emissions and Trend_{Internal} is the trend component due to internal climate variability.
The problem now is that we neither know Trend_{External} nor
Trend_{Internal} but can only estimate Trend_{Effective}.
Now we can assume that Trend_{Effective} = Trend_{Internal} and try to reject this possibility and establish that Trend_{Effective} has a component due to external factors. Of course, Trend_{External} will influence this analysis to some extent.
Alternatively, as you propose in your blog, we can assume that Trend_{Effective} = Trend_{External} but then Trend_{Internal} will influence this analysis to some extent again. The signal is now contaminated by ‘noise’. You are also a priori assuming that there is an externally forced trend present which will bias you towards accepting trends.
This comes down to how you formulate your NUll hypothesis but both approaches are equally valid and both will be contaminated to some extent by ‘misfitting’ the true externally forced trend. Both approaches will be biased either towards accepting trends as externally forced when they actually internal trends and the other towards rejecting trends even though they are externally forced.
I actually did both approaches but only reported the first in the paper because the second gives similar results which wouldn’t change the major conclusion of the study. I now realise that I better should have mentioned that in the paper.
I think the real problem analysing station data is that the signal to noise ratio seems to be generally low. Because of that I think your figure ‘Signal, noise and data’ is misleading because station data look different; also the ACF of station data decays much faster than in your example. Detrending station data has a much lesser influence on the ACF then your example implies. Your example fits better to global mean or hemispheric mean temperatures where the signal is much more pronounced because the spatial averaging has reduced the intrinsic climate fluctuations. For the global mean temperature you can see the trend by eye which is generally not the case for station data. Such a strong trend will have a strong impact on the ACF.
One way of improving the analysis would be to simultaneously estimate Trend_{External} and a statistical model for the intrinsic climate fluctuations. That is something I am currently working on with a PhD student. Here we have to specify parametric models for Trend_{External} and the statistical model. This introduces model error which will affect the outcome to some extent. We again cannot be sure to have accurately identified Trend_{External}.
One could also think about computing the forced response from a set of CMIP5 model simulations and take this as an approximation of Trend_{External}. But we would need to deal with model error and model bias and also would need to relate the model grid to station data or aggregate station data so that it better corresponds to model output. This approach also wouldn’t be the ‘perfect’ solution.
Christian,
It is interesting that it doesn’t matter much whether you identify Trend_{Effective} = Trend_{Internal} or Trend_{Effective} = Trend_{External} for the purpose of determining significance.
Would any of the following be correct?
It seems that your using daily data is significant.
For the AR(1) process you will get scale separation. I.E. the amount of Trend contaminating a period of daily data of length similar to the AR(1) time constant will be very small.
For the ARFIMA process, the parameter can determined at any time scale due to its fractal nature and there are many more high frequency components than the small handful of low frequency components that dominate the cubic fit. The greater amount of high frequency data thus overwhelms the component due to Trend_{Effective} whether it is included or not.
The case of phase scrambling is not so clear to me. I think that once again the use of daily data implies the law of large numbers is in effect and the Fourier components, at least for an AR(1) assumption have expected covariances approaching zero so the phase can be thought of as a random variable with a uniform distribution on [0,2pi). In that case and given that any cubic Trend_{Effective} will have a characteristic set of phase relationships one can ask whether that characteristic set was likely.
By way of an illustration, a linear slope is approximated by a saw-tooth function which not only has components with amplitudes 1/f but consists solely of sine components (each with zero phase angle). The likelihood of that occuring by chance is very small were all phase angles equally likely.
That said, I am not sure I could convince myself that this applies in the LRD (fractal) case as I would expect that over any fixed length period such a noise model would have a non-zero expectation for the covariance between the components, (and especially the critical low frequency components) both in terms of amplitude and phase, but I am truly unsure of such being the case.
Many Thanks
Alex
The phase randomization method is a neat one. Good to see it used. I think it originates in a paper by Theiler et. al in 1992 (see exact reference in Franzke’s article). Glass and Kaplan discuss it in their nice book on Non-linear dynamics
(http://www.amazon.com/Understanding-Nonlinear-Dynamics-Applied-Mathematics/dp/0387944230 ).
It is a deceptively simple method, that uses the facts that a) the autocorrelation and the spectrum are Fourier couples, and b) that all phase information is lost when a complex number is squared, to generate surrogate time series that have the same spectrum as an original time series, – and thus the same autocorrelation.
It is my favorite method to generate surrogate time series, but one thing to know is that while the autocorrelation is (by design) conserved the distribution is not. If this is likely to cause problems there are methods around this.
For those Realclimate readers who are R-affictionados you can find the surrogate function in the tseries package (http://cran.rstudio.com/web/packages/tseries/index.html). It can do both standard and distribution conserving surrogates.
Dr. Franzke,
I’ll disagree with you and agree with Rasmus. He is not “a priori assuming that there is an externally forced trend present which will bias you towards accepting trends.” He is positing including a trend term, which may be zero if the coefficients so dictate, but its impact will not bias the result toward trends so long as the number of degrees of freedom is properly accounted for. I suggest that it’s a mistake not to allow for a trend when estimating the ACF. You surely can’t demonstrate the lack of a trend by assuming that there isn’t one.
You say that doing it the other way gives similar results, and I believe you. You also say that what’s really going on is that the signal-to-noise ratio is so low it makes trends in single-station records extremely difficult to detect, and I’ve seen enough of the data to know that’s true. But I have to wonder, what’s the real purpose of your study? Since all single-station records have such low signal-to-noise, and this is even more true for Arctic stations, haven’t you demonstrated nothing more than the low signal-to-noise ratio itself?
There’s also the fact that the bulk of your stations are in Scandinavia. Given the strong spatial correlation of temperature records, this hardly represents over 100 independent tests. It’s an interesting question just how many degrees of freedom are present in the selected sample, but it’s certainly much smaller than the number of station records examined.
Finally, the data reveal obvious seasonal heteroskedasticity. For Arctic stations it’s so extreme that if one wants to be truly rigorous, both the AR(1) and ARFIMA models (with coefficients based on daily data) are in serious doubt.
Christian,
Thank you for your response. While any individual station has a low signal to noise ratio, would it be possible to group similarly sited stations in order to improve the ratio? Granted, grouping the entire set Siberian stations may not yield much improvement, you have an abundance of Scandinavian data that may yield a higher ratio, if grouped together. If the data is largely random variation, then the grouping would not change much, but if several stations showed similar results, then you may achieve higher confidence in the trends. Of course, there is always the difficulty in assessing short term trends using data which is not significant in the short term.
A little bit of “told you so” here. http://www.alternet.org/environment/climate-risks-have-been-underestimated-last-20-years
I’ve been offering this very analysis since as long ago as 2007, and certainly since the thermokarst issue arose n 2007 via Walter, et al. The problems with underestimation are multi-layered, but the most important, imo, at the end of the day is the lack of trust in interdisciplinary approaches that include non-scientific analysis based in risk assessment and areas of knowledge that are informative, but not well-parameterized. But, if there are people and/or groups doing excellent predictive/scenario generation, year after year, should we not begin to listen?
It is time to acknowledge there are issues with CH4, issues with Earth System Sensitivity, and issues with Rapid Climate Change… and simple forms of analysis that can help us work these things out and create solutions. The natural world holds answers that are becoming increasingly measurable. That is, science is beginning to back up what we have known for a very long time about how natural systems work, and how to maximize them to generate solutions.
A recent article and study found *gasp!* that diversity and complexity in ecosystems, and food systems, is really healthy. Observing nature told us that a long, long time ago, and some of us know how to design such things either for remediation or to integrate human systems with the natural world.
The same knowledge base helps to understand why the Rapid Climate Change is already upon us.
Thanks for an interesting discussion. Many good points have been made. What Christian does is to test the hypotheses that the observed record is a realization of two particular noise processes, one with short-range memory (AR(1)) and one with long-range memory (ARFIMA). Then this is formulated as the null hypothesis and the test is to find out whether this hypothesis is rejected by the data. Of course the trend should not be incorporated in the test of this null hypothesis. Tamino (Jan 2.) misses the point when he writes: “You surely can’t demonstrate the lack of a trend by assuming that there isn’t one.” What Christian does is not to demonstrate the lack of a trend, but to demonstrate that you cannot reject the hypothesis that there isn’t one.
What Rasmus does is to illustrate, by one sample of an AR(1) process, that adding a strong 3. order polynomial trend gives a long-tailed ACF which is easily distinguishable from the exponential ACF for AR(1). This is really quite trivial, obvious, and deceptive. What he should have done, is to use a real observed record, instead of the synthetically generated y(t) (gray curve) in his figure, and compute the ACF. If this record is global temperature it would look similar to the curve shown by Rasmus, and the ACF would have a long tail similar to the gray ACF shown in his figure. By performing a Monte Carlo study (generating an ensemble of realizations of the AR(1) process) he could estimate the confidence limits on the ACF of the AR(1) and he would find that the null hypothesis that global temperature is described by an AR(1) is rejected. This is not surprising, and not in contradiction to Christian’ work, because Christian is not analyzing global data with monthly resolution, buit rather local data with daily resolution.
The situation would not be so clear if Rasmus would do what he has done, but with the ARFIMA null hypothesis. We have done this with another long-range memory process (fractional Gaussian noise-fGn) as null hypothesis, and find that the cubic trend is significant, i.e., the fGn null is rejected. However, if the cubic trend is subtracted, and the test is performed on the residual signal (which contains a prominent 60 yr oscillation), the null hypothesis is not rejected. This means that we cannot exclude that this oscillatory “trend” is an undriven internal fGn fluctuation. These results are contained in a manuscript submitted to JGR, and can be downloaded from:
https://dl.dropbox.com/u/12007133/LRM%20in%20Earth%20temp.pdf
As Christian points out, Rasmus would also have arrived at a different conclusion if he would use single-station records with daily resolution, even if he would use the AR(1) null. Again, there is no contradiction between Rasmus and Christian, other than emphasizing different null models and different observation data.
Having said this, Tamino makes a very interesting point by questioning Christian’s use of localized station data with daily resolution for trend estimates. According to our analyses, an fGn long-range memory model works well on both local and global data, but the persistence (Hurst exponent) is much higher in the global data. On the other hand, as pointed out in several of the comments, the noise variance is much higher in the local data. The confidence limits for the ACF for an fGn depends only on the Hurst exponent H and are wider for higher H. On the other hand a given trend has a smaller effect on the tail of the ACF if the noise variance is higher. Hence, these two effects act in the opposite direction when it comes to trend detection. We can only find out which data (local or global) are optimal for trend detection by analyzing both. By analyzing the global temperature records and the Central England record in the JGR submission mentioned above, we find that the trends stand more clearly out of the noise in the global data, indicating that Christian is not using the optimal data for trend detection.
Thanks for the interesting comment Kristoffer. I agree with your comments. Just a comment on ‘optimal data for trend detection’.
I agree that using spatially averaged data reduces the amount of intrinsic climate fluctuations and, thus, is making the trends more pronounced. Since understanding regional climate change becomes more and more important it would then be important to know what the ‘optimal’ spatially averaging area is. I suspect that global averaging will give you the most reduction in intrinsic climate fluctuations and, thus, being the ‘optimal’ data for trend detection. That might be the optimal way to decide whether the Earth as a whole is warming due to anthropogenic forcing. But that does not tell us anything about regional or local climate change which I am interested in.
Thanks for your prompt respone, Christian. I agree that global trends do not tell you all about regional and local change, but to say that it tells you nothing is perhaps an overstatement. If there is a global warming, there must also be local changes, but they may of course be different in different regions.
If only 1 out of 109 arctic stations shows a significant trend by analysis of individual station data it would perhaps be an idea to analyze a suitably weighted average over these stations as one time series. That should reduce the noise level and make trend detection easier.
But even more important is time averaging, I think. By analyzing time series with daily resolution you drag along with, not only climate noise, but weather noise. You don’t lose any local or regional information by analyzing monthly averages rather than daily averages, but you get rid of a lot of fluctuations which are related to weather rather than climate, and which probably obeys quite different statistics than the fluctuations on time scales from months to decades.
[Response: I think we must be on different wavelengths here. I want to refer to your previous comment also, where you discuss the ACF example and the use of actual data. My point is that we do not know what is signal and what is noise. Hence we need a synthetic example where these have been specified – and the demonstration that the signal, the trend in this case, does indeed affect the ACF, as well as the Hurst exponent. Agree, for lesser trends, the differences will not be as marked. But the ACF will still be contaminated by the signal.
If you assume that the trend (signal) is noise, then you will find that your time series does not have a statistically significant trend – by circular reasoning. In fact, when you test a number of different cases, you’d expect that a small number will seem to satisfy the criterion of being statistically significant just as in Franzke’s paper: for the 5% confidence interval, you’d expect to find that 5% of tests made on random samples will ‘qualify’. For many parallel test, you will have to apply something like the Walker test: See Wilks, 2006.
The choice of method is less of an issue here, whether AR(1), ARFIMA, or phase scrambling. They have different capabilities of describing the noise characteristics for sure, but neither provide a distinction between what is noise and what is signal. When applied, one usually assumes all to be noise.
One way to try to answer this question could be to do a regression analysis against the global mean on e.g five-year mean sequences (to emphasis the longer time scales), use the regression model to predict the local temperature series, and then apply the ACF to the residuals of the regression results, however, one difficulty is if non-linear trends are present. One could also repeat the analyses on results from climate models to see if there are accounted-for mechanisms indicating that such non-linear links are present. -rasmus]
Kristoffer,
I didn’t mean to imply that global mean data won’t tell us anything. Far from it, the global mean temperature curve is very useful. I just wanted to state my personal motivation for looking at station data and when I started working on that paper I was mainly interested in local scale climate change.
I agree with you and other comments that looking at spatially averaged data might be better in identifying the trend signal. I will do this in my future research.
Response to Rasmus’ response. I agree that we may be on somewhat different wavelength. For instance your phrase “If you assume that the trend (signal) is noise…” is very confusing to me. In my conceptional framework we have the equation
observation = trend (signal)+noise,
hence I cannot assume that trend is noise. On the other hand a trend ESTIMATE (by regression or other methods) can be erroneous and therefore in reality should be relegated to the noise background.
What I need to fully understand what you mean, Rasmus, is that you formulate clearly your approach to hypothesis testing. In my world, and I am sure also in yours, hypotheses cannot be verified by observation, they can only be falsified. Therefore you have to formulate an hypothesis to reject; a null hypothesis. Loosely formulated this hypothesis is “the observation is pure noise.” If the observation is inconsistent with this hypothesis (outside the confidence intervals for realizations of this noise) we can conclude that the trend (signal) is not vanishing, and hence that some sort of trend exists. The result obviously depends on how we define “pure noise” so we need to specify a model for the noise. Trends identified as significant under a white-noise null hypothesis may not be significant if the noise is red (e.g., an AR(1) process), and a trend that is significant under AR(1) noise may not be significant if the noise is long-range dependent. It is not a question of method, it is a question of choice of null hypothesis. The choice of null hypothesis (noise model) defines what we mean by “a trend” because ”trend=observation – noise.” I cannot see any circularity in this reasoning.
So why do you think there is circular reasoning? Maybe it is associated with the choice of the right noise model. Here it is possible to get caught in circular reasoning if the assumption “observation=noise” is used. For instance, a simple variogram analysis of an observed record which is white noise superposed on a strong trend may return a result that looks like a strongly persistent fractional Gaussian noise (fGn) with a Hurst exponent close to unity. Using this fGn as a null hypothesis the hypothesis test will likely accept the observed signal as pure noise, i.e., the null hypothesis is not rejected. In fact, a sufficiently persistent long-range memory noise (or motion, if the Hurst exponent is >1) has so strong variability on long time scales that it will hide any trend, so we need criteria for a reasonable choice of noise model.
This dilemma is the essence of the proverb, “one man’s signal is another man’s noise.” It is to some extent a subjective choice, based on what part of the underlying dynamics we want to represent as a signal and what we would relegate to noise. In climate science a useful criterion is to define forced change as a signal, while internal variability is noise. It can be systematically studied in climate models, which can give us an idea about the nature of the internal variability by running them with constant forcing. Another approach that we have had considerable success with lately is to explore a statistical dynamic response model for the climate system against known data for global forcing and temperature response. With only white-noise forcing such a model yields the climate noise, and with the known deterministic forcing it yields the “signal” (or trend). Various models for the climate response can be investigated and tested against the observations, and for each response model the model parameters can be obtained by maximum-likelihood estimation (MLE). In this approach the trend is simply the deterministic response to the known forcing. We have tested the noise component obtained by subtracting this estimated trend from the observed global temperature record against the response model that produces AR(1) noise and the response model that produces fGn noise, and it turns out to be inconsistent with the former and consistent with the latter, and the Hurst exponent is close to 1.
There are also methods that do not make use of forcing data. On synthetic data nonparametric detrending methods like the detrended fluctuation analysis or wavelet variance analysis have proven effective in eliminating trends and returning the correct Hurst exponent. Among parametric methods, maximum-likelihood estimation may be used to estimate the most likely noise- and trend parameters if the signal is assumed to consist of a noise of a particular type superposed on a polynomial trend of a given order with unknown coefficients.
In conclusion: some degree of ambiguity will probably always exist, but the picture is not as bleak as you draw it, Rasmus.
Thanks for your explanation, Kristoffer – very much appreciated! Also very interesting and difficult. I’ll try to make clear my position.
I do agree 100% that observation = trend (signal)+noise, that signal/trend estimates are subject to errors, and that null-hypotheses are used for falsification, and hypotheses cannot be verified by observation, they can only be falsified.
My primary concern is that choosing a null-hypothesis is a subjective choice – often a null-model is chosen because the investigator expects that it will fit the observations. The null-models should be chosen to fit the noise.
My concern is that some of the persistence may be due to the signal itself, and not necessarily the noise. Hence, the noise model may be deceptive (possible circular, at least in the synthetic example that I provided).
In some ways, it’s a question about the amount of information there is – if the data record only fits a couple of periods/oscillations of the long-term behaviours, then it is extremely difficult to say whether these are part of background variability or if they are indeed the signal.
I think it would be fun to test some of these ideas out. Your suggestion are very interesting. We can also look to the pealeo-data – e.g. GISP2 data capturing the ice ages. What would the long-term-persistance (LTP) null-models like ARFIMA give you for noise? I’m open for persuation.
One could also look at the problem in two parts: (1) is the recent distribution statistically different to previous distributions (purely a statistical test with no regards to LTP noise; (2) If so, what’s the cause. If the reason is LTP internal variations, these surely take place due to certain physical processes – what are these? Is it possible to isolate these and simulate these processes?