Climate sensitivity is a perennial topic here, so the multiple new papers and discussions around the issue, each with different perspectives, are worth discussing. Since this can be a complicated topic, I’ll focus in this post on the credible work being published. There’ll be a second part from Karen Shell, and in a follow-on post I’ll comment on some of the recent games being played in and around the Wall Street Journal op-ed pages.
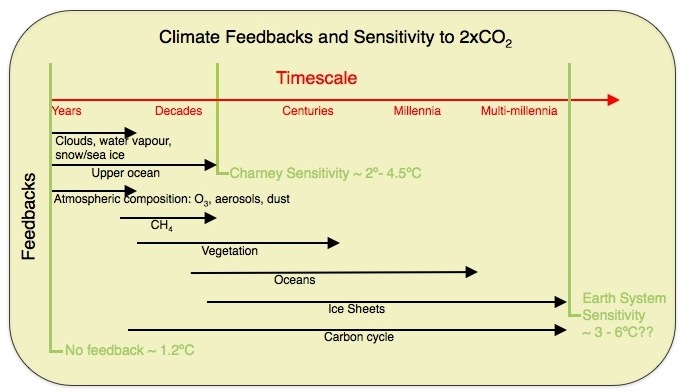
What is climate sensitivity? Nominally it the response of the climate to a doubling of CO2 (or to a ~4 W/m2 forcing), however, it should be clear that this is a function of time with feedbacks associated with different components acting on a whole range of timescales from seconds to multi-millennial to even longer. The following figure gives a sense of the different components (see Palaeosens (2012) for some extensions).
In practice, people often mean different things when they talk about sensitivity. For instance, the sensitivity only including the fast feedbacks (e.g. ignoring land ice and vegetation), or the sensitivity of a particular class of climate model (e.g. the ‘Charney sensitivity’), or the sensitivity of the whole system except the carbon cycle (the Earth System Sensitivity), or the transient sensitivity tied to a specific date or period of time (i.e. the Transient Climate Response (TCR) to 1% increasing CO2 after 70 years). As you might expect, these are all different and care needs to be taken to define terms before comparing things (there is a good discussion of the various definitions and their scope in the Palaeosens paper).
Each of these numbers is an ’emergent’ property of the climate system – i.e. something that is affected by many different processes and interactions, and isn’t simply derived just based on knowledge of a small-scale process. It is generally assumed that these are well-defined and single-valued properties of the system (and in current GCMs they clearly are), and while the paleo-climate record (for instance the glacial cycles) is supportive of this, it is not absolutely guaranteed.
There are three main methodologies that have been used in the literature to constrain sensitivity: The first is to focus on a time in the past when the climate was different and in quasi-equilibrium, and estimate the relationship between the relevant forcings and temperature response (paleo constraints). The second is to find a metric in the present day climate that we think is coupled to the sensitivity and for which we have some empirical data (these could be called climatological constraints). Finally, there are constraints based on changes in forcing and response over the recent past (transient constraints). There have been new papers taking each of these approaches in recent months.
All of these methods are philosophically equivalent. There is a ‘model’ which has a certain sensitivity to 2xCO2 (that is either explicitly set in the formulation or emergent), and observations to which it can be compared (in various experimental setups) and, if the data are relevant, models with different sensitivities can be judged more or less realistic (or explicitly fit to the data). This is true whether the model is a simple 1-D energy balance, an intermediate-complexity model or a fully coupled GCM – but note that there is always a model involved. This formulation highlights a couple of important issues – that the observational data doesn’t need to be direct (and the more complex the model, the wider range of possible constraints there are) and that the relationship between the observations and the sensitivity needs to be demonstrated (rather than simply assumed). The last point is important – while in a 1-D model there might be an easy relationship between the measured metric and climate sensitivity, that relationship might be much more complicated or non-existent in a GCM. This way of looking at things lends itself quite neatly into a Bayesian framework (as we shall see).
There are two recent papers on paleo constraints: the already mentioned PALAEOSENS (2012) paper which gives a good survey of existing estimates from paleo-climate and the hierarchy of different definitions of sensitivity. Their survey gives a range for the fast-feedback CS of 2.2-4.8ºC. Another new paper, taking a more explicitly Bayesian approach, from Hargreaves et al. suggests a mean 2.3°C and a 90% range of 0.5–4.0°C (with minor variations dependent on methodology). This can be compared to an earlier estimate from Köhler et al. (2010) who gave a range of 1.4-5.2ºC, with a mean value near 2.4ºC.
One reason why these estimates keep getting revised is that there is a continual updating of the observational analyses that are used – as new data are included, as non-climatic factors get corrected for, and models include more processes. For instance, Köhler et al used an estimate of the cooling at the Last Glacial Maximum of 5.8±1.4ºC, but a recent update from Annan and Hargreaves and used in the Hargreaves et al estimate is 4.0±0.8ºC which would translate into a lower CS value in the Köhler et al calculation (roughly 1.1 – 3.3ºC, with a most likely value near 2.0ºC). A paper last year by Schmittner et al estimated an even smaller cooling, and consequently lower sensitivity (around 2ºC on a level comparison), but the latest estimates are more credible. Note however, that these temperature estimates are strongly dependent on still unresolved issues with different proxies – particularly in the tropics – and may change again as further information comes in.
There was also a recent paper based on a climatological constraint from Fasullo and Trenberth (see Karen Shell’s commentary for more details). The basic idea is that across the CMIP3 models there was a strong correlation of mid-tropospheric humidity variations with the model sensitivity, and combined with observations of the real world variations, this gives a way to suggest which models are most realistic, and by extension, what sensitivities are more likely. This paper suggests that models with sensitivity around 4ºC did the best, though they didn’t give a formal estimation of the range of uncertainty.
And then there are the recent papers examining the transient constraint. The most thorough is Aldrin et al (2012). The transient constraint has been looked at before of course, but efforts have been severely hampered by the uncertainty associated with historical forcings – particularly aerosols, though other terms are also important (see here for an older discussion of this). Aldrin et al produce a number of (explicitly Bayesian) estimates, their ‘main’ one with a range of 1.2ºC to 3.5ºC (mean 2.0ºC) which assumes exactly zero indirect aerosol effects, and possibly a more realistic sensitivity test including a small Aerosol Indirect Effect of 1.2-4.8ºC (mean 2.5ºC). They also demonstrate that there are important dependencies on the ocean heat uptake estimates as well as to the aerosol forcings. One nice thing that added was an application of their methodology to three CMIP3 GCM results, showing that their estimates 3.1, 3.6 and 3.3ºC were reasonably close to the true model sensitivities of 2.7, 3.4 and 4.1ºC.
In each of these cases however, there are important caveats. First, the quality of the data is important: whether it is the LGM temperature estimates, recent aerosol forcing trends, or mid-tropospheric humidity – underestimates in the uncertainty of these data will definitely bias the CS estimate. Second, there are important conceptual issues to address – is the sensitivity to a negative forcing (at the LGM) the same as the sensitivity to positive forcings? (Not likely). Is the effective sensitivity visible over the last 100 years the same as the equilibrium sensitivity? (No). Is effective sensitivity a better constraint for the TCR? (Maybe). Some of the papers referenced above explicitly try to account for these questions (and the forward model Bayesian approach is well suited for this). However, since a number of these estimates use simplified climate models as their input (for obvious reasons), there remain questions about whether any specific model’s scope is adequate.
Ideally, one would want to do a study across all these constraints with models that were capable of running all the important experiments – the LGM, historical period, 1% increasing CO2 (to get the TCR), and 2xCO2 (for the model ECS) – and build a multiply constrained estimate taking into account internal variability, forcing uncertainties, and model scope. This will be possible with data from CMIP5, and so we can certainly look forward to more papers on this topic in the near future.
In the meantime, the ‘meta-uncertainty’ across the methods remains stubbornly high with support for both relatively low numbers around 2ºC and higher ones around 4ºC, so that is likely to remain the consensus range. It is worth adding though, that temperature trends over the next few decades are more likely to be correlated to the TCR, rather than the equilibrium sensitivity, so if one is interested in the near-term implications of this debate, the constraints on TCR are going to be more important.
References
- . , "Making sense of palaeoclimate sensitivity", Nature, vol. 491, pp. 683-691, 2012. http://dx.doi.org/10.1038/nature11574
- J.C. Hargreaves, J.D. Annan, M. Yoshimori, and A. Abe‐Ouchi, "Can the Last Glacial Maximum constrain climate sensitivity?", Geophysical Research Letters, vol. 39, 2012. http://dx.doi.org/10.1029/2012GL053872
- P. Köhler, R. Bintanja, H. Fischer, F. Joos, R. Knutti, G. Lohmann, and V. Masson-Delmotte, "What caused Earth's temperature variations during the last 800,000 years? Data-based evidence on radiative forcing and constraints on climate sensitivity", Quaternary Science Reviews, vol. 29, pp. 129-145, 2010. http://dx.doi.org/10.1016/j.quascirev.2009.09.026
- J.D. Annan, and J.C. Hargreaves, "A new global reconstruction of temperature changes at the Last Glacial Maximum", 2012. http://dx.doi.org/10.5194/cpd-8-5029-2012
- A. Schmittner, N.M. Urban, J.D. Shakun, N.M. Mahowald, P.U. Clark, P.J. Bartlein, A.C. Mix, and A. Rosell-Melé, "Climate Sensitivity Estimated from Temperature Reconstructions of the Last Glacial Maximum", Science, vol. 334, pp. 1385-1388, 2011. http://dx.doi.org/10.1126/science.1203513
- J.T. Fasullo, and K.E. Trenberth, "A Less Cloudy Future: The Role of Subtropical Subsidence in Climate Sensitivity", Science, vol. 338, pp. 792-794, 2012. http://dx.doi.org/10.1126/science.1227465
- M. Aldrin, M. Holden, P. Guttorp, R.B. Skeie, G. Myhre, and T.K. Berntsen, "Bayesian estimation of climate sensitivity based on a simple climate model fitted to observations of hemispheric temperatures and global ocean heat content", Environmetrics, vol. 23, pp. 253-271, 2012. http://dx.doi.org/10.1002/env.2140
Ray Ladbury #93
“I agree that Jeffrey’s Prior is attractive in a lot of situations. However, it is not clear that it would help in this case, is it? I mean in some cases, JP is flat”
The form of the Jeffreys’ prior depends on both the relationship of the observed variable(s) to the parameter(s) and the nature of the observational errors and other uncertainties, which determine the form of the likelihood function. Typically the JP is only uniform where the estimation is of a simple location parameter, with the measured variable being the parameter (or a linear function thereof) plus an error whose distribution is independent of the parameter.
Where (equilibrium/effective) climate sensitivity (S) is the only parameter being estimated, and the estimation method works directly from the observed variables (e.g., by regression, as in Forster and Gregory, 2006, or mean estimation, as in Gregory et al, 2002) over the instrumental period, then the JP for S will be almost of the form 1/S^2. That is equivalent to an almost uniform prior were instead 1/S, the climate feedback parameter (lambda), to be estimated.
The reason why a 1/S^2 prior is noninformative is that estimates of climate sensitivity depend on comparing changes in temperature with changes in {forcing minus the Earth’s net radiative balance (or its proxy, ocean heat uptake)}. Over the instrumental period, fractional uncertainty in the latter is very much larger than fractional uncertainty in temperature change measurements, and is approximately normally distributed.
There is really no valid argument against using a 1/S^2 prior in cases like Forster & Gregory, 2006 and Gregory et al, 2002, and that is what frequentist statistical methods implicitly use. For instance, Forster and Gregory, 2006, used linear regression of {forcing minus the Earth’s net radiative balance} on surface temperature, which as they stated implicitly used a uniform in lambda prior for lambda. When the normally distributed estimated PDF for lambda resulting from that approach is converted into a PDF for S, using the standard change of variables formula, that PDF implicitly uses a 1/S^2 prior for S. However, for presentation in the AR4 WG1 report (Fig. 9.20 and Table 3) the IPCC multiplied that PDF by S^2, converting it to a uniform-in-S prior basis, which is highly informative. As a result, the 95% bound on S shown in the AR4 report was 14.2 C, far higher than the 4.1 C bound reported in the study itself.
Where climate sensitivity is estimated in studies involving comparing observations with values simulated by a forced climate model at varying parameter settings (see Appendix 9.B of AR4 WG1), the JP is likely to be different from what it would be were S estimated directly from the same underlying data. Where several parameters are estimated simultaneously, the JP will be a joint prior for all parameters and may well be a complex nonlinear function of the parameters.
I’m in need of some clarification on what we should be now using as a GWP for methane.
From Archer 2007:
…..so a single molecule of additional methane has a larger impact
on the radiation 5 balance than a molecule of CO2, by about a factor of 24 (Wuebbles and Hayhoe, 2002)……
…..To get an idea of the scale, we note that a doubling of methane
10 from present-day concentration would be equivalent to 60 ppm increase in CO2 from present-day, and 10 times present methane would be equivalent to about a doubling of CO2. A release of 500 Gton C as methane (order 10% of the hydrate reservoir) to the atmosphere would have an equivalent radiative impact to a factor of 10 increase in atmospheric CO2……
…..The current inventory of methane in the atmosphere is about 3 Gton C. Therefore, the release of 1 Gton C of methane catastrophically to the atmosphere would raise the methane concentration by 33%. 10 Gton C would triple atmospheric methane.
(so doubling atmos methane requires 3 Gton release, 10x present methane requires 30 Gton released?)
Here also GWP methane is taken as 24. As we know 20yr GWP methane is commonly stated as 72 (IPCC) or 105 (shindel).
Factoring in findings of :
Large methane releases lead to strong aerosol forcing and reduced cloudiness 2011 T. Kurt ´en1,2, L. Zhou1, R. Makkonen1, J. Merikanto1, P. R¨ais¨anen3, M. Boy1,N. Richards4, A. Rap4, S. Smolander1, A. Sogachev5, A. Guenther6, G. W. Mann4,K. Carslaw4, and M. Kulmala1
-That previous GWP methane figures need x1.8 correction factor….
We should be using 20yr GWP methane of 130 or 180. This is 5.4 or 7.5 times the 24 GWP that Archer 2007 appears to be using?
So maybe the above should say, looking at a 20yr period(using the 100 becomes 180 gwp)?:
…..To get an idea of the scale, we note that a [100% increase/7.5= 13% increase] of methane from present-day concentration would be equivalent to 60 ppm increase in CO2 from present-day, and [10 times/7.5= 1.333times] present methane would be equivalent to about a doubling of CO2. A release of [500/7.5=66.7] Gton C as methane (order [10%/7.5=1.3%] of the hydrate reservoir) to the atmosphere would have an equivalent radiative impact to a factor of 10 increase in atmospheric CO2……
Aaron Franklin (102)
I wouldn’t go so far to say that the collective climate science community has completely moved on from the idea, but I’d argue that GWP is a rather outdated and fairly useless metric for comparing various greenhouse gases. It is also very sensitive to the timescale over which it is calculated.
It’s correct that an extra methane molecule is something like 25 times more influential than an extra CO2 molecule, although that ratio is primarily determined by the background atmospheric concentration of either gas, and GWP typically assumes that forcing is linear in emission pulse, which is not valid for very large perturbations. But because there’s not much methane to begin with, it’s not true that 1.33x methane has more impact than a doubling of CO2 (we’ve already increased methane by well over this amount)…a doubling of methane doesn’t even have nearly as much impact as a doubling of CO2.
The key point, however, is the much longer residence time of CO2 in the atmosphere…GWP tries to address this in its own mystical way, but there are much better ways of thinking about the issue. See the recent paper from Susan Solomon, Ray Pierrehumbert, and others.
Re: The Norwegian findings (#96-100), they’re still under review. Scroll down to “update”:
http://www.forskningsradet.no/en/Newsarticle/Global_warming_less_extreme_than_feared/1253983344535/p1177315753918?WT.ac=forside_nyhet
Clicking the Cicero link provided there takes you round trip — RealClimate is extensively referenced.