

Gavin Schmidt and Stefan Rahmstorf
John Tierney and Roger Pielke Jr. have recently discussed attempts to validate (or falsify) IPCC projections of global temperature change over the period 2000-2007. Others have attempted to show that last year’s numbers imply that ‘Global Warming has stopped’ or that it is ‘taking a break’ (Uli Kulke, Die Welt)). However, as most of our readers will realise, these comparisons are flawed since they basically compare long term climate change to short term weather variability.
This becomes immediately clear when looking at the following graph:
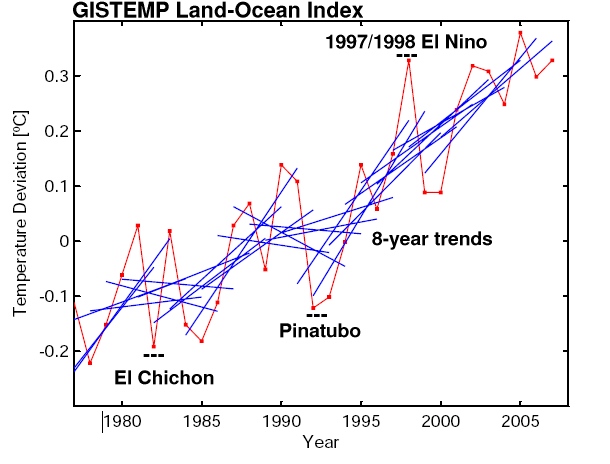
The red line is the annual global-mean GISTEMP temperature record (though any other data set would do just as well), while the blue lines are 8-year trend lines – one for each 8-year period of data in the graph. What it shows is exactly what anyone should expect: the trends over such short periods are variable; sometimes small, sometimes large, sometimes negative – depending on which year you start with. The mean of all the 8 year trends is close to the long term trend (0.19ºC/decade), but the standard deviation is almost as large (0.17ºC/decade), implying that a trend would have to be either >0.5ºC/decade or much more negative (< -0.2ºC/decade) for it to obviously fall outside the distribution. Thus comparing short trends has very little power to distinguish between alternate expectations.
So, it should be clear that short term comparisons are misguided, but the reasons why, and what should be done instead, are worth exploring.
The first point to make (and indeed the first point we always make) is that the climate system has enormous amounts of variability on day-to-day, month-to-month, year-to-year and decade-to-decade periods. Much of this variability (once you account for the diurnal cycle and the seasons) is apparently chaotic and unrelated to any external factor – it is the weather. Some aspects of weather are predictable – the location of mid-latitude storms a few days in advance, the progression of an El Niño event a few months in advance etc, but predictability quickly evaporates due to the extreme sensitivity of the weather to the unavoidable uncertainty in the initial conditions. So for most intents and purposes, the weather component can be thought of as random.
If you are interested in the forced component of the climate – and many people are – then you need to assess the size of an expected forced signal relative to the unforced weather ‘noise’. Without this, the significance of any observed change is impossible to determine. The signal to noise ratio is actually very sensitive to exactly what climate record (or ‘metric’) you are looking at, and so whether a signal can be clearly seen will vary enormously across different aspects of the climate.
An obvious example is looking at the temperature anomaly in a single temperature station. The standard deviation in New York City for a monthly mean anomaly is around 2.5ºC, for the annual mean it is around 0.6ºC, while for the global mean anomaly it is around 0.2ºC. So the longer the averaging time-period and the wider the spatial average, the smaller the weather noise and the greater chance to detect any particular signal.
In the real world, there are other sources of uncertainty which add to the ‘noise’ part of this discussion. First of all there is the uncertainty that any particular climate metric is actually representing what it claims to be. This can be due to sparse sampling or it can relate to the procedure by which the raw data is put together. It can either be random or systematic and there are a couple of good examples of this in the various surface or near-surface temperature records.
Sampling biases are easy to see in the difference between the GISTEMP surface temperature data product (which extrapolates over the Arctic region) and the HADCRUT3v product which assumes that Arctic temperature anomalies don’t extend past the land. These are both defendable choices, but when calculating global mean anomalies in a situation where the Arctic is warming up rapidly, there is an obvious offset between the two records (and indeed GISTEMP has been trending higher). However, the long term trends are very similar.
A more systematic bias is seen in the differences between the RSS and UAH versions of the MSU-LT (lower troposphere) satellite temperature record. Both groups are nominally trying to estimate the same thing from the same data, but because of assumptions and methods used in tying together the different satellites involved, there can be large differences in trends. Given that we only have two examples of this metric, the true systematic uncertainty is clearly larger than the simply the difference between them.
What we are really after is how to evaluate our understanding of what’s driving climate change as encapsulated in models of the climate system. Those models though can be as simple as an extrapolated trend, or as complex as a state-of-the-art GCM. Whatever the source of an estimate of what ‘should’ be happening, there are three issues that need to be addressed:
- Firstly, are the drivers changing as we expected? It’s all very well to predict that a pedestrian will likely be knocked over if they step into the path of a truck, but the prediction can only be validated if they actually step off the curb! In the climate case, we need to know how well we estimated forcings (greenhouse gases, volcanic effects, aerosols, solar etc.) in the projections.
- Secondly, what is the uncertainty in that prediction given a particular forcing? For instance, how often is our poor pedestrian saved because the truck manages to swerve out of the way? For temperature changes this is equivalent to the uncertainty in the long-term projected trends. This uncertainty depends on climate sensitivity, the length of time and the size of the unforced variability.
- Thirdly, we need to compare like with like and be careful about what questions are really being asked. This has become easier with the archive of model simulations for the 20th Century (but more about this in a future post).
It’s worthwhile expanding on the third point since it is often the one that trips people up. In model projections, it is now standard practice to do a number of different simulations that have different initial conditions in order to span the range of possible weather states. Any individual simulation will have the same forced climate change, but will have a different realisation of the unforced noise. By averaging over the runs, the noise (which is uncorrelated from one run to another) averages out, and what is left is an estimate of the forced signal and its uncertainty. This is somewhat analogous to the averaging of all the short trends in the figure above, and as there, you can often get a very good estimate of the forced change (or long term mean).
Problems can occur though if the estimate of the forced change is compared directly to the real trend in order to see if they are consistent. You need to remember that the real world consists of both a (potentially) forced trend but also a random weather component. This was an issue with the recent Douglass et al paper, where they claimed the observations were outside the mean model tropospheric trend and its uncertainty. They confused the uncertainty in how well we can estimate the forced signal (the mean of the all the models) with the distribution of trends+noise.
This might seem confusing, but an dice-throwing analogy might be useful. If you have a bunch of normal dice (‘models’) then the mean point value is 3.5 with a standard deviation of ~1.7. Thus, the mean over 100 throws will have a distribution of 3.5 +/- 0.17 which means you’ll get a pretty good estimate. To assess whether another dice is loaded it is not enough to just compare one throw of that dice. For instance, if you threw a 5, that is significantly outside the expected value derived from the 100 previous throws, but it is clearly within the expected distribution.
Bringing it back to climate models, there can be strong agreement that 0.2ºC/dec is the expected value for the current forced trend, but comparing the actual trend simply to that number plus or minus the uncertainty in its value is incorrect. This is what is implicitly being done in the figure on Tierney’s post.
If that isn’t the right way to do it, what is a better way? Well, if you start to take longer trends, then the uncertainty in the trend estimate approaches the uncertainty in the expected trend, at which point it becomes meaningful to compare them since the ‘weather’ component has been averaged out. In the global surface temperature record, that happens for trends longer than about 15 years, but for smaller areas with higher noise levels (like Antarctica), the time period can be many decades.
Are people going back to the earliest projections and assessing how good they are? Yes. We’ve done so here for Hansen’s 1988 projections, Stefan and colleagues did it for CO2, temperature and sea level projections from IPCC TAR (Rahmstorf et al, 2007), and IPCC themselves did so in Fig 1.1 of AR4 Chapter 1. Each of these analyses show that the longer term temperature trends are indeed what is expected. Sea level rise, on the other hand, appears to be under-estimated by the models for reasons that are as yet unclear.
Finally, this subject appears to have been raised from the expectation that some short term weather event over the next few years will definitively prove that either anthropogenic global warming is a problem or it isn’t. As the above discussion should have made clear this is not the right question to ask. Instead, the question should be, are there analyses that will be made over the next few years that will improve the evaluation of climate models? There the answer is likely to be yes. There will be better estimates of long term trends in precipitation, cloudiness, winds, storm intensity, ice thickness, glacial retreat, ocean warming etc. We have expectations of what those trends should be, but in many cases the ‘noise’ is still too large for those metrics to be a useful constraint. As time goes on, the noise in ever-longer trends diminishes, and what gets revealed then will determine how well we understand what’s happening.
Update: We are pleased to see such large interest in our post. Several readers asked for additional graphs. Here they are:
– UK Met Office data (instead of GISS data) with 8-year trend lines
– GISS data with 7-year trend lines (instead of 8-year).
– GISS data with 15-year trend lines
These graphs illustrate that the 8-year trends in the UK Met Office data are of course just as noisy as in the GISS data; that 7-year trend lines are of course even noisier than 8-year trend lines; and that things start to stabilise (trends getting statistically robust) when 15-year averaging is used. This illustrates the key point we were trying to make: looking at only 8 years of data is looking primarily at the “noise” of interannual variability rather than at the forced long-term trend. This makes as much sense as analysing the temperature observations from 10-17 April to check whether it really gets warmer during spring.
And here is an update of the comparison of global temperature data with the IPCC TAR projections (Rahmstorf et al., Science 2007) with the 2007 values added in (for caption see that paper). With both data sets the observed long-term trends are still running in the upper half of the range that IPCC projected.
The response in #367 (raypierre) doesn’t jive with climate station data in the Midwest and West. Another station plot (1897-2007, link below) shows Benton Harbor, MI annual mean temperatures in 1931 was very warm in 1931 (still the warmest on record for that station). Other stations, in rural and forested areas, were also hot in 1931.
http://picasaweb.google.com/npatnew/TemperaturesAtUSClimateStations
501
There is nothing wrong withwhat he said…the earlier warming, say, 1900-40 was caused by anthropogenic, solar, internal, lack of volcanic…interrupted mainly be aerosols, and everything since then is mainly us. Also, I’m not sure what you’re trying to get from a single weather station, but it probably won’t work for any discussion on global warming.
473 Nick Gotts> That is rather a tasteless offer: if Alastair accepts it, he puts himself in the position of standing to win money through an increase in the number of people dying of hunger.
You are correct; I should have added the usual terms for these bets: The winnings go to a charity of the winners choice. In this case a famine prevention charity should be specified.
483 Alastair McDonald> If I am correct there is a strong possibility of social disorder. In that case it is unlikely that I would be able to collect my bet. Would you really hand over $1000 dollars to me rather than use it to by food for your wife and kids?
There are betting brokers that will hold the stakes in low risk investments. Are there any other objections? $1000 is OK with me (with the proceeds going to a famine charity).
Re #439 Alastair: what you are saying is correct, but IMHO irrelevant. Indeed partial pressure ratios are the same as molar or ppm-by-volume ratios — but when computing weights, you must take molecular masses into account as Barton does.
From what I see he does his calculations right and comes up with two correct answers. Only, them being different is counter-intuitive.
#492 Timothy,
So #485 Buckner’s lag is caused by ocean convection. And #463 ocean upwelling can be a major source of heat loss. Two questions:
1. What is the characteristic time-scale of this heat flux? Shorter or longer than, say, the solar cycle?
2. You say ocean heating leads to H2O vapor, a (+) feedback GHG. Does it also not generate clouds, a (-) feedback? How much of each? Do you have a reference handy?
Thanks.
Re # 467 Joseph Sullivan
I’m curious about your comment that “the socratic method is the normal method in that arena [ meaning Law School]”
I have no doubt that some law professors do use the Socratic method, but there is a common misperception about this teaching method in law school based on John Houseman’s character, Professor Kingsfield, in the 1973 movie, Paper Chase (http://news-service.stanford.edu/pr/03/socratic528.html). I hope this movie is not the source of your comment.
I’m also curious about your assertion that the socratic method “will be misunderstood by people, like scientists, who have been trained in a completely different way.”
That is just not true. While most science and engineering courses dwell on factual knowledge, not all do – some aim to get students to think more clearly about scientific issues. And the Socratic method of discourse can be quite useful in forcing science students to think clearly (http://news-service.stanford.edu/pr/03/socratic528.html; http://humbugonline.blogspot.com/2005/01/socratic-method.html). In fact, I had an undergraduate biology professor who taught that way, and years ago the journal American Scientist published a very clever essay that made use of Socratic dialog to examine the logic of hypotheses for the evolution of larger brains in primates feeding on fruits in trees (sorry, but I can’t locate the reference at this moment).
random question
what is the real emissivity of the Earth, I’ve seen 0.769 here, 0.95, 0.615…and don’t you need to compute that when doing radiation calculations like (sigma)T^4 * (0.95) = OLR. That goes from 240 W/m2 to 227, but I never see that done. Why all these values, and where do you actually compute that?
In # 40 Gavin said “The variance of weather is larger than the seasonal warming from 10-17 April. Do exactly the same exercise for a two-month period rather than 8 days, and it will make sense”
That makes total sense, so I ask Gavin or anyone who can answer or point me where I can find the answer to this question: Would not the Earth’s precession and it’s variable orbit around the sun have a significant influence on our climate, since they are the primary factors behind theories related to the ice ages? Geologist point to earth surface features which demonstrate, for example, the Atlantic Ocean was 400’feet higher than present during peak melting and coastal shoreline were 50 miles farther east during peak ice.
Thank you – Dan
[Response: Yes. Search on Milankovitch forcing – this is the primary driver of climate variability in the 10,000 to 400,000 year range. – gavin]
#506 Chuck Ooth*
I have not seen Paper Chase. I am basing my assertion on my own experience when I was a student in law school and when I was a biology major as an undergraduate.
What I had in mind was the standard practice in law school where a student takes a position and the professor will bring up arguments to counter the student’s position, and the student will in turn defend his position. The professor’s arguments at times have no validity, but the process develops the student’s legal reasoning and rhetoric skills.
Knowingly advancing an incorrect position in a public debate would not be acceptable to the scientific community. A lawyer may push a legal theory in court that he considers incorrect if it would help his client, and as long he followed the code of ethics that behavior would be acceptable in the legal community.
The excellent Ziman(2000) paper that Raypierre links on The debate is just beginning – on the Cretaceous post explains what I mean in more detail.
*If I’m Joseph Sullivan, then you’re Chuck Ooth. ;)
#486
huh? I have no idea what the Hadley Centre says about arctic warming (searching for “Arctic” on their site yields something about increased river flows into the arctic but by all means let me know if you find some categoric statement that they think it is or isn’t warming).
The point of their response was the methodology of their approach, which they contrast with GISS. Hadley says that GISS has a very small amount of data which they interpolate from. Hadley meanwhile says “we don’t know” and adjusts its error bars accordingly.
[edit]
[Response: The random error bars on both are around 0.1 deg C in any one year – smaller than the difference the treatment of Arctic points make. However, GISS shows a graph of what happens if you leave out the very highest latitudes so you can see for yourself that this is not a ‘random’ issue. As the Arctic warms faster than the rest of the globe, there is a systematic bias that occurs if you assume that it is simply unknown. It’s good that different groups adopt different strategies in this case, because that demonstrates the importance more clearly. – gavin]
Inquirer, cloud fomation is a bit complicated. Yes, one might expect more cloud for higher H2O vapor content, but if the upper troposphere warms substantially, you might not get more clouds. And if you do, keep in mind that clouds have both a cooling effect (keeping sunlight out) and a warming effect (keeping IR in, especially at night).
RayPierre’s comment on the 3 degree issue is unarguable, (466) as is Hanks (454). They are saying that whatever caused past changes in the energy balance of the planet, the resulting temperature changes will appear much later.
We have no way of quantifying the effects of the delays, so over short current timescales (hundreds of years?, more?) it is impossible to attribute any particular change in temperature (the emergence from the little ice age, the fall from the forties to the seventies, the medieval warm period) to any particular cause.
The problem, however, is that politicians and journalists do just that – the increase in concentration of one of the lesser greenhouse gases. A is happening, B is happening, so A must be causing B.
Scientists should not make that mistake, and should attempt to support the theory with validated laboratory experiments, carefully measuring the saturation effect, for example, and its range of application. We should not attempt to explain Angstrom away (What Angstrom did not Know, here) – if we do not accept his results we should repeat and extend his experiment.
Otherwise we have only the temperature measurenents (themselves very uncertain, and subject to debate) to validate the model theory.
I used RayPierre’s logn law data in my first comment on 3 degrees (451). If we are half way to the effect of doubling the CO2 concentration, and if the initial rise from the 19th century to 1940 (about 0.4 degrees) had nothing to do with CO2, (the concentration seems to have increased from 280 to 300 ppm) we can expect less than half a degree increase from the forties to the end of this century.
Arrhenius was expecting 6 degrees from doubling CO2. Would it have been a good idea to have taken him seriously, and cancelled the Western industrial revolution?
Are we sufficiently certain to ask China and India to take that view today? More to the point, will they be sufficiently certain to agree?
[Response: Staple’s whole line off argument is completely invalidated by the fact that all GCM’s make use of the very same physics that gives you the logarithmic law for radiative forcing, yet they can give a great deal of additional warming — even up to Arrhenius’ value in some cases — when run out to 2100. You don’t have to believe the GCM’s have everything “right” to get my point. The point is that these models show that the same physics Staples is arguing on the basis of undeniably is compatible with several degrees C of additional warming in the future.
As to Arrhenius, if people had paid him more attention it wouldn’t have cancelled the industrial revolution. It would only mean we would not have put so much reliance on fossil fuels. We’d be fifty or more years ahead of the game on engineering for a more renewable based economy. To be fair, the moment when it became clear there was a problem was much later in the 1950’s when Revelle and Suess developed the ocean chemistry showing that CO2 really could be increased by fossil fuel burning. On the other hand, the carbonate chemistry used by R&S is standard high-school stuff, and there’s a good chance it would have been discovered much earlier if people had paid more attention to Arrhenius, and if Ångström hadn’t set back the field by a highly publicized but botched experiment. –raypierre]
Question for whomever, from Timothy, and #505 which says, “…2. You say ocean heating leads to H2O vapor, a (+) feedback GHG. Does it also not generate clouds, a (-) feedback? How much of each? Do you have a reference handy?…”
I don’t hear anything about the larger cooling effect on the ocean (surface) stemming from increased evaporation via increased ocean temps. Is this all assumed in the current discussion, or/and what is its impact?
Well Chris,
Your reply in 502 about “single weather stations” ignored what I said in 501 and 399 that many other stations in rural and forested areas in both 1931 and 1921 were part the 1920s-1940s global warm period.
U.S. and global hydrologic and meteorological data from 1880-2007 show no significant global cooling from the 1950s-mid 1970. Instead, there were two warm periods: 1. 1920-1940s and 2. late 1970s – current, which were sandwiched between an “apparent cool dip” from the 1950s-1970s.
The “apparent cool dip” was actually just getting back closer to the normal trend which had been occurring in the late 1800s and early 1900s. The 1950s-1970s “apparent cool dip” was influenced by the dominance of La Nina rather than by El Nino (which dominated the mid 1930s-1940s period).
It’s wrong to tell the public that a reduction in aerosols is the culprit behind the 1950s-1970s “apparent cool dip”. Many scientists have done that and are now refusing to admit the mistake. As a result, public confidence in interpretations by many climate scientists continues to be low on many subjects – a big problem. Public confidence would improve if more scientists speak honestly about what they see happening, including those scientists who work in weather prediction.
Greg posts:
[[what is the real emissivity of the Earth, I’ve seen 0.769 here, 0.95, 0.615…and don’t you need to compute that when doing radiation calculations like (sigma)T^4 * (0.95) = OLR. That goes from 240 W/m2 to 227, but I never see that done. Why all these values, and where do you actually compute that?]]
0.95 is the emissivity of the Earth’s surface, 0.615 is the emissivity of the Earth-atmosphere system as seen from space. The 0.769 figure is from treating the atmosphere as a single slab and asking what fraction of energy from the ground would need to be absorbed to reach the correct surface temperature.
Re #512 (Fred Staples) “Arrhenius was expecting 6 degrees from doubling CO2. Would it have been a good idea to have taken him seriously, and cancelled the Western industrial revolution?”
It’s too early to say :-).
Fred Staples embraces mysticism:
“We have no way of quantifying the effects of the delays, so over short current timescales (hundreds of years?, more?) it is impossible to attribute any particular change in temperature (the emergence from the little ice age, the fall from the forties to the seventies, the medieval warm period) to any particular cause.”
Fred, now come on. Fess up. Did you really have a straight face as you were typing this? Your contention completely ignores the fact that we have physics to help us out. The fact that we don’t know everything does not invalidate the fact that there are some things we do know.
And I refuse to embrace the false assumption that anyone who is persuaded by the science and evidence of climate change must want to “cancel the industrial revolution”. Are fossil fuels the only source of energy? Do we really need a market place where imported tropical fruits are cheaper than locally grown produce?
Sorry, Fred, this is a weak effort.
Re #516 (Nick Gotts) [Re #512 (Fred Staples) “Arrhenius was expecting 6 degrees from doubling CO2. Would it have been a good idea to have taken him seriously, and cancelled the Western industrial revolution?”
It’s too early to say :-).]
To expand a little, the only way we can try to answer this question is by constructing one or more counterfactual scenarios, and comparing them with the world as it is. So, let’s suppose there had been much less fossil fuel readily available, or some religious taboo had prevented its use. Significant use of fossil fuels actually came quite late in the “Western industrial revolution”, which has medieval roots, and is just the latest stage of a much broader, more or less global acceleration of technological innovation, which has lasted many millennia. By 1600, before any significant fossil fuel use, many key prerequisites of the Western industrial revolution had been borrowed from other parts of the world (e.g. paper, clear glass, steel, magnetic compass, gunpowder, “Arabic” numerals), others were invented in Europe before 1600 (e.g., ocean-going ships, guns, moveable-type printing, clockwork, spectacles, telescopes, perspective drawing). Accessible fossil fuel “supercharged” European technical innovation (and the Great European Land Grab it made possible), but there is no reason to think that technical development would have stalled altogether without it, since the acceleration of innovation, and its spread around the world, go back so far. It seems possible people might have done less damage to each other and the environment in a slower industrialisation process, but by no means certain: our doppelgangers in such a possible world might well find a way to screw things up without using fossil fuels!
It would be interesting to think about a planet where a lot of fossil fuel was not readily available. If people there developed an advanced technology, presumably they would start out burning wood, and later perhaps refine methanol from it. Cars and factories would still be possible. They might make more use of wind and solar power. There’s no reason to think they couldn’t figure out nuclear fission, or eventually, fusion. (Assuming the latter can, in fact, be figured out, something I’m increasingly dubious about.)
Sadly, Raypierre, I have not made my point clear.
I am not saying that the logn law is unarguable. Applied to current temperature changes and concentrations it may prove accurate; equally, it may not if the temperature effects are delayed.
What we cannot do is validate the GCM’s by appealing to the GCM results for temperatures changes 100 years from today.
It is the degree of certainty claimed for the GCM models that I object to, not the GCM theory itself.
Take, for example, Steve Sherwood’s contribution on the issue of troposphere temperatures versus surface temperatures
“The non-warming troposphere has been a thorn in the side of climate detection and attribution efforts to date. Some have used it to question the surface record (though that argument has won few adherents within the climate community), while others have used it to deny an anthropogenic role in surface warming (an illogical argument since the atmosphere should follow no matter what causes the surface to warm)”
He seems to put the issue fairly, except that his parentheses are irrelevant. He should have concluded that, on the measurement evidence, the troposphere warming is not sufficient to support the AGW theory, and if the theory is correct the surface temperature increase looks to be exaggerated.
And on the mysticism point, Ray, (517) I am inviting you to go back 100 years, look at the energy sources available then, and take a view.
[Response: You are misinterpreting Steve’s quote. It has to be read in the context of the subject he was working on. He is referring to problems with the data itself, and the nature of the difficulties in getting good tropospheric temperature trends, particularly in the tropics. It’s still hard to do, but the best estimates now are that the troposphere is indeed warming along with the surface. With regard to the GCM’s, what I’m saying is that your physical argument is utterly bogus, since if it were correct it would apply to the GCM’s as well, and they don’t show the behavior you infer. –raypierre]
Fred, that’s precisely the problem–you keep insisting on going back 100 years. And your point is irrelevant, as by 1950, nuclear power was an option, and most of the CO2 emissions post-date this era. Moreover, to expect that human innovation would have stagnated is not reasonable.
Not only is your understanding of climate models severely outdated, so is your understanding of the data. The discrepancy between theory and measured tropospheric warming is now within reasonable error bars.
An Inquirer (#505) wrote:
It might be better to phrase this a little more exactly. Ocean upwelling can be a major source of heat loss from the surface. However, the heat still exists. It has simply been redistributed to greater depths.
*
An Inquirer (#505) wrote:
There shouldn’t be any one characteristic time-scale involved. This is a large part of the reason why today’s climate models will divide the ocean into 40 levels rather than the 20 they might have made due with in the 1990s or used two slabs (one on top of the other) instead of one — which is what would seem to be implied when speaking of just one “characteristic time-scale” in accordance with which heat is exchanged between the two. Indeed, with thermohaline circulation, the cycle itself is such that individual molecules take on the average 3500 years to complete. However, this isn’t relevant for our purposes.
Thermal inertia and ocean circulation imply that the “full response” takes time, they imply a form of “latent heating,” but the strongest response is immediate. Neglecting natural variability due to various climate oscillations, temperature change is to a first approximation proportional to the rate in change of the forcing at the time of the change in the total forcing and diminishes after that.
Thus if solar irradiation rises rapidly to say 1950 but then goes flat, the strongest response should be while it is rising or just after it has risen. What one should not expect is for the response to be small, but then pick up with temperatures acceralating nearly 30 years later in 1979. Likewise, when the world economy recovered at the end of World War II, sulfates and forcing due to sulfates greatly increased, leading to a period of global cooling that began immediately. The initial effects weren’t delayed for several years or several decades — although the full effects certainly would be.
*
An Inquirer (#505) wrote:
Increasing the temperature is leading to increased water vapor, or alternatively, increasing absolute humidity.
For one study that looks specifically into this and its attribution to anthropogenic greenhouse gases, please see:
Santer et al., Identification of human-induced changes in atmospheric moisture content, PNAS, 25 Sept 2007, vol. 104, no. 39, pp 15248-15253
http://www.pnas.org/cgi/content/short/104/39/15248
However, water vapor feedback is expected to and appears to leave relative humidity roughly constant.
Please see:
Some of those who have argued for a lower climate sensitivity have argued that relative humidity would actually decrease due to increased precipitation. But we aren’t seeing this either in the models or empirical studies.
*
An Inquirer (#505) wrote:
Global warming could result in increased or reduced cloud cover. It will largely depend upon the temperature profile of the atmosphere. Moreover, clouds have both a greenhouse effect in which they trap thermal radiation and an albedo effect in which they reflect sunlight. These nearly cancel, and the net effect for a given layer of clouds is dependent upon cloud height, thickness — among other things. At night, for example, clouds tend to keep in thermal radiation but their albedo effect is of little use.
In fact, people like Lindzen have claimed that global warming would result in fewer clouds — with the skies opening up to let out additional thermal radiation, acting as a negative feedback that would dampen global warming.
Now at most latitudes, the models have done well at projecting trends in cloud cover. However, we have seen cloud cover decrease over the past fifteen years in the tropics which is not predicted some models. Whether this is due to diminished aerosol load, global warming or natural variability (e.g., ENSO) is still an open question inasmuch as the trend has been relatively short.
But the net effect at the top of the atmosphere has been a reduction in reflected sunlight which almost exactly matches the increase in outgoing longwave radiation, implying no net warming or cooling as the result of diminished cloud cover, and over the same period, the temperature of the tropics has continued to rise.
Please see:
As such decreasing cloud cover in that region has no net effect upon the trend in global warming.
*
Of course what you appear to be interested in is climate sensitivity. One way of cutting through what uncertainty exists with respect to some of the feedbacks is to see what the climate system has done in the past.
Bringing together the results of over 40 different paleoclimate studies of periods over the past 420,000 years, the following paper…
Royer DL, Berner RA, Park J. (2007), Climate sensitivity constrained by CO2 concentrations over the past 420 million years. Nature, 446: 530-532.
… arrived at a fairly consistent best fit for a climate sensitivity of roughly 2.8 C/doubling of carbon dioxide. However, there is still a fair range of uncertainty associated with this, but given the statistical analysis performed, it is more likely that 2.8 C significantly underestimates the actual climate sensitivity than overestimates it.
Rre 509 Joseph [O]Sullivan
Sorry for misspelling your name – I had it correct in my original comment, which disappeared when I hit [Post] and I couldn’t retrieve it, so I had to retype it in a hurry. And I apologize for questioning your familiarity with the Socratic Method in law school..you might enjoy Paper Chase, by the way.
I agree that knowingly advancing a false position in a public debate would not be acceptable to the scientific community, but I see nothing wrong with doing so in a science class in order to help students see the flaws in their logic. My point is still that many scientists are quite familiar with the Socratic method – they may have studied Greek philosophy, they may have taken courses from professors who use the Socratic method (apparently, you missed that as an undergraduate, which is unfortunate), and they may use it themselves in the classroom. And many scientists, biologists especially, are very familiar with the conscious advancement of false propositions as a rhetorical trick – that’s how creationists and ID proponents frequently argue their cause. ’nuff said.
Gracias por la traduccion en espaniol – it is extremely useful when trying to explain to my Spanish speaking colleagues and family members.
469:
The “reduction…1980 to 2000” is basically IPCC assessment spin. Here is a quote from the section:
“The most recent study (Stern, 2005) suggests a decrease in global anthropogenic emissions from approximately 73 to 54 TgS yr–1 over the period 1980 to 2000,…”
But if you go to Stern, 2005, the emissions as late as 1991 are about 72 TgS yr-1. So it’s not like Stern, 2005 is saying that emissions peaked circa 1980, and declined steadily thereafter.
So once again, we’re left with the question of why surface temperatures started rising in the mid-1970s, even though sulfur dioxide emissions did not decline.
Nick (518), an added tidbit: Ford’s (at least) early cars were built to run on ethanol because gasoline was still very new and costly.
Can Declining Sulfur Emissions Explain the Timing of the Modern Era of Global Warming?
Mark Bahner (#525) wrote:
Well, I couldn’t find a copy of Stern 2005, but I found:
David I Stern, Reversal of the trend in global anthropogenic sulfur emissions, Global Environmental Change 16 (2006) 207–220
http://web.archive.org/web/20070101084353/http://www.rpi.edu/~sternd/GEC2006.pdf
…. which I presume is almost as good.
*
Looking at world emissions, I see a very steep climb until some time in the mid 1960s at which point the sulfur emissions continue to rise, but not anywhere as steeply. Then I see the emissions barely rise from 1978-1979, fall during early 1980s, rise again for perhaps four years, fall a little, then fall precipitously. That’s from figure 1.
Another good graph is figure 4, “Northern and southern hemisphere emissions 1850–2000.” It breaks things out according to hemisphere. According to this graph, sulfur emissions in the Northern hemisphere had pretty much leveled off a little before 1975 and was faultering shortly afterward. Both North America and Western Europe were declining at least since about 1975.
*
Mark Bahner (#525) wrote:
I can think of at least two reasons. First, its not like sulfur emissions are the only forcing in the climate system. Second, they don’t get evenly distributed, either.
Carbon dioxide is still growing, so even if sulfur emissions remained flat, we would see temperatures begin to rise. But more importantly, it really matters where the sulfur is being emitted. If sulfur emissions are dropping in the Northern Hemisphere but rising in the Southern Hemisphere, the Northern Hemisphere will tend to matter more because that is where there is more land mass. Land has less thermal inertia than ocean, and therefore with a given forcing, land temperature will change more rapidly than ocean.
Sulfates don’t stay put, but get carried by the wind. However, they will get carried only so far.
Please see:
On average, they will travel 1600 km before being cut in half. As such, wind circulation matters a great deal…
Please see:
NASA Scientists Use Satellites to Distinguish Human Pollution from Other Atmospheric Particles
NASA’S Earth Observatory, RELEASE NO: 02-137
September 17, 2002
http://earthobservatory.nasa.gov/Newsroom/Aerosols/
As such, even within the Northern Hemisphere, sulfates will be more effective at arresting the rise in temperature in some places more than others.
If they are emitted too far north, we will have white on white with ice and snow below and no net effect upon the albedo. And even then, in the far north, a small carbon content will of a little more than 5% will tend to result in a change in the sign of the forcing.
If they are too far south, they will tend to pass over less land and more water, or perhaps even drift into the Southern Hemisphere. If they are emitted along west coasts, they will tend to drift over land, but when emitted along the east coasts they will drift over water.
*
Looking at Stern 2006 figure 4, “Regional trends in sulfur emissions in the 1980s and 1990s,” North America and Western Europe were beginning to reduce their emissions around 1970-5. Eastern Europe had nearly leveled off by the late 1970s and faultered in the early 1980s, with some recovery in the late 1980s. In the Northern Hemisphere, the only continent that experience continuous strong growth was Asia until the mid to late 1980s — further to the south with the Pacific Ocean to the West.
Not simply the sign matters, but the actual magnitude of the change in emissions. But the magnitude isn’t enough, either. You have to know where it is distributed in order to be able to estimate the effect. Emissions in the Northern Hemisphere leveled off and dropped before global emissions. Emissions in the mid-latitudes of the Northern Hemisphere (principally North America and Western Europe) dropped before the rest of the Northern Hemisphere between 1970 and 1975. Emissions to the north of the mid-latitudes will be more be more susceptible to carbon content due to more ice and snow, and emissions to the south of the mid-latitudes will have a greater tendency to be blown out over open water where they will have less of an effect upon global average temperature, particularly along the east coasts of Asia.
Given the graphs in Stern 2006, the fact that the modern era of global warming began in 1979 doesn’t present much of a mystery, at least from what I am able to gather. Judging from what I looked at above, any time after 1975 wouldn’t be problematic. And my focus was principally upon sulfates — without regard for the changes to the other forcings, or for that matter climate oscillations like ENSO or the Atlantic Oscillation.
Mark Bahner writes:
[[So once again, we’re left with the question of why surface temperatures started rising in the mid-1970s, even though sulfur dioxide emissions did not decline.]]
Because CO2 was high enough then to have a larger effect.
@ Chuck Booth 523
There’s a big difference between knowingly advancing a false position for the purpose of helping someone learn to think more clearly by finding the flaws in your argument, and knowingly advancing a false position for the purpose of actually convincing others of that false position. I for one am idealistic enough to think that the latter should be shunned in any forum, be that publications in journals, discussion on blogs, or courtroom trails. There are clearly a few people who believe otherwise…but they’ll never identify themselves as such. We can only recognize them by realizing that they’re taking an unsupported position when they really ought to know better.
It’s tough for us lay people to sort out, though. I’m a smart guy–I even think I could learn some of the relevant math and physics if I had the time and strong enough motivation–but often when the equations start flying in a post I skim down to summary/conclusion statements to try and get the gist. I can’t, or at least am very unlikely to, check all the work for myself. I think it’s safe to say most other people won’t, either. So here’s what I do. I think of the hierarchy of evidence I learned in college: true experiment>correlational study>case study>anecdote>expert opinion>personal opinion. Lab experiments verify the properties of CO2 that lead to it functioning as a greenhouse gas, as well as a lot of (all?) the other physics in the models. The balance of experimental and correlational research leads to a pretty coherant picture of what’s going on, summarized by the IPCC. There are margins of error around all the terms, but things are constrained enough to make it seem profoundly unlikely that some new finding will fundamentally disrupt the big picture. People regularly tell stories about being able to grow certain plants in zones where they formerly wouldn’t grow, spring coming earlier, winters being milder, etc. News reports about changes in the Arctic are frequent, I’ll also count that as anecdote. You can find “professional” opinion going either way, but when bodies of scientists have issued official positions, it has AFAIK always been to endorse the IPCC synthesis. The only place where I encounter as much support for the position that the current warming isn’t anthropogenic (or has stopped, or whatever) is at the lowest tier of evidence: personal opinion. However, there are several very vocal “experts” of the non-anthropogenic position, so I’ll grant that there is some debate at the lowest two tiers of evidence.
But my impression is that many if not most people put expert opinion much higher in the hierarchy, and then weight expert opinions differentially according to how closely the various experts match their own preexisting beliefs. So in effect, the determining factor in how many laypeople evaluate the evidence is…how well it accords with what they already believe, or want to.
Here’s where I’m going with all this–the professional and amateur climate scientists here, and at Tamino’s place, and Eli’s, etc. often recommend that we laypersons educate ourselves about climate physics so we can grasp the significance of the evidence. I agree. But given that we know, or at least strongly suspect, that for most people that will never happen, I recommend that the climate folks also educate themselves about another professional field: social psychology, particularly persuasion and attitude change. I think it’s important. And I think those who have set themselves up as your idealogical opponents are ahead of you on this. I’m not suggesting that you use any of the “dirty tricks” of marketing that the other side is already using–going over to the dark side would ruin your credibility with us idealistic people. But I really, really do think you should get more savvy about the social psychology of attitude change.
I have tried on several previous occasions to thank Ray, Hank, Rod B and Chris for taking the trouble to reply to my previous posts (#443 and #477). Unfortunately they all disappeared when I clicked the post command. I hope I’ll be more fortunate this time.
I think I now know the following:
1) There is no current satellite orbiting in space capable of measuring changing brightness temperature in the 15 micron CO2 absorption band. (Needs yet-to-be-launched DISCOVR, re Ray)
2) A photon cannot be emitted from a CO2 molecule that is itself incapable of being absorbed by a second CO2 molcule.
3) SO2, as a gas, absorbs in the UV range but, in fact, acts as an aerosol (in droplet form) in the atmosphere and reflects solar energy but absorbs and emits nothing.
4) The atmosphere is currently saturated in the 13.5 – 17 micron part of the CO2 absorption band. If I interpret Ray Pierrehumbert correctly (his M and M candy analogy and his CO2 columns),no free photons in the 13.5-17 range can pass through the level of saturation to the high dry atmosphere.
5) I had assumed, therefore , that all radiation in this upper part of the atmosphere must have been created in situ by non radiative convected energy reacting with CO2. I think Ray Ladbury suggested, to the extent that I understood him correctly, that they could also be transported to this region by covection while in the grip of excited CO2 molecules. (Not sure of the relative time scales of energy transmission by convection and radiation in a ghg containing atmosphere).
I would still like to know how energy reaching the high dry atmosphere could get back to the surface if there were an underlying layer of saturation which would presumably block access to downwelling radiation in exactly the same way as upwelling radiation from the surface is blocked. Can you have reverse convection? I thought that heat energy rose.
What is meant by top of atmosphere? I am shrewd enough to appreciate that it is not a cellophane wrapper that divides atmosphere from space (but not that much more shrewd). Why doesn’t the atmosphere just keep expanding as extra energy is uplifted and ultimately dissipated by molecular separation by pressure drop?
Can someone please discuss saturation with respect to water vapour? One can only assume a positive feedback with water vapour in the absence of pre-existing saturation. (I know that it won’t be saturated over dry areas but models, I think, suggest that warming won’t increase water vapour over such areas.) To what extent will a CO2/water vapour combination in the CO2 wings cause saturation equivalent to that caused by CO2 alone in the centre of its absorption band?
Presumably, increasing ghgs will reduce the height from the ground at which saturation will occur. Why is it not more plausible to suppose that this trapping of energy nearer the surface will have more warming effect than anything happening miles up in the atmosphere?
Thanks.
[Response: Sorry your previous posts disappeared. I have found that things sometimes (maybe always) disappear when entered into the comment box you get on the pop-up window, as opposed to comments accessed at the end of the article itself. Might be browser dependent. –raypierre]
[Re: # 528]
But NOAA CMDL data shows that CO2 has been increasing in a linear fashion since measurements began in the late 1950s.
http://www.esrl.noaa.gov/gmd/ccgg/trends/co2_data_mlo.html
Douglas Wise,
OK, we’re close. Sorry if what I wrote gave the impression that excited CO2 molecules transported via convection were a significant source of energy. Rather, it is thermal energy that is so transported. But thermal energy (e.g. molecular collisions) can excite CO2 in the upper atmosphere–both there and down in the lower troposphere.
WRT saturation, be careful. Yes, a photon in that wavelength range radiated from the surface probably would not escape. However, as more CO2 is added, you get more absorption in the wings of that absorption line. Look at it this way, the depth of the absorption spectrum can be viewed as measure of the probability that a single molecule of CO2 will absorb the photon in that range. As you move out into the wings, the probability of absorption by a single photon decreases a lot, but if you add enough CO2, you’re still likely to absorb the photon even out in the wings.
Likewise, as you move higher in the troposphere, temperature decreases, and the thermal energy (of order ~kT) is well under the energy needed to excite the vibrational mode of CO2. However, the molecules follow a Maxwell distribution~exp(-E/kT), so there will be some that are sufficiently energetic to knock a CO2 molecule into its excited state. It can emit an IR photon as it decays. In the absence of CO2 above, that photon would escape. Add more CO2 and it will most likely be trapped. It all comes down to probabilities, but add the probabilities together and you come up with a certainty–you trap more energy.
Energy transport to the surface from the upper troposphere can occur via convection (again, thermal energy) or backradiation. Yes, a CO2 photon will likely be absorbed on the way down, so maybe that heats the atmosphere. But a warmer atmosphere will have more thermally excited CO2 molecules, and so more IR photons, and so on. The main thing to realize is that if the energy doesn’t escape, it has to warm the climate. It may take several steps to do so, but if it doesn’t escape, those steps will happen.
Re: #529 (Kevin Stanley)
An excellent comment, and I agree. I would add that scientists need to recognize that we’re not always the most persuasive (or charismatic) public speakers.
Perhaps it would be a good idea to identify those individuals with exceptional charisma and persuasive speaking skills to carry the banner of public communication. This is especially important in debate; the “winner” (meaning, the one who is most persuasive) isn’t necessarily the one who is correct, or presents arguments most logically and correctly; all too often it’s the one the listeners like, and therefore want to believe.
I’m reminded of the 2004 vice-presidential debate between Dick Cheney and John Edwards. I’m no fan of Cheney (or Bush), and I was hoping for Edwards to “clean his clock.” But Cheney was better-prepared with logical (sometimes false, but logical) arguments and facts (sometimes distorted). I concluded, after watching the debate, that Cheney had won going away (much to my chagrin).
But poll results the following morning showed how wrong I was. The general public viewed Edwards as the winner by a nontrivial margin. I believe this is because Edwards is likeable and good-looking, while Cheney is neither. The “winning” of the debate had nothing to do with fact (distorted or not) or logic (false or not) — it had to do with charisma.
So, all you RC guys — who in the climate science community has the most charisma, and the most persuasive public-speaking skills? I want someone who looks like Brad Pitt and talks like JFK. Maybe we could persuade Johnny Depp to finish his Ph.D. and join the team?
Douglas Wise posts:
[[I would still like to know how energy reaching the high dry atmosphere could get back to the surface if there were an underlying layer of saturation which would presumably block access to downwelling radiation in exactly the same way as upwelling radiation from the surface is blocked.]]
If the upper levels are absorbing more radiation from lower levels, due to there being more CO2 in the said higher levels, they will warm up. And radiate. The radiation doesn’t have to get all the way to the ground. It just has to fall on the level under it, which then heats up a bit, and heats the level under that, etc. You can warm the ground a little bit even by warming the very topmost layer. Let me know if you want to see the math.
[[ Can you have reverse convection? I thought that heat energy rose.]]
Convective heat transfer does rise (though there is also such a thing as sideways “advection”). Radiation can travel in any direction, however.
>528, 531
Pat, the rate of increase hasn’t been linear, and your cited page doesn’t support that belief. See also
ftp://ftp.cmdl.noaa.gov/ccg/co2/trends/co2_gr_mlo.txt
Half the fossil fuel burned was burned up to about 1970; the second half through about 2000; we’re on the ‘third half’ now.
See also
http://www.globalwarmingart.com/images/5/52/Carbon_History_and_Flux_Rev.png
Re #532 Ray Ladbury
Quote
“Likewise, as you move higher in the troposphere, temperature decreases, and the thermal energy (of order ~kT) is well under the energy needed to excite the vibrational mode of CO2. However, the molecules follow a Maxwell distribution~exp(-E/kT), so there will be some that are sufficiently energetic to knock a CO2 molecule into its excited state. It can emit an IR photon as it decays. In the absence of CO2 above, that photon would escape. Add more CO2 and it will most likely be trapped. It all comes down to probabilities, but add the probabilities together and you come up with a certainty–you trap more energy.”
Unquote
Please will you explain what happens to the energy which is trapped?
Mr. Banner, the answer hasn’t changed from the many other times you’ve asked the same question — a greenhouse gas molecule in the atmosphere can transfer energy by collision to oxygen and nitrogen molecules.
Mr. Banner, c’mon, you’ve posted your disbelief — a detailed statement of the physics you don’t believe in — over at CA repeatedly. Most recently p=2572#comment-193276.
Belief isn’t something we can help with; physics, you need to either understand, or trust someone’s answer for. You won’t get a different answer by asking the same question over and over, seems to me.
Re #537 and #538 Hank Roberts
Mr Roberts, thank you for responding to my post #536, but I’m still hoping for a reply from Ray Ladbury. I get a sense that you do not like the message I’m trying to send. Yes, I did try to get it across before in a different thread, but the thread was unfortunately cut before I received a reply which I found convincing.
I have said already that although a sceptic about the enhanced GHG effect, nevertheless I am fully prepared to be convinced by a properly reasoned explanation based on physics. So it is not a case of “belief” as far as I am concerned, but what I have come to understand from my own consideration of the physics involved. I do, indeed, understand the physics and this is why I am not prepared to trust someone’s answer when it clearly is either wrong or, more likely, incomplete. Perhaps you, yourself, should consider whether you are simply “believing” something because you want to. If not, then I think it would be appropriate to give full consideration to an alternative, or additional, explanation based only on the physics.
It may be that there is some other factor which is crucial to the way the GHG effect works, but which has not been mentioned so far. In such a case, I should be very keen to learn about it.
With reference to your #537, I quote
“a greenhouse gas molecule in the atmosphere can transfer energy by collision to oxygen and nitrogen molecules.”
Unquote
Yes, this was the sort of reply I was expecting. So it is agreed that when the CO2 molecule which had absorbed a photon next decays by collision, its excited internal energy is transferred to the atmosphere. But this is where the energy came from in the first place! So nothing has changed. The temperature of the atmosphere has not been changed as a result of this process. It is just as if nothing had happened.
Re #539
“With reference to your #537, I quote
“a greenhouse gas molecule in the atmosphere can transfer energy by collision to oxygen and nitrogen molecules.”
Unquote
Yes, this was the sort of reply I was expecting. So it is agreed that when the CO2 molecule which had absorbed a photon next decays by collision, its excited internal energy is transferred to the atmosphere. But this is where the energy came from in the first place! So nothing has changed. The temperature of the atmosphere has not been changed as a result of this process. It is just as if nothing had happened.”
No, the photon originally emitted by the surface is then absorbed by a CO2 molecule which then transfers it to surrounding N2 & O2 molecules, approximately 8 kJ/mole of CO2 is thereby added to the atmosphere. However, any excess energy in N2 and O2 molecules can not be radiated into space, the only way this can occur is if sufficient energy can be collisionally transferred back to a CO2 (or other GHG) sufficiently high in the atmosphere so as to radiate into space. According to the Boltzmann distribution only about 1% of CO2 molecules will be in that state at the top of the troposphere.
AEBanner: So it is agreed that when the CO2 molecule which had absorbed a photon next decays by collision, its excited internal energy is transferred to the atmosphere. But this is where the energy came from in the first place! So nothing has changed. The temperature of the atmosphere has not been changed as a result of this process. It is just as if nothing had happened.
I think your focus is too narrow. You have just agreed that the absorption of a photon can heat a gas. Now step back and compare an atomsphere with no CO2 with our current atmosphere. The IR from the surface escapes directly to space; no effect on the atmosphere. But in our atmosphere, IR photons get captured and the energy heats the gas.
So how can CO2 not be heating our atmosphere?
Not all the IR came from the atmosphere.
AEBaner, well if energy is not escaping the system–and IR radiation is the only way it can escape–then it must go into heating the system. The primary mechanisms are via collisional relaxation and backradiation. The relative importance of these two mechanisms depends on density and temperature, of course and therefore on altitude.
You say: “Yes, this was the sort of reply I was expecting. So it is agreed that when the CO2 molecule which had absorbed a photon next decays by collision, its excited internal energy is transferred to the atmosphere. But this is where the energy came from in the first place! So nothing has changed. The temperature of the atmosphere has not been changed as a result of this process. It is just as if nothing had happened.”
I must say, this is a rather myopic view. If the CO2 molecule had not been present, what would have been the fate of the photon? Escape to space, no? So, something most certainly has happened. Energy that would have left the sysem is transformed to thermal energy, which cannot escape the system. Meanwhile, more shortwave radiation is coming from the sun. Energy in is roughly constant; energy out has decreased. And when that happens, what does the system do?
Also I must apologize to Douglas Wise. When I referred to convective heat transport, I was speaking rather liberally and including the thermal energy transported when the air descends to the ground again. If it is less cool because it has lost energy, it will cool the ground a bit less. My use of the term was a bit too loose, and Barton graciously corrected my loose language.
AEBanner, as a fellow skeptic maybe I can shed some light re #539. What you describe in the last paragraph is true if the CO2 molecule excited its vibration energy from a collision with another gas molecule (of any kind). That collision should lower atmospheric temperature. Then when the CO2 relaxes by another collision and passes the energy to another gas molecule, the temperature will go back to where it was.
But this does not cover the excitation of CO2 vibration energy with infrared radiation, which is the predominate way CO2 gets excited (vibrationally). This does provide a net heating of the atmosphere when the CO2 collides and loses that energy.
Though the question remains on the cooling of the earth surface as it radiates (which ought to be a little greater than the subsequent atmospheric heating) and how that gets mitigated/reversed with back radiation, which is just a little less than the outgoing surface radiation. This gets a little complicated, in my view, and I have questions about it. But this is different, I think, from what you are asking.
Re AEBanner @ 539: “So it is agreed that when the CO2 molecule which had absorbed a photon next decays by collision, its excited internal energy is transferred to the atmosphere. But this is where the energy came from in the first place! So nothing has changed. The temperature of the atmosphere has not been changed as a result of this process. It is just as if nothing had happened.”
Not quite nothing. What’s happened is that energy has been kept in the atmosphere rather than emitted to space. And since more energy is continuously being added to the atmosphere from the surface, the atmosphere must therefore warm. And it will continue to warm until the energy of the photons making it to space equals the energy being added to the atmosphere from the surface.
It’s not hard to understand. Really.
Mr. Banner, have you counted the various threads where you’re asking this same question? You won’t get a logical proof without math. E.g.
http://forum.physorg.com/index.php?showtopic=19006&st=45&# or
lofi.forum.physorg.com/global-warming_6077.html or
lofi.forum.physorg.com/Photon-At-High-Altitudes_19783.html or
http://www.climateaudit.org/?p=2560 or
http://www.climateaudit.org/?p=2572 or
http://www.theenvironmentsite.org/Forum/viewtopic.php?t=5367 or
http://www.theenvironmentsite.org/Forum/viewtopic.php?p=112349
That’s not a complete list, just a few among many.
You’re getting lots of attention but not enough help.
[Response: I think this subject and Mr Banner’s concerns have been more than adequately dealt with. No more on this please (that’s to everyone of course). – gavin ]
Hank, I understand that the rate increase in CO2 has not been linear. Thanks for clearly pointing that out.
My comment in 531 was in ref to 528 and 501. I was explaining that while surface temperatures began rising in the late 1970s (even though sulfur dioxide emissions did not decline) BPL was wrong in his explanaion (“Because CO2 was high enough then to have a larger effect.”). I was merely trying to say that there was no abrupt increase in CO2 in the mid-1970s to explain the abrupt increase in the rate of increase in global temperature in the late 1970s. I mistakenly used the words linear fashion in describing CO2 increase, which skepics have used erroneously many times in the past in describing the rate of CO2 increase.
pat n (#546) wrote:
Actually CO2 levels increased quite substantially during the 1970s relative to the previous decades. I believe the following chart will give you some idea as to how it compared to previous decades, as well as how well-correlated temperature has been with CO2 concentration since 1880.
Please see:
Global Average Temperature and Carbon Dioxide Concentrations, 1880-2006
http://www.whrc.org/resources/online_publications/warming_earth/images/Fig2-CO2-Temp.gif
… from:
Scientific Evidence
Increasing Temperatures & Greenhouse Gases: Woods Hole Research Center
http://www.whrc.org/resources/online_publications/warming_earth/scientific_evidence.htm
*
Of course numbers are better than charts and physical principles are better than mere correlations. We know as a matter of physics that due to CO2’s absorption spectra, forcing due to CO2 rises as the log of the concentration.
Going to:
Trends in Atmospheric Carbon Dioxide – Mauna Loa
NOAA Earth System Research Laboratory: Global Monitoring Division
http://www.esrl.noaa.gov/gmd/ccgg/trends/
… I was able to get the annual mean growth rate in carbon dioxide for 1959-2007, the CO2 concentration for 2003, calculate CO2 concentration for each year, then calculate the percent change in CO2-forcing from 1970 to 1980 as: 100*(Ln(CO2[1980]/280)/Ln(CO2[1970]/280)-1) where CO2[1980]=341.13 and CO2[1970]=328.54.
The result?
23.52%.
That one decade alone added nearly as much forcing due carbon dioxide as a quarter of all of the previous decades since the beginning of the industrial revolution.
Jim (544), you (among others) also ignore the cooling effect of radiation leaving the surface. Though maybe that just expands and confuses the question too much. Though I’m still curious.
Re Rod @ 548: “you (among others) also ignore the cooling effect of radiation leaving the surface.”
I don’t ignore it, Rod, but don’t forget that the surface is then rewarmed by solar insolation during the next daylight period. Energy continues to be added to the system.
Re #534. Barton Paul Levenson, in answering an earlier question of mine, states that you can warm the ground a little even by warming the very topmost layer of the atmosphere. He offers a math based explanation which, I regret, would almost certainly be beyond my ability to understand. I would, however, like to ask him a few supplementaries.
1)Given that we have ruled out “downward” convection, why doesn’t heat (energy) at the very topmost layer of the atmosphere just travel on up, thus causing atmospheric expansion. In other words, what constraints does the so-called top of the atmosphere represent.
2)Barton says that heat at the very top will cause a small degree of warming at the bottom(ground). Surely, the closer the source of heat to the surface, the greater the warming would be? If such is the case, wouldn’t the lowering of altitude of the “almost” saturated layer, occasioned by greenhouse gas increases, be a much more important source of surface temperature increase than anything happening at the top of the atmosphere?
I am sorry if I am being completely naive. I would also be very grateful if one of you out there could address the subject of radiative saturation with respect to water vapour in a manner similar to that which has been applied to CO2 in isolation.
[Response: Douglas,I appreciate your desire to attain a better degree of understanding of the finer details of how the greenhouse effect works, but you’re not going to get that by a dialog like this in the comments. If you just need the broad-brush explanation, ask yourself if you understand how adding insulation to your house allows you to maintain a higher temperature inside while burning the same amount of fuel in the furnace. If you understand that, you understand the greenhouse effect, since the greenhouse effect is just planetary insulation. The fact that the greenhouse effect works through its influence on radiative heat loss out the top of the atmosphere rather than convective heat loss from the outside of your house does not change the way the energy balance argument works. Now, the questions that you are asking about how CO2 affects infrared loss are answered at the broad-brush level in the “A Saturated Gassy Argument,” and if that’s not enough for you, there’s simply no alternative to actually learning the math and physics, at least to the level of Chapter 3 and 4 of my book (draft still available online). Water vapor radiative saturation is discussed in Chapter 4. Water vapor, unlike CO2, actually does come close to being radiatively saturated in the tropics near the ground (and becomes fully radiatively saturated around 310 or 320 K). I emphasize that because of the “thinning and cooling” argument even a gas that’s radiatively saturated through a considerable depth of the atmosphere gives you greenhouse warming. If Weart’s verbal discussion of this isn’t enough you just have to learn the greygas calculation or accept the authority of people that have. In the case of water vapor, an additional — and more important — factor is that water vapor concentration becomes low in the cold upper parts of the troposphere, because of Clausius Clapeyron. Generally speaking, I’m getting a little tired of these endlessly recurring drawn out exchanges about how the greenhouse effect works. Past a point, if the verbal explanations are unsatisfying, you just have to go read the textbooks or go take a course. –raypierre]