

Gavin Schmidt and Stefan Rahmstorf
John Tierney and Roger Pielke Jr. have recently discussed attempts to validate (or falsify) IPCC projections of global temperature change over the period 2000-2007. Others have attempted to show that last year’s numbers imply that ‘Global Warming has stopped’ or that it is ‘taking a break’ (Uli Kulke, Die Welt)). However, as most of our readers will realise, these comparisons are flawed since they basically compare long term climate change to short term weather variability.
This becomes immediately clear when looking at the following graph:
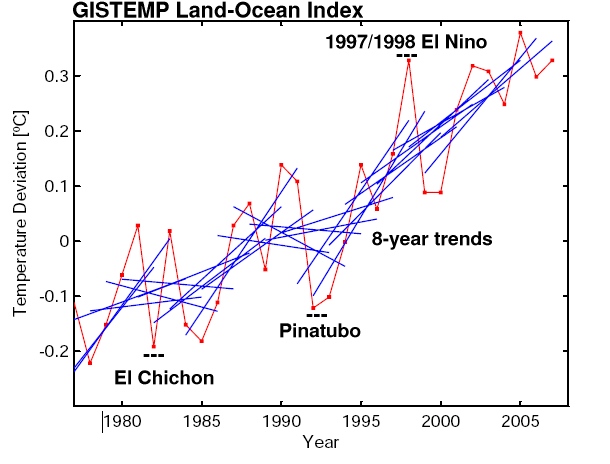
The red line is the annual global-mean GISTEMP temperature record (though any other data set would do just as well), while the blue lines are 8-year trend lines – one for each 8-year period of data in the graph. What it shows is exactly what anyone should expect: the trends over such short periods are variable; sometimes small, sometimes large, sometimes negative – depending on which year you start with. The mean of all the 8 year trends is close to the long term trend (0.19ºC/decade), but the standard deviation is almost as large (0.17ºC/decade), implying that a trend would have to be either >0.5ºC/decade or much more negative (< -0.2ºC/decade) for it to obviously fall outside the distribution. Thus comparing short trends has very little power to distinguish between alternate expectations.
So, it should be clear that short term comparisons are misguided, but the reasons why, and what should be done instead, are worth exploring.
The first point to make (and indeed the first point we always make) is that the climate system has enormous amounts of variability on day-to-day, month-to-month, year-to-year and decade-to-decade periods. Much of this variability (once you account for the diurnal cycle and the seasons) is apparently chaotic and unrelated to any external factor – it is the weather. Some aspects of weather are predictable – the location of mid-latitude storms a few days in advance, the progression of an El Niño event a few months in advance etc, but predictability quickly evaporates due to the extreme sensitivity of the weather to the unavoidable uncertainty in the initial conditions. So for most intents and purposes, the weather component can be thought of as random.
If you are interested in the forced component of the climate – and many people are – then you need to assess the size of an expected forced signal relative to the unforced weather ‘noise’. Without this, the significance of any observed change is impossible to determine. The signal to noise ratio is actually very sensitive to exactly what climate record (or ‘metric’) you are looking at, and so whether a signal can be clearly seen will vary enormously across different aspects of the climate.
An obvious example is looking at the temperature anomaly in a single temperature station. The standard deviation in New York City for a monthly mean anomaly is around 2.5ºC, for the annual mean it is around 0.6ºC, while for the global mean anomaly it is around 0.2ºC. So the longer the averaging time-period and the wider the spatial average, the smaller the weather noise and the greater chance to detect any particular signal.
In the real world, there are other sources of uncertainty which add to the ‘noise’ part of this discussion. First of all there is the uncertainty that any particular climate metric is actually representing what it claims to be. This can be due to sparse sampling or it can relate to the procedure by which the raw data is put together. It can either be random or systematic and there are a couple of good examples of this in the various surface or near-surface temperature records.
Sampling biases are easy to see in the difference between the GISTEMP surface temperature data product (which extrapolates over the Arctic region) and the HADCRUT3v product which assumes that Arctic temperature anomalies don’t extend past the land. These are both defendable choices, but when calculating global mean anomalies in a situation where the Arctic is warming up rapidly, there is an obvious offset between the two records (and indeed GISTEMP has been trending higher). However, the long term trends are very similar.
A more systematic bias is seen in the differences between the RSS and UAH versions of the MSU-LT (lower troposphere) satellite temperature record. Both groups are nominally trying to estimate the same thing from the same data, but because of assumptions and methods used in tying together the different satellites involved, there can be large differences in trends. Given that we only have two examples of this metric, the true systematic uncertainty is clearly larger than the simply the difference between them.
What we are really after is how to evaluate our understanding of what’s driving climate change as encapsulated in models of the climate system. Those models though can be as simple as an extrapolated trend, or as complex as a state-of-the-art GCM. Whatever the source of an estimate of what ‘should’ be happening, there are three issues that need to be addressed:
- Firstly, are the drivers changing as we expected? It’s all very well to predict that a pedestrian will likely be knocked over if they step into the path of a truck, but the prediction can only be validated if they actually step off the curb! In the climate case, we need to know how well we estimated forcings (greenhouse gases, volcanic effects, aerosols, solar etc.) in the projections.
- Secondly, what is the uncertainty in that prediction given a particular forcing? For instance, how often is our poor pedestrian saved because the truck manages to swerve out of the way? For temperature changes this is equivalent to the uncertainty in the long-term projected trends. This uncertainty depends on climate sensitivity, the length of time and the size of the unforced variability.
- Thirdly, we need to compare like with like and be careful about what questions are really being asked. This has become easier with the archive of model simulations for the 20th Century (but more about this in a future post).
It’s worthwhile expanding on the third point since it is often the one that trips people up. In model projections, it is now standard practice to do a number of different simulations that have different initial conditions in order to span the range of possible weather states. Any individual simulation will have the same forced climate change, but will have a different realisation of the unforced noise. By averaging over the runs, the noise (which is uncorrelated from one run to another) averages out, and what is left is an estimate of the forced signal and its uncertainty. This is somewhat analogous to the averaging of all the short trends in the figure above, and as there, you can often get a very good estimate of the forced change (or long term mean).
Problems can occur though if the estimate of the forced change is compared directly to the real trend in order to see if they are consistent. You need to remember that the real world consists of both a (potentially) forced trend but also a random weather component. This was an issue with the recent Douglass et al paper, where they claimed the observations were outside the mean model tropospheric trend and its uncertainty. They confused the uncertainty in how well we can estimate the forced signal (the mean of the all the models) with the distribution of trends+noise.
This might seem confusing, but an dice-throwing analogy might be useful. If you have a bunch of normal dice (‘models’) then the mean point value is 3.5 with a standard deviation of ~1.7. Thus, the mean over 100 throws will have a distribution of 3.5 +/- 0.17 which means you’ll get a pretty good estimate. To assess whether another dice is loaded it is not enough to just compare one throw of that dice. For instance, if you threw a 5, that is significantly outside the expected value derived from the 100 previous throws, but it is clearly within the expected distribution.
Bringing it back to climate models, there can be strong agreement that 0.2ºC/dec is the expected value for the current forced trend, but comparing the actual trend simply to that number plus or minus the uncertainty in its value is incorrect. This is what is implicitly being done in the figure on Tierney’s post.
If that isn’t the right way to do it, what is a better way? Well, if you start to take longer trends, then the uncertainty in the trend estimate approaches the uncertainty in the expected trend, at which point it becomes meaningful to compare them since the ‘weather’ component has been averaged out. In the global surface temperature record, that happens for trends longer than about 15 years, but for smaller areas with higher noise levels (like Antarctica), the time period can be many decades.
Are people going back to the earliest projections and assessing how good they are? Yes. We’ve done so here for Hansen’s 1988 projections, Stefan and colleagues did it for CO2, temperature and sea level projections from IPCC TAR (Rahmstorf et al, 2007), and IPCC themselves did so in Fig 1.1 of AR4 Chapter 1. Each of these analyses show that the longer term temperature trends are indeed what is expected. Sea level rise, on the other hand, appears to be under-estimated by the models for reasons that are as yet unclear.
Finally, this subject appears to have been raised from the expectation that some short term weather event over the next few years will definitively prove that either anthropogenic global warming is a problem or it isn’t. As the above discussion should have made clear this is not the right question to ask. Instead, the question should be, are there analyses that will be made over the next few years that will improve the evaluation of climate models? There the answer is likely to be yes. There will be better estimates of long term trends in precipitation, cloudiness, winds, storm intensity, ice thickness, glacial retreat, ocean warming etc. We have expectations of what those trends should be, but in many cases the ‘noise’ is still too large for those metrics to be a useful constraint. As time goes on, the noise in ever-longer trends diminishes, and what gets revealed then will determine how well we understand what’s happening.
Update: We are pleased to see such large interest in our post. Several readers asked for additional graphs. Here they are:
– UK Met Office data (instead of GISS data) with 8-year trend lines
– GISS data with 7-year trend lines (instead of 8-year).
– GISS data with 15-year trend lines
These graphs illustrate that the 8-year trends in the UK Met Office data are of course just as noisy as in the GISS data; that 7-year trend lines are of course even noisier than 8-year trend lines; and that things start to stabilise (trends getting statistically robust) when 15-year averaging is used. This illustrates the key point we were trying to make: looking at only 8 years of data is looking primarily at the “noise” of interannual variability rather than at the forced long-term trend. This makes as much sense as analysing the temperature observations from 10-17 April to check whether it really gets warmer during spring.
And here is an update of the comparison of global temperature data with the IPCC TAR projections (Rahmstorf et al., Science 2007) with the 2007 values added in (for caption see that paper). With both data sets the observed long-term trends are still running in the upper half of the range that IPCC projected.
Thank you, Timothy Chase. I understand (now) the search facility on this site and will employ it in the future.
I’m new to this stuff and have several colleagues (interestingly, all of conservative tendency) who keep suggesting that AGW is on a shaky foundation. So be patient with my naive questions (not that you are otherwise).
Burgy (www.burgy.50megs.com)
I have been tracking the measured annual global mean surface temperature versus the IPCC trend predictions, 1995 and 2000.
While the IPCC made no annual predictions, I see no reason one can not construct annual bounds based on their trendline predictions to facilitate gauging the performance of their predictions to date.
To do this I extended their prediction, uppper and lower bounds, by 1.28 std. deviations (90% confidence limit) to account for natural interannual variation. The variance was calculated as twice the variance in the residuals of a linear regression on the annual surface temperature data: 1970-2000. This is to account for the natural variability one can expect between any year of interest and an arbitray reference year: 1990 in this case.
A link to the graph:
http://i161.photobucket.com/albums/t231/Occam_bucket/IPCCTempPredictions.jpg
Dave Occam (602) — Thank you!
Aren’t you lumping all models together, than saying a short trend doesn’t invalidate model X, therefore all models are still plausible?
For example, I would think a small downward trend or flatline over an 8 year period, should make the forecasts of larger warming like 6C less likely than the 2C scenario.
Dave Occam #602, is that right? A two-sided 90% confidence interval is +/- 1.645 sigma for the normal distribution.
MikeN (604) — The major uncertainty is human behavior; are we or are we not going to add lots of extra carbon dioxide to the atmosphere?
“Aren’t you lumping all models together, than saying a short trend doesn’t invalidate model X, therefore all models are still plausible?”
Nope, a short trend doesn’t invalidate model X therefore it doesn’t prove model X is wrong.
There is no flatline or downward trend.
It was going up before 1998.
It has gone up after 1998.
And when in the 80s the AGW theory was just beginning and well into the 90s, it was all “you haven’t got enough data to say there’s even been any warming”.
That was 80 years of data.
Now 8 years is enough???
MarkN (604),
The 90% confidence limit does not apply to the probability of annual temperatures falling within the two bounds but rather the confidence limits of the best and worst case scenarios only. You can’t put a confidence limit on the aggregate because none were supplied by the TAR or SAR for their trendline prediction.
1.281 std devs leaves 10% (one tail) of the population outside the limit of interest if temperatures are tracking one of the envelope trendline bounds. Only one tail is relevant for each bound. If for example temperatures are running close to the lower bound then they are testing the slowest temperature rise model/scenario(s); the upper range of natural variability would fall well within the upper bounds. So while in this example you might have 10% of the years falling below my lower confidence limit it’s highly unlikely you will have any above the upper limit.
Martin Vermeer (605),
Unfortunately, I thought quantifying the confidence limit might cause some confusion.
The 90% confidence limit does not apply to the probability of annual temperatures falling within the two bounds but rather the confidence limits apply to the best and worst case scenarios only. You can’t put a confidence limit on the aggregate because none were supplied by the TAR or SAR for their trendline prediction.
1.281 std devs leaves 10% (one tail) of the population outside the limit of interest if temperatures are tracking one of the envelope trendline bounds. Only one tail is relevant for each bound. If for example temperatures are running close to the lower bound then they are testing the slowest temperature rise model/scenario(s); the upper range of natural variability would fall well within the upper bounds. So while in this example you might have 10% of the years falling below my lower confidence limit it’s highly unlikely you will have any above the upper limit.
Dave OK, thanks.
Dave, so were you agreeing with me that a 10 year flatline, if it happens, would have to lower the confidence ranges for temperature increase by 2100? Don’t want get confused by terminology. I’m saying that the 6.4C upper range temperature is less valid given a flatline. Not debunked or invalidated, but less likely than it already was, since a flatline is more likely under a 2.4C scenario than a 6.4C scenario.
MikeN #611. Not if you find the reason for the flatline is something that isn’t going to continue.
Without that, the most likely candidate is that the errors will get WIDER.
And note: it isn’t flatlining.
But even if it were, if that reason turned out to be that the ocean chemistry was changing into a new mode and about to exhaust all the stored methane in it, the temperature by 2100 would be higher than predicted.
If it were, and that reason were that the sun is reducing its output and will for the next thousand years, then the temperature by 2100 would be lower than predicted.
But since either could be happening, if it WERE flatlining (which it isn’t), we don’t know why and so our uncertainty would be higher. We’d have, in the words of Rummy, a known unknown. And each of those increases the uncertainty, not the trend.
Well going off the post at the top which shows various trends over short periods as part of general ‘weather’ variability.
I’m assuming a flatline comes from this and not some external forcing not in the models.
In that case, then I think basic math would suggest that the lower end of warming is more likely than the higher end. A flatline should be more likely in a 2C model than a 6C model correct?
Hi MikeN. :-)
This question has come up in another discussion, and both Mike and I would love to get a more informed third opinion. If I may rephrase the question I think Mike is asking…
What does the frequency of “lulls” tell us, if anything, about the climate sensitivity? Sensitivity estimates for climate range from about 1.5C to 4.5C per 2xCO2, or (equivalently) from about 0.4 to 1.2C per unit forcing (W/m^2).
Should different sensitivities result in a different frequency of “lulls”? Can we use information about the range of variation in the short term 8-year slope to help constrain the sensitivity estimates?
You’d have to know how the chaotic system reacts.
Short answer: no.
Long answer, theoretically and in general.
An example is to take the variations in temperature and go “how much of that is matched out by solar variation”. you then subtract a variation at that frequency until you get a line that is more straight than before.
And do that with all other variables.
Though that gives more the attribution rather than the sensitivity. And is subject to a lot of error.
But that’s not looking at the lulls either.
“Dave, so were you agreeing with me that a 10 year flatline, if it happens, would have to lower the confidence ranges for temperature increase by 2100?”
Are you addressing me, MikeN? I accidentally double posted – I meant to direct my post to Martin Vermeer.
In case you were asking my opinion: Statistically speaking, I would not look at a select 10 year period, a selection already biases the result, but rather the full record from the date of the prediction/s. I would consider the prediction suspect if we got a couple years outside my bounds over the next decade (exempting years of a major episodic event).
I think if temperatures hug the lower bound over the next few years it would make the upper 2030 bound an unlikely occurrence, but not necessarily the upper 2100 bound. Some models and scenarios produce very slow increases in temperatures in the first couple decades but accelerate more in the later years. For example scenario A2 of the 6 SRES scenarios (Fig 9.15 of my reference) produces the smallest increase in temperature in 2030 but the second highest in 2100 – for all models.
So far the IPCC predictions are holding their own. Hypothetically speaking, if they should require modification in the future to levels outside current bounds then I don’t think we can say at this point if it is because of inaccurate models, forcing sensitivities, initial conditions or natural changes that were not anticipated. So we couldn’t say much about 2100 temperatures till that was resolved.
>I think if temperatures hug the lower bound over the next few years it would make the upper 2030 bound an unlikely occurrence, but not necessarily the upper 2100 bound.
OK, not necessarily unlikely, but wouldn’t it then make the lower 2100 bound more likely than the upper 2100 bound?
Duae has hypothesized that a high positive feedback model that produces a 6C warming is as likely to produce lulls as a low feedback model that produces warming of 2C. Any opinion on this?
By the way, I don’t wish to compare models of different carbon scenarios, but rather models with different feedback variables.
Re 617: “By the way, I don’t wish to compare models of different carbon scenarios, but rather models with different feedback variables.”
But the IPCC prediction envelope encompasses both; when the authors determined the bounds of this envelope they had both in mind. The bounds of their prediction were based on expert judgment, not statistical computation.
If you want to tease out more information than what they summarized you need to address specific models and/or specific scenarios – but then how do you choose – statistically speaking? And then adding confidence limits for a chosen model is problematic – for experts not to mention lay readers.
Re 617: “OK, not necessarily unlikely, but wouldn’t it then make the lower 2100 bound more likely than the upper 2100 bound?”
Short answer, I am not qualified to say, but IMO I still think not necessarily – despite the intuitive attractiveness of your assumption. It all depends on how you determine likelihood and how well the causes of the slower than expected warming are understood in the future of your hypothetical scenario.
But we are just splitting hairs. By the time we reach 2030 they will have greater understanding of climate, better data and models and be able to narrow the range of plausible outcomes. However there will always be some natural variation that is beyond prediction. At this point in time I don’t see that it matters in terms of decisions that have to be made today regarding policy around GHG emissions that affect resource spending prior to 2030.
“but wouldn’t it then make the lower 2100 bound more likely than the upper 2100 bound?”
It doesn’t MAKE the upper bound less likely than before.
You can make a ***guess*** that it should, but unless you know why your model and reality are disagreeing, you don’t ***know*** that your assumption will hold.
That’s the thing. It isn’t one model, but a range of model possibilities.
Re 620: “That’s the thing. It isn’t one model, but a range of model possibilities.”
Right. As I understand it, capturing the results from a range of models is a proxy for capturing all the uncertainties in modeling. This might seem like they are sandbagging by playing it so safe, but I believe the models are using a nominal value for climate sensitivity to various forcings. If they were to choose only one model then it would make sense to capture the uncertainty in the sensitivities by running them with a range of values. Probably how it will be done in the future, after they get confidence in more evolved models and when they can do a better job of independently bounding the sensitivities.
Re: #602
I have updated the data and added near term statistical projections to the plots; i.e. projections free of any climate specific assumption.
http://i161.photobucket.com/albums/t231/Occam_bucket/IPCCStatTempPrediction.jpg
Captured in these four plots we see that the global annual mean surface temperature, through 2008, is tracking within International Panel on Climate Change projections.
[IMG]http://i161.photobucket.com/albums/t231/Occam_bucket/IPCCTemperatureProjection.png[/IMG]
The top chart shows actual mean temperatures relative to 1990 and annual bounds derived from IPCC’s multi-decadal trend bounds – values on left scale. These bounds capture uncertainty in the model, emissions scenario, and inter-annual noise. Also a linear trend-line is plotted from the measured temperature points and extrapolated out to 2030 so we can see the projected 40 year change – right scale, based on data through 2008.
The next two charts are the associated multi-decadal temperature trend projections published by the IPCC in the Third Assessment Report, based on climate models run in the late 1990s. As it turned out, per the last chart in the lower right (published in the Copenhagen Climate Report – 2009) emissions have so far closely followed SRES A1F1. I have circled the point in the IPCC chart where model ECHAM4/OPYC predicts the 40 yr temperature change given emission scenario A1F1. You can see it (0.72C) falls right on top of the actual trend to date.
Of course 19 years of data do not definitively define a 40 year trend, but we now have enough data to get a meaningful indication of how these 1990s models are tracking reality. So far actual temperatures are closely following median model projections.
It is disturbing to note that should these models continue to hold true and we continue on the emissions path of scenario A1F1 we are facing a global temperature increase of around 4.5C or 8.1F before the end of the century.
Link to plots for preceding post
http://i161.photobucket.com/albums/t231/Occam_bucket/IPCCTemperatureProjection.png