I don’t tend to read other blogs much, despite contributing to RealClimate. And I’m especially uninterested in spending time reading blogs full of ad hominem attacks. But a handful of colleagues apparently do read this stuff, and have encouraged me to take a look at the latest commentaries on our Antarctic temperature story. Since I happen to be teaching about principal component analysis to my graduate students this week, I thought it would be worthwhile to put up a pedagogical post on the subject. (If you don’t know what principal component analysis (PCA) is, take a look at our earlier post, Dummy’s Guide to the Hockey Stick Controversy).
 For starters, consider the following simple example. Suppose we have measured two variables over some time period (say, temperature and humidity, call them x and y). We manage to get 10 observations of x and y simultaneously, but unfortunately one of our instruments breaks and we wind up with 10 additional measurements of x only, but none of y. Fortunately, we know that x and y are physically related to one another, so our hope is that we can use the paired observations of x and y to estimate what y should have been, had we been able to measure it throughout the experiment. We plot the variables y vs. x and try fitting some function to the data. If we get the function right, we ought to be able to estimate what y is for any arbitrary value of x. The obvious thing one might try, given the apparent curve to the data, is to use a 2nd-order polynomial (that is, a parabola):
For starters, consider the following simple example. Suppose we have measured two variables over some time period (say, temperature and humidity, call them x and y). We manage to get 10 observations of x and y simultaneously, but unfortunately one of our instruments breaks and we wind up with 10 additional measurements of x only, but none of y. Fortunately, we know that x and y are physically related to one another, so our hope is that we can use the paired observations of x and y to estimate what y should have been, had we been able to measure it throughout the experiment. We plot the variables y vs. x and try fitting some function to the data. If we get the function right, we ought to be able to estimate what y is for any arbitrary value of x. The obvious thing one might try, given the apparent curve to the data, is to use a 2nd-order polynomial (that is, a parabola):
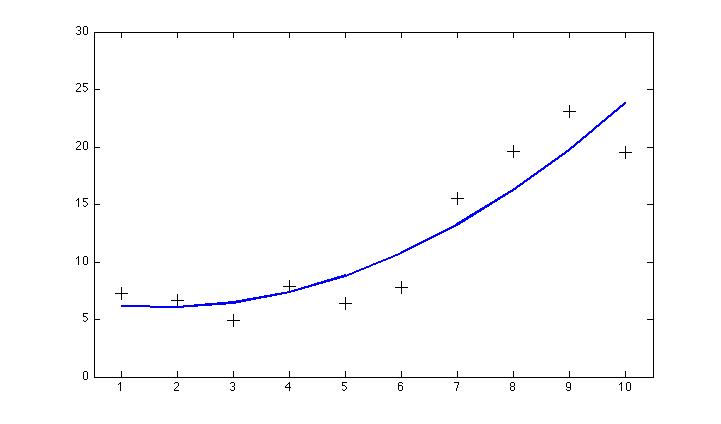
Looks pretty good right?
Well, .. no. Actually, in for this particular example, we should have just used a straight line. This becomes obvious after we fix the broken instrument and manage to increase the size of the data set:
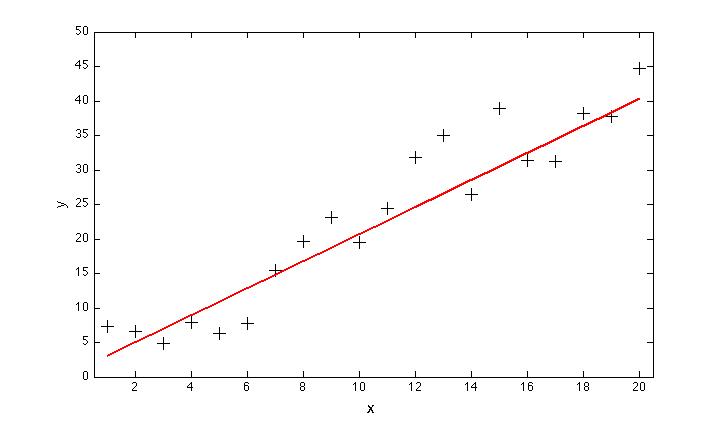
Of course, our estimate of the best fit line to the data is itself uncertain, and when we include more data, we wind up with a slightly different result (shown by the dashed green line, below). But we are a lot closer than we would have been using the parabola, which diverges radically from the data at large values of x:
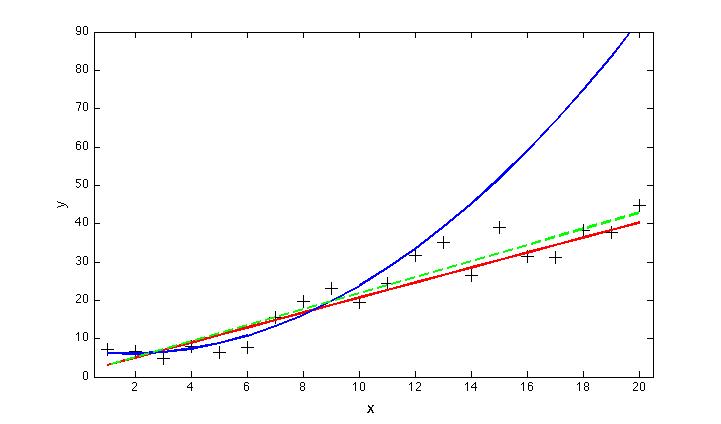
Of course, the parabola looked liked it might be a better fit — after all, it is closer to more of the data points, which really do seem to be curving upwards. And we couldn’t have known in advance, could we? Well, we could have increased our chances of being right, by using some basic statistics (a chi-squared test for example). The results would have shown us that there were not enough degrees of freedom in the data to justify the use of the higher-order curve (which reduces the degrees of freedom by from 8 to 7 in this example). Choosing the parabola in this case is a classic example of overfitting.
The basic lesson here is that one should avoid using more parameters than necessary when fitting a function (or functions) to a set of data. Doing otherwise, more often than not, leads to large extrapolation errors.
In using PCA for statistical climate reconstruction, avoiding overfitting means — in particular — carefully determining the right number of PCs to retain. Just as in the simple example above, there are two different — but both important — tests to apply here, one a priori and one a posteriori.
First, we are interested in distinguishing those PCs that may be related to the true ‘modes’ of variability in the data. In our case, we are interested in those PCs that represent variations in Antarctica temperature that are related to, for example, changes in the circumpolar wind strength, variations in sea ice distribution, etc. While linear methods like PCA are inherently just an approximation to the real modes in the climate system, in general the first few PCs — which, by construction capture that variability that occurs over large spatial scales — do bear a strong relationship with the underlying physics. At the same time, we want to avoid those PCs that are unlikely to represent physically meaningful variability, either because they are simply noise (whether instrumental noise or true random variability in the climate) or because they represent variations of only local significance. This is not to say that local or ‘noisy’ parts of the system aren’t important, but this kind of variability is unlikely to be well represented by a network of predictor variables that is even sparser than the original data field from which the PCs are obtained.
The standard approach to determining which PCs represent to retain is to use the criterion of North et al. (1982), which provides an estimate of the uncertainty in the eigenvalues of the linear decomposition of the data into its time varying PCs and spatial eigenvectors (or EOFs). Most of the higher order PCs will have indistinguishable variance. In the case where the lower order PCs (which explain the majority of the variance) also have indistinguishable variance, caution needs to be applied in choosing which to retain, because PCA will usually scramble the underlying spatial (and temporal) structure these PCs represent. One can easily demonstrate this by creating an artificial spatio-temporal data set from simple time functions (say, a bunch of sines and cosines), plus random noise. PCA will only extract the original functions if they have significantly different amplitudes.
The figure below shows the eigenvalue spectrum — including the uncertainties — for both the satellite data from the main temperature reconstruction and the occupied weather station data used in Steig et al., 2009.

It’s apparent that in the satellite data (our predictand data set), there are three eigenvalues that lie well above the rest. One could argue for retaining #4 as well, though it does slightly overlap with #5. Retaining more than 4 requires retaining at least 6, and at most 7, to avoid having to retain all the rest (due to their overlapping error bars). With the weather station data (our predictor data set), one could justify choosing to retain 4 by the same criteria, or at most 7. Together, this suggests that in the combined data sets, a maximum of 7 PCs should be retained, and as few as 3. Retaining just 3 is a very reasonable choice, given the significant drop off in variance explained in the satellite data after this point: remember, we are trying to avoid including PCs that simply represent noise. For simple filtering applications (image processing for example), the risk of retaining too much noise is small. For extrapolation in time – the climate reconstruction problem — it is critical that the PCs approximate the dynamics in the system. In that application, retaining fewer PCs — and in particular only those that are distinguished by a large break in slope (i.e. PCs 3 or 4 in the actual data, above) is the choice least likely to unnecessarily inflate possible noise.
In short, we a priori would not want to retain more than 7, and as few as 3 PCs is clearly justifiable. We would most certainly not want to retain 9, 11, or 25 since doing so is almost certain to result in extrapolation errors. Which leads us to our a posteriori test: how well do the various reconstructions do, as a function of the number of retained PCs?
As in the simple x,y example above, we now want to take a look at how our extrapolation compares with reality. To do this, we withhold some of the data, calibrate the model (a separate calculation for each number of PCs we want to consider), and then compare the resulting reconstruction with the withheld data. Such calibration/verification tests, were, of course, done in our paper and is the major thing that distinguished our paper from previous work.
As shown in the figure below, there is not much change to the goodness-of-fit (as measured in this case by the correlation coefficient of the withheld and reconstructed data in the split calibration/verification tests), whether one uses 3, 4, 5, or 6 PCs. There is a significant (and continuous) drop off in skill, however, if one uses more than 7. We can therefore eliminate using more than 7 PCs by this a posteriori test. And since little was gained by using more than 3 or 4, parsimony would indicate using no more.

Now the alert reader may point out that the reconstruction skill (as calculated with simple PCA and correlation scores at least) seems to be the greatest in West Antarctica when we use 4 PCs, rather than 3 as in the paper. However, as shown in the first figure below, choosing more than 3 PCs results in the same or even larger trends (especially in West Antarctica) than does using 3 PCs. Of course, we can get smaller trends if we use just two PCS, or more than 10, but this can’t be justified under either a priori or a posteriori criteria — no more so than using 13, or 25 can.* The result is the same whether we use a simple PCA (as I’ve mostly restricted myself to here, for simplicity of discussion), or the RegEM algorithm (we used both methods in the paper):
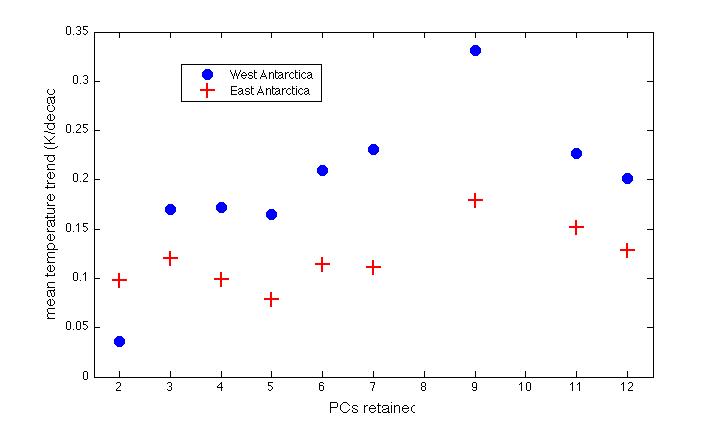
In summary: our choice to retain 3 PCs was not only a reasonable a priori choice, but it produces comparable or smaller trends to other reasonable a priori choices. Using 4, 6 or 7produces larger trends in West Antarctica, and little change in East Antarctica. Using more than 7 (at least up to 12) increases the trend in both areas. So much for the claim, reported on several web sites, that we purposefully chose 3 PCs to maximize the estimated warming trend!
All of this talk about statistics, of course, can distract one from the fact that the key finding in our paper — warming in West Antarctica, akin to that on the Peninsula — is obvious in the raw data:
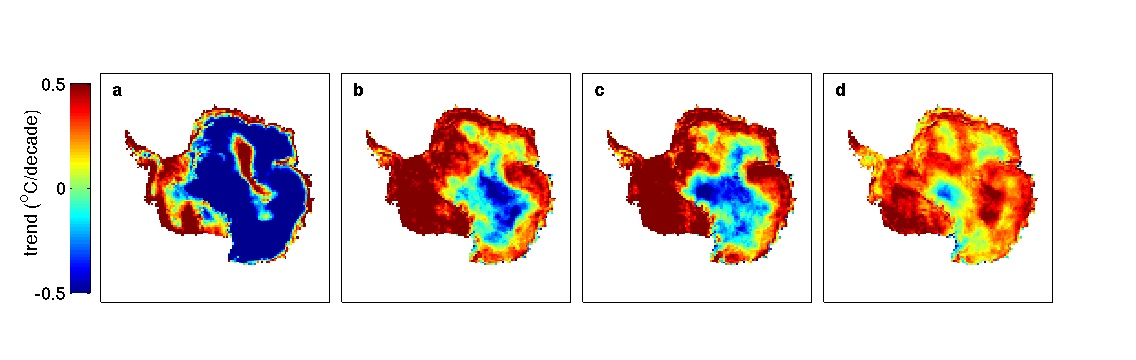
Raw trends in temperature — in different versions of the monthly cloud-masked temperature data (a) Comiso (decadal trends 1982-1999), (b) Monaghan et al. (1982-1999) c) Steig et al. (1982-1999), (d) Steig et al., (1982-2006).
It is, furthermore, exactly what one would expect from the atmospheric dynamics. Low-pressure storms rarely penetrate into the high polar plateau of East Antarctica, and temperatures there are radiation dominated, not-transported dominated as they are in West Antarctica and on the Peninsula. This is why those general circulation models that properly simulate the observed atmospheric circulation and sea ice changes — increasing around most of East Antarctica, but decreasing off the coast of West Antarctica and the Peninsula — also match the pattern and magnitude of the temperature trends we observe:
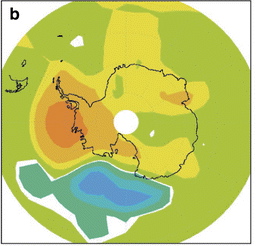
Figure 3b from Goosse et al., 2009, showing temperature trends (1960-2000) simulated by an intermediate complexity coupled ocean-atmosphere model that uses data-assimilation to constrain the model to match observed surface temperature variations at surface weather stations. No satellite temperature data are used. Yellow areas are warming at 0.1 to 0.2 degrees/decade in the simulation and light orange 0.2 to 0.3 degrees/decade.
A final point is that it is actually rather bizarre that so much effort has been spent in trying to find fault with our Antarctic temperature paper. It appears this is a result of the persistent belief that by embarrassing specific scientists, the entire edifice of ‘global warming’ will fall. This is remarkably naive, as we have discussed before. The irony here is that our study was largely focused on regional climate change that may well be largely due to natural variability, as we clearly state in the paper. This seems to have escaped much of the blogosphere, however.
*While I was working on this post, someone called “Ryan O” posted a long discussion claiming that he gets better verification skill than in our paper using 13 PCs. This is curious, since it contradicts my finding that using so many PCs substantially degrades reconstruction skill. It appears that what has been done is first to adjust the satellite data so that it better matches the ground data, and then to do the reconstruction calculations. This doesn’t make any sense: it amounts to pre-optimizing the validation data (which are supposed to be independent), violating the very point of ‘verification’ altogether. This is not to say that some adjustment of the satellite data is unwarranted, but it can’t be done this way if one wants to use the data for verification. (And the verification results one gets this way certainly cannot be compared against the verification results based on untuned satellite data.)
Further, the claim made by ‘Ryan O’ that our calculations ‘inflate’ the temperature trends in the data is completely specious. All that has done is take our results, add additional PCs (resulting in a lower trend in this case), and then subtract those PCs (thereby getting the original trends back). In other words, 2 + 1 – 1 = 2.
Since I said at the outset that this is a pedagogical post, I will end by noting that perhaps something has been learned here: it appears that using our methods, and our data, even a self-professed ‘climate skeptic’ can obtain essentially the same results that we did: long term warming over virtually all of the ice sheet.
Great artcile RC. This just goes to explain why you guys work for GISS and submit your work for the required and proper scientific process of peer review and further work to fully integrate it into current earth science knwledge whist the blogosphere does not and hence is prone to getting it all wrong.
I see articles from the physicst John Nicol www
(A Fundamental Analysis of the Greenhouse Effect)paper which is full of complex math equations but has had very little reply in the AGW sphere but is rife on the blogs to some degree and is used by people from downunder to seemingly prop their misunderstanding of AGW.
http://climaterealists.com/faqs.php?id=1347
I have learnt to only come here for science and a lot of other places for convincing the public either way.
Dr. Steig – the response is much appreciated.
Without replying now to your points about overfitting here, I do want to say that nobody posting at tAV is hoping to embarrass you or your comrades. It is as I pointed out from the beginning just an exercise in understanding.
Most of us don’t even care that the Antarctic isn’t warming as much as your method shows, it’s more about the ‘very clever’ method at this point and how easily it can mislead.
BTW: I certainly don’t expect the absolute reality of a warming globe to go away either, and ascribing such hopes to myself or others is unfortunate.
Dr. Steig, the choice of 3 PC’s, a low order processing scenario, does not allow peninsula warming to be properly expressed. It does not allow the possibility that peninsula warming may be an entirely regional phenomenon. By definition, the “predictor” impact of a cluster of correlated, warming stations cannot be regionally constrained in a 3 PC reconstruction. Please clarify why such a scenario would not yield spurious smearing.
I know nothing about statistics, but the editor in me suggests it should be \principal\ rather than \principle\ component analysis…
[Response: Corrected. Thanks. Silly typo.]
Thanks for a very clear explanation of the choice of 3 PCs. It exposes this as the [poorly edited and ungrammatical] nonsense that it undoubtably is …
It is my view that all Steig and Michael Mann have done with their application of RegEm to the station data is to smear the temperature around much like an artist would smear red and white paint on a pallete board to get a new color “pink” and then paint the entire continent with it.
It is a lot like ‘spin art’ you see at the county fair. For example, look (at left) at the different tiles of colored temperature results for Antarctica you can get using Steig’s and Mann’s methodology. The only thing that changes are the starting parameters, the data remains the same, while the RegEm program smears it around based on those starting parameters. In the Steig et al case, PC and regpar were chosen by the authors to be a value of 3. Chosing any different numbers yields an entirely different result.
So the premise of the Steig et al paper paper boils down to an arbitrary choice of values that ‘looked good’.
Only the best Blog Science makes it onto the Science Blog of the Year.
Commenting on that which I am qualified to comment on (a very small subset of what goes on at Climate blogs), I don’t understand the statement
I read a lot of blogs on both sides of the issues and the blogs behind the other side of this debate (CA & tAV) have few if any ad homs. In my opinion, less than RC. And that’s taking into account comments (where it’s debateable whether or not the blog proprieter should be held accountable for the comments of others). WUWT has it’s problems, but it’s no worse there than at deltoid.
Re# WUWT has its problems? Yes its anti science.
I didn’t read the JeffID/RyanO work but have read JeffID’s earlier “I’ve mathematically proven the hockey stick is an artifact of the analysis” piece and it was garbage. It was explained to him that it was garbage, and why it was garbage, but he didn’t budge.
So don’t expect any backtracking by them on this piece of work.
to BillB(6) & JeffID — your comments seem a bit disingenuous as the blogs in question are full of ad-hom & plenty of snarky comments, even from the “principal components” a la McIntyre defending Ryan O’s faulty analysis:
“In this example, we all realized pretty quickly that Steig was spreading the Peninsula around Antarctica….It’s hard not to imagine that they didn’t do runs retaining more than 3 PCs. Perhaps they are in the CENSORED directory.”
Seems to make sense to a layman; will be interesting whether this goes any further. One question; I’m guessing the slight increase in ice in the Antartic over the decades is possibly attributed to increased precipitation (due to the slightly warmer weather; contrary to what the average joe would naturally assume?)
[Response: Be careful about what ‘ice’ you are talking about. There is the glacial ice in the interior of the continent (where warming would be expected to lead to increases in snowfall), there is the glacial ice along the edge of the continent where increased losses due to ice dynamics (for instance in parts of West Antarctica and the Peninsula) probably overwhelm any potential increases in snowfall, and then there is the sea ice (which is formed in situ on the ocean). The sea ice changes are much more susceptible to changes in wind patterns and so have very regionally specific trends – big reductions to the west of the peninsula, increases to the east (and a slight increase over all), but they aren’t really affected by changes in snow fall. -gavin]
I love the smell of red herring in the morning, but that’s an argument we need not have here; it’s done:
http://www.google.com/search?q=blog+ad+hominem+idiot
“…it is actually rather bizarre that so much effort has been spent in trying to find fault with our Antarctic temperature paper. It appears this is a result of the persistent belief that by embarrassing specific scientists, the entire edifice of ‘global warming’ will fall.”
I don’t think you can have it both ways. If the effort to find fault is bizarre, then there was no need to respond to it, and there is absolutely no need to be embarrassed by it. If the effort has been to question and thereby help validate your study by encouraging the clarifications that you have provided, then that effort will have been to the good.
“Most of us don’t even care that the Antarctic isn’t warming as much as your method shows”
Is it not? You seem very sure of that. What’s your evidence?
“A final point is that it is actually rather bizarre that so much effort has been spent in trying to find fault with our Antarctic temperature paper.”
I’ve been following the effort to replicate your results and wonder how you get the impression that this has been an attempt to find fault.
Ryan O followed the analysis where it took him, and with great personal effort, replicated your results, and then produced what he considers to be a better analysis. He’s thoroughly documented his results, his reasoning, and his source code online. I am sure he is more than willing to debate the relative merits of the respective reconstructions.
Pete Best asks about the paper by Jon Nicol that essentially refutes the whole AGW understanding. One clue: It is loaded with statements of fact about current conclusions and results of analyses without citing a single reference. 27 pages of analysis and not a single reference. That is not the work of a scientist.
The conclusion seems to be nonsense, but I will leave it to an expert to say why.
Jeff Id writes:
“It is as I pointed out from the beginning just an exercise in understanding. ”
I hope he understands better now, but somehow I doubt that, given the inability to address the points made and the general snark.
Addressing supermarket tabloid-quality analysis is a tricky business. On the one hand, it tends to appear to the layperson to elevate such dubious material to the level of credible peer-reviewed science. On the other hand, such claims can propagate easily if never addressed. If few ever read supermarket tabloids, the latter wouldn’t be an issue.
Eric,
The fact that those skeptical of your results replicated your analysis themselves is certainly a step up from the usual rhetoric in climate blog debates, even if they may have erred in including too many PCs. After all, independent replication is an essential check for the validity of one’s results, especially when complex statistics are involved!
[Response: Indeed. This is a far cry, however, from “debunking”, which is what is being trumpeted.–eric]
Jeff Id writes:
“It is as I pointed out from the beginning just an exercise in understanding.”
I hope he understands better now, but I somehow doubt that given the inability to address the points made and general snark.
Addressing supermarket tabloid-quality material is tricky business. On the one hand, it tends to appear to elevate the material to the level of objective peer-reviewed research. On the other hand, dubious claims are often easily propagated if not addressed head-on. The latter wouldn’t be an issue if tabloid-quality material was read by few.
Hank,
I performed the suggested google. I presume that your reference was to Stephan Bond’s “the ad hominem fallacy fallacy”?
If so, it was a good read and I agree with Mr. Bond.
So, was your comment directed at me, Dr. Steig or someone else?
#11, I doubt I will be able to ‘address the points’ here. Ninety percent of my polite and on topic comments have been moderated to either. I will reply in time on tAV.
Ryan O has made a detailed first pass at some of the points above currently in moderation in this comment thread. He has repeated much of what I would add but has done a better job than I could. There are a variety of rules for choosing PC’s. My own results, Jeff C’s and Ryan’s have all shown the same thing which is a more similar trend in comparison to surface stations shown at this link titled according to the famous blogger ‘TCO’s’ language.
http://noconsensus.wordpress.com/2009/04/27/maximum-triviality-reconstruction/
What was telling early on was a correlation vs distance plot by CA which showed the clear smearing of covariance info across the Antarctic. What Jeff C and I have shown in past RegEM, is that increasing PC’s improves this flaw resulting in a better match to surface station trend and improved verification statistics demonstrated by RyanO.
If I get Dr. Steig’s permission to comment here, I will try to do a more thorough job, otherwise I can reply on tAV.
[Response: No comments of yours have been deleted that I’m aware of, at least not to this post. Still, I’m not at all interested in debating you — I’ve got much better things to do. Let me be very clear, though, that I’m by no means claiming our results are the last word, and can’t be improved upon. If you have something coherent and useful to say, say it in a peer reviewed paper. If your results improve upon ours, great, that will be a useful contribution.–eric]
Glad to hear that, I’d hate to see your hopes dashed.
I’d be more likely to believe you if I hadn’t read some of your other posts on other blogs, including your own … in fact I’d say that Steig’s comment …
is substantiated by Jeff Id’s comment on the thread devoted to his and Ryan O’s work over at WUWT, where he says:
It is hard to reconcile this statement with Jeff’s post above in which he says
#19, You are conflating the need for better models with the reality that the globe has warmed.
No one argues the need for improving models. Why do you think Gavin has a job?
You don’t *improve* a model that’s been “contradicted”, especially when the physics upon which they’re based has been contradicted, as you claim: “any reasonable Antarctic temperature math contradicts predicted CO2 based warming”.
You would throw it out and start over.
My main reason for posting is to encourage lurkers to investigate you themselves, as your oh-so-polite, watered-down act here is … an act.
I agree with Eric (and various others who’ve said the same at WUWT): submit your work for publication at a reputable journal and see where it goes.
Eric — Well done!
Jeff Id (20) — The internet is best effort, but without guarantees. Sometimes comments are simply lost.
Pete Best (#1), the Nicols text seems after twenty-odd pages to just end up with some variant on the saturation argument, which has been very educationally demolished on RC before, here with more technical detail here.
Re: #23,
“I agree with Eric (and various others who’ve said the same at WUWT): submit your work for publication at a reputable journal and see where it goes.”
Although this is good advice, it’s not as fun as (and in some ways less rewarding than) getting promoted on popular contrarian blogs and slinging mud at scientists. Doing objective research is also a lot more difficult.
But remember…if a contrarian can’t get their work published in one of dozens of reputable journals, it’s just more evidence of the grand “AGW conspiracy” as opposed to evidence that something might be wrong with their argument.
Your example addresses extrapolating a data set with limited information and demonstrates the risks of extrapolating your predicted trend with higher order fits. Of course the fictitious “new data” could just as easily have been along the second order fits trend, or curved the opposite direction. Extrapolation is always just a best guess.
I thought the Antarctic Study was related to interpolating data sets and evaluating historic trends within the time period.
Aren’t you “comparing apples to oranges” with regard to the best processes for extrapolating vs. interpolating?
The uncertainty curves that you presented do show adjacent PCA with little or no overlap around 10-11 and 13-14. When interpolating a data set, why would keeping more information be bad? Computer methods reduce the historic need to be careful with the number of calculations.
[Response: Read paragraph 8 again “First, we..” – gavin]
“any reasonable Antarctic temperature math contradicts predicted CO2 based warming”
Inappropriate selection of PCs aside and assuming Antarctic temperature trends lag CO2 predictions, such an argument is only valid in the absence of all other variability, natural…or not:
http://www.nytimes.com/2002/05/03/us/ozone-hole-is-now-seen-as-a-cause-for-antarctic-cooling.html
This reminds me of when the scientific community thought the earth was flat, the sun was the center of our universe, etc., and the skeptics where burned at the stake or hung. Just because there is a popular belief/statistical methodology used does not mean it is correct or the underlying science is correct. When will society realize we know very little, much less prove any different. What Ryan and others have shown, if you take the time to read the work, is that the methods use for the reconstruction and trending calcs are suspect. It does not in any shape or form address AGW,they have been addressing the viability of the mathematical methods used, trying to determine the robustness.
Oh, one last thing, for all the people out there crying for a peer reviewed paper, all that means is that that paper was “peered reviewed”, it does not mean it is correct. Many peered reviewed papers have been retracted, so don’t forget that.
Eric,
As the “Ryan O” to which you refer, I would like to have the opportunity to respond to the above.
First, the discussion in North about statistical separability of EOFs is related to mixing of modes. Statistical separability is never stated or implied as a criterion for PC retention except insofar as degenerative multiplets should either all be excluded or all be retained. I quote the final sentences from North (my bold):
The criteria set forth in North do not suggest, in any way, shape or form, that only statistically separable modes should be retained. As statistical separability is not a constraint for either SVD or PCA, mixed modes often occur. Indeed, there is a whole subset of PCA-related analyses (such as projection pursuit and ICA) dedicated to separating mixed modes. PP and ICA by definition would not exist if statistical separability were a criterion for PC retention, as both PP and ICA require the PC selection be made ex ante. Calling statistical separability a “standard approach” to PC retention is unsupportable.
Second, as far as verification statistics are concerned, the improvement in both calibration and verification using additional PCs is quite significant. This obviates the concern that the calibration period improvement is due to overfitting. I have provided fully documented, turnkey code if you wish to verify this yourself (or, alternatively, find errors in the code). The code also allows you to run reconstructions without the satellite calibration being performed to demonstrate that the improvement in verification skill has nothing do to whatsoever with the satellite calibration. The skill is nearly identical; and, in either case, significantly exceeds the skill of the 3-PC reconstruction. The purpose of the satellite calibration is something else entirely (something that I will not discuss here).
Thirdly, this statement:
is misguided. I would encourage you to examine the script more carefully. Your results were not used as input, nor were the extra PC’s “subtracted out”. The model frame of the 13-PC reconstruction – which was calculated from original data (not your results) was used as input to a 3-PC reconstruction to determine if 3 PCs had sufficient geographical resolution. The result is that they do not. I refer you to Jackson ( http://labs.eeb.utoronto.ca/jackson/pca.pdf ) for a series of examples where similar comparisons using real and simulated data were performed. Contrary to your implication, this type of test is quite common in principal component analysis.
Lastly, I take exception to the portrayal of the purpose of this to be, in your words:
Nowhere have I stated my purpose – nor have I ever even implied – that my analysis makes any statement on AGW whatsoever. The purpose was to investigate the robustness of this particular result.
[Response: Ryan: Unlike most of your fellow bloggers, you have been very gracious in your communications with me. They could learn something from you. Nevertheless, I think you have greatly jumped the gun in claiming to have demonstrated anything. I understand and appreciate your points, and I do not wish to imply that I think every point you have made is wrong. To the contrary: you may well be that you are able to show that a different methodology, and retaining a different number of PCs, gives a better result than ours. That would be great, because it will move the science forward. But you have by no means demonstrated anything of the sort. I by no means discourage you from trying, but as I said to Jeff Id I’m not interested in an endless debate on this. Write a good paper on the subject, and submit it. What you will need to do for anyone to take such a paper seriously, among the several other things I could have pointed out, is to be more thoughtful about how you use the AWS data. By combining these the occupied weather station data (not to mention imputing the weather station data using the satellite data, which makes it even worse) prior to deciding how many PCs to retain you are greatly overestimating the amount of resolvable information. You claim to be using 98 weather stations (which means in principle you could retain up to 98 PCs!). But there are no AWS data available during the reconstruction period, so this is meaningless. Using just the occupied weather stations — which is the only sensible thing to do — gives you (by your own analysis) at most 6 PCs. Retaining 13 PCs makes absolutely no sense a priori, no matter how good the a posteriori ‘verification’ appears to be.–eric]
Eric,
The counter claim now appears to be that the calibration of the AVHRR data with the surface station data makes no difference to the reconstruction verification statistics. This seems somewhat counter intuitive. It also seems to raise the possibility of other methodological differences between your study and Ryan O’s work. Any ideas?
I am maybe misunderstanding something here, but I fail to see how your “a priori” test is in anyway a priori.
Is an a priori test not one which is “derived by or designating the process of reasoning without reference to particular facts or experience”?
As far as I see it you are making your a priori test by looking at the eigenvalues of the results and then making your choice. Surely this is an a posteriori test?
Confused…
Al
[Response: I take ‘a priori’ to mean before the verification tests are done. – gavin]
[Gavin has this right.–eric]
When will skeptics realize that actually we know a lot. The breadth and width of modern scientific knowledge is immense. There’s far more to learn, but a lot has been learned.
You’re one step better than those who say “since we don’t know everything, we know nothing”, but really, it’s not much of an improvement to believe that “since we don’t know everything, we know almost nothing”.
I’m not familiar with Ryan’s work, but I am familiar with a pseudo-mathematical attack on the “hockey stick” written by Jeff ID, and as I stated above, it was garbage.
Though the rah-rah crowd clung to it with an enthusiasm similar to that being shown over Ryan and Jeff’s “debunking” of Steig’s paper.
So I’d suggest your statement is one of faith, nothing more.
Let me put it this way: Ryan and Jeff’s methodology is suspect, as pointed out in Eric’s post. Using suspect methodology to claim that someone else’s work is suspect is … not very convincing.
True, unreviewed blog science papers are never retracted, therefore blog science must be better …
Comment 27 says: “The uncertainty curves that you presented do show adjacent PCA with little or no overlap around 10-11 and 13-14. When interpolating a data set, why would keeping more information be bad? ….
[Response: Read paragraph 8 again “First, we..” – gavin]”
Paragraph 8 says:
First, we are interested in distinguishing those PCs that may be related to the true ‘modes’ of variability in the data. In our case, we are interested in those PCs that represent variations in Antarctica temperature that are related to, for example, changes in the circumpolar wind strength, variations in sea ice distribution, etc
Are you suggesting that there are are only three three important variations in antartica temperature? What is the other one apart from circumpolar wind strength and variations in sea ice distribution? Are these all one dimensional?
[Response: No…. read all the way to the end. – gavin]
One question I have, is not linked to the mathematics (Way beyond my level of competance), but why have islands that are closer to New Zealand & Chile been included in temperature measurement data for Antarctica?
I just want to add that having read several of Ryan O’s comments at WUWT – a site that is typically raucous at best – his track record there fully backs up Eric’s statement above. He’s been very careful not to personally attack the authors of the paper, and has been very modest in his claims as to what he’s shown, and has tried to caution others at WUWT to do so as well.
In other words, he’s been very professional, right or wrong.
Re: #29 from WhyNot:
“Oh, one last thing, for all the people out there crying for a peer reviewed paper, all that means is that that paper was “peered reviewed”, it does not mean it is correct. Many peered reviewed papers have been retracted, so don’t forget that.”
Let me add another response alongside dhogaza’s. Yes, many peer-reviewed papers have been retracted, which is exactly the point. The peer reviewed journals provide the forums for the ongoing discussion and debate. The blogosphere does not serve that capacity in science: at least, not yet. I would second Eric’s comment: let JeffID, RyanO and others try to get their material published, and if such work is published, let the scientific community have at it. And if such work advances scientific understanding, we all win.
Dr. Steig,
Thank you for your reply to Ryan. What you say about AWS stations makes some sense. I wonder if it’s helpful in de-weighting some of the dominant satellite covariance which isn’t ideal. Dr. Comiso did an excellent job with it, after looking at the raw data I was amazed at how much he was able to clean it up.
Still the long term trend of the sat data doesn’t match surface stations, I haven’t done a significance analysis but it isn’t very close. Therefore in the verification statistics as well as the covariance of the reconstruction in your paper as well as Ryan’s work and others, the short term fluctuations are dominant.
It seems to me therefore, that the goal would be a redistribution of superior accuracy ground station data according to spatial covariance of the satellite data. Something I think RegEM can do a reasonable job of.
What are your thoughts on a higher order correction of the satellite data in an effort to match more closely the trends of surface stations? The point would be that covariance information is maintained yet surface station trends are minimally disturbed.
[Response: This could be useful. However, another reason we didn’t try this kind of correction is that the satellite data are *particularly* suspect precisely at the locations where most of the occupied weather stations are. That’s because the weather stations are mostly located on the coastline, in areas of considerable topography. No matter how reliable the weather stations are for measuring local variability, they probably contain a lot of variability that isn’t important on the ice sheets. Indeed, one of the reviewers on our papers was initially concerned that we had done such a correction, and that this disqualified our analysis, making it doubly ironic that you are now criticizing our paper in precisely the opposite way. Using AWS to correct the satellite data might make sense, but as you know well, the AWS have their own significant issues. In short, there is no simple answer to this, but if you guys are serious about making a contribution, you can’t gloss over these kinds of issues. Cheers, –eric]
well outside my area of expertise, but I was slightly peturbed by a line in the north 1982 paper you quoted:
“The problem focused upon in this paper occurs when near multiplets get mixed by sampling error….. …However, in choosing the point of truncation one should take care that it does not fall in the middle of an “effective multiplet” created by the the sampling problem, since ther is no justification for choosing to keep part of the multiplet and disarding the rest. Other than this, the rule of thumb unfortunately provides no guidance in selecting a truncation point ”
This Jeff Id fellow appears to be toning it down here a bit. On the contrarian blog being questioned, the following comments (on the “…falsified” blog post) of his fit right in with much of this crowd. I’ve included my replies, which might take the edge off from reading the comments uninterrupted.
Ad hom 1:
“As far as agenda, I don’t care if the Antarctic is warming as I don’t have any climate computer models I’ve devoted my life to designing.”
Reply: No agenda? Let our readers decide…
“The current models ‘apparently’ predict significant warming in the Antarctic based on evil CO2. This is an extremely important point for AGW”
Reply: As explained in a post above, it’s not quite as significant as Jeff makes it out to be, unless you believe CO2 is the only driver in regional climate.
“as if the Antarctic won’t melt, the flood disasters don’t happen.”
Reply: It appears to be melting, on balance,
http://scienceblogs.com/deltoid/2009/05/the_australians_war_on_science_38.php
although Jeff Id appears to think contintental ice melt is completely correlated with temperature rise. Rising temperatures can result in more precipitation. With cold temperatures, that still falls as snow. This is partially the case with a handful of world glaciers that are growing in contrast with the vast majority of them.
“It is critical to AGW that the Antarctic melts.”
Reply: AGW theory is not critically dependent on Antarctica melting.
“Without rebuttal, this paper and those which Dr. Steig claimed at RC are being developed by others will be the new poster children for the IPCC.”
Reply: While he clearly appears to be over-estimating the significance of this study, the comments so far appear to be revealing of a possible agenda.
“They know the temps aren’t even close to melting the ice but the papers can proclaim warming (already have) so people will a priori ‘know’ it’s coming. ”
Reply: Antarctic ice appears to be melting on balance (see Dr. Allison’s quotes in the Deltoid link above), although I don’t think the Steig et al study addresses this. Jeff is barking up the wrong tree.
“AGW has placed the burden of proof on the rational rather than the extremist predictions. How else does the highest trend ever published (that I know of) for the Antarctic become the cover of Nature?”
Reply: I don’t think most predictions are “extremist” any more than I think smaller predictions are “denialist”. I prefer to examine the methodology used and not immediately hand-wave away results that doesn’t agree with any pre-conceived notions or hopes. The comment above appears to indicate a bias.
Ad hom 2:
“…Steig et al, mashes, blends and crushes the numbers into a continuous uptrend – consistent with models as Gavin stated in celebration when this paper was acclaimed on RC.”
Ad hom 3:
The frustrating part is that even if climatology rejects this unreasonable paper outright (as it should), gavin and modelers will just shift positions. Models will again show local cooling followed by doom-filled warming. Pinning a modeler down is like putting a railroad spike through a jar of jelly on a hot day – mush.”
Eric Steig’s comment regarding some the zealotry seen in the blogosphere didn’t entirely make sense to me. Now it does:
“A final point is that it is actually rather bizarre that so much effort has been spent in trying to find fault with our Antarctic temperature paper. It appears this is a result of the persistent belief that by embarrassing specific scientists, the entire edifice of ‘global warming’ will fall. This is remarkably naive, as we have discussed before. The irony here is that our study was largely focused on regional climate change that may well be largely due to natural variability, as we clearly state in the paper. This seems to have escaped much of the blogosphere, however.”
Furthermore, I think Steig’s suggestion to Jeff regarding submitting his argument for peer review is very appropriate. Discourse in such venues tends to be much more rational, certainly more civil, and a place where high quality science (as opposed to politics) is conducted.
Eric,
Thank you for the reply. If you get a chance and can bring yourself to visit either WUWT or the Air Vent, I hope you will see the comments I made where I expressed that all of your responses to me had been courteous, professional, and nearly immediate. I hope you will also see that I asked many of the posters to cease the ad hom attacks on you – especially anything insinuating fraud or academic dishonesty. I do not believe in those kinds of attacks.
I also hope you remember that when everyone was pointing to Harry as invalidating your results, I posted on both Lucia’s site and Climate Audit (as well as dropping a note here) a brief set of calculations that I felt indicated that Harry was a non-issue as far as the fundamental conclusions of the paper went. My interest in this was not to manufacture some reason to disregard your results; if I found that I agreed with the methodology and results you can rest assured that I would have posted that in just as much detail as I posted my contrary findings.
With that aside, I would invite you to look here:
http://noconsensus.wordpress.com/2009/06/01/rc-replies-dr-steig-claims-overfitting/#comment-6113
I have included plots of the verification statistics demonstrating that the calibration step does not artificially inflate the skill. There is no discernible difference. I have included the instructions for you to be able to replicate this yourself using the script provided here:
http://noconsensus.files.wordpress.com/2009/05/recon.doc
I would respectfully disagree that our reconstruction does not already demonstrate significantly improved skill.
When it comes to your comment about the AWS data, I believe you have misunderstood our use of the data (WUWT also misunderstood, as the inclusion of the AWS data during the ground station imputation step does not significantly affect the results; you can verify this by examining the reconstruction “r.13.man” in the script), as well as the PC selection. The 13 PCs applies to the AVHRR data only; not to the number of eigenvectors used in the RegEM imputation. We determine that separately by using the broken stick model as the selection tool after the ground station matrix has been fully imputed. The reason for including the AWS stations in one of the reconstructions was to use the AWS stations as a verification target in a reconstruction that did not include them.
[Imputing the ground stations using the AVHRR data, and then determining how much information (how many PCs) is in the ground stations makes no sense. Again, the right answer here (by your own analysis!) is a maximum of six PCs.–eric]
When it comes to your statement about publication, I do understand. It is not productive for you to spend your time debating every issue that every blogger wishes to raise. I do not mean that sarcastically – I really do mean it. So I do understand your desire not to endlessly debate this here.
I also understand that there is a certain amount of “put up or shut up” when it comes to publication. You and I both know that it is much easier to put together some fancy plots for a blog; the wicket for publication is much more difficult and forces more critical thought than blogging. If you do not wish to discuss this until/unless a peer-reviewed paper is forthcoming, I respect that.
[Response: Thank you. Whether from you, me or someone else, there are sure to be published updates to the question of Antarctic temperature change, and some of them may well be an improvement to our work. If you are one of the authors on such a paper good on ya’. Meanwhile, I’d appreciate your pointing out to the various folks who have used your blog posts to justify claiming that our work has been debunked that they are a tad premature. And with that, I’m closing comments on this post.-eric]