According to some recent reports (e.g. PlanetArk; The Guardian), the public concern about global warming may be declining. It’s not clear whether this is actually true: a poll conducted by researchers at Stanford suggests otherwise. In any case, the science behind climate change has not changed (also see America’s Climate Choices), but there certainly remains a problem in communicating the science to the public.
This makes me think that perhaps a new simple mental picture of the situation is needed. We can look at climate models, and they tell us what we can expect, but it is also useful to have an idea of why increased greenhouse gas concentrations result in higher surface temperatures. The saying “Everything should be made as simple as possible, but not simpler” has been attributed to Albert Einstein, which also makes me wonder if we – the scientists – need to reiterate the story of climate change in a different way.
Gavin has already discussed this (also see here and here), but it may be necessary to tell story over again, with a slightly different slant. So how can we explain how the greenhouse effect (GHE) work in both simple terms and with a new angle? I also want to explain why the middle atmosphere cools with increasing greenhouse gas concentrations associated with an increased GHE. Here I will try to present a conceptual and comprehensive picture of GHE, explaining both the warming in the lower part of the atmosphere as well as the cooling aloft, and where only the most central features are included. Also, it is important to provide a good background, and we need to start with some very fundamental facts.
Four main physical aspects
Several factors are involved, and hence it may be useful to write a simple recipe for the GHE. This recipe then involves four main ingredients: (i) the relationship between temperature and light, (ii) the planetary energy balance, (iii) the distance light travels before being absorbed, and (iv) the relationship between temperature and altitude.
(i) Temperature and light
Energy can be transmitted in many different ways, involving photons (light or electromangetic radiation), conduction, and motion. Most of these require a medium, such as a gas, fluid, or a solid, but space is basically a void through which photons represent virtually the only form for energy transfer. Hence, planets tend to gain or lose energy to space in the form of photons, and we often refer to the energy loss as ‘radiative heat loss’.
A fundamental law of physics, known as the Planck’s law, says that radiative heat loss from any object depends on its temperature. Planck’s law also explains the colour of the light, or its wavelength, and hence explains why iron gets red hot when heated sufficiently.
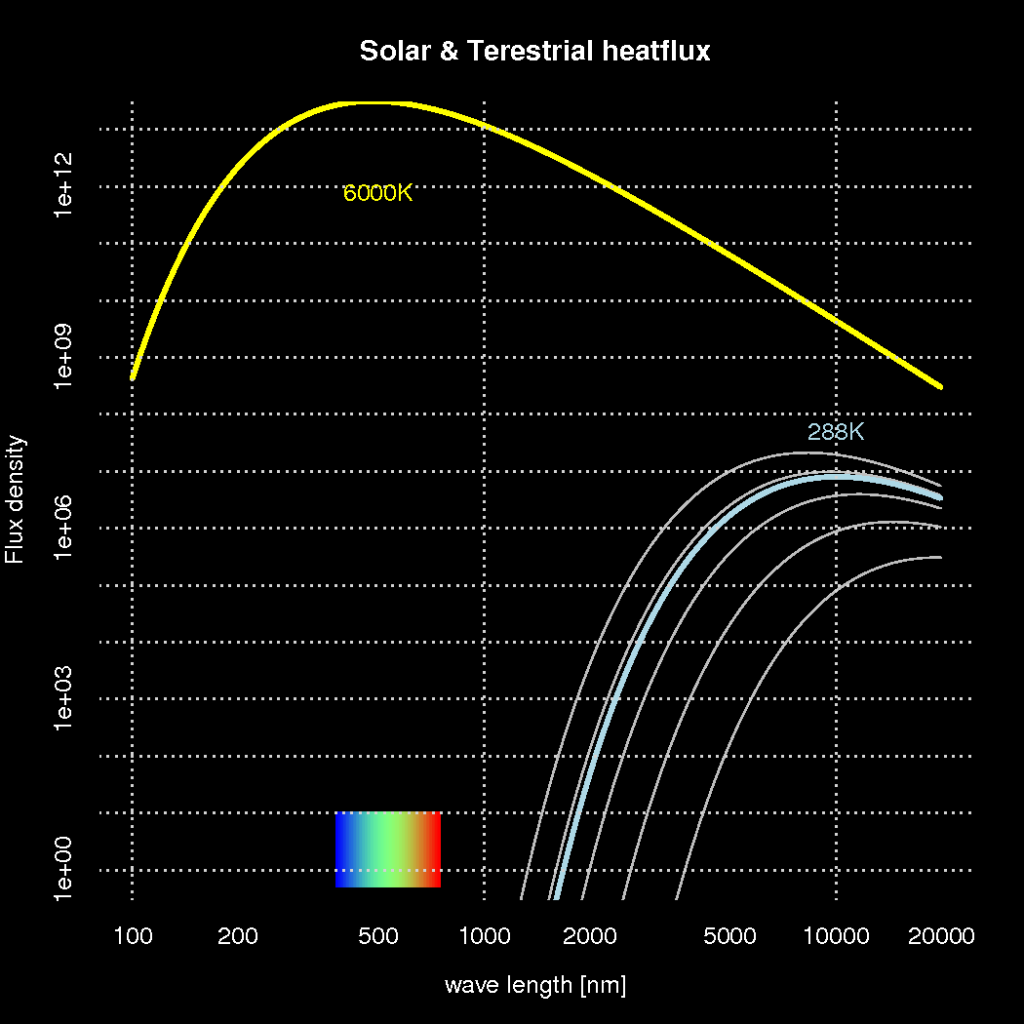
Planck’s law predicts that the light from an object with a temperature of 6000K – such as the solar surface – produces light that is visible, whereas objects with a temperature of 288K produce light with a wavelength that our eyes are not able to see (infra red). This is illustrated in Figure 1 showing how the light intensity (y-axis; also referred to as ‘flux density‘) and the colour of the light (wave length) vary for objects with different temperatures (here represented by different curves). The yellow curve in the figure represents the solar surface and the light blue curve the earth.
(ii) The planetary energy balance
The planetary energy balance says that our planet loses heat at the same rate as it receives energy from the sun (otherwise it would heat or cool over time). This is because energy cannot just be created or destroyed (unless it involves nuclear reactions or takes place on quantum physics scales).
The planets’ distance from the sun and the brightness of its surface dictates how much energy it receives from the sun, as the light gets dimmer when it spreads out in space, as described by Gauss’ theorem.
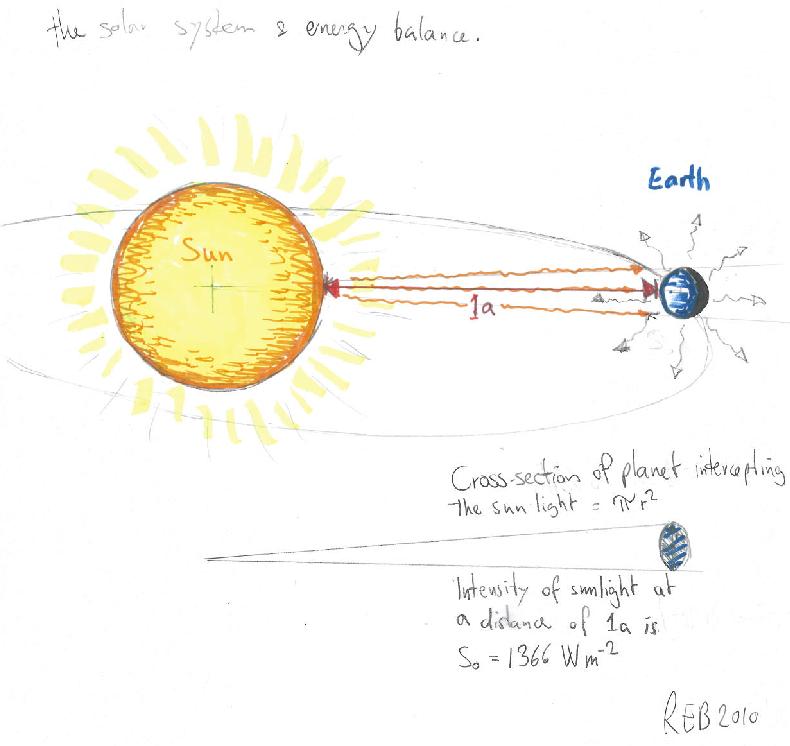
The energy flowing from the sun is intercepted by the earth with energy density described by the ‘solar constant‘ (S0=1366W/m2), and the amount of energy intercepted is the product between this flux density and the earth’s disc (minus the reflected light due to the planet’s albedo: A ~0.3). The average heat loss is given by the product of earth’s surface and its black body radiation:
S0/4 (1-A) = σT4,
where σ=5.67 x 10-8W/(m2 K4) is the Stefan-Boltzman constant. This gives a value of 255K, known as the emission temperature.
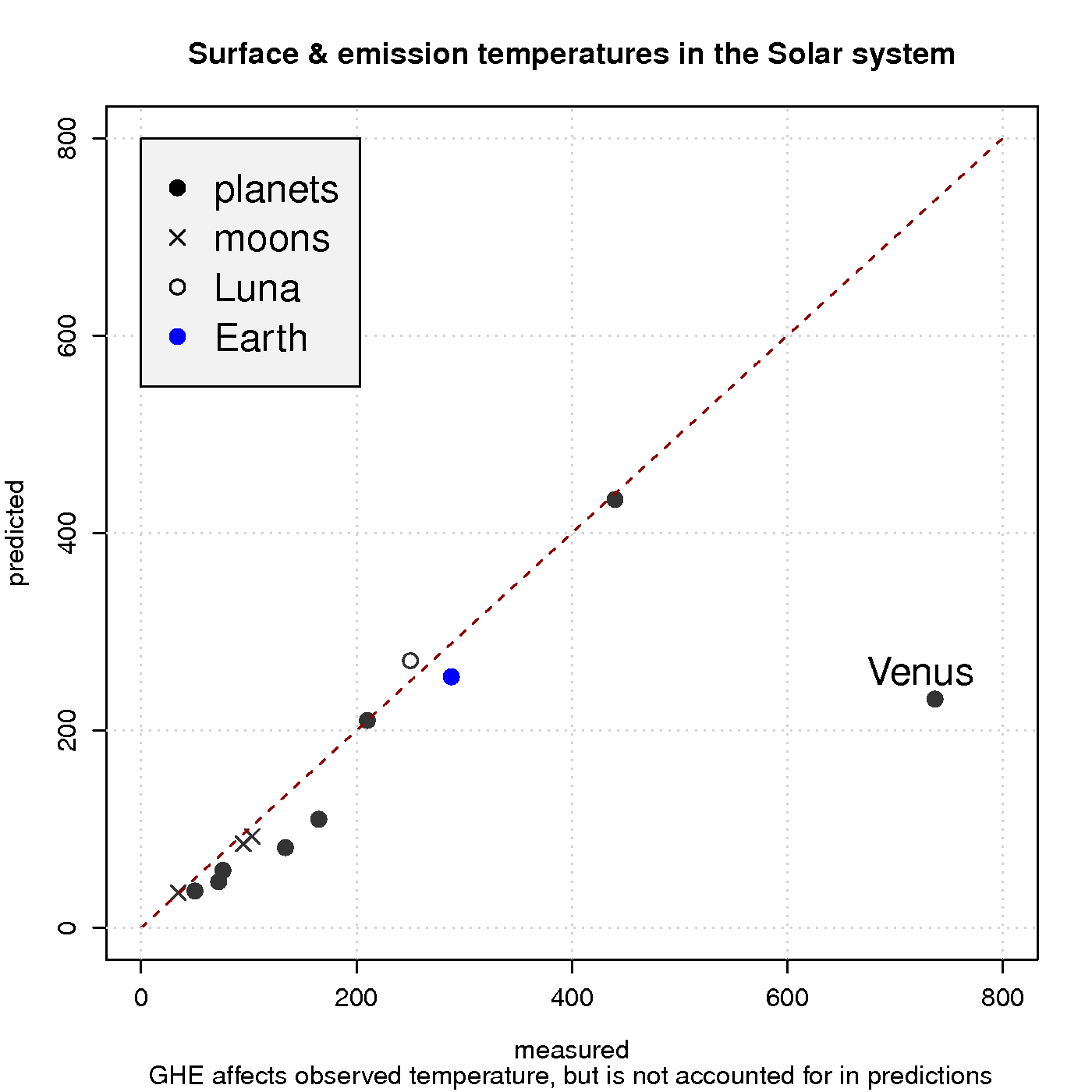
Figure 3 shows a comparison between observed surface temperature and calculated emission temperature for the planets in the solar system, based on the balance between energy from the sun and heat loss due to black body emission. In these simple calculations, the greenhouse effect is neglected, and the black body radiation can be derived from Planck’s law. The calculations agree quite well with the observations for most of the objects in our solar system, except for Venus which is known to harbour a strong GHE and has a hotter surface than Mercury despite being about twice as far away from the sun.
(iii) Light absorption
It is also clear that our planet is largely heated at the surface because the light from the sun – which is visible for our eyes – penetrates the atmosphere without much absorption (hence we can see the sun from the ground). However, the atmosphere is a medium of gas and particles that can absorb and scatter light, depending on their wavelength (hence explain why the sky is blue and sunsets orange).
The distance light travels before being absorbed – optical depth – can vary with the light’s wavelength and the medium through which is travels. The optical depth in our atmosphere is different for visible and infra-red light.
Infra-red light is absorbed by molecules, which in turn get more energetic, and the excited molecules will eventually re-emit more infra-red light in any random direction or transfer excess energy to other molecules through collisions. In a optically thick (opaque) atmosphere, there will be a cascade of absorption and re-emission.
Hence, whereas the planet is heated at the surface, it’s main heat loss takes place from a height about 5.5 km above the ground, where most of the radiation is free to escape out to space. The optical depth dictates how deep into the planet’s atmosphere the origin is for most of the planet’s infra-red light (the main planetary heat loss) that can be seen from space. Furthermore, it is the temperature at this level that dictates the magnitude of the heat loss (Planck’s law), and the vertical temperature change (lapse rate) is of course necessary for a GHE. The temperature at this level is the emission temperature, not to be confused by the surface temperature.
We know that the optical depth is affected by CO2 – in fact, this fact is the basis for measuring CO2 concentrations with infra-red gas analysers. Molecules composed of three or more atoms tend to act as greenhouse gases because they can possess energy in terms of rotation and vibrations which can be associated with the energy of photons at the infra-red range. This can be explained by theory and be demonstrated in lab experiments. Other effects are present too, such as pressure and Doppler broadening, however, these are secondary effects in this story.
(iv) The relationship between temperature and altitude
There is a well-known relationship between temperature and height in the troposphere, known as the ‘lapse rate‘ (the temperature decreases with height at a rate -6K/km). The relationship between temperature and altitude can also be seen in the standard atmosphere. The lapse rate can be derived from theory for any atmosphere that is the hydrostatically stable condition with maximum vertical temperature gradient, but it is also well-known within meteorology. Thus, given the height and value of the emission temperature, we can get a simple estimate for the surface temperature: 255K + 5.5km * 6K/km = 288K (=15oC; close to the global mean estimated from observations given by NCDC of ~14oC).
Enhanced greenhouse effect
The term known as the ‘enhanced greenhouse effect’ describes a situation where the atmosphere’s becomes less transparent to infra-red light (reducedincreased optical depth), and that the heat loss must take place at higher levels. Moreover, an observer in space cannot see the infra-red light from as deep levels as before because the atmosphere has become more opaque.
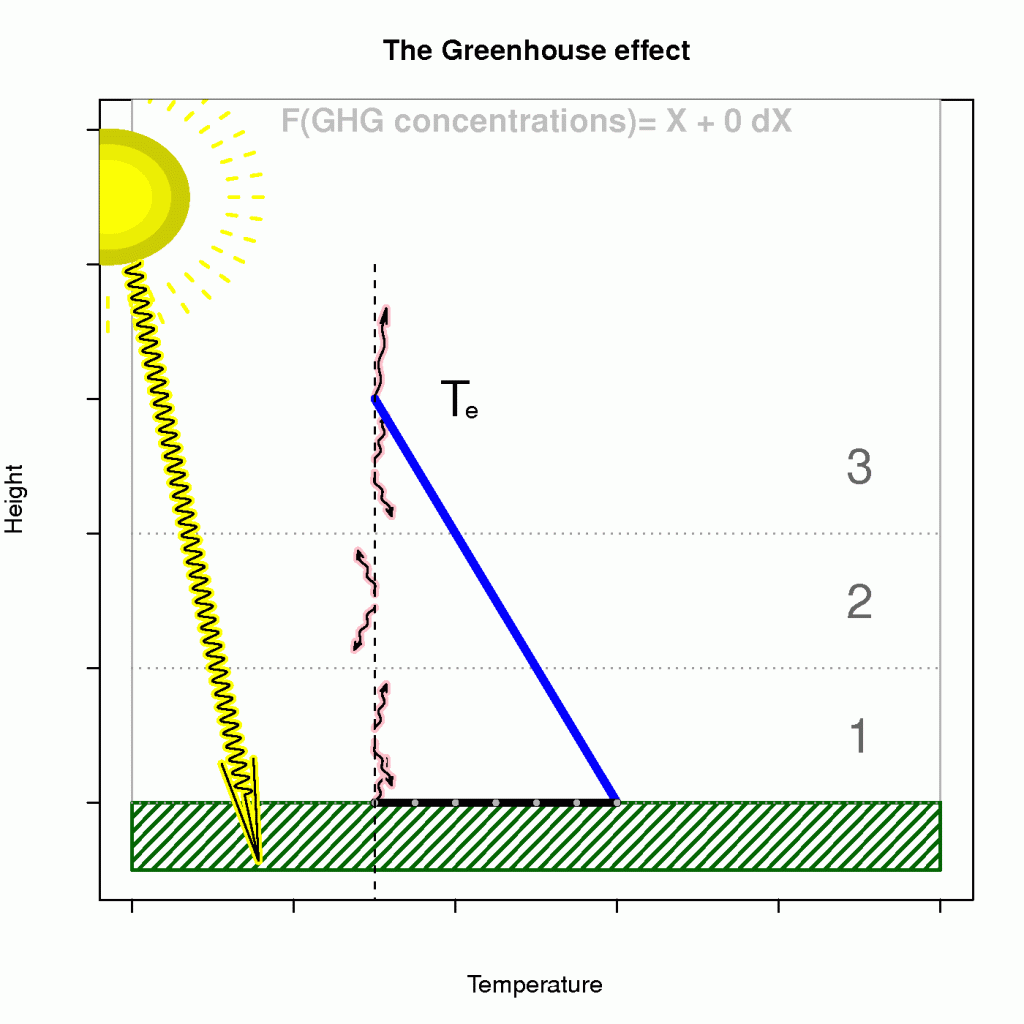
The effect of heightened level of heat loss on the surface temperature is illustrated in Figure 4, where the emission temperature and lapse rate are given if we assume an energy balance and a hydrostatically stable atmosphere on average (a generally hydrostatically unstable atmosphere would be bad news).
Hence, a reducedincreased optical depth explains why atmospheres are not easily ‘saturated‘ and why planets such as Venus have surface temperatures that are substantially higher than the emission temperature. Planets with a thin atmosphere and insignificant greenhouse effect, on the other hand, have a surface temperature that is close theto the estimates from the planetary energy balance model (Figure 3).
Feedback processes
The way the atmosphere reacts to changes in the optical depth is more complicated, due to a number of different feedback mechanisms taking place. But to get a simple overview, it is useful to keep in mind that the optical depth is sensitive to how much water vapour (humidity) there is in the air, and that the lapse rate is sensitive to the composition of the atmosphere (i.e. humidity). Furthermore, the albedo A is affected by clouds, snow, ice, and vegetation, all of which affect the way the earth receives energy from the sun.
In our simple picture, feedback processes affect changes in the height of the level where most heat loss takes place, the slope of the lapse rate, and heating at the surface (and hence the emission temperature).
So why is the upper atmosphere cooled then?
The upper atmosphere, comprising the stratosphere and mesosphere, is expected to cool during an AGW, as shown by the GCMs. So what is happening there? This is when the picture becomes more complicated.
Since CO2 mostly absorbs/re-emits infra-red light at around 14 microns, an increased concentration in the troposphere will reduce the upward infra-red radiation at this band. The total energy is roughly constant, but it is made up from increased emissions at other bands because it’s warmer. There is less absorption by CO2 of upwelling infra-red light above the troposphere, but increased emission as a function of increased concentrations. Thus there is a cooling.
Controversy?
Can this picture be falsified, e.g. if other factors were to play a role too? For instance, can this situation be altered by changes in the sun?
Changes in the sun can of course affect the amount of energy received by the earth through changes in its output, variations in the intensity of UV-light, or perhaps even clouds through galactic cosmic rays. But it’s hard to see any systematic long-term trend in the level of solar activity over the last 50 years, and it is difficult to see how solar activity may have an effect while other factors, such as GHGs, don’t. Gavin and I recently published a study on the response to both solar activity and GHGs, and found similar magnitude for both forcings in both observations and the GISS GCM.
There have been claims of negative feedbacks, such as the “iris effect“. One would expect negative feedbacks in general to dampen the response to most forcings, unless they involve a particular process that is active for a particular forcing. In other word, why would a negative feedback act for GHGs but not for solar forcing? Many feedbacks, such as changes in atmospheric moisture, cloudiness, and atmospheric circulation should be similar for most forcings.
Another question is why we do see a global warming trend if the negative feedbacks were most important (Figure 5). Negative feedbacks usually imply quiet conditions in a complex system, whereas positive feedbacks tend to lead to instabilities, often manifested as internal and spontaneous oscillations (see Figure 5). It is reasonable to expect the feedback processes to affect natural variations as well as forced changes such as an enhanced GHE, orbital changes, volcanoes, or changes in the sun.
The point about negative feedback also brings up another interesting issue: Negative feedbacks usually act to restore a system to a particular zero-level state. What would the zero-state be for our climate? No greenhouse effect or some preferred level of greenhouse warming? There is already a natural GHE that, together with other atmospheric effects, can account for about 32oC higher global mean surface temperature. What makes this state so special, and can we explain the present natural GHE in the presence of negative feedbacks (consider starting from a state with no GHE)?
Hence, claims of negative feedback is controversial because all these tough questions then need to be addressed. We can write down a simple recipe for the GHE, but it is indeed challenging to reconcile a presence of a negative feedback with our observations, or explain the current observed global warming in any other terms.
L. David Cooke (#297),
You are mistaken. The 32C figure includes all gases and CO2’s greenhouse effect can not be deduced quite so straighforwardly from its concentration in the atmosphere. With the current amount of CO2 in our atmosphere, the effect is logarithmic: a doubling of the amount of CO2 in the atmosphere would raise temperatures by about 1.2C. To that figure, one should indeed add the feedbacks (or “secondary effects” as you put it).
You should research the accepted scientific findings a bit more before indulging in such speculation, me thinks. At the top of RealClimate’s home page, you’ll find a link labelled “start here”.
Gordon:
I think Gordon is right about human nature, but wrong in thinking that scientists can lead by modelling the sacrifices required from everyone. Chris G @273 has it right: AGW is a tragedy of the commons. It’s been discussed previously on RC.
Hey Anonymous Coward,
I am quite aware of the effects of CO2 in the atmosphere. What apparently you are missing is the point I am trying to make.
An average person is going to apply a simple rule set based on the words of an expert. When such a one suggests that the warming in the atmosphere of 32 Deg. C is directly related only to CO2 then the response is going to be as I outlined. CO2 would have to rise in a linear manner because the expert implied it was so, without adding the caveat, as you indicate.
Generally, if I recall correctly, the rule is roughly that a doubling of CO2 density in the atmosphere should result in roughly a 4 Deg. C rise in surface temperature. So if we apply this rule then the change between 385 and 280ppm of CO2 should only provide a change of about 1 Deg. C. (Your 1.2 Deg. C works just fine for this example.)
However, if as the expert explained earlier that the CO2 in the atmosphere was responsible for a 32 Deg. rise from the insolation baseline then we need to discuss the initial value and the points of doubling. By inference I believe you are suggesting that the CO2 levels had to double 8 times between 0ppm and 280 ppm.
Hence, what I see as being proposed in your inference is that the initial CO2 concentration had to be approximately 1.09ppm, doubling to 2.18, then 4.4, 8.9, 18, 35, 70 140 and finally 280ppm with each rise forcing a rise in temperature of 4 Deg. C each time. Sorry, but this line of thinking is absolutely ludicrous.
It is likely that the change in temperature due to the change in concentration was more like when CO2 reached 280ppm from 140ppm the global average temperature would have rose roughly 2 Deg. C. Going back further, 70ppm would be 1 Deg. and so on down the slope. However, we also have to keep in mind that early Earth’s atmosphere appears to have been dominated by Carbon Oxides, so it is unlikely the Earth had CO2 levels below roughly 240ppm in the last billion years. If the levels had been much lower it would have reduced the level of the flora on the planet to subsistence levels not unlike during “Snowball Earth”.
(As we know plants in the presence of light generally generate O2 from CO2 and in the Dark we see sugars being consumed causing flora to emit CO2. Hence, it is unlikely that after flora became common place the balance between CO2 and O2 was ever much out of sync. until the presence of fauna. (Such as Blue-Green Algae which could both emit and consume both CO2 and O2 having characteristics of both flora and fauna.))
The heating ratio between IR re-emission and CO2 density seems to be a factor of doubling (double the concentration/double the intensity for the same distance from the surface), unlike the radiant outflow from a black body (double the distance from the surface, 1/4 the intensity). Hence, the rise in temperature may not be logarithmic. The rise in emitted energy seems a much simpler ratio, emitted energy in the case we are discussing does not change at a constant rate, it changes in relation to the intensity of the emitter, this change over time is a linear function due to the systemic processes which we are still working to describe, sorry.
Would you like to explore this further? I for one would like to see a follow up of the current work by Dr. Benestad that more clearly defines the means of “cause and effect” and how this is resulting in high surface temperatures. However, I would prefer to start the discussion not with the anthropogenic influence baseline; but, the natural baseline. From here we could build the description of the basic physics in regards to the Earth and Sun’s relationship and the variances in insolation, emissions, reflections and re-emissions. If instead you would like to discuss this further here, I am interested.
Cheers!
Dave Cooke
If you do the calculations as the formula is written, you get a T of over 300K
The formula should be (So/4)*(1-A)=sigma*T^4
That will give a T of 255K
I think the explanation is too complex and certainly too long. Considering the public are acustomed to movies starring aliens who can see in the infrared I would propose that it would make a bigger impact on people’s understanding if they could “see” the sky with and without CO2, both from the ground and from orbit.
Well, Mal, I agree that it is a crisis of the commons. I went to look at the post you referenced, and, lo and behold, the solution to the fishing crisis is instigated by…what?…by leaders making sacrifices (the top 5 fisher-folk deciding to reduce their catch by 80%). Hmmm…
Ray, please say whether you’re worrying about your great-great-grandchildren.
Simon Abingdon,
No children implies no further progeny. I leave no hostages to fortune.
#307–
I’d have thought you’d been hanging around RC long enough to know this: Ray has previously stated that he has no children, and does not expect to have any.
Your point, Simon? (Or, if you prefer, ‘simon.’)
Inquiry ad hominem, rather than refutation ad hominem?
Patrick and Chris Colose,
Referring to Chris’:
“…only similar in that regions above the tropopause are typically optically thin enough to not matter much for the net radiative budget…”
I’m sure you know your stuff, but only about 75% of the mass of the atmosphere is below the tropopause. If CO2 is relatively well mixed, I’d be surprised to learn that the last 25% of the CO2 has negligible effect.
The first point I’m trying to make is that, in my opinion, if what we are talking about is the wavelength(s) absorbed by CO2, then where the partial pressure (or optical density) of C02 drops to near-0 is a lot more interesting than where the sum of all gas partial pressures, where the majority of other gases do not absorb at the wavelength of CO2, drops to near-0, which is the more traditional meaning for TOA.
Uh Gordon, I assume you mean that the leaders of the fishers where the ones catching the most fish. I don’t think you originally meant that the scientists were leading in the sense that they were the ones producing the most CO2.
Sure, if the top 5 producers of CO2, by absolute, over time, or per capita (different top 5 depending on how you measure it, US, Australia, UK, China, whomever), were to reduce their production by 85%, we’d be well on our way to a solution.
Re 303 L. David Cooke
The shape of the CO2 absorption spectrum: roughly, there is a peak in the absorption near 15 microns, with an overall tendency of exponential decay of the optical thickness outward from 15 microns (within limits). This means that, for any optical thickness smaller than the peak value, doubling the CO2 (which doubles the optical thickness from CO2 at every wavelength) shifts the wavelength at which that optical thickness occurs outward from the center by some amount. Thus, the absorption band widens a certain amount for each doubling (out to a point where parts of the spectrum that don’t fit this shape become important). But at the center of the band, the optical thickness increases.
For sufficiently small intervals, any smooth continous function can be approximated as linear; for sufficiently small changes in optical thickness, two identical successive increments will have nearly the same effect. Thus starting at zero CO2, adding some small amount of CO2 has some effect, and doubling the amount of CO2 approximately doubles that effect. This would apply to sufficiently small amounts of any gas.
But when optical thickness gets to a significant value (such that the overall spatial temperature variation occurs on a spatial scale comparable to a unit of optical thickness), each successive increment tends to have a smaller effect – when optical thickness is very large relative to the spatial scale of temperature variation, the flux at some location approaches the blackbody value for the temperature at that location, because the distances photons can travel from where they are emitted becomes so small that everything ‘within view’ becomes nearly isothermal. This is called saturation.
In the approach to this limit, when optical thickness is sufficiently large, a linear approximation can be made (remember what was said earlier about small intervals), wherein each doubling results in half the change of the last doubling (that’s based on an approximately linear change in temperature relative to optical distances, and an approximately linear change in the Planck function over temperature – applicable for the small distances and small temperature variations implied).
Within a continuum of material (ie not at TOA, but within the atmosphere), temperature generally varies continuously (at least if you are willing to use high enough resolution, so this should tend to apply to the surface as well), so a pair of oppositely directed fluxes will both eventually saturate, and at that point they will be the same, so that there is no net flux (assuming the optical thickness is also distributed continuously; net fluxes can persist where there is a transparent gap, for example (such as at TOA)).
At sufficiently large amounts of CO2, the center of the band becomes saturated, so the band-widenning effect acts alone, thus a doubling of CO2 widens the absorption band by about the same amount as the last or next doubling.
At present, the effect of CO2 is or is close to saturated at the tropopause (small or zero net flux at the tropopause), and because parts of the lower stratosphere are nearly isothermal while the upper stratosphere has a negative lapse rate, the effect CO2 at TOA is saturated in a sense (OLR reaches a minimum, beyond which, farther increases in optical thickness result in increasing OLR).
PS (TOA forcing – Tropopause forcing = **forcing of the stratosphere (and mesosphere, etc, but almost all of that is the stratosphere by mass); increasing CO2 has a larger forcing at the tropopause than at TOA (this is dependent on the lapse rate of the stratosphere), hence stratospheric cooling; stratospheric adjustment returns the stratosphere to equilibrium by increasing the net flux out of the stratosphere by the same amount as the initial stratospheric forcing; thus, a portion of stratospheric cooling can be transfered to the forcing at the tropopause level (resulting in the tropopause-level forcing with stratospheric adjustment/equilibration). Warming must occur below the tropopause to increase the net LW flux out of the tropopause to balance the tropopause-level forcing; there is some feedback at that point as the stratosphere is ‘forced’ by the fraction of that increase which it absorbs, and a fraction of that is transfered back to the tropopause level – for an optically thick stratosphere that could be significant, but I think it may be minor for the Earth as it is (while CO2 optical thickness of the stratosphere alone is large near the center of the band, most of the wavelengths in which the stratosphere is not transparent have a more moderate optical thickness on the order of 1 (mainly from stratospheric water vapor; stratospheric ozone makes a contribution over a narrow wavelength band, reaching somewhat larger optical thickness than stratospheric water vapor) (in the limit of an optically thin stratosphere at most wavelengths where the stratosphere is not transparent, changes in the net flux out of the stratosphere caused by stratospheric warming or cooling will tend to be evenly split between upward at TOA and downward at the tropopause; with greater optically thickness over a larger fraction of optically-significant wavelengths, the distribution of warming or cooling within the stratosphere will affect how such a change is distributed, and it would even be possible for stratospheric adjustment to have opposite effects on the downward flux at the tropopause and the upward flux at TOA).
**-it is correct to say that, right?
————–
Plants don’t necessarily stabilize the amount of atmospheric CO2; they could actually destabilize it in some ways (forest fires, etc.). What would affect atmospheric CO2 directly is the changes in the total amount of stored C in vegetation and soil, which is changed by imbalances between C-fixation and respiration/decomposition/oxidation.
The geologic burial of organic C would contribute to an increase in free O2, but the impression I’ve gotten is that the dominant source of free O2 (at least before the Phanerozoic?) has been the escape of H to space (which is limited by the abundance of H above the tropopause (it must diffuse upward to feed the escape), which is limited by sources of H (which would also diffuse to feed dissociation reactions). Not so much by direct photolysis of water vapor (not generally a lot of that in the stratosphere), but from CH4, which could build up in a nearly oxygen-free atmosphere, and being largerly of biotic origin, with the H coming from photosynthesis (releasing O); O2 buildup itself was delayed because of geologic O2 sinks (in particular, the conversion of ferrous Fe (naturally present in the crust and mantle and which can dissolve in the oceans) to ferric Fe (precipitates out of the water, the source of banded-iron formations, which humans have used to get Fe).
PS because of the lack of O2 and the presence of methanogens, CH4 could have had a more important role in the total greenhouse effect of the (late?) Archean Eon.
Both geologic organic C and gelogic inorganic C are sources of CO2 to the atmopshere, ocean, and vegetation and soil. They are typically relatively small fluxes of CO2, as are the sequestration of C from those reservoirs to gelogic reservoirs either as organic C or inorganic C (carbonate minerals) – an exception being the result of recent human activity.
Over geologic time, geological processes can change the amount of CO2 in the atmosphere+ocean+vegetation+soil (let’s say, AOVS) significantly via changes in the geologic emission rate. Chemical weathering (favored by warm wet conditions, and a supply of mechanically-weathered debris bearing some kinds of silicate minerals) can act, depending on the distribution of continents, and their topography (and minerology (?)) relative to weather patterns, as a negative feedback to climate changes, tending to stabilize the atmospheric CO2 level by allowing the climate to shift until the rate of removal balances the rate of supply (it has been suggested that the mechanism is relatively ineffective when the continents are concentrated at low latitudes – see articles about “Snowball Earth”). Because the flux involved is usually quite small (exception could occur in the hot, CO2 rich, glacially-eroded aftermath of a Snowball), this is ineffective in preventing larger changes over the short term. It is also possible for cold climates to increase chemical weathering in some ways, by lowering sea level to expose more land to erosion (though I’d guess this can also increase oxydation of C in sediments) and by supplying more sediments via glacial erosion for chemical weathering (of course, those sediments must make it to warmer conditions to make the process effective – downhill and downstream, or perhaps via pulsed ice ages (?)).
(Chemical weathering supplies ions that are able to combine with CO2 to form carbonate minerals. Higher temperatures below the surface tend to favor the release of CO2.)
More rapid fluxes occur within AOVS that tend to redistribute C towards some equilibrium for a given climate and given amount of C in total, etc (this doesn’t necessarily mean that the fraction of the total in each one tends to be constant). However, exchange with the deep ocean is still relatively slow, and the amount that the upper ocean can hold for a given atmospheric CO2 amount depends on various ions present, which are generally supplied at a slow rate (this involves chemical weathering and also the dissolution of carbonate minerals). Redistribution of C has acted as a positive feedback to orbitally-forced glacial-interglacial variations (ice ages) – but this depends on some particulars and isn’t necessarily a general feature applicable to every geologic age (?).
———-
The sun has gotten gradually brighter over geologic time. Thus more CO2, or more CH4, or ____, would have been required earlier in Earth’s history to maintain the same temperature.
———-
A signficant hysteresis is involved in Snowball episodes. Depending on meridional heat transport, when freezing temperatures reach deep enough towards low-latitudes, the ice-albedo feedback can become so effective that climate sensitivity becomes infinite and even negative (implying unstable equilibrium for any ‘ice-line’ (latitude marking the edge of ice) between the equator and some other latitude). For a combination of CO2, CH4, and solar brightness that would allow such an unstable equilibrium, there will be at least two stable equilibria – one is a Snowball (very cold), the other being significantly warmer. During a Snowball, chemical weathering is essentially shut-down, so CO2 from geologic sources can build up. When their is enough CO2 to start thawing near the equator, a runaway positive feedback would tend to ensue, not stopping until the climate is much warmer.
Chris G (# 310),
Sorry– after going back to my previous comment which you quoted I see that I did not get that point across clearly or correctly. Indeed, the TOA and tropopause forcing can be quite similar, but also very different depending upon the nature of the forcing (see Hansen et al., 1997 for specifics). For instance, if the solar irradiance were to increase in a spectrally-uniform manner (over all wavelengths) then some fraction would be absorbed in the stratosphere, a region not well coupled by atmospheric motions to the lower atmosphere, and so a certain amount of energy will be radiated back to sapce without affecting the surface temperature. However, the traditional RF often used now (defined in IPCC 2001, 2007 although deviations from this exist, especially for aerosol evaluations) already incorporates stratospheric adjustment which occurs on timescales of several months and so TOA/tropopause forcings become comparable.
No, Chris, I didn’t intend to imply that scientists (as a group?) produce the most CO2. However, if I understood Mal Adapted correctly, he implied that scientists wouldn’t (shouldn’t? couldn’t?) be leaders in the fight against global warming. (Is that anything like the “war against drugs?” And how successful the “government” has been in that one?)
But, I expect that leaders are where you find them, not where they are “supposed” to be.
Dear rasmus,
You stated:
“Thus, given the height and value of the emission temperature, we can get a simple estimate for the surface temperature: 255K + 5.5km * 6K/km = 288K (=15oC; close to the global mean estimated from observations given by NCDC of ~14oC).”
Can you relate that to works like “Effect of CO2 line width on 15 μm atmospheric emission”, B. Kivel et al. (1976), which use the emission from CO2 to explore the Troposphere temperature? While the emission is a function of frequency and height, the general average for CO2 is usually assumed to come from a region with -53 deg. C which relates to almost double the height you use in your statement.
[edit]
“There is less absorption by CO2 of upwelling infra-red light above the troposphere, but increased emission as a function of increased concentrations. Thus there is a cooling.”
It would help me (and perhaps others)to understand CO2-related stratospheric cooling if you would clarify where the energy comes from for the increased emission by the greater concentration of CO2 in the stratosphere.
Any clarification would be appreciated.
[Response: It doesn’t matter. In the stratosphere, it from solar and LW absorption by ozone, and a small amount from water vapour, but what ever the temperature is, there is radiation from the CO2. – gavin]
#311:
It’s kind of important to know which countries are the largest emitters I think. And the UK is not close to being on either top 5 list. So there you are…
Top 5 emitters (2007): China, USA, India, Russia, Japan
Top 5 per capita emitters (2006, ignoring small countries emitting less than 0.5% of the world total which would other crowd the list): USA, Australia, Canada, Saudi Arabia, Khazakstan
Regarding
mircea (26), Thomas (34), and (46) Chris Colose:
I think Thomas had it right, and Gavin and Chris Colose were misinterpreting mircea’s question.
Ture, the sun’s radiation output at the sun’s surface, with a temperature of 5780K, is higher at any frequency than the earth’s output at the earth’s surface, at a temperature of 287 or 288 K, but we don’t receive the sun’s radiation at the sun’s surface. The radiation is attenuated by that
factor in figure 2, which is what Gavin and Chris Colose should have referred to.
The sun has a radius of 695,600 km, the earth is 1 astronomical unit away at 149,600,000 km, so we only receive
(149,600,000/695,600)^-2 = 1/46,253 of the sun’s output at any frqueency.
The net result is, earth receives a lot less infrared radiation from the sun than it radiates away.
Dave Cooke (#303),
+4C per doubling is a somewhat higher than usual (but still reasonable) number that includes feedbacks such as an increasing amount of atmospheric H2O but also non-greenhouse effects such as a diminshed reflective ice cover on the surface of the planet. +1.2C per doubling does not take such feedbacks into account. These numbers only apply in conditions similar to the ones we experience now.
If we assume +4C per doubling, the effect of going from 280 to 385 ppm would be +1.8C.
The atmospheric CO2 concentration seems to have fallen a good bit below your estimate several times in the past million (never mind billion) years during glaciations and these episodes were quite cold indeed.
You’re confusing the rate at which radiation intensity drops from the surface of a sphere as opposed to a point source.
And so on… please take some time to inform yourself before engaging in such reckless speculation. I think you’ll find that these things are better understood than you suspect.
Gordon @306:
Um, you may want to read that post again. It refers to the actual collapse of the Newfoundland cod fishery. The crisis wasn’t solved, and the cod population of the Grand Bank has yet to recover. It’s a classic example of the TotC.
234 Gilles, and Patrick,
Thaks for your answers. I’m still learning them.
I wondered why Hansen says we must stop below or at 350 ppm of co2.
Suppose we get a co2 doubling by 2100 to 540 ppm, and a +3,4k temp, then stabilization. What’s so catastrophic about that ?
[Response: What was the sea level rise the last time the planet was even close to that warm? – gavin]
RE: 319
Hey Anonymous Coward,
Okay, I agree that for hard and fast values you are correct, that the value of change for the suggested 240ppm non-anthropogenic baseline for the last 614ky the values has varied by as much as 22ppm.
ref: http://www.nature.com/ngeo/journal/v1/n5/full/ngeo185.html
http://www.epa.gov/climatechange/science/pastcc_fig1.html
To try to extend this back through geologic proxies is still a science in it’s infancy and I will abide by known accepted measurements. However, even this 614Ky period contained substantial glaciation, orbital, astronomical and volcanic events. The combination of flora and fauna bio-mass CH4 production and geologic sources have provided a fairly stable CO2 source. This was balanced by the land and marine flora conversion of CO2. (Though some have claimed in this thread that the balance of O2 generation may be related to the reduction of hydrogen by gravitational loss; most of the isotopic record still suggests that the balance of O2 appears to have a biologic influence and was not the result of planet wide respiration of H2.)
As to “charges of speculation”, I have yet to see a reasonable explanation as to the 32 Deg C. offset above the accepted TOA insolation value as being founded in the CO2 balance. (Roughly the difference between the 255 Deg. K levels from the est. 1366 watts/m^2 at the TOA, plus the retention of roughly 284 Watts/m^2 insolation by all GHG and “Warming” contributors, resulting in a roughly averaged 283/284 Deg. K base temperature of the atmospheric column.) I would prefer that rather trying to change the subject we concentrate on the issue I have requested we focus on.
The most recent paper I read from this past Spring does suggests that the CO2 levels have varied more; however, there is not sufficient geologic evidence that I have seen (Even with the examination of the foraminifera O2 isotope record. http://en.wikipedia.org/wiki/Delta-O-18 see side panels for graphs to compare to the ones from the URLs above and below.), except for Pre-Cambrian “Snowball Earth” and the Carboniferous period; of significant swings (>35%) in the CO2 and O2 balance, to my knowledge. The basis of the recent work appears to be primarily model based.
ref:
http://en.wikipedia.org/wiki/File:Phanerozoic_Carbon_Dioxide.png
However, as I have entertained this issue in the past here in RC, I am willing to keep an open mind.
(BTW Note: The 4 Deg. C doubling was the estimate change for between the 280 and 560 ppm values. I made a mistake earlier suggesting the 1 Deg. C was between 280 and 460 when it should have been 280 and 560ppm, sorry. Thanks for the correction, (105/280ppm)=@.37 37%*4 should be near 1.5 Deg.)
Cheers!
Dave Cooke
#321 [Response: What was the sea level rise the last time the planet was even close to that warm? – gavin]
gavin, I am interested in what an x feet (for various x) increase in sea level means as a reduction in actual global land area but perhaps more relevantly in the resultant increase/decrease in habitable land area (increased I imagine in Canada, Siberia, Antarctica etc).
I don’t think mass migrations have ever been a problem for the human race. When flying along the eastern seaboard of the USA I was always amazed that the cities I saw had been there for barely 200 years.
Hey Patrick,
Okay, for starters to clarify, you seem to be suggesting
that the absorption window of the atmosphere to re-
emitted (300nm-1.2um initialy) solar energy has a center
frequency of roughly 15um. The first issue I am have with your explanation is you are not defining the bandpass bandwidth. Also, I seem to be having an issue in trying to understand what is the ratio of the bandpass window frequency in relation to the center frequency intensity.
In short, at the attenuation levels of 15um say +/- 1um;
how many db down would you suggest the throughput would
be at +/- 1um? Also, we should would need to determine
the db of Earth emitted 15um +/- 1um to try to determine
the radiant output being emitted outside beyond the central frequency.
As to the idea that the bandwidth changes in relation to
the intensity I find difficult. The attenuation should
remain constant, if only the initial value is greater
hence, more energy “leaks past” the “filter”, then we are fine.
Next as to what determines a “significant value”
regarding the idea of optical translucence. The initial
description of the acceptance window acting as a optical
wave guide is fine. As the intensity increases yes the
sidebands will begin to pass through to a point at which
the attenuation exceeds the intensity of the signal. At
this point it would appear you are suggesting that
radiation of the energy no longer operates as the
transport or waveguide. This would suggest that
convection or conduction would have to take place to
transport energy beyond the “Irising” of the absorption
frequency of the atmosphere. So far I do not have any
problem with that idea.
Now as to the idea of then saturation of the CO2 window
we have a problem. Saturation cannot expand the window
beyond the attenuation limits of the bandpass or
absorption limitation as defined by the photonic emission spectrum of the working material. It would depend on the various energy bands of the working materials making up the “filter”.
I have seen absolutely nothing that suggests that the
15um band at the tropopause has reached saturation. Were
this true, if you removed convection, there would be
virtually no release of the insolation from the
atmosphere. We currently believe no less then 1080
Watts/m^2 has to be released from the Earth’s atmospheric system. By the same token if saturation were true then we could continue to emit CO2 to our hearts delight as the maximum potential retention of insolation by GHG has been reached.
There is a corundum in regards to your discussion of the
Stratospheric forcing at this time, as I see it. When we consider that the average Ozone change between 1950 and 2000 in was approximately 280 Dobson units we have another contributor to the reduction in the Stratospheric temperatures that are missing from your strawman. I tend to disagree, in that I do not think the effect of the Ozone Optical translucence (300nm to 1.2um) of the Stratosphere is insignificant. As the higher frequency (300nm-1.2um) energy level in relation to that being returned at the lower frequency of 15um should be proportionally higher.
(In short a cool Stratosphere does not a 15um Optical
Saturation argument make, as at 280 Dobsons, more O3
there should result in roughly 6-18watts not reaching the tropopause, depending on the season…)
Okay, leaving that subject, if we examine the total
estimated annual CO2 respiration it would appear to be,
according to the old Carbon Cycle cartoons, approximately 202Gt of CO2. Looking at the Mauna Loa graph it would appear that the normal seasonal fluctuation is around 7ppm globally at what, 7km? This change includes all normal seasonal variations forest fires, dead fall, harvesting, anthropogenic influences… (Albeit with a rising trendline.)
ref:
http://www.esrl.noaa.gov/gmd/ccgg/trends/co2_data_mlo.htm
l
As to the idea of CH4 contributing to an increase in O2
in the atmosphere we are leaving out the recent examples
of increased water vapor in the Stratospheric region. In short, it is much more likely that the H4 is combining with the O3 forming water-vapor in the Stratosphere causing the rise in Polar Stratospheric Clouds or the PSC’s that were such an interest 4 years ago.
Finally the conclusion that chemical weathering has a
greater impact on the reduction in the atmospheric CO2
during a Earth Snowball event then biologic functions
seems slightly humorous to me…; however, if you can
support the idea I would entertain looking at the data.
However, the point is we still have not addressed the
difference between the 255 Deg, K and the global 283/4
Deg K bottom of the atmospheric column and the role a an
increasing CO2 level plays. Can we please try to get
back to this issue as it would help many of us out a lot
if this could be explained clearly.
Cheers!
Dave Cooke
Re 303 L. David Cooke – I was reminded by 317 Anonymous Coward that you brought up the inverse square law. Absent emission, absorption, reflection, scattering, and refraction outside of a sphere with radius 1, and assuming steady state, the flux coming out of such a sphere is the same as the flux coming out of any closed surface enveloping that sphere; the area of a sphere is proportional the square of the radius, so the average flux per unit area going through successively larger spheres follows an inverse square law.
Hence the solar flux/area in space reaching Earth is only about 1366 W/m2.
(Remember that the Earth’s surface area is about 4 times it’s cross section and it has an albeod of approximately 0.3, so the global time average solar heating of the Earth is approximately (1366/4 * 0.7) W/m2 ~= 239 W/m2 (ignoring significant figures there)).
The vast majority of the mass of the atmosphere, and hence the vast majority of the optical thickness, is concentrated into a vertical distance that is very small relative to the radius of the Earth. Thus, to a first approximation, the Earth’s curvature and the increasing global area with height can be ignored. It isn’t really important to the Earth’s energy budget what the outgoing flux is at some great distance of the Earth; for the OLR, I think TOA can be approximated as having a radius on the order of 1 % larger – or less – than the radius at the surface. That would make a 2 % difference or less to the global area. Actually, though, most of the OLR originates from below the tropopause (can get up around 18 km in the tropics, generally lower) – with a majority of solar radiation absorbed at the surface, a crude approximation can be made that the area emitting to space is less than 2*(20/6371)*100 % ~= 0.628 % more than the area heated by the sun, so the OLR per unit area should be well within about 0.6 % of the value calculated without the Earth’s curvature (I’m guessing it would actually be closer to if not less than 0.3 % different).
(Another effect of the Earth’s curvature is that photons emitted downward that manage not to be absorbed first can end up going upward eventually. The refraction by the atmosphere also has effects that tend to counteract the effects of the Earths curvature: it tends to bend radiation downward around the Earth, and it magnifies the lower levels when seen from above, as if the atmosphere were more vertically compressed into a narrower range of radii (blackbody radiation intensity is actually a function of the refractive index; without any reflection/scattering/absorption/emission etc. in between, a blackbody embedded within a material with different refractive index n = n2 from it’s surroundings n1 will appear on the outside (where n = n1) to be emitting the blackbody flux and intensity for the n1 value, and it will appear to come from a larger or smaller object depending on whether n2 is larger or smaller than n1). Because the index of refraction stays very close to 1, and because of the relative thinness of the atmosphere relative to the radius of the Earth, these are all quite minor effects.)
Re 323 simon abingdon –
the resultant increase/decrease in habitable land area (increased I imagine in Canada, Siberia, Antarctica etc).
If there were any significant increase in habitable land in Antarctica, it would come at a horrific price (where are you going to put that ice? – just removing ice isn’t enough, it will still be cold and often dark, and there’s not going to be much soil.
How are you going to move the soil? The infrastructure? Moving has a cost. Some species are photoperiod sensitive. Civilization was built around things being roughly the way they are. Don’t forget ecosystem services.
I don’t think mass migrations have ever been a problem for the human race. When flying along the eastern seaboard of the USA I was always amazed that the cities I saw had been there for barely 200 years.
It’s easy to migrate if there are no people in your way (or if you are willing to remove those people). It’s easy to move when you aren’t used to modern comforts.
Re 323 simon abingdon
It’s not the “human race” that will suffer, but individual humans. Where will the people who live in places like Bangladesh go when they are forced to abandon their homes?
simon abingdon @323
It’s not the “human race” that will suffer, but individual humans. Where will the people who live in places like Bangladesh go when they are forced to abandon their homes?
Hey Patrick,
Again thanks for your input; however, I still fail to see how the points you elicit explain the 32 Deg. C related to GHGs and other warming contributors as well as support the 4 Deg. C doubling potential between 280 and 560ppm of CO2. In your calculations please remember to consider that the area of the disk has two sides, one for collection, the other for emission.
As it seems I am encountering a few “bugs” from this site I accept that it may be that I am being asked to refrain from further participation. To that end, “Good Bye and Thanx for all the Fishes….”
Cheers!
Dave cooke
“increase in habitable land in Antarctica”…. A lot of Antarctica’s rock surface is below sea level – the present sea level, that is. If all the ice melted, then – well – even more of it would be below sea level, wouldn’t it?
The good news? The tiny remaining human population of Earth would be able to survive happily by exploiting all the coal and oil previously trapped under the ice.
(Joke. Ha ha.)
Re 323 simon abingdon – let me put that last part another way: it may seem easier to leave everything behind when there isn’t much to leave behind.
Dave Cooke,
You seem preoccupied about the relationship between the 32C and CO2 but that’s a waste of time. Again, these 32C are not explained by CO2 alone but by the total greenhouse effect (including clouds). An Earth without atmospheric CO2 would likely be more than 32C colder than now. The 255K theoretical value depends on the albedo and is an upper limit which can only be reached with constant temperatures across the globe and the day/night cycle.
Your calculation in #322 is erroneous as it neglects the logarithmic aspect.
Stratospsheric Cooling Redux
I’ve been involved in some provocative discussions of the stratospheric cooling issue on Chris Colose’s Climate Change blog – with both Chris and Patrick, two well-informed contributors. It has helped me to refine my own perspective. Without belaboring the process, I thought it might be worthwhile to summarize that perspective here, because stratospheric cooling continues to fascinate and bedevil those who hear about it. We are now far down in the thread, but I expect that at least a few of the expert and knowledgeable readers and bloggers may read it, offer responses, identify flaws, and perhaps take account of these ideas in arriving at their own perspective.
Stratospheric Cooling by CO2 as a Mechanism Based on Ozone
The first point, made earlier, is that a plausible explanation exists involving the presence in the stratosphere of a powerful absorber of solar UV radiation – ozone. Ozone is also present in small quantities above the stratosphere, but there, other solar absorbers such as O2 and N2 may be more important. The essence of the argument is simple: much stratospheric warmth is derived from ozone-mediated UV absorption. Added CO2 contributes to the dissipation of this heat to space while contributing less to additional heat absorption in the stratosphere because it absorbs only in the infrared, whereas much of the heat comes from absorbed UV, and CO2 can dissipate that heat as well as heat it absorbs from upwelling IR. The imbalance is responsible for cooling.
This analysis is discussed more quantitatively by Raymond Pierrehumbert in his upcoming book, “Principles of Planetary Climate”, but Raypierre also mentioned it in a 2007 RC thread, and it was mentioned in an RC thread in 2005 by IBM mathematician James B. Shearer. In Raypierre’s analysis, added CO2 in the absence of ozone should warm rather than cool the stratosphere.
Although an adequate explanation involving ozone might suffice, it must compete with alternative explanations for cooling that do not involve ozone. One of these asserts that cooling results from the reduced flux of IR into the stratosphere due to trapping in the troposphere from the increased CO2. This explanation fails, because models show that under equilibrium conditions, with OLR restored to its level prior to the extra CO2, the stratosphere persists in a cooler state when the CO2 concentration is higher.
The Spectral Shift, Pivot Point Argument
A second alternative acknowledges an unchanging OLR, but posits that less is now entering the stratosphere in wavelengths absorbable by CO2 because a heated surface is now radiating more IR to space in wavelengths where CO2 does not absorb (“window regions”). This “spectral shift” argument, along with other arguments for a cooling in the stratosphere associated with an enhanced greenhouse effect in the troposphere, requires that there must be a transition layer of the atmosphere – a “pivot point” – where warming below is associated with cooling above.
The spectral shift argument is superficially plausible, because it acknowledges cooling despite an unchanging OLR, and because theory, models, and observations all demonstrate that a spectral shift does occur. The argument appears to fail on a more subtle level.
WHY THE PIVOT POINT ARGUMENT IS PROBABLY UNTENABLE – subtitle, “Why You Can’t Cool An Object By Heating It.”
My analysis requires some simplifying assumptions, but the pivot point argument doesn’t posit a mechanism that depends on these being wrong, so we can proceed with them, at least until we need to abandon them.
1. Cooling occurs even if ozone is absent or plays no role.
2. Stratospheric cooling is a strictly radiative phenomenon, with no significant influence of non-radiative factors such as convection, turbulence, etc.
3. At a given insolation and albedo, CO2 and other absorbers, such as water, that obey the same principles, are the determinants of atmospheric temperatures. I will confine the discussion to CO2 as though it alone determined temperature, but including the other absorbers should not contradict the conclusions. Increases in water consequent to CO2 increases should in fact reinforce the point. In actuality, if we get rid of ozone, CO2 will be by far the predominant radiative component in the stratosphere.
4. Absorption of solar radiation by CO2 is minimal, and increasing CO2 should not change it in a way to mediate cooling. Therefore, for practical purposes, the sole source of excess heat if we increase CO2 is IR emitted by the surface from absorbed solar radiation,. Because of atmospheric absorption and emission, IR at any level will not be coming only from the surface, but that is where it will all originate. (I neglect here atmospheric absorption of IR by water, but that should not mediate cooling at any level. Aerosols exert complex effects, but they have not been incorporated into these arguments, and so I won’t include them).
5. The heat sink for atmospheric emissions is space, and is unchanging.
Armed with these assumption, let’s examine the claim for a pivot point altitude in the atmosphere. We will confine the discussion to changes within the CO2 absorption wavelengths, because regardless of how much or how little OLR is emanating within these wavelengths, if the principles of radiative physics are violated there, the argument fails. We can divide the atmosphere into a lower part (LP), which includes the surface and is the source of IR, and an upper part (UP), which we are asked to assume will cool when CO2 increases, in conjunction with the expected warming of LP from the enhanced greenhouse effect. By established principles of radiative physics, a warmer LP should emit more IR within the CO2 wavelengths, including IR upward into the UP. Some of the excess upward IR will escape to space, but some will be absorbed within the UP. We are now asked to conclude that the UP, which was cooler to start with, will now cool still further. (If the heat sink, space, were changing, this might provide a cooling outlet, but it’s not). How can a warmer object, warming further and transmitting some of that increased heat to a cooling object, cause the latter to cool even more? It can’t.
At this point, a clever reader will say, “Aha, you’ve omitted an important new element. The UP is not only absorbing more heat from below, but we’ve added an IR emitter, CO2, to the UP layers, and so it can rid itself of more heat.” That argument fails also, as long as we make assumption #3 above, that UP temperatures are determined by CO2 and other moieties that will act in the same direction. If CO2 determines temperature, adding more CO2 increases a layer’s emissivity, but it also increases its absorptivity by the same fractional increment, and so the effects cancel out. We are still left then, with the requirement that a warming object transmitting more heat to a cooler object somehow causes it to cool.
I’m too hot. Put more wood on the fire!
It may be worthwhile to pursue a simple analogy – a room with a fireplace and an open window – the fireplace equivalent to the Earth’s surface as a source of IR and the window the equivalent of space as a fixed heat sink. We are being asked to believe that if we turn up the heat in the fireplace, the room will cool, which is to say it will increase its heat loss more than its heat gain from the fire. In a real room with a real fireplace and a real window with a fixed opening, would that happen? We can also bring in the absorptivity/emissivity argument here, by asking whether we can help the room to cool by increasing its absorptivitiy and emissivity. One way to do that would be to paint the walls black. Will this make the room cooler? Note that black walls would absorb over a broad spectrum of wavelengths, whereas CO2 absorbs in the IR. In the IR, though, it acts like a black body.
We can extend the same reductio ad absurdum logic to show that the involved principle – a warm object causing a cooler object to emit even more heat than it gains – is a Second Law violation. Let’s keep the principle but change the scenario slightly. Imagine an isolated chamber filled with air and having a small container at one end. We position a thermometer in the container and another to measure air temperature. We start out by placing a warm object – say a heated piece of iron – in the chamber, and then sealing the chamber, Our principle tells us that the heat from the iron will cause the air to cool by emitting even more heat than it receives. However, in the isolated chamber, that heat can only flow back to the iron. Since we are claiming that the iron is therefore receiving more heat than it emitted, it will warm further, thereby allowing it to cool the air further – a cool object heating up a hot one in violation of the Second Law. (Notice a bit of sleight of hand here. I’m applying the ability to emit excess heat to the air on cooling and to the iron on warming, which converts a Second Law violation into a combined Second/First Law violation. If we omit the claim that the iron will heat further, only the Second Law is violated.)
Endless Electricity Without Fossil Fuels
We can vary this theme to create a perpetual motion (or at least perpetual energy) device by not allowing the iron to continue heating further, but rather siphoning off some of the heat to a boiler creating steam to generate electricity. We do this just enough to keep the iron temperature constant. We end up with an endless stream of electricity sufficient to power the world’s growing energy demand, with no need for any more fossil fuels.
Obviously, the atmosphere is different from a room with a fireplace and a window. It seems to me, though, that the burden falls on those who predict a different outcome for the atmosphere to show why the differences obviate the need to postulate that a warmer system, upon further warming, will cause a cooler system to cool further. Because of the many assumptions made here, I may have overlooked subtle flaws, but that’s the purpose of inviting comment.
Re 324 L, David Cooke – Come again? Perhaps there is a language barrier between us, because I can’t make out much of what I actually intended to say in the way you describe what I said. Judging from the terminology I get the impression you might be an electical engineer or work with fiber optics perhaps? The same terms (band widenning) may have different implications in different fields of study.
(You also misunderstood my points regarding oxygen and H escape, etc, but I’ll leave that for later.)
(Sorry, I’ve heard of decibels but I haven’t worked with them much. Is a db supposed to be 1/2 of a power of ten? By the way, the symbol db could be mistaken in the atmospheric sciences to be 1/10 of a bar).
1.
I think of a waveguide as being a guide of waves through space. The flow of radiation at different frequencies (wavelengths) don’t follow waveguides in that sense, though they can be thought of as different channels of communication. No ‘waveguide’ is necessary to keep a photon from changing its frequency; absent doppler and relativistic effects and certain kinds of scattering like Raman and Compton scattering, photons conserve their frequency while they propagate. Something specific has to happen in order to change a photon’s frequency, and that isn’t a big player in radiative fluxes through the Earth’s climate system.
(Photons also tend to conserve their wavelength, except as changes are required to conserve frequency while propagating through variations in the index of refraction n. Often we speak of photons as if their wavelengths are unchanging – this is approximately true for radiation flowing though the atmosphere because n is very very close to 1, but in case the issue becomes significant, often when I’ve refered to the wavelength of radiation, I’ve been refering to the wavelength that a photon would have in a vacuum.)
So I think I need to start over and explain some basics:
2. The global average solar heating of the Earth is approximately 240 W/m2 (or maybe 235 W/m2 ?). This is about 0.7 * 1/4 of the solar flux incident on a unit area facing the sun at the position of Earth. The reason for this is that the area of a circle is π*radius^2, while the area of a sphere with the same radius is 4 times that value. The Earth is approximately spherical, but it intercepts solar radiation through an area facing the sun (recieving the approx. 1366 W/m2 solar flux per unit area) equal to it’s circular cross section. For at least near present-day conditions, it reflects about 30 % of the solar radiation it intercepts.
3.
Intensity is the amount of radiant power going in a direction, per unit area facing that direction, per unit solid angle (a range of directions).
Flux per unit area in direction Q2
= integral over solid angle of [intensity in direction Q1 * cos(θ)],
where θ is the angle between Q1 and Q2.
(The unit area that the flux goes through is perpendicular to Q2, while intensity in direction Q1 is given per unit area perpendicular to Q1; a unit area facing Q2 will appear to have a smaller area in direction Q1 in proportion to cos(θ))
A flux per unit area can be found by integrating the intensity over a hemisphere of directions that all pass through the unit area in the same direction (in the sense of being from one side of the unit area to the other side, even though they do so at different angles).
A net flux is the difference between a pair of fluxes in opposite directions. A net flux through a unit area can also be found by integrating the net intensity over a hemisphere of directions.
Examples of units (sr = steradian = a meaure of solid angle; a solid angle of directions is equal to the surface area of a unit sphere onto which those directions project, where those directions are from the center of the sphere. There are 2*π steradians in a hemisphere of directions; all directions over a whole sphere occupy 4*π steradians.
Intensity: W/(m^2 * sr)
Flux per unit area: W/m^2
A flux or intensity can be for the whole spectrum of frequencies, or some part of that spectrum (LW or SW, for example), or for a smaller band. One can also refer to monochromatic (spectral) fluxes and intensities, which is the flux or intensity at a particular frequency ν (or wavelength λ, or photon energy E) per unit of the spectrum (per interval of ν or λ or E, or even per unit log(ν), etc.). Integrating these values over ν or λ gives the flux or intensity for the whole spectrum or some subset of the spectrum.
When one refers to a flux or intensity at some ν or λ, etc, it is implied that this is a flux or intensity per unit of the spectrum:
at a particular ν (units of Hertz, Hz)
Intensity: W/(m^2 * sr * Hz)
Flux per unit area: W/(m^2 * Hz)
at a particular λ (units of microns, μm)
Intensity: W/(m^2 * sr * μm)
Flux per unit area: W/(m^2 * μm)
Etc.
Often the term flux is used when one is actually refering to a flux per unit area (I caught myself doing this below in a few spots, but it is too cumbersome to fix now; usually one can distinguish what is meant by context).
If polarization ever matters, one could refer to flux or intensity for some subset of the ‘polarization spectrum’, or to a flux or intensity at a particular polarization – if I ever do this, assume it is per unit of the polarization spectrum. I wouldn’t know how to express that formally but the concept is easy to understand – you would have to integrate such values over the polarization spectrum to find a total for all polarizations. If I use the Planck function in the context of polarized radiation, assume if I don’t otherwise specify it, that it is the original Planck function (monochromatic blackbody intensity as a function of temprature) divided by some value that represents the range of polarizations, so that it is an intensity per unit of the polarization spectrum.
The following assumes LTE**. Refraction and some other complexities (Raman and Compton scattering, other…) are set aside for now.
4. At a particular frequency ν and polarization P:
4a.
Along a path with optical thickness τ, if intensity going into one end of the path is I0, the intensity coming out the other end of that path that is of the same photons that were going in is I0*exp(-τ). exp(-τ) is the fraction of intensity that is transmitted. This must be the same in both directions, So τ is the same in both directions along the same path. τ can include absorption and scattering of the original photons out of the path. Note that I0*exp(-τ) does not include contributions from emission of photons within the path or scattering of photons into the path from other directions.
Different contributions to τ of different types (absorption, scattering) from different sources (different gases, particles, and different segments of the total path length) add linearly. τ per unit length is equal to the extinction cross section per unit volume. Cross sections of different types from different sources also add linearly. The absorption cross section density for radiation coming from a direction = emission cross section density for emission of radiaton into that direction; this is a form of Kirchhoff’s Law. Absorption cross section density is the fraction of radiation absorbed per unit distance. Emission cross section density is the fraction of Bν(ν,T) emitted into a direction per unit distance. Bν(ν,T) is the Planck function for frequency ν and temperature T and is the monochromatic intensity (intensity per unit frequency) that would be emitted by a perfect blackbody at temperature T. Notice that if the intensity coming from a direction is equal to Bν(ν,T), then the emitted intensity into that direction by a small length of path with temperature T is equal to the intensity from that direction absorbed by that same length of path. Scattering cross section density is the fraction of intensity that is scattered out of a path per unit path length.
There is an ‘I can see you as well as you can see me’ rule. If I have this correctly *** For the same frequency, the fraction of photons at a location r1 going into a direction Q1 with polarization P1 that reach location r2 from direction Q2 with polarization P2 is the same as the fraction of photons at r2 doing into Q2 with polarization P2 that reach r1 from Q1 with polarization P1. Combined with Kirchhoff’s law, this ensures that the net flux of photon energy, from emission to absorption, between two volumes, is from higher to lower temperature, thus satisfying the second law of thermodynamics.
(If I have this correctly: for a frequency ν, for an intensity I1 of polarization P1 from direction Q1 incident either on some scattering agents or a partially reflecting surface, a fraction f of that is scattered/reflected/transmitted into direction Q2 with polarization P2. The same fraction f of an intensity I2 reaching the same location from direction Q2 with polarizaton P2 is scattered/reflected/transmitted (respectively) into direction Q1 with polarization P1.)
Note that if the extent to which you can ‘see’ is proportional to your absoptivity and the extent to which you can be seen is proportional to your emissivity, the ‘I can see you as well as you can see me’ rule includes Kirchhoff’s Law.
Note that the ‘I can see you as well as you can see me’ rule is not violated by one-way mirrors (the room on one side of such a window is relatively dark, so what people on the other side see of that room is darkness, and any details tend to be drowned out by the reflection of the brightly lit room.)
—— ——– ——–
Combining Kirchoff’s Law with everything else: EWF: Consider an unit intensity of photons (of a particular frequency, and if necessary, polarization) directed in some direction from some location. The absorption of photons is distributed as a density over space in some way (along a path, exponentially decaying with distance if the absorption cross section density is constant over distance; if their is (partial reflection), it may be along a bent or branching path; if there is scattering, the distribution may fill a volume. If there is a lack of absorption nearby, the distribution is projected onto where it could be absorbed; scattering and reflection will redirect that projection. This distribution is equal to the emission weighting function. Locally multiplying the EWF by Bν(ν,T), and then integrating over the distribution over space (along a path or over a volume) gives the value of the intensity of the radiation coming from that direction and reaching the same location. EWF can be integrated over directions the same way intensity is integrated to find a flux per unit area; the result is an EWF for the flux per unit area (which I’ll refer to as EWFf). EWFf is also equal to the distribution of absorption of a flux per unit area, through the same area, going in an opposite direction, provided that the flux is isotropic (constant intensity) over the whole hemisphere of directions, with intensity = 1.
Increasing optical thickess of the absorption type compresses the EWF and EWFf into a smaller volume closer to the location considered; increasing scattering optical thickness does the same if absorption is significant, and also can cause the EWF and EWFf to surround the location considered. Otherwise, scattering redistributes the EWF and EWFf so that they may be more evenly distributed around the location, though possibly at some distance away.
When absorption is a signficant contributor to optical thickness, increasing the optical thickness (increasing the cross section densities) shortens the distances that photons can travel from where they are emitted, and to where they are absorbed. If the optical thickness and temperature distributions are such that the dominant spatial tendency in temperature is to either increase or decrease (as opposed to fluctuate) from a location out to a substantial optical thickness away, then farther increases in optical thickness will bring the flux and intensities coming from that direction toward the values they would have for a blackbody with a temperature equal to the temperature at that location. This approach to a particular asymptotic value is called saturation.
When there aren’t any gaps in space with zero optical thickness (there is approximately a gap above TOA) and temperature varies continously over space (at sufficient spatial resolution, this is generally true everywhere within the climate system), increasing optical thickness eventually saturates the fluxes going in opposite directions, at which point they become equal, so that the net flux is zero. Saturation at TOA still leaves a nonzero net LW flux into space.
________________________________
For LW radiation in the Earth’s climate system, scattering is a minor issue and to a first approximation one can assume only absorption and emission occur. For SW (solar) radiation, there is generally no significant emission (volcanoes and lighting don’t cover enough space and aurora are too weak) within the Earth’s climate system, but scattering is important.
_______________________________
(PS when refraction occurs, the intensity in the absence of scattering, absorption, emission, or reflection, changes because the same amount of radiation is compressed or expanded to different solid angles as the real component of the refractive index n changes. The blackbody intensity varies as a function of n in the same way. So one can take the actual value of intensity I and divided it by some function of n to find I#, which is conserved in the absence of other processes (specifically, at least in the case of isotropic n, I# = I/n^2);
then, if I’m not mistaken, for a particular ν, the I# scattered/reflected/transmitted into a direction Q2 with polarization P2 from an incident I#1 from direction Q1 with polarization P1 is the same fraction of I#1 as the fraction of I#2 is the I# scattered/reflected/transmitted, repectively, into direction Q1 with polarization P1 from an incident I#2 from direction Q2 and polarization P2. And I# is emitted and absorbed by emission and absorption cross sections and emissivities and absorptivities that are equal for emission into a direction and absorption from that direction at the same location or over the same path length for the same frequency and polarization. The net flux of radiant energy (from emission to absorption) is from higher to lower temperature. I at any location is determined by I# reaching that location and the n at that location.)
______________________________
For the CO2 absorption band (the one of greatets importance in Earthlike conditions) centered at 15 microns (the corresponding frequency ν at this peak is νpeak), the shape of the band can be roughly***** described as per unit mass path of CO2 (mass per unit area along a path length), the optical thickness decays approximately exponentially moving away from the center of the band. As a function of frequency ν, log(τ) ~= τpeak – M1*(νpeak-ν) for ν νpeak.
The τ from CO2 increases in proportion to the amount of CO2 at all ν; this includes τ = τpeak at ν = ν0. Thus, for all τ smaller than the initial τpeakν value, after increasing the amount of CO2 by a factor of 10, the same τ value can be found at a different ν that is farther out from the center of the band by an amount equal to 1/M1 or 1/M2, depending on which side of the center is being considered. Thus the CO2 absorption band effectively widens by an amount equal to 1/M1 + 1/M2. This has an effect on radiative fluxes by increasing the range of frequencies for which the EWFf’s are compressed by more than some amount. It also has an additional effect by compressing the EWFf’s near the center of the band. Eventually, the fluxes approache asymptotic values – the effect saturates. But when this first happens in the center of the CO2 band, there is still the band widenning effect; the CO2 effect is not saturated at the ‘edges’ of the band, which shift outward over the spectrum with increasing CO2. This pattern continues until there is so much CO2 that other parts of the absorption spectrum with different shapes become important.
Note that I am refering to the effect of a change in CO2 amount on radiative fluxes while holding the climate steady. In some conditions, saturation can occur while holding temperatures steady, but the climate response can still change the fluxes – this won’t generally add a significant net flux where optical thickness has brought the net flux to zero, but it can change the net flux at TOA even if the effect of optical thickness has been saturated at TOA, and the climatic response could ‘unsaturate’ the effect at TOA by creating a thinner layer of different temperature. If the tropopause level LW flux were ever saturated over the whole LW portion of the spectrum, and there were still significant solar heating below that level, then the tropopause would tend to shift upward to where the LW flux is not saturated at some frequencies; in an equilibrium climate, the net LW flux out of the tropopause has to balance SW heating below the tropopause (in the approximation of zero non-radiative flux out of the tropopause), and thus cannot be zero.
The effect of CO2 is to cause some sort of a valley or hill*&* in the monochromatic flux graphed over the spectrum (*&*depending on vertical level relative to temperature variations and whether one is considering upward or downward fluxes or the net upward flux). Consider the values of ν on either side of the band where the monochromatic flux is roughly halfway up or down the height or depth of that hill or valley; call these ν1 (lower than νpeak) and ν2 (higher than νpeak).
To a first approximation, the CO2 radiative forcing can be approximated by taking the net upward monochromatic flux Fνup in the vicinity (in terms of position in the spectrum) of the CO2 band.
Let
Fνup(no CO2) be the value if there were no CO2 (holding climate steady),
while
Fνup(peak) is the value at the peak of the CO2 band.
The height or depth (as a negative height) of the hill/valley is equal to
Fνup(peak)-Fνup(no CO2) = Fνup(CO2).
The effect of band widenning is a reduction in net upward LW flux (this is called the radiative forcing), which is proportional to a change in area under the curve (a graph of flux over the spectrum); the contribution from band widenning is equal to the amount by which the band widens (in units ν) multiplied by -Fνup(CO2). For a doubling, that would be:
forcing from band widenning, per doubling = -log(2)*(1/M1+1/M2) * Fνup(CO2)
(the negative sign is there because Fνup(CO2) is positive if CO2 increases the net upward flux, while positive forcing is a decrease in a net upward flux.)
When the band is saturated at the center, Fνup(CO2) reaches an asymptotic value Fνup(CO2saturated), the difference in the net upward monochromatic flux between a saturating amount of CO2 at that frequency, and no CO2 (notice that Fνup(CO2saturated) can be defined for any particular frequency).
When the band is not saturated at the center, there will be an additional contribution to radiative forcing per doubling of CO2, that will be on the order of
-1/2 * log(2) * (1/M1+1/M2) * 1/2 * [Fνup(CO2saturated)-Fνup(CO2)] if the peak is close to saturated
(ie the area may be approximated as a triangle with a height that is half the difference between the net flux at the peak of the CO2 band and the net flux at saturation, though it will tend to be distorted a bit from that shape),
or
-1/2 * log(2) * (1/M1+1/M2) * Fνup(CO2) if the CO2 effect at the center of the band is still quite small,
though the exact values will vary depending on how the temperature varies over height as measured in terms proportional to optical thicknesses.
That is sufficient so long as Fνup(CO2) doesn’t reverse it’s tendency at some point. If it reverses, we can treat the value at the point of reversal (marking a maximum height or depth of the hill or valley in the net upward flux spectrum) as the saturation value, and then include some additional effect at the center of the band for additional increases in CO2 that have the opposite sign as the band widenning in their contributions to radiative forcing. This can happen for radiative forcing at TOA because the upper stratosphere, directly heated by the sun, is warmer than the lower stratosphere and tropopause. It tends not to happen within the atmosphere because the net flux saturates at zero and won’t increase again after saturation – although it is hypothetically possible to set up a situation where increasing CO2 would result in one or more ‘pseudosaturations’ (*%* can I use that term?) (where the trend in net monochromatic flux reverses) before reaching the ultimate saturation; if this situation came up, after each ‘pseudosaturation’, the radiative forcing can still be estimated with a band-widenning effect outside the central region where the last ‘pseudosaturation’ has taken effect, minus the contribution from whatever is happenning in the center (think in terms of positive and negative areas on the graph). But the spectrum of net upward flux at the tropopause for Earth is approximately a valley (Fνup(CO2) is negative) with a continual downward slope toward the center on each side (this is an approximation, though*****).
Note that this approximation assumes that the same optical thickness from CO2 will make the same change to the net upward monochromatic flux at each ν. This can be true to a first approximation. Variations are due to variations in the optical thicknesses already provided by water vapor and clouds, and variation of the Planck function over the spectrum. To deal with such variations, to a first approximation, one can use different values of monochromatic flux (in place of a single Fνup(CO2) value) for the widenning effects at each side of the band and for the the center of the band. For example, once the band is saturated at the center, the forcing from the band widenning could be estimated as:
forcing from band widenning, per doubling = -log(2)*[ 1/M1 * Fνup(CO2saturated)ν1 + 1/M2 * Fνup(CO2saturated)ν2),
where
Fνup(CO2saturated)ν1 and Fνup(CO2saturated)ν2 are the differences between the net upward fluxes with CO2 saturated at ν1 and ν2 and with no CO2, evaluated at ν1 and ν2, respectively; they could be considered the ‘potential’ monochromatic forcing for CO2 at those frequencies.
______________________
**At LTE (local thermodynamic equilibrium) within a small volume of material (small enough to be isothermal) that is still large enough to contain a large enough population of molecules/atoms/electrons/etc, each population of a type of particle has the same temperature, and the distribution of energy among all particles and all forms it can take (translational, vibrational, rotational, potential, electronic, latent, etc) is an equilibrium distribution).
(This is not a full thermodynamic equilibrium – it doesn’t require chemical mixtures to be at equilibrium, or for the radiative intensities to be in equilibrium with the non-photon matter. As long as the chemical and physical (and nuclear, etc.) reactions that do occur are occuring slowly enough for energy to be redistributed among particles, LTE can be approximately maintained. In some non-LTE conditions, a subset of particles may act as if they have a particular temperatue with respect to radiation but actually have a different temperature with respect to something else (applicable to photovoltaic devices; quasi-thermodynamic equilibrium). It is hypothetically possible to have populations of different temperatures within the same volume; as long as each seperate population is at LTE within itself, the radiative physics as described above can apply in a modified way – for example, the density distribution of an EWF would have to be distributed over space and over the different populations within that space.)
(In full thermodynamic equilibrium, all photon-non-photon interactions, including Raman and Compton scattering, would sustain that equilibrium; all such interactions tend to eventually bring a system towards such equilibrium provided that photons (as well as other particles) are not entering or leaving the system from other systems with different conditions.)
The vast majority of the mass of the atmosphere and surface material is approximately at LTE. LTE can be approximately maintained by redistributions of energy by molecular collisions or other such microscopic interactions among atoms, electrons, etc, as long as these occur rapidly relative to other processes that would selectively add or remove energy from a subset of the particles or forms of energy. Effective maintenance of LTE allows a subset of molecules to absorb radiation or emit radiation with the temperature of the emitting and absorbing population being nearly the same as the temperature of all the local matter, and with any net absorption or emission of radiant energy changing the temperature or physical or chemical state according to the heat capacity or latent heat of all the matter.
________________________
***** The CO2 spectrum deviates from the simple shape described above in some ways. There are some bumps, and there is also some finer-scale texture associated with the individual lines that make up the absorption band. To the extent that this fine-scale texture is self-similar over intervals of the spectrum that are narrow enough to resolve the band-widenning, they don’t affect the overall behavior so much; one can break up the spectrum into intervals sufficiently small to resolve the overall shape, and assign fractions of each interval to different absorption bands with different peak values but with the same shape and same slope when optical thickness is graphed on a logarithmic scale. The effect is a continuum of different absorption spectra that all have the same band-widenning per doubling and same effects at the center at various stages between no effect and saturation, though they are at different stages in that process for any given amount of CO2; the radiative forcing is a weighted average of the effects of each of those absorption spectra; once the center of the band is saturated for all of the spectra, the band widenning effect is the same for each and thus the forcing from the band widenning is the same as it is in the original simplified picture.
However, their are other deviations from the simple picture that still render the logarithmic proportionality an approximation.
There could also be some such complexity in the radiative flux per unit area absent CO2, which would affect the relationship between changes in CO2 and radiative forcing; for sufficient self-similarity of finer scale texture, the effect might be treated the same way as the texture of the CO2 spectrum (?).
Still, the logarithmic proportionality works as an approximation for the radiative forcing of changes in CO2 amount once the center of the band has become saturated.
___________________________
Part of this paragraph got cut-off:
For the CO2 absorption band (the one of greatets importance in Earthlike conditions) centered at 15 microns (the corresponding frequency ν at this peak is νpeak), the shape of the band can be roughly***** described as per unit mass path of CO2 (mass per unit area along a path length), the optical thickness decays approximately exponentially moving away from the center of the band. As a function of frequency ν, log(τ) ~= τpeak – M1*(νpeak-ν) for ν smaller than νpeak, and τpeak – M2*(ν-νpeak) for ν larger than νpeak.
The τ from CO2 increases in proportion to the amount of CO2 at all ν; this includes τ = τpeak at ν = ν0. …
sa 323: I don’t think mass migrations have ever been a problem for the human race.
BPL: Or abandoning trillions of dollars worth of coastal infrastructure? And consider how the US has reacted to 10 million illegal aliens from Mexico. How will the red states respond to 100 million refugees from California, New York, and Florida? Or India to 100 million refugees from Bangladesh? Then there’s the fact that agriculture is likely to collapse if GW continues. Any of this concern you?
Fred (#333),
Your LP/UP model doesn’t take the lapse rate into account. I’m no atmospheric scientist and haven’t really considered the stratospheric cooling issue but, if an increase in the amount of atmospheric CO2 raised the average altitude from which the stratosphere receives radiation in the CO2 bands, wouldn’t it receive less radiation in those bands? It wouldn’t be the warming of the troposphere which cools the stratosphere but the lapse rate combined with the increased opacity in the CO2 bands. Does this explanation hold up?
To 337 (Anonymous Coward): For clarity, we are discussing the explanation that discounts a role for ozone, in which case I argue the atmosphere would warm at every level if CO2 is added. If we compare a given level with the same altitude prior to the extra CO2, we will find it is receiving more IR from below, because the Earth and troposphere below that level are warmer, and it will be emitting more than before, because having received more IR, it is warmer itself. However, less of that IR will escape, because of the increased optical thickness above it. The result is that the effective radiating altitude rises until it reaches a higher altitude than before, optically thin enough to permit adequate IR to escape. That altitude is cooler than was the earlier radiating altitude (hence the reduced escape via the CO2 wavelengths), but it is warmer than the new altitude was before the CO2 addition, since previously, the new altitude was not the radiating altitude but above it.
Replying to you also gives me a chance to clarify assumption #1 in my comment #333. That particular assumption is limited to proponents of explanations that discount the role of ozone. It is probably incorrect, but I was using their assumption for a reductio ad absurdum analysis of their explanation.
#321 Jacob
#323 simon monckton
In addition to sea level considerations for a warmer world there are myriad other considerations. Sea level is catastrophic because of infrastructure near the water and the costs associated with sea level rise. How much would it cost to move or rebuild all the infrastructure of New York City?
Also, you need to consider the reality that all our current food infrastructure has been built during the relative radiative forcing of the Holocene and now we have altered that forcing.
How much will in cost to reestablish the global food infrastructure at new latitudes? Consider this also though: how much will it cost to move that infrastructure multiple times? The climate system and the warming is non linear, so how much will it cost to do this multiple times?
There are many other costs associated with climate change as well. So it all depends on what you consider catastrophic. Personally I think the economy is under enough stress already. But this is just the tip of the iceberg, so to speak.
Think about it this way, we are already seeing economic impacts at 389ppm. so how much stress is okay? 540ppm is a lot of stress from pretty much every reasoned view that has examined it.
As to simon’s question, well, infrastructure cost. Hundreds of thousands of years ago, no one had invested billions of dollars of investment in Manhattan. Consider also the economic strains of human migration.
I do disagree with the perspective that this will only affect individuals. This is a global affect that unfolds and gets increasingly more expensive for the entire human race, but also we must consider the costs to the economic system itself, oceans, land, air.
It’s the whole nine yards.
—
A Climate Minute The Greenhouse Effect – History of Climate Science – Arctic Ice Melt
‘Fee & Dividend’ Our best chance for a better future – climatelobby.com
Learn the Issue & Sign the Petition
Re 333,338 Fred Moolten
That particular assumption is limited to proponents of explanations that discount the role of ozone.
I don’t think that’s necessarily the intent. I think at least some fraction of the equilibrium and also transient stratospheric cooling depends on the solar heating of the stratosphere; the question is whether there is some amount of cooling that would would still occur in the absence of that solar heating.
Because of atmospheric absorption and emission, IR at any level will not be coming only from the surface, but that is where it will all originate.
Actually there can be convection from the surface that is balanced by some of the radiation from within the troposphere, but in the approximation of zero non-radiative transfer above the tropopause, all the flux into the stratosphere must be from below (absent solar heating).
How can a warmer object, warming further and transmitting some of that increased heat to a cooling object, cause the latter to cool even more? It can’t.
True, but reducing the transmission to the cooler object can cause the cooler object to cool even more.
Re 337 Anonymous Coward re Fred Moolten Your LP/UP model doesn’t take the lapse rate into account.
Actually it does. I had forgotten something about the lapse rate when I earlier argued that there was some equilibrium stratospheric cooling that would occur absent direct solar heating of the stratosphere.
—
I think it’s easier to look at this as a function of lapse rates. The lapse rate within the troposphere is largely determined by convection, which redistributes any changes in radiative heating or cooling within the troposphere+surface so that all levels tend to shift temperature similarly (with some regional/latitudinal, diurnal, and seasonal exceptions, and some exceptions for various transient weather events).
When there is no solar heating above some level, the net non-SW heat flux must be upward and constant at all levels from the tropopause to TOA in equilibrium, to balance solar heating below that level. Radiation transfers heat across different scales at different optical thicknesses for different frequencies; the net radiant flux depends more on temperature variations that occur over distances on the order of a unit of optical thickness, so the net flux can be through smaller-scale temperature variations. However, there is no way to cause vertical fluctuations in equilibrium temperature if the total net LW flux is upward at every level, with all that energy ultimately coming from below, and there is no solar heating. So the lapse rate, though smaller than in the troposphere, will still be positive in the stratosphere; it might approach zero but it will not quite reach zero and will never be negative.
Much of the absorption of fluxes going into the stratosphere and emission of fluxes going out from within the stratosphere may actually be due to stratospheric water vapor, because it has moderate optical thickness (on the order of unit optical thickness) over a wide band of wavlengths (though it is transparent in the vicinity of the 15-micron-centered CO2 band); the optical thickness is much greater in the CO2 band, but it covers a narrow range of wavelengths.
However, for any sufficiently thin slice of the stratosphere, the water vapor will be almost transparent everywhere, while the CO2 still has a significant effect near 15 microns; thus, the fluxes among thin layers are mediated more by CO2 and occur near 15 microns.
Thus, a very thin layer near the top of the stratosphere will essentially only be heated (absent solar heating) by radiation from below at the peak of the CO2 band near 15 microns. At equilibrium, it will have a temperature at which the blackbody flux at 15 microns would be half of the actual OLR at 15 microns. Thus, adding an infinite amount of CO2 would reduce the 15-micron OLR by 50 % (before the climatic response). This is the very important detail I forgot to consider earlier.
to be cont…
A simple recipe for GHE is both good and useful. Better still would be to also make sure that accurate definitions and concepts are included as part of the GHE recipe.
For example, the distance light travels before being absorbed is the mean-free-path for absorption, and not the optical depth. The mean-free-path is not typically utilized in radiative transfer calculations. On the other hand, the optical depth is a direct measure of absorber amount (with a distinction to be drawn between absorption optical depth and extinction optical depth to account for the scattering part of the total optical depth, or optical thickness). For greenhouse gases in the IR, since scattering is negligible, the extinction optical depth is essentially equal to the absorption optical depth. More important, the optical depth is a dimensionless quantity, being the ratio of the total absorption cross-section per unit area, to the unit area itself.
The optical depth, TAU, can also be expressed as the negative of the logarithm of the transmission, i.e., TAU = – log [ exp(–TAU) ]. For greenhouse gases, TAU is a highly variable function of wavelength, ranging from near-zero in the far-wing areas of absorption lines, to many thousands within the core regions of strong absorption lines. TAU = 1 is the amount of absorber that if laid side by side without overlapping would just cover the unit reference area, implying 100% absorption of the incident light beam. But the gaseous absorbers are very small, very numerous, and randomly distributed. The transmission by one such particle is (1 – TAU/N). The transmission by all N particles is (1 – TAU/N)**N, which in the limit of large N, gives the transmission as being equal to exp(–TAU).
It is noted that the stratosphere is expected to cool, while the troposphere and surface warm in response to GHG increases, as shown by GCMs, but that the picture might be more complicated.
First, the Earth has a stratosphere because of the local heating due to solar radiation being absorbed by ozone. Without such absorption of solar radiation high in the atmosphere there would be no stratosphere, and the temperature would decrease monotonically with height.
Second, that GCMs produce stratospheric cooling in response to GHG increases is and indication that the radiative transfer modeling is being done reasonably correctly, i.e., the spectral nature of IR absorption is being modeled, rather than using spectrally grey absorption. Spectrally grey absorption and spectrally integrated fluxes (sigmaT**4) cannot reproduce the stratospheric cooling.
The explanation for the stratospheric cooling is actually straightforward. Stratospheric cooling arises because the IR window region allows radiation emitted by the ground to go directly out to space, and thus allows a combination of surface temperature change and stratospheric temperature change to contribute to defining the effective temperature, rather than forcing the stratospheric temperature alone to define the effective temperature. Consider a somewhat extreme example where half of the spectral outgoing LW flux is within the window region (emitted by the ground surface), with the other half being emitted within the radiatively opaque part of the spectrum from regions high near the top of atmosphere. In equilibrium we would have that:
(Te)**4 = 0.5 * [(Ts)**4 + (Tt)**4 ]
where Te is the effective temperature (as defined by the absorbed solar radiation), Ts is the surface temperature, and Tt represents the stratospheric temperature that is being defined by the opaque spectral region.
With a GHG increase, say doubling of CO2, upon reaching equilibrium there will be a surface temperature increase by dTs, and a change in the stratospheric temperature by an amount dTt. The effective temperature Te will remain fixed, since we are not allowing changes in absorbed solar radiation (for simplicity). In the new equilibrium,
(Te)**4 = 0.5 * [(Ts + dTs)**4 + (Tt + dTt)**4 ].
Expanding the terms gives
(Te)**4 = 0.5 * [(Ts )**4 + (Tt)**4 + 4dTs (Ts)**3 + 4dTt (Tt)**3].
Since Te does not change, it then follows that the stratospheric temperature change has to be a cooling effect in order to maintain SW / LW energy balance and to conserve energy. Thus
dTt = – dTs (Ts/Tt)**3
In the above, the slight spectral shift of the Planck spectral radiation distribution has been neglected. Note that since Ts is substantially larger than Tt, it follows that the magnitude of the stratospheric cooling dTt will be larger that the surface warming dTs.
Note also that the added LW opacity due to the CO2 increase will have little effect in the troposphere where convective energy transport is active. But the added opacity will have its full effect in the stratosphere (which is in radiative equilibrium). Opacity added to a radiative layer increases the temperature differential across the layer. The lower stratosphere will warm, and will communicate this warming to the troposphere and ground, while the upper stratosphere will cool because of reduced upwelling radiation.
Andy (#341)
In my earlier comment (333), I described the reasoning behind the conclusion that increased CO2 only cools the stratosphere in the presence of ozone. Without ozone, the stratosphere should warm. I also attempted to demonstrate that a warming troposphere can’t cool the stratosphere by itself (e.g., without ozone). That rationale holds, I believe, until demonstrated false.
I have some significant reservations about your analysis. You state:
With a GHG increase, say doubling of CO2, upon reaching equilibrium there will be a surface temperature increase by dTs, and a change in the stratospheric temperature by an amount dTt. The effective temperature Te will remain fixed, since we are not allowing changes in absorbed solar radiation (for simplicity). In the new equilibrium,
(Te)**4 = 0.5 * [(Ts + dTs)**4 + (Tt + dTt)**4 ].
You appear to be adding the new Ts to the new Tt as though their sum were Te, but Te is a radiating level temperature, not an average temperature in either stratosphere or below. In fact, with increased CO2 (absent ozone), the radiating temperature will rise to a higher altitude. In the presence of a spectral shift, the stratospheric radiating temperature in the CO2 wavelengths will decline, but the overall stratospheric temperature will rise. As I mentioned in 333, I see no way for the increased emissions emanating from a warmer surface and troposphere to cool the stratosphere.
Along the same lines, you also state:
The lower stratosphere will warm, and will communicate this warming to the troposphere and ground, while the upper stratosphere will cool because of reduced upwelling radiation.
There is an increase rather than a decrease in upwelling radiation, because the radiation is coming from a warmer surface and troposphere. Note that the radiation escaping from the stratosphere will decline because of the spectral shift, but the radiation entering the stratosphere will increase because more radiation is coming from below. The reduction in the escaping radiation is due to the fact that it would be coming from a higher, cooler layer. Within the stratosphere, each layer will warm (to a declining extent with altitude) because of the increased opacity combined with the increase in the upwelling radiation.
Not to belabor the point, but as I suggested in 333, for one part of the atmosphere to warm, transmitting that extra warmth to a second, higher part, can’t lead to a cooling of the higher part through any known thermodynamic mechanism
Thanks Dr. Lacis…
Fred– I still believe you misunderstood the section in Dr. Pierrehumbert’s book which specifically deals with the grey gas model and ignores the fact that a sensor from space will see the stratosphere at the opaque regions (~15 microns). This is where temperature increases with height resulting in an increase in the 15 micron irradiance (decreases in the 15 micron spectral flux into the stratosphere), and increased emission to space in the window region from the lower atmosphere and surface. In the weaker “wing” regions between 14 and 17 um the sensor is seeing the troposphere where irradiance decrease as CO2 is increased.
In a grey atmosphere, then I would no longer agree with Dr. Lacis to the extent that there is an upper-level absorber present. This is because if you increase the GHG then you can get more cooling (at a given temperature) balancing the same solar heating. If we take a thin slice of isothermal stratosphere being heated by UV radiation (S_ozone)and outgoing longwave radiation from below (εσTe**4) and the stratosphere radiates up and down at εσTt**4 (assuming the emissivity to be constant over all wavelengths, and a factor of two for up and down direction), then the energy balance for that layer is
(1-ε)S_ozone + εσTe**4 = 2εσTt**4
From which it follows that
Tt**4=[S_ozone/ε – S_ozone + σTe**4]/2σ
If the OLR and absorbed UV are the same for heightened CO2 (at equilibrium), then the only change comes from ε which appears in the denominator of a term forcing the whole expression to become smaller with higher CO2. Thus the stratosphere can cool even in a grey model, although if S_ozone is zero then this term no longer matters. This is obviously not a realistic model through for real atmospheres.
The fact that the mesosphere/thermosphere cools with higher CO2 (where the temperature declines in the mesosphere), and indeed that the high atmosphere of Venus is even colder than Earth, should also be independent validation that ozone is not a pre-requisite for upper atmosphere cooling.
Re Andy Lacis –
Spectrally grey absorption and spectrally integrated fluxes (sigmaT**4) cannot reproduce the stratospheric cooling.
Unless there is sufficient solar heating in the upper atmosphere, specifically within the layer that can emit significantly directly to space.
What if, in addition to increasing optical thickness within a band, you also add some optical thickness in a new band (CO2 is a bit like that because of the shape of the absorption spectrum)?
The stratosphere can have a positive lapse rate, just so long as it is not large enough to make it part of the troposphere.
——–
It almost seems like whether the stratosphere or parts thereof would cool from increased GHGs in the absense of direct solar heat is a question balanced on a knife’s edge, and could go either way depending on specifics…
Hi Chris – Let’s take things one at a time. If you read Raypierre’s chapter, you’ll see that he was not invoking a grey gas model to require the presence of ozone for stratospheric cooling. He was explicitly using that mechanism to explain stratospheric cooling observed here on Earth during recent decades (or rather that part of cooling not attributable to ozone depletion). He added that in our own, non-grey gas atmosphere, increased CO2 should raise stratospheric temperatures in the absence of ozone. In that sense, if you disagree, you should probably take it up with him as someone best qualified to defend his assertions.
Let’s next consider Andy’s equation that he believes requires the stratosphere to cool if the surface warms., presumably without invoking ozone. In his example split between a transparent window region and a very opaque region, he averaged (using the appropriate fourth powers) the surface temperature with the radiating temperature of emissions from the opaque region, calling the latter “the stratospheric temperature”. It isn’t. Rather, as opacity increases due to increased CO2 or other ghgs, the stratospheric temperature deviates more and more from the radiating temperature in the stratosphere for the opaque region. That is because the radiating layer risis to a higher altitude. In essence, the stratosphere warms, while the radiating temperature remains constant if there is no spectral shift, and declines if there is (as one would expect to happen). The latter is what we should see on Earth, with its spectral shift – a warmer stratosphere at all levels with increasing CO2, combined with a reduced temperature at which the stratosphere radiates to space.
Here is where the grey gas model does help illustrate my point. Assume we increase the ghg responsible for the greyness. If insolation and albedo don’t change, the radiating temperature won’t, but clearly both the surface temperature and atmospheric temperature will rise. The radiating temperature will remain constant because its altitude is elevated.
What appears to be a prerequisite for cooling is not ozone per se, but a UV absorber – ozone in the stratosphere, but more likely O2 and N2 in higher levels.
Finally, the laws of thermodynamics must apply. As I discussed in #333, requiring a warmer lower part of the atmosphere, on warming further and emitting more IR, to cause a cooler part receiving the excess IR to cool further, violates radiative transfer principles and/or the Second Law. For anyone following this discussion, I would urge them to find my own conclusions best described in #333, but they should also visit #14, for Raypierre’s perspective on the topic.
this a great analysis but I will also echo something said earlier. the laymen just want to know, how can high altitude areas be cooler than than at sea level yet the energy is coming from above[ the sun].
granted, over-simplification would merely serve to mislead scientists. my suggestion: two replies side by side, one to the laymen and another about photons, wavelengths, frequencies, planck, einstein.
good article nevertheless.
Fred, are you distinguishing the stratosphere temperature
–during the period of nonequilibrium from
–during the new equilibrium period after CO2 stops increasing and the warming has leveled off at a higher temperature?
Re Chris Colose, Andy Lacis, Fred Moolten – Okay, I’ve figured it out. (I now agree with Chris Colose and Andy Lacis). I wouldn’t have taken so long if I hadn’t been flipping between different ways of picturing the problem:
The forcing of a doubling of CO2, in the approximation of a band where optical thickness halves over a spectral interval of BW (BW1 or BW2 depending on the side of the peak) going away from the peak
and in the approximation that other sources of optical thickness and the Planck function don’t vary much over the width of the CO2 band so – or their combination of variations is such – that the baseline spectral flux for no CO2 as well as the value at any given optical thickness from CO2 is approximatly constant over wavlength – or else so that the baseline and other levels of spectral flux for a given additional optical thickness, or at least the differences among them, vary over the band is such that as the band widens, decreasing effect on one side is balanced by increasing effect on the other – but for now I’ll just use the simplification of a constant baseline and additional optical thickness effect on spectral flux over the width of the band:
Consider a graph of the spectal flux (per unit area, of course) over wavelength, with some baseline flux for the absence of CO2, and some saturation value when CO2 optical thickness is very large. The effect of CO2 is a hill or valley that has some height or depth from the baseline; it’s maximum height or depth is achieved when the central portion of the band saturates. The magnitude of the radiative forcing per doubling is equal to the effect of band widenning, which is (BW1+BW2)*depth of valley or height of hill, plus some additional effect in the center of the band, which is on the order of 1/2 * (BW1+BW2) * increase in height or depth of hill or valley; the central contribution could be more or less than that, but it will be less than double (because the shape of the absorption spectrum won’t allow a square shape in the graph of the spectral flux). This last part becomes insignificant when the center of the band becomes saturated; however, if the temperature fluctuatuates over thin vertical layers near the level for which this flux is evaluated, an initial saturation effect can be reversed. Hypothetically it could reverse multiple times; each time, the height or depth of the hill/valley at the point of the the most recent ‘saturation’ can be multiplied by the BW1+BW2 to find the magnitude of the radiative forcing from band widenning, with the only remaining part to consider being the reversal of the trend in the flux near the center since the most recent ‘saturation’.
At the tropopause, there is a baseline net upward spectral flux, which is the upward – downward baseline fluxes. Absent CO2, the stratosphere is essentially transparent near the CO2 band, so the net upward baseline flux is equal to the upward baseline flux from below, and it is equal to the baseline OLR spectral flux at TOA. Thus the baseline of the net upward spectral flux is the same at the tropopause, TOA, and everywhere in between.
The radiative forcing is the decrease in net upward flux.
CO2 puts a valley in the upward flux; at the tropopause it puts a hill in the downward flux, which combine to form a valley in the net upward flux. The generally positive lapse rate in the troposphere down to the surface means that the valley in the upward flux at the tropopause (I’m going to say TRPP, for short) has no reversals in the depth of the valley until ultimate saturation. Depending on the lapse rate in the stratosphere, the hill in the downward flux could reverse at some point, particularly if their is a large negative lapse rate in the base of the stratosphere – but I don’t think this tends to be the case; anyway, let’s assume that the CO2 valley in the TRPP net upward flux only deepens until it saturates at zero (it saturates at zero because at that point the upward and downward spectral fluxes at the center of the band are equal to the blackbody value for the temperature at TRPP).
There is thus a greater maximum depth that the CO2 valley can achieve at TRPP (or within the stratosphere) than at TOA because the baseline net upward flux is the same but the net flux can be brought all the way to zero except at TOA, where there is no source of downward flux. Thus, if the CO2 band center is sufficiently close to saturation at TRPP, the forcing per doubling will be smaller at TOA, implying some cooling of the space in between (equal to the difference in forcing between TRPP and TOA; the climatic response will, via cooling, reduce the fluxes out of the stratosphere by the same amount; some fraction of this can go into the troposphere, and since it is a reduced downward flux, it cancels out some of the initial TRPP forcing, resulting in a smaller TRPP forcing (the forcing with stratospheric adjustment) that the surface+troposphere must respond to. When the troposphere+stratosphere respond by warming, an increase in the net upward flux at TRPP occurs that is equal to the TRPP forcing with stratospheric adjustment – the stratosphere is warmed by this, but only by the fraction of that which it absorbs; if that is sufficiently small, than the stratospheric warming is smaller than than the initial cooling, so some cooling remains (there will be feedback from this stratospheric warming that results in some additional warming of the troposphere+surface, which adds some more stratospheric warming, but an infinite number of iterations will converge to a small finite effect if the stratospheric absorption of the changes in upward fluxes from below is small enough). Depending (?) on how the temperature varies with height and how other gases, etc, within the troposphere that lower the baseline, are distributed relative to temperature, it may in general be the case that the valley at TRPP will be deeper than the valley at TOA even if it is not saturated at TRPP (?).
With solar heating, particularly of the upper stratosphere, the upper stratosphere is warmer than otherwise; with sufficient heating (as it is now on Earth), the upper stratosphere is warmer than the lower stratosphere. The valley in net flux at TOA can, at sufficient CO2 amounts, develops a hill at the bottom. The effect of the growth of this central region partly cancels the band-widenning (which is itself proportional to the depth of the valley, which may tend to be less than the depth of the valley at TRPP). Thus, a given amount of solar heating results in increased stratospheric cooling for a doubling of CO2.
But without direct solar heating of the stratosphere (and in the approximation of no non-radiative energy fluxes throught the stratosphere), while the temperature should decline through the stratosphere, it will not go to zero. The CO2 valley for the OLR at TOA still cannot get as deep as it can at TRPP, although it won’t reverse after saturation (lack of reversal would also be true for an isothermal stratosphere).
Approaching TOA, the temperature falls toward a skin temperature (see last paragraph of my 340, see Chris Colose’s comment for the reason why), which is lower than the brightness temperature of the OLR at the wavelengths at which the skin layer absorbs OLR from below; specifically, the skin temperature is such that, were the skin layer to become very optically thick, the OLR at those wavelengths would drop to half of what they are. Let’s assume that it is the 15 micron OLR that controls the skin temperature; the blackbody OLR (at 15 microns) for the skin temperature will be half of the actual OLR. In a linear approximation (that the blackbody spectral flux as a function of local temperature changes linearly over optical thickness going down from TOA, down to a sufficient optical depth), a doubling of CO2 will bring the depth of the valley halfway towards half of the OLR (the OLR at 15 microns will decrease by 25 % per doubling – remember this is before the temperature responds).
So, assuming the same baseline net upward flux (transparent (except for CO2) stratosphere in the vicinity of the CO2 band), if the CO2 valley in net upward flux is saturated (at the center) at TRPP, the depth of the TRPP valley is deeper than the valley at TOA both before doubling, after doubling, and even at TOA saturation. The forcing for an unsaturated valley, per doubling of CO2, is more than the (BW1+BW2) * initial valley depth, but it is less than the (BW1+BW2) * final valley depth, which will be less than the (BW1+BW2) * saturated valley depth at TOA, which is still less than (BW1+BW2) * saturated valley depth at TRPP.
Thus, at least if the CO2 band is sufficiently close to saturated at it’s center at TRPP, and maybe even if it is not, the TRPP radiative forcing will be greater than the TOA radiative forcing for a doubling of CO2, so their will still be initial stratospheric cooling. It will be, as in the case with direct solar heating, larger than the final equibrium cooling, but it could still be a cooling even after surface+tropospheric warming, though both the initial and final cooling will be smaller than in the case with direct solar heating.
(PS to deal with the shift in the tropopause, we could take TRPP to be the higher final tropopause position.)
——-
(the other approach I was thinking of involved considering how the lapse rate equilibrates so that the net flux is constant over some thickness for the whole LW spectrum (approximately true for equilibrium above the tropopause). This won’t generally be the case at every LW frequency. Thus, at some frequencies, there will be layers with net radiative heating; which means at others, there will be net radiative cooling of the same layers. So what happens when optical thickness is changed at one or the other of those sets of frequencies?
——-
Of course, though some of the flux up at the tropopause escapes directly to space, and some is absorbed by CO2 (over the whole stratosphere in the wings of the CO2 band, concentrated towards the base of the stratosphere for larger optical thicknesses), some is absorbed by ozone (with variable concentration), and some by water vapor. The troposphere+surface have to warm up enough so that the upward flux at TRPP balances both the TRPP forcing and TRPP feedbacks from changes below TRPP. That doens’t affect the equilibrium increase in the upward flux at TRPP in response, though it may change how much of that is absorbed by the stratosphere (perhaps a reduction due to shielding of water vapor and CO2 wings in the stratosphere by increased tropospheric water vapor (as it would by an increase in clouds, particularly higher clouds) – PS feedbacks also change the baseline spectral flux in the vicinity of the CO2 band.
But then there’s feedbacks within the stratosphere (water vapor), which would increase the stratospheric heating by upward radiation from below, as well as add some feedback to the downward flux at TRPP that the upward flux at TRPP would have to respond to via warming below TRPP. (In general, the troposphere+surface have to warm to balance the TRPP forcing and feedbacks (in terms of net flux, thus depending on stratospheric feedbacks), and the stratospheric temperature has to respond to both forcing and feedbacks in the TOA net flux – TRPP net flux.)
PS what if their where a substance within the stratosphere that provided significant optical thickness in the vicinity of the CO2 band. This would tend to reduce the potential for TOA forcing even more, leading to more stratospheric cooling in response to an increase in CO2; however, the presence of such a substance would itself make the inital stratospheric temperature warmer than otherwise.
Patrick27, 340, 344–
I hesitate to comment on a discussion I am not prepared (for the most part) to understand in any depth; however, perhaps others will be confused, as I was, by your comments WRT the stratospheric lapse rate.
Surely the stratospheric lapse rate is in fact negative, as every “general science”-level discussion of the matter I’ve ever read states? After all, the stratopause is what, about -3C?
Re 346 ziarra – the flow of heat (between adjacent layers of material via conduction, convection, or mass diffusion, or potentially across larger distances via emission and absorption of photons) will be from hot to cold (or from higher to lower concentrations of a substance carrying heat, which might end up being from cold to hot in some conditions, such as a wet surface cooling by evaporation into warm dry air).
But this flow of heat is spontaneous because the energy (or matter than embodies it) tends to spread out from whereever it is. It is spreading out even from cooler regions; but because the concentration is less, the flow of energy out of lower concentrations is less than the flow out of higher concentrations (other things being equal). Thus the flow of heat, which is a net flow of energy, is from higher to lower concentrations of that type of energy.
The radiation from a cooler upper atmosphere can warm the surface because it counteracts the even greater amount of radiation in the other direction, thus reducing the net flow of heat.