According to some recent reports (e.g. PlanetArk; The Guardian), the public concern about global warming may be declining. It’s not clear whether this is actually true: a poll conducted by researchers at Stanford suggests otherwise. In any case, the science behind climate change has not changed (also see America’s Climate Choices), but there certainly remains a problem in communicating the science to the public.
This makes me think that perhaps a new simple mental picture of the situation is needed. We can look at climate models, and they tell us what we can expect, but it is also useful to have an idea of why increased greenhouse gas concentrations result in higher surface temperatures. The saying “Everything should be made as simple as possible, but not simpler” has been attributed to Albert Einstein, which also makes me wonder if we – the scientists – need to reiterate the story of climate change in a different way.
Gavin has already discussed this (also see here and here), but it may be necessary to tell story over again, with a slightly different slant. So how can we explain how the greenhouse effect (GHE) work in both simple terms and with a new angle? I also want to explain why the middle atmosphere cools with increasing greenhouse gas concentrations associated with an increased GHE. Here I will try to present a conceptual and comprehensive picture of GHE, explaining both the warming in the lower part of the atmosphere as well as the cooling aloft, and where only the most central features are included. Also, it is important to provide a good background, and we need to start with some very fundamental facts.
Four main physical aspects
Several factors are involved, and hence it may be useful to write a simple recipe for the GHE. This recipe then involves four main ingredients: (i) the relationship between temperature and light, (ii) the planetary energy balance, (iii) the distance light travels before being absorbed, and (iv) the relationship between temperature and altitude.
(i) Temperature and light
Energy can be transmitted in many different ways, involving photons (light or electromangetic radiation), conduction, and motion. Most of these require a medium, such as a gas, fluid, or a solid, but space is basically a void through which photons represent virtually the only form for energy transfer. Hence, planets tend to gain or lose energy to space in the form of photons, and we often refer to the energy loss as ‘radiative heat loss’.
A fundamental law of physics, known as the Planck’s law, says that radiative heat loss from any object depends on its temperature. Planck’s law also explains the colour of the light, or its wavelength, and hence explains why iron gets red hot when heated sufficiently.
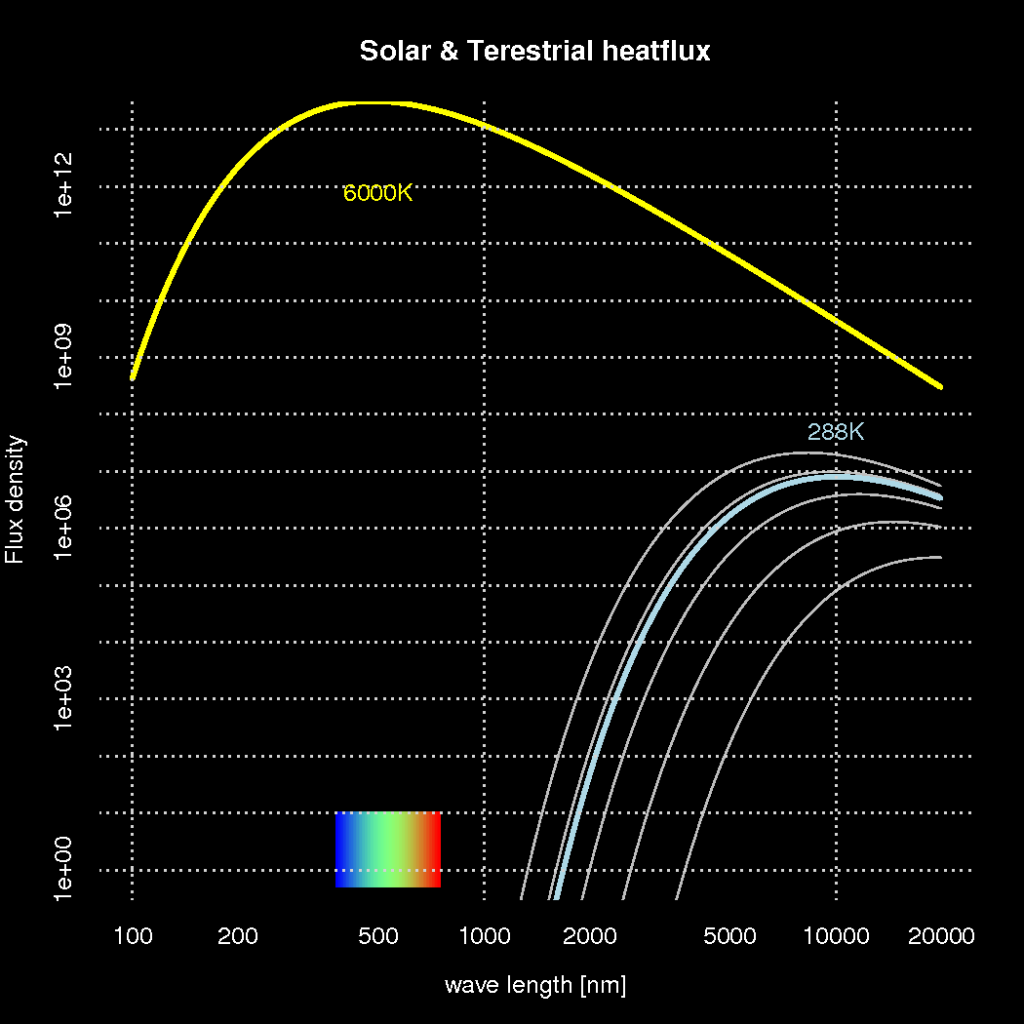
Planck’s law predicts that the light from an object with a temperature of 6000K – such as the solar surface – produces light that is visible, whereas objects with a temperature of 288K produce light with a wavelength that our eyes are not able to see (infra red). This is illustrated in Figure 1 showing how the light intensity (y-axis; also referred to as ‘flux density‘) and the colour of the light (wave length) vary for objects with different temperatures (here represented by different curves). The yellow curve in the figure represents the solar surface and the light blue curve the earth.
(ii) The planetary energy balance
The planetary energy balance says that our planet loses heat at the same rate as it receives energy from the sun (otherwise it would heat or cool over time). This is because energy cannot just be created or destroyed (unless it involves nuclear reactions or takes place on quantum physics scales).
The planets’ distance from the sun and the brightness of its surface dictates how much energy it receives from the sun, as the light gets dimmer when it spreads out in space, as described by Gauss’ theorem.
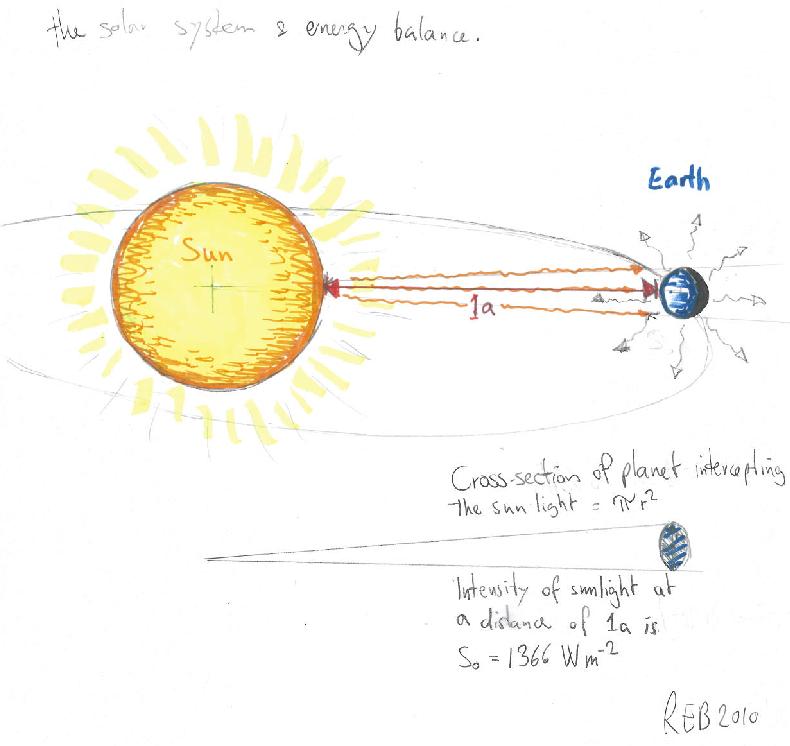
The energy flowing from the sun is intercepted by the earth with energy density described by the ‘solar constant‘ (S0=1366W/m2), and the amount of energy intercepted is the product between this flux density and the earth’s disc (minus the reflected light due to the planet’s albedo: A ~0.3). The average heat loss is given by the product of earth’s surface and its black body radiation:
S0/4 (1-A) = σT4,
where σ=5.67 x 10-8W/(m2 K4) is the Stefan-Boltzman constant. This gives a value of 255K, known as the emission temperature.
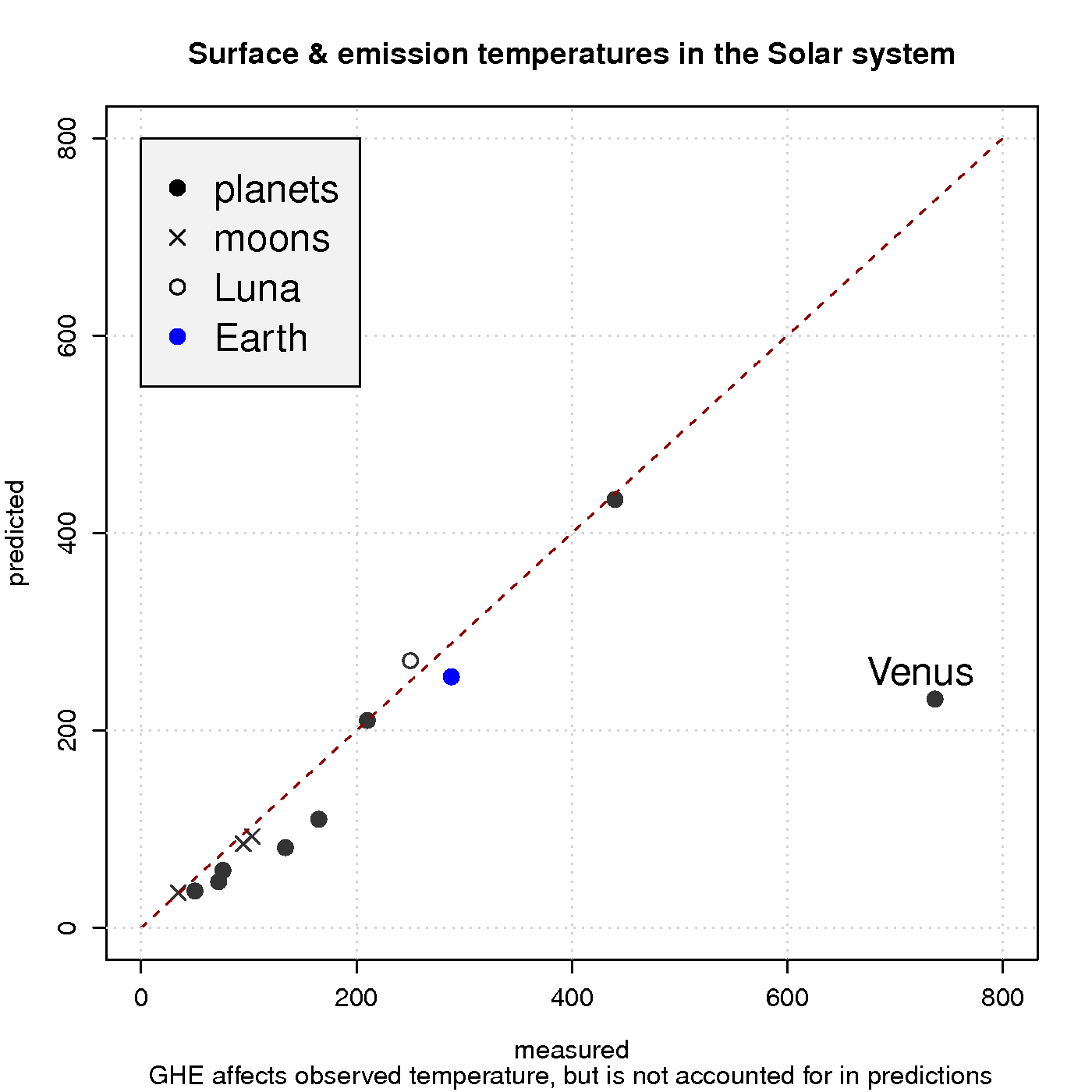
Figure 3 shows a comparison between observed surface temperature and calculated emission temperature for the planets in the solar system, based on the balance between energy from the sun and heat loss due to black body emission. In these simple calculations, the greenhouse effect is neglected, and the black body radiation can be derived from Planck’s law. The calculations agree quite well with the observations for most of the objects in our solar system, except for Venus which is known to harbour a strong GHE and has a hotter surface than Mercury despite being about twice as far away from the sun.
(iii) Light absorption
It is also clear that our planet is largely heated at the surface because the light from the sun – which is visible for our eyes – penetrates the atmosphere without much absorption (hence we can see the sun from the ground). However, the atmosphere is a medium of gas and particles that can absorb and scatter light, depending on their wavelength (hence explain why the sky is blue and sunsets orange).
The distance light travels before being absorbed – optical depth – can vary with the light’s wavelength and the medium through which is travels. The optical depth in our atmosphere is different for visible and infra-red light.
Infra-red light is absorbed by molecules, which in turn get more energetic, and the excited molecules will eventually re-emit more infra-red light in any random direction or transfer excess energy to other molecules through collisions. In a optically thick (opaque) atmosphere, there will be a cascade of absorption and re-emission.
Hence, whereas the planet is heated at the surface, it’s main heat loss takes place from a height about 5.5 km above the ground, where most of the radiation is free to escape out to space. The optical depth dictates how deep into the planet’s atmosphere the origin is for most of the planet’s infra-red light (the main planetary heat loss) that can be seen from space. Furthermore, it is the temperature at this level that dictates the magnitude of the heat loss (Planck’s law), and the vertical temperature change (lapse rate) is of course necessary for a GHE. The temperature at this level is the emission temperature, not to be confused by the surface temperature.
We know that the optical depth is affected by CO2 – in fact, this fact is the basis for measuring CO2 concentrations with infra-red gas analysers. Molecules composed of three or more atoms tend to act as greenhouse gases because they can possess energy in terms of rotation and vibrations which can be associated with the energy of photons at the infra-red range. This can be explained by theory and be demonstrated in lab experiments. Other effects are present too, such as pressure and Doppler broadening, however, these are secondary effects in this story.
(iv) The relationship between temperature and altitude
There is a well-known relationship between temperature and height in the troposphere, known as the ‘lapse rate‘ (the temperature decreases with height at a rate -6K/km). The relationship between temperature and altitude can also be seen in the standard atmosphere. The lapse rate can be derived from theory for any atmosphere that is the hydrostatically stable condition with maximum vertical temperature gradient, but it is also well-known within meteorology. Thus, given the height and value of the emission temperature, we can get a simple estimate for the surface temperature: 255K + 5.5km * 6K/km = 288K (=15oC; close to the global mean estimated from observations given by NCDC of ~14oC).
Enhanced greenhouse effect
The term known as the ‘enhanced greenhouse effect’ describes a situation where the atmosphere’s becomes less transparent to infra-red light (reducedincreased optical depth), and that the heat loss must take place at higher levels. Moreover, an observer in space cannot see the infra-red light from as deep levels as before because the atmosphere has become more opaque.
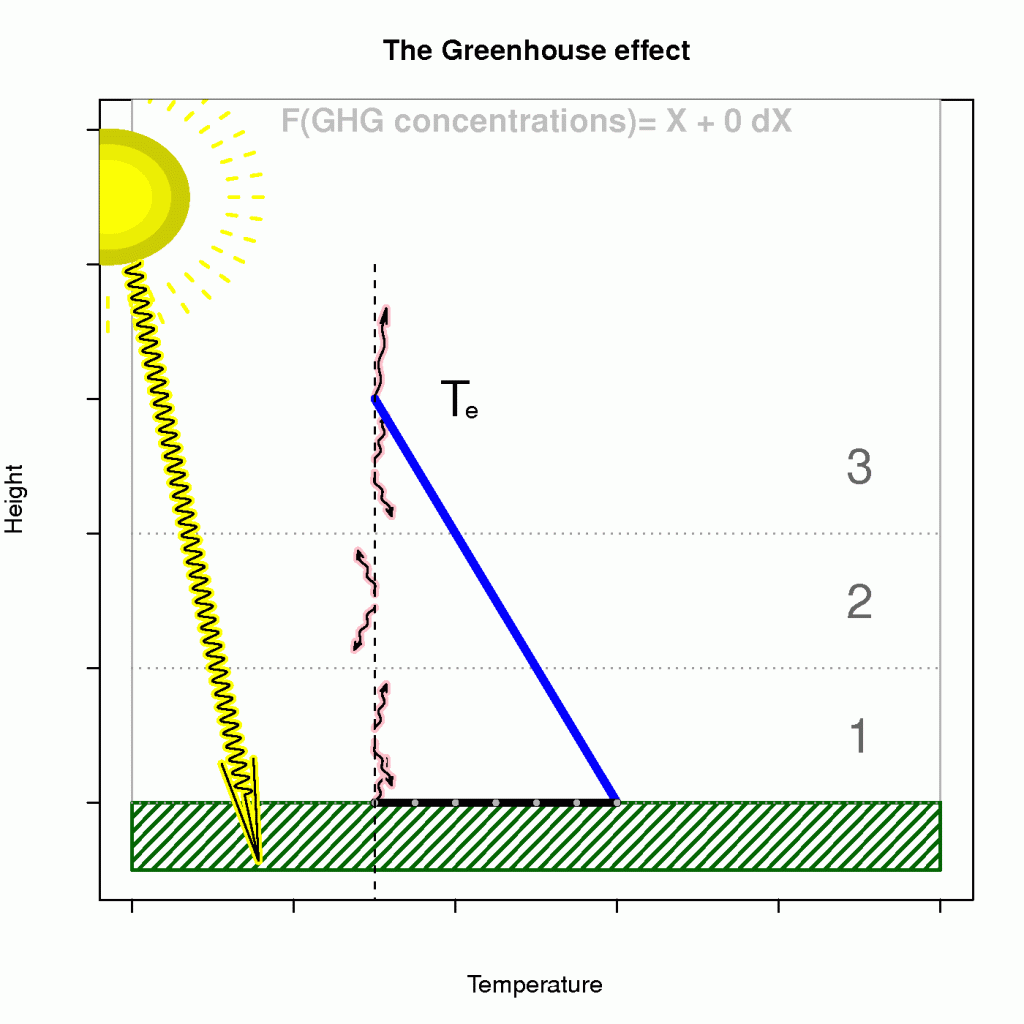
The effect of heightened level of heat loss on the surface temperature is illustrated in Figure 4, where the emission temperature and lapse rate are given if we assume an energy balance and a hydrostatically stable atmosphere on average (a generally hydrostatically unstable atmosphere would be bad news).
Hence, a reducedincreased optical depth explains why atmospheres are not easily ‘saturated‘ and why planets such as Venus have surface temperatures that are substantially higher than the emission temperature. Planets with a thin atmosphere and insignificant greenhouse effect, on the other hand, have a surface temperature that is close theto the estimates from the planetary energy balance model (Figure 3).
Feedback processes
The way the atmosphere reacts to changes in the optical depth is more complicated, due to a number of different feedback mechanisms taking place. But to get a simple overview, it is useful to keep in mind that the optical depth is sensitive to how much water vapour (humidity) there is in the air, and that the lapse rate is sensitive to the composition of the atmosphere (i.e. humidity). Furthermore, the albedo A is affected by clouds, snow, ice, and vegetation, all of which affect the way the earth receives energy from the sun.
In our simple picture, feedback processes affect changes in the height of the level where most heat loss takes place, the slope of the lapse rate, and heating at the surface (and hence the emission temperature).
So why is the upper atmosphere cooled then?
The upper atmosphere, comprising the stratosphere and mesosphere, is expected to cool during an AGW, as shown by the GCMs. So what is happening there? This is when the picture becomes more complicated.
Since CO2 mostly absorbs/re-emits infra-red light at around 14 microns, an increased concentration in the troposphere will reduce the upward infra-red radiation at this band. The total energy is roughly constant, but it is made up from increased emissions at other bands because it’s warmer. There is less absorption by CO2 of upwelling infra-red light above the troposphere, but increased emission as a function of increased concentrations. Thus there is a cooling.
Controversy?
Can this picture be falsified, e.g. if other factors were to play a role too? For instance, can this situation be altered by changes in the sun?
Changes in the sun can of course affect the amount of energy received by the earth through changes in its output, variations in the intensity of UV-light, or perhaps even clouds through galactic cosmic rays. But it’s hard to see any systematic long-term trend in the level of solar activity over the last 50 years, and it is difficult to see how solar activity may have an effect while other factors, such as GHGs, don’t. Gavin and I recently published a study on the response to both solar activity and GHGs, and found similar magnitude for both forcings in both observations and the GISS GCM.
There have been claims of negative feedbacks, such as the “iris effect“. One would expect negative feedbacks in general to dampen the response to most forcings, unless they involve a particular process that is active for a particular forcing. In other word, why would a negative feedback act for GHGs but not for solar forcing? Many feedbacks, such as changes in atmospheric moisture, cloudiness, and atmospheric circulation should be similar for most forcings.
Another question is why we do see a global warming trend if the negative feedbacks were most important (Figure 5). Negative feedbacks usually imply quiet conditions in a complex system, whereas positive feedbacks tend to lead to instabilities, often manifested as internal and spontaneous oscillations (see Figure 5). It is reasonable to expect the feedback processes to affect natural variations as well as forced changes such as an enhanced GHE, orbital changes, volcanoes, or changes in the sun.
The point about negative feedback also brings up another interesting issue: Negative feedbacks usually act to restore a system to a particular zero-level state. What would the zero-state be for our climate? No greenhouse effect or some preferred level of greenhouse warming? There is already a natural GHE that, together with other atmospheric effects, can account for about 32oC higher global mean surface temperature. What makes this state so special, and can we explain the present natural GHE in the presence of negative feedbacks (consider starting from a state with no GHE)?
Hence, claims of negative feedback is controversial because all these tough questions then need to be addressed. We can write down a simple recipe for the GHE, but it is indeed challenging to reconcile a presence of a negative feedback with our observations, or explain the current observed global warming in any other terms.
“Thus the flow of heat, which is a net flow of energy, is from higher to lower concentrations of that type of energy.”
Although one may refer to the individual flows of that type of energy as flows of heat, but they aren’t *THE* (net/total) flow of heat.
Hank (347) – I’ve restricted my discussion to equilibrium conditions. While I’m commenting, I want to agree with Patrick above that as long as there is a solar absorber, there will be conditions permitting increased opacity in a grey gas atmosphere to result in stratospheric cooling. I also agree that if complicating factors are introduced that invalidate my assumptions in #333 about an explanation excluding ozone, one might see cooling without ozone, but I’m not aware of any factor that would actually change the assumptions sufficiently to do that. I therefore must stick with the conclusion that a solar warmer is needed for increasing CO2 to cool the stratosphere.
Chris C – In reviewing Raypierre’s chapter, I note that he introduced his equations using a grey gas model, but my point was that he then applied the results to our own atmosphere. Regarding Venus, it appears that the solar absorber is CO2, primarily in the near infrared.
To all – now that we’re airing some disagreements, I want to restate my respect for all those participating. I present the logic of my conclusions as convincingly as I can, but that doesn’t diminish my respect for those who disagree as thoughtfully as is the case here.
Re 346 ziarra, again:
“The radiation from a cooler upper atmosphere can warm the surface because it counteracts the even greater amount of radiation in the other direction, thus reducing the net flow of heat.”
In other words, the greenhouse effect reduces the radiative heat loss of the surface, which is being heated by the sun; the surface has to warm up enough so that it can lose heat at the same rate that it gains heat from the sun (though changes in radiative heating at the surface can be made up for by convection, which is why we tend to focus on the effect of net heat loss at the tropopause, which is approximately an upper boundary to convection; the surface and troposphere together are cooled by the net radiative heat loss at the tropopause, which can be reduced both by greenhouse gases and clouds within the troposphere (reducing the upward flow of radiation because they are cooler than the surface and block the greater flow of radiation from the surface) as well as by the greenhouse gases within the stratosphere (by increasing the downward flow of radiation; withoug the greenhouse gases, the stratosphere would not emit any radiation).
The surface and troposphere are linked by convection so that they tend to warm up and cool down together in response to changes in either the greenhouse effect or in solar heating.
Air expands and cools as it rises (to lower pressure) and does the opposite when it sinks (to higher pressure), which is why convection cannot make the troposphere as warm as the surface. Convection tends to occur where radiative processes alone would make the temperature drop with height faster than the rate that air cools as it rises (the greenhouse effect is important for that, too).
Since you’ve taken it upon yourself to explain climate science to us, there’s one subject that has always confused me. If the atmosphere is a big window to space, it seems not to be transparent to very many wavelengths of infra red light. What is particularly bad about CO2? Does it block one of the few open pathways? How about methane, SF6, and others – do they block the same wavelengths as CO2, or do they stake out other wavelengths. I find it amazing that CO2, present in such tiny amounts, can cause such mayhem.
ref. #10
Neaaaaa….what’s up Doc?
Sorry Edward…I could not help myself.
Great lecture Gavin…
lucien
In the grey gas case with no solar heating above the stratosphere, the equilibrium temperature at TOA is fixed by the equilibrium OLR (such that the blackbody flux for T(TOA) is half of actual OLR; by the way, for some purposes it may be easier to refer to values of temperature in terms of the corresponding blackbody or Planck function value – ie the surface has warmed up to 390 W/m2, etc…).
The temperature from the tropopause to TOA drops in such a way as to keep the net upward LW flux constant. For large optical thicknesses, this can be achieved (within limits – see below) by having T^4 decrease linearly over distance measured in terms of optical thickness, so that the corresponding blackbody flux changes linearly over optical thickness – in that case, an evenly distributed increase in optical thickness reduces the net upward flux by the same amount at different vertical positions, so that no layer experiences an initial heating or cooling (this is before temperatures change elsewhere, such as at the surface and troposphere).
However, if the temperature outside some region breaks from this pattern (in the troposphere or at the surface, above TOA in effect), this changes LW fluxes entering the region where the pattern holds, requiring some compensating deviation from that pattern in those locations. Both the deviations from such a pattern outside the stratosphere and the deviations necessary within the stratosphere may allow an increase in optical thickness to cause some initial warming or cooling within the stratosphere.
Effect of additional optical thickness on the skin layer: The OLR is reduced, which cools the skin layer. This is entirely transient since the OLR has to return to the same equilibrium value when the full climatic equilibrium response occurs (absent SW feedbacks, of course). For an optically thick stratosphere, for full equilibrium, the same temperature profile is compressed towards TOA, except where the flux from the troposphere+surface requires some deviation.
Patrick (348) – I wonder whether you’re using the terms “upward flux” and “net upward flux” interchangeably. They are very different. With a warming troposphere due to increased CO2, the upward flux must inevitably increase via the Planck function. This warms any atmosphere above it. In the absence of ozone, there would be no well-defined stratosphere, but what we now call the stratosphere would also warm due to its increased opacity, and an increased upward flux from below in the CO2 wavelengths. This is why, barring some unusual extraneous factors, we would predict “stratospheric” warming rather than cooling from a CO2 increase.
I feel like I’m belaboring the point, but I would refer anyone interested to go back to #333 for the thermodynamic/radiative transfer analysis. Despite the fact that I see the logic there as sound in its own right, my confidence is reinforced by the explanation I quoted from Raypierre in #14.
Pete Baldo (354):
Please refer to this diagram which will be helpful for your question
http://chriscolose.files.wordpress.com/2010/03/upwelling_toa1.png
For the top part of the figure: The “window” regions are those levels where radiation from the surface and lower troposphere can easily escape to space, and so the blue squiggly curve tracks the blackbody spectrum for hotter temperatures (between 280 and 300 K). This can be found primarily between 800 and 1200 cm**-1 except for the ditch caused by ozone (the units here are wavenumbers, which is the inverse of wavelength). CO2 absorbs between the 600-800 cm**-1 region, a very important part of the spectrum for planets or moons which radiate at Earth-like temperatures, and so yes, this substantially reduces the outgoing radiation of the planet for a given temperature.
By the way, how effective a new greenhouse will be for altering the global climate depends very much on whether another absorber is present at those wave numbers of strong absorption. Introducing a greenhouse gas that absorbs in the window regions would have a much larger effect than introducing a new greenhouse gas that absorbed where CO2 already did. This is why CFC’s have a stronger molecule-by-molecule impact than CO2.
To Patrick, Fred, and other interested in this discussion on the technical details of stratospheric cooling. I have just had a brief e-mail correspondence with Ray Pierrehumbert asking for clarification on the relevant section in his book; he is currently in New Zealand and busy with work and so he cannot explore our conversation here. Having his permission, I am posting his remarks from two emails here (psst…I am dubbing this ‘raypierre-gate’ but don’t tell anyone). He didn’t seem to directly answer the question of whether you get upper-atmosphere cooling with no UV-absorbers at all, which my impression from his message goes beyond a simple thought experiment. He is also leaving us with work exercises for the readers:
………….
Email 1
Hi, Chris,
[irrelevant discussion]
I’m glad the analytic grey gas solution
has gotten people thinking. It’s what it’s for.
The grey gas version doesn’t actually do the complete job of accounting
for what is going on regarding stratospheric cooling/tropospheric warming.
The main points of that solution are to show that (1) for making
temperature increase with height, it’s not enough
to have a stratospheric absorber; you need one with the right vertical
profile, and (2) you can get stratospheric cooling in response to
increased IR opacity because you get rid of more of the absorbed solar
locally. The tricky part is getting stratospheric cooling together with
tropospheric warming. My analytic solution doesn’t even try to do the
whole problem, since the analytic solution is just pure radiative
equilibrium. In the pure radiative equilibrium, you can get it into a
range where the grey model gives you surface warming and stratospheric
cooling (that’s in one of the problems), but you have to work at it a bit,
and also remember to plot things in pressure coord, not optical depth
coordinates. That’s still
not the whole story, though, since the full story involves
radiative-convective equilibrium. I’m pretty sure you can get the grey
version of that into a strat-cooling/trop-warming situation if you pick
the strat absorbers right, but Andy is certainly right that non-grey
effects play a crucial role in explaining quantitatively what is going on
in the real atmosphere (that’s connected with the non-grey explanation for
the anomalously cold tropopause which I have in Chapter 4, and also with
the reason that aerosols do not produce stratospheric cooling, and
everything depends a lot on what level you are looking at). Remember,
too, that ozone changes are part of the observed stratospheric cooling.
I hope those remarks help to set things in the right direction. The book
is in production, and will go to the printers in August if I return the
proofs on time. Still takes until December for it to get distributed and
go on sale. I have started cleaning up the web site and online materials.
A complete set of data sets and scripts is now available at the new
web site (still embryonic, but growing):
http://geosci.uchicago.edu/~rtp1/PrinciplesPlanetaryClimate/index.html
[irrelevant discussion]
–Ray
……………….
Email 2
……………….
Hi,
I see what the discussion is centered on. These are interesting and
thought provoking issues. Certainly, it is true that you can’t get the
stratospheric cooling in a grey model without shortwave absorbers, not if
you keep the OLR fixed (i.e. constrain things to satisfy the TOA radiation
budget). In the full radiative-convective case, it’s rather tedious to
work that out analytically (though you can, in the optically thick limit),
but exploring it numerically is fairly simple. The basic idea, though, is
that the stratosphere temperature scales with the skin temperature, and
that doesn’t change if you hold OLR fixed.
For a real gas it’s a lot harder to do the reasoning analytically,
especially since you have to keep in mind the effects of changing the
tropopause height. It would be instructive to work this out for the
window-grey atmosphere, which has a lot of the basic features of the real
gas in this regard. I don’t really have a suitable plot in Chapter 4 to
address this question, since the real-gas results in Chapter 4 are
computed holding the surface temperature fixed while you make the
atmosphere more optically thick (in which case you do get stratospheric
cooling, but that’s not the same thing you’re talking about). I’d suggest
doing a simple CO2 plus dry air radiative-convective calculation for
either the NCAR model or my homebrew radiation code, using the Python
scripts I have provided for the purpose. There are always more questions
than can be covered by an static set of graphs, which is why I worked so
hard to provide software so people can explore this sort of thing on their
own.
–Ray
……………..
Hopefully these help for the discussion we’re having, of which I don’t know if I can add anything more
Chris
Re: #354
The main reason is that your phrase “present in such tiny amounts” has led you astray. If you see such a remark in science ask yourself tiny compared to what ?> The concentration of CO2 is the wrong measure for deciding whether it is ‘tiny’, because it compares the amount of CO2 with the amounts of oxygen and nitrogen which don’t absorb infra-red at normal pressures.
Thus CO2 is important because
(a) There is a lot of it compared to all the other greenhouse gases except water vapour.
(b) If we increase the amount , the increase will stay around for an unusually long time.
(c) The level of water vapour depends on the global temperature , so it is roughly fixed until something else warms the atmosphere when it increases in amount producing more warming. The CO2 is often the something else, especially during the last few decades i.e. the CO2 has been acting as a driver for the water vapour.
Ray’s answer makes it obvious (for me) that reality is very complex and far from being explainable by simple, hand-made arguments for the general audience; that’s why I think that trying to explain “simply” the very complex phenomena involved in radiation transfer is just lost time- and in my opinion the REAL issues associated with social impacts of GW are not primarily associated with the detailed physics of the phenomenon.
Concerning the stratospheric cooling, I have the impression that they’re two different explanations that are often mixed and confused.
* increasing CO2 concentration of the opaque (lower) layer of the troposphere absorbs more LWR , which decreases the heating of the upper layers and eventually produces a cooling.
* increasing CO2 concentration in the optically thin (upper) layer in the stratosphere increases the LWR emissivity and hence increases the cooling.
Correct me if I’m wrong, but I think that the first effect can only be a transient effect, because it holds only during the warming phase of the Earth surface. Actually to reach a new, higher equilibrium temperature, the Earth surface (including oceans) must warm and thus the radiative budget MUST be unbalanced, less radiation must be emitted in space compared to the (unchanged) incoming solar radiation. So during this phase, the increased absorption actually lowers the temperature of TOA. But eventually, this will be exactly compensated by the increased emission from the surface (because it’s getting warmer and warmer), until by definition both fluxes compensate exactly and a new steady state is reached. But the the radiation emitted in space is again exactly the same, and so the “photosphere ” (TOA defined by IR optical depth around one) , what I understand being the “skin”, is the same. And ABOVE this skin, there is no reason why the stratosphere should cool – IMHO the argument that the temperature gradient must still be larger is INCORRECT, because in the transparent regime, the heat flux is no more linked to temperature gradient (hence the temperature increase with altitude…)
so once the new equilibrium temperature is reached, the increased absorption of the lower level is compensated by the increased emission from the ground, and this shouldn’t change the stratosphere temperature. That’s how I understand Ray’s assertion “The basic idea, though, is that the stratosphere temperature scales with the skin temperature, and that doesn’t change if you hold OLR fixed.”
So the ONLY permanent effect is the second one : stratosphere temperature (which is NOT related to heat flux but is the result of heating and cooling process far from LTE) is mainly dominated by heating from the incident UV flux and cooling by the IR emissivity from (optically thin) GES. Increasing GES concentration increases the cooling and hence lowers the equilibrium temperature.
#354 Pete Baldo
Pete, probably the best way to explain how much mayhem such a tiny amount of CO2 can cause, is to consider what the earth would be like without that ‘tiny’ amount.
Frozen.
—
A Climate Minute The Greenhouse Effect – History of Climate Science – Arctic Ice Melt
‘Fee & Dividend’ Our best chance for a better future – climatelobby.com
Learn the Issue & Sign the Petition
Andy Lacis 341,
your equation should read
T = exp(-tau)
where T is transmissivity. Having tau on both sides of the equation just overcomplicates things.
Kevin McKinney 349,
The stratosphere is isothermal in its lower altitudes and has a negative lapse rate in the upper part.
#360, Geoff Wexler:
An additional point:
– H2O vapor quits at about 10 km altitude
– CO2 goes on strong until about 90 km
Since the cooling due to radiation at a frequency is controlled by the temperature at the photosphere (optical depth = 1) at that frequency, the gas on top is most important for the 15-micron band.
(Numbers are from http://www.spectralcalc.com)
The stratospheric cooling that takes place when GHG concentrations are increased is independent of the ozone heating. As I was suggesting in my earlier (341) post, UV absorption by ozone is responsible for creating a stratosphere that is substantially warmer than the tropopause point. With no ozone, the atmospheric temperature would decrease monotonically, and we would instead have to speak of cooling of the “upper atmosphere” in conjunction with the surface warming due to increasing GHGs. The key factor for this model work as the real atmosphere is having a transparent window in the spectrum.
To help illustrate what is happening, it is useful to consider a simple radiative system consisting of a fixed-temperature ground surface (Ts), and a homogeneous, isothermal, single layer atmosphere (of temperature Ta) with spectrally grey absorption. I follows that the ground will it emit Planck radiation according to Bs = sigma (Ts)**4. The atmospheric layer will absorb the amount Bs*[1 – exp(–TAU)], where TAU is the optical depth of the atmospheric layer. By Kirchhoff’s radiation law, the layer emissivity is also equal to the layer absorptivity. Thus the atmospheric layer must emit radiation according to Ba*[1 – exp(–TAU)], where Ba = sigma (Ta)**4, in both the upward, as well as the downward directions. Radiative energy balance for this atmospheric layer requires that
Bs * [1 – exp(–TAU) ] = 2 * Ba * [1 – exp(–TAU) ].
Interestingly, this means that the temperature of this isothermal layer will be independent of the LW optical depth TAU, and is equal to Ta = (1/2)**0.25 Ts, or Ta = 0.84 Ts. This solution is robust for an optically very thin layer, since both the top section of the layer (Tt), and the bottom section of the layer (Tb) will see the same surface temperature. Note that both the top and bottom sections of the atmospheric layer will absorb a tiny fraction Bs*[1 – exp(–dTAU)], and they will similarly radiate the essentially equal amounts of energy 2*Ba*[1 – exp(–dTAU)]. Thus, the temperature gradient that is established within the layer will indeed be close to isothermal. Isothermal layers as such are unphysical for finite optical depths since there is no infinitely fast acting physical process to redistribute the absorbed heat uniformly within the layer. Accordingly, as the optical depth is cranked up, a temperature gradient will be established within the atmospheric layer as the layer bottom temperature Tb becomes hotter than the layer mean temperature, and the layer top temperature Tt becomes colder than the layer mean.
This seems like an ideal problem to assign in a physics class. Given a homogenous spectrally grey slab sitting on a hotplate of fixed temperature, what will be the equilibrium temperature gradient that is established within the homogenous slab?
While an analytic solution is possible, is is anything but straightforward. This is because the analytic solution requires integration over all angles and the evaluation of fredholm integrals of the second kind. Thus, it is preferable to simply solve the problem numerically. Numerical calculations show that the equilibrium temperature gradient within the homogeneous atmospheric slab will be essentially linear in Planck, i.e., a straight line in TAU space can be drawn between Bt = sigma (Tt)**4 at the top of the layer, and Bb = sigma (Tb)**4 at the bottom. We derived analytic formulas for expressing the emitted radiance in the upward and downward directions from such an atmospheric layer in our correlated k-distribution paper (Lacis and Oinas, 1991, JGR).
Now, in this particular example with the fixed surface temperature (assuming the heat capacity of the ground to be infinite, or that there is some thermostat regulating the energy input to the ground to maintain the fixed temperature), as the optical depth is cranked up to infinity, the layer bottom temperature Tb will approach the surface temperature Ts, while the layer top temperature will approach zero. A small temperature discontinuity must remain between the ground and atmosphere in order to transfer heat energy to the atmosphere to maintain the temperature gradient. (If the heat source at the ground were set equal to zero, the only heat source would be the 3K cosmic background input at the top of the atmosphere. The temperature gradient would then collapse, and the laws of thermodynamics would only permit an isothermal (3K) atmosphere to exist.) This simple radiative example (convective transport is not being allowed) shows that any finite surface temperature Ts can be supported in radiative equilibrium with any arbitrarily cold “upper atmosphere” temperature Tt, by prescribing the appropriate LW opacity TAU for the atmospheric layer, with the energy required to maintain a fixed Ts adjusted accordingly.
Note that the above example with the fixed surface temperature is not descriptive of the operation of the terrestrial greenhouse effect. The terrestrial greenhouse effect requires that there is significant solar energy deposition at the ground surface. Then, if the atmosphere were to consist of opaque isothermal layers, each layer of the atmosphere (as in the above example) would be colder by 0.84 than the layer below, thus establishing a decreasing temperature trend with height. As it is, atmospheric layers are not really totally opaque, nor are they isothermal. Moreover, the atmospheric temperature gradient is mitigated by the absorption of solar radiation within the atmosphere (also latent heat deposition), thus a more moderate temperature gradient is established within the ral atmosphere.
Furthermore, the key global energy balance consideration for the terrestrial greenhouse that is in hydrostatic and thermal equilibrium, is that the solar energy that is absorbed by the ground surface and atmosphere must be balanced by the outgoing LW emission to space. This means that for a spectrally grey atmosphere, the “upper atmosphere” represented by the temperature Tt (more specifically the TAU = 1 level as measured from the top of the atmosphere), must be at such a temperature (Te) as to be able to radiate away the absorbed solar energy. Thus, in the spectrally grey atmosphere, Tt is constrained to be equal to the effective temperature Te. Then as atmospheric opacity TAU is increased (doubled CO2, and beyond), the surface temperature Ts can increase essentially without bound as LW TAU is increased (assuming no change in SW albedo, Te will stay fixed). As a result, for this grey opacity model, the surface temperature can continue increasing (as LW TAU is increased) until the Planck surface radiation starts spilling into the solar part of the spectrum. But the “stratosphere”, or “upper atmosphere”, will not able to cool since Tt is constrained to be equal to Te.
From this it is clear that the transparent spectral window is the key factor in limiting and constraining the radiative behavior of the terrestrial greenhouse. As in my earlier (341) post, where half of the spectral outgoing LW flux is assumed to be within the window region (and thus emitted by the ground surface), with the other half being emitted within the radiatively absorbing part of the spectrum, it follows that:
(Te)**4 = 0.5 * [(Ts)**4 + (Tt)**4 ].
Note that in this situation, Tt can vary just as in the fixed surface temperature example described above. But with the transparent window, Tt is now decoupled from being constrained to maintain the planetary energy balance requirement as set by Te. In the case where the LW opacity is negligibly small, Tt will approach the value of the surface temperature Ts. If LW TAU is increased toward infinity, Tt will approach zero, independent of the value of Ts, in which case we will have Ts = Te. Since the absorbed solar radiation is deemed to be 240 W/m2, it follows that Te = 255K, and Ts = 255K will represent the no-greenhouse surface temperature (again assuming there are no changes in solar albedo). With the LW opacity of the atmosphere increased to infinity, we then have [(Ts)**4 = 2*(Te)**4, so that Ts = 303K. This limiting situation represents the maximum possible greenhouse effect that is achievable with an atmosphere that has a spectral window that covers half of the spectrum.
The real world spectral window is of course significantly smaller than half of the spectrum, which would allow the surface temperature to go significantly higher than 303K. Also, the real world spectral window is not spectrally contiguous, nor is it fully transparent for the entire atmospheric column. Nevertheless, the contrasting behavior of the spectrally grey atmosphere, and of the atmosphere with the transparent spectral window, provides a clear indication of how the existence of a transparent spectral window decouples the stratospheric temperature from having to maintain (all by itself) the global energy balance set by the effective temperature Te. That is why it is important to accurately model the radiative transfer within the climate system.
Giles (361)
But a substantial amount of increased emission at the surface (to reach equilibrium) is in the window region (e.g. 10 microns) where CO2 is pretty transparent.
Re 349 Kevin McKinney
On Earth, because of solar heating of the ozone layer (PS the maximum solar heating density will be above the maximum ozone density because the heating is proportional to the solar flux (of relevant wavelengths), which decreases through an absorbing medium), the upper stratosphere is warmer than the lower stratosphere and tropopause. This would actually not be true at sufficiently high latitudes in the winter hemisphere, except that some circulation in the upper atmosphere is driven by kinetic energy generated within the troposphere (small amount of energy involved) which, so far as I know, doesn’t result in much of a global time average non-radiative energy flux above the tropopause, but it does have important regional effects, and the result is that the top of the stratosphere is warmer than the tropopause at all latitudes in all seasons so far as I know.
However, away from lower latitudes, the lower stratosphere is nearly isothermal, and at higher winter latitudes, it has a positive lapse rate.
Because of conditions on Earth, we may think of the stratosphere as being defined by temperature increasing with height (or at least not decreasing by much), but in general, the stratosphere is just the region above the tropopause, and the lapse rate can be positive, just as long as it isn’t large enough to become part of the troposphere.
(PS I had once read that without an ozone layer, the atmosphere could be divided into two layers (by temperature trends – of course there is also compositional and electromagnetic distinctions (homosphere, turbopause, heterosphere; ?electrosphere?, ionosphere, magnetosphere) – the troposphere and the thermosphere. There might be different conventions in labeling in cases where there is no mesosphere?)
———————-
Re 357 Fred Moolten (and Gilles)
Patrick (348) – I wonder whether you’re using the terms “upward flux” and “net upward flux” interchangeably. They are very different. With a warming troposphere due to increased CO2, the upward flux must inevitably increase via the Planck function. This warms any atmosphere above it. In the absence of ozone, there would be no well-defined stratosphere, but what we now call the stratosphere would also warm due to its increased opacity, and an increased upward flux from below in the CO2 wavelengths. This is why, barring some unusual extraneous factors, we would predict “stratospheric” warming rather than cooling from a CO2 increase.
I agree with all that, regarding the stratospheric response to the increased upward flux from below.
I am very aware aware of the distinction between upward and net upward fluxes; if I slipped up and called one the other, it was a typo – except maybe in my 224
https://www.realclimate.org/index.php/archives/2010/07/a-simple-recipe-for-ghe/comment-page-5/#comment-180237 – it’s been a while so I don’t remember whether I slipped up or not in that one; I kept the concepts distinct in my more recent 340,344,348 comments.
What you didn’t include just now, though, is that the increased upward flux at the tropopause is in response to a decreased net upward flux from the tropopause. Before allowing the temperature to respond, we can consider the forcing at the tropopause (TRPP) and at TOA, both reductions in net upward fluxes (though at TOA, the net upward LW flux is simply the OLR); my point is that even without direct solar heating above the tropopause, the forcing at TOA can be less than the forcing at TRPP (as explained in detail for CO2 in my 348, but in general, it is possible to bring the net upward flux at TRPP toward zero but even with saturation at TOA, the nonzero skin temperature requires some nonzero net upward flux to remain – now it just depends on what the net fluxes were before we made the changes, and whether the proportionality of forcings at TRPP and TOA is similar if the effect has not approached saturation at TRPP); the forcing at TRPP is the forcing on the surface+troposphere, which they must warm up to balance, while the forcing difference between TOA and TRPP is the forcing on the stratosphere; if the forcing at TRPP is larger than at TOA, the stratosphere must cool, reducing outward fluxes from the stratosphere by the same total amount as the difference in forcings between TRPP and TOA. Some fraction of that may (depending on the distribution of temperature change within the stratosphere and the optical thicknesses) be transferred to the TRPP forcing, reducing the TRPP forcing that the surface+troposphere must respond to. Some fraction of the increase in upward flux at TRPP can also be transferred to the stratosphere, requiring it to warm again (if that is a small fraction, or if the fraction of that which is transferred to the TRPP flux again is small), then the resulting iteration of additional warming will converge relative quickly so that this feedback is a small effect. In the end, there is some increase in upward flux at TRPP, which is equal to a value between the TRPP forcing before stratospheric cooling and the TRPP forcing with initial stratospheric adjustment (unless … *&&*); if the fraction of that which is absorbed by the stratosphere is sufficiently small (which it may be if the stratosphere is nearly transparent over a sufficient portion of the spectrum), then some net stratospheric cooling will remain.
Given the much more rapid respons time of the stratosphere to radiative forcings, there is(can be) some initial stratospheric cooling (or at least some cooling somewhere in the stratosphere), which consists of a transient component, and a component that remains at full equilibrium. Solar heating of the stratosphere, properly distributed as pointed out above, will increase both, but it is possible to have some cooling, even at full equilibration of the climate system, even with direct solar heating above the tropopause.
Re 361 Gilles
The skin is not the Earth’s effective photosphere (in analogy to the sun); it is above that layer. This is why (absent sufficient solar or other non-LW heating) the skin temperature is lower than the effective radiating temperature of the planet (in analogy to the sun, the SW radiation from the sun is like the LW radiation, and the direct ‘solar heating’ of the part of the atmosphere above the photosphere may have to due with electromagnetic effects (as in macroscopic plasmas and fields, not so much radiation emitted as a function of temperature). The skin layer planet is optically very thin, so it doesn’t affect the OLR significantly, but (absent direct solar heating) the little bit of the radiant flux (approximatly equal to the OLR) from below that it absorbs must be (at equilibrium) balanced by emission, which will be both downward and upward, so the flux emitted in either direction is only half of what was absorbed from below; via Kirchhoff’s Law, the temperature must be smaller than the brightness temperature of the OLR (for a grey gas, Tskin^4 ~= (Te^4)/2, where Te is the effective radiating temperature for the planet, equal to the brightness temperature of the OLR – ***HOWEVER, see below***).
————
*&&* – if the stratosphere were optically thick and warmed at the bottom even if the whole experiences net cooling, then the stratospheric feedback adds to the initial TRPP forcing, and the end result could require warming below TRPP to change the flux at TRPP to an amount greater than the TRPP after stratospheric adjustment, because of the additional warming that would occur in the (lower) stratosphere.
*** – will get back to that.
Re #366 (Andy Lacis) – Although we appeared to have concluded the stratospheric cooling discussion earlier, you have brought it up again, and so perhaps a response is appropriate. Based on the entire previous discussions over several pages, it now seems reasonable to conclude that solar absorption is a critical element needed for stratospheric cooling, but whether any cooling at all can occur without solar absorption was left unsettled. I would argue that if we use a simple radiative model with a variety of assumptions, no upper atmosphere cooling but only warming will occur with increased CO2 (see #333), based on the radiative transfer equations and the Second Law of thermodynamics, but when other complexities are introduced, this might change.
Regarding your most recent comment, I believe you are making the same mistake you made earlier by confusing Tt with the temperature of the upper atmosphere (without ozone, it would be hard to call it a “stratosphere” so I’ll use that term in quotes). Tt is not the temperature of the “stratosphere” but rather the effective temperature at which radiation is emitted to space from the “stratosphere”, and the two diverge more and more as opacity is increased. In the absence of a solar absorber, the “stratosphere” won’t be isothermal, but will be cooler at higher altitudes until it asymptotes to the skin temperature, which won’t change. In essence, all parts of the “stratosphere” below that limit will be warmer. Basically, what happens, I would argue, is that increased opacity raises the height of the “stratospheric” radiating layer. In the absence of a spectral shift, its former temperature would be restored, at that higher altitude. Because a spectral shift would occur, the radiating layer of the “stratosphere” will be cooler than before, but the rest of the “stratosphere” would be warmer. To conclude otherwise would be to assert that a warmer body, the troposphere, on warming further and transmitting some of that heat to a cooler body, the “stratosphere”, could cause the latter to cool further, in what would seem to be a Second Law violation.
I have a sense that we are all repeating ourselves at this point, but I’ll look forward to any new insights.
*&&* – if the stratosphere were optically thick and warmed at the bottom even if the whole experiences net cooling, then the stratospheric feedback adds to the initial TRPP forcing, and the end result could require warming below TRPP to change the flux at TRPP to an amount greater than the TRPP after stratospheric adjustment, because of the additional warming that would occur in the (lower) stratosphere. … there could be other ways to make the full response of the stratosphere+troposphere greater than the largest of these – initial (instantaneous) TRPP forcing, TRPP forcing after initial stratospheric adjustment … OF course, here and in my last comment, I am not including any non-Planck feedbacks.
Re my own comment #369 above, a correction: Not only will the effective radiating temperature of the “stratosphere” described there decrease when opacity increases, as stated, but so will the skin temperature, with both now located at higher altitudes. At any given altitude, temperatures will be warmer.
Re 366 Andy Lacis –
I agree that the non-grey nature of atmospheric optical properties is important to the issue of stratospheric cooling and that an increase in a greenhouse gas like CO2 can cause stratospheric cooling even without solar heating of the stratosphere.
However, I think, given some solar heating of the stratosphere, stratospheric cooling from an increased GHE can be enhanced, and that it could happen for a grey gas GHE as well – maybe not for the whole stratosphere, but for part of it.
As pointed out by Ray Pierrehumbert via 359 Chris Colose, the distribution of solar heating is important. Without going into detail of how, I’ll just point out that the temperature profile is what determines how LW fluxes respond to a change in optical thickness at the relevant wavelengths. The solar heating affects the equilibrium temperature profile of the stratosphere. Before the response of the surface+troposphere, what allows stratospheric cooling is the TOA forcing being less than the tropopause-level forcing; both are affected by the stratospheric temperature profile.
For a grey gas, the skin layer temperature is such that the corresponding blackbody flux is 1/2 of the OLR, absent solar heating of the skin layer. If there is solar heating of the skin layer, the temperature will be larger so that the skin layer’s emission balances it’s heat gain from both absorption of LW radiation from below and SW radiation. Doubling the optical thickness effectively halves the thickness of the skin layer, removing (if the solar heating had been evenly distributed over the skin layer) half of the solar heating. It is true that this lost solar heating now adds to the LW flux coming from below, but the skin layer only absorbs a tiny fraction of that, so the increase in absorped LW flux from below is less than the decrease in the absorbed SW radiation. So the skin layer will cool.
Re 366 Andy Lacis
Numerical calculations show that the equilibrium temperature gradient within the homogeneous atmospheric slab will be essentially linear in Planck, i.e., a straight line in TAU space can be drawn between Bt = sigma (Tt)**4 at the top of the layer, and Bb = sigma (Tb)**4 at the bottom.
That makes some intuitive sense to me (as allowed by optical thickness, photons moving out of a region in proportion to concentration; constant photon concentration gradient can be sustained with constant T^4 gradient, etc.), though then I have to correct something I said earlier – within the region where T^4 varies linearly (over optical distance), the radiation will be anisotropic. The surface and space are both analogous to infinite optical thicknesses that are isothermal; the flux originating from them (in the case of space, in this approximation, zero) will be isotropic. If not for the temperature discontinuity, then the radiation coming from the surface would be less than what fits the linear T^4 pattern, with the biggest difference at angles near vertical. With the temperature discontinuity, the intensity of radiation could still be smaller than what would fit the T^4 pattern at nearly vertical angles; but that could be balanced by intensities larger than what would fit the T^4 pattern at greater angles from vertical (the same intensity would be larger than the T^4 anisotropic pattern at greater angles from vertical and smaller than the T^4 pattern closer to vertical) – so the flux per unit area could fit the T^4 pattern, but now, this would lead to (relative to the T^4 pattern) anomalous heating next to the surface and anomalous cooling just above that, because the anomalously larger intensities would be absorbed closer to the surface (being at greater angles from vertical) while the anomalously smaller intensities would be absorbed over a thicker vertical extent. And for the lack of downward radiation at TOA … etc. So I’m wondering how that works out… is there any way to explain besides the number crunching?
… interestingly in the grey gas case with no solar heating of the stratosphere, increasing the optical thickness of the atmosphere would result in an initial cooling of and in the vicinity of the skin layer (reduced OLR), and an initial radiative warming of the air just above the surface (increased backradiation) – of course, the first of those dissappears at full equilibrium.
PS where I said earlier that direct solar heating (properly distributed) can enhance both the transient and full equilibrium cooling of the stratosphere, or portions of the stratosphere, I did not mean – or should not have meant – that the solar heating enhanced the transient component of the response – the component that dissapears at full equilibrium. It may or may not, I haven’t made any general arguments for it. What I did mean was that the initial cooling, which is the sum of the transient and full equilibrium cooling components, can be enhanced, as well as the full equilibrium cooling.
About skin temperature – *** – will get back to that. –
The OLR will not generally be isotropic unless the whole atmosphere is optically quite thin (entirely within the skin layer except for the troposphere) or if an optically thick upper portion is isothermal.
The skin layer will absorb a larger fraction of the intensity coming from closer to horizontal than from closer to vertical. Depending on optical thicknesses and lapse rates, the skin layer may preferentially absorb the OLR intensities with lower brightness temperature than the whole OLR flux/area.
If either the skin layer’s absorptivity were isotropic or the OLR were isotropic, the skin layer would have the temperature with the corresponding blackbody flux of half of the OLR. But if the skin layer’s absorptivity is greater at angles where the OLR intensity is less, then the equilibrium skin temperature will be colder.
So far so good, but then, what about the top part of the skin layer where absorptivity is small at large angles from vertical and essentially zero everywhere else. This skin of the skin layer would be absorbing radiation mostly emitted from layers above where the OLR is emitted. The temperature would be even colder. The skin of the skin of the skin of the skin might be absorbing radiation primarily emitted from the first skin. Etc. (I have to say, I don’t like where this is going (toward absolute zero – PS this wouldn’t completely change the argument about CO2 causing cooling; the nature of the skin temperature is such that at equilbrium, the center of the CO2 band can never be saturated at TOA absent solar heating.).) I would guess something is wrong with this argument, since I’ve never heard of this. And it would seem to apply to cases where the OLR would otherwise be isotropic.
Re my 348 last paragraph:
PS what if their where a substance within the stratosphere that provided significant optical thickness in the vicinity of the CO2 band. This would tend to reduce the potential for TOA forcing even more, leading to more stratospheric cooling in response to an increase in CO2;…
Depending on the temperature where that substance is. If it is in an isothermal layer, it will radiate upward as much as downward; it will decrease the baseline TRPP net flux and increase the baseline TOA flux by the same amount, but it will decrease the baseline TOA flux by a greater amount if it is absorbing radiation with a higher brightness temperature from below (the baseline upward flux at TRPP), so it will increase the amount by which the baseline net flux at TRPP is greater than that at TOA. If the lapse rate is positive, the effect will be reduced; if it is negative, the effect will be increased.
CORRECTION however, the presence of such a substance would itself make the inital stratospheric temperature warmer than otherwise.
No. By absorbing radiation from below; but it would radiate both upward and downward, thus making the layer cooler; but if it is optically thick, it could make the lower part warmer.
———–
In general: even if the stratosphere as a whole cools (in terms of a decrease in total flux going out, to balance radiative forcings + radiative response from below), this doesn’t necessarily mean cooling occurs throughout; there could be some portions that warm. And vice vera – with stratospheric warming as a whole there could still be cooling in places. As with forcings and responses in fluxes at TOA and TRPP, one could consider them at TOA and some other level to find the effect for an upper portion of the stratosphere, etc.
First part of last comment: If the lapse rate is positive, the effect will be reduced; if it is negative, the effect will be increased.
reverse that.
Patrick, I don’t know if anybody but you can follow what you’re explaining. I can’t – and as far as I can judge, some of the things you’re saying are erroneous.
In the wavelengths where the atmosphere is opaque, the radiation field is almost isotropic, because photons are constantly absorbed and reemitted. As I mentioned before, the fact that a CO2 molecule absorbing a photon will preferentially loose its energy by collisions doesn’t mean that the total photon density in the line strongly decreases, because it’s compensated almost exactly by the opposite effect : the very large number of collisions will excite also CO2 molecules, a small part of them reemitting a photon, which almost cancel the number of absorptions. So basically thinking of a “global absorption ” exp(-tau) throughout the atmosphere is not particularly relevant : it holds for the initial photons emitted for the ground, but not for the total amount of photons. In the absorption lines, the atmosphere is mostly like fog : you can’t see the sun, but you see light all around you. Actually the radiation is not absorbed but scattered and thermalized.
In all what I said before, the “almost” refers to the fact that the atmosphere is not isothermal , but there is a temperature gradient. So the radiation field is not perfectly isotropic, it’s a little bit brighter (hotter ) from below and a liitle bit colder from above; this insures a small anisotropy responsible for the outwards flux in the line. It makes also the total number of photons slightly decrease with distance, following the blackbody temperature, until the photosphere is reached, then we have basically only the 1/r^2 law.
This holds only in the opaque lines. In transparent windows, the radiation field basically tracks the source : the sun in the sky and the ground, and is strongly anisotropic, and not thermalized : it keeps the spectrum of the source, not of the local BB temperature.
This is the main reason why the effective temperature is different from the local temperature : because the radiation field is only partly thermalized. Effective temperature is defined such as the emergent power is sigma Teff^4 whatever the spectrum is. But in the transparent windows, the radiation field is “hotter” (being a combination of reflected SWR and emitted “hot” ground LWR) , so in the lines, it is “colder” : the lines appear thus as absorption lines from the space, with a lower brightness temperature than the continuum.
So actually the local radiation field is much simpler that what you’re trying to describe : in the transparent windows, it’s just the emitted intensity from the source (sun + ground), and in the opaque lines, it is nearly isotropic with the excitation temperature of the molecules close to the local kinetic temperature if collisions are numerous enough, with a small anisotropy linked to the net radiation flux. All “memory ” of where the photons come from has almost be forgotten, except this small anisotropy.
Our climate changes are accompanied by storms li “KYrill” with 202 km/h and more (re: research-eu No. 63)will get an do so constantly more strengh. Aren’t those cyvlones not only steadily tugging more on the earth’s surface on our seas (e. g. the so-called monsterwaves) but pulling also on our firm crust in certain places, thereby provoking unusual outbreaks of volcanoes, like in Iceland, and with that maybe also causing every more a little change on the polar axis of our planet? Research and forecast in this direction?
[Response: No. Far too small. – gavin]
RE: 332
Hey Anonymous Coward,
The central theme of the relationship between GHG and the non-GHG planetoid I see as crucial in the understanding of how a change in GHG can effect surface temperatures. You asked why this is important it is only so that I and other less educated people can understand the principles better.
As to the issue of the formula I think I got it right. If as the 2006 basis suggested that the doubling of the 1750 level should have been near 280ppm. (I believe there was a 2005 paper suggesting the pre-anthropogenic emission should have balanced around 240ppm.) If the total change between 1750 and the doubling of the density value should occur somewhere between 2075 and 2125, the percentage change in the temperature offered by the increase in CO2 today should be roughly 40% of 4 Deg. C. As the IPCC has suggested that the contribution of total Global Warmth contributors both positive and negative CO2 should average out to be approximately 40%. Hence, the total temperature potential of the current temperature rise due to the change to the current CO2 levels should be approximately 3.7 Deg of the total potential change of roughly 10 Deg. C if all other things remained proportionally similar.
That the trend in GAT surface temperatures we are seeing demonstrate roughly a 0.65 Deg. C change suggests that much of the rest of the change has to be radiated elsewhere. Hence, given the idea of 360 Deg. radiation would suggest that 1/2 of the estimated 1.48 Deg C. suggested should be roughly a net gain at the surface of around 0.74 Deg. C while at the same time the net gain at 560ppm of CO2 should be approximately 1/2 of 10 Deg. C or roughly 5 Deg. C.
Now back to the original issue, to get a surface temperature differential of 32 Deg. C at 280ppm of CO2 would seem to require that the net Warming gain would have to of been roughly 64 Deg. C. Of which, if the proportions were the same, CO2 should have been responsible for 25.6 Deg. C. From here we then would need to determine the rough amount of doubling cycles between the CO2 voided planetoid and the suggested pre-anthropogenic 240ppm content.
All I am asking is for the value of change required to achieve the current doubling potential of 4 Deg. C at 280ppm from the estimate of the 2006 paper and the total potential change of 25.6 Deg C above the 0ppm theoretical baseline. So far no one has stepped up with the logarithmic value and the estimated doubling points. (Note: You may have missed my suggestion that the systematic change would likely be linear or proportional while the CO2 level was logarithmic.)
Cheers!
Dave Cooke
Thanks to Barton & Patrick for responses to my #349–helpful, and appreciated.
An additional response to Pete Baldo @ #354:
IMO, the “but 390 ppm is so small” theme comes from failing to think quantitatively. That’s ironic coming from me, as I’m an artsy whose eyes tend to glaze (or, in extreme cases, cross) when confronted with actual equations. . . however, sometimes you gotta do what you gotta do.
And what you gotta do in this case (IMO) is look at the actual numbers of molecules involved, in a rough back-of-the-envelope sort of way.
So, by Avogadro’s number you’ve got about 6 x 10e23 molecules per mole of air, and that’s about 22 liters (according, at least, to some random website I once consulted–corrections welcomed.) (For perspective, an average human male has a lung capacity of around 6 liters.) 390 ppm is .00039; multiply that by Avogadro’s number (or my lazy approximation of it, rather) and you get 2.34 X 10e20 (unless I dropped a decimal or something.) But the point is that there is still, at 390 ppm, a whole bunch of CO2 molecules per unit of atmosphere.
People go wrong about this, I think, because their everyday experience doesn’t lead to a gut-level understanding of just how numerous molecules actually are. (A point made with a vivid irony by Arthur C. Clarke at the end of one of his “Tales From The White Hart” (paraphrased): “It’s quite probable that even now, molecules of the late professor are passing through the very seawater filter that he devised. . .”)
Hence, they focus on that .00039 with a tacit assumption that 1 x .00039 is always neglible. But if you think of .00039 x 6 x 10e23, as we have just done, that doesn’t seem quite so negligible after all!
“neglible”–ugh! Sorry. . .
Gilles (378), in following this discussion I have a number of sidebar questions. But for fear of hijacking or deviating the main topic let me try just one… for now. I was under the impression that in a collision the tendency to transfer CO2 excitation energy to other kinetic energy is much greater than for kinetic energy to transfer to the excited levels of CO2, at least at low altitudes. You seem to say otherwise. Further you say that the kinetic-to-excitation transfer is great enough to cause the now re-excited CO2 molecules to relax with emission at near the same level as the original absorption, instead of collision-to-kinetic transfer, which normally greatly exceeds the emission type relaxation as I asked about above. This sounds like the radiation energy field at the absorption frequencies (say 15um, e.g.) would not vary nor diminish, other than for same short transient, as the total emissions (primary and after-collisions secondary) “almost exactly” matches the absorption. This strikes me as incorrect.
Can you further explain this? Or did I miss the point?
Great article for those of us who have had a physics education years ago and have left physics for other careers. I will suggest that for engineering/science graduates (at least a master’s level) it ought to be used.
I see little chance a journalist will read and understand it — but who knows? Worh a shot.
An exception to the first statement may be oilfield engineers. Here in Houston, so many jobs depend on oil that global warming is a gnat to be swatted away. I can have a reasoned discussion with an oil engineer of some topic we disagee on — not on climate change.
Thanks again.
John
Kevin McKinney (381), smarter guys than I can reply: your math is pretty good. The interesting part of this has been pointed out by others (Ray Ladbury comes to mind) and relates to the number of acceptable photons that are shot into the air. This math requires some very sensitive assumptions which can result in a wide range of answers, but one is: your 22.4 liters of atmosphere that has 2.34x10e20 CO2 molecules can be put in a cylinder 100m high with a 2.24cm^2 base. At 290 degrees between 14.3 and 15.6um (one of the highly variable assumptions) the 2.24cm^2 base area emits (I think) 0.0056watts = 0.0056joules/sec. Based on harmonics physics and math (something down a musician’s alley I suspect ;-) ) the center frequency of CO2 absorption is 15um and equates to 1.325x10e-20 joules/photon. That means the base area is emitting 4.26x10e17 absorbable photons each second with a total of 2.34x10e20 CO2 molecules to absorb them — roughly 500 molecules to absorb a photon every second within a 100 meter path. This can vary by magnitudes depending on the assumptions, but it describes the main idea within a ballpark: there may be a tiny number of CO2 molecules but — though depending on a bunch of stuff!! — there are probably much fewer photons for them to absorb.
Rod ” This sounds like the radiation energy field at the absorption frequencies (say 15um, e.g.) would not vary nor diminish, other than for same short transient, as the total emissions (primary and after-collisions secondary) “almost exactly” matches the absorption. This strikes me as incorrect.”
sorry but it is correct : close to the thermal equilibrium, emission and absorption “almost” cancel : actually AT the thermal equilibrium, the photon density must remain constant and equal to the Planck law density – this means of course that any absorbed photon is exactly compensated by an emitted photon. Now consider a single molecule that is supposed to loose more rapidly its energy by collision after absorption of a single photon. Just after the absorption, this molecule has no idea if it is in a thermal bath and if the photon density is the Planck law or not , so it will transfer its energy by collision in any case. So IF the thermal equilibrium is reached, the absorbed photon must be exactly offset by an emitted one – and of course the source of energy can be nothing but a inelastic collision if the photon has to been created. So the Planck photon density is exactly the value for which absorption and emission rates cancel.
Now the matching is just “almost perfect” if there is a temperature gradient, because the photon density must slowly decrease to match the local excitation temperature. So actually there is a small warming term from the lower layers, exactly compensated by a cooling towards the upper layer. This is neither a net absorption , or a warming (in the sense that the atmosphere tends to reach an equilibrium local temperature, but an energy transfer . )
cheers
Re 378 Gilles – yes at least one comment I have made is erroneous, but I wouldn’t disagree with any of what you just posted (of course the T^4 relationship is for a grey gas; when you get into different parts of the spectrum you have to follow the Planck function’s temperature dependence. But yes, as optical thickness gets large on the spatial scale of temperature variation, the anisotropy in the radiation field gets smaller (assuming isotropic optical properties, of course, although if there were a direction with minimum optical thickness, increasing the optical thickness in all directions with constant proportionality would eventually bring all directions towards an ultimate saturation), and the brightness temperature in all directions approaches the actual local temperature (this happens faster toward more isothermal directions – ie typically nearly horizontal in the atmosphere) – which is the situation at the ultimate saturation.
However, the skin layer, absent solar heating, has an equilibrium temperature that is smaller than the brightness temperature of the radiation from below at those wavelengths where the skin layer absorbs. That means saturation will not have occured; the OLR brightness temperature will be larger than the skin temperature, though the difference will be smaller for intensities in nearly horizontal directions – not just because the skin layer is colder but because some portion of the atmosphere below that is colder (the temperature will gradually approach the skin temperature going upward from the ‘photosphere’ (effective emitting level) as you would call it in analogy with the sun).
Re my 376,377 – go ahead and ignore that as well as the last paragraph of my 348; I made one or more silly algebraic errors (if you could call it that; I was doing it in my head and apparently flipped some things around and maybe left out a couple of ‘terms’).
I’ll post the correct version later.
#385, Rod B.:
The “fewness” of IR photons is not relevant. What is relevant is the probability that such a photon will be absorbed by (or more generally interact with) a susceptible molecule (CO2) within the given length. So the argument does not hang on the rate of emission of IR photons.
In accordance with the original posting: the issue is whether you have enough added CO2 to move the level of the IR photosphere (the point at which optical depth, as measured from outer space inward, = 1) significantly.
As I noted earlier, CO2 is quite pervasive in the atmosphere up to 90 km, whereas H2O seems to quit at about 10 km. That means that CO2 is in a leveraged position (near the top) to influence the altitude of the photosphere. If the CO2/H2O ratio of concentrations were constant, I believe the skeptics would have a valid point that “CO2 can’t be important, compared to water vapor”.
(It’s true that CO2 absorbs more IR in the window around 15-micron than H2O, but by eye, the difference is not that impressive, maybe a factor of 2; whereas the ratio of total H2O to CO2 is quite large.)
In other words, if the ratio of local CO2 concentration to H2O concentration were constant throughout the atmosphere, I believe the enhanced greenhouse effect would be indeed be negligible at current levels.
If someone sees an error in this analysis, I would be pleased to be corrected.
Re 383 Rod B – That is all taken care of by the LTE approximation. The frequency at which photons are emitted or absorbed is small relative to the rate of energy redistribution among molecules and their modes, so the fraction of some molecules that are excited in some way is only slightly more or less than the characteristic fraction for that temperature (depending on whether photons absorption to generate that particular state is greater than photon emission from that state or vice versa, which depends on the brightness temperature of the incident radiation relative to the local temperature).
I think the LTE approximation is still valid through the stratosphere; where it does break down, there can still be a greenhouse effect still works, but to the extent that atoms and molecules are emitting photons of the same frequencies that they absorb without redistribution of energy to other states/molecules in between absorption and emission, it would be analogous to scattering; the mathematical relationships will be a bit different. Hypothetically, you could even have a greenhouse effect with fluorescence or phosphorescence.
Re 380 L. David Cooke –
If you want to see how the total GHE can be approximately calculated, see, for example, Kiehl and Trenberth 1997, from links here:
http://chriscolose.wordpress.com/2008/12/10/an-update-to-kiehl-and-trenberth-1997/
– Kiehl and Trenberth 1997: http://www.atmo.arizona.edu/students/courselinks/spring04/atmo451b/pdf/RadiationBudget.pdf
– see also the link for K
In Kiehl and Trenberth 1997, they find a 155 W/m2 total greenhouse effect for approximately present-day Earth conditions (among the approximations: surface is a perfect (isothermal**) blackbody, and the use a representative 1-dimensional atmospheric column (instead of seperate calculations for each location over the globe at each time over the course of a period of time sufficient to describe a climatic state – but note righthand side of p. 200, just past halfway down the column) … a few other things).
**(the nonlinearity of blackbody flux/area relative to temperature means that for the same emitted flux, one can have a lower average temperature if there is more temperature variation. In spite of the temperature difference from Antarctic winter to Saharan midday summer, this effect is actually rather small for the Earth (PS horizontal and temporal temperature variations within most of the mass of the atmosphere are of the same order of magnitude or smaller than at the surface), so a global average flux computed from global time average temperature will not have a large error; more extreme temperature variations that occur on bodies like the moon or Mercury would be more important.)
**(the existence of some correlation between variable gases and clouds and different surface temperatures and vertical temperature distributions could affect the average effects – though at least for water vapor, I’d guess this tends to even out the OLR distribution over the globe (?). There would also be some correlation between local/regional climate and surface emissivity (I think sea ice is different than open ocean, for example).)
——–
See Fig 1 which shows the spectrum of OLR (outgoing LW radiation) – the smooth curve is the Planck function for 288 K, approximate surface temperature, scaled (by a factor of pi steradians) to be in terms of flux per unit area per unit of the spectrum.
The other curve is a calculated actual OLR for the amount and distribution of water vapor, CO2, CH4, etc, and clouds, for a vertical temperature profile, representative of the global atmoosphere.
The area between the two curves is the TOA radiative forcing of the total greenhouse effect, calculated to be about 155 W/m2 …
(Since the net upward LW flux balances the net downward SW flux in equilibrium, and without a GHE, the same net upward flux would be found at all vertical levels, one could add the solar heating of the stratosphere (roughly, 3 % * 342 W/m2 ~= 10 W/m2) to find the tropopause-level total GHE forcing.) (PS don’t mistake this dependence on solar heating in this context to equate to an argument that all full-equilibrium stratospheric cooling in the increase of a GHE requires stratospheric solar heating; also, this additional 10 W/m2 doesn’t include any stratospheric adjustment effect.)
This area is shown (upside down) in Fig 2; the contribution made by clouds after the rest is shown in Fig 3. Why ‘after the rest’? Because there are overlaps – clouds alone could accomplish more; the presence of the gases reduces the additional radiative forcing caused by the addition of clouds. These overlap issues are summarized in table 3.
(Note that radiative forcing is not necessarily proportional to reduction in atmospheric transparency, because relatively opaque layers in the lower warmer troposphere (water vapor, and for the fractional area they occupy, low level clouds) can reduce atmospheric transparency a lot on their own while only reducing the net upward LW flux above them by a small amount; colder, higher-level clouds will have a bigger effect on the net upward LW flux above them (per fraction of areal coverage), though they will have a smaller effect on the net upward LW flux below them. (Water vapor and low-level clouds can have a big effect on the radiative balance of the surface.)
(Because convection can balance imbalances in radiative fluxes, and the troposphere+surface will tend to respond (to a first approximation) about the same in response to changes in radiative inputs and outputs of their whole, it is the tropopause-level forcing which is really key.)
Look at Fig 1 again – keeping all the other greenhouse agents, removing CO2 would remove the valley in OLR between roughly 13 and 17 microns (or 13 and 18?) – you could draw in a line across the top of that valley to approximate what water vapor and clouds, etc, would do without CO2; the area of the valley created by adding CO2, given everything else, is 22 W/m2 (from table 3).
What does this mean for CO2 forcing? A doubling of CO2 in present conditions would add a forcing of about 3.7 W/m2 (+/- ? mabye 0.5 W/m2, I don’t remember exactly offhand, but the error bar is not very large). This is for the tropopause level with stratospheric adjustment. A halving of CO2 would do about the same in reverse, -3.7 W/m2. Removing all CO2 would result in a radiative forcing of -22 W/m2, TOA – I don’t know the tropopause level with stratospheric adjustment value; assuming it is similar to in proportion to the TOA forcing as for doubling CO2, removing all CO2 might have a tropopause level with stratospheric adjustment forcing somewhere roughly around -30 W/m2, though that proportionality may break down as we get to a point where CO2 is not saturated… But using 22/3.7 and 30/3.7, it appears for a rough estimate that the logarithmic proportionality for CO2 may break down before about 6 to 8 halvings of CO2. The proportion of forcing to CO2 amount eventually becomes linear as the amount of CO2 goes to zero – this is nothing special; any continuous smooth function can be approximated by a straight line over a sufficiently short interval; adding a sufficiently small amount of any greenhouse gas will have about half the effect as adding twice as much.
What does this mean for climate sensitivity? If a doubling of CO2 resulted in a temperature increase of approximately 1 K before any non-Planck feedbacks (before water vapor, etc.), then assuming the same climate sensitivity to the total GHE, removing the whole GHE would result in about a (setting the TOA/tropopause distinction aside, as it is relatively small relative to the 155 W/m2 value) 155/3.7 * 1 K ~= 42 K. Which is a bit more than 32 or 33 K, though I’m not surprised by the difference. (This doesn’t include any solar-heating (albedo, etc.) feedbacks, which is necessary for a direct comparison; the GHE warming of about 33 K is only the effect of the atmopheric LW optical thickness, and thus doesn’t include any feedbacks on solar heating)
Climate sensitivity, even excluding non-Planck feedbacks, can’t be expected to be constant over all climates – we can start, if not knowing otherwise, with an assumption that it will be nearly constant for a sufficiently small range of temperatures (ie the same forcing that causes 2 K warming may be about half the forcing that would cause a 4 K warming) – for the same reason that any sufficiently small addition of a greenhouse gas will have about half the forcing as double that addition – linear approximations are generally valid for sufficiently small intervals.
… to be cont.
Andy (#366),
Actually, in the totally optically thick case it is easy to calculate the temperature gradient. Each layer must transport the same energy as the layer below and its emissivity is perfect (optically thick) so it transports according to R^2T^4 where R is the radius from the center of the planet and T is absolute temperature. T is thus proportional to sqrt(R). Your factor of 0.84 gets washed out by this surface area limit on energy transport. This is the temperature gradient throughout most of the Sun, for example.
Nice article. Different articles are needed for different audiences; this one fills a need. If technically interested audiences get an understanding, their less technical friends notice. Regular people rely on various kinds of authorities, including their technically minded friends.
What regular people should hear most often is this: “I am a scientist, and I am concerned. I think the future looks very worrisome.” Give the public hundred such statements, preferably with a photograph of the scientist.
Next level would be simple statements like “I assure you that I am not conspiring just to get research grants. If I were not worried about the future climate, I would be applying for other grants and researching other things. The reason I win grants for climate research is that the guardians of the research funds are feeling worried too by the climate prospects.” and “The attacks on the climate research are very unfair, trust me. They are often like saying car engines are not possible because the spark plug would expand in the heat and crack the engine block. Sounds plausible if you have heard about thermal expansion, but in reality there are millions of cars running just fine.”
So the emphasis has to be on the “trust me” part. That is how people decide must issues. How many have verified in any serious way that the Earth is really round, not flat? People pick their beliefs through social mechanisms. Use them.
But some people struggle to make the various pieces they know about fit together. This article helps doing that, but mostly for people that already wanted to know how Planck’s law fit in the big picture.
There is still a lack of good, convincing, and correct descriptions at a simpler level. The “Start here” articles in RC deserve much wider dissemination. I would have preferred a big “Beginners Click Here” button centered prominently below the banner picture on the home page.
But even those could improve. Consider the water bucket model. It shows buckets with different inflows. It should have been buckets with different size stones lodged in the outlet hole, as the GHE acts to impede the outflow of energy while the solar irradiation is essentially constant. And the outflow water rays should have been made to show more prominently the difference in pressure, with the trickle ray going almost straight down, and the strongest ray flowing farther horizontally. Forces are not directly visible, make them more so using a playbook from Walt Disney comics.
In the end, I think that public relations is a non-trivial science, and this science should be brought to bear on this problem. I have no background in it, so in the above paragraphs I am just another “idiot with an opinion”. It’s my best effort, though, for whatever it is worth.
Neal J. King, you’re right of course. I just thought that was one level deeper into the science that would complicate rather than help McKinney’s ballpark query.
Re 392 Chris Dudley – I don’t understand what you mean by R^2T^4 – and there should be something about how optical depth is proportional to R, and also, if you’re going a significant distance toward the center of such an object, there is the issue of spherical geometry; if the optical thickness is large enough across small changes in radius, then you don’t need to account for the spherical geometry in the calculation of the flux per unit area as a function of the temperature profile and optical thickness; however, the flux per unit area outward will drop as an inverse square, except of course within the layers that are being heated through a different process (SW heating for a planet, radioactivity, latent and sensible heat loss associated with a cooling interior, gravitational potential energy conversion to enthalpy via compression (adiabatic warming) and settling of denser material under gravity (the later both leads to compression via increased pressure via increased gravity within the interior, and also is a source of kinetic energy which can be converted to heat)…
(Kinetic energy in a molten metal core or plasma can under the right conditions sustain a magnetic field (dynamo); this process extracts energy but can return some of that energy via electrical resistance heating; PS off on a tangent here but I actually came across a study of the possibility of a process of sustaining a dynamo via motions induced by such things as precession (precession being caused by tidal torques on the Earth’s equatorial bulge) when thermal or chemical buoyancy wouldn’t be sufficient to drive motions (possibly before an inner core forms and grows, releasing latent heat and rejecting some less dense liquid) (PS the differential heating/cooling available to drive convection can be reduced by thermal conduction withint the liquid metal core)
… and nuclear fusion within the core of a star).
Re 392 Chris Dudley – while it makes intuitive sense that a spatially-invariant net photon flux could be sustained by a constant gradient in local equilibrium photon concentration (proportional to T^4 for a grey gas, assuming constant real component of index of refraction), the calculation of what that gradient should actually be is made a bit more complicated by the fact that photons travelling in different directions will on average be absorbed over longer or shorter vertical distances.
But so long as T^4 (for a grey gas – use Planck function for a particular wavelength) has a constant gradient over vertial optical depth out to a sufficient distance beyond a level being considered, (and assuming isotropic optical properties, and assuming only absorption and emission – no scattering, etc.) the intensity in each direction will,
being the average of T^4
weighted by the emission weighting function
which will decay exponentially (over optical depth in that direction) away from the point of view, with an e-folding scale of unit optical depth in that direction,
and given that T^4 varies linearly over optical depth in all directions (but at different rates),
… the intensity will thus be the blackbody intensity for the temperature found at unit optical depth distance from the point of view.
With a vertical local blackbody intensity (B_wholespectrum = σ/(π sr) * T^4) gradient, varying over vertical optical depth such that d(B_wholespectrum)/d(optical depth, positive downward) = BVGRAD, then the intensity I’ in the vertical direction, relative to the blackbody value at the point of view, will be +/- BVGRAD (+looking down, -up); the intensity at an angle θ from vertical will be +/- BVGRAD/sec(θ) = +/- BVGRAD*cos(θ), because optical depth per unit vertical distance is proportional to sec(θ).
The flux F’ (relative to the blackbody value, σ*T^4, for T at the point of view) will then be the integral over solid angle of the intensity (relative to blackbody intensity for T at the point of view) * cos(θ) (this other factor of cos(θ) is due to the way a unit area facing vertical projects onto a smaller area in other directions), which will be
F’
= integral (θ = 0 to π/2) of (I’ * area projection factor * d(solid angle) )
= integral (θ = 0 to π/2) of (I’ * cos(θ) * 2*π*sin(θ)*dθ )
= integral (θ = 0 to π/2) of (+/- BVGRAD*cos(θ) * cos(θ) * 2*π*sin(θ)*dθ )
= +/- π * integral (θ = 0 to π/2) of (BVGRAD*cos(θ) * sin(2*θ) * dθ )
= +/- π/2 * integral (θ = 0 to π/2) of (BVGRAD * [sin(θ) + sin(3*θ)] * dθ )
= +/- π/2 * BVGRAD * [-cos(θ) + -cos(3*θ)/3](difference from θ = 0 to π/2)
= +/- π/2 * BVGRAD * [0 – -1 + 0 – -1/3]
= +/- π/2 * BVGRAD * 4/3
= +/- 2/3 * π * BVGRAD
Gilles (386) and a bit of Patrick 027, I still can’t get a grasp of the practicalities of it all. The simple conclusion from your analysis would seem to say that the radiation intensity of say the 15um band through the atmosphere would not diminish (other than by the inverse square.) Maybe it’s the LTE that is a bother (the atmos is nor really in LTV..??, as Ray said), or that “brightness temperature” is confusing me (what is your exact definition and use of the term?) Or maybe I simplify too much (though I think complex things ought to pass the simple aspects, too….)
Although molecular energy transfer is excruciatingly complex, I think it is reasonably understood that in at least the lower atmosphere the probability of a collision transferring CO2 vibration energy to translation energy is much greater than the other direction. But this is at odds with your assertion.
What am I (or maybe you??) missing?
…
F’
= +/- 2/3 * π * BVGRAD
= +/- 2/3 * π * d(B_wholespectrum)/d(optical depth)
= +/- 2/3 * d(σ*T^4)/d(optical depth)
The net upward flux would be 2*|F’| = 4/3 * d(σ*T^4)/d(optical depth)
Which means that, if modelled as a series of isothermal layers that each radiate up and down as blackbodies, each layer would correspond to a layer of atmosphere with 4/3 vertical optical depth.
Re 397 Rod B –
Brightness temperature = the temperature that a blackbody would need to have to emit the same intensity of radiation (or if applied to a flux per unit area, the temperature of a blackbody emitting the same flux per unit area).
Inverse square law – see my 325 https://www.realclimate.org/index.php/archives/2010/07/a-simple-recipe-for-ghe/comment-page-7/#comment-180849
– you don’t really need it much in the context of the atmospheres of terrestrial planets regarding most of the mass of those atmospheres.
Going in a direction, The intensity in that direction decreases if it’s brightness temperature is higher than the local temperature, and increases if it is smaller than the local temperature (because the material emits less or more than it absorbs depending on whether it’s temperature is lower or higher than the brightness temperature of the incident radiation) – this assuming no scattering or reflection, only absorption and emission.
Re 392 Chris Dudley (cont. from 396,398) – … The net upward flux would be 2*|F’| = 4/3 * d(σ*T^4)/d(optical depth)
Notice that in order for this to hold at some level, the gradient in σ*T^4 has to be constant out to some large optical depth up and down from that level, to ‘insulate’ the level from the perturbation radiative fluxes from perturbations to the pattern.
For the context of atmospheric radiation, the surface (assuming a perferct blackbody) and space can be considered isothermal regions of infinite optical depth (surface at T = Ts, space at T ~= 0 K). This necessarily breaks the pattern. (see also my comment 373)
Let d(T^4)/d(optical depth downward) = T4grad,
Tsa = surface air temperature
T_TOA = air temperature at TOA
The downward radiation at the surface would be σ*(Tsa^4 – 2/3*T4grad)
The upward radiation would have to be σ*(Tsa^4 + 2/3*T4grad) in order for the net upward flux to be constant through the air, which requires
Ts^4 = Tsa^4 + 2/3*T4grad. So the surface is warmer than the air immediately above it, with T^4 larger by the same amount as it is smaller at a unit optical depth above the surface. But the upward flux from the surface (assuming a perfect blackbody) is isotropic, which means that in order for the upward flux per unit area to fit the T^4 pattern, the intensity will be anomalously small (relative to the T^4 pattern) in a range of directions near vertical, and anomalously large in a range of directions closer to horizontal. Because intensities at different angles are absorbed over shorter or longer vertical distances, this leads to anomalous warming in the air just above the surface and anomalous cooling in a layer above that (the anomalous cooling would taper off with height but never quite go to zero). If the air just above the surface were anomalously warmer, the increased emission from that layer would reduce the anomalous warming and decrease the anomalous cooling higher up – however, that would also reduce the net flux at the surface, so the surface would also have to be warmer (also helping to reduce the cooling higher up). I’m not sure exactly what the shape of the resulting pattern would be, but it should a perturbation from the T^4 pattern that gradually decays with height (although a temperature discontinuity at the surface would still be required, as stated by Andy Lacis in 366).
Likewise a perturbation to the T^4 pattern that gradually decays downward into the atmosphere may be necessary to balance the anomolous cooling near TOA and some anomalous warming below that due to the darkness of space (the anomalous warming would be from the intensity in all directions downward from space not only being not more than 0 but also being not less than 0 – continuation of the T^4 pattern would after all require negative values at some point).
Suppose the T^4 held up all the way to TOA.
The upward radiation at TOA would be σ*(T_TOA^4 + 2/3*T4grad) = OLR flux per unit area. But that is supposed to be equal to the net flux within the atmosphere, so
σ*(T_TOA^4 + 2/3*T4grad) = σ*(4/3*T4grad)
which implies
σ*T_TOA^4 = 2/3*T4grad
And notice this fits the skin temperature (the blackbody flux for the skin temperature is half of the OLR).
Given the upward flux/area is the net flux/areat at TOA, the downward radiation would be zero, but let’s consider the formula for the downward flux: it has to be σ*(T_TOA^4 – 2/3*T4grad) in order for the net upward flux to be constant through the air. Letting this equal zero fits the above solution for T_TOA.
But if the T^4 pattern actually continued upward to produce the same zero downward flux, the downward intensity at nearly horizontal angles would be positive, while the downward intensity closer to vertical directions would be negative (at the vertical direction, the brightness T^4 would be the T at a unit optical distance above, which would be T_TOA^4 – T4grad = – 1/3 * T4grad). So the downward intensities are anomalously large near vertical and anomalously small near horizontal, leading to anomalous cooling at and near TOA and anomalous warming below that, tapering off to zero at infinite optical depth below.
Cooling the temperature at and near TOA would help restore balance. There would have to be some warming below to keep the same OLR. Or maybe only warming of the rest of the atmopshere relative to the old T^4 pattern would keep the same OLR and maybe allow the same skin temperature (although the anisotropy in the OLR suggests there should be a colder skin temperature)- this might be equivalent to shifting the T^4 pattern upward toward TOA and compressing it near TOA ?
Or is the same net upward flux maitained by a larger T4grad when the thickness of the atmosphere is reduced?