According to some recent reports (e.g. PlanetArk; The Guardian), the public concern about global warming may be declining. It’s not clear whether this is actually true: a poll conducted by researchers at Stanford suggests otherwise. In any case, the science behind climate change has not changed (also see America’s Climate Choices), but there certainly remains a problem in communicating the science to the public.
This makes me think that perhaps a new simple mental picture of the situation is needed. We can look at climate models, and they tell us what we can expect, but it is also useful to have an idea of why increased greenhouse gas concentrations result in higher surface temperatures. The saying “Everything should be made as simple as possible, but not simpler” has been attributed to Albert Einstein, which also makes me wonder if we – the scientists – need to reiterate the story of climate change in a different way.
Gavin has already discussed this (also see here and here), but it may be necessary to tell story over again, with a slightly different slant. So how can we explain how the greenhouse effect (GHE) work in both simple terms and with a new angle? I also want to explain why the middle atmosphere cools with increasing greenhouse gas concentrations associated with an increased GHE. Here I will try to present a conceptual and comprehensive picture of GHE, explaining both the warming in the lower part of the atmosphere as well as the cooling aloft, and where only the most central features are included. Also, it is important to provide a good background, and we need to start with some very fundamental facts.
Four main physical aspects
Several factors are involved, and hence it may be useful to write a simple recipe for the GHE. This recipe then involves four main ingredients: (i) the relationship between temperature and light, (ii) the planetary energy balance, (iii) the distance light travels before being absorbed, and (iv) the relationship between temperature and altitude.
(i) Temperature and light
Energy can be transmitted in many different ways, involving photons (light or electromangetic radiation), conduction, and motion. Most of these require a medium, such as a gas, fluid, or a solid, but space is basically a void through which photons represent virtually the only form for energy transfer. Hence, planets tend to gain or lose energy to space in the form of photons, and we often refer to the energy loss as ‘radiative heat loss’.
A fundamental law of physics, known as the Planck’s law, says that radiative heat loss from any object depends on its temperature. Planck’s law also explains the colour of the light, or its wavelength, and hence explains why iron gets red hot when heated sufficiently.
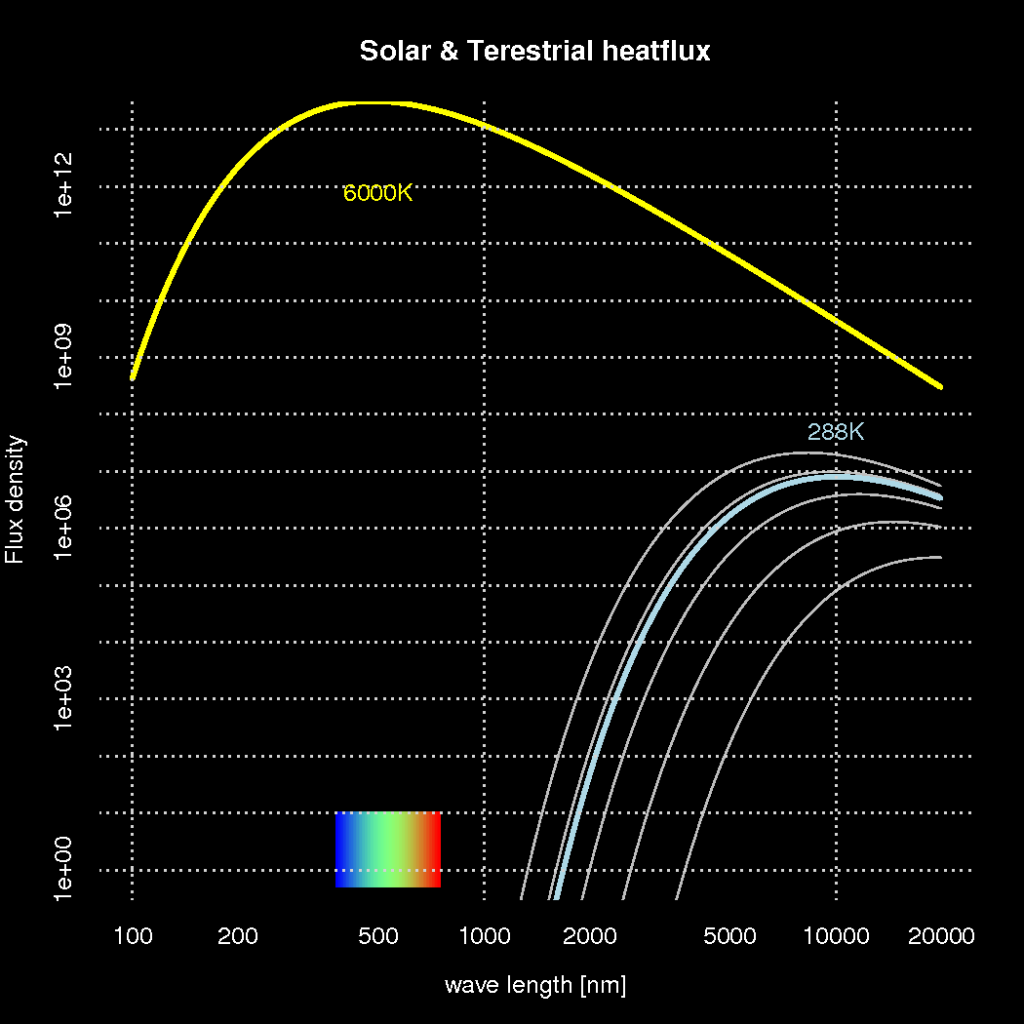
Planck’s law predicts that the light from an object with a temperature of 6000K – such as the solar surface – produces light that is visible, whereas objects with a temperature of 288K produce light with a wavelength that our eyes are not able to see (infra red). This is illustrated in Figure 1 showing how the light intensity (y-axis; also referred to as ‘flux density‘) and the colour of the light (wave length) vary for objects with different temperatures (here represented by different curves). The yellow curve in the figure represents the solar surface and the light blue curve the earth.
(ii) The planetary energy balance
The planetary energy balance says that our planet loses heat at the same rate as it receives energy from the sun (otherwise it would heat or cool over time). This is because energy cannot just be created or destroyed (unless it involves nuclear reactions or takes place on quantum physics scales).
The planets’ distance from the sun and the brightness of its surface dictates how much energy it receives from the sun, as the light gets dimmer when it spreads out in space, as described by Gauss’ theorem.
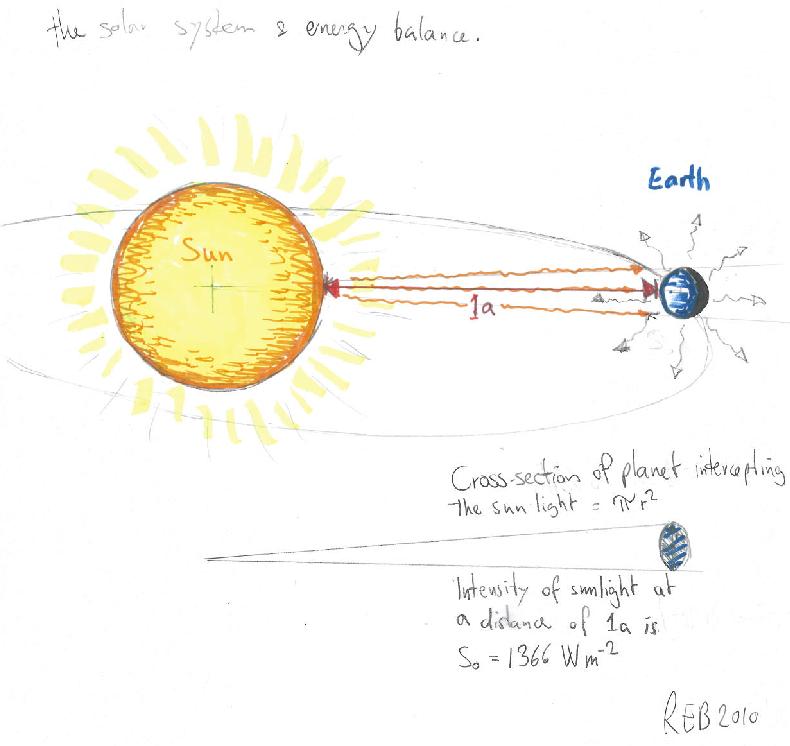
The energy flowing from the sun is intercepted by the earth with energy density described by the ‘solar constant‘ (S0=1366W/m2), and the amount of energy intercepted is the product between this flux density and the earth’s disc (minus the reflected light due to the planet’s albedo: A ~0.3). The average heat loss is given by the product of earth’s surface and its black body radiation:
S0/4 (1-A) = σT4,
where σ=5.67 x 10-8W/(m2 K4) is the Stefan-Boltzman constant. This gives a value of 255K, known as the emission temperature.
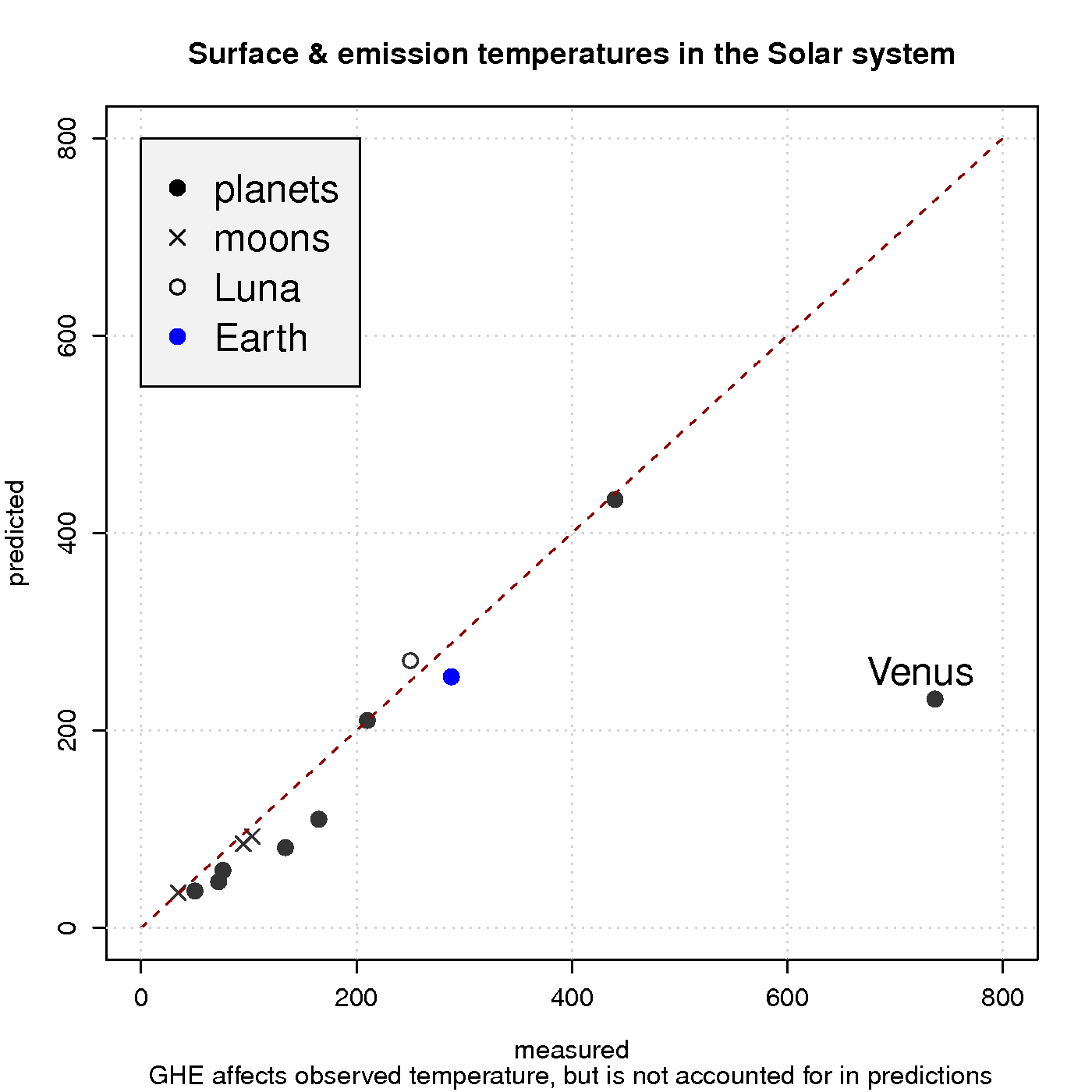
Figure 3 shows a comparison between observed surface temperature and calculated emission temperature for the planets in the solar system, based on the balance between energy from the sun and heat loss due to black body emission. In these simple calculations, the greenhouse effect is neglected, and the black body radiation can be derived from Planck’s law. The calculations agree quite well with the observations for most of the objects in our solar system, except for Venus which is known to harbour a strong GHE and has a hotter surface than Mercury despite being about twice as far away from the sun.
(iii) Light absorption
It is also clear that our planet is largely heated at the surface because the light from the sun – which is visible for our eyes – penetrates the atmosphere without much absorption (hence we can see the sun from the ground). However, the atmosphere is a medium of gas and particles that can absorb and scatter light, depending on their wavelength (hence explain why the sky is blue and sunsets orange).
The distance light travels before being absorbed – optical depth – can vary with the light’s wavelength and the medium through which is travels. The optical depth in our atmosphere is different for visible and infra-red light.
Infra-red light is absorbed by molecules, which in turn get more energetic, and the excited molecules will eventually re-emit more infra-red light in any random direction or transfer excess energy to other molecules through collisions. In a optically thick (opaque) atmosphere, there will be a cascade of absorption and re-emission.
Hence, whereas the planet is heated at the surface, it’s main heat loss takes place from a height about 5.5 km above the ground, where most of the radiation is free to escape out to space. The optical depth dictates how deep into the planet’s atmosphere the origin is for most of the planet’s infra-red light (the main planetary heat loss) that can be seen from space. Furthermore, it is the temperature at this level that dictates the magnitude of the heat loss (Planck’s law), and the vertical temperature change (lapse rate) is of course necessary for a GHE. The temperature at this level is the emission temperature, not to be confused by the surface temperature.
We know that the optical depth is affected by CO2 – in fact, this fact is the basis for measuring CO2 concentrations with infra-red gas analysers. Molecules composed of three or more atoms tend to act as greenhouse gases because they can possess energy in terms of rotation and vibrations which can be associated with the energy of photons at the infra-red range. This can be explained by theory and be demonstrated in lab experiments. Other effects are present too, such as pressure and Doppler broadening, however, these are secondary effects in this story.
(iv) The relationship between temperature and altitude
There is a well-known relationship between temperature and height in the troposphere, known as the ‘lapse rate‘ (the temperature decreases with height at a rate -6K/km). The relationship between temperature and altitude can also be seen in the standard atmosphere. The lapse rate can be derived from theory for any atmosphere that is the hydrostatically stable condition with maximum vertical temperature gradient, but it is also well-known within meteorology. Thus, given the height and value of the emission temperature, we can get a simple estimate for the surface temperature: 255K + 5.5km * 6K/km = 288K (=15oC; close to the global mean estimated from observations given by NCDC of ~14oC).
Enhanced greenhouse effect
The term known as the ‘enhanced greenhouse effect’ describes a situation where the atmosphere’s becomes less transparent to infra-red light (reducedincreased optical depth), and that the heat loss must take place at higher levels. Moreover, an observer in space cannot see the infra-red light from as deep levels as before because the atmosphere has become more opaque.
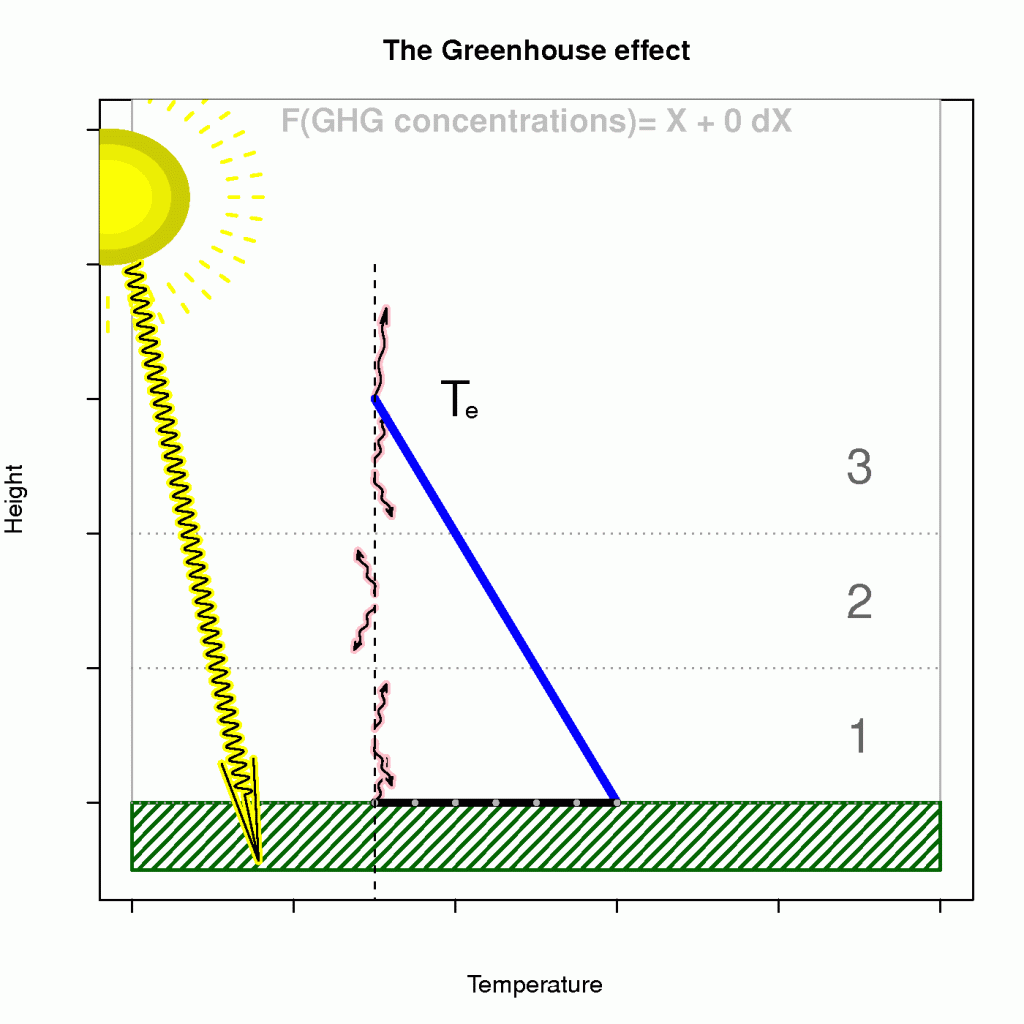
The effect of heightened level of heat loss on the surface temperature is illustrated in Figure 4, where the emission temperature and lapse rate are given if we assume an energy balance and a hydrostatically stable atmosphere on average (a generally hydrostatically unstable atmosphere would be bad news).
Hence, a reducedincreased optical depth explains why atmospheres are not easily ‘saturated‘ and why planets such as Venus have surface temperatures that are substantially higher than the emission temperature. Planets with a thin atmosphere and insignificant greenhouse effect, on the other hand, have a surface temperature that is close theto the estimates from the planetary energy balance model (Figure 3).
Feedback processes
The way the atmosphere reacts to changes in the optical depth is more complicated, due to a number of different feedback mechanisms taking place. But to get a simple overview, it is useful to keep in mind that the optical depth is sensitive to how much water vapour (humidity) there is in the air, and that the lapse rate is sensitive to the composition of the atmosphere (i.e. humidity). Furthermore, the albedo A is affected by clouds, snow, ice, and vegetation, all of which affect the way the earth receives energy from the sun.
In our simple picture, feedback processes affect changes in the height of the level where most heat loss takes place, the slope of the lapse rate, and heating at the surface (and hence the emission temperature).
So why is the upper atmosphere cooled then?
The upper atmosphere, comprising the stratosphere and mesosphere, is expected to cool during an AGW, as shown by the GCMs. So what is happening there? This is when the picture becomes more complicated.
Since CO2 mostly absorbs/re-emits infra-red light at around 14 microns, an increased concentration in the troposphere will reduce the upward infra-red radiation at this band. The total energy is roughly constant, but it is made up from increased emissions at other bands because it’s warmer. There is less absorption by CO2 of upwelling infra-red light above the troposphere, but increased emission as a function of increased concentrations. Thus there is a cooling.
Controversy?
Can this picture be falsified, e.g. if other factors were to play a role too? For instance, can this situation be altered by changes in the sun?
Changes in the sun can of course affect the amount of energy received by the earth through changes in its output, variations in the intensity of UV-light, or perhaps even clouds through galactic cosmic rays. But it’s hard to see any systematic long-term trend in the level of solar activity over the last 50 years, and it is difficult to see how solar activity may have an effect while other factors, such as GHGs, don’t. Gavin and I recently published a study on the response to both solar activity and GHGs, and found similar magnitude for both forcings in both observations and the GISS GCM.
There have been claims of negative feedbacks, such as the “iris effect“. One would expect negative feedbacks in general to dampen the response to most forcings, unless they involve a particular process that is active for a particular forcing. In other word, why would a negative feedback act for GHGs but not for solar forcing? Many feedbacks, such as changes in atmospheric moisture, cloudiness, and atmospheric circulation should be similar for most forcings.
Another question is why we do see a global warming trend if the negative feedbacks were most important (Figure 5). Negative feedbacks usually imply quiet conditions in a complex system, whereas positive feedbacks tend to lead to instabilities, often manifested as internal and spontaneous oscillations (see Figure 5). It is reasonable to expect the feedback processes to affect natural variations as well as forced changes such as an enhanced GHE, orbital changes, volcanoes, or changes in the sun.
The point about negative feedback also brings up another interesting issue: Negative feedbacks usually act to restore a system to a particular zero-level state. What would the zero-state be for our climate? No greenhouse effect or some preferred level of greenhouse warming? There is already a natural GHE that, together with other atmospheric effects, can account for about 32oC higher global mean surface temperature. What makes this state so special, and can we explain the present natural GHE in the presence of negative feedbacks (consider starting from a state with no GHE)?
Hence, claims of negative feedback is controversial because all these tough questions then need to be addressed. We can write down a simple recipe for the GHE, but it is indeed challenging to reconcile a presence of a negative feedback with our observations, or explain the current observed global warming in any other terms.
All of that (396,398, and my last comment) are of course for pure radiative equilibrium, with the particular case studied being a grey gas, though the same principles could be applied to radiation at a particular set of frequencies, provided that the equilibrium is established only at those frequencies (transparency or purely scattering at all other wavelengths).
Interesting aside: The brightness temperature of the downward intensity at TOA that would fit the T^4 pattern would actually be complex (square root of -1 is +/- i, square roots of +/- i are half of each of i+1, -i-1, i-1, -i+1)
Patrick 027 (399), I’m still scratching. If any absorbed radiation is eventually exactly matched by collision caused emission, the radiation field has to remain constant (again after transients). On average the radiant energy in joules absorbed equals the radiant energy in joules later “re”-emitted. Except that the re-emission can go up or down which would make the upward field half of the original and the field between the wrecked molecule and the surface 50% greater — but this is giving me a headache.
Something is amiss. If the emissivity of the earth is 1.0, its brightness temperature is the same as its Planck blackbody temperature. More to the point though, CO2 (or H2O or whatever) absorption of IR radiation does not depend on the earth’s blackbody or brightness temperature being higher than the mean temperature of the atmosphere (and the CO2). Likewise, CO2 at a mean temperature less than the earth’s brightness temperature still absorbs radiation. It seems like you might be confusing Planck function radiation (absorption and emission) with internal molecular energy (vibration and rotation) absorption and emission, which only requires, within certain quantum ground rules, a compatible or synchronized optical collision. The temperature of the molecule(s) is only a minor secondary factor.. Though Planck’s function is used, with some specific gyrations and limits, to analyze and asses vibrotation emission and absorption (and mathematically it does a very good job IMO) the physical processes are not the same and do not follow the same unfettered rules. Or so I maintain (Ray Ladbury’s et al protests not withstanding ;-) )
Am I wrong? Can CO2 at ~1km, ~ 6C colder than the surface and the earth’s brightness temperature, not absorb any of the earth’s IR radiation? Or am I still missing what you are trying to say?
Patrick 027, ps. In reading your post #400 (and I apologized if I missed this in earlier posts or am not reading your posts with sufficient care) it seems you are referring to physical planck-type radiation from atmospheric layers. If that is the case then your analysis sounds correct. But, to be clear, atmospheric planck function radiation (absorption and emission) is still not physically the same as vibrotation internal energy absorption and emission. Even though, as I said above, the mathematics of the planck and associated functions are used to assess the latter. For example, though temperature is a secondary factor, higher temperature CO2 is somewhat less likely to relax through emission than cooled CO2 — the opposite of Planck function.
BTW, and I don’t wish to restart it now, there is major disputes as to how much or even if the atmosphere radiates ala Planck functions, i.e. in proportion to T^4 mitigated with emissivity. I believe it does (but have little clue how much); others (and some with good bona fides) vehemently oppose.
Re 380 L. David Cooke, PART II. – cont. from 391 Patrick 027
It generally makes sense that climate sensitivity, defined per unit radiative forcing (limiting ourselves only to the Planck response, wherein emission of radiation stays proportional the the Planck function as temperature changes, holding optical properties constant) should be larger at smaller temperatures, because of the nonlinear dependence of blackbody radiation on Temperature …
(PS we are considering the climate sensitivity to be in terms of changes in global-time average surface temperature per unit global-time average radiative forcing, though one could also define other sensitivities for other measures of climate).
—————
A 1 % change in T leads to a
4 % change in whole-spectrum blackbody flux per unit area, with larger % changes occuring at higher frequencies (shorter wavelengths):
5 % change in spectral blackbody intensity ( = Planck function) at peak per unit vacuum wavelength (which occurs at a vacuum wavelength λpeak = 2897 μm*K / T; see Wien’s displacement law)
4 % change in the Planck function at peak per unit log(frequency or vacuum wavelength) (which occurs at a vacuum wavelength λ = 5/3 * λpeak)
3 % change in the Planck function at peak per unit frequency (which occurs at a vacuum wavelength λ = 5/4 * λpeak)
approx. 1 % change in the Planck function at very large wavelengths (very low frequencies).
HUGE % changes at much shorter wavelengths (much higher frequencies)
————–
… The GHE TOA forcing of 155 W/m2 is approximatly the difference between the blackbody fluxes at 255 K and 288 K; thus if maitaining 288 K surface temperature, removing it …
(and not allowing surface temperature variation to increase so much that the average temperature drops significantly relative to global average OLR)
(while maintaining solar heating, which is actually a hypothetical excercise in part because removing clouds would change the albedo, though albedo could be artificially maintained by other means for the sake of this thought experiment)
…requires the surface temperature to drop to 255 K in order to restore balance between solar heating and OLR. The difference in radiant flux will be smaller between 222 K and 255 K, and larger between 288 K and 321 K, and it will take a greater GHE TOA forcing to reduce the effective radiating temperature (the temperature of a blackbody that would emit a radiative flux) at TOA from 288 K to 277 K as it would to reduce it from 277 K to 266 K, etc.
As to the other (non-Planck) feedbacks: these are temperature dependent as well. First, for changing just CO2 forcing (or CH4, etc, or for a non-GHE forcing, such as a change in incident solar radiation, volcanic aerosols, etc.) , there will be other GHE radiative ‘forcings’ (feedbacks, though in the context of measuring their radiative effect, they can be described as having radiative forcings of x W/m2 per change in surface T), such as water vapor feedback, LW cloud feedback, and also, because GHE depends on the vertical temperature distribution, the lapse rate feedback (this generally refers to the tropospheric lapse rate, though changes in the position of the tropopause and changes in the stratospheric temperature could also be considered lapse-rate feedbacks for forcing at TOA; forcing at the tropopause with stratospheric adjustment takes some of that into account; sensitivity to forcing at the tropopause with stratospheric adjustment will generally be different from sensitivity to forcing without stratospheric adjustment and both will generally be different from forcing at TOA before stratospheric adjustment; forcing at TOA after stratospehric adjustment is identical to forcing at the tropopause after stratospheric adjustment). global-time average GHE will also depend on horizontal and temporal variations in temperature, so there is a potential for feedback from that as well (that should be small for small changes for the present-day Earth, but they might become significant for a very large cooling.
Then there are also non-GHE feedbacks, such as albedo feedbacks (cloud albedo, snow, ice, vegetation, dust/aerosols).
The snow and ice feedback is generally positive and becomes very large at very cold temperatures; obviously it approaches zero when the temperature is sufficiently warm that very little snow or ice remain and when they occur when and where there is little solar radiation to reflect.
The water vapor feedback (a generally positive feedback) – there is an roughly exponential increase in saturation water vapor pressure with increasing temperature, and the relative humidity (at a given vertical level) overall tends not to change a lot globally, though there will be different regional trends associated with shifting precipitation patterns. However, the mixing ratio of water vapor decreases roughly exponentially with height (in global time-average effect; locally it may vary step-wise or irregularly). So the water vapor profile might simply shift upward by some amount with each unit temperature increase. But the boundary layer of the atmosphere can be moist with dry air above it, and how does the thickness of the boundary layer change, if it does, etc… Anyway, from Hartmann, “Global Physical Climatology”, 1994, p.233, modeling by Manabe and Wetherald (1967) suggests that at least some feedbacks cancel out the nonlinear effect of the Planck response at least betweeen about 250 K and 315 K, and Hartmann states that with some reasonable assumptions and approximations (constant relative humidity, radiative-convective equilibrium, 1-dimensional model), OLR varies linearly with surface temperature just including the Planck response and the water vapor feedback. This seems to imply the water vapor feedback gets stronger at higher temperatures so that the climate sensitivity does not decrease.
At sufficiently high temperatures, the water vapor feedback can get so large that climate sensitivity becomes infinite – this is the runaway water vapor feedback. Unlike the snowball Earth case, there isn’t the same hysteresis following equilibrium climate (not including biogeochemical evolution); the process is reversable so long as water vapor is not lost via H escape to space, etc. When all the water available has gone into the atmosphere, the runaway process stops, and it requires additional external forcing to cause additional climate change. (Within the range where water vapor feedback is runaway, zero change in external forcing ’causes’ a large change in climate; the equilibrium surface temperature, graphed over some measure of external forcing, takes a step at some particular value.) Maintanence of such hot conditions still require an external forcing; if the external forcing is changed to cause cooling and the amount of water vapor in the atmosphere starts to decline via conversion to liquid, the runaway feedback starts again, and doesn’t stop until the climate has cooled back to the value where the runaway would start upon warming.
———————–
to be cont.
CORRECTION Re my 404: in discussing % changes in spectral intensity per % 1 change in temperature:
The 4 % change at peak spectral intensity in terms of per unit log(frequency or wavelength) occurs at λ = 5/4 * λpeak, while the 3 % change at the peak spectral intensity in terms of per unit frequency occurs at λ = 5/3 * λpeak ; I had switched the 5/4 and 5/3 earlier.
Patrick (#395),
Sorry, I was only paying attention to exponents. Each layer transfers 4piR^2sigmaT^4 of power. The transfered power is the same at each layer so we can write T2 at some layer 2 at R2 in terms of T1 at layer 1 at R1 as T2=T1sqrt(R1/R2) so it is really a 1/sqrt(R) dependence rather that sqrt(R) as I originally stated.
At an actual solid gas boundary, the change in opacity will usually lead to convective rather than radiative energy transport so that this will not often be encountered.
One place where this situation does arise is in protostars where pressureless dust provides the opacity and all energy transport is thus radiative as in the original example.
Patrick :”We are considering the climate sensitivity to be in terms of changes in global-time average surface temperature per unit global-time average radiative forcing,”
the problem is that this definition implicitly assumes that the global, time average surface temperature is a definite single valued function of the radiative average forcing, which is far from being true since there are considerable horizontal heat transfer modifying the latitudinal repartition of temperature: the local vertical radiative budget is NOT verified. So of course one could think that the climatic engine will have a complex but definite answer to any variation of the forcing, and that it would define a complicated, but single-valued response of the “average temperature” to the “average forcing” (which is what I understand to be the “fundamental assumption” of climatology). But this is only an assumption since in principle, highly complex systems can have complicated non linear variability at all time scales (for instance through oceanic circulation that needs one millenium to complete a cycle). The time average makes sense only if you are sure to have caught all variability time-scale in the average (i.e., that they are all smaller than 30 years, say) – I’ve never seen clearly where this assumption comes from, apart from computer simulations, which are NOT reliable for this kind of physics.
” But, to be clear, atmospheric planck function radiation (absorption and emission) is still not physically the same as vibrotation internal energy absorption and emission. ”
Rod, absorption and emission always tend to fix the photon density to the Planck value at the excitation temperature of the relevant process. This a general rule that links emission and absorption probabilities, based on the Second Principle (so a very very stringent law ! ) So for a saturated line, the photon density will be close the local excitation temperature if the medium is thermalized. If the medium is transparent, then the radiation temperature is approximately that of the last scattering surface – generally the ground for the transparent windows. The overall spectrum emitted by the Earth is far from a planck distribution basically because the last diffusion surface varies with wavelength, opaque lines being emitted from the TOA, at its local temperature, much lower than the ground.
Re Gilles 407 – I was going to get to that… (but 1. For the benifit of L. David Cooke and/or others at his level, I was starting with the total GHE (global time average) in the approximation of an isothermal blackbody surface. In that context the surface temperature is fixed for a given OLR when the GHE is a given TOA forcing. 2. I never asserted that sensitivity in terms of equilibrium time-average surface temperature change per unit change in TOA or even tropopause-level forcing (with or without stratospheric adjustment) would be the same for each type of forcing for each climatic state and the external forcings that maintain it (or for that matter, for each of those different of forcings (TOA vs tropopause, etc.) with everything held constant. 3. Nonetheless, there is a tendency for similar equilibrium climate sensitivity ECS, especially using a Charney ECS defined as equilibrium global time average surface temperature change per unit tropopause-level forcing with stratospheric adjustment, for different types of forcings (CO2, CH4, solar) if the forcings are not too idiosyncratic. Variations among different climate sensitivies for different agents of forcings are due to their differences and at least in principle can be understood as a consequence of their idiosyncracies (solar forcing causes the same sign of change in stratosphere and troposphere, volcanic aerosol forcing may cause high latitude temperature responses of opposite sign); if their idiosyncracies are outweighed by the similar feedback pattern for a given global average temperature change, then there will be some robust patterns common to ECS change from different kinds of forcings (polar amplification at the surface; enhnaced tropical warming in the upper troposphere, perhaps also the changes in convective heat loss at the surface that balance the surface radiative forcing from water vapor feedback) associated regional changes in storm tracks, precipitation, etc.)… It is specific idiosyncracies in forcings that cause deviations from that, both global average and regional ECS effects.
Gilles (408), the problem might be in part semantics and symbols getting confused with reality. I’m not sure how you define “excitation temperature.” Excited molecules can be ascribed a “temperature of rotation” and a “temperature of vibration” but these are constructs and symbolic to help scientists make comparisons (though as defined may have mathematical units of “temperature.”) They are not temperature in the kinetic and Planck function context — which is real honest-to goodness ‘feels hot’ temperature. Planck radiation is a direct function of the “real” temperature, the radiation intensity or flux being in direct proportion to T^4 (or T^5 depending how you slice it). Vibrotation emission is not directly a function of T^4 or even T. Its connection to temperature is indirect and a function only of the Boltzmann distribution which tells the probability of a molecule within a population of molecules being in an excited state (rotation or vibration for our purposes) within its background temperature. For example, the higher the background temperature the less likely an excited molecule will relax; meaning it is less likely to emit (all else being equal) — the opposite of the Planck function. Secondly, vibrational relaxation is discontinuous in time, staccato if you will; Planck radiation is continuous in time. Thirdly Planck function has more or less a continuous spectrum; the relaxation emission is more or less a single unchanging frequency. Lastly assigning “temperature” to a vibrationally excited CO2 molecule by equating the vibration energy to 1/2kT (as a rule of thumb) gives it a temperature of about 2000K which fits nowhere in this discussion.
Re 402 Rod B
Part of the confusion may be between temporal and spatial variation.
Planck function/blackbody radiation vs radiation from molecules, matter: the physical processes are not the same and do not follow the same unfettered rules.
They are exactly the same because the Planck function and blackbody flux formulas describe something that applies to all radiation. They describe the intensity and flux that would be in thermodynamic equilibrium with matter at a given temperature; which would imply that a population of photons of some frequency and direction which have that particular intensity would have that temperature – their brightness temperature.
Their is no subset of processes on the molecular level that gives rise to ‘Planck type’ radiation. There are processes that emit and absorb photons. The details on a molecular level determine how likely a given transition is likely to occur – in other words, the fraction of photons of some frequency, polarization, and direction, that are absorbed over some path through an amount of material, and the number of photons of the same type which are emitted per unit time. But in full thermodynamic equilibrium, with equilibrium among all photons and non-photons, the rate of emission into a direction and absorption from that direction at some location, of each type of photon, will be equal.
Temporal variation – the tendency toward thermodynamic equilibrium in a closed isolated system
Suppose a bunch of photons and non-photons are thrown into an isolated closed chamber, perfectly mirrored and insulated (or otherwise assume an infinite expanse which is self-similar on a large scale). Whatever the amount of photon energy and other energy, however distributed, over time, absent kinetic barriers, the system will tend to approach equilibrium. The extent to which matter interacts in various ways determines how quickly this occurs. Absent interactions with photons, non-photons will come to a thermodynamic equilibrium wherein there is some equilibrium energy distribution characteristic of that type of material at some particular temperature, and the non-photons will thus have that temperature. Absent interactions with non-photons, the photons have no way of equilibrating amongst themselves, but scattering which preserves photon energy would at least over time redistribute the photons toward an equilibrium distribution over directions, which will be isotropic so long as the real component of the index of refraction is isotropic. Scattering may also drive the distribution over polarizations toward an equilibrium (which would be, at any given frequency and direction, constant over polarizations so long as the real component of the index of refraction is independent of polarization) Interactions wherein photons are scattered by matter with some exchange of energy will eventually redistribute photons toward a Planck-function distribution – a blackbody spectrum – characteristic of some temperature, and because the exchange involves some other type of matter, the photon gas temperature (brightness temperature) will approach the temperature of the material it is interacting with (? unless there is a problem due to scattering preserving the number of photons – in that case, there would be a quasi-equilibrium, analogous to the quasi-equilibrium that can occur when electrons and holes interact with non-photons rapidly to be redistributed within a band while tending to remain within each band so that they are not at equilibrium with each other across bands at the temperature that they have within their bands). Notice that all of these processes involve populations of photons with different brightness temperatures (which are the temperatures of those populations) exchanging energy with a net flux of energy from higher to lower brightness temperatures, bringing larger populations of photons (either all the photons at some frequency, or … etc.) towards the same temperature. Some of these mechanisms preserve the number of photons and the total energy of the photons. An effective way to bring all populations towards the same temperature involves emission and absorption of photons combined with interactions among non-photons; populations of non-photons come to equilibrium with photons of various frequencies, polarizations, and directions, or larger groups of photons depending on how specific the non-photon optical properties are; different populations of non-photons interact to achieve LTE among them, and scattering can drive different populations of photons towards equilibrium with each other, though it is only necessary that the non-photons tend toward LTE to cause different populations of photons to come to the same equilibrium temperature.
Spatial variation – the tendency of photon intensity brightness temperature to approach the temperature of material over a path through that material
Now consider what happens if the photons travel among different systems of non-photons with different temperatures. If there is scattering with photon energy changes – Raman or Compton (or for that matter if there is significant stimulated emission?), then the interaction gets complicated, but if we stick to purely complete emission and absorption of photons, with any scattering preserving photon energy, then, if the non-photons within each local system are at LTE, then they will emit into a direction as much as they absorb from a direction of the same type of photons if their temperature is the same as the brightness temperature of the incident photons. This is because they would be in thermodynamic equilibrium with those photons. As long as LTE is maintained, the fraction of photons in some direction of some type that are absorbed will be the same regardless of the intensity of photons. As long as LTE is maintained and assuming stimulated emission is insignificant, the non-photons would be emitting at the same rate regardless of photon absorbption.
So for a particular type of photon, emitted intensity (I.emitted) into a direction = absorbed intensity (I.absorbed) from that direction if the temperature of the non-photons is equal to the brightness temperature of the incident radiant intensity (I.incident). I.absorbed/I.incident = absorptivity; I.absorbed = I.emitted; I.incident = B.emitted (because they have the same brightness temperature, where B.emitted is what would be emitted by a blackbody, and is what would be in equilibrium with matter at that temperature), emissivity = I.emitted/B.emitted; therefore, given that absorptivity is independent of incident intensity but is fixed for that material at that temperature at LTE, and the emitted intensity is also independent of incident intensity but is fixed for that material at that temperature, emissivity (into a direction) = absorptivity (from a direction). For other reasons, at LTE, the transmission (of a given type of photon) is the same in a pair of opposite directions, so in the absence of scattering, emissivity and absorptivity must each be the same for opposite directions across the same path of material, and thus they will be the same for absorption of photons from a direction and emission of photons into the opposite direction. Even with scattering, if the properties have 2-fold rotational symmetry or are isotropic, emissivity and absorptivity will be the same for the same and opposite directions.
In that case, while holding temperatures constant and non-photon material at LTE, along a path, absent scattering and reflection, the intensity is always tending to approach the local blackbody value; it will not actually reach the blackbody value if the temperature varies along the path with the same tendency. The brightness temperature of the intensity, over distance, is always changing toward the local temperature, at a rate proportional to the absorption cross section density, which is equal to the optical thickness per unit distance, which is equal to absorbtivity per unit distance in the limit of zero distance …
(absorptivity doesn’t increase linearly over distance; optical thickness does;
absorptivity = 1-exp(-optical thickness) (when there is no scattering, etc.);
if we have finite-length path segments that are isothermal, we can use absorptivity and Planck function (for the temperature of the segment) of each segment to determine the change in intensity from one end point to the other, but if temperature is varying continuously over distance, we need to look at a change in intensity over differential lengths ds; where
absorption optical thickness = s* (absorption cross section) density,
absorptivity = 1-exp(-s * absorption cross section density),
d(absorptivity)/ds = (absorption cross section density) *exp(-s * (absorption cross section density))
= absorption cross section density * transmitted fraction over distance s
= fraction of intensity from s=0 that reaches s and is absorbed per distance ds;
the absorptivity of ds itself is just the fraction of intensity incident at ds that is absorbed, which is equal to the absorption cross section density)
So the intensity of radiation (at some frequency and polarization) changes over distance, such that, in the direction the intensity is going, it is always approaching the blackbody value (Planck function) for the local temperature; it approaches this quickly if the absorption cross section density is high; if the cross section density is very high and the temperature doesn’t vary much over distance, the intensity may be nearly equal to the Planck function for that location; otherwise its value is a weighted average of the Planck function of local temperature extending back over the path in the direction it came from. (if there is scattering and absorption, then the intensity at some location will be a weighted average of the Planck function over some volume that may to some extent surround the location; if there is only scattering, then the intensity will be a weighted average of the Planck function at the emitting surfaces (surface, space) depending on how much is scattered from where.)
The intensities from all directions, weighted by the cosine of the angle from vertical, add up over solid angle to equal a flux per unit horizontal area. Summing over a hemisphere upward and hemisphere downward give the downard and upward fluxes, the difference between them being a net (upward or downward) flux (per unit area), which can also be found by summing (Weighted by the cosine of the angle from vertical) the net intensity over a hemisphere, or the intensity over a whole sphere.
Back to time evolution
The difference in net upward flux between the top and bottom of a layer (a flux convergence or divergence) is a net energy absorption/accumulation or emission/depletion of that layer, indicating energy is being gained or lost. This leads to temperature changes (and/or changes of physical or chemical state, of course). In radiative-convective equilibrium, the convergence of different energy fluxes (solar and LW radiation, summed over all frequencies, and convection/conduction/etc.) sum to zero for each layer, so the net upward LW flux plus the net upward non-radiative flux is equal to the net downward solar flux.
Back to Planck function
The Planck function describes an equilibrium intensity for a type of photon, as a function of temperature. Assuming an LTE approximation, setting aside stimulated emission and scattering that changes photon energy (Raman, Compton), how rapidly over space or time the equilibrium may be approached depends on optical properties, which are the aggregate effect of the microscopic processess which themselves are not described by the Planck function, but do obey certain rules (regarding a proportion between likelihood of emission and likelihood of absorption) such that, at LTE, in aggregate, they emit a fraction of the Planck function and absorb the same fraction of incident intensity. (Raman and Compton scattering and, I would assume, stimulated emission, also obey the laws of thermodynamics but if the material is not already in equilibrium with the incident radiation from all directions, the emitted radiation will depend on both the incident radiation and the temperature of the material, etc.)
Re 407 Gilles – it might help to consider what sustains internal variability
There are externally imposed horizontal and vertical differential heating patterns. Temperature tends to respond so that, depending on optical properties, LW emission will tend to reduce the vertical differential heating by cooling warmer parts more than cooler parts (for the surface and atmosphere); also (not significant within the atmosphere and ocean in general, but significant at the interface betwen the surface and the air, and also significant (in part due to the small heat fluxes involved, viscosity in the crust and somewhat in the mantle (where there are thick boundary layers with superadiabatic lapse rates) and thermal conductivity of the core) in parts of the Earth’s interior) temperature changes will cause conduction/diffusion of heat that partly balances the differential heating. It is the remaining differential heating that is available to drive convection, if any is available.
Convection could assume steady state motion to steadily balance, along with LW radiation, etc, the imposed differential heating. In that case the optical property feedbacks, etc, could also be steady. In the absence of horizontal differential heating to anchor convection cells, cells could tend to maintain themselves via the inflow to updrafts and downdrafts being warmed and coolded along the way so that the cells reinforce horizontal temperature variations that organize them. Latent heating would play a role in that in the atmosphere. The kinetic energy produced by thermally-direct overturning would be steadily viscously dissipated. Transport of momentum (linear and angular) within the atmosphere and ocean would be balanced by transfer via pressure gradient and coriolis and viscous forces and by gains or losses at interfaces with each other and the solid Earth.
The pattern would respond to externally forced diurnal and seasonal and orbital-scale cycles with some lag time from thermal and mechanical and compositional, etc, inertia, but with a constant pattern of heat accumulation and depletion over each cycle.
(PS For a given temperature profile within the layer, the layer’s average temperature (and optical properties, etc.) determines whether the fluxes into and out of the layer as a whole are balanced – hence the importance of tropopause-level forcing, but that’s not really the point here.)
But depending on how much differential heating is available, and the underlying physics, such a steady state flow (except for externally imposed cycles) may become unstable to other flow patterns which cannot be steady.
I’ve read that for simple cellular convection in a homogeneous fluid, turning up the differential heating can eventually cause wobbling and more complext behavior and eventually chaotic turbulence; I won’t go into exactly why because I haven’t studied it, I’d guess it has to do with the steady state cell circulation being unable to balance the heat flux via convection while at the same time preventing smaller scale convective instability in the boundary layers where a superadiabatic lapse rate may be required for the transport of heat into and out of the circulating fluid (PS viscosity more effectively impedes convection on smaller scales).
Cumulus convection tends to occur episodically with individual updrafts. Because precipitation removes water, sinking air is often dry, and lapse rates up to dry adiabatic can be sustained even though they would be unstable to moist convection; heat and humidity build up until conditions favor convection, until something triggers it, and then it can sustain itself until the energy is drained.
Hadley cell-type overturning leaves a large horizontal temperature gradient (which has available potential energy, APE) that can be unstable to baroclinic instability (a Rossby-wave instability). Small perturbations on the synoptic scale grow into midlatitude storms; they take APE from the ‘basic state’ and put it into the waves, take some of it and convert it to kinetic energy, which allows them to pull out even more APE, but in the process, they use up some of their energy source; some of the kinetic energy gets put into the ‘basic state’ via a Ferrel cell, some is lost to friction. Storm-track activity patterns are shaped by the momentum distribution and affect the momentum distribution (I think they may tend to reinforce the average momentum distribution).
There is also barotropic instability (also a Rossby-wave instability). Eddies can grow by extracting kinetic energy from a steady-state flow pattern, if there is an elongated horizontal maximum or minimum in potential vorticity; however, the shear can tilt those eddies in such a way that the eddies give back their kinetic energy.
Something very similar to that, tilted on it’s side, can allow vertical wind shear to produce eddies (if the wind shear is strong enough, it can overcome static stabiltiy to do this); on this scale, the eddies lose kinetic energy to smaller scale motions and viscosity more effectively so they tend not to give their energy back to the smooth flow pattern. Momentum can be transfered by the resulting ‘eddy viscosity’ more effectively than by molecular viscosity.
There are some positive momentum feedbacks that can reinforce a momentum redistribution, such as associated with storm track activity, or also (I think this is a good example), with feedback from SST rearrangment, ENSO.
There is an interesting process in the equatorial stratosphere wherein upward transport of momentum and energy by waves is absorbed depending on the wind structure in such a way as to cause the wind to oscillate from easterly to westerly on a timescale that has no direct dependence on the timescales of any forcing – a bit like an internal clock (QBO).
Some of this internal variability can have affect the global average radiative energy balance. For example, episodic deviations in cloud and snow cover, dust and smoke, etc, will have some radiative effect that could cause some global average temperature change. Redistribution of heat (such as vertical transport between the surface and the deeper ocean) could cause some surface and atmospheric temperature change that causes some global average warming or cooling. But these will tend to average out over sufficient time.
The point is, turbulent chaotic episodic motions can develop on various timescales. They do so not because the system is being perturbed from outside, but because (at least on shorter timescales) a steady-state flow is unstable – but the activity is still anchored to external forcing, still relies on a finite imposed energy supply and thus the behavior tends to stay within limits with a predictable overall texture, though the butterfly effect renders prediction of specific events essentially impossible beyond some time horizon (and also means that tiny fluctuations in external forcings (the odd cosmic ray here or there) can affect weather significantly given time, even though they are insignificant to climate). Some low-frequency variability can exist because more slowly evolving internal variability in the oceans may anchor atmospheric patterns, and because of positive feedbacks (not radiative per se – momentum rearrangements may have positive feedbacks while radiative feedbacks may be negative**) within the atmosphere (just as some atmospheric patterns may anchor patterns in smaller scale rapid processes); there can be some positive or reinforcing feedbacks (as in momentum, moisture, snow cover?…), but if internally-generated perturbations that could trigger a shift occur with some frequency, other such perturbations that could trigger a different shift, perhaps the opposite shift, may also occur with some frequency. If they did not, then the climate would, sooner or later, end up stuck in the new state, and thus that would be the equilibrium climatic state.
Re 380 L. David Cooke, PART III (actually it may be part VI, but oh well…)
In addition to climate sensitivity being depenent on climatic state, there is also the fact that radiative forcing, for the same change in optical properties/composition, is dependent on climatic state.
For example, climate affects albedo (and it’s distribution), which affects how much a change in incident solar radiation (globally or regionally as in orbital forcing) forces a change in solar heating. Climate can also affects the vertical distribution of solar heating.
Different climates have different vertical temperature profiles (aside from horizontal and temporal temperature variations), which affects the radiative forcing that an amount and arrangement of greenhouse agents (CO2, CH4, etc, also, water vapor and clouds) will have.
So while, in the isothermal blackbody surface approximation, if the starting surface temperature is 288 K and we know the OLR is reduced from surface emission by 150 W/m2 via GHE, we know that removing all greenhouse agents will have a TOA forcing of -150 W/m2, (and some forcing at the tropopause, etc.) which will cool the surface temperature to about 255 K at equilibrium , absent non-Planck feedbacks. And we know that adding the same greenhouse agents back will (absent hysteresis among equilibria – which should be avoidable if we limit ourselves to considering only the Planck response) warm the climate back up to a surface temperature of 288 K.
But the forcing will be different. In fact, if there is any significant solar heating of the atmosphere, the TOA forcing from adding all GH agents back should tend to be negative! This is because the equilibrium climate without any GHE requires the OLR, which must balance the solar heating of the surface and atmosphere, must be emitted from the surface, requiring heat from solar heating of the air to flow downward to the surface. There could be some weak, shallow overturning due to horizontal differential heating (cooling of sinking air would have to occur via downward diffusion of heat), but to a first approximation, the tropopause level may actually rest near or at the surface. The addition of GH agents will have a positive forcing at the surface and also the tropopause, because, even with stratospheric adjustment, the atmosphere will still be cooler than zero K, and will emit some radiation downward to the surface, which is more than zero (no GHE requires no backradiation to the surface). This highlights the importance of tropopause-level forcing (in this case, at or near the surface) to the surface and tropospheric temperature responses, but we still can’t expect that the tropopause-level forcing would be 150 W/m2.
The same externally-forced change to composition will have the same magnitude of effect on equilibrium climate in the forward and reverse directions provided no hysteresis, but if the change is quite large, the radiative forcing, and the feedback, and the climate sensitivity to the forcing, will be significantly different. The forcing and feedback (including the vertical temperature profile feedback) will be different in complimentary ways to result in the same magnitude of shift in equilibrium climate.
One way in which this works – consider the overlap between CO2 and water vapor and clouds. To isolate this effect, hold the lapse rate (at all levels) steady. Removing CO2 will have some forcing, and their will be a water vapor feedback. Now adding back the CO2 will have a larger magnitude of forcing than the initial removal because there is much less water vapor, and the water vapor feedback in terms of W/m2 will be smaller in magnitude because of the overlap with CO2.
CORRECTION: “because, even with stratospheric adjustment, the atmosphere will still be cooler than zero K,”
Obviously that should be “warmer than zero K”
PS the TOA forcing would be negative initially; after stratospheric adjustment it would be less negative – it could be positive, but that depends on the distribution of solar heating.
Rod : the temperature is not associated with a single state of a system, but with a statistical distribution. A single excited CO2 molecule has no temperature. A large set of CO2 molecules, or the time averaged distribution of the states of one molecule, can often be described by a Boltzmann distribution P \propto exp(-E/kB Texc) where Texc is the “excitation temperature”. If the true thermodynamical equilibrium is achieved, all temperatures will be equal to the temperature of photons (Planck distr.) and the kinetic one (Maxwell distr.). But very often, the temperature will be different and the energy transfer is due to this difference.
Concerning “For example, the higher the background temperature the less likely an excited molecule will relax; meaning it is less likely to emit (all else being equal) — the opposite of the Planck function. ” I don’t know what you means by “the opposite of the PLanck function” (it doesn’t “emit” anything), but your first assertion is wrong. Neglecting coherent (stimulated) emission process, the relaxation of an excited molecule doesn’t depend on the background. Stimulated emission INCREASES the relaxation rate (because the background photon density increases). What happens is that for higher temperature, the absorption rate of ground state molecules increases and the relaxation rate is almost constant – so the density of excited molecules increases.
Patrick 027, a quick response to the first of your 411 post (I’ll get to the rest of it later): In a few words, they ARE NOT the same. The fact that similar math and equations can be applied to different things does not make those things identical. Many of the equations, such as from Beer-Lambert and Kirchhoff laws, can be (are) applied to Planck radiation and to molecular relaxation radiation — provided one puts the proper limits, coefficients and boundaries on the equation. But, the actual Planck Radiation Law and its follow-ons Wien’s Displacement and Stefan-Boltzmann Laws has no relation whatsoever and can not determine the result of any molecular de-excitation radiation. So, I repeat, ARE NOT! Using Planck’s Law along with Beer-Lambert and Kirchhoff and dividing the atmosphere into some number of slabs at the physicist’s choosing is a very convenient way to assess global climate change actions even though greenhouse gases have no actual physical relation with Planck’s Law, and just as the atmosphere is not actually divided up into umpteen slabs, we think that we none-the-less get a very good approximation of what’s happening with the GHGs. But, for these reasons and my earlier post, still ARE NOT the same physical process. In a large ballpark view, it is probably close enough. But in the specific details as to what’s happening at the molecular view, it is NOT close enough; assuming you can analyze this level with inappropriate physics often leads to seriously wrong answers.
What is the brightness temperature of the source of a photon at 2x10E4 gigahertz with an energy of 1.35x10E-20 joules? [And as long as I’m digging, photon sources have temperature; photons do not.]
Gilles, thanks. My understanding is that excitation temperature is a construct more commonly used to describe internal energy levels, especially electronic. I was thinking elsewhere when I asked for the definition.
What I meant was that Planck radiation increases with body or amb ient temperature, but higher temperature, per the Boltzmann distribution, makes it more probable that rotation, vibration, and/or electronic levels will be excited, and therefore less likely to emit relaxation energy, though as you point out this may not be exactly what happens physically — emission radiation is more flat than anything with increasing temperatures. But is sure ain’t increasing in proportion to T^4, as Planck radiation would. This is not talking of stimulated emission.
Patrick 027, PS: While my quip about photon temperature may be true, it’s not very helpful. There is much insight to be gained (as per your post #411) by ascribing a characteristic temperature to an EM field based on the brightness temp and Planck distribution, etc, and there is not much to lose. So, what the hay!
Re Rod B – yes, a single photon has no brightness temperature; a population of photons (via their combined intensity) does have a brightness temperature.
Okay, the Planck function is not the same as the molecular-scale processes that emit radiation, but the Planck function is applicable to describing that radiation in aggregate. (We approximate the atmosphere as some number of layers for the purposes of numerical integration/computer modelling; this is an approximation to a continuum (on scales larger than individual molecules), and we know the approximation gets better at higher resolution. The approximation is not fundamentally different from reality, it will just have some (small) error).
Re my 414,413
PS the TOA forcing would be negative initially; after stratospheric adjustment it would be less negative – it could be positive, but that depends on the distribution of solar heating
Oh, no, that’s not true.
The TOA forcing will be equal to tropopause-level forcing after stratospheric adjustment (their can’t be a net forcing on the stratosphere after it reaches equilibrium).
What I should have said is that the stratosphere will cool – whether it gets cooler than the surface or tropopause or remains warmer (remember this is the case where we started with zero GHE and had some solar heating within the atmosphere) depends on specifics.
Re 380 L. David Cooke ,
Re my 413 (PART III) – and of course, in the case of removing all GH agents and then adding them back and considering only the Planck response – actually, it’s the Planck response plus the vertical temperature profile feedback – which is actually essentially the same as the Planck response except for the troposphere:
1. That was holding the distribution of solar heating steady, which would require removing water vapor, cloud, and ozone LW optical thickness but still leaving behind their SW (solar) optical properties.
2. In that case what makes up the difference in forcing magnitude between the forward and reverse directions is the difference in the temperature-profile feedback. In the case of removing all greenhouse agents, there is no temperature profile feedback to the surface temperature change, because after all greenhouse agents are removed, the vertical temperature profile, while it will respond to the change, will not affect the equilibrium surface temperature. That is not the case when there are greenhoug agents (of the absorbing/emitting kind, as opposed to scattering).
For some reason I kept refering to a 150 W/m2 GHE when I should have been refering to a 155 W/m2 GHE (TOA).
———–
Refraction, specifically the real component of refraction n (describes bending of rays, wavelength changes relative to a vacuum, affects blackbody fluxes and intensities – as opposed to the imaginary component, which is related to absorption and emission) is relatively unimportant to shaping radiant fluxes through the atmosphere on Earth (except on the small scale processes where it (along with difraction, reflection) gives rise to scattering, particularly of solar radiation – in that case, the effect on the larger scale can be described by scattering properties, the emergent behavior).
But I mentioned it earlier and just wanted to clarify: I# is I scaled by n such that I# is conserved over distance in the direction I propagates absent scattering, reflection, absorption; The fraction of I that is absorbed, or scattered, or reflected at a given point is proportional to the fraction of I# that is absorbed, scattered, or reflected. Also, I think the fraction of I# that is scattered from one direction to another is the same as the fraction of I that is scattered from one direction to another. So long as I# is that for the same side of a reflecting interface or the same direction as I – the amount of I that is transmitted or goes in a different direction may be more or less than what was actually taken from another path because of the variation of n, but the amount of I# that is transmitted or goes in a different direction will be equal to the amount that was taken from another path. The emission cross section multiplied by the Planck function for a vacuum will equal the emitted I# per unit distance; multiplying instead by the Planck function for that medium with that refractive index will equal the emitted I per unit distance.
I spreads out or is compressed into a larger or smaller differential solid angle as it moves along a path through variations in n. The total amount of solid angle is always 4*π sr (a whole sphere), so as rays covering some solid angle, such as 2*π sr, spread out going toward smaller n, some have to exit that solid angle to make room as they spread out; thus, if all the rays fill a 2*π sr hemisphere before n declines, some rays have to bend around and go back toward the other hemisphere of directions as n declines, and a smaller fraction of rays will reach a smaller n, as the rest ‘return’ before reaching that n. The rays that get sent back join rays going the other way as more rays get compressed into the same solid angle going back toward larger n. This is the basis for total internal reflection (TIR) – it can occur at an interface between different media, but it can also occur over a continuous distribution of n. A continuous distribution tends not to reflect much radiation (TIR in that case just involves rays taking curved paths).
Patrick 027, O.K., just for fun, what is the brightness temperature of a large pile of photons all at 2×10E4 gigahertz with an energy of 1.35×10E-20 joules having been just emitted from a large pile of relaxing CO2 molecules?
I got called away before finishing my thoughts. Not sure anyone is still following this thread, but for my own piece of mind.
317 by Anonymous Coward,
“…the UK is not close to being on either top 5 list.”
‘Either’? There are a more than two ways to define the top emitters. Where would you put the UK if you measured its cumulative emissions over the last hundred years, total or per capita? Why 100 years? Well, I just picked it; longest period when someone alive today could have benefited from their country’s use of fossil fuels and within the time that most of any additional CO2 would still have an effect.
Patrick 027,
I think I finally came upon a way to properly express my doubt about your comment at #172, my #258.
Pick some density d-saturated moles/m^3 that effectively means the gas is saturated as far as radiative transfer is concerned.
Pick some density d-toa moles/m^3 that effectively corresponds to TOA, near zero I presume.
Not sure how to handle temperature, but if you assume temps close to real world conditions, you’ll stay close enough to what is realistic. You can adjust for a translation between density/partial pressure of your GHG to density/total pressure if you like, but as long as the same partial/total is used on both sides, I don’t think it will matter as far as the conclusion is concerned. Then, you can use the formulas at
http://en.wikipedia.org/wiki/Barometric_formula
to find the difference between h-saturated and h-toa. I don’t think you can create conditions where the height difference is anywhere near zero and still maintain a pressure/density curve that would occur in reality.
Re 422 Rod B – assuming index of refraction is 1 (otherwise an adjustment has to be made to the Planck function):
If either the photons have precisely the same energy, and/or are emitted at precisely the same time from precisely the same location in precisely the same direction, or otherwise are emitted so that they end up in the same direction passing the same point at the same time, then the brightness temperature would be infinity. Of course, photons don’t occupy zero space, … (quantum uncertainty, …) – but the point is, we have to specify the solid angle over which the photons are distributed, and the time period over which the photons pass a given location, and the interval of frequencies over which the photons are distributed, as well as the total number of photons (that’s what gives us the spectral intensity).
PS the complete absence of photons (in a given direction over a given time period at a given frequency, over a given frequency interval) also has a brightness temperature (absolute zero).
Re 423 Chris G – whether the effect saturates at a given density depends on the way the temperature is distributed; if the temperature from TOA downward is isothermal for a sufficient thickness, than the effect could be saturated at TOA (if starting from a large enough optical thickness per unit atmospheric mass path, a change in the density of the gas/etc that contributes optical thickness would then have little to no effect on the flux at TOA, which is what is meant by saturation. Of course, this doesn’t necessarily mean that the resulting temperature response to the forcing (zero forcing at TOA does not mean zero forcing everywhere) can’t ‘unsaturate’ the effect at TOA so that there might be a forcing at TOA for some additional change in the composition of the atmosphere).
Any realistic temperature distribution would allow a sufficient increase in optical thickness per unit atmospheric mass path to approach saturation at TOA (before the temperature response); the realistic limitation to that is that the optical thickness per unit atmospheric mass path can never get to be more than the optical thickness per unit mass path for the ‘strongest’ gas (or whatever material is involved), since the atmosphere can’t be more than 10^6 ppm of anything.
(You could have a more than 10^6 ppm increase in CO2 relative to a reference atmosphere such as the initial atmosphere, but the result would only be an atmosphere that is more than 50 % CO2 and never more than 100 % CO2.)
Re 380 L. David Cooke –
The point of Part III was that there are complexities to very large climate changes, wherein the same change in forcing agent will tend to cause the same magnitude of change in forward and reverse if everything is is held constant, but the change will be a different combination of forcing and feedback, with different climate sensitivity.
For smaller changes, this may not be so apparent or important (a doubling of CO2 from 280 to 560 ppm may have about the same magnitude of forcing and result in the same magnitude of feedback as halving CO2 from 560 to 280 ppm).
Since the 155 W/m2 GHE is the GHE forcing based on the present climate (in the sense that removing all GH agents (only their LW opacity, keeping solar radiation properties constant) results in a forcing of -155 W/m2 at TOA for the present climate, and we know that without any GHE, in the isothermal blackbody surface approximation, the temperature will fall approximately 33 K without any non-Planck feedbacks), it can be compared to smaller climate forcings made in the context of the present climate (such as a doubling CO2.) However, direct comparisons require either only considering the Planck response with radiative-convective equilibrium (maybe also allowing the lapse rate feedback within the troposphere since that is not a change in optical properties – although that is in reality somewhat of a packaged deal with the water vapor feedback), or else including the feedbacks to consider some total W/m2 amount that the climate will be adjusting to. There is also the matter of forcing at TOA vs tropopause level vs tropopause level with stratospheric adjustment.
____________________
I had been preparing comments to explain – how LW radiative forcing (greenhouse effect) works, why forcing from CO2 is approximately linearly proportional to CO2 at sufficiently small amounts of CO2 and approximately logarithmically proportional to CO2 within a range of larger amounts, and then how the climate responds to forcings, but that got very very long and so I’m going to hold off on that.
Here’s what I’ll post for now:
The climate system behavior, including its internal variability (see my 412 above, and also ** below), is anchored to externally-imposed conditions – things that don’t change as a function of climate.
For example, the optical thickness of the CO2 in the atmosphere (if you see an error in this list of things independent of climate, see below), the incident solar radiation and it’s distribution over time and space (latitude), variations in surface albedo between ocean, rock, vegetation, etc.). While the amounts and distribution of water vapor and clouds are feedbacks, the intrinsic properties are ‘externally-imposed’ by the physics, as is the case with snow and ice, etc. These all don’t affect energy fluxes or their spatial-temporal distribution so directly: there’s the heat capacity and viscosity, gravity, the coriolis effect (rotation of the Earth), the distribution of continents and oceans and their topography/bathymetry (aside from albedo, there’s an obvious mechanical forcing to circulation patterns, which, as with the coriolis effect, etc, can have an effect on the radiative feedbacks and sensitivity to radiative forcings (example: changes to geography affect sensitivity to orbital forcing; the coriolis effect (and mountain ranges and ocean geometry) has an affect on horizontal heat transport, which may affect sensitivity by affecting how snow and ice change for the same global average temperature change by affecting temperature gradients).
In hypothetical experiments (modelling), we can pick anything we want to be an externally-imposed condition, alter it and hold it fixed at will and consider how the climate responds.
In reality, the distinction between forcing and feedback depends on perspective; in particular, the time frame.
Over a short-enough time frame, the ocean SST distribution may anchor atmospheric weather patterns, but over longer periods, there is important two-way interaction (the components are more strongly coupled).
There are some things (water vapor, clouds, seasonal snow) that respond rapidly to climate change. Sea ice can also respond relatively quickly.
It is convenient to use a climate sensitivity using predictable rapid feedbacks and holding other things (natural CH4 emissions, ice sheets, vegetation?) fixed. Charney sensitivity is such a concept. If something is expected to change in response to climate change, but there is uncertainty, or maybe just uncertainty in the timing of the response (slow or fast, maybe irregular jumps), we can at least use Charney sensitivity, and treating the left-out feedbacks as a forcing, use Charney senstivity to that forcing to consider what may happen.
Obviously, sensitivity to radiative forcing of greenhouse gases (not water vapor, but CO2 and CH4) can’t include feedbacks of those same gases – those are defined as forcings in such a sensitivity. To consider such feedback, the forcing has to be the actual action that is disturbing the amount of CO2 and CH4 (anthropogenic emissions), and a good description of the response may be time-dependent (trajectory of climate as a function of trajectory of anthropogenic emissions).
Over longer time scales, there is CO2 feedback. There is positive CO2 feedback on the scale of orbitally-forced ice ages and interglacials; this isn’t a general fact – it depends on how the system is set-up (the same is actually true of the ice sheet feedback. With a different overall climatic state or geography, the system might be considerably less sensitive to orbital forcing (obviously it has been less sensitive; orbital forcing has been going on throughout Earth’s history (modulated by tidally-induced changes in Earth’s rotation and the moon’s orbit)). Althoug absent ice age-integlacial response, orbital forcing still affects low-latitude circulation patterns (monsoons).
(Orbital forcing doesn’t have much of a global annual average forcing, and it’s even concievable that the sensitivity to orbital forcing as measured in terms of global averages and the long-term response (temporal scale of ice sheet response) might be approaching infinity or even be negative (if more sunlight is directed onto an ice sheet, the global average albedo might increase, but the ice sheet would be more likely to decay, with a global average albedo feedback that causes warming). Orbital forcing causes ice ages or ends them by redistributing incoming solar radiation over seasons and latitudes so that ice sheet growth or decay is more or less favorable on a regional basis, with a resulting global average albedo feedback.)
—-
The equilbrium global time average response (on a time scale sufficient to characterize externally-forced cycles (day, year) and internal varibility) to an imposed global time average radiative forcing is a change that balances the externally imposed forcing plus any non-Planck feedbacks (where the Planck response is part of the response to the other feedbacks. Within a convecting layer, convective fluxes can also be part of the response, but where convection is bounded within a layer, the layer as a whole must respond with radiation to radiative forcings and feedbacks.)
Patterns in feedbacks can shape the 4-dimensional structure of the climate response; so can patterns in the externally imposed (or just external) forcing, but among external forcings that are not too idiosyncratic, the feedback distribution may dominate so that the climate response is similar in structure. The climate sensitivity to the external forcing will also tend to be similar. Idiosyncracies in the forcings may alter the 4-dimension structure of the climate response so as to change the global average feedback. The climate sensitivity to a forcing divided by climate sensitivity to some reference forcing is called efficacy. Among forcings which have opposite effects on the stratosphere for the same sign of effect on the troposphere+surface, efficacy will tend to be more similar if in terms of tropopause-level forcing with stratospheric adjustment (although there can be mechanical effects on the troposphere+surface from stratospheric changes (and vice versa)).
Anthropogenic aerosols are somewhat more idiosyncratic because of their regional distribution.
Orbital forcing is very idiosyncratic.
————–
** example of internal variability: sound produced by wind blowing through a tree. There is no external forcing with cycles in the frequencies of sound waves; the sound is produced by internal variability. The system is forced by the speed of wind and the type of tree. The energy flux of the sound will tend to increase with greater wind speed. Interestingly, the texture of the internal variability is strongly affected by the type of tree. You can hear the difference between a quaking aspen (rustling-clapping) and a pine-tree (whooshing/rushing/shhhh).
Also, CO2 has non-radiative effects (fertilization (not the panacea it is sometimes assumed to be), acidification), which might somehow feedback on climate (regionally, changes in evapotranspiration, for example – not a tropopause level forcing, but it would have some effects).
Over longer periods of time, there is a negative CO2 feedback (see prior comments)(depending on geography (relative to circulation patterns) and CO2 amount, warming can cause enhanced chemical weathering, which supplies ions that can combine with CO2 to form carbonates. In the absence of that ion supply, abiotic CO2 uptake in the ocean as a function of CO2 in air is at least somewhat limited by ions already present; acification can (over time) dissolve carbonate minerals that supply cations and carbonate ions, buffering pH and reacting with CO2 to form bicarbonate ions; new cations from chemical weathering have to be supplied to actually remove C from the oceans while keeping pH from dropping and without releasing as much CO2 from bicarbonate ions).
(Re L. David Cooke
PS What I meant about H escape – I was refering to a process that could have been important in the Archean eon – it’s importance now would be the leftover oxidized environment, not so much ongoing H escape.
You had mentioned a CO2 – O2 balance; the larger point I should make is that while the organic C cycle affects the CO2 and O2 oppositely, the fluxes are largely balanced (organic C burial is a small term and not all geologic CO2 emissions come from inorganic C in the crust and mantle -some of that organic C returns to the atmosphere+ocean+biota eventually), and there are other processes that affect CO2 and O2 seperately (I think organic C burial is typically ~ 1/5 (?) of the total geologic sequestration; the rest being in the form of carbonate minerals; oxygen reacts with ferrous Fe to form ferric Fe, and there’s H escape to space – these things (so far as I know) might not be so important now but they were at one time).
)
————–
Okay, I’m just going to go ahead and post what I came up with – 4 parts, sorry for the length and poor organization in parts; don’t worry about my time being wasted, because it’s good excercise and whenever I try to explain something, it gives me insight into how I could explain it, and now they’ll be a bunch of paragraphs I might recycle in other discussions rather than reproducing from scratch…
How CO2 changes are related to radiative forcing (I’ve covered this before but it always goes long; I want to try to summarize it neatly).
Part IV. First, reviewing how optical properties shape radiative processes:
———- ————
1.
Note optical thickness of any type, per unit distance = that type of cross section per unit volume. In this context we’ll generally only consider absorption and emission (except for occasional mentions of what other types of CSD can do), and so I will just refer to a cross section density, CSD.
2.
The below generally applies seperately for each frequency (and if necessary, polarization).
3.
In this discussion, we hold temperature constant. (This is how a radiative forcing for a change in optical properties is determined. Starting from an old equilbrium, a change in radiative forcing results in a radiative imbalance, which results in energy accumulation or depletion, which causes a temperature response that approahes equilibrium when the remaining imbalance approaches zero – thus the equilibrium climatic response, in the global-time average (for a time period long enough to characterize the climatic state, including externally imposed cycles (day, year) and internal variability), causes an opposite change in radiative fluxes (via Planck function) (plus convective fluxes, etc, where they occur) equal in magnitude to the sum of the (externally) imposed forcing plus any ‘forcings’ caused by non-Planck feedbacks (in particular, climate-dependent changes in optical properties, + etc.). )
———
4.
Consider any preexisting (baseline) CSD (of the absorbing/emitting type) that exists at some frequency, with some temperature variation over vertical distance. In that case, at a given level L, there is some upward and downward intensity, and net upward intensity at each angle from vertical, and they can be integrated over directions (weighted by the cosine of the angle from vertical) to find an upward, downward, and net upward flux per unit horizontal area.
———
5.
The intensity that comes from some direction, reaching a given location L, is emitted from a spatial distribution that can be called the emission weighting function (EWF). EWF is a density over distance along a line (in the absence of scattering, etc.) or lines (when partial specular reflection occurs), or a density over volume (when scattering contributes to the CSD), where the sum over all space = 1; it matches the distribution over space of the absorption of a unit amount of radiation incident at L from the opposite direction. The effective spatial extent of the bulk of an EWF is on the order of the average distance between photon emission and photon absorption.
6.
If at every point in space, EWF is multiplied by the Planck function for the temperature at that point, the product can be integrated over space (over the extent of the EWF), and the result is the intensity found for the given direction for the given location L. Thus the brightness temperature of the intensity is within the range of temperatures within the EWF; it would be the EWF-averaged temperature were it not for the nonlinearity of the Planck function; but it can be the EWF-averaged temperature for certain temperature distributions; if the temperature varies continously over space and if, over most of the EWF, it varies approximately linearly over space with a small percent change so that the Planck function over that range can be approximated as linearly over that range of temperatures, then the brightness temperature of the intensity can be approximated as being the temperature of the centroid of the EWF.
7.
Greater CSD will compress the EWF into a smaller region, towards the location L.
8.
(This is true for a mixture of absorption and scattering CSD contributions as well as for purely absorbing CSD; it is not true for purely scattering CSD, which tends to redistribute the EWF so that it surrounds L more evenly (partial reflection off a surface can also do the same thing), but the EWF must be found where absorption can occur. Pockets of dense CSD of either type may cast shadows in the disribution of EWF. Aside from the compression or redirection of EWF by CSD, EWF is locally proportional to the CSD from absorption.)
9.
Thus, as CSD increases to large values relative to the spatial scale of temperature variations, the brightness temperature of the intensity at L will approach the local temperature at L (then the effect approaches saturation). If the location L is embedded in a continuous temperature distribution with a continuous CSD distribution, the same will happen for intensities in opposite directions when CSD is large enough, so that the net intensity goes to zero; unless CSD is purely scattering near TOA, this won’t happen at TOA because of the lack of radiation from space (except for solar radiation, or for very tiny solid angles directed at specific objects, which can be ignored for our purposes here)
———— ————-
10.
For the rest of this section:
We’ll assume CSD is horizontally homogeneous. Also we’ll assume each vertical level is approximately isothermal over horizontal distances. We’ll assume CSD is isotropic (same for all directions at any location).
————
11.
Trends as a function of CSD, Saturation: If the temperature varies monotonically over the distance from which most of the radiation reaching that level is emitted, then increasing the CSD will bring the upward and downward fluxes and intensities (at a given angle) toward the same value, reducing the net intensities and fluxes, until eventually they approach zero (or a nonzero saturation value at TOA). If the temperature fluctuates over shorter distances near that level, then the upward/downward/net intensities and fluxes may fluctuate – let’s say whenever they reach a maximum or minimum before reversing tendency, this is a temporary saturation …
(I’m coining a term here because it makes sense to introduce some term, but I’m unaware of a term specifically used for this concept; obviously if another term already exists for this concept, it should be used)
…, but once the optical thickness becomes large over the spatial scale of the nearest maximum or minimum temperature on either side, the net fluxes and intensities will reach a final peak if they have not yet done so, and then decline toward zero (or another value at TOA) – an ultimate saturation (see note about temporary saturation).
12a.
Trends as a function of CSD, different directions: There are larger optical thicknesses over the same vertical distance at larger angles from vertical for the same CSD (assuming isotropic (constant over direction) CSD, which we’ll do here); the intensities at these angles at one value of CSD will be the intensities at smaller angles from vertical at larger values of CSD; thus the intensities are larger angles from vertical lead and the intensities closer to vertical up or down will lag the trends as CSD is increased. If there is some CSD for which the vertical intensity (up, down, net) reaches a maximum or minimum, then the flux (up, down, net, respectively) per unit area, having contributions from intensities in all directions, each in proportion to the cosine of the angle from vertical, will reach a maximum or minimum at a somewhat smaller CSD, while intensities at sufficiently large angles will reach a maximum or minimum at even smaller CSD.
12b. – notice the analogy to how sufficiently self-similar fine-scale texture in an absorption band can be treated.
——– ——–
13.
The exact way that intensities and fluxes vary as a function of CSD depends on the spatial temperature distribution as well as the Planck function, or in combination, it depends on the spatial distribution of the Planck function (for local temperature).
However, it is possible to point out some generalities:
14.
Any smooth continuous function can be approximated as linear over a sufficiently short interval.
15.
15.1.
Thus, for a sufficiently small change in CSD, double that change will result in approximately double the change in intensity at every angle, and thus the same applies to the change in flux per unit area; thus the radiative forcing is linearly proportional to changes in CSD for sufficiently small changes. (This also applies to absorption + scattering CSD, or pure scattering.)
15.2a.
For a particular frequency and a given continuous smooth Planck function distribution, a large enough CSD compresses most of the EWF’s for intensities in all directions to a smaller enough region such that the Planck function can be approximated as following a linear spatial trend within the EWF’s. In that case, for a given direction, a doubling of CSD will halve the difference between the intensity at L and the Planck function for the temperature at L. This occurs for all directions and so occurs for the flux per unit area as well. Thus there will be an approach to an ultimate saturation asymptotic value, with the shape of the flux as a function of CSD being a hyperbola. When this is occuring for upward and downward fluxes, the asymptotic value for the net flux per unit area is zero (provided the Planck function is continuous through the level L, as opposed to what happens in effect at TOA), so that the net flux per unit area halves for each doubling in CSD.
15.2b.
(This actually applies to a doubling of total CSD, and assumes any variations of CSD over vertical position will be held in constant proportionality (CSD changes by the same percent everywhere within most of the EWF’s), but when the additional amount of CSD, relative to a given baseline amount of CSD, is relatively large, the total can be approximated as the additional amount so that doubling the additional amount is approximately the same as doubling the total amount, and also, it will only be necessary to keep the vertical variations in the additional amount of CSD in constant proportionality for the same reason, while the baseline CSD could be distributed differently.)
15.2c.
(I think this should also tend to apply if the CSD comes from a mix of absorption and scattering, provided that the proportionalities among different kinds of CSD are kept constant as CSD is doubled. However, if the CSD around L is purely scattering, the mathematics changes; as EWF’s are redistributed but not compressed toward L).
The largest effects of a doubling of CSD, or a doubling of some additional CSD (given some baseline amount of CSD) will tend to occur somewhere between the ‘linear regime’ and the ‘hyperbolic regime’.
——————–
15.3a.
At a given frequency, if the Planck function B varies over a CSD-weighted distance ztau (using an initial value of CSD so that temperature remains fixed at each ztau) (where ztau = 0 at the level L) in such a way that it can be approximated as a hyperbola
B = a + b/|ztau|^c, with c = 1,
then the linear proportionality of changes in intensity and flux over changes in CSD (provided that total CSD changes by the same percent everywhere) can hold for all CSD.
(If c is larger than 1, then each additional unit increase in total CSD would result in a greater change in the intensities and flux than the previous unit increase of the same size. If c is less than 1, then each incremental change in CSD has a smaller effect at larger CSD.)
If such a distribution occurs on both sides over similar CSD-weighted spatial scales, then the same type of behavior will be true for the net fluxes and intensities.
However, in order for the temperature to remain finite (and if b is negative, in order for the temperature to not be negative), such a Planck function distribution cannot hold at the smallest ztau values (regions close to L), in which case, the linear proportionality must break down at sufficiently large CSD, when the region near L with the different Planck function distribution becomes a significant portion of the EWF’s.
In the case where this happens on both sides of L, the Planck function could have a sharp peak or dip at L or else follow an S-shape going through L, with an approximate B = a + b/|ztau|^c on both sides of L except at small ztau (a and b could be different on each side of L, but for simplicity of behavior of net intensities and flux, keep the same c on each side of L.)
15.3b.
(If there is a mix of scattering and absorption contributions to CSD, then, holding the proportionalities constant while increasing the total CSD can, **I think**, have the same effect for that type of a Planck function distribution, provided that the distribution can be approximated as such a hyperbola on both sides of the location, as described in the last paragraph of 15.3a (because scattering can cause the EWF’s to wrap around the location L)).
———- ———- ———— ———–
PART V.
THE CO2 BAND
16.
The CO2 band with a peak CSD near 15 microns (15 microns vacuum ~= 667 per cm (the inverse of wavelength is often used as a measure of frequency), though I’m not sure how close the peak is to that specific wavenumber. ):
17.
The shape of the CO2 absorption band, in terms of CSD per unit CO2 concentration, can be approximated as having a peak at some frequency (designated ν0) or wavelength (about 15 microns for CO2) with, on each side of that peak, a halving of that optical thickness for each amount BW1 or BW2 that one moves away from the center (toward lower or higher frequency, respectively)
18.
(This can be either in frequency or wavelength; since they are inversely proportional, the absorption band can’t have precisely this shape in both, but it may be approximated this way in whichever unit of the spectrum we decide to use (one might be better than another, though) – if we use wavelength, then we need to use the Planck function for intensity per unit wavelength; if we use frequency, then we need to use the Planck function for intensity per unit frequency. I’ll go by frequency here.)
—–
19.
Linear approximation for small changes:
Starting at any baseline amount of CSD, which may vary over space in some different way from what we will add to it:
For a sufficiently small amount of CO2, adding double the amount would have approximately double the effect on radiant intensities and fluxes – at all frequencies, at all directions. This would be true for a sufficiently small amount of any greenhouse agent.
—–
20.
Now consider a baseline amount of CSD from non-CO2 (which needn’t be mixed with the CSD of CO2 in the same ratio everywhere). Let’s assume it is constant over frequency in the vicinity of the CO2 band.
21.
Consider graphs of upward, downward, and net (spectral/monochromatic) fluxes F or intensities I, as a function of frequency, at some given vertical level. The area under the function is the total for all frequencies.
22.
Let’s measure the amounts in terms of brightness temperature BT, in which case the area is not proportional to the total intensity or flux over all frequencies, but there is an approximate proportionality over small regions of that area. What is convenient is that the baseline CDS will be a flat line on such a graph, and any particular distribution and amount of CDS will produce the same BT at any frequency.
23.
For consideration of net fluxes or intensities, the BT on the graph will be a difference between upward flux/intensity BT and downward flux/intensity BT.
24.
Some amount of CO2 creates a hill or valley in the BT spectrum. Let the difference from the baseline be BTc; BTc at ν0 is BTc0.
35.
The specific shape of the BTc hill or valley depends on the temperature distribution, but there are some generalities due to the convenient shape of the CO2 spectrum.
Doubling the amount of CO2 will change the area under the BT graph in a way that can be divided into two components:
35.1.
Band-widening effect – because on either side of ν = ν0, the CDS halves over an interval BW1 or BW2, in doubling the CO2, the same value of CDS will now be found shifted outward from ν0 by a change in ν equal to BW1 or BW2, respectively. This is true for the entire set of CDS values that were initially found along the graph, and it is true for all directions and thus the band widening effect applies to all intensities and thus to the fluxes per unit area as well.
The change in area from band-widening is equal to
BW1 * BTc0i
and
BW2 * BTc0i
on each side, where BTc0i is the initial value of BTc0, the value before the CO2 was doubled.
35.2.
Band center contribution: change in BTc0: Where the change in BTc0 = ΔBTc0, there will be some additional change in the area that will be on the order of
~ 1/2 * (BW1+BW2) * ΔBTc0 .
It could be smaller than that or larger, depending on the way that temperature varies with height; but it will not be larger than twice that, provided that a temporary saturation doesn’t happen and then significantly reverse in the span of a single doubling – in other words, provided that the process of any temporary saturation and following reversal (wherein BTc0 increases, halts, and then decreases, or in the opposite order) can be sufficiently resolved by the fractional change in CO2.
If we need to, we can use a series of smaller changes than a doubling – for example, we could multiply the CO2 concentration by 2^b, with b between 1 and 0, in which case,
the band widening effect would be
b * BW1 * BTc0i and 1/5 * BW1 * BTc0i,
where BTc0i is the value of BTc0 after the prior 2^(1/5) change and before the next.
The band center contribution would be on the order of
~ b * 1/2 * (BW1+BW2) * ΔBTc0,
where this time, ΔBTc0 is the change in BTc0 for a 2^(1/5) change. The smaller the change (the smaller b is), the better this formula will approximate the actual change.
As long as the changes are small enough that we can stop between increases in CO2 whenever BTc0 reaches a maximum or minimum, this works.
Notice that (for changes small enough to resolve any temporary saturations) as long as ΔBTc0 is not more than BTc0i …
(a condition which tends to be satisfied for a doubling of CO2, unless the temperature variation is sufficiently compressed toward L, analogous the cases discussed in 15.3a with c larger than 1 except for the nonlinear relationship between the intensity or flux and the BT– and preexisting non-CO2 CDS will actually make it harder for ΔBTc0 to be larger relative to BTc0i),
…the band-widening effect will be greater than this band center contribution.
Note that, for sufficiently small changes that b * 1/2 * (BW1+BW2) * ΔBTc0 is a good approximation for the band center contribution, ΔBTc0 would have to be more than 2*BTc0i for the band center contribution to be more than the band widening effect.
—
35.3.
There is no need for special treatment of temporary saturations that might occur due to temperature fluctuations of sufficiently limited spatial extent. If the shape of the hill or valley in BTc has undulations, the band-widening involves positive and negative changes in area on the graph at different points, which are all neatly accounted for by using the BTc0 value at the peak frequency to multiply by the band widening intervals BW1 and BW2.
——-
36.
With a sufficiently small amount of CO2 to start with, a doubling will approximately double BTc0 (and do the same at all other frequencies).
37.
With a sufficiently large amount of CO2, each doubling will approximately halve the difference between BTc0 and the ultimate saturation value BTcsat (which will be the same at all frequencies for the given vertical level, equal to the temperature at that level minus the baseline BT value, or if we are considering net fluxes and intensities, it will be zero except at TOA).
38.
But the band-widening effect is actually at its strongest (assuming any temporary saturations did not take BT outside the range of baseline BT and T at the level L) when ultimate saturation has been reached at the center of the band. When the band center approaches saturation, the forcing by farther changes in CO2 becomes approximately logarithmically proportional to CO2, because there is a certain amount of band-widening per doubling while the height/depth of the hill/valley in BT stays constant (for the simplifying conditions we’ve used).
——-
39.
There is still the matter that the intensity or flux per unit area…
(given by the Planck function or spectral blackbody flux/area, respectively, for T = BT, except when BT is the difference between upward and downward brightness temperatures, in which case the differences between Planck functions or blackbody fluxes must be used)
… is not linearly proportional to BT. Also, the baseline BT value may not be constant over the width of the band.
40.
Changes in the intensity will be approximately linearly proportional to changes in BT if they are sufficiently small, and intensity for a given BT can be approximated as constant over sufficiently short intervals of the spectrum.
41.
If the difference between baseline intensities or fluxes and ultimate saturation intensities or fluxes varies approximately linearly over the vicinity of the CO2, with slopes in inverse proportion to BW1 and BW2 on either side of the peak frequency, then the effect can average out and the radiative forcing for the whole band will be proportional to the area changes on the BT graph.
42.
Otherwise, an approximation can be made by using, in place of BTc0i and ΔBTc0, three corresponding values of upward/downward/net fluxes per unit area, two values for frequencies ν1 and ν2 on either side of the band near the centroids of the areas on the graph for the band-widening effect (works unless there are temporary saturations leaving positive and negative areas, in which case more different values for different frequencies would work better) to multiply by b*BW1 and b*BW2, respectively, to find the band-widenning effect, and one value for the peak frequency ν0, to multiply by something on the order of b* ½ * (BW1+BW2) to find the band center contribution.
43.
But given the narrowness of BW1 and BW2, relative to the scale of the spectral intervals over which the Planck function changes substantially, and given the way water vapor and cloud CDS vary over the spectrum in the vicinity of CO2 (clouds being nearly independent of frequency over much of the LW spectrum as I understand it; water vapor gets stronger over the span of the CO2 band from higher to lower frequencies, but not with big jumps (glossing over some of the finer-scale texture)), the logarithmic approximation is still a good approximation for CO2 forcing (in which the radiative forcing changes by some amount per doubling of CO2 concentration) when the center of the band is saturated.
**(Of course, the above logic was based on an approximation to the CO2 absorption spectrum – but the linear/logarithmic approximation still works and more exact answers can be found with more detailed calculations.
——– ——- ——– ——– ——-
PART VI.
RADIATIVE FORCING, (PLANCK) RESPONSES AND FEEDBACKS
44.
Considering the case where LW scattering and reflection is minor (as it is on Earth):
45a.
The temperature generally decreases with height (positive lapse rate) in the troposphere (see 46,47), so increasing the optical thickness (via increasing CSD) of the troposphere tends to reduce the upward LW flux at the tropopause.
45b.
Space is dark, and increasing the the optical thickness (increasing CSD) of the stratosphere tends to increase the downward LW flux at the tropopause. An exception can occur if the stratospheric temperature increases with height, especially if it does so immediately above the tropopause, in which case, if there is already sufficient optical thickness, the downward flux can be decreased by adding more (this effect is reduced if the temperature increase is concentrated toward the upper stratosphere). (On Earth, the stratosphere is transparent in the vicinity of the CO2 band, so that, given the shape of the CO2 band, increases in CO2 will increase the total LW downward flux at the tropopause for a wide variety of stratospheric temperature profiles.)
46.
(By similar logic, increasing atmospheric optical thickness tends to increase the downward flux at the surface or any other level, and reduce the upward flux at TOA or any other level, but with exceptions due to inversions (layers with increasing temperature with height).
47**.
There can/will be local and regional, latitudinal, diurnal and seasonal, and internal variability-related deviations to the pattern (in temperature and in optical properties (LW and SW) from components (water vapor, clouds, snow, etc.) that vary with weather and climate), but the global average effect is at least somewhat constrained by the global average vertical distribution of solar heating, which requires the equilibrium net convective + LW fluxes, in the global average, to be sizable and upward at all levels from the surface to TOA, thus tending to limit the extent and magnitude of inversions.)
Solar heating is distributed in a certain way; heat must flow from where solar heating occurs to space. With zero LW absorbing optical thickness within the atmosphere, the heat must get to surface (if not already there) before escaping to space. With some LW absorbing optical thickness, the atmosphere can emit radiation to space, so some heat will flow into the atmosphere from where solar heating occurs to get to space. With more LW opacity with some of it being from absorption, more heat must get into the atmosphere before escaping to space, and with more LW opacity, the more heat has to get higher into the atmosphere before escaping to space, with some of that radiant heat taking multiple steps (emission to absorption) to get from solar or convective heating to where it leaves for space (note this refers to the net LW fluxes; photons will generally go back and forth, with the larger flux from higher to lower temperatures). Temperature gradients are generally (see next paragraph) required to drive these flows of heat (continually through layers with convection/conduction/diffusion driven by differential heating, on the scale of distances from emission to absorption for radiant flows), so the temperature tends to decline from where solar heating occurs to where heat escapes to space.
(In the global time average, diffusion of latent heat is in the same direction as sensible heat transport, but latent heat will tend to flow from higher to lower concentrations of water vapor (or equilibrium vapor pressure at the liquid/solid water surface), and regionally/locally, conditions can arise where the latent heat and sensible heat fluxes are oppositely directed.)
48.
(The CSD near a level has the greatest effect on the flux at that level and reduces the effect of CSD at farther distances in the same direction. Thus, the relative concentration of water vapor toward the surface enhances its effect on the surface LW flux and reduces its effect on fluxes at the tropopause and TOA.)
—–
49.
The combination of decreasing upward flux and increasing downward flux add to a decreasing net upward flux (true for both SW and LW radiation).
50.
Radiative forcing RF at a level is equal to a decrease in net upward flux (either SW, LW, or both; the greenhouse effect refers to LW forcing) at that given level, due to a change in (optical) properties, while holding temperatures constant.
51a.
The equilibrium response to an addition of RF at a level is an increase in net upward flux consisting of LW radiation (the Planck response, PR) plus a convective flux response CR; CR is approximately zero at and above the tropopause in the global time average.
51b.
(Within a typical atmosphere, as on Earth, heat transport by conduction and molecular mass diffusion are relatively insignificant for bulk transport (there is some role in smaller-scale processes involving particles in the air), except when the net radiative flux and convective flux are very very small (not a condition generally found on Earth). An exception occurs in a very thin layer of air (~ 1 mm for Earthly conditions) next to the surface (and for a thin layer of water underneath the surface, and for a thicker layer of the land surface material). This is because the surface is a boundary to convection; heat flows across the surface require conduction and diffusion, and over short distances, viscosity is more effective at impeding convection. In the context of climate and weather, the term convection often is meant to include the conduction and diffusion at the surface; these fluxes heat a thin layer as convection cools it, thus the tendency is that approximately the same flux continues from the surface through a short distance of air, changing from conduction and diffusion into convection along the way. Sufficiently vigorous convection will tend to maintain an adiabatic (dry or moist, depending) lapse rate; near the surface there can be a superadiabatic lapse rate when the differential radiant heating is strong enough, so the temperature profile diverges from the convective lapse rate; however, the surface temperature still generally tends to follow changes in the troposphere – see 63. below, 47 above.)
52.
The climate responds to feedbacks from changes in optical properties (at any location above or below the level) in the same general way it responds to externally-imposed radiative forcings, by changing so as to restore balance at a new equilibrium; feedbacks can be described in terms of radiative ‘forcing’ per unit change in climate (such as in terms of surface temperature) . One can consider net PR+CR as a response to externally-imposed RF (external forcing) plus feedback ‘RF’, or one can consider PR + CR – feedback ‘RF’ as the response to the externally imposed RF; the later is perhaps more helpful in picturing the time evolution toward equilibrium (and illustrates why the time it takes for an imbalance,
equal to: externally imposed RF – climate dependent terms (PR + CR – feedback ‘RF’),
to decay is proportional to both heat capacity and climate sensitivity (defined per unit externally imposed RF).
In some contexts, radiative forcing (RF) refers exclusively to externally imposed RF.
53.
With the approximation of geothermal and tidal (and fossil fuel combustion) heat supplies being zero (valid for at least the inner planets), the net flux at a given level is equal to the energy gain or loss rate for the whole climate system below that level. Thus, forcing at TOA is a forcing on the climate system as a whole, and forcing at the tropopause level is a forcing on the troposphere and surface (see next parenthetical paragraph) as a whole.
54.
(The climate system of course includes the ocean and some (relatively thin) layer of the crust / land surface that interacts with the climate system on relevant time scales – with respect to energy balances, that pertains to the depth to which heating changes penetrate beneath the surface on the time scales being considered. In equilibrium, all fluxes into the surface will be balanced by fluxes out of the surface (including momentum, etc, as well as energy), so whatever lies beneath the surface gives the surface an effective heat capacity and also (in the oceans) some ability for local/regional imbalances to be balanced globally, with all of that responding to forcings and PR+CR and other feedbacks at the surface. (And momentum beneath the surface respond to momentum fluxes at the surface, etc.))
———
55.
The variation of RF over a layer, increasing/decreasing with height, means that there is a forced convergence/divergence of radiative fluxes; the RF acting on a layer is equal to the difference between RF at the top and bottom of the layer and is positive/negative if the RF is greater/smaller at the top.
56.
The responses of individual layers (smaller than the whole climate system) are complicated by the fact that some of the PR + CR of one layer goes to other parts of the climate system (as opposed to space). The layers can feedback on each in that way, acting like additional RF (not that it should be called RF, though it might be considered an adjustment to the RF – see below) on any given layer from the portion of PR+CR from the other layers that is absorbed in that layer.
57a.
In this way, the response of LW fluxes (PR) and convection (CR) tend to spread the temperature response vertically from where forcings occur – not generally eliminating the effect of RF distribution over height, although in the case with convection driven by differential radiative heating within a layer, CR can to a first approximation evenly distribute a temperature response over such a layer.
—————
57b.
(In the full 4-dimensional climate, responses can also tend spread horizontally by convection (advection) and temporally by heat capacity, though ‘fingerprints’ of horizontal and temporal variations in RF (externally imposed and feedback – snow and ice albedo, for example) can remain – this spreading is somewhat different as it relies in part on the circulation already present as well as circulation changes)
57c, … – see addendum
————–
58a.
(Regarding PR, the fraction of PR from one layer that is absorbed by another depends on their optical properties (as well as the optical properties of other layers in between, and other layers if scattering/reflection were to occur), including variations over the spectrum and how the temperature change in the layer emitting the PR is distributed, which, along with optical properties, affects how much PR goes out of a layer from the top or bottom, and where it is found in the spectrum. In general, the portion of a layer’s PR emitted at the top needn’t be the same sign as that emitted out the bottom (also true of CR), and thus the equilibrium PR out in one direction can actually be greater than the RF on the layer – what is true is that the sum of equilibrium PR+CR out the top and out the bottom is determined by RF). .
58b.
(The PR from a layer will tend to be more evenly distributed between going out the top and out the bottom if either the change in temperature is evenly distributed within the layer, or if the layer has significant but not large optical thickness over a portion of the spectrum (weighted by the Planck function(s) for the temperature(s) involved) considerably greater than any portion where the optical thickness is large.)
59.
(The effects of PR+CR from all layers at a given level is a net PR+CR at that level, so the net PR+CR at a level includes the PR+CR type feedbacks among layers.)
60.
The RF before such interlayer feedback can be called an instantaneous RF.
——————-
61.
How this works, Earth’s climate system as an example:
For example, consider dividing the climate system into two layers: a surface+tropoposphere layer and a stratosphere…
(on Earth, the mass of the mesosphere and thermosphere are so small that the effect of the entire upper atmosphere above the tropopause on fluxes at TOA and at the tropopause and below can generally be well-approximated by the effect of the stratosphere. (?)In some contexts the term ‘stratosphere’ may refer to everything between the tropopause and TOA(?).)
The instantaneous RF difference between the tropopause and TOA is the instantaneous forcing on the stratosphere RFs1; if the TOA forcing is smaller than the tropopause forcing, then the forcing on the stratosphere is negative, which means that the stratosphere will cool (this doesn’t necessarily mean it will cool everywhere, but the equilibrium response to negative stratospheric RF requires a negative PR+CR response – being the stratosphere, at least in the global time average, CR can be approximated as zero).
62.
Thus, the stratosphere responds to a negative instantaneous RFs1 with an equal negative PRs1. Some fraction, ft1 of that PRs1 is absorbed below (or in this case where ft1*PRs1 is a reduction of flux downward, was absorbed below before it was removed); the fraction of PRs1 that goes to space is then (1-ft1). This adjusts the RF at the tropopause, so that the troposphere+surface must now respond to
the tropopause RF with stratospheric adjustment (RFt2)
equal to:
instantaneous tropopause (RFt1) + ft1*RFs1.
63.
The differential heating imposed on the troposphere+surface layer is sufficient that LW emissions from within the layer are not able to establish pure radiative equilibrium without having the temperature profile become unstable to convection. Thus there is convection within the troposphere that (to a first approximation) tends to sustain some lapse rate profile within the layer – that itself can vary as a function of climate (and height, location, time), but given any relative temperature distribution within the layer (including horizontal and temporal variations and relationship to variable CSD contributors (water vapor, clouds)), the temperature of the whole layer must shift to balance radiative fluxes into and out of the layer (in the global time averae, and in the approximation of zero global time average convection above the troposphere), producing a PRt2 (in the global time average) equal to RFt2.
(see
64.
Some fraction of PRt2, fs2, will be absorbed in the stratosphere. The stratospheric response to this will be PRs2, a fraction ft2 will be absorbed by the troposphere-surface layer. Etc. Approximating the fractions of additional PR of one layer absorbed by another as the same after this point, the total PR from the troposphere+surface will then be the sum of RFt2*(fs2*ft2)^n for n=0 to infinity, equal to
RFt2/[1 – fs2*ft2],
while the total PR from the stratosphere will then be equal to
RFs1 + fs2* RFt2/[1 – fs2*ft2]
(which will be negative if RFs1 is negative and the second term is small enough – even if it is not negative, this wouldn’t necessarily mean that there is no cooling in the stratosphere, but it would mean that such cooling would have to be limited to a portion of the stratosphere with warming in other parts).
These values represent, in terms of fluxes, the warming of the surface+troposphere and stratosphere, respectively, in response to the instantaneous forcings combined with inter-layer flux changes.
65.
Notice that the instantaneous TOA forcing is RFt1 + RFs1, and the end result PR at TOA is the PR from the troposphere+surface that is not absorbed by the stratosphere (first term in next line), plus the PR from the stratosphere that is not absorbed by the troposphere+surface (second and third term):
(1-fs2)* RFt2/[1 – fs2*ft2] + (1-ft2)* fs2* RFt2/[1- fs2*ft2] + (1-ft1)*RFs1
=
RFt2/[1 – fs2*ft2] * [1-fs2 + (1-ft2)* fs2 ] + (1-ft1)*RFs1
=
(RFt1+ft1*RFs1)/[1 – fs2*ft2] * [1 – fs2*ft2 ] + (1-ft1)*RFs1
=
RFt1 + ft1*RFs1 + (1-ft1)*RFs1
=
RFt1 + RFs1
= instantaneous RF at TOA, as expected.
66.
Also, the net PR at the tropopause is the PR from the troposphere+surface (first term in first line below), minus the downward PR from the stratosphere (other two terms):
RFt2/[1 – fs2*ft2] – ft2*(fs2* RFt2/[1-(fs2*ft2)]) – ft1*RFs1
=
RFt2/[1 – fs2*ft2] * [1 – fs2*ft2] – ft1*RFs1
=
RFt2 – ft1*RFs1
=
RFt1
= instantaneous RF at tropopause, as expected.
67.
Note that ft2 is not necessarily equal to ft1 (the pattern of stratospheric response to changes in fluxes from the troposphere alone could be different from the response to the instantaneous forcing, which involves changes in upward and downward fluxes at the troposphere as well as the flux at TOA) , and also, f1 could be negative (see 15,16 above), though f1 is positive for Earthly conditions.
68a.
There can/will also be a shift in the tropopause (relative to mass – I am not referring to thermal expansion, though that happens; thermal contraction happens in layers that cool), which means that some layer of air is reclassified from stratospheric to tropospheric (for an upward shift). The solar heating and LW absorption and emission of that layer will also be transferred to the troposphere. One way to get around that is to consider the RF at the new tropopause level (for an upward shift) or old (for a downward shift); the shift itself would then be like a lapse rate feedback
68b.
(A lapse rate feedback doesn’t directly change fluxes but it changes the relationships of temperatures between vertical levels, so that for a given temperature at one level, a lapse rate feedback changes temperature at another level and thus affects LW fluxes.)
57c – .**
(see 47,63, and second half of
http://chriscolose.wordpress.com/2010/02/18/greenhouse-effect-revisited/#comment-2236 , and
http://chriscolose.wordpress.com/2010/02/18/greenhouse-effect-revisited/#comment-2245 , note I used LSHO instead of LHSO to refer to the same concept)
The troposphere is not everywhere at all times locally vertically coupled by convection; in particular, at night and at high latitudes, especially in winter, and where there is warm air advection aloft, some layer of air can become stable to localized convection.
This locally reduces the convective vertical spreading of the temperature response to forcings.
(57d) Air near the surface gains latent and sensible heat (convective fluxes) from the surface over some fraction of area and time; sometimes air near the surface loses heat to the surface. Deep localized convection where the troposphere is convectively heated by the surface and lower air occurs over some fraction of area and time (where the surface tends to be warm). Horizontal and temporal heat transport/storage brings that heat into regions stable to convection.
(57e) Horizontally large scale circulation still connects all parts of the troposphere. The warm air above nocturnal or polar inversions, or even stable air masses with small positive lapse rates, are warmer than otherwise because of heat capacity and radiant+convective heating during daytime and/or because of heating occurring at other latitudes/regions that is transported to higher latitudes/regions. Some of that heat flows to the surface by LW radiation, reducing the net radiant cooling of the surface.
(57f) When an inversion in the troposphere, in particular near the surface, is sufficiently strong, TOA and tropopause level RF from an increase in LW opacity (with a sufficient amount from absorbing CSD) may actually be negative (blocking radiation from below and replacing it with a larger amount emitted by warmer layers), but it will then be positive at some lower level such as at the surface (increased backradiation), and in such conditions, the temperature response to RF at lower levels (note that surface albedo changes have an RF at the surface) will not be locally vertically spread as much by convection (though there will be some horizontal spreading by advection).
(57h) There is large horizontal-scale overturning (LHSO) that is driven by a combination of differential horizontal net radiant heating and differential vertical net radiant heating; this overturning may be slowed by smaller lapse rates but it can still occur and actually reduce the lapse rate below adiabatic (moist or dry) lapse rates. Slowing such overturning by reducing the horizontal differential heating could tend to allow heat to build up at lower levels until the lapse rate is more favorable to localized vertical overturning (LVO) (The two forms of overturning are not always completely distinct or separate; for example, the Hadley cell, Walker, and monsoon circulations, as well as extratropical storm track activity (developing from baroclinic instability (Rossby wave phenomena)) are driven and organized in part by horizontal differential heating, but in the ascending portions of these circulations, cumulus-type convection can occur).
(57i) The LHSO and LVO described above are thermally-direct circulations, wherein differential heating creates available potential energy (APE) (in the form of internal energy and gravitational potential energy) that is then converted to kinetic energy by adiabatic motions (latent heating also can create APE, or the potential for latent heating can be included in APE, as in CAPE). Thus, some heat gets converted to kinetic energy, but that gets converted back to heat, either by viscosity or by thermally-indirect circulations that produce APE while pulling heat downward in the process (LHSO: Ferrel cell (driven by extratropical storm track activity), Planetary-scale overturning in the stratosphere and mesosphere (includes Brewer-Dobson circulation (I’m not sure if the whole thing is the Brewer-Dobson circulation or if only part of it is)), some motions in the ocean; LVO: wind driven mixing of the boundary layer and of the upper ocean (though mixing itself tends to destroy the APE that the kinetic energy would create by forcing heat downward)). APE produced from kinetic energy may take the form of temperature variations that are farther from radiative equilibrium, and thus may be destroyed by differential radiative heating.
APE can also be due to compositional variations – a generally minor effect in the atmosphere (water vapor makes air less dense; clouds and dust increase the density) but important in the ocean (salinity variations) kinetic energy can be converted from and to this APE as well and this APE can also be destroyed by mixing; within the climate system, it is still ultimately derived from heat (such as via phase changes of water). (Within sufficiently fresh water near the freezing point, the sense of vertical heat flux is reversed between thermally direct and thermally indirect motion.)
At least in the global time average, the non-radiative fluxes through and above the tropopause can be approximated as zero. Whatever kinetic energy goes into the ocean and is dissipated must come out at the surface as heat. Kinetic energy production is small compared to the fluxes of heat involved.
(57j) For surface+tropospheric warming in general, there is (given a cold enough start) positive surface albedo feedback, that is concentrated at higher latitudes and in some seasons (though the temperature response to reduced summer sea ice cover tends to be realized more in winter when there is more heat that must be released before ice forms). The moist adiabatic lapse rate declines with increasing temperature. These shape the 4-dimensional pattern of temperature and other changes – the patterns of circulation, latent heating, and precipitation will shift, as can the cycles driven the imposed diurnal and seasonal cycles in incident solar radiation; the texture of internal variability can also shift. Water vapor also tends to reduce net LW cooling at the surface, which would force increased convection from the surface. There will be Regionally/locally and temporal variations; increased temperature and backradiation tend to reduce the diurnal temperature cycle on land, though regional variations in cloud feedbacks and water vapor could cause some regions to have the opposite effect; changes in surface moisture and humidity also changes the amount of convective cooling that can occur for the same temperature distribution. Regionally, changes in relative humidity near the surface would affect the height at which clouds form…
(57k) When I state that the equilibrium climatic response must balance imposed RF (and feedbacks that occur), I am referring to a global time average RF and global time average response (in terms of radiative and convective fluxes), on a time scale sufficient to characterize the climatic state (including cycles driven by externally-forced cycles (diurnal, annual) and internal variability. Of course, in such a time average, each location’s fluxes (energy, and also momentum and mass) are balanced, with vertical imbalances (generally a net gain in heat at lower latitudes and net loss in higher latitudes, especially in winter) are balanced by horizontal fluxes.
(57l) It would be possible for changes in externally imposed RF involving horizontal and temporal rearrangement with zero global time average to cause a climate change where there is no global average response (except to global average feedbacks).
(57m) However, externally imposed forcings with a global average externally imposed RF may tend to cause similar climatic responses both in the global average and in regional/latitudinal and seasonal (modulation of response to external-forcing cycles that themselves are held constant) and internal variability patterns, provided they are not too idiosyncratic. The effects of some variations among different external forcings with the same global time average RF could be smaller than the effects of horizontal and temporal, and maybe even vertical (as in the water vapor feedback’s effect on convection) variations among feedbacks (surface albedo feedback, moist adiabatic lapse rate changes).
For example, changes in solar brightness (TSI) will have an RF that is largest in the midday at low latitudes with clear skies and dark surfaces (oceans, forests), with a significant amount of RF applying directly to the surface, and some RF of the same sign acting on the stratosphere. In contrast, CO2 forcing by layers changes sign between the surface+troposphere and stratosphere (modulated by the effect of existing solar heating of the stratosphere), and it may have a different distribution of RF over the surface+troposphere layer (which would affect convection) and is more evenly distributed horizontally and temporally. However, there is some similarity: it (or at least the tropopause level forcing) is smallest at high latitudes and greatest in the low latitudes in the absence of at least high-level clouds. But both CO2 and solar-caused surface+tropospheric warming will cause at least some similar latitudinal and seasonal patterns of change within the troposphere+surface via the patterns of albedo feedback and lapse rate feedback.
The efficacy of a forcing is the climate sensitivity (in terms of global average surface temperature change per unit global average RF) of that forcing relative to a standard type of forcing. Efficacies can vary because different patterns of RF can alter the climate response with some global average effect. Among forcings with RF being of different signs in the stratosphere for the same sign at the tropopause, greater similarity in climate sensitivity should be found using the tropopause-level forcing after stratospheric adjustment (see 61-67). For example, the troposphere+surface response is more directly comparable between CO2 and solar forcing for tropopause-level RF with stratospheric adjustment. (Although change in the stratosphere can interact mechanically with changes below.) Forcings which are not too idiosyncratic should tend to have similar efficacies.
Patrick (#395) and further to my #406.
I’d forgotten a rather important aspect of the approximation I was describing. It is used for dust in the interstellar medium which has continuous opacity as a function of frequency but it is not really gray but rather has lower opacity at lower frequency, Thus a layer which is opaque in up welling emission may be transparent in down welling absorption so that the next layer out sees its own down welling emission canceled by emission from the opposite side in the approximation of complete transparency at the appropriate frequencies for the inner shells. T~1/sqrt(R) falls out of that. In radiative stellar interiors the temperature gradient is even less steep.
Additions/clarifications:
Re my 426: Charney Sensitivity – It is convenient to use a climate sensitivity using predictable rapid feedbacks and holding other things…fixed. Charney sensitivity is such a concept. –
1. part of the utility is that Charney sensitivity, using only relatively rapid feedbacks, describes the climate response to an externally imposed forcing change on a particular timescale related to the heat capacity of the system (if the feedbacks were sufficiniently rapid and the heat capacity independent of time scale (it’s not largely because of oceanic circulation), an imbalance would exponentially decay on the time scale of heat capacity * Charney equilibrium climate sensitivity. I’m not quite sure that all the feedbacks in Charney sensitivity are quite that rapid (?). Feedbacks that act on a longer time scale would leave a residual but more persistent imbalance, with a change in the long term sensitivity. Heat capacity that is ‘used’ over a longer period of time (penetration of temperature change through the depths of the ocean and up to regions of upwelling) would leave a more persistent residual imbalance, but the effect would only just stall the full change to equilibrium climate, not change the long term equilibrium sensitivity.)
2. I’m not sure that every feedback not included in Charney sensitivity is less-predictable (with present knowledge or in principle – two different things) than every feedback included in Charney sensitivity.
See also
“Earth system sensitivity inferred from Pliocene modelling and data”
http://www.nature.com/ngeo/journal/v3/n1/full/ngeo706.html
http://www.leif.org/EOS/ngeo706.pdf; first paragraph:
https://www.realclimate.org/index.php/archives/2008/04/target-co2
——
426, 431 (57m) – efficacy:
Not to be taken as a blank check for deciding on a whim that some tiny forcing might be responsible for most of some change with a larger forcing contributing rather little. (There has to be a reason why.)
——-
431 (57i): thermally-indirect circulations that produce APE while pulling heat downward in the process (LHSO: Ferrel cell (driven by extratropical storm track activity)…
The flow of energy between different circulation patterns is dependent on fram of reference (Eulerian vs transformed Eulerian); The Ferrel Cell is the result of some average upward motion poleward of some average downward motion with return flows at lower and higher altitudes, superimposed on the average temperature distribution. Some (not all, I think) of that motion actually occurs where the temperature is perturbed from the average in a particular way so it may not be as thermally indirect as the averages would make it appear – at least that’s my understanding of it. The circulation can be divided among components and the temperature advection by the average motion acting on the average temperature distribution would be one component.
Re 430 add items
69.
The changes in the stratosphere and feedback via Planck response to the troposphere will tend to be more similar for the same tropopause-level forcing after the initial stratospheric adjustment.
70.
The stratosphere will, absent sustained non-radiative perturbations (see 57i), approach radiative equilibrium on a time scale under a year (Holton, “An Introduction to Dynamic Meteorology”, 1992, p. 410), so taking stratospheric adjustment to instantaneous stratospheric forcing first and then applying the adjusted tropopause-level forcing to the troposphere+surface and stratospheric feedbacks is similar to the actual order of events in reality.
Estimate of radiative relaxation time – for small perturbations, using a linearized approximation, wherein imbalances decay exponentially:
Stratospheric temperature ~ 220 K, give or take (this is a rough estimate)
Stratospheric mass ~ 1500 kg/m2 (I recall that being a global average; it’s more in the extratropics, it gets down to ~ 1000 kg/m2 in lower latitudes)
Specific heat cp of air 1004 J/(kg*K)
heat capacity of stratosphere ~ 3 (MJ/m2)/K
From Hartmann, “Global Physical Climatology”, 1994, p.28, stratospheric emission leaving the stratosphere up and down: 11 % (5 % down, 6 % up) of 342 W/m2, or 37.62 W/m2 (ignoring sig.figs).
Grey approximation: 4 % change in emission per 1 % change in temperature
(CO2 band is near the peak wavelength, water vapor bands significant in stratosphere for wavelengths longer than ~ 25 microns and between ~ 5.5 and 7 microns, and ozone between ~ 9.5 and 10 microns, and CH4 and N2O between ~ 7.5 and 8 microns – Hartmann p.44 and 48, rough est. from graphs; signficant stratospheric transparency remains in several of those bands except near the peak of the CO2 band, but especially water vapor from 25 to 50 microns.)
4 * 100 % / 220 K ~= 1.818 %/K,
1.818 %/K * 37.62 W/m2 = 0.684 (W/m2)/K,
3 (MJ/m2)/K / 0.684 (W/m2)/K ~= 50.8 days ~= 0.14 year (that’s an e-folding time scale). Thinner slices of the stratosphere will have less emissivity but also less heat capacity, with the later diminishing faster until the limit is reached where emissivity can be approximated as linearly proportional to thickness. Thus the relaxation time will tend to be larger for thinner layers – except for changes in % change in emission per K change in temperature. The thinnest layers would depend mainly on CO2 for emission (and absorption).
I don’t think there are any significant optical property feedbacks in the stratosphere that don’t require tropospheric+surface changes – except ozone…
Corresponding time for surface+tropospheric equilibration: given 3 K warming (including feedbacks) per ~ 3.7 W/m2 forcing (this includes the effects of feedbacks):
10 years per heat capacity of ~ 130 m layer of ocean (~ heat capacity of 92 or 93 m of liquid water spread over the whole globe)
Re my 433 – wow, thanks for the clean up! But to clarify, the block quote should follow “http://www.leif.org/EOS/ngeo706.pdf; first paragraph:”, not the RC link.
Back to the matter of stratospheric cooling –
if at some wavelengths, the stratosphere has already reached radiative equilibrium involving a positive lapse rate, then adding a greenhouse gas with absorption at some wavelengths could cause cooling if those wavelengths are long enough or warming if those wavelengths are short enough, relative to the spectrum of preexisting absorption, I think … more later if time allows.
… I need to think about that some more, but a key point is:
IF there is some frequency at which absorption and emission occur within the atmosphere, then above the tropopause, in the approximation of zero convection above the tropopause, radiative equilibrium will require some pattern of vertical variation of the Planck function at that frequency.
With the corresponding temperature variation, and using bandwidths (with constant optical thickness within each band) so that the band-integration of the Planck function is constant at some reference level RL among various possible bands, then, if at some reference frequency, the band-integrated Planck function ‘lapse rate’ crosses 1 W/(m2 sr) at RL and is linear (or in a coordinate system where it becomes linear), then all such band integrated ‘lapse rates’ cross the same value at the same RL, but at shorter wavelengths, the ‘lapse rate’ will be steeper at RL and concave, possibly approaching zero at finite height below TOA, while at longer wavelengths, the ‘lapse rate’ will be less steep at RL and convex.
… Well, some things I’ve come up with (assuming only absorption, no scattering, etc.):
For simplicity, assume all solar heating at the surface (so that the lapse rate is (1-dimensional climate model, radiative convective equilibrium) positive or approaching zero but never negative) unless otherwise stated:
1. A band with optical thickess per unit gas decaying exponentially away from a peak: Assuming the peak is saturated at some level within the atmopshere and there are no other absorbers in the same band of wavelengths above that level, increasing the concentration of that gas will result in at least an instantaneous cooling forcing of the layer above (not necessarily all of the layer, but the instantaneous forcing on the layer as a whole will be negative).
(If there were some prexisting non-CO2 absorption between the level and TOA, than the additional forcing that could be accomplished by doubling CO2 would be reduced, and more so at the lower level than at TOA, thus reducing the cooling effect on the layer from doubling CO2.)
Question – what about where the band isn’t saturated?
Consider:
2a. the saturated portion of the band cannot cause (in instantaneous forcing) cooling and may cause warming of the layer above as a whole (no forcing at the base of the layer, but a reduction in OLR at TOA, thus positive forcing of the layer).
Therefore the part of the band that causes cooling must be outside the central saturated portion.
2b. But is it in the far wings? Maybe not. Adding a small amount of absorption at some wavelengths, the each layer of the atmosphere will absorb a fraction of the radiation from the surface (or lower-atmospheric absorbers not found above some level) and emit twice that fraction of the blackbody value at each level. Thus, this would tend to cause cooling in the lower atmosphere and warming in the upper atmopshere, if the temperature decline from the surface (or lower-level emission sources) to TOA is great enough as determined by radiative-convective equilibrium established by preexisting absorption at other wavelengths.
——-
In general:
3. Adding optical thickness in any band reduces OLR in that band initially.
4. Adding a band with some small optical thickness, the atmosphere as a whole cools towards a skin temperature (except where the troposphere forms); the surface warms slightly, and OLR is enhanced at other frequencies. Adding more optical thickness to the same band reduces OLR in that band, cooling at least some portion of the upper atmosphere up to the TOA level, and increases in OLR outside that band results in some portion of that cooling remaining at full equilibrium (as expained by Andy Lacis). This cooling should be larger if the band is at longer wavelengths (see 438).
5. Increasing the width of a band? Well, if we add atmospheric absorption to wavelengths just outside the first band, there could be initial cooling of lower levels and warming of upper levels as explained in 1b, which will be enhanced if this is added at shorter wavelengths (reduced if addeed at longer wavelengths) relative to where the initial atmopsheric absorption was (see 438). But what happens after that…
6. What happens if we start from scratch and just add a wider band? The same temperature increase at lower levels and increased OLR outside the band will be accomplished at smaller optical thickness within the band, so the OLR reduction within the band should be smaller and thus there will be a warmer upper atmsopherer near TOA for the same surface temperature.
7. However, this doesn’t directly address what happens if a band is simply widenned while keeping the optical thickness within the band constant over wavelength.
Keeping within a sufficiently small range of wavelengths that the effects discussed in 438 can be set aside, What such band widenning would do, without a surface temperature increase, is simply increase the range of wavelengths at which the same temperature variation accomplishes the same spectral fluxes through the band, thus not changing OLR within the band – the warming that results from such band-widenning should thus tend to increase the OLR within the band. So band-widenning would warm the upper atmosphere (note this isn’t the same type of band-widenning as described for a CO2-like band).
RE my 439
(If there were some prexisting non-CO2 absorption between the level and TOA, than the additional forcing that could be accomplished by doubling CO2 would be reduced, and more so at the lower level than at TOA, thus reducing the cooling effect on the layer from doubling CO2.)
(Note that this is supposed to concern the effect of adding (more) CO2 to a preexisting equilibrium condition, so the effect of the non-CO2 absorber (with spectral overlap with CO2 within the layer) on temperature is not the issue. Also, this is assuming CO2 is nearly saturated at the peak of the band at the base of this top layer, however thick that layer is supposed to be (it needn’t just be the stratosphere or be the whole stratosphere).)
Possible exceptions exist. The reduction in CO2-cooling (of a layer between TOA and some other level) assumes the increased downward emission at the base of the layer from the non-CO2 absorber within the layer is greater than the decreased OLR at TOA, which is the absorption of radiation from below the layer minus the emission from the layer reaching TOA (refering to the ‘baseline effects’ that would remain if the preexisting CO2 were removed).
For a small amount of absorption, the emission upward and downward would be about the same, so if the upward (spectral) flux from below the layer were more than 2* the (average) blackbody value for the layer temperature(s), the OLR at TOA would be reduced more than the net upward flux at the base of the layer, decreasing CO2 TOA forcing more than CO2 forcing at the base, thus increasing the cooling of the base. Interestingly, in that situation, the non-CO2 absorption within that layer would itself be making the layer warmer than otherwise by absorbing more radiation than it emits. If the blackbody flux of the layer were greater than twice the flux from below, the non-CO2 absorption would tend to cool the layer and reduce the cooling that additional CO2 would accomplish.
If there is some greater amount of non-CO2 absorption, then assuming a positive lapse rate, the decrease in the net upward flux at the base of the layer (from emission from the layer) would be greater than the increase in OLR from TOA from emission from the layer, thus shifting the cutoff between CO2-cooling/non-CO2 warming and the reverse towards a smaller flux from below relative to the average blackbody value for the layer.
———-
To summarize (with the simplifying assumptions of zero non-Planck feedbacks, a perfect blackbody surface for LW, and that all solar heating is at the surface, or at least beneath the tropopause – which is not to say that none of this applies to all other cases):
Starting with zero atmospheric LW absorption, adding any small amount cools the whole atmopshere towards a skin temperature and warms the surface – tending to produce a troposphere (the forcing at any level will be positive, and thus will be positive at the tropopause; it will increase downward toward the surface if the atmosphere were not already as cold as the skin temperature, thus resulting in atmospheric cooling toward the skin temperature; cooling within the troposphere will be balanced by convective heating from the surface at equilibrium, with that surface+troposphere layer responding to tropopause-level forcing.)
In the grey gas(and cloud) case, subsequent addition of absorbing substances reduces OLR initially, but OLR must return to the original value at full equillibrium, so there is a cooling at and near TOA that is temporary. Starting with small amounts of absorption, the transient cooling should extend through most of the atmosphere (except the troposphere) because each layer’s emission and absorption of radiation from the surface would increase equally if not for the increased absorption of radiation from the surface by lower layers, while the increased absorption of radiation from other layers would be a smaller effect due to the small emissivities – this would be true in the troposphere as well except the convective coupling with the surface would prevent it. With larger optical thicknesses, the transient cooling would be more restricted to near TOA.
——-
Refering to bands where optical thickness is constant over the interval of each band, if the atmospheric LW absorption is limited to some band (that doesn’t cover all LW radiation), than increases in OLR in response to surface warming will occur outside that band, so OLR will drop within the band – there will still be some portion of stratospheric or near-TOA cooling that will be transient, but some will remain at full equilibrium.
Widening such a band while holding spectral optical thickness constant within the band will tend to warm the surface+troposphere and the stratosphere and TOA in general because the widenning would not have any forcing effect on layers of air (except for the Planck function’s temperature and wavelength dependence) but will have a positive forcing at the surface, and some of increased upward flux from the surface+tropospheric warming will be absorbed within the band and increase emissions farther up, or else directly increase OLR within the band.
——
Competing bands
With one band (along with the convective lapse rate below the tropopause) establishing the atmospheric temperature profile, adding some other band of absorption may result in some different pattern of temperature change.
In full equilibrium, at any given level, there may be some net radiative heating at some frequencies compensated by some net radiative cooling at other frequencies, with convection balancing the full spectrum radiative cooling of the troposphere and heating of the surface.
Radiative equilibrium at small LW optical thickness occurs when the whole atmosphere has a temperature such that the Planck function is about half of that of the surface (a skin temperature), whereas at larger LW optical thicknesses, the equilibrium profile has a signficant drop in the Planck function through the atmosphere, approaching half the OLR value at TOA and approaching the surface value towards the surface – of course, convection near the surface will bring a closer match between surface and surface-air temperatures.
The ability of a band to shape the temperature profile of the whole atmosphere should tend to be maximum at intermediate optical thicknesses (for a given band width), because at small optical thicknesses, the amounts of emission and absorption within any layer will be small relative to what happens in other bands, while at large optical thicknesses, the net fluxes will tend to go to zero (except near TOA and, absent convection, the surface) and will be insensitive to changes in the temperature profile (except near TOA), thus allowing other bands greater control over the temperature profile (depending on wavelength – greater influence for bands with larger bandwidths at wavelengths closer to the peak wavelength – which will depend on temperature and thus vary with height.
—
Thus, adding absorption to some new band will initially tend to warm the colder upper atmosphere and radiatively cool the lower atmosphere and warm the surface (The forcing at any level will be positive, so the surface+troposphere will warm; if some of the increased flux escaping in parts of the spectrum where the abover layers have sufficiently small optical thickness, some of the upper-level cooling will persist. This also depends on how stratospheric absorption and the change in upward flux from below are distributed over the spectrum.)
As more optical thickness is added to a ‘new’ band, it will gain greater control over the temperature profile, but eventually, the equilibrium for that band will shift towards a cold enough upper atmosphere and warm enough lower atmosphere and surface, such that farther increases will cool the upper atmosphere or just that portion near TOA while warming the lower atmosphere and surface – until the optical thickness is so large (relative to other bands) that the band loses influence (except at TOA) and has little farther effect (except at TOA).
The peak upper level warming that occurs as optical thickness in a ‘new’ band is increased should be larger for a wider band, as it can gain greater dominance over controlling the temperature profile at smaller optical thickness and will have a greater peak in it’s influence.
——-
The equilibrium profile for each band varies over wavelength at the same optical thickness, with larger temperature variations at longer wavelengths. Thus, among competing bands, there may be net radiative cooling in the upper atmosphere or near TOA at longer wavelengths and net heating and shorter wavelengths. The heating of the upper atmosphere and radiative cooling of the lower atmosphere by introducing some small amount of absorption in a ‘new’ band should be enhanced at shorter wavelengths relative to the bands that are/were controlling the profile, and reduced by the opposite arrangement. Less TOA cooling will occur if bands are placed where, in the upper atmosphere or near TOA, they absorb more of the increases in radiation from below from surface+tropospheric(+lower stratospheric) warming.
Question: if the bands controlling the profile are at short enough wavelengths, could adding a ‘new’ absorption band at long-enough wavelengths result in initial cooling of the upper atmosphere? AT sufficiently short wavelengths, the temperature of the upper atmosphere and near TOA would have to be a sizable fraction of the surface temperature in order for the Planck function for higher levels to be a small fraction of the that at the surface (example: at 5 microns, relative to T = 250 K and the Planck function at 250 K, a 20 % reduction in temperature reduces the Planck function by about 94.4 %). At much longer wavelengths, given the surface temperature (which won’t change much by introducing a small amount of absorption), the skin temperature would only be a bit more than half of the surface temperature (example: for a surface temperature of 250 K and a small amount of atmospheric absorption at 200 microns, the skin temperature would be about 56 % of the surface temperature) , which could be less than the temperature even at TOA. So yes, if the profile is originally controlled at sufficiently short wavelengths, introducing some optical thickness at sufficiently long wavelengths would tend to cool the entire atmosphere (above the tropopause, of course). Of course, going to extremes of the spectrum reduces the strength of the effect of a band even if band width extends toward infinity.
——-
Some 1-dimensional radiative-convective equilibrium temperature profiles are shown in Hartmann (Global Physical Climatology) in Chapter 3. Interestingly, going from (among H2O, CO2, and O3) only H2O vapor to H2O+CO2, there is stratospheric warming.
Perhaps this is because of the band-widenning (of the type refered to above) effect, with the initial introduction of some CO2 causing some upper level warming (enhanced by the shorter wavelengths of the CO2 band relative to stratospheric water vapor given the cold temperatures (lack of importance of the ~ 5 to 7 micron band (?)- The cold upper troposphere affects the flux coming up from the troposphere+surface, so the shorter wavelengths have less influence in both absorption and emission within the stratosphere). This doesn’t contradict the argument that, given present amounts, doubling CO2 should cause stratospheric cooling even without solar heating of the stratosphere (with the effect in the far wings being the opposite, and with the effect at the center of the band being restricted towards TOA).
Adding O3 causes much more warming, especially of the upper stratosphere. Interestingly, there is a part of the lower stratosphere where (according to the graphs shown in Hartmann) O3 causes more heating by LW absorption than by SW absorption. Because the O3 mixing ratio rises going into the stratosphere, the ozone layer can absorb some radiation coming directly from signficantly lower and warmer layers and the surface. The upper part of the ozone layer contributes to net LW cooling there – of course, this includes the effect of solar heating on the stratospheric lapse rate.
Also, though, CO2 does absorb a little solar radiation, which would also contribute to the stratospheric warming (second to last paragraph of previous comment) and generally reduce the stratospheric cooling of farther increases in CO2.
Patrick 027,
If you are willing to take a few CO2 questions off forum you can contact me at: burt3845@gmail.com
I would appreciate your response. Thank you
Re my 441 – competing bands – To clarify, the absorption of each band adds to a warming effect of the surface+troposphere; given those temperatures, there are different equilibrium profiles of the stratosphere (and different radiative heating and cooling rates in the troposphere, etc.) for different amounts of absorption at different wavelengths; the bands with absorption ‘pull’ on the temperature profile toward their equilibria; disequilibrium at individual bands is balanced over the whole spectrum (with zero net LW cooling, or net LW cooling that balances convective and solar heating).
(Refering to zero direct solar heating of the air, or at least of the stratosphere:)
The effect where, adding a ‘new’ absorption band and increasing the absorption, there may initially be warming of the colder layers, etc, followed by a stage of upper level or near-TOA cooling – this includes the warming from absorption from increased radiation from the surface+troposphere – which will be greater when more of the spectrum, especially near wavelengths where the emitted spectral flux change is greatest, has a greater amount of absorption. So if more of the spectrum has some amount of absorption, or if absorption is being added to a wider band, etc, it makes sense that the stage of warming of the coldest layers should be prolonged, with greater peak warming of those layers occuring before cooling would take over with farther increases in absorption. If absorption is being added to the most transparent bands, this will eventually bring the situation toward a grey-gas case, and thus cooling of upper levels shouldn’t tend to occur.
(PS in the grey gas case, the whole atmosphere warms with increases in optical thickness, except at TOA; all the same temperatures are found but they are found at higher levels in the atmosphere closer to TOA.)
—–
This link may have been given somewhere above but it deserves emphasis and can illustrate the ‘competing bands’ effect.
http://www.atmosphere.mpg.de/enid/20c.html
See Fig 3 – note that even for well-mixed gases, vertical optical thickness is not proportional to the vertical scale here – it would be proportional to pressure to a first approximation, though there are variations in line broadenning and line strength with height. O3 mixing ratio peaks in the upper atmosphere; water vapor mixing ratio declines from the surface to the tropopause, so that at wavelengths with sufficiently low water vapor optical thickness, LW cooling from water vapor is found at lower levels in the atmosphere.
It must be kept in mind that solar heating of the air is included in this diagram; their is some net LW cooling that balances solar heating above the tropopause, which peaks around the relatively warm stratopause, in bands with sufficient optical thickness. Radiation from this warmer region can contribute to net heating (or reduce net cooling) above and below.
There is cooling (from water vapor) at longer wavelengths even in the cooler layers, which can be explained at least in part by the wavelength dependence of the Planck function’s dependence on temperature.
The most optically thick wavelengths in the upper atmosphere contribute to strong cooling even at 0.1 mb, while less optically thick bands contribute to warming or less cooling at that level.
The warming effect near the tropopause level from CO2 can be explained by the relatively sharp change in the lapse rate. O3 in the lower stratosphere can of course absorb radiation coming from the lower warmer parts of the troposphere and surface.
Cont. from my 443 above –The warming effect near the tropopause level from CO2 can be explained by the relatively sharp change in the lapse rate.
Two points on that:
1. A sharp change in lapse rate will (absent sharp changes in optical thickness per unit distance, which occurs at TOA and at the surface even in wavelength bands dominated by well-mixed gases) tend to differ from radiative equilibrium – the inflection point may correspond to a maximum deviation from radiative equilibrium if the radiative equilibrium profile has some intermediate lapse rate in that vicinity.
2. When optical thickness is large, the net flux will tend to be small, but the flux will vary with lapse rate (according to the corresponding Planck function ‘lapse rate’) and a sufficiently sharp change in that lapse rate could lead to some significant flux convergence or divergence at that level (net radiant heating or cooling).
There is a small amount of warming in the short-wavelength wing of the CO2 band in the lower stratosphere. I would expect that absent solar heating of the ozone layer, the positive lapse rate of the stratosphere may displace this warming upward and the coolness of the upper stratosphere would make it extend upward and be stronger, and perhaps also appear on the other wing of the CO2 band. (If solar heating were absent, radiant cooling near 1 mb would be reduced in general.)
If the CO2 optical thickness in the center of the band is so large, how can there be so much cooling at the 1 mb level in the center of the band, not just in between the peak and wings? Aside from variations in line strength and line broadenning with height, their is the important point that, relative to the mass path of CO2 (distances measured in terms of kg per unit area), temperature variations at those heights occur over small scales.
Recap and some additional points:
In the tugging on the temperature profile (by net radiant heating/cooling resulting from radiative disequilibrium at single wavelengths) by the absorption (and emission) by different bands, the larger-scale aspects of the temperature profile will tend to be shaped more by the bands with moderate amounts of absorption, while finer-scale variations will be more influenced by bands with larger optical thicknesses per unit distance (where there can be significant emission and absorption by a thinner layer). Near TOA, the bands with largest optical thickness per unit distance will have greatest control over the the temperature.
Absent direct solar heating of air and absorption in other bands, when absorption in a band is increased, OLR (at TOA, as well as net upward fluxes at any level (including convection, etc, where that occurs)) would be kept constant following equilibrium if the response were limited to that band; the increased emission at other wavelengths in response to warming at lower levels removes some of upward flux from that band at higher levels (including OLR), thus reducing absorption and leading to cooling near TOA or over some uppermost layer upper in general, depending. But if the optical thickness in that band is sufficiently smaller than in another band (depending on wavelengths), adding some absorption to the optically-thinner band would tend to result in warming of the colder layers (as there would be less temperature variation over height in radiative equilbrium for that band, given the same surface(+tropospheric) temperatures.
What happens when more optical thickness is added to the thickest bands? Then OLR tends to be displaced toward other bands, which don’t have as much influence on temperature near TOA.
What happens to OLR when optical thickness is added to other bands? There would fraction of the increase in emission from warmed lower layers that would pass through all bands, and given all other bands have the same absorption as before, the portion of OLR originating from warmed layers would be displaced from the band with added optical thickness to all other bands, though it would cause smaller changes (depending on wavelength) to OLR in optically-thicker bands; nonetheless OLR would not be reduced in the optically thicker bands from that effect along, it would only be reduced in the band where optical thickness was added. However, some of the OLR and upward fluxes in upper levels in general come from other levels, especially in optically-thicker bands. If the addition of optical thickness to some band is able to sufficiently cool the uppermost layers sufficiently, OLR would be reduced in the optically thicker bands as well; if warming occurs in uppermost layers, OLR would increase in the optically thicker bands. OLR increases in the optically thinner bands would lead to atmospheric warming in general, but this has to be accompanied by OLR decreases somewhere, such as in optically thicker bands (and always in the band where optical thickness was added, assuming positive lapse rates everywhere as is the case in a 1-dimensional equilibrium model with zero solar heating above the tropopause, or at least not too much solar heating in some distributions), which will tend to cause cooling of upper levels.
Re 442 burt – it seems like the conversation here is just a trickle now, so would you like to post your questions here?
OLR increases in the optically thinner bands would lead to atmospheric warming in general – bands that are thin but not transparent.