The “zoo” of global sea level curves calculated from tide gauge data has grown – tomorrow a new reconstruction of our US colleagues around Carling Hay from Harvard University will appear in Nature (Hay et al. 2015). That is a good opportunity for an overview over the available data curves. The differences are really in the details, the “big picture” of sea-level rise does not change. In all curves, the current rates of rise are the highest since records began.
The following graph shows the new sea level curve as compared to six known ones.
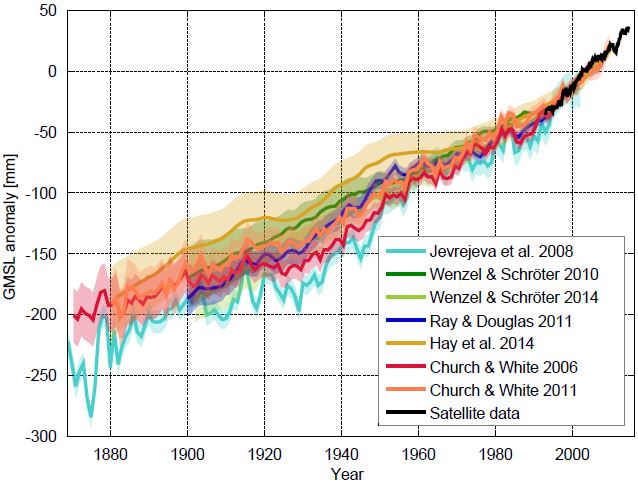
Fig 1 Sea level curves calculated by different research groups with various methods. The curves show the sea level relative to the satellite era (since 1992). Graph: Klaus Bittermann.
All curves show the well-known modern sea level rise, but the exact extent and time evolution of the rise differ somewhat. Up to about 1970, the new reconstruction of Hay et al. runs at the top of the existing uncertainty range. For the period from 1880 AD, however, it shows the same total increase as the current favorites by Church & White. Starting from 1900 AD it is about 25 mm less. This difference is at the margins of significance: the uncertainty ranges overlap.
It is also interesting to compare the rates of sea-level rise.
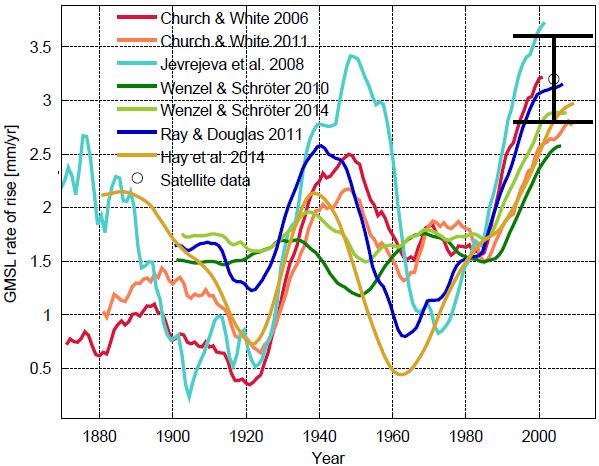
Fig 2 Rates of sea-level rise calculated from the curves in Fig. 1. To calculate the rate of increase, sea level curves were first smoothed with a filter of half-width 15 years and then differentiated. Graph: Klaus Bittermann.
The graph shows that the rates vary over time and also differ between the curves. All reconstructions agree on one point: the rate of rise in the last two decades (about 3 cm per decade) is the highest on record. Hay et al. find that the acceleration of sea-level rise since 1900 AD is larger than in previous reconstructions, but it has been generally questioned whether the quadratic acceleration (derived from a parabolic fit) is a useful number in cases where a parabola doesn’t fit the data well (Rahmstorf and Vermeer 2011, Foster and Brown 2014). Taking a step back, in my view the “big picture” on acceleration is that we have moved from a stable preindustrial sea level to one now rising at 3 mm/year (see Fig. 1 here). The differences between the quadratic acceleration numbers come from differences in the decadal to multidecadal variability in the curves which I don’t consider very robust (we have shown in Rahmstorf et al. 2012 how strongly these can be affected by a small amount of “noise” in the sea-level data).
Why are there at all different reconstructions of the global sea level history? The reason lies in the challenge to calculate global sea level as accurately as possible from a suboptimal data base. Different research groups have developed different approaches for this.
The data problem looks like this:
- Tide gauge measurements are not available in sufficient number (especially in earlier times) and not distributed evenly over the oceans: the Northern Hemisphere, for example, is strongly over-represented and tide gauge stations are located along the coasts.
- Many of the time series have data gaps.
- Tide gauges (unlike satellites) measure sea level relative to the land, so these data are ‘contaminated’ by land uplift or subsidence.
A particular challenge is posed by the positioning of the gauges along the coasts, because coastal sea level can be affected by local effects such as the wind piling up water against the shore. Variability in the prevailing winds (which can extend over decades, England et al. 2014) will therefore lead to variability in the water level along the coasts – but of course we know that the wind cannot change global sea level at all as it merely redistributes the water. Nevertheless such variability induced by winds or currents may give a false impression of global sea level fluctuations in analyses of tide gauge data.
The new reconstruction of Hay et al. is an important addition to the body of sea-level work, coming from top experts. But is it better than previous ones? Which of the curves shown is “the best” is not easy to assess. No one knows the exact true sea-level evolution – so we have to consider what methodology is likely to be the most appropriate to cope with the challenges mentioned. I hope that the authors and other experts might stop by here at Realclimate for a discussion of the advantages and drawbacks of the different methods.
The until now widely favored method of reconstruction is that of Church & White (2006 and updated 2011). It uses the satellite data of sea level to determine the typical variability patterns of the sea surface and thus to establish the link between the locally measured tide gauge values and the global sea level. The big advantage is that one does not need questionable assumptions to extrapolate from the measurements on the coasts into the open ocean, but that empirical data on the actual relationship are used. The disadvantage is that unfortunately the satellite data exist only for about twenty years. This method thus relies on the relationship between sea level on the coast and in the rest of the ocean having remained essentially unchanged.
The new reconstruction of Hay et al. uses statistical methods for dealing with incomplete data which have already proven their worth in other applications. In addition, it also uses knowledge about the physics of sea level rise: it determines the components of the global sea-level rise (e.g. the contribution from ice melt in Greenland and Antarctica) taking into account the knowledge about the spatial pattern, the so-called ‘fingerprint’ associated with each of these components. On the other hand, it does not explicitly take into account the specific patterns of natural variability caused by winds or currents that can masquerade as a false global signal (as described above).
Hay et al perform a test in which they take their reconstruction as “truth” and see how well the method of Church & White performs in reproducing it. They find it to be biased high, although the obtained sea level trend in this case is lower than in the real Church & White reconstruction and fully encompasses the hypothetical “true” range. Although this is an important test, it is thus not entirely conclusive, also considering that it was performed just on one particular sea level pattern (that reconstructed by Hay et al.) so it would be premature to conclude that the method is biased high in general.
To sum up, in my view the strength of the method of Hay et al. is that it uses the expected “fingerprints” of the global warming signal, while the strength of Church & White is to take into account the empirical patterns of natural variability. Ideal would of course be a combination of both, and this could be the next step for further research. Ultimately, it is not clear down to what level of accuracy we will ever know the sea level evolution over the past hundred years or so. But for practical purposes, I don’t think it matters whether the rise from 1900 AD has been 3 centimetres more or less. I do not think this changes our outlook for future sea-level rise in any significant way.
References
- C.C. Hay, E. Morrow, R.E. Kopp, and J.X. Mitrovica, "Probabilistic reanalysis of twentieth-century sea-level rise", Nature, vol. 517, pp. 481-484, 2015. http://dx.doi.org/10.1038/nature14093
- S. Rahmstorf, and M. Vermeer, "Discussion of: Houston, J.R. and Dean, R.G., 2011. Sea-Level Acceleration Based on U.S. Tide Gauges and Extensions of Previous Global-Gauge Analyses. Journal of Coastal Research, 27(3), 409–417", Journal of Coastal Research, vol. 27, pp. 784, 2011. http://dx.doi.org/10.2112/jcoastres-d-11-00082.1
- G. Foster, and P.T. Brown, "Time and tide: analysis of sea level time series", Climate Dynamics, vol. 45, pp. 291-308, 2014. http://dx.doi.org/10.1007/s00382-014-2224-3
- S. Rahmstorf, M. Perrette, and M. Vermeer, "Testing the robustness of semi-empirical sea level projections", Climate Dynamics, vol. 39, pp. 861-875, 2011. http://dx.doi.org/10.1007/s00382-011-1226-7
- M.H. England, S. McGregor, P. Spence, G.A. Meehl, A. Timmermann, W. Cai, A.S. Gupta, M.J. McPhaden, A. Purich, and A. Santoso, "Recent intensification of wind-driven circulation in the Pacific and the ongoing warming hiatus", Nature Climate Change, vol. 4, pp. 222-227, 2014. http://dx.doi.org/10.1038/nclimate2106
- J.A. Church, and N.J. White, "A 20th century acceleration in global sea‐level rise", Geophysical Research Letters, vol. 33, 2006. http://dx.doi.org/10.1029/2005GL024826
- J.A. Church, and N.J. White, "Sea-Level Rise from the Late 19th to the Early 21st Century", Surveys in Geophysics, vol. 32, pp. 585-602, 2011. http://dx.doi.org/10.1007/s10712-011-9119-1
Just eyeballing it, there appear to be differences in the rate of change graphs from the IPCC AR5 graph 13.7 and the graph shown here. For example Church and White 2011 in AR5 shows ~2.3mm yr-1 in 1945, 1975, and 2000. This doesn’t match. The end points are also different.
https://www.realclimate.org/images//IPCC_AR5_13.7ab.png
The acceleration from 1920 to 1940 looks even higher than recent data. What is the explanation for this older acceleration and how much of this same effect may be happening again on ~60 year cycle (AMO?) versus temperature induced changes in sea level?
It appears the rates are decelerating recently. If there is a 60 year signal here, it would seem like you would want to measure change in rates as peak to peak from 1940 to 2000 versus a (1960 to 1980) vs (1980 to 2000) which would not be representative due to the multi-decadal cycle.
[Response: The IPCC used a different method to compute the rates of rise, if I remember correctly they use overlapping 18-year linear trends. For various reasons we prefer the method of Wahl et al. (Ocean Dynamics 2010) – see also response to comment 5. Regarding the supposed 60-year cycle, I am highly sceptical of that as discussed earlier at Realclimate. Btw., you can find stuff like that by entering a search term like “60-year cycle” into the Realclimate search window… -stefan]
Great material … I’m especially glad to see both the overall curves and the rate curves. Our visual systems are a lot better at comparing level differences than they are at comparing slopes of wiggly diagonal lines.
They may also add insight into the relative plausibility of the different curves.
Why sea level rise is expected to be nonlinear? I understand it is difficult to sell 30 cm/century figure as alarming, which motivates for search for “acceleration”. However, here is simplistic argument why sea level rise is linear, at best. The economy grows exponentially, roughly 2-4% in the West, and 10% in the East. Hence notorious exponential atmospheric CO2 concentration curve. But then, the greenhouse effect is logarithmic. So temperature rise is linear, and consequently sea level rise.
[Response: The flaw in your argument is the long response time of sea level. Let’s assume temperature will remain constant from now on. Will sea level remain stable? Of course not, the rise will continue approximately at the current rate, as e.g. the ice sheets will continue to melt due to the elevated temperature – it takes hundreds if not thousands of years until they have finished this response to the past warming. If temperature rises further, the rate at which the ice melts – and hence the rate of sea-level rise will increase. -stefan]
Figured out the answer — ln(2*exp(x)) = x^2. So polynomial growth (but not exponential) is possible even with those simplistic assumptions.
> 1920 to 1940
Looking at what was happening in the background can add an interesting perspective to this sort of thing.
Fishing boomed from 1920 to 1940, a huge run-up in harvesting — then crashed during the world war.
https://www.google.com/search?q=fisheries+recovery+during+“world+war+II”
Fish and whale numbers rebounded dramatically for the six year period (and remember that was species that came to sexual maturity quickly, many other species would only have begun to rebound in that brief time).
We don’t have good information on the base of the food chain for most of the past — that’s just “noise” but now that we start having ways to track trends in primary productivity — what’s being made out of sunlight, water and CO2, by which organisms, and how fast do their populations change (remembering that some plankton populations turn over a new generation in a couple of weeks so relative numbers of different species can change that fast across the oceans).
http://journals.plos.org/plosone/article?id=10.1371/journal.pone.0110355
This is amateur kibitzing on my part but I think it’s very interesting to look at the climate as an outgrowth of Earth’s biology — mostly oceanic biology — which we’re barely beginning to do.
I think I lost an attempted comment; briefly:
> 1920 to 1940
https://www.google.com/search?q=fisheries+recovery+during+%22world+war+II%22
It looks as if the rate-of-rise graph stops at about 2003. Has the rate remaind stable now at about 3 mm/yr over the last ten years or so? Or has the rate continued to increase?
[Response: The rate-of-rise graph is the derivative of 15-year averages, so the midpoint of the last data point is 7.5 years before the end of the data (in some cases, 2010).–eric]
[Response: I hate to say it Eric, but in this case you are wrong (thanks for trying to respond anyway). The actual sea level curves have been smoothed with an SSAtrend filter which has a full width of 30 years, but since the weights of the filter decline away from the central point I cited the half-width – this is like citing an effective width for a Gaussian weighting curve. The filter can produce smooth sea-level curves which are as long as the original unsmoothed curves so it does not end before the original data, and you can see the rate curves go as far as the sea level curves in Fig. 1. Of course the treatment of the end points where data are not available across the full filter width introduces some uncertainty. Luckily this is not a big issue here because the rate at the end, for the last 20 years, we know very well from the satellite data. If one wants to discuss changes in rate within the past twenty years one should really only use the satellite data for that and not the rate curves from the tide gauges shown here. -stefan]
For public consumption, it would be nice have a clean line, but one that can be justified. I would suggest the median of the 7 estimates for each year. Why do the Wenzel & Schroter estimated trends differ in the early years from the others?.
t marvell (5)
As far as I can tell (having read the papers and discussed this with one of the authors) part of the technique Wenzel and Schroter use is to fill the early part of the shorter (nearly always later) records with a linear fit to the existing data – this tends to damp down the variability early in the 20th century, leading to the straight lines/smaller variability earlier in the century in both figures.
One could also argue that the variability in the early part of the century in some of the other time series is too large because of the increasingly sparse data distribution as we go back in time. Some of the estimates have error bars that take this into account. Some don’t. I think it would be interesting to see versions of these figures that only use time series with believable error bars!
Neil
Wili #4 said…It looks as if the rate-of-rise graph stops at about 2003. Has the rate remaind stable now at about 3 mm/yr over the last ten years or so? Or has the rate continued to increase. Wili, I believe the Purkey & Johnson 2014 said 3.4mm. and then we have the following paper.. http://www.atmos.washington.edu/~bitz/514_2013/RecentChangesInGreenlandAntarctica_2013.pdf
Hi Carling, Eric, Bob and Jerry – nice work and very interesting paper! I hope you will join the discussion to better understand the method and differences especially compared to Church & White. Towards this I’d love to see these two tests:
(1) Run your reconstruction method with exactly the same tide gauges as used by Church & White, to see what part of the difference is due to analysis method and what part due to different input data.
(2) You used your reconstructed field as “truth” to test how the Church&White method performs with that. What do you get when you use their reconstruction as “truth” and test how your method performs on that?
Also it would be great to see a map of the different trends in order to understand the regional structure of the differences!
Cheers, Stefan
If I understand correctly, both methods try to calibrate their tide gage data by comparing with the satellite data. And all the non-satellite data has trouble to cope with water being moved around by wind and weather, which can also have effects on time scales as long as those for which we have satellite data.
.. wouldn’t that mean that there is a nearly irreducable systematic effect due to weather & wind pushing around the oceans in the satellite era? The only way to correct for that would be if there are trustworthy models for describing these movements of ocean water in the satellite era.
I’m also very curious if there is an explanation for those periods with a ‘hiatus’ in sea level rise. Are those real, or is there an instrumental explanation?
According to all the curves going back that far, sea levels appear to have begun their rise sometime around 1880. Is there any evidence that worldwide fossil fuel emissions would have been high enough at that early date to already be affecting sea level? And if, as Stefan reminds us above, there is a considerable delay between atmospheric warming and sea level rise, that means FF emissions would have to have been warming the atmosphere to a considerable extent already by mid 19th century or earlier. Does that seem likely?
[Response: Given the multi-decadal variability you can’t really tell when a significant rise above the noise started. Also I don’t believe all this multi-decadal stuff is real global sea level change, rather than data noise. The problem is much worse furthest back in time when there is few tide gauges. -stefan]
Interesting article. But a minor point — I wonder if there is a typo in your first paragraph. You write “Up to about 1970, the new reconstruction of Hay et al. runs at the top of the existing uncertainty range.” OK, I see that, so I guess I’m looking at what you are looking at. But then, next sentence: “For the period from 1880 AD, however, it shows the same total increase as the current favorites by Church & White.” Did you mean 1980 and not 1880? And the following sentence: “Starting from 1900 AD it is about 25 mm less.” Did you mean 2000 AD and not 1900 AD? Are these typos, or am I missing something — wouldn’t be the first time (or do I just need to clean my glasses?).
[Response: I meant it as I wrote it – not sure what is unclear for you? -stefan]
You imply the satellite data does not suffer uncertainty with respect to local conditions like the tide gauges do. How do we know the elevation of the satellite? Is it referenced to some land-based point? If so the satellite data would be subject to those local conditions. How is the change in satellite elevation reflected in its data? Does it have perfect elevation or one at least below the margin of error? These are questions that popped up as I read this good summary article. Thank you.
I see 3.2 +/- 0.4 mm/yr in Purkey(2014), and Hay(2015) gives 3.0 +/- 0.7 mm/yr, so they agree to within error.
Stefan, there are possibly two sources of my confusion. First, when you write “Up to about 1970” I can read that as incorporating “the period from 1880”, and I can read “the period from 1880” as incorporating the period “Starting from 1900.” But you are treating these as 3 distinct periods. Perhaps if you included both start and end dates for the periods you are comparing I would have seen it more clearly. Also, it may be possible that I am confusing the colors — the color for the Hay curve is somewhat similar to the color for the Church&White 2011 curve (at least on my screen). Or perhaps I am missing something else.
[Response: I see. When saying “up to about 1970” I am talking about where the curve runs – Hay is the uppermost. After that I am talking about the total rise from 1880 to present (which is the same in Hay and Church&White) and from 1900 to present (which is about 25 mm less in the former because in 1900 Hay is about 25 mm above Church&White, as you can see in the graph. -stefan]
BobR (#13)
Answers to some of your questions are here: http://www.cmar.csiro.au/sealevel/sl_meas_sat_alt.html
The satellite altimeter data is referenced to an ellipsoid, which is, in turn, referenced to the centre of the Earth, so the satellite altimeter data is, effectively, referenced to the centre of the Earth.
> How do we know the elevation of the satellite?
Triangulation from known points, using the speed of light and accurate clocks. Same method the GPS system uses.
Do you now how long a nanosecond is, physically?
That is, how far light travels during that time?
This far: http://highscalability.com/blog/2012/3/1/grace-hopper-to-programmers-mind-your-nanoseconds.html
In case that link failed, try this one:
http://3.bp.blogspot.com/-zH99SS8Ga0U/Ta36kWgQM0I/AAAAAAAABAs/k6WOz2POw5k/s1600/Nano+hanger.jpgIf you look sideways at the curves of Figure 1 you can discern an acceleration of the rate of sea level rise. This is also apparent in Figure 2. If that acceleration trend continues unabated, through any significant portion of the planet’s ice sheets, then we could lose all seaports (like NYC, Boston, Seattle) and coastal communities, natural and man-made.
Seems like a serious national, and international, security threat to me (as in “clear and present danger”).
Also for BobR — the other important part of how the satellites are located precisely is, many measurements, not only one.
Each individual measurement has some error. If we only had one thermometer, or one satellite altimeter, we’d be limited to that single instrument’s error limits.
Someone with better and newer statistics than I have should explain how accuracy goes up with more measurements — explain it better — it’s a basic tool much used and the reason it works isn’t easily obvious without Stat 101.
> someone
Oh, yeah, it’s 2014.
You can just ‘oogle it:
https://www.google.com/search?q=how+does+taking+more+measurements+increase+accuracy
Hi, everyone!
Responding to Stefan’s response to Wili: I’m not sure I agree that one should always use satellite data over the last 20 years instead of tide gauge data. It depends on the question. Satellite data are denser, but they have different data gaps; for example, they don’t exist in the polar regions, where some of the biggest effects associated with the proximity of shrinking land ice sources occur. They also measure a slightly different vaeiable: sea surface height (aka geocentric sea level, ie the height of the sea surface relwtive to the planet’s center of gravity, rather than sea level proper, aka relative sea level, ie height of the sea surface relative to the solid Earth). Satellite data are better for some questions, but if you want to compare sea level over the last 20 years to earlier sea level, I think you’re actually better off not changing your metric (or using a statistical method that incorporates both and recognizes fhe differences between them).
Stefan: good suggestions in #11. We are working on a reconstruction using only Church & White’s tide gauges, and I’ll have to think about the idea of using their EOF reconstructions. We are preparing to deposit all 622 of our tide gauge reconstructions, and intend to generate some maps when we write the data descriptor.
Nichol: we don’t use satellite data in our calibration. Our physical patterns are based on the physics of glacier/ice sheet melt (static equioibrium fingerprints), glacial isostatic adjustment models, and an ensemble of GCMs to inform the ocean dynamic contribution.
Hank (#22),
It is pretty easy to see why taking many throws of a die can suss out if the die is weighted much better than taking just a few.
This study: http://www.ocean-sci-discuss.net/11/2029/2014/osd-11-2029-2014-print.pdf seems to be going around the denialosphere, where they are claiming it shows that there is no acceleration in the rate of slr. (Interestingly, even that claim implies that they accept that there _is_ some sea level rise.)
They point especially to the right-hand graph in figure 10 (page 2069) as showing a possible recent _decrease_ in rate of slr in the last decade or so. I’m afraid I’m a bit out of my depth in pointing out what might be wrong with this. What exactly _is_ that graph measuring?
It seems to me that this is too short a time frame to tell us much. And it also conveniently (for denialists) apparently ends at 2011 when there was an anomalous drop in sea level because so much of it ended up temporarily on land as deluges in Australia and a few other places.
But I don’t feel particularly confident in assessing this study. Any help would be most appreciated.
Message: The new analysis “suggests that the acceleration in the past two decades is 25 percent higher than previously thought,” Carling Hay
I should note one element of the paper not highlighted in this write-up: the closing of the 1901-1990 sea-level rise budget. In ch. 13 of IPCC AR5 WG1, the authors note that the two reasonably well-modeled components of the sea-level budget — thermal expansion and glaciers — add up to about 1.1 mm/y. Given the previous sea-level trend estimate of about 1.5 mm/y, there is a gap that requires either that these two components both be at the high end of projections or that there is a significant contribution from Antarctica and/or Greenland. The lower trend found by our study is consistent with the median projected sums of thermal expansion and glacier mass loss, implying that no net contribution from polar ice sheets is needed over 1901-1990. By contrast, there is of course a significant contribution over the past 20 years, observed directly and seen (along with greater thermal expansion) in the ~3.0 mm/y rate of rise over 1993-2010.
It seems to me that the biggest difference between the new GMSL curve and most of the others is the flat spot in the new curve from about 1950 to 1970. This more-or-less corresponds to the flat spot in the global-mean temperature series. There is a belief in some quarters that the sea level generally lags behind global-mean temperature.
If you were to replace that bit of the new curve with a section with the same slope as many of the others then all of the curves would more-or-less lie on top of one another.
Many of the other curves have a jump up in the late 1950s, which contributes to the slope over this time span, whereas the Hay et al curve doesn’t. There are jumps in a number of tide gauge records at this time, probably partly related to an El Nino event.
Some other shorter time series (e.g. Holgate and Woodworth, 2004: http://onlinelibrary.wiley.com/doi/10.1029/2004GL019626/full) also show a fairly steep increase in GMSL over this period. This study uses a fairly simple tide-gauge averaging technique.
Why is the Hay et al GMSL curve so flat through this period?
[Response: Hi Neil, I noticed the same thing and wondered whether a “flat bit” can indeed shift the whole curve thereafter – this would be the case if the method reconstructs sea-level increments from the data and then produces the proper sea-level curve by time integration. An equation shown in the methods section suggests that is the case, but when I raised this with the authors they said no. How is this in your method? I think this is a key issue that needs clarification. -stefan]
The satellite estimates show an upward linear trend from 1993-2014 for GMSL.
http://www.aviso.altimetry.fr/en/data/products/ocean-indicators-products/actualitesindicateurs-des-oceansniveau-moyen-des-mersindexhtml.html
The seven estimates in this post show expodental trends, maybe even quadratic trends in recent years. That’s vastly different from a linear trend. The satellite data are better.
There isn’t much difference between satellite data and the seven estimates in the amount of GMSL growth in the past few decades, but the shape of the curves, of course, suggest very different future trends.
wili @26.
If you examine Fig 10 Right-hand panel of Ablain et al (2014), you may be less eager to suggest of the delusionist position “even that claim implies that they accept that there _is_ some sea level rise” The zero rise is actually closer to the top of the graph than the bottom.
What the graph does show is signs of acceleration 1993-2007 but then there are a couple of large negative steps 2007-10 turning the graph into something a denialist could easily claim showed deceleration.
If you look at more recent data since 2010, say this Colorado graph, you will see the blue wiggles start mainly below the linear trend line and by 2006 have become above the trend line. That is that acceleration.
Then in 2007 and again in 2010 the blue wiggle takes a dive down below the trend line. If you remember, this 2010 event was commented on at the time, often called the pothole, and was a result of extreme rainfall events.
But what the graph in Ablain et al (2014) doesn’t capture is the recoverly from the 2010 pothole which, 19mm in two years, would be off the top of the graph by quite a way.
Potholes, the product of a wetter atmosphere, appear to be holding back evidence of acceleration. But then, I don’t think preventing SLR by spreading the excess water over land areas is going to stave off acceleration for too long, not without it becoming a big big problem all of its own.
Minor nitpicking: png or svg for the plots would look better.
> Chris Dudley says:… It is pretty easy to see why …
BobR, if you want more explanation than that, the search suggested above finds a variety of sites explaining how taking more samples increases accuracy.
Here is one exactly on point for your question, in detail:
http://mycoordinates.org/using-satellite-altimetry-to-monitor-and-determine-sea-level/#30–t, I think you may be putting too much weight on the linear fit in the satellite data graph.
There are quite a few curves that can be fit to the data, as this analysis shows:
https://tamino.wordpress.com/2011/03/31/so-what/
# 34 McKinney – The satellite data show a clear linear trend. Tamino argues that the tide data show exponential growth. That is obviously true, as is seen in the second chart in the post. He does not argue that the satellite data (alone) is consistent with exponential growth, and it is not.
The extreme difference between growth patterns of the tidal and satellite data suggest that one procedure is wrong, even though there are only a dozen or so years of overlap. The tidal data have major problems. McKinney gave a response to the Tamino post suggesting that the satellite data also has major problems, that seems to be a minority opinion.
Not everything faster than linear is exponential. Tamino actually fitted a 3rd order polynomial, which is quite a difference.
#35–You may want to reread my comment there for comprehension; it’s not suggesting anything of the kind. Rather, it is twitting denialists infatuated with the satellite *temp* record, who then completely ignore the satellite *SLR* record.
That out of the way, the point is that you can (as Tamino does) fit other curves to the data–notably, that cubic curve in the last graph. You can’t really claim, without more support, that the record is best described by a linear trend line–or to use your language, I don’t agree that it is all that ‘clear,’ yet. It can take a while for a linear trend to diverge measurably from an exponential one.
#36 & 37 – Tamino fitted a cubic polynomial to the residuals (left after fitting tide data) to a linear trend. This curve shows an extreme upward curve since about 1985, which means an extreme (and growing) departure from a linear trend. The tide data depart from the linear trend in a exponential-like way.
That is also shown in the second graph in the post. There is an accelerating growth rate since the early 1980’s. This, like Tamino’s graph, is inconsistent with the linear growth (that is, a decelerating growth rate) suggested by the satellite data.
Maybe the satellite data and tide data will converge with more data, but the changes would have to be very large.
There are advantages if the satellite data are accepted over the tide data: predictions of sea level growth would be quite precise, and it would allow governments to plan better. Also, the neat line produced by the satellite data is probably much more convincing to the public than the messy lines from tidal data.
#38–“Maybe the satellite data and tide data will converge with more data, but the changes would have to be very large.”
– See more at: https://www.realclimate.org/index.php/archives/2015/01/a-new-sea-level-curve/comment-page-1/#comment-623562
The graphs you discuss show that past changes have been very large. A look at the discussion of SLR in AR5 corroborates that:
http://www.ipcc.ch/pdf/assessment-report/ar5/wg1/WG1AR5_Chapter13_FINAL.pdf
Note that the emphasis on how changes in rates of SLR create difficulties in trend analysis even over multi-decadal time spans. Based on tide gauge and proxy records–which reconcile pretty nicely–it’s quite unlikely that the satellite trend will be as ‘neat’ as you imagine over time.
And in fact, it already has some pretty good excursions during the twenty-year existing record–notably that big jag around 2011, but also significant noise around the 1998 El Nino. I’d like to see a trend analysis of the satellite record–I strongly suspect that it could support an exponential fit just as well as a linear one. (Mark I eyeball supports a slight upward ‘dishing’ of the curve–though MIE is, of course, not high-precision/high validity.)
It’s quite likely that over time, SLR is not going to neatly fit either a linear or an exponential model. There’s apparently just too much noise in the global hydrological cycle.
Interesting paper and good write-up discussing the major issues.
I just want to second/emphasize some of the comments from Stefan and Neil on this. Without using the same set of tide gauges, it is difficult to know if the trend difference arises from the method or the tide gauge selection. Having worked on reconstructions myself, I know that the trend in GMSL is quite sensitive to the tide gauges you use. There is a balance between using high-quality long records to capture the GMSL trend, and using enough tide gauges to explain regional variability and trends. Bruce Douglas (among others) has made the argument many times in the past that for the purposes of GMSL, only the longest tide gauges should be used. On long timescales, tide gauges – regardless of where they are located – should reflect/reproduce the GMSL change. The 600+ tide gauges used in the present study concerns me a little bit with regards to making a definitive statement about GMSL.
If I took the 1200+ tide gauges in the PSMSL RLR dataset, I could give you almost any GMSL trend you ask for (within reason) through selective editing of the tide gauges and using a simple (weighted) average. Certainly many of these tide gauges aren’t appropriate for use in a GMSL trend analysis for a range of reasons, but the impact of using 600+ TGs (Hay et al.) vs. ~400 TGs (CW) vs. ~100 TGs (RD) is non-neglible at best.
As a last point, as Neil points out, the difference in the reconstructions during the 1950s appears to be one of the biggest contributors to the lower trend rate. There is decadal and multi-decadal variability in each of these reconstructions, but such variability arises from and is accounted for in different ways (refer to Calafat et al., 2014 for a related discussion). This needs to be kept in mind when analyzing these different trend lines.
#38
Unfortunately, for you at least, both time series will continue to be used.
Mainly because, we all don’t live on a proverbial Waterworld!
“In a future where the polar ice-caps have melted and Earth is almost entirely submerged, a mutated mariner fights starvation and outlaw “smokers,” and reluctantly helps a woman and a young girl try to find dry land.”
Last time I checked, we live on land, many of those that live on land, somewhat unfortunately, live in the coastal zone.
@Hank Roberts said “This is amateur kibitzing on my part but I think it’s very interesting to look at the climate as an outgrowth of Earth’s biology — mostly oceanic biology — which we’re barely beginning to do.”
Yes but not just this past year: http://www.isse.ucar.edu/staff/kleypas/docs/PUBS/moore_etal_dsr2_2002.pdf Deep-Sea Research II 49 (2002) 403–462 An intermediate complexity marine ecosystem model for the global domain
Researching something else, I just came across an item relevant to the conversation at #38-9 (and previous). It’s a 2014 paper in “Nature Communications”, by Haigh et al. Here’s a relevant bit:
Link: http://www.nature.com/ncomms/2014/140414/ncomms4635/full/ncomms4635.html