What is the actual hypothesis you are testing when you compare a model to an observation? It is not a simple as ‘is the model any good’ – though many casual readers might assume so. Instead, it is a test of a whole set of assumptions that went into building the model, the forces driving it, and the assumptions that went in to what is presented as the observations. A mismatch between them can arise from a mis-specification of any of these components and climate science is full of examples where reported mismatches ended up being due to problems in the observations or forcing functions rather than the models (ice age tropical ocean temperatures, the MSU records etc.). Conversely of course, there are clear cases where the models are wrong (the double ITCZ problem) and where the search for which assumptions in the model are responsible is ongoing.
As we have discussed, there is a skill required in comparing models to observations in ways that are most productive, and that requires a certain familiarity with the history of climate and weather models. For instance, it is well known that the individual trajectory of the weather is chaotic (in models this is provable; in the real world, just very likely) and unpredictable after a couple of weeks. So comparing the real weather at a point with a model simulation outside of a weather forecast context is not going to be useful. You can see this by specifying exactly what the hypothesis is you are testing in performing such a comparison in a climate model – i.e. “is a model’s individual weather correlated to the weather in the real world (given the assumptions of the model and no input of actual weather data)”. There will be a mismatch between model and observation, but nothing of interest will have been learnt because we already know that the weather in the model is chaotic.
Hypotheses are much more useful if you expect that there will be a match; a mismatch is then much more surprising. Your expectations are driven by past experience and are informed by a basic understanding of the physics. For instance, given the physics of sulphate aerosols in the stratosphere (short wave reflectors, long wave absorbers), it would be surprising if putting in the aerosols seen during the Pinatubo eruption did not reduce the planetary temperature while warming the stratosphere in the model. Which it does. Doing such an experiments is much more a test of the quantitative impacts then, rather than the qualitative response.
With that in mind, I now turn to the latest paper that is getting the inactivists excited by Demetris Koutsoyiannis and colleagues. There are very clearly two parts to this paper – the first is a poor summary of the practice of climate modelling – touching all the recent contrarian talking points (global cooling, Douglass et al, Karl Popper etc.) but is not worth dealing with in detail (the reviewers of the paper include Willie Soon, Pat Frank and Larry Gould (of Monckton/APS fame) – so no guessing needed for where they get their misconceptions). This is however just a distraction (though I’d recommend to the authors to leave out this kind of nonsense in future if they want to be taken seriously in the wider field). The second part is their actual analysis, the results of which lead them to conclude that “models perform poorly”, and is more interesting in conception, if not in execution.
Koutsoyiannis and his colleagues are hydrologists by background and have an interest in what is called long term persistence (LTP or long term memory) in time series (discussed previously here). This is often quantified by the Hurst parameter (nicely explained by tamino recently). A Hurst value of greater than 0.5 is indicative of ‘long range persistence’ and complicates issues of calculating trend uncertainties and the like. Many natural time series do show more persistent ‘memory’ than a simple auto-regression (AR) process – in particularly (and classically) river outflows. This makes physical sense because a watershed is much more complicated than just a damper of higher frequency inputs. Soil moisture can have an impact from year to year, as can various groundwater reservoirs and their interactions.
It’s important to realise that there is nothing magic about processes with long term persistence. This is simply a property that complex systems – like the climate – will exhibit in certain circumstances. However, like all statistical models that do not reflect the real underlying physics of a situation, assuming a form of LTP – a constant Hurst parameter for instance, is simply an assumption that may or may not be useful. Much more interesting is whether there is a match between the kinds of statistical properties seen in the real world and what is seen in the models (see below).
So what did Koutsoyiannis et al do? They took a small number of long station records and compared them to co-located grid points in single realisations of a few models and correlate their annual and longer term means. Returning to the question we asked at the top, what hypothesis is being tested here? They are using single realisations of model runs, and so they are not testing the forced component of the response (which can only be determined using ensembles or very long simulations). By correlating at the annual and other short term periods they are effectively comparing the weather in the real world with that in a model. Even without looking at their results, it is obvious that this is not going to match (since weather is uncorrelated in one realisation to another, let alone in the real world). Furthermore, by using only one to four grid boxes for their comparisons, even the longer term (30 year) forced trends are not going to come out of the noise.
Remember that the magnitude of annual, interannual and decadal variability increases substantially as spatial scales go from global, hemispheric, continental, regional to local. The IPCC report for instance is very clear in stating that the detection and attribution of climate changes is only clearly possible at continental scales and above. Note also that K et al compare absolute temperatures rather than anomalies. This isn’t a terrible idea, but single grid points have offsets to a co-located station for any number of reasons – mean altitude, un-resolved micro-climate effects, systematic but stable biases in planetary wave patterns etc. – and anomaly comparison are generally preferred since they can correct for these oft-times irrelevant effects. Finally (and surprisingly given the attention being paid to it in various circles), K et al do not consider whether any of their selected stations might have any artifacts within them that might effect their statistical properties.
Therefore, it comes as no surprise at all that K and colleagues find poor matches in their comparisons. The answer to their effective question – are very local single realisations of weather coherent across observations and models? – is no, as anyone would have concluded from reading the IPCC report or the existing literature. This is why no one uses (or should be using) single grid points from single models in any kind of future impact study. Indeed, it is the reason why regional downscaling approaches exist at all. The most effective downscaling approaches use the statistical correlations of local weather to larger scale patterns and use model projections for those patterns to estimate changes in local weather regimes. Alternatively, one can use a regional model embedded within a global model. Either way, no-one uses single grid boxes.
What might K et al have done that would have been more interesting and still relevant to their stated concerns? Well, as we stated above, comparing statistical properties in the models to the real world is very relevant. Do the models exhibit LTP? Is there spatial structure to the derived Hurst coefficients? What is the predictability of Hurst at single grid boxes even within models? Of course, some work has already been done on this.
For instance, Kiraly et al (2006, Tellus) calculated Hurst exponents for the entire database of weather stations and show that there is indeed significant structure (and some uncertainty in the estimates) in different climate regimes. In the US, there is a clear difference between the West Coast, Mountain States, and Eastern half. Areas downstream of the North Atlantic appear to have particular high Hurst values.
Other analyses show similar patterns (in this case, from Fraedrich and Blender (2003) who used the gridded datasets from 1900 onwards), though there is enough differences with the first picture that it’s probably worth investigating methodological issues in these calculations. What do you get in models? Well in very long simulations that provide enough data to estimate Hurst exponents quite accurately, the answer is mostly something similar.
The precise patterns do vary as a function of frequency ranges (i.e. the exponents in the interannual to multi-decadal band are different to those over longer periods), and there are differences between models. This is one example from Blender et al (2006, GRL) which shows the basic pattern though. Very high Hurst exponents over the parts of the ocean with known multi-decadal variability (North Atlantic for instance), and smaller values over land.
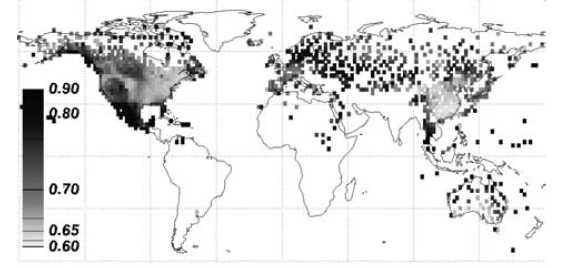
However, I’m not aware of any analyses of these issues for models in the AR4 database, and so that would certainly be an interesting study. Given the short period of the records are the observational estimates of the Hurst exponents stable enough to be used as a test for the models? Do the models suggest that 100-year estimates of these parameters are robust? (this is testable using different realisations in an ensemble). Are there sufficient differences between the models to allow us to say something about the realism of their multi-decadal variability?
Answering any of these questions would have moved the science forward – it’s a shame Koutsoyiannis et al addressed a question whose answer was obvious and well known ahead of time instead.
#47 Hank, they used a grid size of 9km so Albany could fit in one cell, however they only compared observed and simulated results for larger regions based on geography. The paper was meant to point out the ability to get matches between simulations and reality at least in regions.
#49, Patrick, “But don’t you think there are some underlying patterns in the global climate that can be understood even with greatly simplified models? The Hadley cells, for example.” The issue is not developing an understanding, it is testing a model. The greatly simplified or somewhat simplified models cannot be tested because they do not faithfully simulate particular locations that can be compared to the same real world locations.
I do not believe you will find it easier to predict the “amount” without faithfully simulating the distribution. If there’s no match between the distribution in the simulation and the distribution in reality as measured by 8 locations (is that enough I keep asking?) then I would believe the predicted amount either, because the amount depends on the distribution. Parameterizing rates or amounts of anything regionally or globally does yield testability.
Eric, You seem to have some fundamental misunderstandings of how climate models work and even about what climate is. In a climate model, there is a lot of sensitivity to initial conditions and which particular small fluctuations occur in any particular run. You can sort of see this because if Albany starts with a certain energy density, there is no guarantee as to how much energy will stay in Albany and how much will leave that box. If you look at many runs, the importance of the fluctuations tends to diminish, and you are left with the “climate”. You seem to be contending that averaging a single run over a long time will give the same effect, but that is not clear. (Note: Even in statistical mechanics, there is still controversy over whether a time average will yield the same result as an ensemble average. Probably it will in most–but not all–cases.)
If all one has are historical data, then to tell if the climate is changing you need time records that are long in comparison with the main source of weather variability: the yearly seasonal tilt of the Earth.
Say you have the temperature record, hour by hour, from one point – Fairbanks Alaska – over a hundred-year period, and nothing else – that’s your data set. Can we use it to answer the following?
1: What is the average temperature and what is the temperature change trend?
2: What is the average length of one day and is there any change in the length of days over the hundred years? How about for years?
First, is there autocorrelation in the data? Yes. Once a day, temperatures hit a peak, and there is stable yearly behavior – but if every consecutive year, those temperatures are a little warmer at the same times, then you have a warming trend superimposed on a cyclic trend.
Might one see other types of periodicity? It is possible – one might see the effect of quasi-periodic phenomenona like El Nino in the temperature dataset.
Trying to use statistics to answer the second question is obviously ridiculous – one would look instead to physical calculations or observations to get an estimate of year length, not to statistical models based on temperature data – let alone statistical models based on 8 data points.
If you used statistical analysis of temperature data from 8 points over a 100-year period to estimate changes in the length of the year, you’d come up with pretty poor predictions of the future behavior. One could still go around using the result to claim that physical models of planetary orbits are unreliable predictors of future behavior, however, due to their poor performance in the statistical test.
Re #43
I think I understand now. The rock model (climate model) is 100% certain that the rock (temperature of the atmosphere) will go downhill (up) because of gravity (greenhouse gases). The other less important forces like a strong upslope wind, kid holding back the rock (PDO, AMO) are not strong enough to counteract gravity (greenhouse gases). Since we don’t care about the path the rock takes (the weather in the climate model) and we are 100% certain of the result, I guess we don’t need a rock model (climate model) anymore. Oh, but wait. The model is still useful because we want to know how far the rock (how high the temperature) goes. It seems that would depend some on the path of the rock (weather in the climate model). Thanks.
#52, Ray, would you agree that Albany NY and Rome Italy would have distinct, reproducible characteristics of energy density changes based on local topography? When I say reproducible, I don’t mean numerically exact, but that there would be a characteristic curve from an anomalous condition.
I could for example dump 2 feet of snow in Albany NY in January and likewise in Rome (or little north to be exact) and would get predictably different responses back to climatology with normal variations. That is an extreme example I realize.
I think my mention of averaging was somewhat mistaken. The two sources of error discussed by the authors are high frequency noise and micro-climate modeling errors. I don’t think the latter would affect all 8 sampled locations. The former still seems to be somewhat of an open question: does the HF noise integrate into greater or lesser errors over longer time scales?
The area in the model Eric refers to above is huge. In the original paste I got zeros where there should be degree symbols; here is is a bit clearer:
“… LSA-East, defined roughly by 33 – 43[degrees] N latitude and 78 – 89[degrees] W longitude …”
That’s the area they’re talking about.
Think of it as a shotgun pattern on a target, Eric. You can check how the result looks by firing dozens of times. You get roughly the same spread, the same shape, the same accuracy.
You can’t then conclude that any particular tiny circle on the target area will always either be hit or missed by a shotgun pellet.
Even if you have 20 patterns and on none of them was that particular little bit of paper hit — the next time, it might be a hole there.
This analogy brought to you by an ordinary reader, not a climate scientist, and the climatologists may well tell me it’s absurd after they climb back onto their chairs, but it seems to me this is what you’re getting confused about.
#56, Hank, I assume the chaos in your analogy is provided by the turbulence in the explosion and the air that the pellets travel through. Otherwise we would exactly duplicate the physical configuration (cartridge including gunpowder and pellets, etc) for each firing to match the determinism of climate.
In that case I must (like above) amend the analogy to include a real and modeled topology, perhaps various fixed air currents, plus the interactions between the pellets on their way (or not) to each tiny circle on the paper. There will be a predictable probability that each tiny circle will be hit provided the model contains those details.
The turbulence will still result in model-reality mismatches but multiple firings will take care of that. The model will have insufficient topological detail for some of the tiny circles, but we will compare a large enough number of them (probably more than 8).
Eric, No, the results would not be reproducible, because initial conditions when you dump the snow vary. In many successive runs (ensemble), you would have a majority of outcomes that were different in the two cases. In the majority of years, you would also have different outcomes. However, the average over the ensemble and the average over time need not yield the same result. To blithely assume it will be so is a bit risky. Actually Hank’s shotgun blast pattern is a pretty good analogy. Remember, we’re not trying to predict the weather in Albany, NY 100 years hence. We’re trying to look at how changes in the energy in the system will affect TRENDS in global climate. Regional predictions are a long way off, and long-term weather predictions may well be impossible.
#58 Ray, but wouldn’t you agree that the two locations (same latitude but very different topography and thus climate) have distinctly different reactions (in Rome the snow would always melt in a day or two)? Wouldn’t that difference be essentially climate?
Again the paper is trying to validate the models, not use them to determine trends. As the forcings change, will be modeled climate be sufficiently detailed to perform the validation? Will the snow continue to stick around in Albany just as long, or shorter, and how much shorter? Likewise for Rome, the local topography may (for example) create more cooling clouds in winter. If it does, the snow could actually stick around longer.
Re 51:
“The issue is not developing an understanding, it is testing a model. The greatly simplified or somewhat simplified models cannot be tested because they do not faithfully simulate particular locations that can be compared to the same real world locations.”
But one can look for the changes that occur in the Hadley cell in the model data, and then compare that to changes in the Hadley cell in the real world or in other models.
“#42, KevinM: I’m not sure that’s a good analogy of what is being compared. If I were to apply heat to a kettle and take measurements of slight temperature variations within due to heated water circulation, that would indeed not match any simulation of the kettle for those location while the overall temperature in the simulation and real kettle would match quite nicely.
“However, the earth is not a kettle and Albany is not an indistinguishable location, it has specific climate characteristics and weather patterns which can be simulated in climate models. . .
Also the Albany discrepancies are repeated for 7 more locations worldwide, but is that enough locations to say the model is poor? I don’t know.”
Well, no analogy is perfect. But note that in the analogy I *was* asking about specific locations of bubbles–analogous to Albany (or wherever.)
As to your final question, if I understand the OP correctly (and as amplified by various posters throughout this thread), the answer would be no, 7 locations are not enough. The reason is that the GCMs are not intended nor expected to have predictive abilities for specific locations. In my boiling water analogy their analogs would predict things such as (perhaps) the average size of bubbles, their density, curves describing how these change over time, etc., etc. A bubble model is a successful predictor if it can replicate the macro-descriptors even if NO single bubble’s trajectory matches a corresponding observed trajectory. So NO number of locations would be enough, because K’s et al.’s research question is inapplicable in the first place.
To put it very crudely, but maybe usefully, K et al. are criticizing a leaf rake because it makes a very poor salad fork. It is just not true that you need to be able to predict at micro-scales in order to predict at macro-scales. A recent example of this–not highly analagous, but illustrative of the principle–would be the economic model which is able to predict reasonably well national Olympic medal totals without any predictive ability *at all* with regard to any individual sport. (All the model “cares about” is 1) national population, 2) GDP, 3) recent Olympic medal totals, and 4) host team advantage.)
BTW, one of the really interesting aspects of this discussion, to me, is how it leads into the question of damping in chaotic systems. With no damping, presumably your formula that “weather becomes climate” would be 100% correct, and individual locations would in fact have to be accurately modelled for the GCM to maintain accuracy–you’d need to know about the every Brazilian butterfly flapping its wings. But this doesn’t appear to be the case, as far as this amateur can judge at least.
Eric,
Once you are talking about multiple shots, the analogy is multiple runs of the model. And it does not make sense to look at whether a particular point on the target gets obliterated every time, but rather more gross details–average width of the pattern, standard deviation, radius over which target is completely obliterated, etc. It makes no more sense to look at individual points on the target than it does to look at individual stations–from a climatic point of view.
Eric.
When you sneeze, do the bogies always hit the same bits of your hand? Are the sizes of the chewy stuff always the same size and taste?
(this is the closes I get to something like your continued badgering queries).
Eric, the early awareness that climate models could be created came from observing that change is being measured at individual points where we happen to have longterm weather stations, but the actual temperature and humidity and wind changes occur across huge areas.
Watch the weather map — you see reports from point stations but you see the fronts shown and the measurements, wherever they happen to be, change consistently with the large scale event, as the weather front passes.
You’re thinking that weather (and over longer time spans climate) changes in lots of little tiny areas rather than averaged across very large areas.
False premise. You’re imagining that order exists ‘all the way down’ but that’s not true here. Look up “emergent property” — the complicated weather and climate emerge from relatively few specific physical observations in the models.
Yes, a change in a detail will change climate. But the details are things like the Appalachians weathering down from being the biggest mountains, or the continents moving. Those are relatively slow. But if we had a way to remove mountains or move continents, we could cause climate change by doing that rapidly.
Ditto for the background level of CO2 going on an excursion far outside its range. We’re doing that.
Eric,
The difference in climate between Rome and Washington, DC, Denver, CO, etc. all at about the same latitude N) has to do with a lot of factors–the Gulf Stream, topography, altitude… However, initial conditions coud dramatically affect the results of any particular trial. It might be very cold in Rome. You could have a Chinook blowing in Denver. Congress could be producing an exceptional amount of hot air in DC. Only by looking at many runs and over time will the climatic TRENDS. You don’t validate the models by reproducing the weather. The trends are the climate.
#61 KevinM “So NO number of locations would be enough, because K’s et al.’s research question is inapplicable in the first place.” If every point in a model is inaccurate, how would any aggregate statistic from the model have any validity?
#62, Ray, I agree in the shotgun domain that we require multiple simulation runs at least the way that I hypothesized it. But I still believe that the 30 year time frame of the climate simulation will cause most locales to revert to their climate means. The forcing changes in the model and reality will cause predictable changes in those local climates. Over the 30 year period a single point in the locale will reflect the (changed) climate of the locale.
1. Can we redo the Koutsoyiannis analysis using ensembles, rather than single runs? Can we agree that would be valuable?
2. I wonder what percentage of individual model runs produces flat temperature trends for 1998-2008? (Using initial conditions fixed at conditions occurring Jan 1 1997.)
3. How small a sample is too small? Good question. 8 seems small, especially given the free availability of more data. But at least these 8 were chosen at random. Why not redo the analysis with an increasing number of stations and see how the results change? What would it cost to run this analysis? Salary for one research assistant for 6 months?
Thanks again for the OP.
[Response: 1) no point. The spatial scale is still too small to see a forced signal come out of the noise. You need a instead to combine Kiraly’s results with an analysis of the CMIP3 20th Century runs. 2) You can see what the AR4 models gave in a previous post. However, there is no equivalent database of initialised models that all start in 1997 (neither the ocean initial conditions, nor the methodology are sufficiently mature). 3) I have no idea how those eight stations were chosen. But you would be better off looking at the gridded products, not individual stations since you don’t want to re-invent the wheel in making a gridded product in the first place – that’s a big enough job on its own. None of this is time-consuming nor expensive. A grad student could have it done in a couple of months. – gavin]
This is what I get out of this post (without going back for several PhDs): someone can’t see the forest for the trees.
But I still say Katrina was caused (enhanced) by global warming, until someone can prove to me at 95% confidence (in language I understand) that it was not — the null hypothesis being that GW caused Katrina and the research hypothesis being that it did not.
Thanks for the rapid response and especially the link (which I’d missed). The more clarity we can have on what the models say and how they work, the better. The longer that temperatures stay flat, the more important it is going to be to understand how this could be consistent with long-term model predictions of forced warming. LTP cuts both ways. Heat flow – and the asbence of heat flow – can be suprisingly persistent due to slow and uncertain deep ocean mixing dynamics.
#64,65 Hank and Ray, many thanks for your patience. Suppose there was a world without substantial changes in climate forcing except seasons. If we ran a simulation with random initial conditions I would expect that model would match reality in a year or less at a majority of a selected set of points.
This is obviously a deviation from what is being compared in the paper, so we would have to compare parameters like diurnal temperature, precipitation, etc. not long term changes. (1) Would you expect a match? (2) Would the methodology be invalid once major climate forcings were added to the world and the model?
> But I still believe that … Over the 30 year period
> a single point in the locale will reflect the
> (changed) climate of the locale.
What evidence can you point to supporting this belief?
What size “locale” do you believe has its “(changed) climate” different from a “locale” adjacent to it?
Watch this:
http://www.team-6.jp/cc-sim/english/
(from Bryan Lawrence’s weblog, where he writes:
Nearly twenty minutes from Seita Emori. The model he’s describing was the highest resolution model in the AR4 archive. That doesn’t make it right, and he probably ought to caveat more the results beyond temperature, but it’s all very plausible. The fact that it is even plausible should cause concern!
http://home.badc.rl.ac.uk/lawrence/blog
2008/07/18
That movie shows you, as it says, “the highest resolution model” — watch Albany or Rome.
Do you see there what you believe you should see, according to your belief in how the models work?
Lynn, Lynn, Lynn (68), proving a negative is one of the top and common logic fallacies. The default is that the cause does not exist until it is proven otherwise.
Eric, In effect, what you are asking is that if a planet had a climate so simple that it was in effect deterministic, could we predict it? Sure. Mercury comes close. Then there’s the moon. Throw in an atmosphere w/o greenhouse gasses, and things get more complicated, but still mostly tractable. Add ghgs and dust, and you get something like Mars, and that’s pretty difficult if not impossible. Add water in all 3 phases and fuggedaboudit. Now you put all these fossil-fuel burning organisms on it and it’s a wonder Mother Nature herself didn’t throw in the towel… Oh, maybe she did?
Re #70, after posting I realized that modeling without particular forcings is a regular practice (e.g. http://www.nersc.gov/projects/gcm_data/), but not, as far as I can see, used to compare points to observation point.
Eric, no single point measurement is going to show a climate change for a very long time, within the range of accuracy of the instruments.
A thousand thermometers, each accurate to one degree, can be used to detect a trend of a tenth of a degree over a decade. No one thermometer in the group can do that.
Would you make clear whether you do or don’t understand how these temperature trends are being determined from the instruments?
You seem fixated on the idea of measuring at a single point. It can be done but it will take centuries rather than decades to accumulate enough numbers to do the statistics. You understand this?
#74 Hank, the one degree accuracy of the Albany thermometer should not be an issue over the time periods being compared. Not fixated on a single point, but on a set of points since, as postulated in the paper, due to problems with spatial integration of temperatures.
RE #72 & “proving a negative is one of the top and common logic fallacies. The default is that the cause does not exist until it is proven otherwise.”
Well, that may be the case for scientists trying to establish science. But for the rest of us trying to avoid serious problems from climate change, we have to assume GW and its serious effects, until proven at high certainty otherwise, before we stop mitigating.
And even if it could be scientifically established with high confidence that the world were not warming, and/or our GHG emissions were not contributing to the warming, and/or the warming was not causing serious harms, we still would want to reduce those activities that produce the GHGs, since they have many other negative effects — other enviro problems, inefficiencies (waste of money & resources), harm to the economy, war/military actions/costs.
I assume you have some statistical analysis to share to back up your handwave?
Hmmm, why didn’t you supply the analysis in the post, since such an analysis is the only thing that could back up your assertion?
Eric: KevinM “So NO number of locations would be enough, because K’s et al.’s research question is inapplicable in the first place.” If every point in a model is inaccurate, how would any aggregate statistic from the model have any validity?
Just think about fair coin tosses Eric. I cannot predict any individual toss (any predictor will be at best 50% accurate), but I can predict an aggregate statistic (the number of heads per thousand tosses) with great accuracy.
Eric “should not be an issue” according to what source?
What are you relying on for these proclamations?
You have a concept you’re repeating but I don’t see where it comes from.
And to go a little bit further Eric with respect to my last comment; as I’ve thought about it this analogy is not a bad one.
We could build a very complex simulation (a model) of a coin tossing apparatus. Imagine we build a simulator of a mechanical hand and coin using some kind of rigid-body dynamics simulation package. We model fair coin tosses. It would be very dependent on the initial conditions, slightly more force to the hand, slight changes in the positioning of the coin, etc. would result in a different result to the coin toss. Suppose in our simulation we’re careful to not put the coin in exactly the same place we put it before and we’re careful to slightly vary the force of the toss, and we simulate a great many such tosses in a “model run”. A coin tossing “model run” would be an accurate simulation of reality, measured on a toss-by-toss basis, approximately 50% of the time with respect to any real sequence of coin tosses; i.e. toss #1 of the real sequence will match toss #1 of the simulated sequence 50% of the time. Furthermore any two “model runs” will be correct for any particular toss in the run approximately 50% of the time with respect to each other.
However all runs (and reality) will exhibit the property of the aggregate statistic of “the number of heads coming up in a run of a particular length” being nearly identical.
#52 Ray
“In a climate model, there is a lot of sensitivity to initial conditions and which particular small fluctuations occur in any particular run.”
Does this mean that a model, if it was built today, would replicate exactly the earth with no known (or unknown) unknowns?
Does this mean we have a ToE?
Alan K., not sure how what you wrote pertains to what I wrote.
#78 and #80, dhogaza and Hank, my statement was not precise, I should have said the one degree “precision” of the Albany thermometer. I assume the thermometer was accurate (unbiased, in calibration, etc).
K and authors note that they used station data which had a monthly time scale and analyzed at monthly, annual, and 30 year moving average time scales. They had no further discussion of the station measurements.
I assumed that the monthly station reading would be an average of 30 daily readings. From analysis such as http://hadobs.metoffice.com/hadcet/ParkerHorton_CET_IJOC_2005.pdf
I would turn one degree (F) precision into 0.026 variance and divide it by the 30 readings being averaged in the month. That’s why I didn’t think it would be an issue.
Off-topic, but since there’s no “open thread” on this blog, I’m not sure where else to put this.
I’ve detected another mistake in Miskolczi’s paper. Miskolczi’s equation (4) is:
AA = SU A = SU(1-TA) = ED
where
AA = Amount of flux Absorbed by the Atmosphere
SU = Upward blackbody longwave flux = sigma Ts^4
A = “flux absorptance”
TA = atmospheric flux transmittance
ED = longwave flux downward
These are simple identity definitions. I do wonder why Miskolczi used the upward blackbody longwave for the amount emitted by the ground when he should have used the upward graybody longwave — he’s allegedly doing a gray model, after all. Apparently he forgot the emissivity term, which is about 0.95 for longwave for the Earth. One more hint that he doesn’t really understand the distinction between emission and emissivity.
Note that he seems to be saying the downward flux from the atmosphere (ED) must be the same as the total amount of longwave absorbed by the atmosphere (AA).
The total inputs to Miskolczi’s atmosphere are AA, K, P and F, which respectively stand for the longwave input from the ground, the nonradiative input (latent and sensible heat) from the ground, the geothermal input from the ground, and the solar input. P is negligible and I don’t know why he even puts it in here unless he’s just trying to be complete. He’s saying, therefore, if you stay with conservation of energy, that
AA + K + F = EU + ED
Now, from Kiehl and Trenberth’s 1997 atmospheric energy balance, the values of AA, K, and F would be about 350, 102, and 67 watts per square meter, respectively, for a total of 519 watts per square meter. EU and ED would be 195 and 324, total 519, so the equation balances.
But for Miskolczi’s equation (4) to be true, since AA = ED, we have
K + F = EU
That is, the sum of the nonradiative fluxes and the absorbed sunlight should equal the atmospheric longwave emitted upward. For K&T97, we have 102 + 67 = 195, or 169 = 195, which is an equation that will get you a big red X from the teacher.
There is no reason K + F should equal EU, therefore Miskolczi’s equation (4) is wrong. Q.E.D.
hi Ray
my question is suppose you were building a climate model for eg. Albany you need the correct energy density as presumably one of many parameters as an input. You then say that initial conditions are key so you would need not only the correct energy density but the correct everything else. My question is do we know the correct everything else to ensure that initial conditions are replicated in a climate model so that no “loose ends” end up corrupting the model (ie if everything was correct except the energy density value then surely the model would not be as accurate as if the energy density was correctly assessed). So my question about climate models and initial conditions is how close to reality can we get to those initial conditions (=our earth today all of which has an effect on climate)? If we can replicate reality then that is a ToE isn’t it? If we can’t then don’t all those loose ends end up corrupting the model?
They can model the climate at continental scales and that gives a good indication of what might happen should be continye BAU but what about the Biosphere per se? What model has any idea what happens here, not many I would imagine and hence we rely on real world evidence from the geological record, ice cores, organic matter etc to tell us about past climate and the biosphere.
James Hansen tells us that the models are useful but the weakest link the the earth/climate science chain, real world evidence counts for much more of what we know about future climate change. The models seemingly just back up the real world evicence.
Lynn (77), I respect your zeal, but asserting things that are prima facie contraindicated in support of your cause is not a good way to build your credibility viz-a-viz people you may be trying to convince, at least in a logical and scientific environment. (might work well with much of the public as a mass…)
Rod admonishes:
“Lynn (77), I respect your zeal, but asserting things that are prima facie contraindicated in support of your cause is not a good way to build your credibility viz-a-viz people you may be trying to convince, at least in a logical and scientific environment. (might work well with much of the public as a mass…)”
Holy cow, Rod, your own argumentation is a bunch of contraindications, lies and wishful thinking. Please save us from your hypocrisy!
Alan K., Seeking omniscience is the wrong approach for us mere mortals. Rather, you vary the initial conditions and look at the persistent (or robust) results. Averaging over many runs or over space and time can diminish the dependence on intial conditions. Remember, what we’re interested in is climate–persistent global and regional (not local) trends over time.
#81, PatrickC, I like your improved analogy and within a model run of successive tosses, we would probably want the coin placement and tossing force to be a complex function of the previous toss, not simply random. This would help model the analogous LTP from the paper.
One hypothesis in the paper is that the local climate is predictable in some way. I would thus propose that the coins are not equally weighted, that they are each slightly biased but as a set they are not. The question implied by the paper is whether the local climate bias will reflect the global climate changes predictably, or whether that bias will be overwhelmed by weather.
In your analogy it would be simply whether the real and modeled coins (real coins are never perfect) have enough bias in their weighting to make a predictable difference in the measurements or whether that bias will be overwhelmed by the hand position and tossing force changes (i.e. weather).
#90 thanks Ray: omniscience – a “nice to have” :)
but hold on however; isn’t your reasoning circular? Initial conditions are important (“there is a lot of sensitivity to initial conditions”) but you then see what results you get then you vary the initial conditions until you have the “right” initial conditions to suit the results. So either model results result from initial conditions or, if those initial conditions don’t produce the “right” results initial conditions are changed to suit model results. You do not quite have a predictive model, then, do you?
Petro (89), what on earth are you talking about? And, why?
My 2 cents, @ Lynn and responders:
It looks to me like Lynn’s using a risk management philosophy, which is IMO absolutely appropriate for policy decisions, but she made the mistake of expressing it in scientific terms, which as Rod B points out is inappropriate.
Risk management: Once given a credible scenario that a risk exists with probability above some reasonable threshold, that needs to inform policy-making until/unless that risk can be demonstrated to have a low probability, beneath some reasonable threshold.
Science: null hypothesis should usually be that the independent variable has no effect on the dependent variable.
So what Lynn *said* was wrong, but what she seemed to *mean* (taking into account her follow-up post) was right. Sometimes you can tell what people mean even when they say it wrong. In that case, people who make too big of a deal out of what was *said*, neglecting what was pretty clearly *meant*, are rather aggravating to interact with. I feel like Rod B probably understands this in a personal way, after that whole back-and-forth about Monckton’s recent paper.
Alan K, Actually, you are more interested in the behavior that persists across various initial conditions and in spite of fluctuations. You are also interested in the RANGE of behaviors. The results of any single run are not that interesting. That’s why the paper is so baffling. I think of it as analogous to a thermodynamic system–we know a thermodynamic system will spend most of its time near equilibrium because there are so many more possible states there than far from equilibrium. Because of this, we concern ourselves with the properties of the equilibrium system. It also happens to be what we know how to calculate–nonequilibrium thermo is really \near-eqilibrium\ thermo. Does that make sense?
Alan K #92,
You can’t have perfect initial conditions and chaos theory tells us that a small change can make a huge difference. Most people forget the “can” and so we get the butterfly wings meme trotted out which doesn’t explain and actively hinders understanding.
So what you do is run a model with slightly different inital values that still give an overall answer that is correct (e.g. wind speed 10kts +/- 3kts, you pick 5-15kts not 10-90kts because 90kts doesn’t give you a value you “read” with your instruments as 10kts).
And you run lots of these.
Where they all roughly agree on each other is on things that don’t change much on initial conditions. This gives your model sensitivity. And you use that to improve your models.
However, your model must miss things out because we don’t have the computing power to simulate each molecule in the air and in the oceans. Different models miss out or approximate different things. If none particularly disagree, you have a very predictable weather/climate pattern and have a strong indication that your forecast is very close to the truth.
So you run all these models and by virtue of you not forcing the values to conform (in which case, why run the models: just make the numbers up on a spreadsheet and go home), they act slightly differently. But their average should be a lot closer to the truth.
Rather like tossing a coin. The easiest way to see if the coin is weighted is to toss it 100 times. You use the average of all these tosses (which had different throws on them, just like different models have different forces or starting conditions) to decide whether the coin is biased or not.
The more you toss that coin, the more certain you are that the result you get is the correct one. E.g. toss a coin 100 times and you’re confidence in the result is 90%. Toss it 10,000 times and it’s 99%.
This is not a circular argument. It’s statistics. you can prove it yourself by taking a coin and weighting it so it is biased to heads or tails and do the experiment. The first throw tells you NOTHING. The next four don’t tell you much unless they are almost all one side or the other. After 10,000 even a every slight bias in the coin could be discovered.
(Which oddly enough is something Rod B and Monkton seem to have missed out.)
Take a look at the laplace construction that is always shown in chaos theory books. There are areas where the lines are close together: a small change doesn’t make much change in the output. But “small changes make small changes in the output” does not make good copy.
Eric, it’s nuts to refer to just a few weather stations to try to establish anything about longterm climate. You have to RTFM.
http://scholar.google.com/scholar?sourceid=Mozilla-search&q=how+many+surface+weather+stations+to+determine+climate+change
First article found:
http://www.ncdc.noaa.gov/oa/climate/ghcn-monthly/images/ghcn_temp_overview.pdf
Citations to that article:
http://scholar.google.com/scholar?hl=en&lr=&safe=off&cites=7874538422593985630
Note the number of times they’ve been cited by later work — read some of that to see the science in this field. Speculation and wishes don’t change the instruments nor what you can accomplish with the data.
re #79: “If every point in a model is inaccurate, how would any aggregate statistic from the model have any validity?”
I’m not sure how I can say this differently, but. . . if my (imaginary) “bubble prediction model” reliably replicates the larger-scale properties of the observed ensemble of bubbles in my (imaginary) liter of boiling water, then we may not feel that an inability to predict single bubble trajectories is a meaningful deficit. That is, if the model consistently captures the aggregate behaviour–the functions describing densities, sizes, durations, and such–then the modelled bubble ensembles would “look just like” the observed ones. And, more importantly, “act just like” them, too. And we would be able to use the models to make some predictions, with error bars, about what might happen should that liter of water be somehow subjected to temperature or pressure conditions that we are not physically able to set up in our lab. And we still might be utterly unable to predict what any one bubble will do.
I think the problem you are having is in imagining that this is even a possible scenario–your repeated questions all seem to presuppose that prediction on smaller scales is necessary to prediction on larger scales. (“Weather becomes climate.”) Possibly you are imagining causality proceeding “upwards” from small causes to larger ones. But does it really work that way?
kevin (94), I agree. It’s what I said; you just said it much better.
RE #94, thanks, Kevin. That’s exactly what I meant — a focus on the beta error or avoiding the false negative. I call it the medical model, AKA the precautionary principle — one would be quite nervous if the doctor were to say that they are only 94% confident that one’s lump is cancerous, so no treatment was needed until it gets up to that golden 95% (or .05 p that null is correct).
I’d think that the level of confidence required for mitigation or prevention of a problem would be inversely related to the seriousness of the problem and positively related to the costs of mitigation and prevention. Since (1) global warming risks are so very high (throwing in everything that could go wrong, such as extreme warming for 100,000 years from positive feedbacks kicking in, and hydrogen sulfide outgassing snuffing out a huge chunk of whatever live survives the warming), and (2) we haven’t even scratched the surface of cost-effective mitigation strategies that actually save us tons of money, I’d say the standard for deciding to mitigate should be exceedingly low, like what science may have reached well before 1990 (I know it reached 95% confidence or .05 prob of null being correct in 1995).
So basically, the world should have seriously started mitigating this problem before 1990, and we should be at least some 20% below 1990 GHG levels by now, rather than way above them.
Which means that even if this Koutsoyiannis, et al., study in question had failed to reach 95% certainty on GW and its effects in a way acceptable to the community of climate scientists (which apparently it did not bec it confused the random fluctuating noise of weather with the statistical aggregate of climate), it doesn’t really matter from a policy standpoint. It does nothing to derail the urgency of our need to severely mitigate GW, starting immediately, if not 20 years ago as we should have done.
Then once we’ve implemented all the cost-effective mitigation strategies (which should keep up very busy for some 20 years or so), we can then revisit whether or not our GHGs are causing GW, and GW is causing harmful effects, and whether or not we should start sacrificing to mitigate the GW disasters.
So not knowing what the science is here, doesn’t really bother me much; the study in question would not convince me to stop mitigating, even if it did hold some water.