Guest commentary by Martin Vermeer
On December 7, 2009 the embargo expired, and my and Stefan’s joint paper ‘Global sea level linked to global temperature’ appeared in the Proceedings of the U.S. National Academy of Sciences. It had been a long time coming! But this post is not so much about the science as about the process, and about how a geodesist from Helsinki and an oceanographer from Potsdam, who to this day have never even met, came to write, to the surprise of both of us, a joint paper on sea level rise.
My own entry into climatology happened only a few years ago. A significant trigger was RealClimate, which I had learned to appreciate as one of the rare reliable Internet sources amidst the junk. Contributing to the oft-slandered science is my small ‘thank you’ and revenge as a scientist.
As I remember, it was the commenter calling himself Rod B. who enquired, sometime August 2008, what the story really was with Rahmstorf (2007). Trying to answer, I ended up reading the paper and getting interested. What seduced me was the simplicity of this, so-called semi-empirical approach: linear regression of sea level rise dH/dt against temperature T, yielding two unknown parameters: a regression coefficient a, and an intercept, or ‘equilibrium temperature’, T0. See our Ups and downs of sea level projections for a more detailed explanation.
The curve of temperature as a function of time over the 20th century has three parts: a steep rise in the beginning, a flat middle part commonly attributed to aerosols, and a very steep upswing at the end. Physically one would expect for the curve of the sea level rise rate dH/dt as a function of time to look rather similar, as indeed it does: this justifies the Rahmstorf (2007) approach of regressing the one against the other. Looking more carefully however one sees that the dH/dt curve has slightly more of an S-like shape, turning downward in the middle, before swinging up again at the end.
This suggested to me that, in addition to a proportionality to temperature T, sea level rise would also contain a term proportional to the time derivative of temperature, dT/dt. In other words, global sea level would be a good global thermometer, but with a ‘quirk’. I could even think of a physical mechanism for such behaviour.
I contacted Dr. Rahmstorf, proposing the idea: one would expect the ocean surface to warm up rapidly to completion, contrary to the deep ocean and the continental ice sheets. This would argue for a term, in addition to the secular a (T – T0) term, of form b dT/dt. Stefan’s response was cautious; not surprising, as being something of a media figure in Germany surely means that he has to contend with his share of cranks. But he suggested I look myself into the idea, which I subsequently did: in for a penny, in for a pound.
I downloaded Stefan’s script, modified it, did the first computations with the same real tide gauge and temperature data Stefan had used — surprise: negative b. Hmmm, strange. That was for real data from the real Earth; what would happen if I applied the extended relationship to simulated data from the same general circulation model (actually, an Earth system model) for the period 1900-2100 that Stefan had used in his paper for testing his relationship? This model was in one essential way very much simpler than reality: it completely lacked the contribution of land ice melting to sea level.
Stefan helpfully sent me Matlab snippets and model output, and indeed I got it all working. What was more, the disagreement found by Stefan for the late 21st Century — between sea level rise as predicted directly by the model, and indirectly through the semi-empirical relationship between temperature and sea level rise — went almost completely away when using the new, extended relationship. With a positive value for b, just as expected from theory for an ocean surface water response.
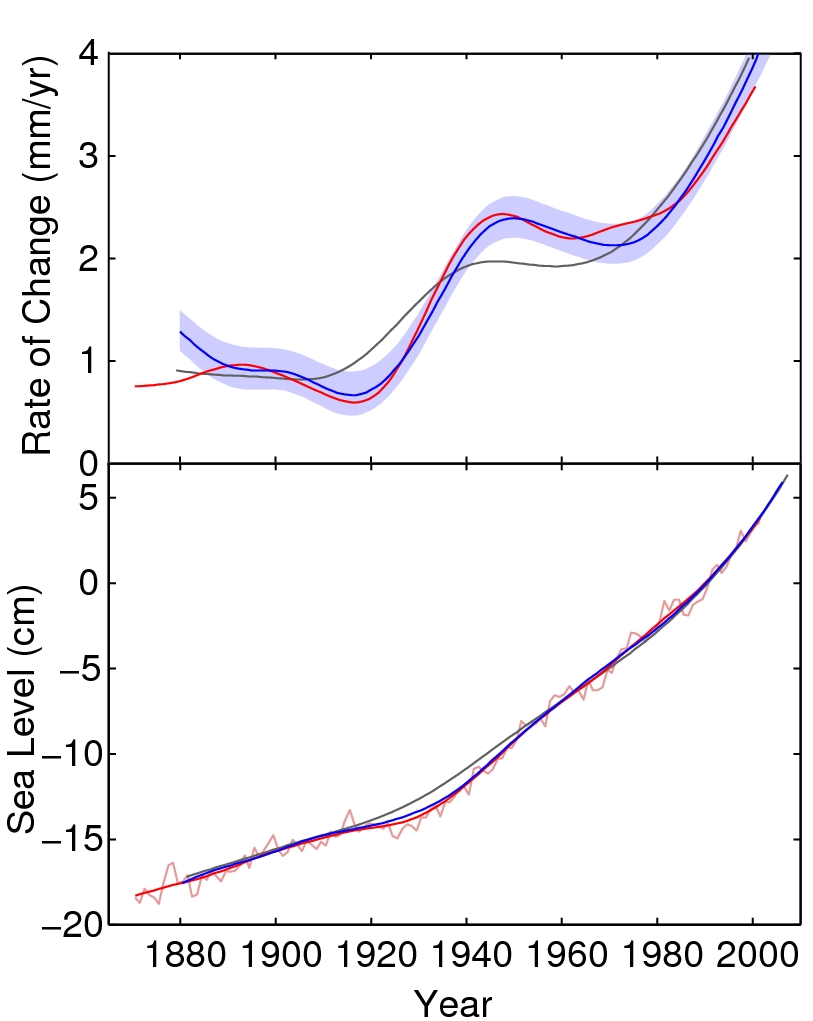 |
| Global sea level against time. Top, sea level rise, bottom, sea level itself. Red, sea level from observations; blue, with uncertainty band, the fit from global temperatures using our new relationship; black, the fit using Stefan’s original relationship. The thin red wiggly curve shows annual sea level values. |
That was encouraging, but what again about the real data? Remember that this is real observational data from tide gauges, altimetric satellites and meteorological stations, warts and all, with a very imperfect spatial sampling both for the tide gauge data and for the surface temperature data. Nothing like the clean, formally perfect model output of truly global mean surface temperature and sea level.
At that point I was about to give up.
I remembered however Stefan mentioning a ‘reservoir correction’ and decided to see if that made a difference. It was not hard to find Chao et al. (2008), who had painstakingly compiled a list of all man-made reservoirs the world over, and the amount of water stored in them. I fitted a simple arctan function through their water storage curve and added that to Stefan’s already extended script. All that water, up to 30 mm sea level equivalent, that should have been in the ocean was progressively kept bottled up on land as dams were being built: a known correction that should be applied.
Wow. Introducing the b term had already improved the Pearson correlation r of fit from 90% for Stefan’s original relationship to 97%; nice, but hardly on its own compelling. Bringing in the Chao et al. man-made reservoir correction brought it up to 99.2%!
Slowly it dawned upon me that, hey, maybe I’m on to something real here, something based in physics: it seems the world ocean can be a remarkably good global thermometer, once you get to know its quirks.
 |
The world ocean, a pretty good global thermometer (drawn using GMT). |
Stefan relates the moment when he realized that I had something worth publishing: January 16, when he saw the results of the ‘millennium run’ that I had done on the data he had sent me. All of the volcanic explosions over the last thousand years, which were translated first into top-of-atmosphere radiative forcing and then turned into sea water thermal contraction and a drop in modeled sea level, were faithfully reproduced in the sea levels obtained from the model temperatures by my new relationship! A beautiful performance on what are large, rapid and erratically occurring excursions in both global temperature and sea level. And that’s how Stefan came on board.
With the small number of independent data points we needed to make sure we were not ‘fitting an elephant‘, so I read up on statistics during winter 2008/2009, and in particular, information theoretical methods like the Akaike Information Criterion. The model intercomparison was useful for just that. I’m not the only one studying these ideas, and I learnt a lot from tamino and James Annan’s Empty Blog. Jaynes (2003) was also on my 2009 Christmas reading list; Hypothesis testing, null and alternative hypotheses, confidence bounds and all that, is a traditional approach to statistics that is easily misunderstood and often misused. Statistical refutations of “silly null” hypotheses abound — like the silly null of no relationship between temperature and sea level rise. If this sounds all cryptic to you, I don’t blame you. Pick up Jaynes (2003), it’s an eye-opener.
As part of his contribution, Stefan tightened up the draft paper to be suitable for submission to Nature. Nature gave us some very helpful reviews which we used to further improve our manuscript. The most useful reviewer remark had to do with the extraction of water from underground aquifers, a process potentially almost as important as the artificial reservoir storage that we did take into account — only, nowhere in the literature was there an equally painstaking accounting exercise to be found as what Ben Chao and colleagues did for the reservoirs. So, we settled for a sensitivity analysis, skillfully whipped up by Stefan.
Nature turned us down, like they do over 90% of manuscripts; had they accepted, the paper would have been out already in summer. We resubmitted to PNAS who obtained three further helpful reviews, the paper was improved yet again and finally published in December. As it happens, this landed it right on top of the Copenhagen meeting.
Stefan tells me that we have exchanged over a thousand emails in the run-up to this paper. I see some poetry in that number being close to that of the East Anglia stolen email selection. Easy, informal email plays a vital role in the work of climatologists, and the loss of trust in its confidentiality could be very disruptive for the science: if the internal discussions of an authoring team would have to be expressed with the same care as the finished product, not a lot of authoring would get done.
Would I have dared, or managed successfully, to submit to a top journal all on my own? Hardly. It is an illusion to think that you can just enter a field that’s not your own and become a productive researcher, whatever you might read or what denialists-of-service may pretend. There is a lot of domain knowledge involved, and precious little of it is simple. In this case, I did learn a lot (and I continue to do so), but this takes both a willingness to learn, and great teachers. RealClimate, and the community it represents, are an indispensable resource for that.
Still waiting for Al Gore’s cheque…
P.s. Over at Nature Stefan has a commentary on sea level today.
References
Martin Vermeer and Stefan Rahmstorf (2009): Global sea level linked to global temperature, Proceedings Nat. Acad. Sci. 2009 vol 106 no. 51 pp. 21527-21532, DOI: 10.1073/pnas.0907765106, open access link
Jonathan Overpeck and Jeremy L. Weiss (2009): Projections of future sea level becoming more dire, Proceedings Nat. Acad. Sci. 2009 vol. 106 no. 51, pp. 21461-21462, DOI: 10.1073/pnas.0912878107 link.
Stefan Rahmstorf (2007): A Semi-Empirical Approach to Projecting Future Sea-Level Rise, Science 315, 368-370, DOI: 10.1126/science.1135456 link
B.F. Chao, Y.H. Wu and Y.S. Li (2008): Impact of Artificial Reservoir Water Impoundment on Global Sea Level, Science, 320, 212-214 link
Edwin Jaynes (2003): Probability theory: the logic of science. Cambridge University Press, ISBN 0-521-59271-2.
Two comments/questions
“The curve of temperature as a function of time over the 20th century has three parts: a steep rise in the beginning, a flat middle part commonly attributed to aerosols, and a very steep upswing at the end.”
Q: What is the difference between “steep” and “very steep” in your statement ?
Second question that I already asked Stefan in the previous post on the subject (sorry, I just discovered the whole topics at this occasion ! ) : do you agree that if there is a very long relaxation time, so that the proportionality of the derivative of sea level to the temperature anomaly is a good approximation , then a sea level rise of around 10 meters throughout the next millenium is already unavoidable whatever we do now, since it is very unlikely that we can contain the warming below 2°C ? ( at zeroth order the rate will continue at least at 3mm*2°C/0.7°C = 1 cm/yr throughout 1000 years in any case)
Martin,
Great post. Its encouraging to see an example of (relative) amateurs and climatologists collaborating together over the internet on a paper. I’m hopefully embarking on something similar myself with remote sensing urbanity proxies and UHI in the near future.
The interdisciplinary nature of climate science really helps in making it possible for folks with different specializations (say, statistical analysis, remote sensing or programming) to work with scientists on projects like these. Tamino’s collaboration with James/Gavin/Mike et al and Nick Barnes and the CCC project are other good examples.
Martin and Stefan:
Fascinating and convincing.
Setting aside your robust projections, the case for warming, to date, is absolutely stunning!
Nice! I second the recommendation of Jaynes 2003, it is very though provoking.
” approach to statistics that is easily misunderstood and often misused. Statistical refutations of “silly null” hypotheses abound — like the silly null of no relationship between temperature and sea level rise. If this sounds all cryptic to you, I don’t blame you.”
Exactly to a high power. Statistics is one of the hardest subjects there is. Don’t expect most people to get anything right in statistics. But everybody should be taught more statistics, starting in the 3rd grade. See: “Probability” by Jeanne Bendix, a book for 8 year olds.
Thanks for this fascinating article. I really enjoyed following how your ideas developed: “Science in the making!”
PS: On my web browser the paragraph beneath the first graph overlaps with the graph and its description.
“Q: What is the difference between “steep” and “very steep” in your statement ?”
I would assume “steep” is a rise that is significant and “very steep” is a rise significantly higher.
Thanks for that article. The historical narrative behind scientific work is impossible to glean from formal publications. The scientists themselves are well aware of the back story because they live it and exchange stories at conferences and, yes, through emails. Science is not some linear process of deduction by Spock-like figures but a more erratic process of discovery and setbacks by humans; stories like this one need to be told more often.
The article shows that, while it is possible for an outsider to make a real contribution to climate science, the biggest barrier to entry is not institutional resistance to new ideas but the difficulty of mastering a new subject.
Also, the fact that the paper was rejected by Nature, even though Stefan Rahmstorf was a co-author, shows that the allegation that scientific publishing is a conspiracy, where the big names get their papers easily nodded through by their cronies while the little guys are the only ones to be rejected, is quite false. Of course this is obvious to any experienced researcher but not so much to outsiders.
[Response: I’ve certainly had more papers rejected than accepted by Nature and Science. And my first two tries got accepted, in 1994 and 1995, although I was single author and completely unknown at the time, with a recent PhD from the quiet scientific backwater New Zealand (sorry friends down under!) and no publication record to speak of. Peer review is not perfect, but it does work to first-order approximation by scientific merit. -stefan]
Excellent narrative, thank you.
I was waiting in suspense to see if the reservoir computation by Chao would come into play, and bingo there it was.
The closeness of fit is amazing, I don’t think I had looked closely at the paper. I wonder does it matter that the (semi-empirical fit) blue curve diverges from the pre-1880 data (red curve)?
I mean in terms of using the obtained relationship to predict future sea level.
There are two articles in Nature Reports: Lowe/Rahmstorf. While Jason Lowe argues the Rahmstorf/Vermeer approach needs to be set against physical plausibility (eg the Pfeiffer et al paper) is it fair to say you don’t disagree fundamentally? Both seem to say in the end that AR4 was too low because it ignored some poorly defined contributions, SLR of 1-2m by 2100 is possible, but >2m is very unlikely.
(clearly there is still some difference of opinion over whether somewhat under 1m or somewhat over 1m is most likely)
[Response: That’s correct – these are respected colleagues and we don’t disagree fundamentally, we just disagree by degrees. And scientists should disagree in this constructive way! Where there’s uncertainty, we debate the strengths and weaknesses of different approaches, we discuss physical plausibility and other issues, people can have different views on those things and that is how science advances. This is the healthy normality of science, it is also why science is so much fun, and the Sunday Times article by Jonathan Leake in January (which I think prompted Nature to invite our commentaries) was complete bogus in claiming that “Climate change experts clash over sea-rise ‘apocalypse’”. But in the meantime we’ve seen more examples of Leake’s special relationship with the truth. -stefan]
Can you comment on this, which is to be published soon.
http://www.jamstec.go.jp/frsgc/research/d2/masayo.ogi/2009GL042356-pip.pdf
[Response: I’ve not read the paper except a quick read through, but I’d say no surprise: “Anticyclonic wind anomalies over the Beaufort Sea during summer favor low September SIE and have contributed to the record-low values in recent summers, perhaps by enhancing the flux of ice toward Fram Strait in the trans-polar drift.” Many scientists have been working on this issue — to what extent was 2007 a freak ‘wind anomaly’ and to what extent is that part of the long term trend? The answer is it’s a little of both. 2007 was ‘sea ice weather’, which can be dramatic from year to year, superimposed on sea ice ‘climate’, which is showing a long term decline (a bit faster than predicted, even if one ignores 2007). This paper seeks to clarify those details and will just be one of many that (I suspect) will reach the same general conclusions.–eric ]
Well done!
Martin,
Thank you for your work and diligence. This article alone is wonderfully illustrative of context and process in care and method.
—
Video: A Climate Minute
History of Climate Science
Arctic Ice Melt
—
Our best chance for a better future ‘Fee & Dividend’
Understand the delay and costs of Cap and Trade
http://www.climatelobby.com/fee-and-dividend/
Sign the Petition!
http://www.climatelobby.com
This is really great to see this, on so many levels :)
Since I’m not actually a blogger (this is the only one I attend), RC is sort of like my family, and it’s as if a family member had made good.
And it’s a feather for RC, that by having this blog, more connections can be made and better science can be advanced.
Also this sheds true light on the arduous peer-review process, esp trying to get into premier journals. There are plenty of top scientists struggling to get published, so lesser scientists should understand it is nothing personal against them or their ideologies.
And this shows how the damaging the effects of stolen and posted emails might have been to this piece of science, had it followed, instead of preceded, the CRU hack. We’ll never know what science could have been in the future without the CRU hack. (I’m wondering if corresponding through some other email format, like hotmail or gmail, might help.)
And last but not least, it’s really great to have some other “thermometer” for global warming, since the denialists take such issue with regular thermometers. So now when they write, “but the temperature data show no warming,” I don’t have to fall back on my “well, look at the ice that’s melting; didn’t you know that heat melts ice?”
Now I can say, “Well, what about the ocean/sealevel thermometer? Even if the sky might lie (and I’m not saying it does), the ocean certainly doesn’t!” It will also make me look smart, because I now know about this great scientific paper.
Magnopere!, Martin & Stefan.
Your seriously cool result reinforces my interest in the possibility of modulating reservoir and lake evaporation and levels in response to future SLR.
Lynn (#14),
Hotmail and Gmail are services provided by Microsoft and Google respectively, not “email formats”. If your current email service is poorly managed, using a reputable service provider instead might help.
But what would really help is encrypting messages you don’t want the world to see. You do not need to use a particular service provider or a special email address to encrypt some of your emails. Encryption is an annoyance but it is worth the bother in some circumstances.
Should we start to evacuate all low-lying areas progressively, is this what they are saying ?
My question is can we expect sea level rise to halt or decline with a decline in mean global temperature? I would like to see some specific predictions if possible.
——-
“At the end of the last ice age, the Earth slowly warmed by 4–7 °C globally14 and lost almost two-thirds of its land ice in the process. That raised sea level by 120 metres, at rates often exceeding a metre per century1. It seems that nothing in the present ice-sheet configuration would rule out similar rates in future15. How much of the remaining 65 metres’ worth of land ice will humans melt if we warm the planet by a further several degrees?”
http://www.nature.com/climate/2010/1004/full/climate.2010.29.html
“In other words, global sea level would be a good global thermometer, but with a ‘quirk’. I could even think of a physical mechanism for such behaviour.”
“Slowly it dawned upon me that, hey, maybe I’m on to something real here, something based in physics: it seems the world ocean can be a remarkably good global thermometer, once you get to know its quirks.”
What do you mean by “good”? Sceptics and alarmists are arguing over small percentage changes in temperatures and you want to use the world’s oceans. Come on!!!!
Lynn Vincentnathan says: 6 April 2010 at 3:45 PM
And this shows how the damaging the effects of stolen and posted emails might have been to this piece of science, had it followed, instead of preceded, the CRU hack. We’ll never know what science could have been in the future without the CRU hack.
Perhaps I’m being too optimistic but I doubt the CRU hack will have much effect on normally unpublished conversations between scientists.
Square kilometers of newsprint were wasted, gigabytes of disk storage and data transfer were poured down a rat hole, several journalists’ reputations needlessly sullied, a Parliamentary committee found its time squandered, finally to what end? None. There was nothing to hide in the first place, no cause for embarrassment, nothing revealed beyond mundane human feelings. Tiptoeing around the thin skins of prima donnas is not in any researcher’s portfolio of responsibilities and it appears failure to do that was the only thing confirmed by all the gullible hue and cry of the past few months. Exact detail of dull gossip was the only new thing exposed to the public eye.
The Senior Laundry Sorter hired by CEI– Chris Horner– has tried a repeat performance of demanding then selectively editing and publishing other people’s emails. Though he loves wallowing in the gutter, Horner’s finding little appetite for his wilted salad of mixed sentence fragments. Once the the first thrill of peering into private correspondence has worn off, crushing boredom is the next and more durable response.
So nothing to hide, no reason to change habits. Smart people recognize this.
[Response: Bold highlighting mine. That pretty much sums it up — well said.–eric]
> what do you mean good?
It’s defined in the paper.
“The impact of Miocene atmospheric carbon dioxide fluctuations on climate and the evolution of terrestrial ecosystems” by Wolfram M. Kürschner, Zlatko Kvaček, and David L. Dilcher:
http://www.pnas.org/content/105/2/449.full
to infer an eventual SLR of about 40–50 meters.
Seattle to become an island at around 10–11 meters SLR.
To expand on my last sentence in #3, above:
Because the oceans occupy a very large portion of the global surface area, and a significant part of the direct radiation is absorbed below the surface, the resulting heating first gets distributed in the mixed ocean layer, before it gets a chance to ‘communicate with’ the atmosphere. That heat remains “in the pipeline” for decades. Part of it is transferred into the atmosphere and then to the land by ‘periodic’ processes like ENSO, AMO, AO, and PDO. These produce large ‘noise’ pulses in the global mean surface temperature (GMST).
Because of the much larger heat capacity of the oceans – in comparison to that of the atmosphere+land – such noise pulses contribute a much smaller fraction to the ocean temperature. And [except for the small lag in the redistribution of volume associated with uneven heating of (various areas of) the ocean], the absorbed heat-induced-volume increase in sea level is ‘instantaneous’. As a result,”the thin red wiggly curve” in the Sea Level vs Time record (in the above Figure) is a much ‘cleaner’ and more robust representation of global temperature trend than is GMST!
Thank you Martin and Stefan!
Martin Vermeer:
On a dark and stormy night in the near future, a black helicopter will land in your backyard. Two men in fine black Armani suits, wearing black sunglasses, will disembark. You will observe that they are handcuffed to a bulky black suitcase, and surrounded by armed and armored guards, also uniformed in black. They will request to enter your home, and show you the contents of the suitcase in your dining room, after the blinds have been closed and the windows covered with black construction paper. You will do as they ask. You will see the suitcase contains US currency. Small and medium bills – $5s, $10s, $20s, and $50s. 11,000 of each. After seeing the money safely secreted away in your safe, they will erase your memory, and vanish into the night, as mysteriously as they came.
[Response: Ah, the ol’ memory erasure! I as wondering where all that cash in my office came from!–eric]
This (and Stephan’s comments in Nature) is a good update on the latest for SLR. However, once again I feel this could be too conservative. This makes no accounting of the potential for positive feedbacks such as methane from tundra. Of course, it is only right that it does not as this is science.
However, as an Engineer, I deal with probabilities of something happening in the future. This requires me to model the likely scenarios. It seems to me that we are already outside the A1B scenario and not likely under the present political atmosphere to be able to get back to it. A1FI is even a bit low for current trends.
Therefore, I feel the risks justify making some sort of assessment as to what might happen if only ONE of the potential positive feedbacks actually occurs. An ALMOST worst case scenario. I would expect there is sufficient expertise under the IPCC to carry out this sort of analysis. Why, when we are asking the world to take the drastic step of abandoning fossil fuels, has this not been done?
This is another pattern for how blogs are actually leading to science. Foster, et al, was another. Well done to all!
Great job. Never imagined a natural phenomenon to produce a 99% Pearson correlation! And now I know which stats handbook to read to get back in shape :-).
CFU “Q: What is the difference between “steep” and “very steep” in your statement ?”
I would assume “steep” is a rise that is significant and “very steep” is a rise significantly higher.”
For me that’s a strange definition, significance is related to signal to noise ratio and not to the absolute value of the slope. But admitting your definition, why is the rise at the end of the XXth century more significant than that at the beginning ?
and for the second question, is it true or false ?
A Rod B sub-thread actually went somewhere!
“However, as an Engineer, I deal with probabilities of something happening in the future. This requires me to model the likely scenarios. It seems to me that we are already outside the A1B scenario and not likely under the present political atmosphere to be able to get back to it. A1FI is even a bit low for current trends.”
The scenario will be mostly constrained by the global amount of fossil fuels we will extract in the century , and this is very poorly related with the current trend. You can relate the current trend with the global curve only with specific hypothesis of the shape of the curve (which can be anything from exponential extrapolation to close peak), and none of these hypothesis has been validated. BTW the “current” trend estimated over the last two years is a – 3% /yr decline.
Gilles #1:
Not necessarily. If by 2100 greenhouse gas emissions have been brought to zero (by that time I expect mankind, or what’s left of it, to have learned its lesson), the CO2 concentration in the atmosphere will start to go down by absorption into oceans and biosphere. As a result, also temperatures will start to go down, but with a delay. Sea level rise will continue as long as temps are above pre-industrial, but at an ever-diminishing rate.
Then, the assumption of a very long relaxation time doesn’t necessarily hold as such. It was found, I think credibly, by Grinsted at al. 2008 that the “infinite” response time scale term a(T-T0) contains a large component with a finite response time scale of several centuries. The instrumental period is too short to discern this, but it too will lead to a gradual levelling-off of sea level rise after several centuries.
Congratulations. Reading the paper I can see why Nature eventually declined. They’re after the new and challenging rather than the refinement, and they seem to prefer much terser constructions. A lot could have been lost as result, so better this way.
I did finally figure the reason for (and implications of) those two different b’s. You might have explained just a little more for us dunces…
As an amateur historian/political scientist, it’s wonderful and quite refreshing for me to see the people and proceses at work here! My sincere thanks.
I’d like to echo Doug’s comments in #20. From what I’ve seen the CRU hack has had more impact outside of science than it has on scientists. Partly I guess because the hack is viewed as an anomalous event – it’ll take more than one or two sets of emails being stolen & published for any real change in behaviour – and partly because, outside climate science & the blogosphere, most scientists I know are only vaguely aware of the details of the hack and, frankly, couldn’t care less.
“[Response: Ah, the ol’ memory erasure! ”
It’s called the “flashy thing”. There’s a big one in the torch of the Statue Of Liberty.
To follow up on Bill’s question (no. 17), what would be the effects, worldwide, of a sea level rise of 124 cm by 2100?
The fact that the number of emails exchanged about this one paper = the entire trove of stolen CRU emails may be a hint of selectivity of the theft.
Your result can’t take into account the threat of a major tipping point, e.g. a large chunk of WAIS floating off, as you hint at the end of the paper. The threat of > 1m sea level rise by 2100 is not a new claim but useful to have further support in the face of the drivelosphere. Good work, and nice that it’s free for all to read.
[spam]
What happens next after this publication ? How is it incorporated into public knowledge and into Govt policy ?
Funny how Gotta didn’t think that
masayo.OGI/2009GL042356-pip.pdf
in his link didn’t have anything to do with the Ogi in this post:
“38
Gotta Believe says:
7 April 2010 at 6:15 AM
Can you comment on the Ogi abstract?”
Then again, it’s a spam link: hosting a sales site and all this barnstack wants to do is sell stuff to the gullible (probably also upping the google rank). Obviously cannot be interested in discussion. Isn’t even listening to what HE says..!
> Gilles … constrained by the global amount of fossil fuels
Please keep it in the one topic you’ve taken over. Not again, please.
> Hunt Janin … what would be the effects, worldwide …
Specific locations expect different results. I gave you cites long ago.
> Bill … what happens next
You read the paper? read the cited papers. Look for more by each author of each paper; watch for new papers citing them over time with Google Scholar.
“At the end of the last ice age, the Earth slowly warmed by 4–7 °C globally and lost almost two-thirds of its land ice in the process. That raised sea level by 120 metres, at rates often exceeding a metre per century. It seems that nothing in the present ice-sheet configuration would rule out similar rates in future. How much of the remaining 65 metres’ worth of land ice will humans melt if we warm the planet by a further several degrees?”
So dramatic sea level rise is not actually unprecedented, and it could rise regardless of what we do?
“But admitting your definition, why is the rise at the end of the XXth century more significant than that at the beginning ?”
Not more significant.
Merely “more”.
As in “4 could be significant. 8 would be significant too. And 8 is greater than 4”.
More.
“and for the second question, is it true or false ?”
Yes.
(where is the second question, or if that WAS the second question, what “it” are you asking for?)
Is it possible that the melting of land ice is, albeit unintentionally, included in this model? There should be some correlation between sea temperature and loss of land ice.
There seems to be no attempt to account for the increased amount of water that should be present in the atmosphere as it warms. Perhaps it is not a significant amount, but it is certainly part of the water balance.
There seems to be no attempt to account for the changes in weight distribution on land, and its effect on land elevation. Resevoir water certainly weighs a great deal, and is believed by some to depress land elevation; this may be one of the factors explaining the faster depression of the US gulf coast than would be predicted by sea level rise alone. Melting land ice is believed to increase land elevation. This may be part of the reason southern Alaska’s elevation is increasing relative to sea level.
I’ve also wondered about the effects of increasing ocean volume: does it cause continents to “float” higher over time? The increasing pressure on the ocean’s bottom perhaps pushes magma under continents.
Hunt (#36),
You keep asking basic questions. Demonstrating that you’ve actually done some research based on the information which has been provided to you might motivate people to give you more substantive answers. Rahmstorf’s latest RC post linked to the report of the Dutch Delta Commission for instance which is very informative. Have you read it? Have you read the IPCC litterature on this topic? Have you looked into the controversies surrounding the expensive public works which are carried out around subsiding locales like New Orleans or Venice (Italy)? Have you read about the effect of SLR on irrigation? And so on…
If you’re undertaking a serious research about this, perhaps you could set up a webpage or a blog about it and lay out some of your findings so as to give back to the community. Perhaps the governments of Bengladesh, Thailand or Nigeria have published pertinent information which has not been adequately communicated to the global public so far for instance. In any case, as a writer, I’m sure you could use your talent to help the public understand the issues you’re researching.
Ed Greisch at comment 5-
Thanks for the recommendation of “Probability” It’s not available from my local library but I will track it down for my 9 yr old.
Good catch by CFU; the blogspambots are getting really nasty here. That one in 38 copied a name used by a previous poster, but put a link to the spam/malware site behind the name, and copypasted apparently relevant text.
Big red flag warning folks:
identical names do NOT mean it’s the same person, or a person at all.
>> “38 Gotta Believe says: 7 April 2010 at 6:15 AM
> it’s a spam link
Needed:
A blacklist reference, one that ISPs or blog owners can use to filter crap.
A tool to compare usernames when repeated and flag inconsistent IP addresses.
A tool to compare the declared user’s blog link to the actual IP posted from.
For Hank Roberts, re #41. I’m very grateful for your input but, understandably, I’d like to know what others think, too. Surely there must be a RANGE of opinions out there…
[Response: Our other commenters have provided you adequate references whereby you can acquaint yourself with the underlying scientific issues. Your pattern of repeat, off-topic commenting is starting to resemble the behavior of a “troll”. Consider this a warning. -moderator]
@ #39 Bill (7 April 2010 at 7:30 AM)
Re public knowledge: it’s up to the newsmedia and science media aimed at the layperson to report items of interest. As well, many non-scientists subscribe to scientific journals in their area of interest (or read them in the library).
Re government policy: Governments have lots of scientific advisers who maintain a watching brief on new science and inform Government Ministers / legislators when something comes up that has implications for policy. Examples of advisers include the various scientific government agencies, Chief Scientists, government scientific advisory panels, special-ists in key roles eg Department of the Premier/Prime Minister and Cabinet etc.
(Plea to RealClimate – would it be possible to do something about the spam filter? Could you at least allow us to edit the post when we use a common word like special-ist? I keep forgetting to copy my post before posting :( )