According to some recent reports (e.g. PlanetArk; The Guardian), the public concern about global warming may be declining. It’s not clear whether this is actually true: a poll conducted by researchers at Stanford suggests otherwise. In any case, the science behind climate change has not changed (also see America’s Climate Choices), but there certainly remains a problem in communicating the science to the public.
This makes me think that perhaps a new simple mental picture of the situation is needed. We can look at climate models, and they tell us what we can expect, but it is also useful to have an idea of why increased greenhouse gas concentrations result in higher surface temperatures. The saying “Everything should be made as simple as possible, but not simpler” has been attributed to Albert Einstein, which also makes me wonder if we – the scientists – need to reiterate the story of climate change in a different way.
Gavin has already discussed this (also see here and here), but it may be necessary to tell story over again, with a slightly different slant. So how can we explain how the greenhouse effect (GHE) work in both simple terms and with a new angle? I also want to explain why the middle atmosphere cools with increasing greenhouse gas concentrations associated with an increased GHE. Here I will try to present a conceptual and comprehensive picture of GHE, explaining both the warming in the lower part of the atmosphere as well as the cooling aloft, and where only the most central features are included. Also, it is important to provide a good background, and we need to start with some very fundamental facts.
Four main physical aspects
Several factors are involved, and hence it may be useful to write a simple recipe for the GHE. This recipe then involves four main ingredients: (i) the relationship between temperature and light, (ii) the planetary energy balance, (iii) the distance light travels before being absorbed, and (iv) the relationship between temperature and altitude.
(i) Temperature and light
Energy can be transmitted in many different ways, involving photons (light or electromangetic radiation), conduction, and motion. Most of these require a medium, such as a gas, fluid, or a solid, but space is basically a void through which photons represent virtually the only form for energy transfer. Hence, planets tend to gain or lose energy to space in the form of photons, and we often refer to the energy loss as ‘radiative heat loss’.
A fundamental law of physics, known as the Planck’s law, says that radiative heat loss from any object depends on its temperature. Planck’s law also explains the colour of the light, or its wavelength, and hence explains why iron gets red hot when heated sufficiently.
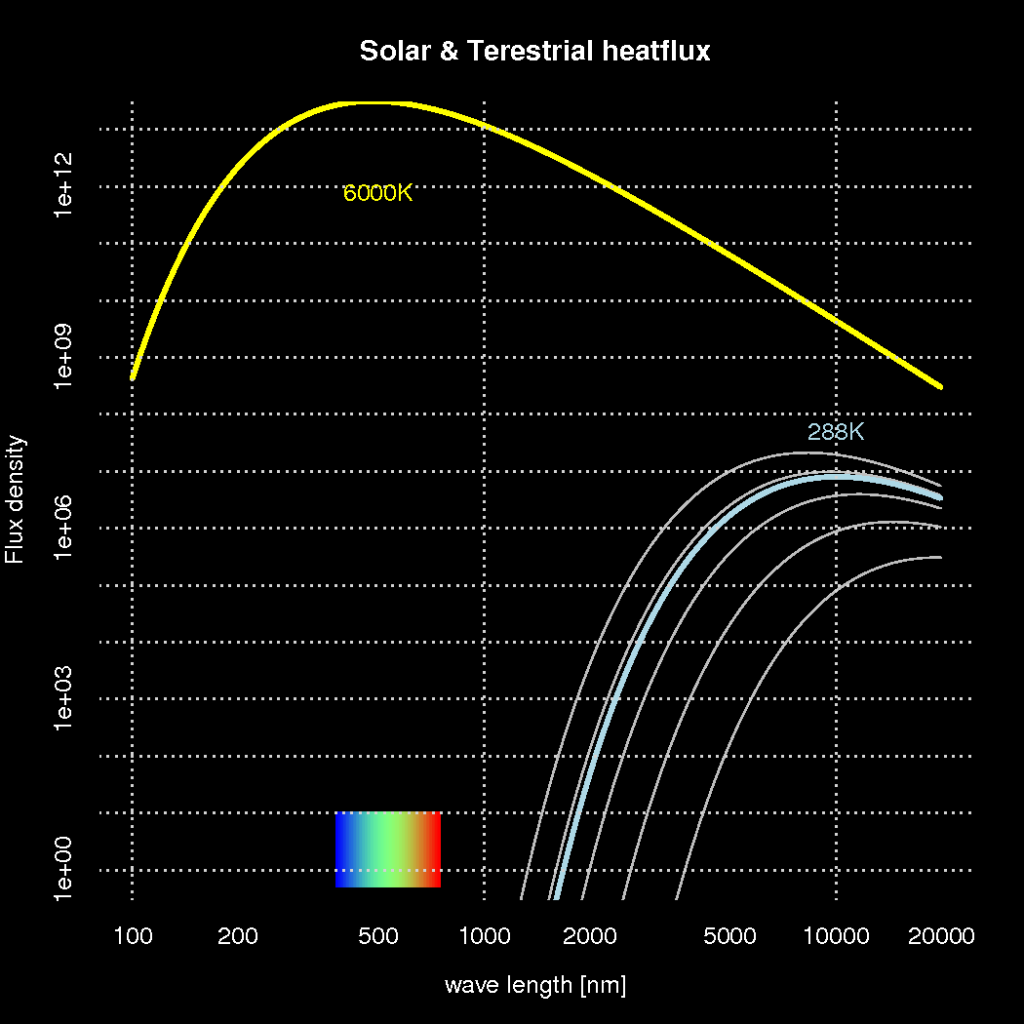
Planck’s law predicts that the light from an object with a temperature of 6000K – such as the solar surface – produces light that is visible, whereas objects with a temperature of 288K produce light with a wavelength that our eyes are not able to see (infra red). This is illustrated in Figure 1 showing how the light intensity (y-axis; also referred to as ‘flux density‘) and the colour of the light (wave length) vary for objects with different temperatures (here represented by different curves). The yellow curve in the figure represents the solar surface and the light blue curve the earth.
(ii) The planetary energy balance
The planetary energy balance says that our planet loses heat at the same rate as it receives energy from the sun (otherwise it would heat or cool over time). This is because energy cannot just be created or destroyed (unless it involves nuclear reactions or takes place on quantum physics scales).
The planets’ distance from the sun and the brightness of its surface dictates how much energy it receives from the sun, as the light gets dimmer when it spreads out in space, as described by Gauss’ theorem.
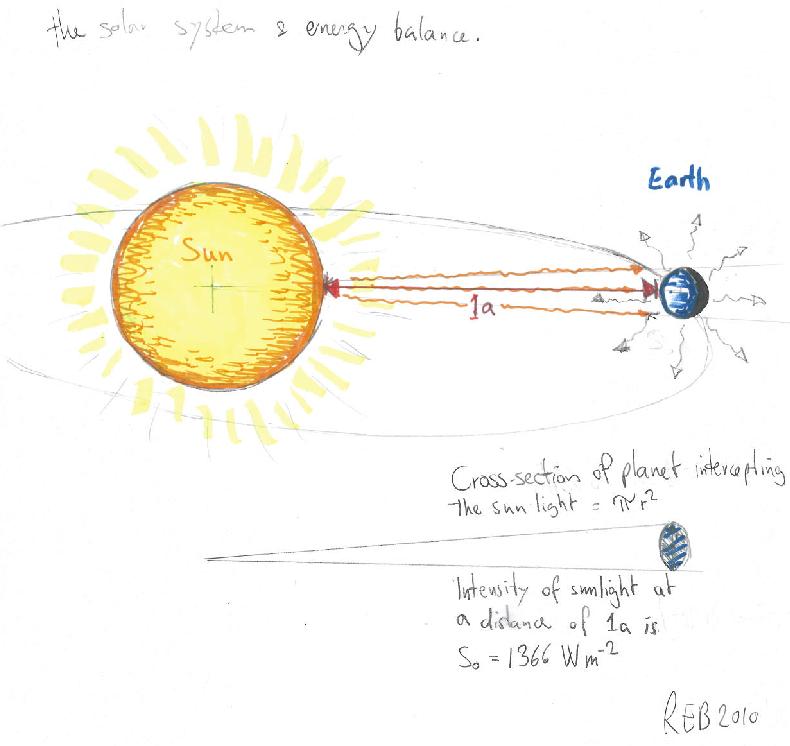
The energy flowing from the sun is intercepted by the earth with energy density described by the ‘solar constant‘ (S0=1366W/m2), and the amount of energy intercepted is the product between this flux density and the earth’s disc (minus the reflected light due to the planet’s albedo: A ~0.3). The average heat loss is given by the product of earth’s surface and its black body radiation:
S0/4 (1-A) = σT4,
where σ=5.67 x 10-8W/(m2 K4) is the Stefan-Boltzman constant. This gives a value of 255K, known as the emission temperature.
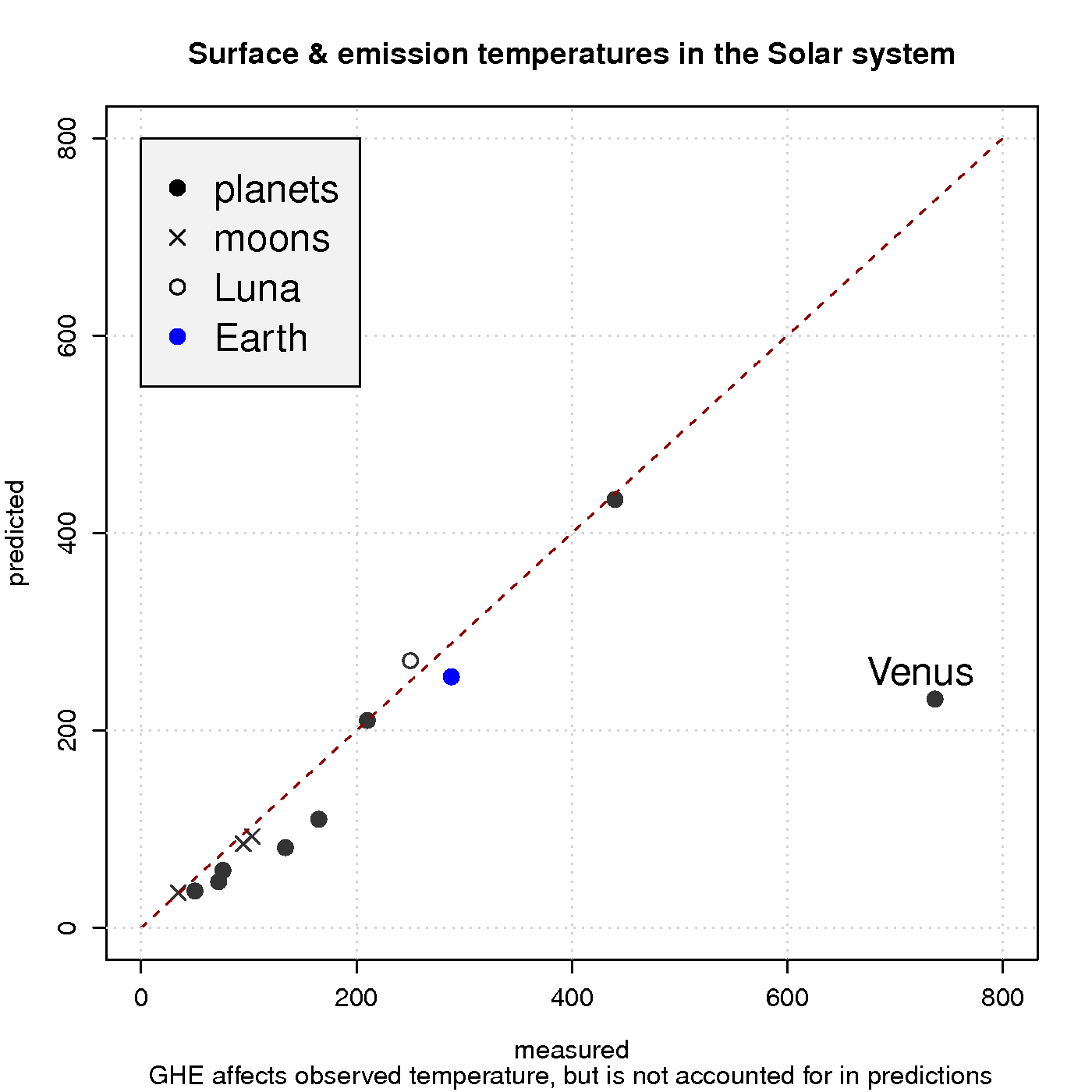
Figure 3 shows a comparison between observed surface temperature and calculated emission temperature for the planets in the solar system, based on the balance between energy from the sun and heat loss due to black body emission. In these simple calculations, the greenhouse effect is neglected, and the black body radiation can be derived from Planck’s law. The calculations agree quite well with the observations for most of the objects in our solar system, except for Venus which is known to harbour a strong GHE and has a hotter surface than Mercury despite being about twice as far away from the sun.
(iii) Light absorption
It is also clear that our planet is largely heated at the surface because the light from the sun – which is visible for our eyes – penetrates the atmosphere without much absorption (hence we can see the sun from the ground). However, the atmosphere is a medium of gas and particles that can absorb and scatter light, depending on their wavelength (hence explain why the sky is blue and sunsets orange).
The distance light travels before being absorbed – optical depth – can vary with the light’s wavelength and the medium through which is travels. The optical depth in our atmosphere is different for visible and infra-red light.
Infra-red light is absorbed by molecules, which in turn get more energetic, and the excited molecules will eventually re-emit more infra-red light in any random direction or transfer excess energy to other molecules through collisions. In a optically thick (opaque) atmosphere, there will be a cascade of absorption and re-emission.
Hence, whereas the planet is heated at the surface, it’s main heat loss takes place from a height about 5.5 km above the ground, where most of the radiation is free to escape out to space. The optical depth dictates how deep into the planet’s atmosphere the origin is for most of the planet’s infra-red light (the main planetary heat loss) that can be seen from space. Furthermore, it is the temperature at this level that dictates the magnitude of the heat loss (Planck’s law), and the vertical temperature change (lapse rate) is of course necessary for a GHE. The temperature at this level is the emission temperature, not to be confused by the surface temperature.
We know that the optical depth is affected by CO2 – in fact, this fact is the basis for measuring CO2 concentrations with infra-red gas analysers. Molecules composed of three or more atoms tend to act as greenhouse gases because they can possess energy in terms of rotation and vibrations which can be associated with the energy of photons at the infra-red range. This can be explained by theory and be demonstrated in lab experiments. Other effects are present too, such as pressure and Doppler broadening, however, these are secondary effects in this story.
(iv) The relationship between temperature and altitude
There is a well-known relationship between temperature and height in the troposphere, known as the ‘lapse rate‘ (the temperature decreases with height at a rate -6K/km). The relationship between temperature and altitude can also be seen in the standard atmosphere. The lapse rate can be derived from theory for any atmosphere that is the hydrostatically stable condition with maximum vertical temperature gradient, but it is also well-known within meteorology. Thus, given the height and value of the emission temperature, we can get a simple estimate for the surface temperature: 255K + 5.5km * 6K/km = 288K (=15oC; close to the global mean estimated from observations given by NCDC of ~14oC).
Enhanced greenhouse effect
The term known as the ‘enhanced greenhouse effect’ describes a situation where the atmosphere’s becomes less transparent to infra-red light (reducedincreased optical depth), and that the heat loss must take place at higher levels. Moreover, an observer in space cannot see the infra-red light from as deep levels as before because the atmosphere has become more opaque.
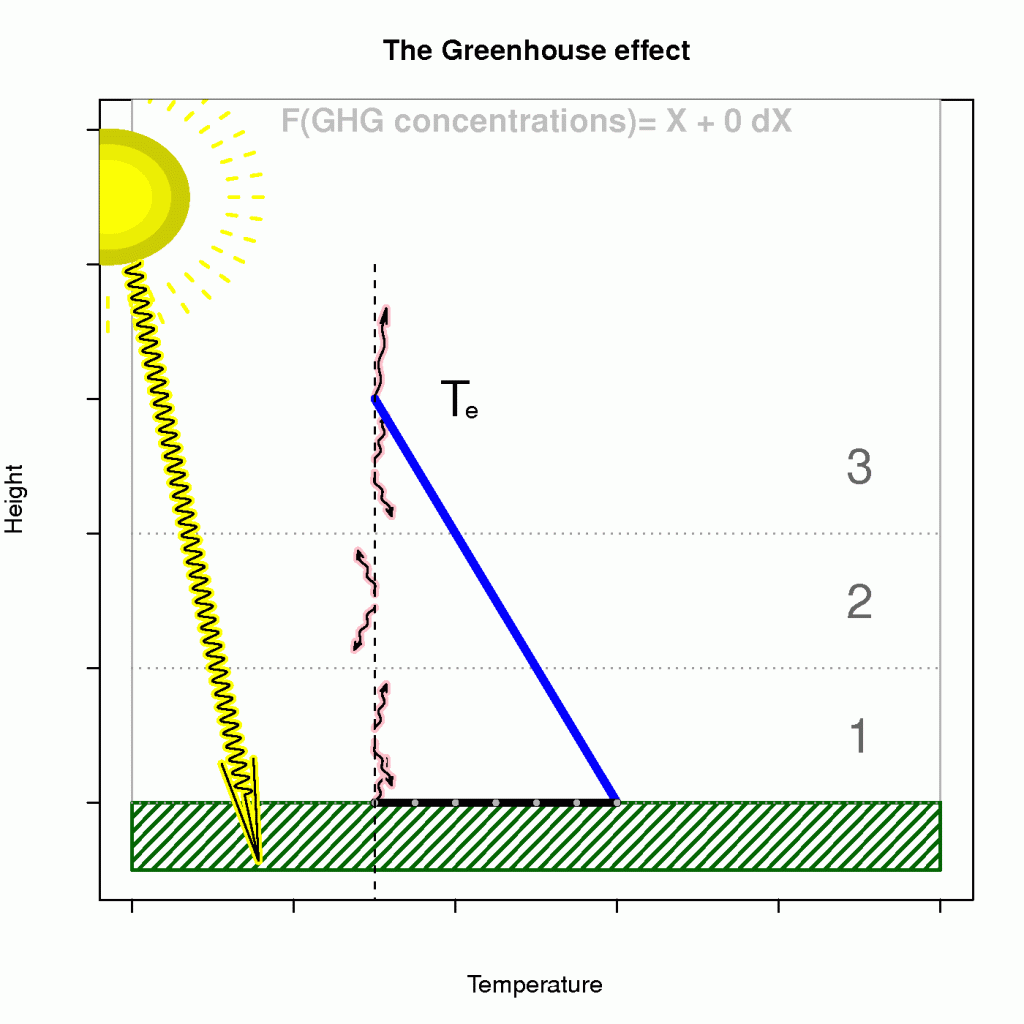
The effect of heightened level of heat loss on the surface temperature is illustrated in Figure 4, where the emission temperature and lapse rate are given if we assume an energy balance and a hydrostatically stable atmosphere on average (a generally hydrostatically unstable atmosphere would be bad news).
Hence, a reducedincreased optical depth explains why atmospheres are not easily ‘saturated‘ and why planets such as Venus have surface temperatures that are substantially higher than the emission temperature. Planets with a thin atmosphere and insignificant greenhouse effect, on the other hand, have a surface temperature that is close theto the estimates from the planetary energy balance model (Figure 3).
Feedback processes
The way the atmosphere reacts to changes in the optical depth is more complicated, due to a number of different feedback mechanisms taking place. But to get a simple overview, it is useful to keep in mind that the optical depth is sensitive to how much water vapour (humidity) there is in the air, and that the lapse rate is sensitive to the composition of the atmosphere (i.e. humidity). Furthermore, the albedo A is affected by clouds, snow, ice, and vegetation, all of which affect the way the earth receives energy from the sun.
In our simple picture, feedback processes affect changes in the height of the level where most heat loss takes place, the slope of the lapse rate, and heating at the surface (and hence the emission temperature).
So why is the upper atmosphere cooled then?
The upper atmosphere, comprising the stratosphere and mesosphere, is expected to cool during an AGW, as shown by the GCMs. So what is happening there? This is when the picture becomes more complicated.
Since CO2 mostly absorbs/re-emits infra-red light at around 14 microns, an increased concentration in the troposphere will reduce the upward infra-red radiation at this band. The total energy is roughly constant, but it is made up from increased emissions at other bands because it’s warmer. There is less absorption by CO2 of upwelling infra-red light above the troposphere, but increased emission as a function of increased concentrations. Thus there is a cooling.
Controversy?
Can this picture be falsified, e.g. if other factors were to play a role too? For instance, can this situation be altered by changes in the sun?
Changes in the sun can of course affect the amount of energy received by the earth through changes in its output, variations in the intensity of UV-light, or perhaps even clouds through galactic cosmic rays. But it’s hard to see any systematic long-term trend in the level of solar activity over the last 50 years, and it is difficult to see how solar activity may have an effect while other factors, such as GHGs, don’t. Gavin and I recently published a study on the response to both solar activity and GHGs, and found similar magnitude for both forcings in both observations and the GISS GCM.
There have been claims of negative feedbacks, such as the “iris effect“. One would expect negative feedbacks in general to dampen the response to most forcings, unless they involve a particular process that is active for a particular forcing. In other word, why would a negative feedback act for GHGs but not for solar forcing? Many feedbacks, such as changes in atmospheric moisture, cloudiness, and atmospheric circulation should be similar for most forcings.
Another question is why we do see a global warming trend if the negative feedbacks were most important (Figure 5). Negative feedbacks usually imply quiet conditions in a complex system, whereas positive feedbacks tend to lead to instabilities, often manifested as internal and spontaneous oscillations (see Figure 5). It is reasonable to expect the feedback processes to affect natural variations as well as forced changes such as an enhanced GHE, orbital changes, volcanoes, or changes in the sun.
The point about negative feedback also brings up another interesting issue: Negative feedbacks usually act to restore a system to a particular zero-level state. What would the zero-state be for our climate? No greenhouse effect or some preferred level of greenhouse warming? There is already a natural GHE that, together with other atmospheric effects, can account for about 32oC higher global mean surface temperature. What makes this state so special, and can we explain the present natural GHE in the presence of negative feedbacks (consider starting from a state with no GHE)?
Hence, claims of negative feedback is controversial because all these tough questions then need to be addressed. We can write down a simple recipe for the GHE, but it is indeed challenging to reconcile a presence of a negative feedback with our observations, or explain the current observed global warming in any other terms.
On point (iv) there is an implication of this that confuses me. This is due to the fact that the atmosphere warms with height in the stratosphere [because of the ozone layer].
In this explanation what is changing is the altitude at which emission occurs, and at higher levels it is colder, so this level needs to warm up to maintain the radiative balance; what would happen once the altitude of radiative emission reaches above the tropopause?
Then temperatures increase with height, so the atmosphere presumably emits more energy, and it would force a cooling..?
Perhaps this isn’t an issue because it would take an impossibly large amount of CO2 [and water vapour] for the emission altitude to reach the tropopause, but it’s an aspect of this sort of explanation that I haven’t been able to work out in my head.
[Response: One key difference is that the troposphere feels warming from below, whereas the stratosphere receives a good portion of the energy from absorption of UV-light. If you contrast the temperature relationship in the troposphere with that of the ocean, you also see different characters, again because the ocean is heated at the top. When the level reaches the tropospause, then this simple picture gets more complicated – after all, I’m only trying to follow the advice “Everything should be made as simple as possible, but not simpler” and try to present a simple comprehensive picture of the situation. -rasmus]
This post was far too complex. Too long, too much math, too advanced for 99% of the population.
[Response: Not everything needs to be written for everyone to understand. Indeed, if we did that we’d rightly be accused of over-simplification and avoidance of complexity in order to bamboozle people ;) Thus, we need to provide information at all different levels. This is not difficult but organising search engines and blogs to reflect that hierarchy is tricky. All suggestions welcome. – gavin]
This is an excellent and cogent summary of basic GHE principles. I would take exception, however, to the explanation offered for stratospheric cooling consequent to increasing atmospheric CO2. In fact, as the atmosphere warms, the “atmospheric window” tends toward closing (particularly because of water vapor effects), and excess escape through this window can’t account quantitatively for the reduction in stratospheric temperatures. A better quantitative explanation appears to involve the presence of upper stratospheric ozone, which absorbs solar UV and visible radiation, warming the stratosphere. That heat must be dissipated to space, and CO2 (which does not absorb in the UV or visible range), adds to the emissivity of the stratosphere at the warmed temperature, while adding much less to the absorptivity. The net effect is essentially that CO2 acts as an escape valve for ozone-trapped heat. In the absence of ozone, added atmospheric CO2 would be expected to warm the stratosphere slightly rather than cool it. (Note that this phenomenon is distinct from the cooling expected from ozone depletion, an entirely separate entity).
[Response:Upper atmosphere cooling as a function of increased CO2 occurs at all levels including the mesosphere, implying directly that the mechanism can’t rely on the presence if ozone or absorbtion of solar uv. -gavin]
I believe that some of the quantitation regarding CO2-mediated cooling can be found in Raypierre’s forthcoming book, “Principles Of Planetary Climate”, due for release in January 2011.
What do you mean by “reduced optical depth” in the sentence “Hence, a reduced optical depth explains why atmospheres are not easily ‘saturated'” ?
Why “reduced” ? (it increases with increasing CO2, isn’t it?)
[Response: http://en.wikipedia.org/wiki/Optical_depth ]
All great stuff if you are a professional or amateur scientist talking to peers or policy makers. Useless if you ar trying to reach Joe Public.
The public are not interested in scientific explanations of the mechanisms, they are interested in the outcome (i.e. the results). More and more data, charts and explanations will simply turn them off.
Try this…one sentance along the lines of ‘Emissions of CO2 and other gases from the buring of fuels allow more sunlight to be trapped by our atmosphere and causing the earth to warm up. Done.
Follow up with relentless and overwhelming numbers of photos of the effects, from Greenland ice moulins to coastal storms to droughts, with comments from locals experiencing these changes.. ‘before’ and ‘after’ are good.
The public will relate to this so much better……and this advice comes from a data junky and trained scientist.
[Response: Thanks for this feedback! To me this is a simple physics exercise, but I do appreciate that it required a bit of training in physics. On the other hand, sometimes it may be useful to reach different segments of the society, and with this post I aimed for the more scientific/technological literate part. I’ll, however, try to write simpler posts in the future more aimed for the average Joe and Mary. -rasmus]
Many thanks to Rasmus for this delightful essay.
The “Iris effect” as proposed by Lindzen is upside down. The more the tropical seas are warm, the more cloud seeds are propagated world wide (I propose the “anvil Seeding theory”), the more Cirrus clouds should be. Precluding cloud seeds, why would, there be less cirrus clouds ? Given warmer seas convective moisture is more shared with the atmosphere. I have read a direct relationship between the number of thunderstorms and El-Nino peaks, which basically confirms
increase cloudiness during El-Ninos. Given that Cirrus clouds are formed in no small part by thunderstorms,
I am at a loss to explain how there should be less Cirrus clouds.
Also there is a link between ENSO cloud driven events and time of year they happen, an El-Nino during winter is best for heating the planet, as opposed to a summer El-Nino, as those in North America may remember summer 2009 great cloudiness (thus cooler wetter summer, as opposed to El-Nino continuing during winter, causing Canada’s warmest winter in history for 2009-2010.
in the “Enhanced greenhouse effect” section you say…
The term known as the ‘enhanced greenhouse effect’ describes a situation where the atmosphere’s becomes less transparent to infra-red light (reduced optical depth)
shouldn’t that be increased optical depth? (i.e., less transparent = increased optical depth) or am I missing something that should be obvious?
[Response: A
reducedincreased optical depth means that the distance you can see things gets smaller – just like murky water which doesn’t let you see the bottom at depth greater than the very shallow parts. -rasmus]tl;dr
That will be the response from your target audience, I fear. And that’s the problem with communicating climate science: the irreducible complexity.
This article is a fascinating angle on the greenhouse effect, and I will give it more attention when I have time. But don’t fool yourself that it is accessible to the general public. Only people with a scientific bent or a strong existing interest in climate change will make it more than half the way through.
[Response: I think you are right about this – but sometimes we also need to try to reach the people who have more training in physics. It also serves to show that certain issues – at least in my mind – are inherently complex and can only be simplified to a certain degree. Hence my reference to the quote from Einstein. -rasmus]
On that Einstein quote: It is from Albert Einstein: On the methods of mathematical physics, Philosophy of Science, vol 1 (1934) 163–169:
“The basic concepts and laws which are not logically further reducible constitute the indispensable and not rationally deducible part of the theory. It can scarcely be denied that the supreme goal of all theory is to make the irreducible basic elements as simple and as few as possible without having to surrender the adequate representation of a single datum of experience.”
Sorry for the slightly off-topic comment.
Thanks much, especially for the downloadable paper. You have made a Great explanation that I can direct some people to. I like your post, but it is too difficult for most people. It has numbers in it, and even worse, equations! Figure 1 has something unfamiliar to most people, wavelength. For that matter, graphs are too hard. ANY graph is too hard. Also, you require a reading comprehension level above second grade, and it is too long for the average attention span by about 4 or 5 times. Optical depth needs to be explained by means of a series of pictures in fog of various densities. Spell out all acronyms every time. Use no acronyms because they require memory.
Use second or third grade students at bad public schools as your test subjects, a different group for each test, and re-write until the students can understand it on their own. Then you will be ready to go public.
Publish as a second grade reading book for all ages and distribute free to elementary schools. Better yet, make it into an animated movie because you shouldn’t assume literacy, never mind numeracy. Keep the movie at the first grade level. Test on first grade students to see if they continue to pay attention until the end of the movie. Hire Bugs Bunny as your narrator.
I think your description of the cooling effect Rasmus is a bit poor!
But having been confused about it, I found Grumbine has one that makes more sense to me. The rest of your post is OK though.
I’ll now have to change my own description of the green house effect on my blog. One day I’ll have it perfected.
I agree that the scientific community should help the general public understand the fundamentals of climate change. And you have presented a very good start.
But, I fear that the article is too complex for the average citizen. I’m not a technical writer, but I would guess that this article is written at a college level. Most Americans read at a much lower level (jr high school level?). Average citizens of other countries are probably at a similar or even lower level.
I find that most people get the concept of the greenhouse effect – that’s why greenhouses work, and why opening the window shades on a sunny winter day helps warm the house.
The most common argument (or point of disbelief) that I hear against AGW is that humans cannot possibly affect something as vast as the global weather. Their view is that the atmosphere is so big and our output of greenhouse gasses is so small. This is the dilution-is-the-solution-to-pollution belief.
A nice added topic would look at the effects of “baseline” (pre-industrial) greenhouse gas levels and 1.5X, 2X, 3X concentration effects. The calculation of burning fossil fuels is straightforward and shows how the atmospheric concentration levels increase.
“A completely transparent medium has an optical depth of zero.”
http://www.daviddarling.info/images/optical_depth.gif
(image credited to NASA)
http://www.daviddarling.info/encyclopedia/O/optical_depth.html
To elaborate on my comment # 3 above, the mechanism for stratospheric cooling consequent to increased atmospheric CO2 appears to be one of the most misunderstood elements of the greenhouse effect. The primary mechanism is attributable to the role of CO2 in discharging heat in the upper stratosphere that results from ozone absorption of solar radiation in mainly the UV plus some in the visible range. – i.e. a “safety valve” for ozone-absorbed heat. Without ozone, added CO2 is predicted to warm rather than cool the stratosphere. Gavin has suggested that the mesosphere would also cool, and while I’m not familiar with the observational data, this result would not be inconsistent with the theorized mechanism, as well as the presence of ozone in the mesosphere.
I hope Raypierre will forgive me for quoting from a recent draft of his upcoming book, “Principles Of Planetary Climate”, where more quantitation is provided. The passages relevant to solar absorption by ozone are the following:
“The solution in Eq. 4.56 also explains why human-caused increases in CO2 over the past century have led to tropospheric warming but stratospheric cooling, as illustrated in Figure 1.17. Increasing the greenhouse gas concentration is equivalent to increasing tau(at infinity). If one plots temperature as a function of pressure for a sequence of increasing tau, the phenomenon is immediately apparent in cases where the upper level solar absorption is sufficiently strong. The behavior is explored in Problems ??. Without solar absorption, increasing tau warms the atmosphere at every level, though the amount of warming decreases with height as the temperature asymptotes to the skin temperature. With solar absorption, however, the increased infrared cooling of the upper atmosphere offsets more and more of the warming due to solar absorption, leading to a cooling there.”
[Response: Perhaps Ray will chime in, but this model (which does not deal with the spectral nature of the emissions) is not a good explanation of the stratospheric or mesospheric cooling, even if it might show similar behaviour in a grey body atmosphere. – gavin]
Is the simple metaphor (“model”) of a thicker blanket reducing the temperature above the sleeping person correct? Or is it wide of the mark?
Thanks, Don
Too complicated for many purposes. How about:
In the absence of carbon dioxide and other greenhouse gases, the temperature of a planet depends on how far away it is from the sun. As we know from laboratory experiments, mathematical calculations, and observations of Venus and other planets in the Solar System, greenhouse gases change things in two ways: they trap heat from the sun in the lower atmosphere, thus making the surface of the planet warmer; and they keep heat from rising, thus making the upper atmosphere colder. This pattern of warmer below, colder above is just what we’ve observed over the last century as the concentration of carbon dioxide in the atmosphere has increased. That’s why scientists don’t believe that an increase in the strength of sunlight is causing the warming of the Earth. It isn’t just that there is no evidence that the sun is shining any brighter. A hotter sun would warm the whole atmosphere, but we know that the upper atmosphere has been cooling. Incidentally, we also know that the extra CO2 results from human activity because lab tests can tell the difference between CO2 produce by burning fuel and CO2 that comes from other sources.
Global warming is definitely happening; it’s not surprising; and we’re causing it.
When you say the optical depth is the depth at which (on average) a photon is absorbed, shouldn’t that be absorbed or scattered. Either way direct beam radiation is reduced, although only the former process results in heat transfer. At least in the visible range (SW to climatologists) scattering is important.
Doesn’t Fred’s argument at (3) carry some truth? The excess warmth of the stratoshere is due to absorption of primarily UV. And the energy is lost via IR thermal radiation. So more CO2 means more thermal radiation from this optically thin region. Of course having lower IR radiation in these bands is also a negative feedback. But it should be possible to quantify the effects of these feedbacks. I would think thermal radiation in an optically thin stratosphere would scale lineraly with CO2 concentration.
Re 1 Timothy – the idea of an effecive emitting altitude is a useful though rough approximation – the photons leaving for space originate over a range of altitudes at any given frequency (wavelength), and that range shifts over different wavelengths.
The condition that portions of the upper atmosphere are significantly warmer than otherwise via direct solar heating should (so far as I know) enhance the GHG-induced cooling at those levels. In the absence of solar heating, there is an equilibrium ‘skin temperature’ that would be approached in the uppermost atmosphere (above the effective emitting altitude) which is only dependent on the outgoing longwave (LW) radiation to space in the case where optical properties in the LW part of the spectrum are invariant over wavelength (this skin temperature will be colder than the temperature at the effective emitting altitude). But when optical properties vary over wavelength, the equilibrium skin temperature will be different.
There is also a difference between the cooling that initially occurs in the stratopshere and above when a change in GHG forcing occurs, and the ultimate equilibrium cooling (relative to prior to change in forcing), which may tend to be smaller. The upper atmosphere has a small heat capacity and reaches equilibrium temperature in considerably under a year; this feeds back on the forcing of the trosphere+surface, which are generally convectively coupled with the ocean (strongly with the upper ocean) and take a number of years to reach equilibrium. During that process, upward LW radiation reaching the upper atmosphere will increase (depending on albedo/ solar heating feedbacks), which will change the equilibrium temperature of the upper atmopshere again. In the case where there is a skin temperature that only depends on solar heating of the planet with no solar heating above the troposphere, an increase in GHG forcing would still result in upper atmospheric cooling, but this cooling would only be transient.
If there is significant solar heating below the tropopause level then there must be a significant net LW flux up through the tropopause (assuming relatively small convective or kinetic energy transfer through that level), so increasing GHG optical thickness can never saturate the tropopause level forcing at all LW wavelengths (by bringing net LW flux at tropopause to zero) in an equilibrium climate. What could hypothetically happen if a very large change in GHG amount/type is made, is that the forcing could increase beyond a point where it becomes saturated at the tropopause level at all wavelengths – what can happen then is that the equilibrium climate sensitivity to the nearly zero forcing from additional GHGs may approach infinity, because in equilibrium the tropopause has to shift upward enough to reach a level where there can be some net LW flux up through it.
How long does a CO2 molecule at 5.5 kms height hold on to that absorbed IR photon before it is released (emitted or transferred though collision to another atmospheric molecule)? How far does an emitted photon travel before it is absorbed again by another molecule? What happens to a non-GHG molecule when it absorbs a photon by collision from a GHG molecule? Do the non-GHG molecules also re-emit those absorbed photons?
I’ve read that the average molecule at sea level experiences 10 billion collisions per second and the length of time a CO2 molecule holds onto an absorbed IR photon is between 1 picosecond (trillionth of a second) to 10 microseconds (millionth of a second). Surely at the quantum level, there is more going on here.
What I like for visualization purposes is to think of greenhouse agents (gases or other) as acting like macroscopic particles – for ease of reference, let’s say Ping-pong balls – suspended in the air. These balls are completely opaque and have a ‘color’ depending on temperature. (To illustrate scattering, through in some mirror-balls and prisms) At any one wavelength The amount of radiation (at that frequency) coming from a direction is equal to the ‘color’ you see. A higher density of these objects reduces the distances that you can see, so that the amount of radiation coming from a direction depends more on the ‘color’ nearby and less on the ‘color’ farther away.
Alternatively, think of an incandescent fog…
I agree that it does not have to be understood by everyone – it´s well within the grasp of an engineer or medical doctor, I think.
I believe that educated people that understand these basics make for good multiplicators of the available information.
Re 15 Don – that can be a part of it. In the most general sense, upper atmospheric cooling is a response to a forcing (reduction in net upward LW + SW radiation) that falls with height through the upper atmosphere.
Great post rasmus.
I don’t agree with some of the comments above who feel that the rasmus’ explanation is too technical, and actually I think it is something that could be understood by a majority of the interested public. It’s a bit more complete than simple cartoons that have a yellow arrow coming into the surface and a red arrow bouncing off the surface and hitting the atmosphere, but it also leaves room for the curious reader with some background to read more into the details of radiant spectra and the influence of the lapse rate, feedbacks, etc that are developed in upper-level undergraduate and graduate texts. In fact it’s one of the easiest ways you can explain the greenhouse effect without over-simplifying it to the point of being wrong. Virtually the entire post is well-rooted in theory and does not require full blown General Circulation Models to appreciate, and my guess is that the general reader will take more kindly to such simple models which can be understood completely.
Fred– hi, it is nice to see you here! You should post more often. I do hope raypierre drops in. Keep in mind the section in raypierre’s book to which you refer strictly applies to an atmosphere where the absorption is independent of wavelength. There cannot be stratospheric cooling in a grey atmosphere with more CO2 (neglecting upper level solar absorption), but in more realistic radiative models (with a window region around 10 um) this phenomena can emerge from increased opacity (And shielding of radiation into the stratosphere) in the 15 um spectral region and increase in the 10 um flux from the ground as the surface is made warmer. The stratospheric emission must be in a limited wavelength band to get cooling and still satisfy planetary energy balance.
I beg to disagree with the basic thesis of this article: that the public are becoming more sceptical about climate change through a failure to understand the science. Most sceptics who are capable of understanding the science accept that GHGs increase temperatures.
Those who understand the science also realise that the increase of temperature in the mid 20th and in the late 20th century were similar, that the current rate of sea level rise is similar to rates at other times in the 20th century. They realise that Arctic sea-ice is low but that the Antarctic ice is at maximum. Until the climate science community explicitly explains why such facts do not invalidate the claims of accelerating climate change their case will remain weak.
It is also a fact that sceptical authors tend to produce more interesting books which tell, possibly fabricated, tales of deceit and skulduggery. There is a crying need for the climate change community to produce popular books that rebut those charges which have got traction with the public.
I remember that Phil Jones said that the Russians and the Japanese also have global temperature records that were a close match to the better known records. I searched for them a while back but had no luck. Can they be accessed online?
I thought I understood the GHE but this article totally confuses me. I am an outsider in this field but I thought that I know at least the basics. So, here is my newbie question:
Fig 1 shows earth receiving higher levels of infrared radiations from sun then the infrared radiation emitted by earth. If this is true then an increase in GHG would cool the Earth. What am I missing?
[Response: The ‘Near IR’ that is part of the solar input to the system is not significantly absorbed by CO2 (though there is some absorption by water vapour). However, absorption of incoming IR does not significantly affect the greenhouse effect or even the surface temperature because of the dominance of convective activity in setting atmospheric temperature gradients. – gavin]
On the Stanford poll at the top of the post: I note that only 1% of Americans think that temperatures have risen but that human activity is not responsible.
This is encouraging, because the 25% who do not “believe” that temperatures have risen are plainly in denial; the evidence for warming is so strong that just about all the prominent so-called sceptic scientists acknowledge it.
Why is this significant? So much emphasis is placed on this 1% position by the deniers, but it simply isn’t an idea that we need to address. Hardly anyone is silly enough to think that temperatures are rising but we didn’t do it. So, what is the real issue for this 25% (up from 15%) of deniers? I suspect it is a political issue for most of them.
Krosnick has a complicated theory about trust and scientists. While no doubt it is true for some people, I feel that politics and plain ignorance of global temperature and region variation plays a much larger role.
Gavin – I don’t mean to belabor the topic of STRATOSPHERIC COOLING (see #3 and #14), but it seems to be an important area of both interest and uncertainty for many people, and so I’d like to pose one more set of comments/questions to you before exhausting my own familiarity with the topic. I believe many readers may appreciate an informative discussion.
Consider, as a thought experiment, an isolated layer of atmosphere, insulated from major conductive or convective influences or other non-radiative processes. Imagine that its only radiatively active moiety is CO2 – no ozone, no water to speak of, etc. – so that its temperature is determined by the balance between absorption of incoming infrared by CO2 and emission of infrared out of the layer by CO2. Do you agree that if CO2 is added to this hypothetical layer, with no change in infrared entering the layer, the layer will warm due to increased absorption, until a new steady state is reached wherein the higher temperature restores emission to a level once again equal to the incoming radiation?
[Response: Yes. – gavin]
Conversely, imagine a different scenario in which much of the heat in the layer comes from something else (e.g., ozone). Again, adding CO2 will increase absorption of incoming infrared (also absorption of ozone-emitted infrared within the layer, but the spectra are different and so that effect is small). Now, however, the extra CO2 does more than radiate away heat due to its own absorptive properties, but also can radiate away heat from the other source. Do you agree that when the heating effect of extra CO2 is due almost exclusively to what it itself absorbs from outside, but the cooling effect entails an ability to dissipate heat from the additional source, cooling can now outweigh warming?
[Response: Depends on the relative size of the two effects. – gavin]
To summarize this concept, do you agree that when a layer’s temperature is due to heat absorbed by CO2 alone, more CO2 will increase the temperature, whereas if the temperature includes heating from something else as well, more CO2 can help rid the layer of that extra heat?
[Response: Yes, but this is not the same as deciding whether increasing CO2 will cause an increase or decrease of temperature. Especially not in the stratosphere or higher where the spectral issues are dominant. – gavin]
Finally, in what ways do you believe the stratosphere is behaving differently from this hypothesized layer, and what data are available to confirm alternative explanations? To the best of my knowledge, increased atmospheric CO2 does not appreciably reduce the flux from below of CO2-absorbable infrared into the stratosphere when a new steady state is achieved at the higher CO2 concentration. Rather, the flux is restored through warming of the troposphere and surface. Thanks.
I don’t think these thread comments have much validity:
“All great stuff if you are a professional or amateur scientist talking to peers or policy makers. Useless if you ar trying to reach Joe Public.”
“This post was far too complex. Too long, too much math, too advanced for 99% of the population.”
If that’s so, why was Steven Hawking’s “A Brief History of Time” so popular, selling over 9 million copies? People appreciate clear scientific explanations, generally speaking – which is why popular science books continue to be top sellers.
The public could probably handle even more detail than included in this discussion. Quantum physics, for example, plays a key role in the fundamental processes involved in greenhouse physics, particularly during this step:
Infra-red light is absorbed by molecules, which in turn get more energetic, and the excited molecules will eventually re-emit more infra-red light in any random direction or transfer excess energy to other molecules through collisions. In a optically thick (opaque) atmosphere, there will be a cascade of absorption and re-emission.
This can be expanded in an interesting manner – From Quantum Physics: A Beginner’s Guide, by A.I.M. Rae (2005)
If you’ve read Stephen Hawking’s “A Brief History of Time”, this next bit is along similar lines:
This explains the absorption characteristics of the atmosphere – high frequency short wavelength radiation is removed by the smaller molecules, like O2 and N2, ultraviolet is screen out by O3, a little longer, and long-wavelength infrared is absorbed by flexible vibrating molecules – CO2, CH4, N2O, H2O, etc.:
Since long wave IR is at the heart of the greenhouse effect, Rae then considers the vibrations of molecules like CO2 and N2O in more detail:
That process is not electronic excitation, as with visible light, but rather vibrational excitation, which is based on oscillation of the atoms in the molecule:
This should also be true for the main gases in the atmosphere, N2 and O2 – why aren’t they absorbing infrared as well? It has to do with the symmetry of charge distribution – consider O=C=O, CO2:
Recall that an electric and magnetic field is associated with light?
It turns out, due to issues related to pressure of gases in the atmosphere, that adding fossil CO2 has the strongest effect around the level of the upper troposphere, some ten miles up in the atmosphere. In the pre-industrial era, more infrared energy would escape to space from this level, but as CO2 levels rose, an increasing amount was sent back to Earth, warming the surface and oceans.
Quantum physics is only part of the story – classical fluid dynamics controls the response to the increased infrared energy. This split between classical physics and quantum physics is also seen in solar energy:
The advantage of taking this approach is that everyone, Joe Public included, is aware that quantum physics is a well-grounded theory with dozens of practical applications. The point should be obvious: if global warming is based on solid physical theories, then you have to discredit those theories if you want to preserve your ‘skeptical stance’ – and that isn’t possible.
It’s similar to the tobacco debate – once people came up with clear evidence of tobacco smoke components, such as benzo(a)pyrene, forming complexes with DNA and damaging gene replication, there was really nothing to say. Such clear evidence already exists with respect to global warming, and has since the mid 1990s at least.
A nice story, but way too simple. Radiation is the source of all terrestial influx of energy, but the atmosphere is not a glass sphere. Water vapour plays an important role, by taking energy at the surface of the oceans when water evaporates. It releases heat when water vapour condeses into rain, at varying levels in the atmosphere. This heat, energy if you like, will be lost to outer space, adding to the radiative loss, and exceeding it by factors. It is a dumd model, as are ALL models. That is why they are models.
[Response: No latent heat is lost to outer space. – gavin]
I think the suggestion to make it clearly understandable by early elementary students is a bridge too far. It would not help the purpose.
I’m sure that this is a good reference for scientific conversation, however, as a non scientist and the type of person that it is trying to reach it is far too complex and introduces confusion and will only deepen any gulf that it tries to bridge.
I did trying reading the article and came across several areas that seem in conflict to what I had previously understood. In one instance the article states about cooling in the upper atmosphere:
“…it’s hard to see any systematic long-term trend in the level of solar activity over the last 50 years, and it is difficult to see how solar activity may have an effect…”
I just dug up what I remembered from a while ago about this same topic:
“For the first time, researchers can show a timely link between the Sun and the climate of Earth’s thermosphere, the region above 100 km, an essential step in making accurate predictions of climate change in the high atmosphere.” (Taken from: Scientists from NASA’s Langley Research Center and Hampton University in Hampton, Va., and the National Center for Atmospheric Research in Boulder, Colo., presented these results at the fall meeting of the American Geophysical Union in San Francisco from Dec. 14 to 18.)
I have also seen several articles about the sun’s activity decreasing of the past 50 years. Take a look at the NASA site for lot’s of info on this.
These sorts of discussions are great and healthy for science to thrash out; however, they show that the science is still in very early stages of development and understanding. Add to this the constant media drip of scary scenario’s and politicians using it to raise taxes, and increase control, IMO, this is where the public starts to loose faith.
Great post, I am gonna need to read it thrice but thats how it should be for us lower beings of lesser ability. I like the way its a simple explanation but still make me head hurt. Great stuff and a challenge to understand, thanks for that as its the challenge that really matters.
Gavin in your response to 26, (if my reading is correct) you misunderstood his difficulty. By my reading mircea was concerned that since at any wavelength the plank function monotonically increases with temperature, the intensity of solar IR exceeds that of terrestrial, at all wavelengths. The resolution is that the plank function is intensity per unit of solid angle (usually expressed as the radiation flowing through a plane of given size), but that the solid angle of sunlight is roughly 6e-5 radians squared (pi times a quarter of a degree squared), whereas the solid angle for terrestrial upward going radiation is the entire half sphere.
As a physicist, I winced when I read “This is because energy cannot just be created or destroyed (unless it involves nuclear reactions or takes place on quantum physics scales).” Energy cannot be created or destroyed, period. Forget nuclear reactions or quantum mechanics; they also can’t create or destroy energy. (As far as we know physics is time-translation invariant, and Noether’s theorem applies to quantum field theory just as much as to classical mechanics….)
The rest is a nice read, though. I’m curious: why is the moon cooler than the naive Stefan-Boltzmann prediction?
In fig 3, why is the measured temp of our moon significantly colder than the expected T?
This summary is extremely useful. The people who want an explanation for lay people are focused on a different audience, which will require a different summary, but that shouldn’t take away from the value this technical summary brings to a more sophisticated audience.
Please explain why a higher humidity reduces optical depth for IR and not for other wavelengths.
We all know that higher WLs have a hard time penetrating the oceans. At very modest depths, only blue remains and just a bit deeper, no visible light penetrates the water, leaving most of the oceans pitch black.
What I mean is that a reduced optical depth due to H2O feedback logically would stop more sunlight from reaching the surface as well, or? The atmosphere and surface might very well heat up from enhanced GHE, but as soon as water vapor feedback kicks in it will actually act as both a positive and a negative feedback. However, the negative one (shielding the surface from sunlight) must “win” in the end, since it actually reduces the energy input across a wide(?) range of wavelengths?
#30 gavin
Why is latent heat once released not then potentially lost to outer space?
Fred Moolten says:
5 July 2010 at 10:22 AM
This is an excellent and cogent summary of basic GHE principles. I would take exception, however, to the explanation offered for stratospheric cooling consequent to increasing atmospheric CO2. In fact, as the atmosphere warms, the “atmospheric window” tends toward closing (particularly because of water vapor effects), and excess escape through this window can’t account quantitatively for the reduction in stratospheric temperatures. A better quantitative explanation appears to involve the presence of upper stratospheric ozone, which absorbs solar UV and visible radiation, warming the stratosphere. That heat must be dissipated to space, and CO2 (which does not absorb in the UV or visible range), adds to the emissivity of the stratosphere at the warmed temperature, while adding much less to the absorptivity. The net effect is essentially that CO2 acts as an escape valve for ozone-trapped heat. In the absence of ozone, added atmospheric CO2 would be expected to warm the stratosphere slightly rather than cool it. (Note that this phenomenon is distinct from the cooling expected from ozone depletion, an entirely separate entity).
I agree with your point Fred, the upper atmosphere is also heated from above, ozone where it exists is a factor but even moreso is O2 and O, which absorb the very energetic UV photons. Collisional transfer to CO2 allows this energy to be radiated to space. Rasmus’s description applies at night, during the day direct heating from the sun must be considered, photodissociation of O2 produces O(D) which is quenched by N2 (which can’t radiate itself) which then can collisionally activate CO2 which then radiates (this is a very efficient process, it’s the basis of the CO2 laser).
I believe Mars and Venus share an equal atmosferic composition almost 96% CO2, but the density is dramatically lower on mars, is this the reason of the difference in temperature on Venus and Mars? If so, How does atmospheric density affect the temperature?
Re: onymous (#36 on the moon):
The formula So*(1-albedo)*0.25 = sigma T^4 is valid only for an isothermal blackbody “bare rock” in space. It can serve as an approximation which is only useful for bodies such as Earth or Venus which, from a planetary climate perspective, are relatively uniform in temperature. For the moon or Mercury which exhibit day-night temperature gradients on the order of several hundred Kelvin it is not really appropriate to define a mean “effective temperature” in the preceding way. It is more useful to average over a hemisphere, or maybe a latitude band, or even at a single point that responds instantly to the solar flux (removing the factor of 1/4 from the equation) depending upon the nature of the problem.
As a visualization,
(T_night + T_day)/2 which becomes a flux upon dividing by sigma and taking the fourth root. Call this value “A.” Or, we can convert the temperatures into fluxes right away and then find the average flux. i.e., (Flux_day + Flux_night)/2…call this value “B.” In general, A=/= B due to the non-linear relationship between radiant flux and temperature. As you can see, it is more appropriate to divide the planet up into a bunch of patches which are relatively uniform in temperature (and surface emissivity). I’m not sure exactly how rasmus defined the “observed” surface temperature for the bodies in Fig.3, especially the ones that depart significantly from the uniform-temperature approximation, but a comparison results from the mathematics of the equation given in the post and has little physical meaning.
Gavin,
All heat is lost to outer space, not only latent heat.
[Response: No it isn’t. Only radiative fluxes are lost to outer space. You know, there is a vacuum and all…. – gavin]
Whether or not this post is too complex for us lay people it should certainly be required reading for any journalist reporting on climate issues. If they are not able to understand the maths and science presented here then hopefully they will think twice before offering their analysis.
mircea (26), Thomas (34):
Clearly the intensity of the solar spectrum is greater than that of the Earth spectrum in the infrared since the derivative of the Planck function with respect to temperature, dB/dT, is positive at all values of wavelength lambda. Though, it is useful to define a threshold at where both the Earth and sun emission are very small, which occurs at around 4 microns. See this image. This allows us to treat the fluxes independently. Note the solar spectrum is scaled by a factor of a millionth in order to see them together, since the total area under the curve is about (6000/300)^4 = 160,000 times larger for the hotter object.
Dear Gavin,
Temperature is defined as being the energy in the motion of individual molecules/atoms or ions. Collisions between molecules etc. will cool down the upper atmosphere by expanding the upper layer of the atmosphere. And there is no vacuum, there is only a lower concentration of matter. That is why the void of space has a temperature of 2 to 4 K.
[Response: Let’s imagine how much water vapour we can be losing to space for it to be an important number for climate purposes: For instance, let’s imagine it is as important as the geothermal heat flux (itself too small to pay much attention to): 0.075 W/m2. What amount of water loss (as vapour) would that be? Divide by the latent heat and multiply by number of seconds in a year to get a mass flux per year ~ 1 kg/m2/yr. If that was coming from the ocean (70% of the area), that would imply 1.5 mm each and every year in sea level loss. I think we would have noticed. Given that the uncertainties in the sea level budget are on the order of 0.1 mm/year, that implies that the ‘latent heat’ loss to space has to be some many times less than what I first postulated. There is no climatically important latent heat loss to space. – gavin (Note: numbers corrected (made smaller) after initial posting – sorry for the confusion)]
I find that I best identify with the “great unwashed” inspite of education, training, technical expertese and interest. The alternative seems to be elitism. I enjoy a re-iteration of basics as others seem to capture nuances either in wording or perspective that helps me learn and refine, which, I guess is the whole point of the exercise. There are fundamental issues not addressed but this was never a discourse on the whole pie. Thank you.
Unfortunately, better communication from scientists will have only limited effectiveness as long as the press continues to drop the ball. Take Washington Post for example. I’ve noticed it takes at least 2 reporters now to write every story concerning global warming. One to write the original article, and one to walk down the street and have lunch with CEI, for the contrarian paragraph. I’m not sure if anyone has alerted them to the fact that CEI representatives will recognize AGW when hell freezes over.
The article on the exoneration of Michael Mann last week is one of many examples of their lazy and inaccurate style.
oops I didn’t read the point iv before asking, sorry about that.
Anyway, the question I had in mind is, corrected the surface temperature with the lapse rate how do temperatures fit with measurements? could you replot figure 3 taking into account the lapse rate correction?