


Global warming is turning 35! Not only has the current spate of global warming been going on for about 35 years now, but also the term “global warming” will have its 35th anniversary next week. On 8 August 1975, Wally Broecker published his paper “Are we on the brink of a pronounced global warming?” in the journal Science. That appears to be the first use of the term “global warming” in the scientific literature (at least it’s the first of over 10,000 papers for this search term according to the ISI database of journal articles).
In this paper, Broecker correctly predicted “that the present cooling trend will, within a decade or so, give way to a pronounced warming induced by carbon dioxide”, and that “by early in the next century [carbon dioxide] will have driven the mean planetary temperature beyond the limits experienced during the last 1000 years”. He predicted an overall 20th Century global warming of 0.8ºC due to CO2 and worried about the consequences for agriculture and sea level.
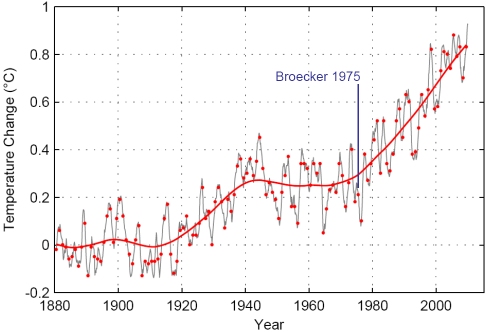
Global temperature up to June 2010 according to the NASA GISS data. Grey line is the 12-month running average, red dots are annual-mean values. The thick red line is a non-linear trend line. Broecker of course did not have these data available, not even up to 1975, since this global compilation was only put together in the late 1970s (Hansen et al. 1981). He had to rely on more limited meteorological data.
To those who even today claim that global warming is not predictable, the anniversary of Broecker’s paper is a reminder that global warming was actually predicted before it became evident in the global temperature records over a decade later (when Jim Hansen in 1988 famously stated that “global warming is here”).
Broecker is one of the great climatologists of the 20th Century: few would match his record of 400 scientific papers, a full sixty of which have over 100 citations each! Interestingly, his “global warming” paper is not amongst those highly-cited ones, with “only” 79 citations to date. Broecker is most famous for his extensive work on paleoclimate and ocean geochemistry.
It is very instructive to see how Broecker arrived at his predictions back in 1975 – not least because even today, many lay people incorrectly assume that we attribute global warming to CO2 basically because temperature and CO2 levels have both gone up and thus correlate. Broecker came to his prediction at a time when CO2 had been going up but temperatures had been going down for decades – but Broecker (like most other climate scientists at the time, and today) understood the basic physics of the issue.
Basically his prediction involved just three simple steps that in essence are still used today.
Step 1: Predict future emissions
Broecker simply assumed a growth in fossil fuel CO2 emissions of 3% per year from 1975 onwards. With that, he arrived at cumulative fossil CO2 emissions of 1.67 trillion tons by the year 2010 (see his Table 1). Not bad: the actual emissions turned out to be about 1.3 trillion tons (Canadell et al, PNAS 2007 – estimate extended to 2010 by me).
A shortcoming, from the modern point of view, is that Broecker did not include other anthropogenic greenhouse gases or aerosol particles in his calculations. He does however discuss aerosols, which he calls “dust”. In fact, the first sentence of the abstract (quoted above) in full starts with an if-statement:
If man-made dust is unimportant as a major cause of climate change, then a strong case can be made that the present cooling trend will, within a decade or so, give way to a pronounced warming induced by carbon dioxide.
That is a nod to the discussion about aerosol-induced cooling in the early 1970s. Broecker rightly writes:
It is difficult to determine the significance of the next most important climatic effect induced by man, “dust”, because of uncertainties with regard to the amount, the optical properties and the distribution of man-made particles,
citing a number of papers by Steve Schneider and others. Because he cannot quantify it, he leaves out this effect. Here luck was on Broecker’s side: the warming by other greenhouse gases and the cooling by aerosols largely cancel today, so considering only CO2 leads to almost the same radiative forcing as considering all anthropogenic effects on climate (see IPCC AR4, Fig. SPM.2).
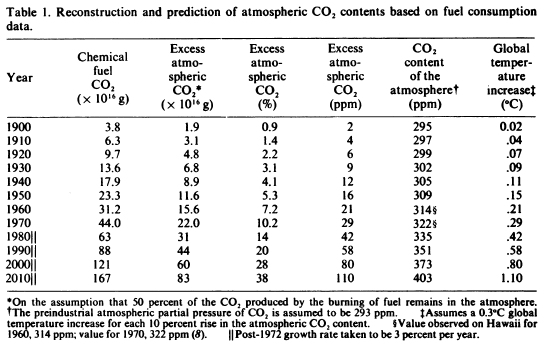
Table 1 of Broecker (1975)
Step 2: Predict future concentrations
To go from the amount of CO2 emitted to the actual increase in the atmosphere, one needs to know what fraction of the emissions remains in the air: the “airborne fraction”. Broecker simply assumed, based on past data of emissions and CO2 concentrations (Keeling’s Mauna Loa curve), that the airborne fraction is a constant 50%. I.e., about half of our fossil fuel emissions accumulates in the atmosphere. That is still a good assumption today, if you look at the observed CO2 increase as fraction of fossil fuel emissions. Broecker calculated that about 35% of the emissions is taken up by the ocean and the other 15% by the biosphere (again not far from modern values, see Canadell et al.). On this basis he argued that if the ocean is the main sink, the airborne fraction would remain almost constant for the decades to come (his calculations extend to the year 2010).
Thus, with a 3% increase in emissions per year and 50% of that remaining airborne, it is easy to compute the increase in CO2 concentrations. He obtains an increase from 295 to 403 ppm from 1900 to 2010. The actual value in 2010 is 390 ppm, a little lower than Broecker estimated because his forecast cumulative emissions were a little too high.
Step 3: Compute the global temperature response
Now we come to the temperature response to increased CO2 concentration. Broecker writes:
The response of the global temperature to the atmospheric CO2 content is not linear. As the CO2 content of the atmosphere rises, the absorption of infrared radiation will “saturate” over an ever greater portion of the band. Rasool and Schneider point out that the temperature increases as the logarithm of the atmospheric CO2 concentration.
Based on this logarithmic relationship (still valid today) Broecker assumes a climate sensitivity of 0.3ºC warming for each 10% increase in CO2 concentration, which amounts to 2.2ºC warming for CO2 doubling. This is based on early calculations by Manabe and Wetherald. Broecker writes:
Although surprises may yet be in store for us when larger computers and better knowledge of cloud physics allow the next stage of modeling to be accomplished, the magnitude of the CO2 effect has probably been pinned down to within a factor of 2 to 4.
The AR4 gives the uncertainty range of climate sensitivity as 2-4.5ºC warming for CO2 doubling, so there still is about a factor of 2 uncertainty and Broecker used a value near the very low end of this uncertainty range. Modern estimates are not only based on model calculations but also on paleoclimatic and modern data; the AR4 lists 13 studies that constrain climate sensitivity in its table 9.3.
In Broecker’s paper the warming calculated with the help of climate sensitivity happens instantaneously. Today we know that the climate system responds with a time lag due to ocean thermal inertia. By neglecting this, Broecker overestimated the warming at any given time; accounting for thermal inertia would have reduced his warming estimate by about a third (see AR4 Fig. SPM.5). But again he was lucky: picking ~2ºC rather than the more likely ~3ºC climate sensitivity compensates roughly for this, so his 20th-Century warming of 0.8ºC is almost spot on (the actual estimate being closer to 0.7ºC, see Fig. above). (A modern version of this back-of-envelope warming calculation is found e.g. in our book Our Threatened Oceans, p.82.)
Natural Variability
Broecker was not the first to predict CO2-induced warming. In 1965, an expert report to US President Lyndon B. Johnson had warned: “By the year 2000, the increase in carbon dioxide will be close to 25%. This may be sufficient to produce measurable and perhaps marked changes in climate.” And in 1972, a more specific prediction similar to Broecker’s was published by the eminent atmospheric scientist J.S. Sawyer in Nature (for a history in a nutshell, see my newspaper column here).
The innovation of Broecker’s article – apart from introducing the term “global warming” – was in combining estimates of CO2 warming with natural variability. His main thesis was that a natural climatic cooling
has, over the last three decades, more than compensated for the warming effect produced by the CO2 [….] The present natural cooling will, however, bottom out during the next decade or so. Once this happens, the CO2 effect will tend to become a significant factor and by the first decade of the next century we may experience global temperatures warmer than any in the last 1000 years.
The latter turned out to be correct. The idea that the small cooling from the 1940s to 1970s is due to natural variability still cannot be ruled out, although more likely this is a smaller part of the explanation and the cooling is primarily due to the “dust” neglected by Broecker, i.e. due to the rise of anthropogenic aerosol pollution (Taylor and Penner, 1994). However, the way Broecker estimated and even predicted natural variability has not stood the test of time. He used data from the Camp Century ice core in Greenland, arguing that these “may give a picture of the natural fluctuations in global temperature over the last 1000 years”. Ironically, Broecker’s own later work on Atlantic ocean circulation changes showed that Greenland is likely even less representative of global temperature changes than most other places on Earth, it being strongly affected by variability in ocean heat transport (see our recent post on the Younger Dryas, or Broecker’s latest book The Great Ocean Conveyor). However, Broecker was right to conclude that the buildup of CO2 would sooner or later overwhelm such natural climate variations.
Overall, Broecker’s paper (together with that of Sawyer) shows that valid predictions of global warming were published in the 1970s in the top journals Science and Nature, and warming has been proceeding almost exactly as predicted for at least 35 years now. Some important aspects were not understood back then, like the role of greenhouse gases other than CO2, of aerosol particles and of ocean heat storage. That the predictions were almost spot-on involved an element of luck, since the neglected processes do not all affect the result in the same direction but partly cancel. Nevertheless, the basic fact that rising CO2 would cause a “pronounced global warming”, as Broecker put it, was well understood in the 1970s. In a 1979 TV interview, Steve Schneider rightly described this as a consensus amongst experts, with controversy remaining about the exact magnitude and effects.
Reference
BROECKER WS, 1975: CLIMATIC CHANGE – ARE WE ON BRINK OF A PRONOUNCED GLOBAL WARMING?
SCIENCE Volume 189, Pages 460-463.
Yeah!!!
Global Warming!!!
woohoo!!!
Happy birthday!!!
Wishing you a wonderful. . .
uh,
hmmm. . .
Nevermind.
—
A Climate Minute: The Natural Cycle – The Greenhouse Effect – History of Climate Science – Arctic Ice Melt
‘Fee & Dividend’ Our best chance: – Learn the Issue – Sign the Petition
Most depressing “Happy Birthday” ever.
And, in a comment with a bit more substance: that paper’s held up really well over time. I guess there’s a damn good reason it was published in Science. The existence of this paper is also good to use against the folks who talk about “global cooling” (yes, I know there’s another RC thread devoted just to that topic!).
I’d also love to have the “problem” of one of my better papers having “only” 71 cites :)
Wally has always been the king of the back-of-the-envelope calculation. This is just one example, and shows how he developed a simple model of CO2 and warming that got within 15% of what actually occurred over 35 years.
A note on early predictions of CO2-induced warming: the New York Times published an editorial on March 24, 1953, entitled “How Industry May Change Climate.” I have a PDF of it, which begins “The amount of carbon dioxide in the air will double by the year 2080 and raise the temperature an average of at least 4 per cent…” The editorial also mentions a recent paper presented by Gilbert Plass at AGU, which I haven’t looked up.
So the potential effects of CO2 on climate have been appreciated for a long, long time.
[Response: Interesting. Not to be picky about a 50 year old newspaper article but… I wonder what 4% temperature increase is supposed to mean, though. They can’t mean 4% of 288 K, which would be 11 °C! 4% of 15K. They could mean 4% of 15 C, which is about 0.6. Of course, they were probably thinking F, not C, so perhaps they mean 4% of 59, or 2 F? –eric]
[Response: Surely the author meant degrees (F or C is the question). For some reason non-scientists often confuse this – at least a dozen times in the last couple of years I’ve heard people talk about limiting global warming to 2%. -stefan]
Stefan wrote: “… warming has been proceeding almost exactly as predicted for at least 35 years now …”
Too bad that other things have not been proceeding exactly as predicted:
The path not taken …
Thanks very much for posting this. I normally try to stay aware of such milestones and anniversaries, but this one completely slipped by me.
This raises an issue that I think will increasingly become a sticking point in humanity’s response to this situation: When can we fairly say that we knew with reasonable certainty that climate change was real and that it was largely human caused? I do NOT want to bring up here the arguments about which country or group of countries (i.e. the OECD) is responsible for how much of our predicament, although that’s largely the context in which this question is asked.
Putting the political aspect aside, I would really like to hear the opinions of the RC regulars, both real scientists and the scientist wannabes (like me), on what date you would pick on a time line and say, “by this point we knew about the A in AGW and there was very little doubt, even if we had a lot of uncertainty about the amount of warming and interactions between various parts of the environment, and we should have started to take action to reduce our emissions”.
I know about the report to LBJ from the Presidential Science Advisory Committee in 1965 (and its Appendix Y4) and the 1958 booklet from the NAS that talked about CO2 and water vapor being greenhouse gases, but it’s never been clear to me exactly when it would be reasonable to say that the evidence was not just strong enough but also widely accepted enough by scientists that the rest of us should have taken notice and done something other than buy more cars and bigger houses.
[Response: I like to ponder what must have been going through the minds of some of these guys as they were looking at the results of their calculations and model outputs and getting a first glimpse of what was going on.–Jim]
Ben(5): How long is that NY Times article? I couldn’t find it online, and would love to see it.
By the way, the two documents I referred to in my prior post:
The 1958 NAS booklet “Planet Earth”:
http://dl.dropbox.com/u/3476601/tcoe%20cc%20history/IGYBook_PlanetEarth_PDF.pdf
The 1965 report to LBJ (CO2 appendix only):
http://dl.dropbox.com/u/3476601/tcoe%20cc%20history/PSAC%2C%201965%2C%20Restoring%20the%20Quality%20of%20Our%20Environment.pdf
I’m a bit too young to celebrate this one.
I am curious about the apparent lack of warming observed over the 20th century for North America. I wonder if perhaps the increase in ‘dust’ from Asia that was occurring just as the ‘dust’ generated in North America could perhaps be responsible.
Anyone have any idea?
[Response: Hmm. I just got back from central British Columbia, which has warmed about 3 C in the last 50 years… Last time I checked, BC was in North America.–eric]
7 (Lou Grinzo),
As a scientist-wish-I-were, I’d go with the answer provided by this post, and seemingly backed up with evidence:
[Side comment: Excellent post. Historical perspective is an important and often overlooked factor in “the debate.”]
Our understanding in 1979 may not by itself have implied a call to action at that point, but we’d already suffered through the 1973 oil embargo, knew that U.S. strategic and economic fortunes were tied to a resource we could not necessarily control, knew of other reasons to switch (pollution, ultimate limits to fossil fuel availability, etc.), and knew that other technologies were seemingly within our grasp.
Imagine if we’d started taking action in 1979, where we’d be environmentally, climatically, economically and strategically. Imagine how small the expense (which is the denier’s sticking point) would have been if the issue had been approached gradually but continuously since 1979.
Heck, we might never have fought two wars in the Persian Gulf.
Which leads to another side point. Why haven’t we developed and implemented acceptable solar energy solutions? There are three sources of power on this planet; nuclear, tidal, and solar. 99.99% of all power we see on earth (plants growing, animals moving, winds and waves moving, light and heat) are a result of solar energy. Even fossil fuels are, in fact, solar energy.
So if the sun is in effect the source of almost all power on the planet, and nature has been able to easily transform it into wind, waves, life, movement, and hydrocarbons on a daily basis, why are we so crippled and incompetent in extracting what we need from it?
re:8
Those are interesting reads. It looks like the fundamentals have been in place for a long time.
It’s depressing that so little has been done to mitigate things — it’s like turning around an aircraft carrier with a paddle.
Stefan, do you have any Happy Birthday insights re future prospects for sea level rise?
Best,
Hunt
[Response: You find my current views on this here. -stefan]
I really like the older video clips of people talking about global warming. I added The Frank Capra clip and the Steve Schneider clip to my version of Spencer Wearts climate history page:
http://www.ossfoundation.us/projects/environment/global-warming/climate-science-history/
Does anyone have a clip of Svante Arrhenius talking about AGW. . . back around 1896??? Hmmm… I better try Google.
—
A Climate Minute: The Natural Cycle – The Greenhouse Effect – History of Climate Science – Arctic Ice Melt
‘Fee & Dividend’ Our best chance: – Learn the Issue – Sign the Petition
@7 Lou: When did we know with reasonable certainty that AGW was real? What you mean, “we”? Wally and Steve Schneider and lots of others knew it by the late 1970s, but many scientists and still more non-scientists found lots of valid reason for doubt. I think you can’t pick a better date than 2001, when the IPCC officially announced that there was a “discernible” human effect on climate. At that point “we” included the overwhelming majority of experts and the official consensus of most of the world’s governments. At any time before that, you could say there were defensible reasons for doubt.
Another possible date would be 1988, when the international Toronto conference of experts called for strict, specific limits on greenhouse gas emissions. This represented a consensus (incomplete) of scientists that there was reasonable certainty that AGW was, if not beyond doubt, at least enough of a risk to warrant real action.
FWIW, I personally became convinced in the late ’90s. The last straw was evidence that GCM’s had correctly reproduced the very different conditions of ice-age tropical ocean temperature; I suppose everyone has their own personal last-straw. Bore-hole demonstrations of 20th century warming also played a role in convincing me. Although in all science,conviction should never mean more than, say, 95% sure… there’s always a remote possibility of being wrong.
[Response: Scientific consensus was already strong at the Villach conference in 1985, convened by ICSU, WMO and UNEP. Another possible date would be 1990, when in December the German parliament unanimously voted to reduce CO2-emissions by 25% by the year 2005, following a detailed parliamentary inquiry into the issue that was started in 1987. I think if you get parliamentarians of one of the major industrial nations of the world unite across party lines to back action, the evidence must have been very strong to anyone who cared to properly look at the issue. The latest possible date you could name in my view is the Rio Earth summit of 1992, where the nations of the world decided to stabilise greenhouse gas concentrations in the atmosphere and the UNFCCC was born. -stefan]
oops, my bad, “discernible” was from the 1995 IPCC report (another milestone). The 2001 report more definitely declared that “most of the observed warming over the last 50 years is likely to have been due to the increase in greenhouse gas concentrations” where “likely” falls only a little short of reasonable certainty.
Thanks Stefan for that news.
A triumph for science, not so good news for humans and the planet.
But I guess that is the issue. The message is negative and that goes against the grain for many humans.
Excellent post on an excellent paper. I’m surprised this paper isn’t the standard response to the denier “point” that global cooling was imminent according to scientists in the mid 70s.
5 Ben said, “I have a PDF of it, which begins “The amount of carbon dioxide in the air will double by the year 2080 and raise the temperature an average of at least 4 per cent…” ”
That’s quite a trick. Assuming they meant “degrees F” they were quite accurate for 57 years ago.
Good article. I recall Richard Alley in his book “Two Mile Time Machine” mentioning that if you’re a climate scientist, and you think you have a good idea, chances are Broecker already got to it first. He has done extraordinary work and this paper is no exception.
In response to John Reisman (14), Arrhenius was not interested in anthropogenic global warming. He did do the first quantitative outlook of the effects of CO2 changes on global temperature (of which he got very lucky in being close to modern estimates), but his target was largely to examine the coming and going of ice ages.
If you want to go back and extend the “birthday of global warming” Callendar is probably the first person to look at.
Thanks Chris, I seem to recall something about Arrhenius saying if humans increase CO2 it would be great because we don’t want to go into another ice age. It might have been from Spencers work, but I will have to dig around.
Yes, Callendar was on top of this. I think as early as 1924 or 26?
#7 Lou Grinzo. For me, the A-part of GW became evident a bit after 1995 report, probably 1997/8 winter after checking some things in the report from the original articles in the university chemistry library. C13/14 uptake by plants produced some confusion afterwards, but this was cleared soon after, 1999?
#19, #14, #5–
There isn’t that much readily available online about Callendar, but Fleming wrote what will likely prove to be the definitive biography. I drew heavily upon it for this web article:
http://hubpages.com/hub/Global-Warming-Science-And-The-Wars
Towards the end, I include an image of a 1953 Popular Mechanics “sidebar” squib on global warming sourced to Gilbert Plass–a scientific correspondent of Callendar’s (as was Keeling.) I haven’t read the letters beyond a few excerpts quoted by Fleming, but I’ve the idea that Callendar was a bit of a long-distance mentor–to Plass especially.
There’s also a lot about Broecker in this “review” of “Fixing Climate,” which includes a lot of Broecker biography:
http://hubpages.com/hub/Climate-change-resources–Fixing-Climate–A-review
And–as others have said–excellent post! Love the historical context (obviously!)
‘International Environmental Problems–A Taxonomy’, Russell & Landsberg (1971) [Science 25 June 1971 172: 1307-1314 [DOI: 10.1126/science.172.3990.1307], is supposed to have the following sentence…
“For example, a global warming trend is a “greater” effect than is the extinction of a species.”
Perhaps it laid the seed in Broecker’s mind?…. or maybe it didn’t… I’ll get my coat…
The NY Times article can be found at
http://select.nytimes.com/gst/abstract.html?res=F10D12F63858117B8EDDAD0A94DD405B8389F1D3&scp=1&sq=industry+change+climate&st=p
A copy costs $3.95.
Perhaps someone with connections can persuade the NY Times to open it for free viewing.
Hope this won’t be considered off-topic, given the interconnectedness of the issues (no intention of instigating a debate):
Rickover on Energy in 1957, Rep. Bartlett commenting: http://energybulletin.net/node/31022
Stefan, thank you for an absolutely fascinating post.
A terrific review and reminder, both the post and the linked references, thank you. The situation was already sketched out in the 60’s and 70’s, becoming increasingly clear ever since. Making the world’s (mostly non-) reaction all the more tragic, in the sense of a horrific outcome due to ineradicable human flaws.
There is still time to make the future better than it would be without recognition and action, though probably not time to avoid many heartbreaking losses.
SecularAnimist, how about this paraphrased quote from T. Edison in 1910: The nickel-iron battery will put the gasoline buggies out of existence in no time?
Hmmm. Stefan, at the top of your post you list the Broecker paper as “Are We on the Brink of a Pronounced Global Warming?”
But Science (and your “References” section at the end of the post) give the full title as “Climatic Change: Are We on the Brink of a Pronounced Global Warming?”
If Broecker’s original title included the “Climatic Change” part, then it’s kind of remarkable that this foundational paper that first introduced the term “global warming” also exemplifies the tension between the use of that term versus the use of “climate change” … in its very title.
I don’t think much could be done until the theoretical framework was coupled with observed temperature rise. That didn’t start until the 80s, so the first real opportunity was 1988 – Jim Hansen’s congressional testimony. That was when everything kicked off – formation of the IPCC, Thatcher forming the CRU the year after…
That was when we should have made global warming a non-event.
On the question of when did “we” collectively have enough evidence to know a response was required: I’d point to the Rio Earth Summit in 1992. The nations of the world agreed to create the Framework Convention on Climate Change (UNFCCC), which collectively acknowledged the evidence and the need for a response. This framework treaty came into force in 1994, with near universal support worldwide, including the U.S., Europe, China, Russia, India, basically everybody:
http://unfccc.int/essential_background/convention/items/2627.php
The framework Convention is a legally binding treaty, but it simply states that we all see there is a problem, and does not tackle how to go about solving it. That was left for the 1997 Kyoto Accord, which was a Protocol to the Framework Convention. The UNFCCC set up the annual meetings known as “Conference of the Parties” or COP. We’ve kept holding those, recently completing COP-15, and are working up toward COP-16 in Cancun, Mexico this coming December.
The Kyoto Protocol did pass its own thresholds to come into force as an international agreement (>=55 countries totaling at least 55% of emissions), but it was vitiated by the refusal of the U.S. Senate to ratify the treaty, highlighted in the July 1997 Byrd-Hagen Resolution:
http://www.nationalcenter.org/KyotoSenate.html
The Kyoto Protocol is still in force today, for those Parties (countries) who ratified it. It governs the period from 2008-2012 for Annex I parties, who are obliged to meet whatever target they set for themselves in the course of the negotiations, stated as a % reduction in emissions from a 1990 baseline.
Some parts of Europe are actually on track to meet their Kyoto commitments. Canada, which ratified the treaty, has admitted this now far beyond the realm of possibility for us, as we’re perhaps 25 or 30% over our 1990 levels and have very little policy in place yet to achieve any cuts or even to slow the growth of emissions. “Oh, well…” (national shrug?)
So by the reckoning that 1992 was the year the world community acknowledged the problem, we’re now in year 18 of dithering over whether to do anything to slow and someday start cutting emissions.
To avoid ending on a down note, I will point out that China is taking serious steps to start slowing their own emissions growth:
http://af.reuters.com/article/energyOilNews/idAFTOE66L02M20100722
http://news.xinhuanet.com/english2010/indepth/2010-07/28/c_13418759.htm
This could at least remove one of the main stated objections behind Byrd-Hagel in the U.S., though other objections such as “devastate the economy”/ “it’s a tax” may remain key moves in U.S. inactivists’ playbook.
J wrote: “… this foundational paper that first introduced the term ‘global warming’ also exemplifies the tension between the use of that term versus the use of ‘climate change’ … in its very title.”
What “tension”?
Global warming causes the climate to change. Seems pretty straightforward to me.
My Jr. High School science teacher told us about global warming. This was in the 1950’s.
C. Mather says: 28 July 2010 at 12:01 PM
Perhaps someone with connections can persuade the NY Times to open it for free viewing.
Paging Andy Revkin. .Earth?
Forgot to mention, what a great post, thank you Stefan. Humbling to see somebody wade through so much material and make it tractable for those of us a mile wide and an inch deep.
One part makes no sense. You state that “based on this logarithmic relationship (still valid today) Broecker assumes a climate sensitivity of 0.3ºC warming for each 10% increase in CO2 concentration, which amounts to 2.2ºC warming for CO2 doubling.” I certainly understand the logarithmic relationship – that’s straight 2nd law stuff. But then you go on to linearly extrapolate the temperature. This doesn’t make sense.
Assuming the first 10% increase in CO2 leads to a 0.3C warming, then ln(10) = 2.303. 0.3 and 2.3 should be proportional – the ratio is 0.13.
Doubling the CO2 concentration requires taking ln(100), or 4.6. Employing the same ratio yields a temperature increase of 0.6 C, not 2.2.
I have never understood this. From the second law, chemical activity is proportional to the logarithm of the concentration, and yet the temperature increase is always calculated linearly, as in your example. On a logarithmic scale, the doubling of CO2 concentrations is, frankly, not especially significant.
Please explain.
[Response: The logarithmic impact of CO2 is not related to the 2nd Law in any direct way. It is simply a function of the climate state and the atmospheric composition we have. The forcing for increases in CO2 is approximated by ~ 5.35*log(CO2/CO2_orig) in W/m2 (Myhre et al, 1998), and the planet responds (to first order) linearly to changes in the forcing. The forcing for a 10% increase in CO2 is 5.35*log(1.1) = 0.5 W/m2, and so if that gave 0.3 deg C, you would expect 3.7*0.3/0.5 =2.2 deg C for when you get to 2xCO2. Hope that is clearer. – gavin]
A little reminiscing circa 1979…
Actually back in early 1979 I would have been writing up my final project report for my diploma at a further education college here in the UK. It was titled ‘Sun Tracking for Solar Cells and Parabolic Reflectors’.
I remember making the mechanism out of Meccano and burning out the only transistors I had trying to drive the motors.
I still have the (rather good) report, which has a hand drawn graph of the spectrum of sunlight reaching the ground, with the visible band clearly marked. I’m sure I probably copied the graph out of a book.
Dan King – I think you are getting confused with percentages. It’s not log of 10 or 100 that you need to take, it’s log of 1.1 and 2 – log 2 is a bit more than 7 times log 1.1, so the increase in temperature for a doubling of CO2 is a bit more than 7 times the warming you get from a 10% increase in CO2.
Sorry, but that still makes no sense. The absorption and emission of IR radiation by CO2 is a chemical process, and MUST be related to the second law. There is no escaping that.
I don’t know what “forcing” means, so I don’t really understand. But whatever it is, I can’t believe it turns a logarithmic process back into a linear one.
[Response: Sorry, but nothing is turning a logarithmic process into a linear one. Calculating the difference that increasing CO2 makes on the radiation at the top of the atmosphere (i.e. the forcing) depends logarithmically on CO2 concentrations. The planet to first approximation reacts linearly to whatever forcing is imposed (whether it is from the sun or from a volcano or from CO2). Two separate processes. – gavin]
Re: #36 (Dan King)
10% doesn’t imply log(10). It implies log(1.1), since a 10% increase of 1 (being the “present” level) is 1.1. And, log(1.1) (using natural log) is 0.0953.
Meanwhile, log(2) is 0.693. The ratio log(2)/log(1.1) is 7.27, so we need 7.27 increases of 10% (compounded) to achieve a doubling. If each 10% increase raises temperature by 0.3 deg.C, then 7.27 of them would raise temperature by 2.2 deg.C.
Someone mentioned Callendar:
The Artificial Production of Carbon Dioxide and its Influence on Temperature
http://dl.dropbox.com/u/3476601/tcoe%20cc%20history/qjcallender38.pdf
(Please note with this and the other links I posted above that they’re in a DropBox account and sometimes won’t load a PDF correctly. If that happens, just hit refresh and try again. It’s not clear to me what issue DB has with PDFs, but it’s usually not a significant issue.)
Dan King: You obviously made a basic error, because if you are right that “Doubling the CO2 concentration … yields a temperature increase of 0.6 C” then clearly a rise of 0.6 is the same as two rises of 0.3 each. And if 0.3 is produced by a 10% increase, then two 10% increases are plainly not the same as a doubling.
Reductio ad absurdum.
Gavin,
Thank you for your patience, and I admit I’m a novice to this. But I do know my thermodynamics. Taking your statement as correct – that “forcing”, whatever it is, is proportional to the log(CO2), then increasing the CO2 concentration from 1.1x to 2x should result in multiplying the temperature by a factor of 1.8. It doesn’t matter how many processes are involved: 1, 10, 135. There is no way that anything can depend exponentially on the concentration, which is what the ratio log(2)/log(1.1) implies.
OK – so I’ll shut up and leave you folks alone. Thanks again.
[Response: Sorry again, but just work through the maths: Temp change ~= sensitivity * forcing. (T = a * F). For a 10% change in CO2, the temperature change is posited to be 0.3 deg C, thus sensitivity a=0.3/(5.35*log(1.1)). For a doubling of CO2, the temperature change is thus: T = 0.3/(5.35*log(1.1)) * 5.35*log(2) = 0.3*log(2)/log(1.1) = 2.2 deg C. – gavin]
Really sixty publications with over 100 citations? Wow. Impressive.
[Response: Indeed. And I thought I was doing OK with a dozen. -stefan]
My wife was a researcher on James Burke’s documentary “After the Warming”, which came out in 1990. It was already abundantly clear then that warming was going to happen, and that it was largely due to anthropogenic causes.
We watched it again recently, and it is scary how accurate JB’s predictions were – although things that he said would only start happening in the 2020s or 2030s are already happening now.
Every time I hear someone declare that climate science is an “immature” science, or that we need to wait for more evidence, I want to sit them down in front of “After the Warming”, and ask how much longer we need to wait.
Dan King, I think you are confusing the relationship between CO2 concentration and radiative forcing, and the relationship between global temperature and radiative forcing. The “forcing” by the way is just a measure of how the net radiative balance of the planet is perturbed by a change in solar irradiance,greenhouse gases, etc. That alone doesn’t tell you anything about the temperature change realized at the surface, since this also depends on how sensitive the system is to that forcing, which depends on feedbacks.
For a change in CO2 concentration, the forcing is given as RF_CO2=k*ln[CO2(t)/CO2(0)] where k ~ 5.35 W m**-2 and CO2(t), CO2(0) represent the final and initial concentration. Thus, a 10% change in CO2 (e.g., from 300 ppm to 330 ppm) corresponds to a forcing of 5.35*ln(1.1)=0.5 W m**-2. A doubling of CO2 would be RF_CO2=5.35*ln(2)=3.7 W m**-2.
The global mean temperature response to the imposed forcing is:
dT=λ*RF
where λ is a sensitivity parameter expressed in degrees C temperature change per unit radiative forcing (whose value is a diagnostic of how strong various feedbacks are, and thus of the climate sensitivity). In the discussion with you, gavin and other commenters have assumed λ to be invariant over the range of climate change we are interested in. A central estimate of λ is ~0.75 degrees C/(W m**-2), so
dT (1.1xCO2)=0.75*5.35*ln(1.1)=0.38 C
dT (1.5xCO2)=0.75*5.35*ln(1.5)=1.6 C
dT (2xCO2)=0.75*5.35*ln(2)=2.8 C
note that previous comments are using λ closer to 0.59 degrees C/(W m**-2) but the implications for this discussion are the same.
It follows from this that the logarithmic dependence of the outgoing longwave radiation (which by the way, has to do the the exponential decay of the absorption coefficient away from the center of the absorption line) can still lead to significant temperature changes, particularly since water vapor enhances the value of λ and smoothes out a plot of the outgoing radiation vs. temperature (making it more linear than T**4). The log dependence though does mean that incremental changes of CO2 produce forcings smaller than the last similar incremental change (e.g., the forcing from 200 to 400 ppm is the same as the forcing from 500 to 1000 ppm, not 500 to 700 ppm). This is fortunate because if it were not the case, then CO2 doubling would be lethal and the Earth would be subject to extreme changes in climate. This is not the case, but it doesn’t mean the Earth is insensitive to change.
Here is a scientific article from 1960 that uses the term:
http://www3.interscience.wiley.com/journal/119763462/abstract?CRETRY=1&SRETRY=0
I doubt it is the first.
In an odd case of cinematic symmetry, two films came out in 1973 with bearing on climate change: “Soylent Green,” and “American Graffiti.” “Soylent Green,” dystopian sci fi set in 2022, with Charlton Heston and Edward G. Robinson (Robinson’s last film), includes this dialogue between them:
How can anything survive in a climate like this?
A heat wave all year long.
A greenhouse effect. Everything is burning up.
“American Graffiti,” set in 1962, is in part a love affair with cars.
un–Happy Birthday.
Now we know where the denialists cherry picked the “saturation” idea from.
7 Lou Grinzo: I pick 1898 when Arrhenius wrote his paper. See:
http://www.slrtx.com/blog/climate-science-timeline/
When should we have done something: Without the influence of coal industry propaganda and lobbying: There would have been zero large fossil fueled electric power plants after 1970.
A world of scientists would not be in this pickle. There is an evolutionary hurdle here. Can we get over it? Per SETI, E.T. seems not to have gotten over the evolutionary hurdle.
I’m so grateful that RealClimate exists. Today I read a news article about global warming on Yahoo (nothing startling in it, just that yes, the world is getting warmer, like we’ve been saying), and after reading the comments, remembered why I never read the comments. (It was this one, if you want to get a taste of what I mean: http://news.yahoo.com/s/ap/20100728/ap_on_sc/us_sci_state_of_the_climate) Post after post after post decrying that global warming exists, that it’s caused by humans, that it’s even a bad thing. Ignorant, blind excuses for reasoning are offered up as if they’re fact, making me wonder if we have any hope at all. After all this time, after the mountains of data, after the lives dedicated to finding the truth, people still look away, still deny its existence. Happy birthday, global warming, you may have the last laugh at our stupid species.
But then … I come here … and I have a flicker of hope. Thank you.