Guest commentary by Tamino
Update: Another review of the book has been published by Alistair McIntosh in the Scottish Review of Books (scroll down about 25% through the page to find McIintosh’s review)
Update #2 (8/19/10): The Guardian has now weighed in as well.
If you don’t know much about climate science, or about the details of the controversy over the “hockey stick,” then A. W. Montford’s book The Hockey Stick Illusion: Climategate and the Corruption of Science might persuade you that not only the hockey stick, but all of modern climate science, is a fraud perpetrated by a massive conspiracy of climate scientists and politicians, in order to guarantee an unending supply of research funding and political power. That idea gets planted early, in the 6th paragraph of chapter 1.
The chief focus is the original hockey stick, a reconstruction of past temperature for the northern hemisphere covering the last 600 years by Mike Mann, Ray Bradley, and Malcolm Hughes (1998, Nature, 392, 779, doi:10.1038/33859, available here), hereafter called “MBH98” (the reconstruction was later extended back to a thousand years by Mann et al, 1999, or “MBH99” ). The reconstruction was based on proxy data, most of which are not direct temperature measurements but may be indicative of temperature. To piece together past temperature, MBH98 estimated the relationships between the proxies and observed temperatures in the 20th century, checked the validity of the relationships using observed temperatures in the latter half of the 19th century, then used the relationships to estimate temperatures as far back as 1400. The reconstruction all the way back to the year 1400 used 22 proxy data series, although some of the 22 were combinations of larger numbers of proxy series by a method known as “principal components analysis” (hereafter called “PCA”–see here). For later centuries, even more proxy series were used. The result was that temperatures had risen rapidly in the 20th century compared to the preceding 5 centuries. The sharp “blade” of 20th-century rise compared to the flat “handle” of the 15-19th centuries was reminiscent of a “hockey stick” — giving rise to the name describing temperature history.
But if you do know something about climate science and the politically motivated controversy around it, you might be able to see that reality is the opposite of the way Montford paints it. In fact Montford goes so far over the top that if you’re a knowledgeable and thoughtful reader, it eventually dawns on you that the real goal of those whose story Montford tells is not to understand past climate, it’s to destroy the hockey stick by any means necessary.
Montford’s hero is Steve McIntyre, portrayed as a tireless, selfless, unimpeachable seeker of truth whose only character flaw is that he’s just too polite. McIntyre, so the story goes, is looking for answers from only the purest motives but uncovers a web of deceit designed to affirm foregone conclusions whether they’re so or not — that humankind is creating dangerous climate change, the likes of which hasn’t been seen for at least a thousand or two years. McIntyre and his collaborator Ross McKitrick made it their mission to get rid of anything resembling a hockey stick in the MBH98 (and any other) reconstruction of past temperature.
Principal Components
For instance: one of the proxy series used as far back as the year 1400 was NOAMERPC1, the 1st “principal component” (PC1) used to represent patterns in a series of 70 tree-ring data sets from North America; this proxy series strongly resembles a hockey stick. McIntyre & McKitrick (hereafter called “MM”) claimed that the PCA used by MBH98 wasn’t valid because they had used a different “centering” convention than is customary. It’s customary to subtract the average value from each data series as the first step of computing PCA, but MBH98 had subtracted the average value during the 20th century. When MM applied PCA to the North American tree-ring series but centered the data in the usual way, then retained 2 PC series just as MBH98 had, lo and behold — the hockey-stick-shaped PC wasn’t among them! One hockey stick gone.
Or so they claimed. In fact the hockey-stick shaped PC was still there, but it was no longer the strongest PC (PC1), it was now only 4th-strongest (PC4). This raises the question, how many PCs should be included from such an analysis? MBH98 had originally included two PC series from this analysis because that’s the number indicated by a standard “selection rule” for PC analysis (read about it here).
MM used the standard centering convention, but applied no selection rule — they just imitated MBH98 by including 2 PC series, and since the hockey stick wasn’t one of those 2, that was good enough for them. But applying the standard selection rules to the PCA analysis of MM indicates that you should include five PC series, and the hockey-stick shaped PC is among them (at #4). Whether you use the MBH98 non-standard centering, or standard centering, the hockey-stick shaped PC must still be included in the analysis.
It was also pointed out (by Peter Huybers) that MM hadn’t applied “standard” PCA either. They used a standard centering but hadn’t normalized the data series. The 2 PC series that were #1 and #2 in the analysis of MBH98 became #2 and #1 with normalized PCA, and both should unquestionably be included by standard selection rules. Again, whether you use MBH non-standard centering, MM standard centering without normalization, or fully “standard” centering and normalization, the hockey-stick shaped PC must still be included in the analysis.
In reply, MM complained that the MBH98 PC1 (the hockey-stick shaped one) wasn’t PC1 in the completely standard analysis, that normalization wasn’t required for the analysis, and that “Preisendorfer’s rule N” (the selection rule used by MBH98) wasn’t the “industry standard” MBH claimed it to be. Montford even goes so far as to rattle off a list of potential selection rules referred to in the scientific literature, to give the impression that the MBH98 choice isn’t “automatic,” but the salient point which emerges from such a list is that MM never used any selection rules — at least, none that are published in the literature.
The truth is that whichever version of PCA you use, the hockey-stick shaped PC is one of the statistically significant patterns. There’s a reason for that: the hockey-stick shaped pattern is in the data, and it’s not just noise it’s signal. Montford’s book makes it obvious that MM actually do have a selection rule of their own devising: if it looks like a hockey stick, get rid of it.
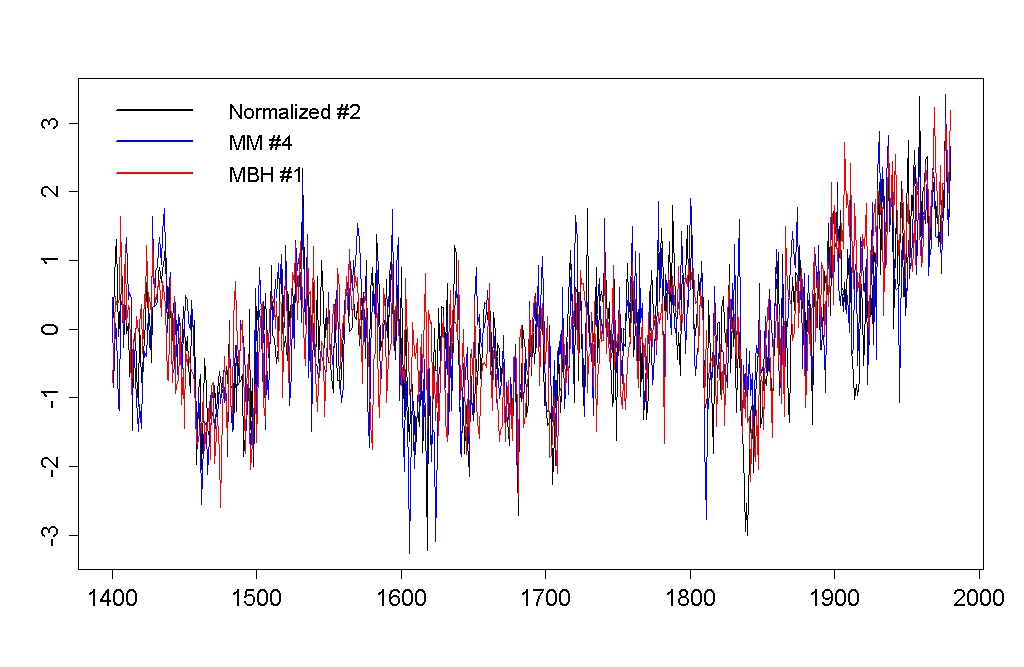
The PCA dispute is a prime example of a recurring McIntyre/Montford theme: that the hockey stick depends critically on some element or factor, and when that’s taken away the whole structure collapses. The implication that the hockey stick depends on the centering convention used in the MBH98 PCA analysis makes a very persuasive “Aha — gotcha!” argument. Too bad it’s just not true.
Different, yes. Completely, no.
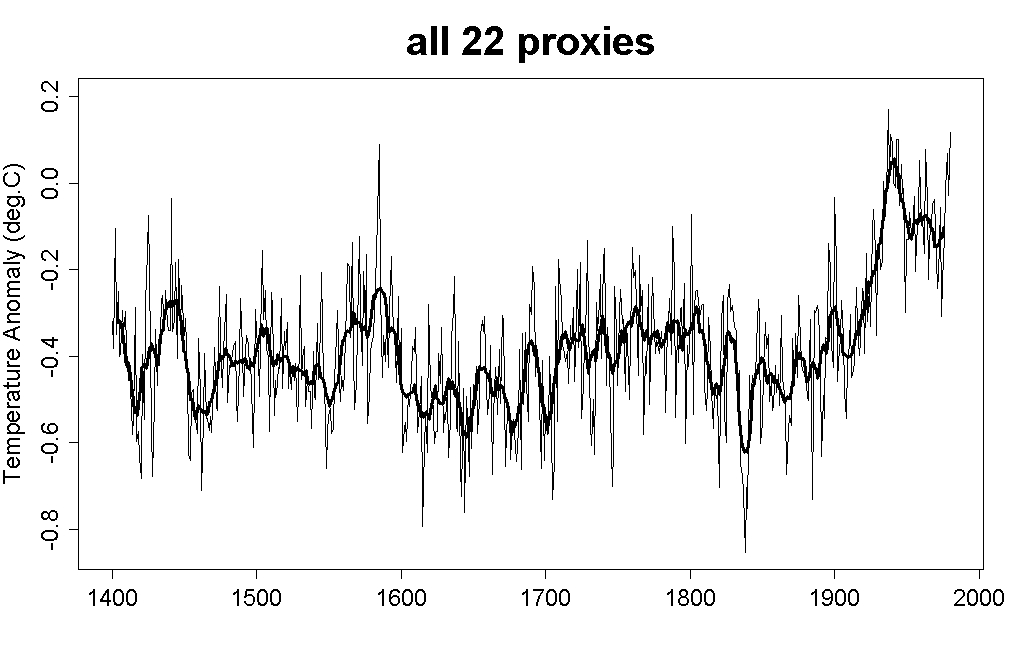
As another example, Montford makes the claim that if you eliminate just two of the proxies used for the MBH98 reconstruction since 1400, the Stahle and NOAMER PC1 series, “you got a completely different result — the Medieval Warm Period magically reappeared and suddenly the modern warming didn’t look quite so frightening.” That argument is sure to sell to those who haven’t done so. But I have. I computed my own reconstructions by multiple regression, first using all 22 proxy series in the original MBH98 analysis, then excluding the Stahle and NOAMER PC1 series. Here’s the result with all 22 proxies (the thick line is a 10-year moving average):
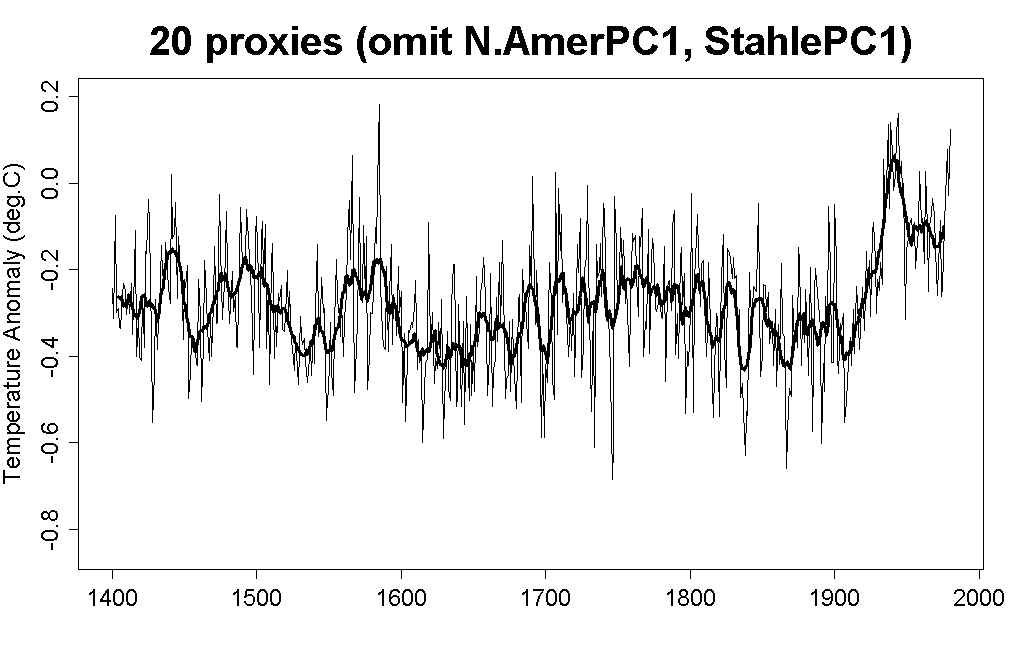
Here it is with just 20 proxies:
Finally, here are the 10-year moving average for both cases, and for the instrumental record:
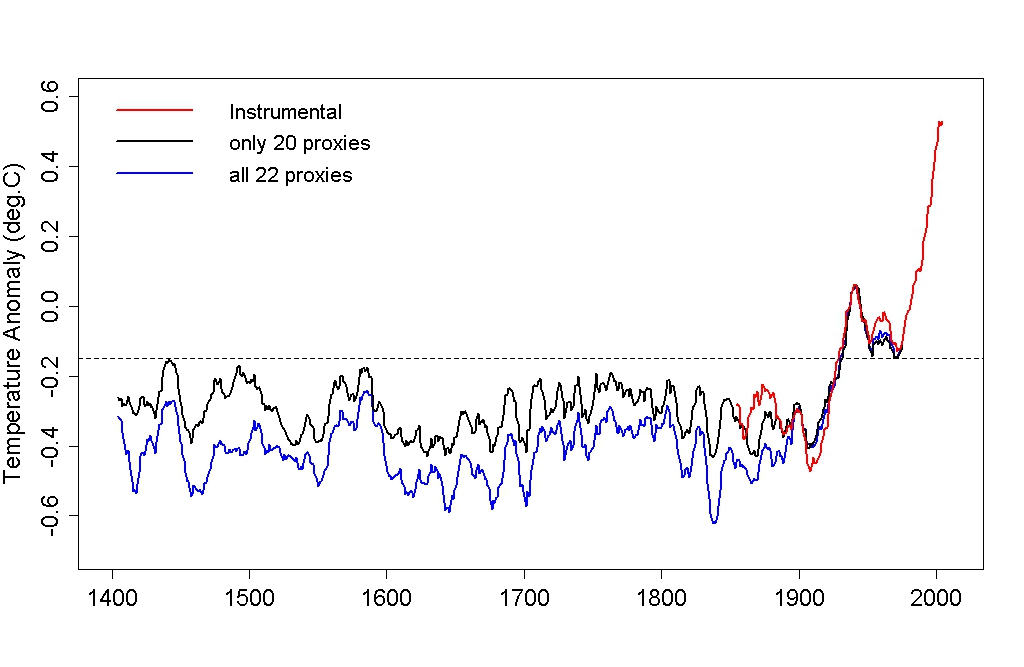
Certainly the result is different — how could it not be, using different data? — but calling it “completely different” is just plain wrong. Yes, the pre-20th century is warmer with the 15th century a wee bit warmer still — but again, how could it not be when eliminating two hand-picked proxy series for the sole purpose of denying the unprecedented nature of modern warming? Yet even allowing this cherry-picking of proxies is still not enough to accomplish McIntyre’s purpose; preceding centuries still don’t come close to the late-20th century warming. In spite of Montford’s claims, it’s still a hockey stick.
Beyond Reason
Another of McIntyre’s targets was the Gaspe series, referred to in the MBH98 data as “treeline-11.” It just might be the most hockey-stick shaped proxy of all. This particular series doesn’t extend all the way back to the year 1400, it doesn’t start until 1404, so MBH98 had extended the series back four years by persistence — taking the earliest value and repeating it for the preceding four years. This is not at all an unusual practice, and — let’s face facts folks — extending 4 years out of a nearly 600-year record on one out of 22 proxies isn’t going to change things much. But McIntyre objected that the entire Gaspe series had to be eliminated because it didn’t extend all the way back to 1400. This argument is downright ludicrous — what it really tells us is that McIntyre & McKitrick are less interested in reconstructing past temperature than in killing anything that looks like a hockey stick.
McIntyre also objected that other series had been filled in by persistence, not on the early end but on the late end, to bring them up to the year 1980 (the last year of the MBH98 reconstruction). Again, this is not a reasonable argument. Mann responded by simply computing the reconstruction you get if you start at 1404 and end at 1972 so you don’t have to do any infilling at all. The result: a hockey stick.
Again, we have another example of Montford implying that some single element is both faulty and crucial. Without nonstandard PCA the hockey stick falls apart! Without the Stahle and NOAMER PC1 data series the hockey stick falls apart! Without the Gaspe series the hockey stick falls apart! Without bristlecone pine tree rings the hockey stick falls apart! It’s all very persuasive, especially to the conspiracy-minded, but the truth is that the hockey stick depends on none of these elements. You get a hockey stick with standard PCA, in fact you get a hockey stick using no PCA at all. Remove the NOAMER PC1 and Stahle series, you’re left with a hockey stick. Remove the Gaspe series, it’s still a hockey stick.
As a great deal of other research has shown, you can even reconstruct past temperature without bristlecone pine tree rings, or without any tree ring data at all, resulting in: a hockey stick. It also shows, consistently, that nobody is trying to “get rid of the medieval warm period” or “flatten out the little ice age” since those are features of all reconstructions of the last 1000 to 2000 years. What paleoclimate researchers are trying to do is make objective estimates of how warm and how cold those past centuries were. The consistent answer is, not as warm as the last century and not nearly as warm as right now.
The hockey stick is so thoroughly imprinted on the actual data that what’s truly impressive is how many things you have to get rid of to eliminate it. There’s a scientific term for results which are so strong and so resistant to changes in data and methods: robust.
Cynical Indeed
Montford doesn’t just criticize hockey-stick shaped proxies, he bends over backwards to level every criticism conceivable. For instance, one of the proxy series was estimated summer temperature in central England taken from an earlier study by Bradley and Jones (1993, the Holocene, 3, 367-376). It’s true that a better choice for central England would have been the central England temperature time series (CETR), which is an instrumental record covering the full year rather than just summertime. The CETR also shows a stronger hockey-stick shape than the central England series used by MBH98, in part because it includes earlier data (from the late 17th century) than the Bradley and Jones dataset. Yet Montford sees fit to criticize their choice, saying “Cynical observers might, however, have noticed that the late seventeenth century numbers for CETR were distinctly cold, so the effect of this truncation may well have been to flatten out the little ice age.”
In effect, even when MBH98 used data which weakens the difference between modern warmth and preceding centuries, they’re criticized for it. Cynical indeed.
Face-Palm
The willingness of Montford and McIntyre to level any criticism which might discredit the hockey stick just might reach is zenith in a criticism which Montford repeats, but is so nonsensical that one can hardly resist the proverbial “face-palm.” Montford more than once complains that hockey-stick shaped proxies dominate climate reconstructions — unfairly, he implies — because they correlate well to temperature.
Duh.
Guilty
Criticism of MBH98 isn’t restricted to claims of incorrect data and analysis, Montford and McIntyre also see deliberate deception everywhere they look. This is almost comically illustrated by Montford’s comments about an email from Malcolm Hughes to Mike Mann (emphasis added by Montford):
Mike — the only one of the new S.American chronologies I just sent you that already appears in the ITRDB sets you already have is [ARGE030]. You should remove this from the two ITRDB data sets, as the new version should be different (and better for our purposes).
Cheers,
Malcolm
Here’s what Montford has to say:
It was possible that there was an innocent explanation for the use of the expression “better for our purposes”, but McIntyre can hardly be blamed for wondering exactly what “purposes” the Hockey Stick authors were pursuing. A cynic might be concerned that the phrase actually had something to do with “getting rid of the Medieval Warm Period”. And if Hughes meant “more reliable”, why hadn’t he just said so?
This is nothing more than quote-mining, in order to interpret an entirely innocent turn of phrase in the most nefarious way possible. It says a great deal more about the motives and honesty of Montford and McIntyre, than about Mann, Bradley, and Hughes. The idea that MM’s so-called “correction” of MBH98 “restored the MWP” constitutes a particularly popular meme in contrarian circles, despite the fact that it is quite self-evidently nonsense: MBH98 only went back to AD 1400, while the MWP, by nearly all definitions found in the professional literature, ended at least a century earlier! Such internal contradictions in logic appear to be no impediment, however, to Montford and his ilk.
Conspiracies Everywhere
Montford also goes to great lengths to accuse a host of researchers, bloggers, and others of attempting to suppress the truth and issue personal attacks on McIntyre. The “enemies list” includes RealClimate itself, claimed to be a politically motivated mouthpiece for “Environmental Media Services,” described as a “pivotal organization in the green movement” run by David Fenton, called “one of the most influential PR people of the 20th century.” Also implicated are William Connolley for criticizing McIntyre on sci.environment and James Annan for criticizing McIntyre and McKitrick. In a telling episode of conspiracy theorizing, we are told that their “ideas had been picked up and propagated across the left-wing blogosphere.” Further conspirators, we are informed, include Brad DeLong and Tim Lambert. And of course one mustn’t omit the principal voice of RealClimate, Gavin Schmidt.
Perhaps I should feel personally honored to be included on Montford’s list of co-conspirators, because yours truly is also mentioned. According to Montford’s typical sloppy research I have styled myself as “Mann’s Bulldog.” I’ve never done so, although I find such an appellation flattering; I just hope Jim Hansen doesn’t feel slighted by the mistaken reference.
The conspiracy doesn’t end with the hockey team, climate researchers, and bloggers. It includes the editorial staff of any journal which didn’t bend over to accommodate McIntyre, including Nature and GRL which are accused of interfering with, delaying, and obstructing McIntyre’s publications.
Spy Story
The book concludes with speculation about the underhanded meaning of the emails stolen from the Climate Research Unit (CRU) in the U.K. It’s really just the same quote-mining and misinterpretation we’ve heard from many quarters of the so-called “skeptics.” Although the book came out very shortly after the CRU hack, with hardly sufficient time to investigate the truth, the temptation to use the emails for propaganda purposes was irresistible. Montford indulges in every damning speculation he can get his hands on.
Since that time, investigation has been conducted, both into the conduct of the researchers at CRU (especially Phil Jones) and Mike Mann (the leader of the “hockey team”). Certainly some unkind words were said in private emails, but the result of both investigations is clear: climate researchers have been cleared of any wrongdoing in their research and scientific conduct. Thank goodness some of those who bought in to the false accusations, like Andy Revkin and George Monbiot, have seen fit actually to apologize for doing so. Perhaps they realize that one can’t get at the truth simply by reading people’s private emails.
Montford certainly spins a tale of suspense, conflict, and lively action, intertwining conspiracy and covert skullduggery, politics and big money, into a narrative worthy of the best spy thrillers. I’m not qualified to compare Montford’s writing skill to that of such a widely-read author as, say, Michael Crichton, but I do know they share this in common: they’re both skilled fiction writers.
The only corruption of science in the “hockey stick” is in the minds of McIntyre and Montford. They were looking for corruption, and they found it. Someone looking for actual science would have found it as well.
What’s really shameful is that M&M managed to get their crappy analysis into a peer-reviewed science journal. How did that happen?
Thank you Tamino for, as always, a very clear and logical presentation. I am pleased that you emphasized how the hockey stick is visible in the actual data. It is truly extraordinary the lengths that McIntyre and Montford go to to avoid this obvious point. Science requires both the ability to handle the nitty-gritty details, and the ability to stand back and see the big picture. This is something that the self-styled “auditors” have spectacularly failed to grasp.
We are reminded by this dissection/flaying of Montford of the quote attributed to Daniel Moynihan–everyone is entitled to his own opinion, but not to his own facts. Kudos, Tamino! You make Papageno proud.
The other “damning evidence” of misconduct by Mann I hear recirculated by the likes of M&M is that the proxies don’t match the observed temperatures after about 1980. What’s the explanation for why the proxies aren’t used to show warming in the last 30 years?
[Response: At the time (late 1990s), most of the data in the archives had been collected in the 1980s or even earlier, and so the number of proxies decreased rapidly after 1980. There are also some technical reasons for that (for instance, for some proxies, such as lake sediments or ice cores, it is harder to retrieve the most recent data). Now (in 2010) that is not so much of a problem and more recent multi-proxy reconstructions go up to 1995 or so (Mann et al, 2008 for instance). – gavin]
Infinite thanks, very useful.
If one goes to the amazon.com entry for this tome, one can read all sorts of adoring accolades from the already convinced. One can also comments on comments—and dissenting comments (e.g. ones that disagree with the adoration, or cite Realclimate.org) can be censored by other readers as “inappropriate”. Quite revealing–have a look, and vote the dissenters back on the island.
Note, of course that Montford’s “extensive” research failed to uncover:
earlier attacks on the hockey stick
Essex&McKitrick’s 2002 book [Essex isn’t even in the Index]
McKitrick, and then M&M recruitment by CEI + George Marshall Institute
paying for visits to Washington, DC
introducing them to Singer, Baliunas, Soon, Michaels for review of their talks
adding them as GMI Experts (2004)
sponsoring talks for Congress
introducing them to Inhofe
helping get publicity in WSJ
and then of course the whole Barton/Whitfield … Wegman Report effort.
For a detailed chronology, see Crescendo to Climategate Cacophony, especially section 5, and look around for all the references to A.HOCKX and A.Hockey, i.e., the two parts of the attack on the hockey stick. Sooner or later, that will get updated … and it will certainly include a link to tamino’s post…
Thanks, Tamino. Now Judy can get back to doing science, right?
Tamino wrote: “But if you do know something about climate science and the politically motivated controversy around it …”
It is not a “politically” motivated “controversy” around climate science.
It is a financially motivated attack on climate science.
The attacks on climate science have nothing to do with any actual political ideology, and everything to do with the ONE BILLION DOLLARS PER DAY PROFIT that the fossil fuel corporations want to keep raking in for as long as they can get away with it.
Anybody following James Annan’s blog will get a hearty laugh from the idea that he’s a member of the imaginary conspiracy. What a joke, really.
Thanks for the link to my dissection of how little context can be drawn from the CRU emails, Tamino. Based on the text of the ICCER (Sir Muir Russell) report, the Review independently came to same conclusions I did – the emails weren’t damning on their own, weren’t necessarily reliable, and lacked sufficient context to justify the broad conclusions drawn by folks like Montford, McIntyre, McKitrick, et al.
For amusement, one may consult The Hockey Stick Illusion, Wikipedia talk page.
I was going to mention tamino’s post there … but discovered that the Dark Lord of Wikipedia (or something similar) otherwise known as WMC was too quick and had already done so.
SecularAnimist – I did some research into grants for climate science vs. revenues for fossil fuel-related industries and found that in 2008 (the latest year for which all the data I needed was available), globally governments spent about $3.8 billion on researching climate science (and that’s a high estimate, given how much of that money goes to multi-purpose satellites) while the fossil fuel-related industries I could track had revenues of about $9 trillion, or 15% of the entire global economy. And that number was a minimum, not a max, given the way I did my analysis.
And yet Montford et al still claim that climate scientists are all in it for the grant money. If that were the case, they’d be far more likely to perform research for a corporate employer instead of working for government labs or in academia, given that there’s about 2400x more money available than there is in government or academia.
[Response: Indeed. It’s worth emphasising that the vast bulk of the climate science money goes on observing platforms like satellites. For instance, NASA’s budget for Earth Science is around $2 billion dollars, and GISS accounts for about 0.5% of that. – gavin]
How does the Midieval warm period suppose to appear or disapper when the reconstructions you supply in this artical only go back to the year 1400 and the Midievel warm period is aroung the year 1000?
[Response: It doesn’t. This is one of those frequent (and false) ideas that pop up in Monckton’s presentations and elsewhere, such as this book apparently – even as they discuss the reconstruction back to 1400 only. – gavin]
Gavin – I know someone who works reasonably high up in a government lab (won’t say who or which lab), and when the OCO failed to separate from the rocket, the money lost on that one satellite would have funded his/her entire lab budget for at least 3 years. Owie.
[Response: Only 3 years? It would have funded GISS for 25. – gavin]
[Response: BTW, a contract for the rocket propulsion was just awarded for a launch of OCO2 in 2013, according to Nature–Jim]
What a valid waste of time Tamino dedicated himself to do. King contrarians harping about a vast conspiracy, while outside their homes weather is the warmest ever recorded! A kin to wind mills attacking Don Quixote, the world is not what it really seems. Their basic premise of corruption is an inversion, pure and simple, they are the ones corrupting science with malicious claims, along with this action they make money, appear on Fox news or some British tabloid to further book sales. I pity their legacy, meanwhile they enjoy their 15 minutes of shame.
Medieval in Greenland:
Vinther, B.M., Jones, P.D., Briffa, K.R., Clausen, H.B., Andersen, K.K., Dahl-Jensen, D. and Johnsen, S.J. 2010. Climatic signals in multiple highly resolved stable isotope records from Greenland. Quaternary Science Reviews 29: 522-538.
“temperatures during the warmest intervals of the Medieval Warm Period,” which they defined as occurring “some 900 to 1300 years ago, “were as warm as or slightly warmer than present day Greenland temperatures”
[Response: What is your point? This is neither relevant to MBH98 (which only goes back to 1400), nor to any papers written in 1998 (since it came out in 2010), nor to the claims made in this book. If you wanted to discuss the regional patterns of medieval climate anomalies, there was a thread a couple of months back (and almost certainly there will be another at some other time). Claims about medieval times are OT on this thread. – gavin]
I think part of the problem with the hockey stick is that it has been used so heavily by the IPCC and others that it has become rather totemic for both sides of this debate. There is all sorts of evidence for and against natural climate change at various stages of history (and prehistory) that bears discussing, but we rarely ever get to it because everyone is banging on about the hockey stick being inaccurate or accurate (depending on your point of view).
Indeed, Gavin responds on this thread to “Medieval in Greenland” that “Claims about medieval times are OT on this thread”. Strictly speaking, of course, they are. But the hockey stick has been used to slap down talk about previous (natural) warm periods when it should not have been because it only went back to 1400.
It is such a shame everyone seems fixated on this one graph.
[Response: We couldn’t agree more. The study of past climate variations is fascinating and is so much more than simply relative medieval warmth. The fact that people are still arguing about a decade old paper is frankly mystifying from a scientific point view, but all too understandable from a political view. Despite what Montford would have you believe, this study just isn’t that important to the science (as we tried to make clear years ago). You are correct in pointing to the iconisation of a single graph as being the heart of the problem – that tends to bring out the iconclast in everyone. But where it all goes wrong is when people take something that is representative of a whole suite of scientific study and act as if that was the totality of the understanding. Thinking mistakenly perhaps that by undermining one symbolic graph they change the underlying knowledge. The same situation occurs with Kilimanjaro – a representative picture of glaciers melting almost everywhere that is sometimes assumed to be the sole proof of the wider phenomena. And similarly, the iconclasts point to specific issues that might be relevant for Kilimanjaro as if that meant that no glaciers anywhere are retreating. Why does this occur? Something to do with the need to have shorthand for complex issues in the public discourse in ways that don’t occur to anything like the same manner in science perhaps? – gavin]
Excellent, excellent piece.
My only complaint is the single phrase minimizing the unusual PCA centering technique Mann used. While I understand what was done, and it actually makes sense to me as a non-statistician, the comments by Professor Ian Jolliffe on your own blog suggest to me that it is simply wrong to do so, although maybe not entirely that black and white. The fact that it makes minimal difference in the end result should be highlighted, but I think you go overboard in minimizing the basic MM argument by using the following phrasing:
I don’t want to wordsmith it on you, but use of words like “claimed,” “convention,” and “customary” seem to make the MM complaint seem arbitrary and misguided when to me it was not. It wasn’t merely claimed, they were right. It wasn’t a convention, it was a technique. It wasn’t simply not customary, it was wrong to do so. Use of double quotes around the word “centering” also hints at something intangibly nefarious, probably because the deniers so often put quotes around terms they don’t like, simply to silently imply that everything behind the term is arbitrary, or lacking truthiness, or not even relevant (like “global temperature record” or “computer models” or so called “climate scientists”).
The centering method Mann used (based on what I’ve read) was, to statisticians, both irregular and incorrect. Come out and say it, or your post starts off sounding a bit like the denier’s posts. Call a spade a spade, and let the truth stand on it’s own, without crutches.
[Or, if I’m wrong on this, please correct me.]
[Response: I don’t agree. One can perform an SVD on any matrix you like, and that will provide a set of basis functions that have certain properties. The interpretation of the vectors will certainly depend on this, but it is much less important if you are simply doing a data reductions step. In this case, this was being used for data reduction, and so the particular SVD decomposition needs to be combined with a selection rule to see what is retained. I’m sure that given the subsequent furore, Mann et al would have been happier if they had used full centering, but it would have made very little difference either to the results or the reaction. – gavin]
But again, this is an excellent, concise deconstruction of something that MM have spent years and years trying to compile. It’s a wonder that their position gets any air time at all, except that there are obviously so many people out there who only ever see what they want to see, and the bigger the danger is, the more tightly they shut their eyes and try to imagine their happy place.
Thanks Tamino, great post. Would it be possible to get links to larger versions of the images?
Thanks
I’m glad to see this issue being given attention by Tamino & RC.
Deep Climate could have some worthwhile observations to add too.
Montford’s pernicious drivel, encouraged on his website, is the most serious attack on science imaginable without invoking Godwin’s Law.
I’m looking at the first graph in this article. There is a definite upward trend at the end of the graph starting in the middle of the 19th century.
Is the prevailing opinion that that upward trend is primarily caused by human emissions of greenhouse gases or am I looking at a natural phenomenon that humans are now adding to? Is the cause of warming during that period different from the cause of warming now (ie soot vs CO2)?
I have been told that the warming caused by human emissions of greenhouse gases is happening far faster than natural trends normally do and that the fear is that natural systems won’t be able to cope quickly enough to this warming. It looks like the upward trend in the late 15th and early 16th centuries has the same slope, though. Would you say that the most damaging global warming is not shown on that graph? (The graph ends at 1980, I think?) Or is it partially the duration of the trend that is a concern? Or would you say that nature can adapt to these changes?
Finally, this is somewhat unrelated to the article here, but it’s something I’m curious about. Can you comment or point me towards information about what parts of the world are most likely to become more habitable for humans or remain largely unaffected? I have heard a lot about what areas are at higher risk (coastal areas, for instance) but more rarely hear about areas that should fare well.
The Wegman Report (ostensibly an examination of the M&M critique) studiously omitted any discussion of PC selection/retention criteria. Not so co-incidentally, they also excluded any substantive discussion of the two peer-reviewed comments (Huybers and von Storch) and the Wahl and Ammann Climatic Change paper (then in press), which remains to this day the most substantive peer-reviewed treatment of M&M “hockey stick” critique.
Wegman even claimed as “fact” that “it is not a published refereed paper”. Like much of Wegman’s commentary, this was highly misleading. The paper was in press at Climatic Research (as seen in the report’s own reference list). So the paper had been reviewed, finalized, accepted and had been published online, even though the journal publication came later.
http://deepclimate.files.wordpress.com/2010/04/stupakresponse-no-appendix.pdf [p. 14]
Hence the title of an upcoming DC post: “Wegman’s trick to hide the deletion … of Wahl and Ammann”
BTW, Wahl and Amman can be found at:
http://www.cgd.ucar.edu/ccr/ammann/millennium/refs/Wahl_ClimChange2007.pdf
As for M&M’s PC selection criterion, it appears to have been “Take two PCs and call me in the morning”.
It seems to be a hallmark of crank denial to attack the pioneering work in a field (and frequently, the scientists responsible for it). Creationists attack Darwin. HIV denialists attack Gallo. And Global Warming denialists attack Mann.
To some extent, I think this reflects a cartoon notion of science that prevails among cranks. Cranks tend to imagine that the early studies constitute a foundation of conclusions and that are accepted without question by subsequent researchers. Destroy that foundation by discrediting the early work, they imagine, and the entire edifice will collapse.
This tends to be mystifying to working scientists to whom the early (and in an active field of science, 10 years ago is early) work is largely of historical interest. However groundbreaking the early studies were, they will inevitably have been replicated with improved methods and better data since that time.
I think this misconceptioin about science reflects two factors. One of course is simply unfamiliarity with the primary literature. Few cranks have the patience or background to read it, and few have any conception of just how much of it there is. It is not uncommon to hear a crank demand “the single paper that proves {denial target).” When they are given a list of hundreds or thousands of references, they see it as mere obfuscation.
I don’t think that there is much that scientists can do about this, aside from writing popular reviews, and even these must inevitably understate the mass of the literature.
However, a second factor may be that scientific papers rarely give much attention to results that confirm or replicate previous work. There is an understandable wish to highlight the findings that are new or different, which are what will sell the paper to the reviewers, and also what one’s colleagues are going to be most interested in. Others in the field will recognize replication, anyway, so at most it tends to be mentioned obliquely (“Consistent with previous findings…”). I can’t help wondering if some more attention given to highlighting confirmation in “crank target” fields could be helpful.
#20
Montford’s discussion of the two “competing” panels (NRC and Wegman) is all wrong as well. Something else to get into …
Not to mention the upcoming GWPF Climategate investigation by none other than … Andrew Montford:
http://www.thegwpf.org/climategate/1204-investigation-into-climategate-inquiries-announced.html
When will this madness end? When will the media wake up and do their job?
This is a bit off-topic, but perhaps related.
SPPI has just issued a new paper authored by Joe Aleo that alleges Hansen and CRU are manipulating graph lines by changing them from what they were years ago.
The paper refers on page 4 to “Hadley’s CRU,” even though it is dated 7-21-10.
This mistake about the name of the organization was sorted out last November when the story of the hacking broke.
I think the author means CRU because he mentions Wigley, but why would he say “Hadley’s CRU”? What am I missing? Later he just says CRU.
QUOTE:
“Hadley’s CRU has changed significantly just in the last decade in much the same way. The 1940 warm blip that worried Wigley and others was minimized which minimized the three decade cooling from 1940 to the late 1970s. The same issues mentioned above have exaggerated the recent warming.”
http://scienceandpublicpolicy.org/originals/progressive_enhancement.html
The author claims that moving the lines on the graph “have exaggerated the recent warming.”
I can’t judge that, but is strange to write “Hadley’s CRU.”
[Response: This is a very frequent error (Watts has made it many times before), and stems from their confusion between the HadCRUT data set (which is a collaboration between the Hadley Centre (providing SST and sea ice cover) and the CRU (which provides the met station analysis) and the actual institutions (which are completely independent and separated by a couple of hundred miles). – gavin]
re: #18
I’ve long argued that this is an “evidence vs representation” issue, that the emphasis on the hockey stick in the TAR seemed due to fact that of the huge numbers of papers and lines of evidence, very few offer a simple, compelling graphic … which is why it has been subject to such attack.
People may recall that Gerald North ran the NRC panel in 2006, by request of Rep. Boehlert, that reviewed all this.
It is well worth watching/listening to his August 2006 seminar, although the beginning music is a bit much.:-)
He discusses this topic, among others.
Re: #19 (Ken W)
If you right-click on the graph, then select “view image” from the menu, you’ll see a larger version (it’ll fill your browser screen).
I’ve a better grasp of exactly what the “noise” about the hockey stick generated by the deniers is about. The raw data shows the hockey stick so the quibbling about statistics (always a suspect activity) is just so much hot air.
Personally, I see no reason that somebody who is being harassed can’t complain about in private. In purple tones, if that’s their style. I’ve never known anyone being actively harassed who was calm about it. It’s not a character deficiency!
13 Brian Angliss or somebody: Could you please trace where M&M get their money to do all of their anti-science? We know it has to be the fossil fuel industry, but more a specific path and the information on how much would be useful.
Dr. Tamino: Your very last sentence doesn’t flow right. Great article. Thanks. People with Paranoid Personality Disorder will never be convinced of the truth.
Tamino,
Help. I’m struggling with your first paragraph where you talk of Montford claiming ‘all of modern climate science, is a fraud perpetrated by a massive conspiracy of climate scientists and politicians, in order to guarantee an unending supply of research funding and political power. That idea gets planted early, in the 6th paragraph of chapter 1.’
Montford, describing the growth of the modern global warming hypothesis (para 5 ch 1 of his book), then gives para 6:
“Work continued quietly but steadily in the background. Then in 1977 the pace started to quicken. The impulse was provided by the creation of a separate climate bureaucracy under the auspices of the World Meteorological Organisation (WMO). The WMO had organised the first World Climate Conference,, which was held in Geneva two years later, and it is to that first meeting that the beginnings of the global warming movement can be traced.”
I just can’t find anything conspiratorial in paragraph 6 of ch 1. Just a description of the growth of the global warming hypothesis. Or did I miss something.
Well done Tamino.
21 (Peter),
I can’t vouch for the accuracy of the site, and you must make your own inferences from projected temperature and precipitation changes, as well as knowledge of the climate being changed (e.g. the southwestern U.S. is already hot and dry), but I find this site to be informative and fun (in a rather depressing way)…
Climate Wizard
Of course, this still doesn’t fill in many missing bits of information (such as the knowledge that even if parts of Canada or Siberia get warmer, they will not necessarily have arable soil, or growing seasons of the proper duration (i.e. number of months with a minimum amount of sunlight per day) to make them viable for crops.
When I read the Wegman report some time ago, the main message I got was that the climate science community did not adequately involve the statistical community in their work, even though climate science tends to be heavy in statistics. Has the climate science community increased involvement of statisticians in recent years, perhaps including them in the statistical work or at least including them in peer review of climate science papers prior to publication? I realize Wegman is a statistician and perhaps its human nature to maximize one’s profession, but he could have a point. Scientists of various disciplines and even applied statisticians may be more inclined to use plug & play canned statistical tools. Theoretical statisticians may be more capable of recognizing unique conditions of specific data analyses and be able to formulate more appropriate statistical tools for specific applications.
[Response: Sure, there are multiple programs to do just that – the recent meeting on statistical climatology in edinburgh was full of people involved in that. – gavin]
Another point I remember from the Wegman report was that the peer review of climate science papers was sort of a closed circle due to the relatively small number of qualified climate scientists. Is that a valid observation? If so, have steps been taken to improve the independence of peer reviewers?
[Response: Since Wegman had no information at all on the identities of any peer reviewers, his comments on the issue are content-free. He did make an analysis of co-authorship (not the same thing at all), and found, to no-one’s surprise that Mann’s coauthors were a network of people with Mann at the center. The same thing will be trivially true for any reasonably collaborative scientist. Contrary to Wegman’s assertions, editors do strive and have always striven to get objective peer reviews for all the papers they deal with. Suggestions to the contrary without any actual evidence are just insinuations, not issues. – gavin]
Re: #29 (Edward Greisch)
The last paragraph is a paraphrase of Dee Snider’s testimony before a Senate committee, about the “Parent’s Music Resource Committee” request for warning labels on music albums.
Re: #30 (Cameron Rose)
By my count, what you’ve called paragraph 6 is actually paragraph 5.
The actual paragraph 6 (the following one) ends with these sentences: “One can almost detect the germ of an idea forming in the minds of the scientists and bureaucrats assembled in Geneva: here, potentially, was a source of funding and influence without end. Where might it lead?”
“And if Hughes meant “more reliable”, why hadn’t he just said so?”
This (and the full paragraph) gets at the heart of why private correspondence between scientists is inherently of limited value, and also why it’s a boon for political hacks (context that is lacking can be created to suit one’s goals). Of many things, it presumes that scientists are writing emails to each other with the idea that the general public will be reading it, and thus will go out of their way to provide the full background in each message – that the relationship between colleagues is no different from the relationship with the general public. I’m certain that someone looking for dirt can find messages to/from colleagues of mine that have plenty of ambiguity, and seen through the eyes of conspiracy nuts, can be spun to mean something nefarious. Montford is hoping these presumptions are lost on his readers, many of whom probably have a nutty leaning to begin with.
To clarify: Dee Snider was frontman for the band “Twisted Sister.” Their song “Under the Blade” was falsely accused by the PMRC (specifically, Tipper Gore) of being about sadomasochism, bondage, and rape. In reality (as Snider testified at Senate hearings in Sept. 1985) it was about fear of an impending surgery.
The false accusation is fine example of someone finding evil, not because it’s there but because that’s what they’re looking for.
One aspect of this saga that I think needs to be disabused is the notion that these were “private” emails. They may have been perceived by the communicators as private conversations, but nearly all of the e-mail exchanges were done by people operating with public funding or, in some cases, on government e-mail accounts.
Some background, from the Union of Concerned Scientists:
http://dotearth.blogs.nytimes.com/2010/02/02/climate-information-wants-to-be-free/
[Response: I strongly disagree. Emails written prior to FOIA legislation even existing, written on university computers that do not belong to the government are not ‘public’. Even emails existing on government computers with FOIA legislation are not ‘public’. There are multiple filters that need to be operated before an email held by a government entity can be released – filters for whether it is associated with official business, filters for privacy concerns, filters for pre-decisional discussions, anything related to Congress etc. Now, while working for an institution with IT policies and the like, people have no expectation to absolute privacy (since the IT department can examine servers and the like), but this is vastly different to assuming that all email is automatically in the public sphere. Your medical records can be viewed by other medical practioners and so similarly do not have an absolute privacy guarantee, but they are a long way from public domain. People certainly had, and should have, an expectation that they can discuss issues frankly without needing to be mindful that everything is being published. That is true in science, it is true in government and it is true at the New York Times. No-one works and lives in glare of 100% openness and nor could they. – gavin]
Andy Revkin wrote: “One aspect of this saga that I think needs to be disabused is the notion that these were ‘private’ emails.”
One aspect of this saga that I think needs to be disabused is the notion that illegal hacking into servers to steal emails has anything whatever to do with FOIA, or openness, or transparency.
We are not talking about information that was obtained, for example, consequent to a lawsuit.
We are talking about information that was stolen by criminals. Which is an “aspect of this saga” that you seem inclined to ignore.
It’s really too bad that you haven’t seen fit to give even a fraction of the attention to the very real, very serious question of who broke into the computer system and stole the emails that you have given to legitimizing the baseless, slanderous and inflammatory charges that various fossil fuel corporation stooges made about the emails.
This is an excellent rebuttal, but it’s a pity that such a piece is necessary at all.
The way I analyse the global warming story over the past 20 years is that various players with a strong interest in not moving quickly to a post-carbon economy (the task of filling up the blanks I’ll leave to you) begin a quiet disinformation campaign almost before the science was settled. It took a long time, but eventually (by the early 2000s) this had generated a head of steam so that rubbish like this book could be seen to be some sort of valid comment by the serially deluded, and a whole denial movement seemed to exist in its own right.
Meanwhile, politicians, whilst in main subscribing the science, found it too difficult to fight against, on the one hand, the official opposition of the carbon industries, and on the other this opposition from ostensibly independent public opinion. And so little was done to mitigate global warming.
And so the actual intention of the oil-companies and their sector was accomplished by a two-flank attack, a public one, on global warming policies, and a covert one, by whipping up a denial movement to do what the industries could not do publicly without appearing foolish.
Andy Revkin:
http://quotationsbook.com/quote/19331/
You are using a publicly funded email system — the Internet.
Look at the path records for the email that reaches you.
Did any of it ever go through a government-funded machine?
Is your email public?
What of anyone who contacts you by email?
What about the other 99 percent or whatever it is, that’s apparently been stolen but not disclosed? What about other archives? All public?
Mr. Revkin-
There are also Data Protection Issues.
The Email Review’s (FAQ’s) notes:
“This review is not a criminal investigation. However, Norfolk Constabulary are investigating criminal offences in relation to the hacking incident. The Information Commissioner is examining Freedom of Information and Data Protection issues. The Review has met Norfolk Constabulary and the Information Commissioner’s Office and will remain in touch on matters of mutual interest.”
This is the address of the http://www.ico.gov.uk/
Compliance with this gets very complicated.
There are caveats like information doesn’t have to be shared “if there’s a good reason not to,” etc.
I thought the Information Commissioner Graham Smith just shot his mouth off without knowing any facts. He is a lawyer and should not be making judgments based on what is in the newspapers. He didn’t even talk to CRU.
Sometimes there are proprietary or sensitive issues when you share data with some government organizatons. For example, CRU works with the MET, and that is technically part of the British Ministry of Defense.
I’d really like to see #38 clarified. I’m hoping there’s some sort of miscommunication going on, because otherwise it sounds an awful lot like excusing or condoning the emails’ theft and dissemination.
[Response: That it does. – mike]
Tamino, hi,
Reading this article prompted me to have another go at digesting Gavin’s also excellent Dummies guide to the latest “Hockey Stick” controversy. And this time through, it finally sunk in that if you change the way the PCs are normalised, you may need to include more PCs else you risk losing crucial data. Got it! A real eureka moment for me.
But the main reason I’m writing is about another apparent loss of crucial data. One of my all-time favourite articles illustrating the undeniably significant role that GHGs play in climate change is by you: Not Computer Models. I always had difficulty interpreting your graphs, however, so I wanted to try employing the “trick” you described above in post #28 to blow up the images (most people would assume that if you don’t explicitly link to a larger image, then one is not available, BTW).
Alas, none of your articles from more than a few weeks back seem to be accessible any longer. I believe that you are in the process of moving servers. Will your older articles be restored in the near future? I surely hope so, because they are a great resource.
Considering the important and sometimes crucially determinative role of journalism in public policy debate, I think it’s reasonable to wonder why journalists’ notebooks and professional communications are not transparently available to the public on demand.
It would be entirely more healthy for us to be able to trace the path of information or disinformation represented as journalism to the printed page when such matter is consumed by the public and its representatives as an important constituent of civic activity. For instance, how is a particular story instantiated, organically by an editor or reporter, or at the behest of a publisher? What research was included in a story and what was not? What was struck by editors?
Naturally such a system would require some means for necessary redaction, perhaps via a board of review composed of journalism academics, but at the end of the day information of such importance to the public interest should be available on demand. Conversely, a journalist’s work product should never be simply stolen and then published without proper vetting.
[edit – sorry OT]
re: #34 John Philips
As it happens, in the near future, you may want to revisit the Wegman Report…
– For example, Wegman & co were so expert at Social Network Analysis that pp.17-22 of the WR bear “striking similarity” (that’s the legal term, most people say plagiarism) from Wikipedia, Wasserman&Faust(1994) and deNooy, Mrvar, and Bateglj(2005), as shown by Deep Climate in April.
Did the WR itself have any peer review in the normal sense?
No.
Re; #19 (Bob Sphaerica)
I only put the word “centering” in quotes because in this context its meaning is different from what the average lay reader thinks of — it’s a technical term and I hoped to emphasize that. Any other interpretation is incorrect. I probably should have used italics instead.
Professor Jolliffe’s comments on my blog objected to the implication that he had endorsed the MBH98 procedure, but did *not* say that “it is simply wrong to do so.” He has made it clear, repeatedly, that he doesn’t consider himself sufficiently knowledgeable of the details to comment on the correctness of the procedure.
You’re certainly entitled to believe MM were right. I call ’em as I see ’em, so to call a spade a spade: I disagree.
What cannot be denied rationally is that whether the MBH98 PCA methodology was a convention or a technique, customary or not, correct or not, doesn’t invalidate either the MBH98 hockey stick or those which have followed in its groundbreaking footsteps.
Deep Climate writes “When will the media wake up and do their job?”
Indeed. Maybe the hackers covered up their tracks really well. That’s the real story, isn’t it? I look forward to your next post.
What’s important to realize is that the true test of a paper’s worth is whether the studies can be replicated and built upon. Obviously, temperature reconstruction by proxies has become a nice field of study, and the papers by Mann, et al. in PNAS (2008) and Science (2009) show where the field is now and provide better information about the Medieval Climate Anomaly, LIA, to the level where regional temperatures can be constructed. Montfort, McIntyre, et al. are fighting last decade’s battle while the science has gone past them.
Nice analysis, tamino.
Shorter #38
Scientists and public employees should be 100% transparent. Journalists and think tanks, not so much.
=================
Well I beg to differ.
For example, a preview of the Wegman Report appeared in the Wall Street Journal on July 14, 2006, the day of its official release. Shouldn’t the Wall Street Journal make public all preceding communication with Joe Barton’s satff?
Another example:
A rare front-page science feature appeared on the front page of the Wall Street Journal in February, 2005. That report featured an account of the just-published GRL article by Steve McIntyre and Ross McKitrick.
Which PR disinformation outfit contacted the Wall Street Journal to arrange this prominent coverage? My guess is APCO Worldwide. Or perhaps the Wall Street Journal got the idea from coverage in the National Post, then in the thrall of APCO Worldwide operative Tom Harris. No one knows because the Wall Street Journal has consistently refused to discuss the matter.
I’ve said it before, but it bears repeating. The likes of Patrick Michaels and CEI’s Chris Horner are not legitimate sources for “balance” from the “other side”. Rather, they are appropriate subjects for journalistic investigation. At the very least, they should not be allowed access to reputable journalistic platforms until they come close to the same transparency that most scientists have always exhibited.
The “hockey stick” scientific “scandal” has been manufactured from the start on non-existent evidence, and promoted diligently on behalf of powerful interests. “Climategate” is the real hoax, one perpetuated by complaisant media outlets like Fox News, the National Post and the Wall Street Journal.
It’s high time Andrew Revkin recognized that awful truth. His continued silence on the real issues is a disgrace.