Progress has been made in recent years in understanding the observed past sea-level rise. As a result, process-based projections of future sea-level rise have become dramatically higher and are now closer to semi-empirical projections. However, process-based models still underestimate past sea-level rise, and they still project a smaller rise than semi-empirical models.
Sea-level projections were probably the most controversial aspect of the 4th IPCC report, published in 2007. As an author of the paleoclimate chapter, I was involved in some of the sea-level discussions during preparation of the report, but I was not part of the writing team for the projections. At the core of the controversy were the IPCC-projections which are based on process models (i.e. models that aim to simulate individual processes like thermal expansion or glacier melt). Many scientists felt that these models were not mature and understated the sea-level rise to be expected in future, and the IPCC report itself documented the fact that the models seriously underestimated past sea-level rise. (See our in-depth discussion published after the 4th IPCC report appeared.) That was confirmed again with the most recent data in Rahmstorf et al. 2012.
As a result of the IPCC-discussions, in 2006 I developed a complementary approach to estimating future sea-level rise and offered it to IPCC (but it was not used); this was published in Science in 2007 (and with over 300 citations to date it turned out to be the second-most-cited of the ~10,000 sea-level papers that were published since 2007). This “semi-empirical approach” linked the rate of global sea-level rise to global temperature in a simple physically motivated equation, calibrated with past data. It suggested that sea-level might rise about twice as much by 2100 AD as predicted by IPCC. My main conclusion was not that semi-empirical models are necessarily better, but that “the uncertainty in future sea-level rise is probably larger than previously estimated”. We will come back to this issue, i.e. the overall uncertainty across different model types and using all available information, in part 2 of this post.
Much higher projections than IPCC are also a consistent feature of more recent assessments published since 2007, e.g. the Antarctic Science Report, the Copenhagen Diagnosis, the Arctic Report of AMAP and the recent World Bank Report. Higher projections are also commonly used in coastal planning, e.g. in the Netherlands, in California and North Carolina, and included in the recommendations of the US Army Corps of Engineers. And last month NOAA published the following new sea-level scenarios for the US National Climate Assessment:
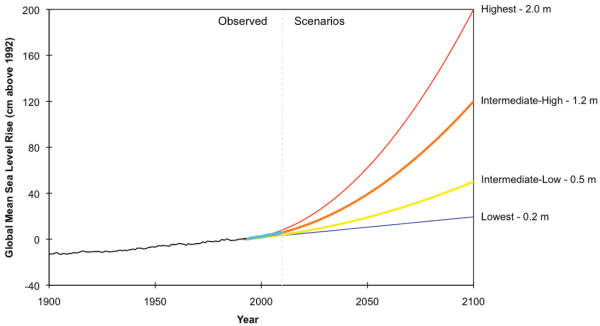
Fig. 1. Source: Global Sea Level Rise Scenarios for the United States National Climate Assessment, NOAA (2012)
The range intermediate-low to intermediate-high of 0.5-1.2 meters is almost the same as the range 0.5-1.4 meters of my 2007 Science paper.
This week an expert elicitation by Bamber and Aspinall was published in Nature Climate Change, which confirms that the body of expert opinion expects much higher sea level rise than the 4th IPCC report. The median contribution from ice sheets alone by 2100 was estimated as 29 cm, with a 95th percentile value of 84 cm. The paper compares a range for total sea-level rise for the RCP4.5 scenario of 33-132 cm based on their expert elicitation to our recent semi-empirical range (Schaeffer et al., Nature Climate Change 2012) of 64-121 cm.
Recent progress in understanding sea-level rise
Just before Christmas an overview of process-based sea-level estimates for the 20th Century was published by Gregory et al in Journal of Climate, a paper with many authors that presents a whole suite of estimates for individual sea-level contributions, partly data-based and partly model-based. The paper then looks at the sum of all these components, see Fig. 2.
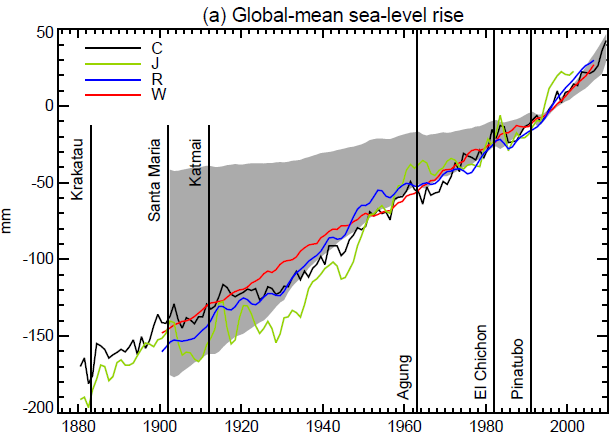
Fig. 2: Comparison of timeseries of annual-mean global-mean sea-level rise from four analyses of tide-gauge data (lines) with the range of 144 synthetic timeseries (grey shading). Each of the synthetic timeseries is the sum of a different combination of thermal expansion, glacier, Greenland ice-sheet, groundwater and reservoir timeseries. Source: Gregory et al in Journal of Climate.
This diagram shows the range of sea-level histories that is obtained by combining all the single estimates in various combinations. It shows that the observed sea-level history can be obtained when combining the individual components in all possible combinations (144 in all), but the observations lie at the very edge of the range. The authors write:
We would judge that a given synthetic timeseries gave a satisfactory account of observed global mean sea-level rise if it lay within the uncertainty envelope for 90% of the time. Very few of the synthetic timeseries pass this test.
If we take the mid-point of the grey range, this shows that the central estimate of 20th Century sea-level rise, based on adding up all processes, is ~11 cm. The central estimate of observed rise is ~16 cm and ~40% larger.
The authors conclude that a residual trend is needed to make up for the discrepancy and argue that this must come from a long-term ice loss in Antarctica. They write:
If we interpret the residual trend as a long-term Antarctic contribution, an ongoing response to climate change over previous millennia, we may conclude that the budget can be satisfactorily closed.
I guess it depends on how easily one is satisfied. The estimated required residual trend is given as 0 – 0.2 mm/year, so it explains at most 2 cm of rise over the 20th Century and does not make up for the shortfall mentioned; as I understand it, it just increases the synthetic range enough to bring most observations into its 90% confidence interval, though still near its edge.
In any case the now higher sea-level estimates from process models for the 20th Century naturally also imply higher projections for the 21st. Here it is important to compare like with like – same emissions scenario, same time interval. E.g. for the A1B scenario over the interval 1990-2095, the 4th IPCC report’s central estimate is 34 cm while the semi-empirical estimate of Science in 2007 is 78 cm. While we do not want to enter discussions about the draft 5th IPCC report (this would be premature, given there will still be numerous changes), given that it is in the public domain now it is no secret that for this scenario it projects 59 cm – a whopping 73% increase over the 4th report and much closer to my 2007 semi-empirical estimate. However, the more recent semi-empirical models have tended to give higher projections, so there remains a substantial gap between these two modelling approaches.
Personally, for various reasons I expect that process-based estimates may well keep edging up in future as the models are improved, considering e.g. the recent Nature-Paper by Winkelmann et al. and the remaining tendency to underestimate past rise. I dearly hope, however, that the truth will turn out to be a lower rise than suggested by semi-empirical models, for the sake of all people who live near the sea or love the coast.
Is 20th C sea-level rise related to global warming?
The Gregory et al. paper was greeted with enthusiasm in “climate skeptics” circles, since it includes the peculiar sentence:
The implication of our closure of the budget is that a relationship between global climate change and the rate of global-mean sea-level rise is weak or absent in the past.
The abstract culminates in a similar phrase, which can easily be misunderstood as meaning that global warming has not contributed to sea-level rise. That is wrong of course, and the claimed closure of the sea-level budget in this paper is only possible because increasing temperatures are taken into account as the prime driver of 20th Century sea-level rise.
When read in full context, the true meaning of the statement becomes clear: it is intended to discredit semi-empirical sea-level modelling. That is both fallacious and odd, given that the paper does not even contain any examination of the link between global temperature and the rate of global sea-level rise which is at the core of semi-empirical models, and which has been thoroughly examined in a whole suite of papers (e.g. Rahmstorf et al. 2011). Instead, it dismisses semi-empirical models offhand based on two arguments.
The first is that individual contributions to the sea-level budget do not show a clear link to global temperature. That is simply a fundamental misunderstanding of the semi-empirical approach: its principal idea is to cut through the uncertainty and complexity surrounding the time evolution of the individual components by considering only the overall sea-level rise and its link to global temperature. The usefulness of this idea is based on the following factors:
1. More accurate data. We may assume that the observational data for the time evolution of global sea-level rise are much more accurate than those for any individual component. A particular irony is that the glacier melt component of “process models” is in fact estimated by a semi-empirical equation quite similar to the one we use for sea level, but poorly validated since data are available only for ~350 of the world’s ~ 200,000 glaciers. Thus results from questionable semi-empirical modelling are used to dismiss rather better-validated semi-empirical modelling.
2. Partial cancellation of regional climate variability. It is obvious that e.g. the Greenland ice sheet responds to local and not global temperature, so it is not surprising that the Greenland component alone shows little relation to global temperature in the past. However, the ice sheet contributions come from both polar areas, the mountain glacier components from global land masses across a range of latitudes (with a mid- to high-latitude bias), while thermal expansion is particularly sensitive to warming over low-to mid-latitude oceans since the thermal expansion coefficient is much larger there than in colder waters. This broad mix of different regions contributing to sea-level rise makes it likely that the total rise is more clearly linked to global-mean temperature than any single component.
3. Future dominance of global warming over natural regional variability. Since the global warming signal increases over time while the amplitude of natural climate variability does not (much), the effect of global warming on sea level will become more dominant in future, making it likely that semi-empirical models are an even better approximation in future than they were in the past.
The counter-argument that with progressive warming we run out of glacier ice is an artifact of the split between mountain glaciers and larger ice masses and does not apply if total sea level is considered. As shown in Rahmstorf et al. 2011, the argument vanishes if we consider all continental ice together as a continuum (see their Fig. 13), in which melting progressively affects the colder ice surfaces as climate heats up.
Has sea-level rise accelerated?
The second argument for dismissing semi-empirical models in Gregory et al. is that “acceleration of global-mean sea-level rise during the 20th Century [is] either insignificant or small”. That argument was also put forth by Houston and Dean (2011) (see our discussion of this paper), and in our published comment on this we showed why it is false (Rahmstorf and Vermeer 2011). The argument is based only on considering the acceleration factor from a quadratic fit, an almost meaningless statistic (see our tutorial explanation). In fact, if the rate of sea-level rise perfectly follows global-mean temperature, then such a small acceleration factor is exactly what one gets, due to the specific shape of the global temperature curve. Thus, a small quadratic acceleration factor in no way speaks against semi-empirical models, but rather is what one would find if the semi-empirical model were perfect. Frankly, I am quite surprised that the authors (ten of whom are also authors of the sea-level chapter of the upcoming IPCC report) display such unfamiliarity with the fundamentals of (and prejudice against) semi-empirical models.
As John Church phrased it right after the paper was published:
I would argue that there is an unhealthy focus on one single statistic — an acceleration number — and insufficient focus on the temporal history of sea level change.
That is well said – and the temporal histories of the Church&White sea-level data and global temperature match rather well, as the following graph shows.
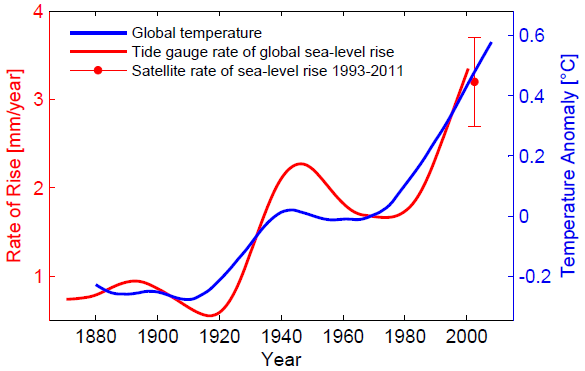
Fig. 3: Rate of global sea-level rise based on the data of Church & White (2006), and global mean temperature data of GISS, both smoothed. The satellite-derived rate of sea-level rise of 3.2 ± 0.5 mm/yr is also shown. The strong similarity of these two curves is at the core of the semi-empirical models of sea-level rise. Graph adapted from Rahmstorf (2007).
If we do focus on the temporal history, we find that in all but one of the sea-level reconstructions shown in Gregory et al. (their Fig. 6) the most recent rate of rise is unprecedented since the start of the record, despite the curves ending already in 2000 and all below the more reliable satellite rate of 3.2 mm/year. Early in the 20th Century, all show rates around 1.5 mm/year. In addition there is good evidence for very low rates of SLR in centuries preceding the 20th (presented e.g. in the 4th IPCC report or more recently in Kemp et al. 2011).
The one curve that does not show an unprecedented recent rate in Gregory et al. is the data of Jevrejeva et al. (2008). That contrasts with our treatment of the same data in Rahmstorf et al. 2011 (Fig. 5), where we applied a stronger and more sophisticated smoothing (as compared to the running average used by Gregory et al) which lowers the temporary high peak in the rate around 1950. This peak is not found in any of the other data sets, and as shown in Fig. 2 above, it makes the Jevrejeva data run outside the grey range found by combining all contributions.
I think this peak is spurious and results from the fact that the data of Jevrejeva et al. cannot be considered an estimate of global-mean sea level on such relatively short time scales (a couple of decades). For example, in this data set the North Atlantic data (including Arctic and Mediterranean, overall 16.6% of the global ocean area) provide 31% of the global average and are weighted four times as strongly as the Indian Ocean, although the latter is larger (19.5% of the global ocean). The Northern Hemisphere is weighted more strongly than the Southern Hemisphere, although the latter has a greater ocean surface area. (For more on the Jevrejeva weighting scheme, see our reader’s exercise below.) That is not to say that other tide-gauge based estimates guarantee a properly area-weighted global sea-level history, but it means that Jevrejeva et al. are guaranteed to not represent an area-weighted global mean, while e.g. Church and White (2006, 2011) are making a decent attempt at representing a global mean.
All reconstructions to a different extent are affected by spurious variability that is not real variability in global sea level. The satellite data are least affected by this because they almost cover the entire global ocean (and they show a remarkably constant rate of sea-level rise since 1993). The spurious variability is bound to increase further back in time due to the fewer early tide gauges. It is bound to be much reduced by time-averaging, because in the longer run the effect of water “sloshing around” the global ocean under the influence of winds and currents (due to natural variability) will largely average out, given the restoring force of gravity. Hence, the further back in time one looks, the more time averaging is required to see a signal rather than noise, and the tide gauge data sets generally require much more averaging than the satellite data.
My bottom line: The rate of sea-level rise was very low in the centuries preceding the 20th, very likely well below 1 mm/yr in the longer run. In the 20th Century the rate increased, but not linearly due to the non-linear time evolution of global temperature. The diagnosis is complicated by spurious variability due to undersampling, but in all 20th C time series that attempt to properly area-average, the most recent rates of rise are the highest on record. At the end of the 20th and beginning of the 21st Century the rate had reached 3 mm/year, a rather reliable rate measured by satellites. This increase in the rate of sea-level rise is a logical consequence of global warming, since ice melts faster and heat penetrates faster into the oceans in a warmer climate.
Update 14 January: Today I received this 200-page report on sea-level rise by the National Research Councils of the National Academies in the post. The committee that wrote it derived their own sea-level rise projections which are highly consistent with those of NOAA and my 2007 Science paper: “Global sea level is projected to rise 8-23 cm (3-9 in) by 2030, relative to 2000 levels, 18-48 cm (7-19 in) by 2050, and 50–140 cm (20-55 in) by 2100.”
Continue to Part 2 of this post, with some thoughts on “cycles” of sea level rise, the maturity of process models and the IPCC process.
—
A reader’s exercise: the “virtual station method” of Jevrejeva et al.
A thorough, critical assessment of different climate data sets is of course not the job of blogs but of the IPCC, and its experts get several years to prepare this. Nevertheless, some insights can already be obtained by the sea-level amateur spending half an hour on the following exercise.
In the virtual station method the global ocean is subdivided into 13 ocean regions. The global mean sea level is computed as the arithmetic average over these 13 regions. As mentioned above, this does not provide an area-weighted global average, since e.g. the North Atlantic consists of four regions (western and eastern North Atlantic, Arctic and Mediterranean) while the entire Indian Ocean is just one region. The North Pacific is two regions and a half: the western and eastern North Pacific, and the Central Pacific which stretches across both hemispheres.
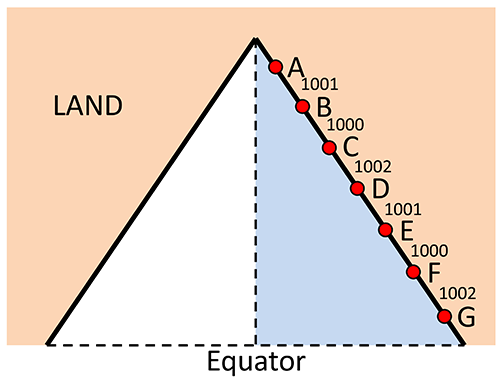
But now let us look at how the average sea level change within each region is computed. Take the example in the graph shown below, where the light-blue ocean region (think of it as eastern half of a northern hemisphere ocean basin) is covered by 7 tide gauges A-G. These are spaced about 1000 km apart – the exact distances are shown in the graph. Maybe you want to ponder first how you would average those stations to obtain a reasonable average over the light-blue ocean region!
The virtual station method averages the rise observed at these stations (over a given time interval) by application of the following simple set of rules:
1. Take the two stations closest to each other and average them.
2. Replace those two stations by a new “virtual station” which consists of the above average, located at the mid-point between the two stations.
3. Go back to step 1 with this new set of stations.
Repeat this until you are left with only one virtual station, which now is your regional average.
So here is our reader puzzle: with what weighting factors do the above 7 stations enter the final regional average?
Update 10 January: Our reader MARodger was the first to give the right answer:
A, G: 1/4
B, C, D: 1/8
E, F: 1/16
So the weights attached to these gauges differ by up to a factor of 4, apparently for no good reason. To be fair, the method was not designed to deal with regular spacing of tide gauges as in this idealised example, but with cases where spacing is highly irregular. I think it is a reasonable method e.g. to average a cluster of gauges into one number before averaging it with one far-away gauge. Nevertheless I think the example illustrates important limitations of this method, and the point that the weights by design must differ by factors of 2, 4, 8, 16… Maybe this post will inspire some mathematically-minded reader to propose a better scheme.
There is an additional issue in that the weights change over time, since the number of tide gauges available changes over time. That is another avenue by which spurious variability can enter the final average curve.
[With thanks to Svetlana Jevrejeva for answering my questions on the virtual station method.]
References
- S. Rahmstorf, G. Foster, and A. Cazenave, "Comparing climate projections to observations up to 2011", Environmental Research Letters, vol. 7, pp. 044035, 2012. http://dx.doi.org/10.1088/1748-9326/7/4/044035
- S. Rahmstorf, "A Semi-Empirical Approach to Projecting Future Sea-Level Rise", Science, vol. 315, pp. 368-370, 2007. http://dx.doi.org/10.1126/science.1135456
- J.L. Bamber, and W.P. Aspinall, "An expert judgement assessment of future sea level rise from the ice sheets", Nature Climate Change, vol. 3, pp. 424-427, 2013. http://dx.doi.org/10.1038/nclimate1778
- M. Schaeffer, W. Hare, S. Rahmstorf, and M. Vermeer, "Long-term sea-level rise implied by 1.5 °C and 2 °C warming levels", Nature Climate Change, vol. 2, pp. 867-870, 2012. http://dx.doi.org/10.1038/nclimate1584
- J.M. Gregory, N.J. White, J.A. Church, M.F.P. Bierkens, J.E. Box, M.R. van den Broeke, J.G. Cogley, X. Fettweis, E. Hanna, P. Huybrechts, L.F. Konikow, P.W. Leclercq, B. Marzeion, J. Oerlemans, M.E. Tamisiea, Y. Wada, L.M. Wake, and R.S.W. van de Wal, "Twentieth-Century Global-Mean Sea Level Rise: Is the Whole Greater than the Sum of the Parts?", Journal of Climate, vol. 26, pp. 4476-4499, 2013. http://dx.doi.org/10.1175/JCLI-D-12-00319.1
- R. Winkelmann, A. Levermann, M.A. Martin, and K. Frieler, "Increased future ice discharge from Antarctica owing to higher snowfall", Nature, vol. 492, pp. 239-242, 2012. http://dx.doi.org/10.1038/nature11616
- S. Rahmstorf, M. Perrette, and M. Vermeer, "Testing the robustness of semi-empirical sea level projections", Climate Dynamics, vol. 39, pp. 861-875, 2011. http://dx.doi.org/10.1007/s00382-011-1226-7
- "Sea-Level Acceleration Based on U.S. Tide Gauges and Extensions of Previous Global-Gauge Analyses", Journal of Coastal Research, vol. 27, pp. 409, 2011. http://dx.doi.org/10.2112/JCOASTRES-D-10-00157.1
- S. Rahmstorf, and M. Vermeer, "Discussion of: Houston, J.R. and Dean, R.G., 2011. Sea-Level Acceleration Based on U.S. Tide Gauges and Extensions of Previous Global-Gauge Analyses. Journal of Coastal Research, 27(3), 409–417", Journal of Coastal Research, vol. 27, pp. 784, 2011. http://dx.doi.org/10.2112/JCOASTRES-D-11-00082.1
- A.C. Kemp, B.P. Horton, J.P. Donnelly, M.E. Mann, M. Vermeer, and S. Rahmstorf, "Climate related sea-level variations over the past two millennia", Proceedings of the National Academy of Sciences, vol. 108, pp. 11017-11022, 2011. http://dx.doi.org/10.1073/pnas.1015619108
- S. Jevrejeva, J.C. Moore, A. Grinsted, and P.L. Woodworth, "Recent global sea level acceleration started over 200 years ago?", Geophysical Research Letters, vol. 35, 2008. http://dx.doi.org/10.1029/2008GL033611
- J.A. Church, and N.J. White, "A 20th century acceleration in global sea‐level rise", Geophysical Research Letters, vol. 33, 2006. http://dx.doi.org/10.1029/2005GL024826
- J.A. Church, and N.J. White, "Sea-Level Rise from the Late 19th to the Early 21st Century", Surveys in Geophysics, vol. 32, pp. 585-602, 2011. http://dx.doi.org/10.1007/s10712-011-9119-1
Nice article.
Just doing a quick pictorial attempt at the puzzle, I get A,G at 1/4, B,C,D at 1/8 and E,F at 1/16. (Doing the numbers would be no fun!). That is indeed an unusual method.
A latitude-average based method would give linearly increasing weights to the stations based on the width of the ocean. Kriging – I can’t that in my head.
Thanks Stefan.
Could you elaborate on the reasons for the discrepancy between semi-empirical and process-based projections of SLR?
There seems to be this peculiar situation where adherents of both approaches don’t think anything of the competing approach. E.g. from glaciologists I sometimes hear that there is no evidence for mechanically enhanced melt of ice sheets (which would be needed to arrive at higher estimates than their current process-based projections). One could say that absence of evidence is no evidence of absence of course, but that’s rather unsatisfying.
What reasons could there be for process-based methods underestimating the (speed of) response of SLR to temperature? And what potential reasons could there be for semi-empirical methods overestimating the same? (This is not to imply that the truth would necessarily be in the middle; just trying to understand the differences between the different methods)
[Response: Bart, I can’t fully answer this, but note that the expert elicitation cited specifically asked glaciologists, and if they are right this would close much of the gap between process models and semi-empirical models. -Stefan]
Reader puzzle answer (spoiler alert):
Station i in [0, n] gets weight factor (n over i)/2^n. So in this case, with n=6 and where A corresponds to i=0 and G to i=6, we get:
A: 1/64
B: 6/64 = 3/32
C: 15/64
D: 20/64 = 5/16
E: 15/64
F: 6/64 = 3/32
G: 1/64
Doesn’t seem like a balanced average to me…
[Response: Here is one solution, but is it right? What do other readers think? -Stefan]
Here I compare Rahmstorf (2007) sea-level rise and global temperatures with Vukcevic 2009 negative magnetic field change due to the convection in the underlying mantle associated with the Post-glacial Laurentide uplift
http://www.vukcevic.talktalk.net/SeaLevel.htm
I would like to see a graph plotting the project sea-level rise by 2100, 2200, 2300 and so on (as data allow) against the year the year the projection was made.
Well I am confused. Half an hour? I must have missed something.
Assuming there is no linear/area weighting & there being no other ambiguity that I know of with the averaging of just two numbers, the seven stations get the following weighting in the final all-encompassing virtual station. A&G 4, BC&D 2, E&F 1. It would appear not to be an averaging method that immediately recommends itself.
[Response: You mean it took you just five minutes? In any case, you got what I got, too. Although to get a total of 1 you then have to divide the numbers by 16. Thanks for participating! -Stefan]
I would find a weight for each station by integrating a decreasing function of distance over the ocean area.
For example, take all available satellite data and find the correlation between sea level at a point in the ocean and level measured at a station of interest. To find the station weight add this up over the whole ocean.
However, I have no detailed knowledge of how sea level works, so this may suffer from a fatal flaw…
I am confused, too, after reading the solution of MARodger. How do you come to that conclusion? I have the same solution as Deen (A: 1/64, B: 6/64, C: 15/64, D: 20/64, E: 15/64, F: 6/64, G: 1/64).
Ah, I see what I did in my first comment. It appears I interpreted the virtual station method as first replacing A-G with virtual stations AB, BC, …, FG, and then replacing those with virtual stations ABC, BCD, …, EFG, and repeat until you get a single virtual station ABCDEFG. In this interpretation, you get the answer I gave above.
Doing it the way you meant it (i.e. first merging B and C into BC, then E and F into EF, then A and BC into ABC, etc) I get the same answers as you:
A, G: 1/4
B, C, D: 1/8
E, F: 1/16
Either way, it’s a peculiar method for doing averages.
Jan W.: read the instructions. Step one is to combine the closest stations together – that would be the stations that are 1000 units apart, eg, E&F and B&C. Because step one turns E&F and B&C into one virtual station each, E&F _have_ to have the same weight, as do B&C.
@MMM: Thank you. As Deen pointed out, Deen and I made the same mistake. IMHO the instructions could easily be misinterpreted.
“The implication of our closure of the budget is that a relationship between global climate change and the rate of global-mean sea-level rise is weak or absent in the past.”
Scientists have an obligation to not provide global warming deniers opportunities like the above quote to misinterpret the meaning of a paper. Without compromising the integrity of their research, scientists must be aware that climate science is under attack by commercial and ideological forces that are not interested in the truth. Clear communication is essential and whether the scientific community likes it or not, the ambiguous and sometimes convoluted academic language of journals will be scoured by those with an ax to grind and every phrase that can be misunderstood will be misunderstood.
Thanks for the great post. I can’t tackle the quiz right now, but I wondered if Stefan would mind commenting on this video by Prof. Alley? Particularly the last ten minutes or so where he suggests that a relatively sudden sea level rise of about three meters can not be ruled out.
http://climatestate.com/climate-state/videos/item/slip-slidin-away-ice-sheets-and-sea-level-in-a-warming-world.html
The video has attracted some interested comments from other posters here on the open thread, so I thought it would be valuable for all of us to hear another expert’s evaluation of it while we are discussing slr. Thanks ahead of time for any insight you can throw on this troubling/horrifying possibility.
[Response: I’m a huge fan and friend of Richard’s, but I do not think this is plausible at all, if by “sudden” it is meant within 100 years or less. Even if all the glaciers in Greenland start flowing at 5 times their current rate, and do so for the next 100 years, we still perhaps 2 m of sea level rise. That would be catastrophic, but it’s probably impossible, and definitely at the upper end of possibilities. Having said all that, >3 is probably inevitable over the next several hundred years if we continue to burn fossil fuels at the current rate.–eric]
[Response: Like Eric, I’m a fan of Richard and consider myself a friend – I have not had time to look at this video, so can’t comment specifically. Also, I am by no means an expert on the stability of the WAIS which appears to be the theme of his lecture. -Stefan]
Wouldn’t it be interesting to start map water distribution with SLR, to get a map with Hotspots? I think this would help with policy making, since SLR along the U.S. Atlantic Coast is increasing about three to four times more than the global average. And ofc to include the potential for abrupt SLR, which would mean +2 meters.
I agree with 12 Larry Saltzman. Intentional misunderstanding deserves a new word. I call it “disunderstanding” to indicate intention. Disunderstanding is also used by provokers. Provokers are people who intend to get people angry.
wili #13
I too would like Stefan to comment on Prof Alley video. My memory of it is that if we are considering risks of sudden sea rises of a few meters from ice sheets, we should
1. not worry too much about Greenland – it’s underlying rock keeps in in place.
2. not worry too much about the East Antarctic Ice Sheet. It’s stable, high and cold.
3. not worry about one part of the West Antarctic Ice Sheet in a long rock valley because edge friction will slow it down
4. begin to worry about another part of the the WAIS which has underlying rock formation which can allow a rapid incursion of salty warmer water underneath it.
There is some evidence that the latter has shown signs of rapid movement in the past.
This may be a tipping point situation which could contribute a couple of metres of seal level rise.
Prof Alley wasn’t exactly panicking – he didn’t seem to know what the odds were.
I’d like to know more.
If the inter-tidal gauge distances were not integers, wouldn’t the most isolated gauge always get a weight of 1/2 ?
2008 Alley slides here (.ppt); some are familiar from the recent video.
http://www.victoria.ac.nz/antarctic/about/events/s-t-lee-lecture/lecture-2008
The 2008 lecture video link is broken, but maybe it’s findable
Stefan, thank you for this very important post.
I have for a long time been puzzled by the scepticism many experts have for the semi-empirical model approach to project future sea level rise. This scepticism has prevailed until this day, despite that by now many papers have been published based on the method in good scientific journals, and despite that, to my knowledge, no fatal criticism to the semi-empirial methodology have yet been published in a scientific journal. The paper that you discuss in this post is perhaps the best attempt to discredit the semi-empirical method, but the arguments used in the paper seem flawed, as you show in this post. I think this kind of methodological discussions are very important and I hope that you will also publish a reply in the journal.
Another point that I would like to hear your thoughts on is the relevance of potentially greater than linear rate of sea-level rise contribution from the great ice-sheets. As I understand it, the semi-empirical models presume linear responses. Given that there is a risk of supra-linear responses (e.g. as indicated by the views of some of the glaciologists who participated in the study by Bamber & Aspinall), this would imply that the semi-empirical models represent LOWER BOUNDS, rather than the upper bounds that they often are used as.
Furthermore, this would mean that while semi-empirical methods are only able to make accurate hindcasts and forecasts when the response can be approximated by a linear function, the model would break down when the non-linear responses become dominant. Is this correct understood?
[Response: Correct, I already discussed this in my original 2007 Science paper. And semi-empirical models have been criticised for potentially underestimating non-linear ice-sheet responses, like what Richard Alley talks about in his lecture. I think there are some arguments why these models might underestimate and some why they might overestimate future sea-level rise, but ultimately we do not know. -Stefan]
GeoffBeacon #16:
Yes, some experts think that something fast could happen at the WAIS. Take a close look at Figure 8 in the Supplementary Material in the Bamber & Aspinall paper which can be found here:
http://www.nature.com/nclimate/journal/vaop/ncurrent/extref/nclimate1778-s1.pdf
Four experts estimate the upper limit of contribution from WAIS ONLY in year 2100 to be (30 mm/year, 20, 15 and 10 mm/year respectively).
If you liked the R.B Alley video, I think you will also like this video lecture by Robert (Bob) Bindschadler:
http://www.youtube.com/watch?v=hnVtjnGRyDY&feature=player_embedded
I’m seeing this quote various places not cited to wherever it begins — often with no date so it seems to be contemporary.
But the earliest I notice with a quick scan is 1998.
Does it still represent something being said recently?
—–> “make a hole in the side of the ice sheet” “The remaining ice would drain through that hole.”
If we are averaging the sea level rise based on area and expect a dependence on latitude, then each station will be weighted according to the area it represents in its latitude band. Therefore, given the triangular shape of the ocean, the weights will be proportional to the distance from the pole. So the area weight for A = 1/49, B= 3/49, C=5/49 etc up to G=13/49.
Brian @ 6:44pm If the inter-tidal gauge distances were not integers, wouldn’t the most isolated gauge always get a weight of 1/2 ?
Integers or not, only if it stays isolated to the very end. As other gauges are merged, the positions change and distances change. You can end up with groupings that are farther apart (more isolated) than any individual station was, so the original isolated station will get merged with a group before the final groups get merged.
FYI, the merge order I get from the example is:
A B C D E F G (original individual stations)
A BC D EF G (doesn’t matter if you do BC and EF together, or as discreet steps in this case)
ABC DEF G (again, same result if two steps)
ABC DEFG
ABCDEFG
Before the second last merge, the two distances are 3003 (ABC to DEF) and 2252.5 (DEF to G), so distances are much more variable between groups than they ever were between individual gauges.
Eric (moderator response at #13) – I’m assuming you haven’t watched Dr Alley’s lecture because your comment is a mischaracterization of it. The Greenland ice sheet is not the concern, the West Antarctic ice sheet is. I’m sure you’re familiar with the topography, and the buttressing effect which slows the flow of the glaciers into the ocean.
Now many “warmist” commenters tend to get a bit carried away with possible future rates of sea level rise, and that may be what you responded to, but the fact that global sea level rose rapidly during the last interglacial highstand, when only the Greenland and Antarctic ice sheets existed (i.e. no gigantic Laurentide or Fennoscandian ice sheets) suggests that scientists cannot get too complacent about this. Especially when we’ve warmed the planet so rapidly, and process-based modelling of ice sheet behaviour is presently out-of-kilter with observations.
As Dr Hansen notes, comparison between rates of paleo-sea level rise driven by a much slower warming, and present rapid global warming, may not be valid. I, of course, hope he is wrong, but…….
[Response: You are right I haven’t watched Richard’s lecture (I will do so), but I stand by what I said, including Antarctica. >3 m is less than 100 years is virtually unpossible (h/t Walt Kelly). Saying “we can’t rule it out” is accurate, but misleading. I am sure Richard agrees. –eric]
@Eric Steig, responding to wili #13:
Alley wasn’t talking about Greenland, but most specifically about Thwaites glacier, West Antarctica. His position seems to be we can’t rule out upto 3m in less than a century once Thwaites would start draining, all the way to the Trans-Antarctic Mountains.
The question is how soon that process could start. Alley says we don’t really know, but it could maybe just as well be wihtin decades as after centuries or millennia.
Deepest thanks, eric, for addressing my request for an evaluation of Alley’s video. Alley actually seems to agree with you (between minutes 18 and 21) that Greenland is probably not going to be able to flow into the sea in a shorter time period than centuries or millennia because of it’s ‘gnarly’ bedrock.
From that point in the video, though, he moves on to a discussion of parts of West Antarctica that he claims do show characteristics that would allow for a relatively rapid rise, and he has models of exactly how that could happen. This is the section of concern and the process I was interested in a second opinion on, not the Greenland issue (which, though ultimately worrying, does not seem, as you said, to be likely to achieve the rates of flow to pose an extreme short-term risk on its own).
So, sorry to be a pest, but I would still like to hear you or someone’s response to the claims made especially in the last ten minutes or so of the video (and it sounds as if I am not alone in this request here).
Thanks ahead of time, and for all you folks do.
[Response: I’ll watch it and get back to this thread to comment. It is very unlikely Richard and I disagree about this, based on numerous conversations I have had with him; it’s more a matter of whether we tend to emphasize the likelihoods or the unlikelihoods.–eric]
Thanks, Stefan, for your response at both 13 and for the related response at 19. It is interesting that there are reasons to think that models may underestimate and that they may overestimate. Uncertainty indeed.
(Unfortunately, unlike what many denialists seem to think, uncertainty is not necessarily our friend. It makes it harder to plan. I still think that if Alley is setting forth even a rather remote possibility, it is something worth worrying about and starting to plan for–and especially to stop pushing the system toward! By the way, if you don’t want to watch the whole of the Alley video, the gist is really in the last ten minutes or so.)
Again, many thanks for your very important work.
Climate communicators have a duty to put this in locar perspective by raising awareness of local rates of land elevatiion change from post-glacial isostatic rebound and tectonic processes.
In the long run these issues have serious ramifications for preparing for storm surges.
Eric, wili needs help understanding what Alley is saying in that video.
Starting around 34:15 (the last 10 minutes as Wili says), Alley is using slides from Christianson et al. 2011. There he talks about loss of the ice shelf on the end of the Thwaites, and about the deep basin behind that ice front, and that _if_ the calving front retreats to that deep hole we could get an ‘insane’ amount of ice breaking off. He says you don’t sleep right next to El Capitan because even a little rock falling off a face that tall is a lot, and points out the ice is enormously thick over that deep basin but it’ll be easily melted _if_ the calving front retreats to that area.
Then he talks about what the ice is actually doing, and how a little bump of sediment out at the calving front blocks warm sea water from getting in under the ice — but if the front retreats behind that little bump, suddenly water can get far back under the ice.
Then he cites Christianson and assorted PSICERS, in review — perhaps you have access to the paper? at 36:49 in the video.
There’s the rub. He says the calving front is almost off that bump — and once it passes that point, a very long span of ice will be floating and subject to tidal and storm flexing.
He mentioned earlier that you can see the ice 80km up the glacier changing its speed with the tidal cycle, so it’s expected to be very sensitive to loss of that obstruction at the calving front.
I do think it’d be good if several of the scientists could get together a review _of_ the videos out there. Above I mentioned that I’d been asking about stuff that seemed to be fringe speculation six or seven years ago at William Connolley’s blog about how fast erosion happens under the ice — stuff like the first ever observation of creation of a drumlin under the ice, and how astonished people were at the speed of change below a glacier.
That stuff and the stuff about groundwater surging up from sediments under a glacier as it lifts, increasing the flow rate — is still pretty new.
There’s probably a blind-men-and-elephant problem with ice cap science just because there’s so much information flooding out that nobody has time to go deeply into other people’s research, but at this rate of change I think the risk is that the assumptions underlying one person’s work are apt to be changed by the news from someone else’s work.
Eric, see the video at minute 37:00-38:00 for Alley’s description of the “big jump”
At about 40:00 he states the uncertainties — the ice might survive this entire interglacial; we have some paleo evidence it has gone away in previous interglacials.
And there is where he says we can think of one disaster scenario that gives three meters “and rather than talking about centuries to millenia you start talking about centuries to decades. And would I pound on the table about any of that? No! We do not have the physics of a mile high cliff in anybody’s calving model ….”
Thanks, Hank. As usual, you are much more articulate, precise and thorough than my blundering self. I rib you sometimes, but you really are a rare treasure here (especially when you manage to resist the temptation to feed trolls ‘-).)
I hadn’t heard of that (potential? observed?) effect of “groundwater surging up from sediments under a glacier as it lifts” before. Is that in the Stoat discussion that you linked to earlier, or do you have another linky to point me to?
(I know, I know, I should get off my lazy @$$ and find it myself, but perhaps you can spare me the endless two minutes of the hard labor of google-scholar-ing ‘-).)
I vote something like eadler2’s latitude-band method (@22): Apply a smoothing kernel over the stations’ measurements, defining their positions by latitude, then project the resulting smoothed estimator over latitude-bands across the ocean width.
“A kernel smoother is a statistical technique for estimating a real valued function f(X)…by using its noisy observations, when no parametric model for this function is known. The estimated function is smooth, and the level of smoothness is set by a single parameter.” (Wikipedia, “kernel smoother”)
This is (1) mathematically mechanistic, (2) much better than the virtual station method, and (3) actually sensible.
The averaging exercise takes on real importance when we remember that wind and thermohaline currents can affect local sea level by significant fractions of a meter. Global warming is changing atmospheric circulation patterns and and we are seeing thermal anomalies in sea surface temperatures. Thus, some local sea levels are likely to change much more than the global average, no matter how it is calculated. How we do the average makes a huge difference in the global average number. And, the global average number may not reflect the extent and impact of local sea level rise.
When one does take a mile high calving front on an ice structure that has been warmed by many moulins, one possible result is a progressive structural collapse. A tiny example is http://www.guardian.co.uk/environment/video/2012/dec/12/chasing-ice-iceberg-greenland-video . They call it calving, but it is progressive structural collapse.
Ice melts from the bottom up. (Most of the heat required to melt big ice is collected by oceans somewhere else.) Glaciers move downhill from cold to warm, so they still have cold cores. And, glaciers sit on rock. When the bottom of a glacier melts, the upper parts of the glacier still sit on rock. When the bottom of an ice sheet melts, the top of the ice sheet falls into the melt zone. The fallen ice then melts (drop a 10 ton block of ice a few kilometers and see how fast it melts), and the process repeats. As the buttresses fail, ice from the bottom of the central ice massif is forced horizontally outward by the pressure of the ice above it. High speed hydraulic flows are generated. Such flows can pass through the narrowest fjords with the greatest of ease.
I am sure the folks here will tell me to go read the literature just as they did when I first brought up moulins way back in 2003.
Your loyal Alarmist
Hank @29:
Good summary! However, I cannot find the paper Alley refers to “Christianson et al. 2011”? (Even after 10 minutes of google sholar!) Does anyone know or can make a good guess?
[Response: Correct, I already discussed this in my original 2007 Science paper. And semi-empirical models have been criticised for potentially underestimating non-linear ice-sheet responses, like what Richard Alley talks about in his lecture. I think there are some arguments why these models might underestimate and some why they might overestimate future sea-level rise, but ultimately we do not know. -Stefan]
We’re on track to reach 450 ppm CO2 in about 30 years, and that won’t be the max. What was sea level the last time CO2 was 450?
26 wili says, ” Alley actually seems to agree with you (between minutes 18 and 21) that Greenland is probably not going to be able to flow into the sea in a shorter time period than centuries or millennia because of it’s ‘gnarly’ bedrock”
Google Greenland bedrock map. You’ll see that the middle of Greenland, as currently squished by ice, is a huge inland sea mostly to the north, and some minor seas scraggling off to the south and west. At the end of those southern seas is a great canyon that not only cuts 100+km through the mountains to the sea, but cuts deep below sea level. At the ocean it’s -500?ft, but get back 30-40km and it dives to -1400?ft. Visualize the Grand Canyon at sea level directly draining the interior of Greenland. Maybe you’ll live long enough to see it…
wili,
Getting through the mountains, carving up the south, and then marching northwards towards ever-colder climes… conquering the Greenland ice sheet isn’t a “decades” type of project. “Centuries to millennia” opens the door to a whole new order of magnitude in the debate.
http://www.sciencedirect.com/science/article/pii/S001282521200013X
Tunnel valleys: Concepts and controversies — A review
http://dx.doi.org/10.1016/j.earscirev.2012.02.002
Powerpoint at: http://services.elsevier.com/SDWebExport/export/figure/S001282521200013X/1-s2.0-S001282521200013X-gr6.jpg/ppt
(see also references to “tunnel gully” formation)
Being a sometime fizicist an such, i like to count both the mass flux and the heat.
1e20J into land ice melt is 1mm of SLR or close enuf. Radiative imbalance is say 0.5e22J/yr
So 1% or 2% of the radiative imbalance is going into melting ice.
GRIS put in about 1.5 mm (574Gton, 1.5e20J) in 2012. The Box et al paper
The Cryosphere, 6, 821-839, 2012
http://www.the-cryosphere.net/6/821/2012/
doi:10.5194/tc-6-821-2012
estimates 4.5e19J into GRIS in 2011 from albedo increase. Is the rest coming from ocean or rain or air ? Pfeffer (2008) says 300Km^2 gate area for GRIS. So if we were to melt all the 1.5mm for 2012 in place, we need around 1-10 KW/m^2 thru those gates to make up the rest of the heat from the ocean into the ice. Don’t think so, I think the rest is ice exporting itself to the ocean to melt at leisure.
WAIS and APIS ? 1/2 mm from there lately. No albedo change or rain. Heat gotto go into ice thru the ocean or ice has to export itself. The latter is more likely. Mile high, hundred mile wide, 2mile deep calving front, anyone ?
Model mass flux thru (possibly fractal) phase change boundaries is messy, but we need to deal with the mess, or else we will deal with other, bigger messes.
A number I like to keep in mind is a mole of Joules. 6m SLR, all of GRIS or all of WAIS. Also about 100 yr of current radiative imbalance. The ocean has a few tenths of a mole of Joules to throw around, but will cool perceptibly if it does, as Hansen states.
All numbers subject to error, love to see corrections.
sidd
Eric Steig “>3 m is less than 100 years is virtually unpossible (h/t Walt Kelly)”
Maybe. But sea level rise during the last interglacial highstand may have reached rates of 0.6 – 2.5 metres per century (Rohling et al [2007]) above present-day. Only the Greenland and Antarctic ice sheets remained then. If correct, this infers that collapse of the West Antarctic ice sheet may indeed be very possible in the future. The topography and other issues discussed by Richard Alley, provide a physically-based starting point for how this geologically-rapid jump in sea level rise may have occurred.
Rather than proclaiming something is unpossible, it would indeed be very handy to see some modelling of the physics of ice sheet behaviour that gives some confidence that the current “mainstream” view is correct.
The West Antarctic ice sheet may, or may not, respond dramatically during this century. But whenever it does it’s possible that sea level rise is going to be faster than is presently anticipated.
And one last thing, I do agree with Dr Hansen that direct comparison between slow paleo-planetary warming, and rapid present-day warming, is a flawed approach insofar as the ice sheet response is concerned. Yet to be convinced of anything approaching 5 metres this century though – not sure I understand the rationale behind that.
[Response: This isn’t an argument about the science, but about what is responsible reporting of the science. We had a little argument about this here at RC a few years ago, and it’s telling that the argument was not about whether 5 m was likely, but whether anyone had claimed it was likely! My view comes from published modeling work e.g. by David Pollard, Penn State and Ian Joughin at University of Washington. Pollard’s results with their state-of-the-art ice sheet model shows that if you crank up the heat to the ice shelves in Antarctica by a huge amount (factor of four, as I recall), you might get West Antarctica to contribute 50cm/century. Jougin’s model focusses on Pine Island / Thwaites glacier and he get even slower rates. There simply isn’t a known way to evacuate that much ice, notwithstanding Richard Alley’s point that we don’t have a good model of the physics of calving yet. Another point is that the rapid rise at the end of the glaciation occurred when the Antarctic ice sheet was expanded to the edge of the continental shelf. That was a lot of ice at the edge of very deep water. Evacuating ice across shelf — as would have to happen today — is much harder; the icebergs would get stuck. Finally, Tad Pfeffer has done the relevant calculation here) including the possible contributions from Antarctica, and finds there is no way to get more than 2 m in the next century. See our friendly discussion with Pfeffer about this, here. A key sentence from that paper’s abstract: We find that a total sea-level rise of about 2 meters by 2100 could occur under physically possible glaciological conditions but only if all variables are quickly accelerated to extremely high limits.
The bottom line is that until we discover something new that suggests otherwise, the current state of knowledge is that a rise in sea level above 2 m in the next century is extremely hard get, and should not be discussed seriously as a possibility. The likely value of 1 m or more from Stefan and others’ work is serious enough! –eric]
Eric – You appear to be arguing a strawman, and you links are strawmen too. I’m not sold on the idea that rates of sea level above 2 metres are likely to occur this century. Other commenters may have done so, so you’re probably lumping me in with them. What I’m pointing out is that the West Antarctic may collapse as some future point and bring with it much higher rates of SLR – hence my earlier comment that the West Antarctic ice sheet may, or may not, respond this century.
“Another point is that the rapid rise at the end of the glaciation occurred when the Antarctic ice sheet was expanded to the edge of the continental shelf. That was a lot of ice at the edge of very deep water.”
Do you have references for that? Save me some time digging through the peer-reviewed literature. I wasn’t aware we had such accurate assessments of the state of the ice sheets at the last interglacial highstand.
[Response: I agree it is a bit of a stawman, but I was responding to points other raised, suggesting 3 m of “sudden” sea level rise was plausible. Yes, the modeling is not mature. No, in my assessment, no amount of maturing is going to change my point. Regarding the continental shelf, I’m not talking about the last integlacial, but the last glacial. No reference I can think of that makes my specific inference, but the glacial limit (at the shelf edge) is well known, many many references going back to Scott and Amundsen. Start with the name “Denton” and you’ll find a bunch of stuff. –eric
]
Eric, thanks for a clear and candid assessment in your answer to post #41. This is a very helpful and useful discussion to me.
Did you see this from Stefan’s new post here:
“A factor-two revision and a newly discovered first-order mechanism are both not exactly signs of a mature stage of modelling having been reached. I know enough about modelling the Greenland and Antarctic ice sheets and mountain glaciers to be certain that a lot of work remains to be done before these models can be called mature.”
Do you agree with this assessment of the state of the modeling? If so, how certain can we be of your 2 meter limit? When you use a phrase like “the current state of our knowledge” do you think you should add “which is not very mature”?
Thanks again for clear responses and for all you very important work.
[Response: Read the Pfefffer paper in detail regarding the 2 m limit. That’s the best answer to your question. Of course, *anything* can happen in science, but some things are more likely than others. This point changing is not likely. But I agree with you and Stefan that the state of the modeling is not mature; I’m very supportive of additional work in this area. But I think it is exceedlingly unlikely that the basic picture will change; significant contributions of Greenland and Antarctica to sea level rise are certain, but their rates being dramatically larger than the upper estimates (which are already very liberal) given e.g. in Pfeffer et al. are simply not supported by any analysis I’m aware of. –eric]
“Since the global warming signal increases over time while the amplitude of natural climate variability does not (much)“
Can someone point me to a good resource about natural climate variability increasing (not much)? I had always just assumed things had not changed enough for natural variability to have changed (pretty ignorant on this point).
Thanks in advance
Foster and Rohling report in PNAS (in press):
http://www.pnas.org/content/early/2013/01/03/1216073110.abstract
that in the longer run even current levels of atmospheric [CO2] will likely lead to sea level rise of over 9 metres above current levels on near-equilibrium timescales…
Very nice review but I am disappointed that you didn’t address Goelzer et al. 2012. Educators like me who are not experts are lost as to why Goelzer’s millennial scale projections seem to suggest a much smaller sealevel rise by 2100 than provided by most other recent papers. Local sealevel rise skeptics in North Carolina (remember House Bill 819?) are all over this.
Skeptics are pointing to Figure 3 in Goelzer et al. 2012 to argue that the LOVECLIM model suggest a maximum sealevel rise of ~50cm (~20 inches) by 2100 which puts us closer to the low AR4 estimates again. Why is their model projection so low? What am I missing here? Any clarification would be much appreciated.
See article:
Millennial total sea-level commitments projected with the Earth system model of intermediate complexity LOVECLIM
H Goelzer et al 2012 Environ. Res. Lett. 7 045401
chris, thanks for the link to the new paper by Foster & Rohling.
Some bad news: +2C of global warming (400-450 ppm CO2) will eventually lead to between 9-31 meter of sea level rise, in equilibrium.
Some good news: Not much additional response in SLR until 650 ppm. “sea level stays more or less constant for CO2 changes between 400 and 650 parts per million and it is only for CO2 levels above 650 parts per million that the researchers again saw a strong sea level response for a given CO2 change.”
This indicates the relative stability of the East Antarctic Ice Sheet. However, I don’t think we should take this as an excuse for burning fossil fuels up to 650 ppm, as the additional forcing will probably cause a faster rate of sea level rise.
Quotation from the press release here: http://noc.ac.uk/news/new-study-documents-natural-relationship-between-co2-concentrations-sea-level
I have been looking forward to this paper since Eelco Rohling’s lecture at AGU11. Here is a link to the lecture: http://climatevideos.wordpress.com/2011/12/18/james-hansen-eelco-rohling-and-ken-caldeira-at-agu11/
Alex, I’d also be interested in an expert consideration of Goelzer et al. From my brief perusal of their paper, the rather slow and relatively limited sea level response relates to a very low climate sensitivity in their preferred model (climate sensitivity of 1.6 oC). That’s very, very much on the low side of the range broadly accepted as conforming to observational, paleo and modelling evidence, and seems particularly low as the time scale of their analysis (extending to the year 3000) would seem to require a consideration of some of the longer term feedbacks inherent in the earth system sensitivity. On the other hand their model has a high polar amplification….
But I might well be mssing something, and I should probably read their paper more thoroughly. Better ‘though would be to have an expert viewpoint on Goelzer’s choice of model/parameterization…
The averaging question looks like one common in geostatistics; not my field but that of a few who I frequent. I suspect there may be good, defendable approaches that are significantly more sophisticated than the one described. In orebody and oilfield evaluation, many millions of dollars can depend on rigorous probabilistic answers to questions of highly under-sampled averaging. I think Robert Rohde at Berkerly has recently been applying some of these techniques to climate science.
[Response: Robert Rohde is using kriging, and I agree this could be helpful here. But I think the best answer would come from a spatial pattern/data assimilation approach that used information from the spatial variations seen by the satellites to estimate the correlations between the far field and the gauge data. – gavin] [… which is what Church&White (2006) have done. – stefan]
Apparently, many of the synthetic time series severely underestimate past sea level rise (fig. 2). Doesn’t that give rise to questions on using them to predict future sea level rise?