Time for the 2012 updates!
As has become a habit (2009, 2010, 2011), here is a brief overview and update of some of the most discussed model/observation comparisons, updated to include 2012. I include comparisons of surface temperatures, sea ice and ocean heat content to the CMIP3 and Hansen et al (1988) simulations.
First, a graph showing the annual mean anomalies from the CMIP3 models plotted against the surface temperature records from the HadCRUT4, NCDC and GISTEMP products (it really doesn’t matter which). Everything has been baselined to 1980-1999 (as in the 2007 IPCC report) and the envelope in grey encloses 95% of the model runs.
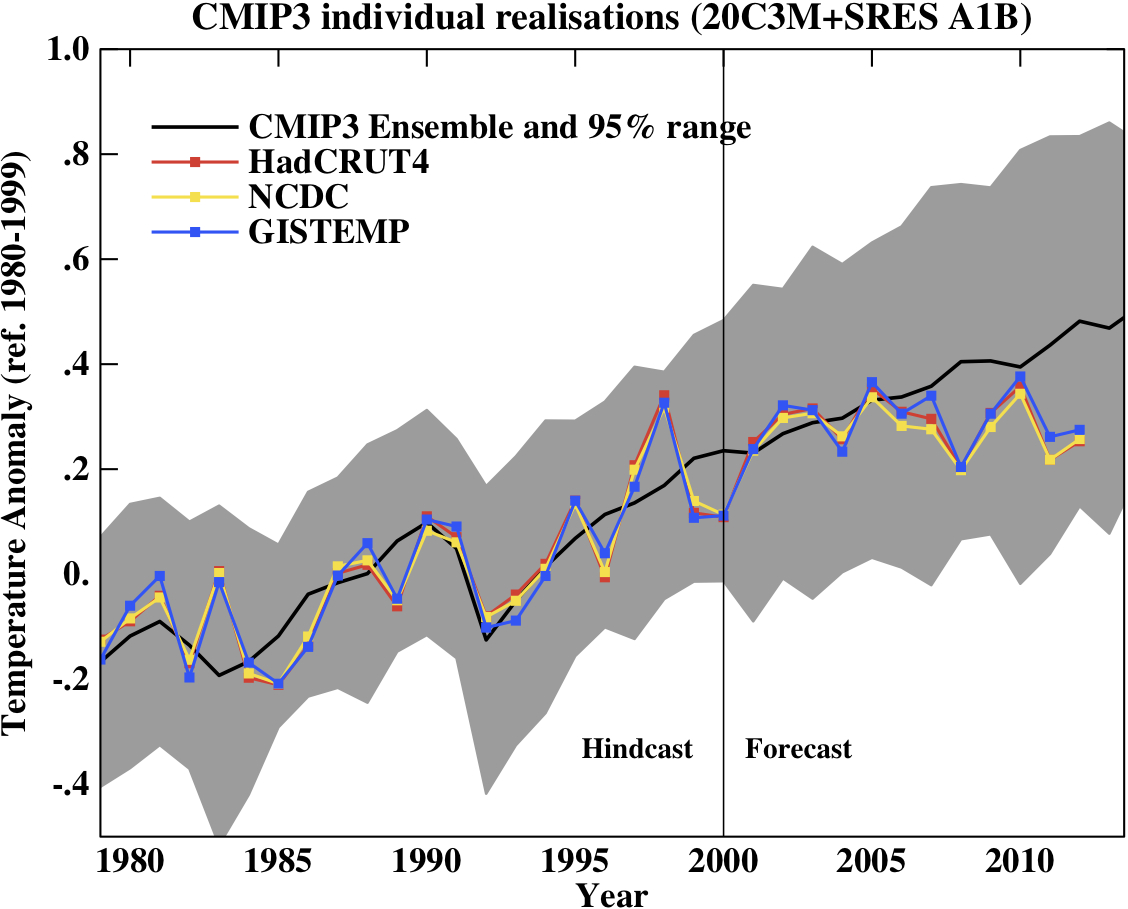
Correction (02/11/12): Graph updated using calendar year mean HadCRUT4 data instead of meteorological year mean.
The La Niña event that persisted into 2012 (as with 2011) produced a cooler year in a global sense than 2010, although there were extensive regional warm extremes (particularly in the US). Differences between the observational records are less than they have been in previous years mainly because of the upgrade from HadCRUT3 to HadCRUT4 which has more high latitude coverage. The differences that remain are mostly related to interpolations in the Arctic. Checking up on the predictions from last year, I forecast that 2012 would be warmer than 2011 and so a top ten year, but still cooler than 2010 (because of the remnant La Niña). This was true looking at all indices (GISTEMP has 2012 at #9, HadCRUT4, #10, and NCDC, #10).
This was the 2nd warmest year that started off (DJF) with a La Niña (previous La Niña years by this index were 2008, 2006, 2001, 2000 and 1999 using a 5 month minimum for a specific event) in all three indices (after 2006). Note that 2006 has recently been reclassified as a La Niña in the latest version of this index (it wasn’t one last year!); under the previous version, 2012 would have been the warmest La Niña year.
Given current near ENSO-neutral conditions, 2013 will almost certainly be a warmer year than 2012, so again another top 10 year. It is conceivable that it could be a record breaker (the Met Office has forecast that this is likely, as has John Nielsen-Gammon), but I am more wary, and predict that it is only likely to be a top 5 year (i.e. > 50% probability). I think a new record will have to wait for a true El Niño year – but note this is forecasting by eye, rather than statistics.
People sometimes claim that “no models” can match the short term trends seen in the data. This is still not true. For instance, the range of trends in the models for cherry-picked period of 1998-2012 go from -0.09 to 0.46ºC/dec, with MRI-CGCM (run3 and run5) the laggards in the pack, running colder than the observations (0.04–0.07 ± 0.1ºC/dec) – but as discussed before, this has very little to do with anything.
In interpreting this information, please note the following (mostly repeated from previous years):
- Short term (15 years or less) trends in global temperature are not usefully predictable as a function of current forcings. This means you can’t use such short periods to ‘prove’ that global warming has or hasn’t stopped, or that we are really cooling despite this being the warmest decade in centuries. We discussed this more extensively here.
- The CMIP3 model simulations were an ‘ensemble of opportunity’ and vary substantially among themselves with the forcings imposed, the magnitude of the internal variability and of course, the sensitivity. Thus while they do span a large range of possible situations, the average of these simulations is not ‘truth’.
- The model simulations use observed forcings up until 2000 (or 2003 in a couple of cases) and use a business-as-usual scenario subsequently (A1B). The models are not tuned to temperature trends pre-2000.
- Differences between the temperature anomaly products is related to: different selections of input data, different methods for assessing urban heating effects, and (most important) different methodologies for estimating temperatures in data-poor regions like the Arctic. GISTEMP assumes that the Arctic is warming as fast as the stations around the Arctic, while HadCRUT4 and NCDC assume the Arctic is warming as fast as the global mean. The former assumption is more in line with the sea ice results and independent measures from buoys and the reanalysis products.
- Model-data comparisons are best when the metric being compared is calculated the same way in both the models and data. In the comparisons here, that isn’t quite true (mainly related to spatial coverage), and so this adds a little extra structural uncertainty to any conclusions one might draw.
Given the importance of ENSO to the year to year variability, removing this effect can help reveal the underlying trends. The update to the Foster and Rahmstorf (2011) study using the the latest data (courtesy of Tamino) (and a couple of minor changes to procedure) shows the same continuing trend:

Similarly, Rahmstorf et al. (2012) showed that these adjusted data agree well with the projections of the IPCC 3rd (2001) and 4th (2007) assessment reports.
Ocean Heat Content
Figure 3 is the comparison of the upper level (top 700m) ocean heat content (OHC) changes in the models compared to the latest data from NODC and PMEL (Lyman et al (2010) ,doi). I only plot the models up to 2003 (since I don’t have the later output). All curves are baselined to the period 1975-1989.

This comparison is less than ideal for a number of reasons. It doesn’t show the structural uncertainty in the models (different models have different changes, and the other GISS model from CMIP3 (GISS-EH) had slightly less heat uptake than the model shown here). Neither can we assess the importance of the apparent reduction in trend in top 700m OHC growth in the 2000s (since we don’t have a long time series of the deeper OHC numbers). If the models were to be simply extrapolated, they would lie above the observations, but given the slight reduction in solar, uncertain changes in aerosols or deeper OHC over this period, I am no longer comfortable with such a simple extrapolation. Analysis of the CMIP5 models (which will come at some point!) will be a better apples-to-apples comparison since they go up to 2012 with ‘observed’ forcings. Nonetheless, the long term trends in the models match those in the data, but the short-term fluctuations are both noisy and imprecise.
Summer sea ice changes
Sea ice changes this year were again very dramatic, with the Arctic September minimum destroying the previous records in all the data products. Updating the Stroeve et al. (2007)(pdf) analysis (courtesy of Marika Holland) using the NSIDC data we can see that the Arctic continues to melt faster than any of the AR4/CMIP3 models predicted. This is no longer so true for the CMIP5 models, but those comparisons will need to wait for another day (Stroeve et al, 2012).

Hansen et al, 1988
Finally, we update the Hansen et al (1988) (doi) comparisons. Note that the old GISS model had a climate sensitivity that was a little higher (4.2ºC for a doubling of CO2) than the best estimate (~3ºC) and as stated in previous years, the actual forcings that occurred are not the same as those used in the different scenarios. We noted in 2007, that Scenario B was running a little high compared with the forcings growth (by about 10%) using estimated forcings up to 2003 (Scenario A was significantly higher, and Scenario C was lower), and we see no need to amend that conclusion now.
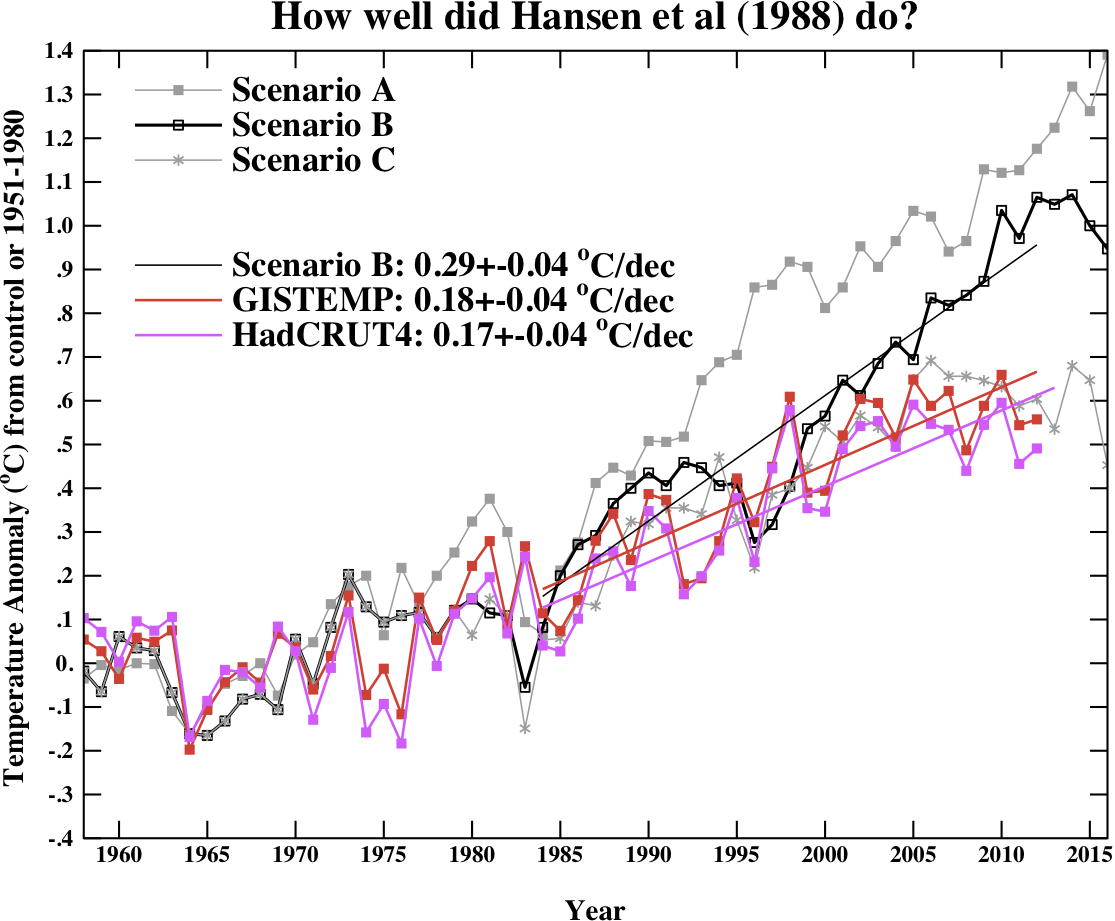
Correction (02/11/12): Graph updated using calendar year mean HadCRUT4 data instead of meteorological year mean.
The trends for the period 1984 to 2012 (the 1984 date chosen because that is when these projections started), scenario B has a trend of 0.29+/-0.04ºC/dec (95% uncertainties, no correction for auto-correlation). For the GISTEMP and HadCRUT4, the trends are 0.18 and 0.17+/-0.04ºC/dec respectively. For reference, the trends in the CMIP3 models for the same period have a range 0.21+/-0.16 ºC/dec (95%).
As discussed in Hargreaves (2010), while this simulation was not perfect, it has shown skill in that it has out-performed any reasonable naive hypothesis that people put forward in 1988 (the most obvious being a forecast of no-change). However, concluding much more than this requires an assessment of how far off the forcings were in scenario B. That needs a good estimate of the aerosol trends, and these remain uncertain. This should be explored more thoroughly, and I will try and get to that at some point.
Summary
The conclusion is the same as in each of the past few years; the models are on the low side of some changes, and on the high side of others, but despite short-term ups and downs, global warming continues much as predicted.
References
- G. Foster, and S. Rahmstorf, "Global temperature evolution 1979–2010", Environmental Research Letters, vol. 6, pp. 044022, 2011. http://dx.doi.org/10.1088/1748-9326/6/4/044022
- S. Rahmstorf, G. Foster, and A. Cazenave, "Comparing climate projections to observations up to 2011", Environmental Research Letters, vol. 7, pp. 044035, 2012. http://dx.doi.org/10.1088/1748-9326/7/4/044035
- J.M. Lyman, S.A. Good, V.V. Gouretski, M. Ishii, G.C. Johnson, M.D. Palmer, D.M. Smith, and J.K. Willis, "Robust warming of the global upper ocean", Nature, vol. 465, pp. 334-337, 2010. http://dx.doi.org/10.1038/nature09043
- J. Stroeve, M.M. Holland, W. Meier, T. Scambos, and M. Serreze, "Arctic sea ice decline: Faster than forecast", Geophysical Research Letters, vol. 34, 2007. http://dx.doi.org/10.1029/2007GL029703
- J.C. Stroeve, V. Kattsov, A. Barrett, M. Serreze, T. Pavlova, M. Holland, and W.N. Meier, "Trends in Arctic sea ice extent from CMIP5, CMIP3 and observations", Geophysical Research Letters, vol. 39, 2012. http://dx.doi.org/10.1029/2012GL052676
- J. Hansen, I. Fung, A. Lacis, D. Rind, S. Lebedeff, R. Ruedy, G. Russell, and P. Stone, "Global climate changes as forecast by Goddard Institute for Space Studies three‐dimensional model", Journal of Geophysical Research: Atmospheres, vol. 93, pp. 9341-9364, 1988. http://dx.doi.org/10.1029/JD093iD08p09341
- J.C. Hargreaves, "Skill and uncertainty in climate models", WIREs Climate Change, vol. 1, pp. 556-564, 2010. http://dx.doi.org/10.1002/wcc.58
Re 100 (Ray Ladbury)
let’s go to basics first.
Multiple linear regression is no magic tool to “discover” unknown behavior “buried” under some noise and unwanted influences. It is based on statistical calculation of the best fit for the measured/observed variable as function of some independent variables. For example the intro text in http://www.statsoft.com/textbook/multiple-regression/ puts the basic equation as follows:
“In general then, multiple regression procedures will estimate a linear equation of the form:
Y = a + b1*X1 + b2*X2 + … + bp*Xp,
where Xp are the control variables.
F&R used 4 such variables: global warming signal (linear – please do read the quote I provided, or the paper in full) and MEI, AOD and TSI. They found the best fit coefficients for the various datasets are slightly different. Let me quote F&R again:
“Using multiple regression to estimate the warming rate
together with the impact of exogenous factors, we are able to improve the estimated warming rates, and adjust the temperature time series for variability factors”
The assumed form of the warming was linear. When one chooses some independent variables for the multiple regression – from that moment they are all treated on equal footing. And out of the four: MEI, AOD and TSI were provided by independent data, while global warming was assumed to be linear.
Linearity with respect to time should not be confused with linearity with respect to the feedback parameter f. That is why, over ‘shortish’ time intervals, the present low signal regime appears to be approximately described by a non accelerating (linear t dependence) and a positive feedback.
Ref. E.g. Chris Colose Part 2.
Thank you, PAber. I do know what linear regression is. My question is why would you expect the first order effects of those influences NOT TO BE LINEAR? What is more the fact that the 4 independent products wound up marching in lockstep once the analysis was applied is surely not fortuitous. Even if the effects were highly nonlinear, it surely strains credulity to imagine that such an error would actually improve the signal, does it not. So, I would say that in this case, linear regression kicked some serious tuckus and illuminated some important relations–and that is what science is about. The approach is certainly a lot better than throwing up one’s hands and saying “Oh, it’s all too hard,” as you would have us do.
@103 Ray Ladbury
I do not know if anybody is still reading such a late post – but I feel that we may be getting closer to a common ground, so I’ll try posting once more.
Coming back to my post 101, please consider this:
The form of the multiple regression is Y = a + b1*X1 + b2*X2 + … + bp*Xp.
Y is the measured global average temperature. No matter which dataset. I hope you agree, that once a method for spatial averaging, smoothing and getting rid of noise there would be one. true, global average. The many raw datasets are but approximations or versions and they are pretty much close to each other (Fig 1).
First assume, as F&R that X1 is linear in time, where we seek the appropriate warming rate and X2, X3 and X4 are MEI, AOD and TSi profiles. We minimize the residual difference for the best fit looking for the a, b1, … b4 factors. Then we get rid of the b2*X2+b3*x3+b4*x4. What we are left with is the b1*X1 + noise.
Showing this as a proof that “underlying temperature growth is linear” is a trick.
Suppose instead that X1 is in the form of sine wave sin(c(T-T0)) with a period of about 60 years and phase shift T0 at about 1985 (see figure 2 or Armando’s post). This would give linear-like behavior between 1973 and 1998 (roughly), and slow down after 2000. Keep X2, X3 and X4 as before. Look for the new values of best fit a, b1, b2, b3, and b4 coefficients. My guess is that the solar index would be smaller. Then as before, get rid of the b2*X2+b3*x3+b4*x4, leaving only the “global warming” part. What will be left? Sine wave + noise.
Now, you might ask: why sine wave? Well, why not? For a purely statistical procedure there is no way of telling which form is better, other than the value of the minimized R^2. It is only physics that can tell us if the time evolution is roughly linear or if it slows down, speeds up, oscillates. And let me remind that historically periods of linearity were quite limited.
So the statistical procedure is the thing I object to. I insist that unless we have the coefficients giving the MEI, AOI and TSI contributions from PHYSICS, the procedure does not lead to unique results. And using “adjusted data” figure to prove that there is no change in average global warming rate, as has been done here is circular argument. Let’s stick with raw data, and try to understand it better.
> why sine wave? Well, why not?
Because CO2. Physics, as you say.
PAber, Why not a sine wave? Well, for starters, because you are fitting 35 years of data to a function with a periodicity of 60 years. I’d call that kind of a problem. Second, if we are to posit a periodic function, we must have in mind a periodic driver of said function. As Hank pointed out, the reason for a linear term is the physics of increasing anthropogenic CO2 forcing. This is not arbitrary.
Also, what you seem to be missing is that if a simple model is wrong, there is no reason why it should actually improve agreement between disparate datasets. That is does certainly suggests that it has elements of correctness. Of course the proof of any statistical model is not in how it fits the data, but rather in its predictive power–we’ll have to wait and see. However, information theory shows us that a simple theory that explains the theory well is much more likely to have predictive powr than a complicated theory that explains the data equally well.
@105 Hank Roberts
AFAIK the dependence of temperature on CO2 concentration is logarithmic (e.g. Royer et al 2007). And the growth of CO2 is (approximately) linear.
More seriously, please look at the Armando’s link and see for yourself.
PAber, Dan H. tried that talking point here a few days back. It’s been debunked.
Monckton Myth #3: Linear Warming
> look at the Armando’s post and see for yourself
As others already pointed out, see how by using a very short timeline carefully selected, a mistaken impression is created, compared to using all the information available as, e.g. Tamino does.
PS: PABer:
For those outside the paywall, Stoat provided this pointer for Royer et al. (2007)
It’s not support for the claim you’re making.
PAber, Uh, no. CO2 growth is most certainly exponential or even faster:
http://tamino.wordpress.com/2010/04/12/monckey-business/
Please, where do you get this crap?
From Foster & Rahmstorf:
Linear it is. Better believe it ;-)
CO2 growth according to NOAA:
http://www.esrl.noaa.gov/gmd/webdata/ccgg/trends/co2_data_mlo_anngr.png
This shows that the rate of growth is perhaps linear with time, i.e R=k*time.
That means the growth itself is C=1/2*k*time^2, which is accelerating, but not exponentially accelerating.
R = dC/dt
The interesting point is when you plug the concentration into the CO2 log sensitivity. Then you get
log( C ) = log(1/2*k*time^2) = 2*ln(1/2*k*time)
which is sub-linear with time because the power can be moved outside the logarithm.
So it really does take an exponential (or faster) acceleration to make the sensitivity linear or higher with time.
That is not to say that an exponential growth may not suddenly take off. When one considers the possibility of mining oil shale or other energy intensive fossil fuels in the future, the multiplier effect will kick in and the amount of CO2 may indeed increase exponentially. Or some other tipping point such as methane outgassing may hit a critical temperature and activate its release.
> CO2 growth according to NOAA:
> This shows that the rate of growth is perhaps ….
Hard to tell much from a bar chart. Try this from Tamino recently.
Interesting that the topic is still alive.
First of all thanks to WebHubTelescope (#112), this is what I meant. I specifically put the “approximately” linear in the growth of CO2 – I allow it may have slight rate increase – but this is not the point I was stressing.
My main point is focused on the application of the results of fitting a linear form of global temperature as function of time and presenting it as if it were a “cleared”, “true” signal.
Locally, any smooth function is “approximately” linear. The issue lies in the meaning of “locally”. Looking at the raw temperature records since 1800 or 1900 I guess all of you would agree that they are not linear, showing periods of increases and decreases. (On the other hand the CO2 concentration is supralinear, maybe quadratic maybe better – but always increasing). Ray: The reason I mentioned sine wave (60-year oscillation) is that the temperature record since 1940 to 2012 resembles a half of a sine wave. I use the word resembles WITHOUT suggesting any physical oscillatory mechanism. Regarding your remark for the scope of the fit: why should we limit our fits to 30 years instead of 60? Even so, for statistical analysis sine wave is as good as the linear form. So, in principle, one could repeat the F&R analysis using as X1 the sine wave and publish “discovery” that the adjusted signal is oscillatory. Would anyone believe such claim? As Ray rightly notes: there should be physical mechanism behind it. And this is why I object to using the F&R fit results as physical.
Is there any physical explanation why the b2, b3, and b4 coefficient have the values resulting from statistical fit?
As for the Martin Vermeer remark and quote from F&R. The quote excludes specifically the ACCELERATED global temperature record as not giving a better fit for 3 datasets. There is no information on other forms of functions. Exclusion of the acceleration does not automatically mean that “linear it is”.
Lastly, I fully agree with Ray (#106) and his concluding remark: to see if the model is correct “we’ll have to wait and see”.
WHT (112),
Another approach might be to notice that the concentration growth rate seems bare some relationship with the emissions growth rate of 1.6% annually. http://www.eia.gov/forecasts/ieo/emissions.cfm
That seems to describe the chart you linked to as well as a linear description might. And, the exponential description has been more successful when longer time periods have been considered.
#114–
Really? (And yes, read that with a strong rising intonation!)
I’ll readily admit to mathematical naiveté, but the position that though linear fits work well for all data sets while quadratic fits are poor except for UAH, realistically leaves open the possibility that a sine curve (or something) might just possibly work as well or better seems, er, not very realistic.
Call me a skeptic on that one…
The discussion of trends seems to mix up three issues: CO2 vs time, temperature vs time and temperature vs CO2.
The increase of CO2 with time is highly correlated with CO2 emissions, and these correlate to world economic growth which is roughly exponential. A logistics curve might be better, the growth has to stop sometime!
The increase in temperature is more complicated, but is, as expected, quite well correlated to the increase of CO2. For example, between 1880 and 2011 the temperature anomaly correlates linearly to CO2 level on a yearly basis with R-sq~.8
{ data used is NASA’s CO2 series for 1850 -2011 http://data.giss.nasa.gov/modelforce/ghgases/Fig1A.ext.txt) and NASA’s temperature anomaly series http://data.giss.nasa.gov/gistemp/graphs_v3/Fig.A2.txt).
While it might seem more appropriate to use the natural log of the CO2 level, it makes little difference for the specified time period because the CO2 level increases by “only” 35%, and so only the linear term of the Taylor series expansion is important. However, using logarithms leads to the statistical relationship
Temperature Anom =0.17+3.12ln(CO2/341) deg K Rsq.~0.86
{341ppm is the average of the beginning and end point levels}
If the CO2 level doubles this statistical model predicts a 2. deg K temperature rise (a linear model would give 2.5 deg K). So the statistical model agrees pretty well with the results of the big models for the transient climate sensitivity.
Muller’s Berkeley Group has a nice graphic showing the results of what appears to be a similar analysis (http://berkeleyearth.org/results-summary/), but they don’t give details of their analysis.
Subtracting the trend curve from the raw data leaves “random” fluctuations (noise) with a standard deviation of 0.1 deg K. Fourier analysis of the noise for the period 1880-2007 (128 years) shows a big component at f=.0156 y-1(i.e. 64 year period). This surprised me, but when I overlaid the equivalent sine-wave on the time signal it appeared to be a very real effect. There were also several very noticeable harmonics. This may be just some strange artifact of the particular time period I analyzed – but it does seem to me that it would be worth the attention of a graduate student.
for Dave Griffiths: you might compare what you discovered to some of the mentions of similar ‘cycles’ e.g. here or in these.
PAber,
Just because one is doing a statistical fit does not mean one should toss physics out the window. If you look at the temperature record, it is clear that there are breakpoints–one in 1945, corresponding to a rapid economic growth that happened to be producing a lot of sulfate aerosols as well as CO2, then one again in about 1975. The latter likely represents the effects of clean air legislation in most of the industrial world, as the output of sulfate aerosols falls quite significantly.
Thus, it makes no sense to attempt to fit a single trend to the period 1945-2013. And fitting an oscillatory trend is especially problematic since 1)we are still dealing with less than a single period (remember my favorite exercise with the digits of e, the base of Napierian logarithms), and 2)there is no oscillatory forcing that will give rise to a sinusoidal shape.
On the other hand, the physics clearly says the trend due to warming ought to be roughly linear. Were it not roughly linear, it is unlikely that several independent datasets would agree better after the analysis than before it.
And this is the point I was making that you have conveniently ignored–a simple analysis that agrees with the available data if far more likely to have predictive power than one that is complicated. F&R 2011 is admirable in its simplicity. It produces far better agreement than could be expected purely by chance. It very likely yields important insight into both the signal and the noise. That is the point.
Dave Griffiths @117 — It is at least conceivable that AMOC has a 60-70 year quasiperiod. Looking for such in a mere 128 years of data is highly dubious. Looking into various ice cores [Chylek et al., 2012]
http://onlinelibrary.wiley.com/doi/10.1029/2012GL051241/full
does not offer convincing support.
Hank Roberts @118 — The second link appears to be broken.
@119 Ray Ladbury
I guess we’re coming to a real common ground. You provide arguments regarding the changes in behavior in the separate time domains – plausible, although not ironclad. This is what I called for.
Unfortunately I still disagree with your point “Were it not roughly linear, it is unlikely that several independent datasets would agree better after the analysis than before it.”
Not really. John von Neumann famously said “With four parameters I can fit an elephant, and with five I can make him wiggle his trunk.” The four independent statistical procedures, resulting in slightly different output parameters b1 … b4 and with the assumed linear main trend X1 could minimize the differences between the “adjusted” global temperature trends. And these raw records are hardly independent – they are attempts to measure the same quantity. In fact I am quite satisfied with the agreement between the four raw datasets.
Reiterating: my objection is to propagandist use of the adjusted data as *proof* of continuing linear increase of the temperature. I’d prefer better averaging methods (or even better: improved measurement quality, global coverage, station quality etc.) and therefore more trust in the raw data, rather than adjustments.
@PAber
John von Neumann did not say this, but he was one of the first promoters of general circulation models for climate and weather prediction and understanding. He loved computer and who is a better sponsor than military? You should read “A vast machine” by Paul Edwards where you can find the history of climate data collection and GCMs. It is a good book. In this book, you also find an answer to your “raw-adjustment” confusion.
PAber and ghost,
First, according to wikiquote, von Neumann did in fact say:
“With four parameters I can fit an elephant, and with five I can make him wiggle his trunk.”
Note, however, that he did not say that he could fit 4 independent elephants with 4 parameters. And the measurements are in fact independent, relying on very different techniques. The satellite measurements in particular are strongly affected by ENSO.
And it is fascinating that you refer to the citation of the results of a research paper as “propagandist”. The paper does in fact show that continued warming is an essential element to understanding global temperatures over the past 35 years. If you wish to attack the methodology of the paper, fine. However, you’ve yet to raise any substantive point I can see–just a general distrust of statistical fitting, which amounts to uninformed prejudice rather than a technical argument.
> propagandist
Resistance is futile. You will be assimilated.
@ Ray
Please read my statements carefully:
1. The four datasets are NOT independent – they aim to measure the same quantity. Hopefully they are related to each other.
2. I wrote: I object to the “propagandist use of the adjusted data as *proof* of continuing linear increase of the temperature”. Not to the paper by F&R. While I have my reservatyions regarding the methodology (in particular lack of recognition that ENSO and global temperatures might be correlated), the paper has to stand on its own. It does explain the methodology and in principle allows anyone to rework the calculations.
The problem is that the “adjusted” figure from this paper is presented in various blogs and web pages as *proof* that the warming has not stopped (opposing the usage of the raw data and the calls that the warming hiatus since 1998), without any explanation as to the origin of the “adjustments”. Many Internet users, who do not know much about multiple regression and statistical procedures would think that the adjusted data is the true global temperature average. This creates some confusion – and this is why I wrote about propaganda.
PAber,
So it would be your contention that a measurement of a temperature using a mercury thermometer and an IR thermometer are not independent measurements of the temperature? Interesting. By this logic, we should throw out experimental confirmation entirely, then? And we can shut down all but one experiment at CERN, since we certainly wouldn’t every want to measure the Higgs mass with two independent experiments! Dude, you sure you are a scientist?
And let me see if I’ve got your second point right. We should not quote the results of a paper, because there might be some ignorant food tube out there who misunderstands it? F&R 2011 provides pretty good evidence that the forcing due to anthropogenic CO2 continues unabated. In so doing, it is supported by physics. The paper provides a good measure of what that forcing would be ceteris paribus. It does not claim ceteris are paribus, but that doesn’t make that quantity any less valuable for planners, legislators (were they to extract their heads from their own anuses and their noses from those of lobbyists) and even scientists. You have done nothing that raises any doubts about those two results.
#125–” I wrote: I object to the “propagandist use of the adjusted data as *proof* of continuing linear increase of the temperature”.”
Well, I don’t recall seeing anybody claim the result to be “proof.” Those citing F & R have, in my experience, generally known better than to claim that even robust results amount to ‘proof’ of anything.
I have seen it presented as good reason to expect that warming is continuing more or less linearly–and I would think that that’s a pretty good conclusion to draw from F & R. Pending further work, as always.
It’s certainly much better than the ‘fruity’ conclusion, promulgated ad nauseam recently, that because the observed warming since 1998 is not large–let alone statistically significant!–that the long-term trend must therefore have changed. That’s the meme in response to which I’ve usually seen F & R cited. And it’s much more misleading–dare I say, intentionally so?
PAber (#125)
“The four datasets are NOT independent.”
This statement worries me. Are you saying that we may not take multiple measures of the same thing to defeat noise and perhaps even systematics? That does not seem to me to correspond with measurement theory. In fact, we seek statistically independent measures for this very reason.
I’m also not persuaded by your claim that Foster & Rahmstorf’s method yields what you claim. So long as the result is reasonably orthogonal to the fitted functions, it should come out fairly clearly. Things that resemble the fitted functions will be aliased of course, but a line or an arc would show up if they were the residual.
Hank (118) thanks for the reference to Atlantic Multi-decadal Oscillation. I downloaded the NOAA data for the AMO Index ( http://www.esrl.noaa.gov/psd/data/correlation/amon.us.long.data) and, after computing yearly averages, Fourier analyzed the same period as I used for the “noise”. I found the AMO index for this period to be dominated by a ~ 1/64 cycle/y signal with almost exactly the same phase as that of the noise signal at 1/64 cycle/y (the phase is very close to zero i.e. a cosine wave for t=0 at 1880).
Since I used a 128 year time period, the Fourier components were separated by 1/128 cycles/year, so I can’t be too precise about the frequency. However, in both cases there was very little leakage, so the basic frequency must be very close to 1/64 cycle/year. The amplitude of the AMO signal is about 2.6 x the noise signal. The North Atlantic covers about 1/5 of the Earth’s surface, so the AMO signal must have a considerable impact on the “noise”.
Judging from what I’ve read about the AMO, this topic is being looked at by some of the experts.
This should be helpful for future model accuracy. Any chance this gets into the 5th assessment?
http://www.cbc.ca/news/politics/story/2012/11/29/pol-ice-sheets-melting-greenland.html
Dave Griffiths,
I am sure some folks are getting tired of this example, but it is pertinent. Consider the following series of ordered pairs
1,2
2,7
3,1
4,8
5,2
6,8
7,1
8,8
9,2
10,8
Predict the y-value for the 11th pair. If you said 7 or 8, you are wrong. It is in fact 4, because the y values are the digits of the base of Napierian logarithms, e. e is transcendental, and so cannot be periodic.
One should be very careful about positing periodicity with only a few cycles unless one knows a periodic forcing is extant.
Yes.
That paper, your link says, was published in November/December 2012
@ Chris Dudley and Ray Ladbury
I stand by what I wrote: the four datasets are NOT independent.
Chris – you wrote “This statement worries me. Are you saying that we may not take multiple measures of the same thing to defeat noise and perhaps even systematics? ”
Of course we can and should make multiple measurements, using all available techniques: ground bases, satellite, whatever and all the good methods for improving the data quality. Still, the goal of all global methods, again, provided that the averaging methods are consistent, is to arrive at a single number: global temperature for each year or month or date. Multiple approaches reduce error and provide better final value.
What I objected to (track the origin of my remark) was the statement by Ray, that using 4 independent fitting procedures by F&R one arrives at “better agreement” of the adjusted data than the agreement of raw data. This is to be expected: the assumed form of the global trend (linear function) is the same in all cases. The resulting fitting parameters b1 … b4 (to keep my notation) are different for each dataset. Resulting better agreement of the X1 (global signal) in all 4 datasets is a very weak argument for the “proof” of linearity.
As for the capacity to discover the nonlinear residue that you mention – there is a simple explanation. The divergence of the raw data from linear growth, used by the sceptics, is mainly visible post ’98. Looking at the volcanic, solar and oceaninc contributions one can see that volcanic activity is gradually diminishing, mei has some ups and downs for the period but the solar activity component is negative and rather strong in the post 1998 period. Thus the multiple regression would ascribe most of the downward deviation from linearity to this trend.
Now suppose that the main (global change) component is not linear but the sine wave, or any other form in which there is a marked decrease of the growth of the X1 function. The result would be a smaller coefficient linking the solar influence to raw data. Depending on the choice of the input functions, the results are different. And while the solar, volcanic and oceanic influences are given by independent measurements, the linear global part is put in by hand.
PAber (#133),
Fitting independently is fine, and appropriate in this case since it seems to be physically motivated. Somewhat different regions are being measures.
I also do not see an assumed form in the residual. High frequency functions were fit so a low frequency signal could survive in the residual. You may have a case that one particular bend could have been aliased, but I think you need to demonstrate that quantitatively. You can’t just take one section of the data and one portion of a fitting function and make that claim. Something will pop up elsewhere if you do that.
PAber, It would appear that you have not worked with data much. The only way in which you would expect agreement among 4-5 datasets gathered via independent measurements to line up after adjustments is if they were in fact measuring the same underlying physical quantity AND measuring it well AND if the “corrections” applied were indeed correct!
It utterly astounds me that anyone with any familiarity with the satellite and terrestrial datasets could contend that they are not independent measurements! It seems that you want it both ways–you want to claim (but never quite do) that the results of F&R 2011 are spurious. But at the same time, you need to contend that the datasets are not independent–which could only happen if there were in fact an actual linear trend that they were measuring. And you avoid the contradiction by never following anything to its logical conclusion. It is an attitude reminiscent of the approach denialists take with climate models–they are careful to preserve their ignorance, because it is the only way to avoid contradictions.
Ray @ 131:
Personally, I don’t get tired of it. It’s the example that keeps on giving and giving…
Dave Griffiths @ 129:
What is so special about a Fourier-derived period that turns out to be just half your entire data length? And why does it show up in both the AMO and the noise? Could it perhaps be just a coincidence?
Regarding the different data sets analyzed in Foster & Rahmstorf 2011: while the surface temperature data sets share much of the same root data, the satellite data sets are entirely separate from them. They don’t even measure the same thing (surface temperature vs lower-troposphere temperature). Hence, independent — except for the fact that they reflect related physical phenomena.
Regarding different coefficients for the different data sets: they’re not that different. Look at figure 3 in that paper. The only significant differences are between surface and satellite data for volcanic and el Nino influences. And they should be different, those factors really do have a different influence on the surface temperature and lower-troposphere temperature. In fact that’s one of the results of the paper.
Regarding Ray Ladbury’s example in #131: it’s just as relevant this time as it was the first. Repeat as often as necessary.
Regarding the so-called “period” in both global temperature and AMO: in case you didn’t know, AMO is temperature. That’s all it is. Unlike ENSO (which can be quantified in many ways, including some like the SOI which don’t use any temperature data at all), AMO is just temperature. So — global temperature is correlated with north Atlantic temperature. What a shocking result.
This is in response to the comments on the apparent 1/64 cycle/y. Sorry if some of this is a little repetitive.
If you correlate the temperature anomaly to the CO2 level you find pretty good correlation (RSq~.94 for 10 year rolling averages). If you subtract the derived trend curve from the raw data you are left with that part of the anomaly not correlated to the CO2 level, let’s call this noise.
I just happened to be interested in the Fourier spectrum of this noise. I had assumed it was mostly relatively high frequency due to El Nino’s etc, say in the range .1 to.4 cycle/yr. So I was surprised when I looked at the spectrum for the period 1880-2007 and found a large component at 1/64 cycle/year. Hank Roberts suggested that AMO might look similar so I checked it, and it did (at least the time series I analyzed has the 1/64 cycle component). This implies that there is some correlation between the “noise” and the AMO signal. In fact the RSQ is ~0.5. Is this a coincidence? Perhaps.
I don’t claim that you can use this information to make any predictions. In fact I would not like to make any predictions simply from statistical analysis if there was no physics back-up. For example, the statistical correlation of CO2 levels with temperature anomaly agrees quite well with models based on the laws of physics, so I think it has some predictive capability.
There seems to be quite a lot of evidence for the AMO both from data and models. According to the 4-th IPCC (r-4 modelling section, p623)
(a) “The Atlantic Ocean exhibits considerable multi-decadal variability with time scales of about 50 to 100 years (see Chapter 3). This multi-decadal variability appears to be a robust feature of the surface climate in the Atlantic region, as shown by tree ring reconstructions for the last few centuries (e.g., Mann et al.,
1998).
(b) “ In most AOGCMs, the variability can be understood as a damped oceanic eigenmode that is stochastically excited by the atmosphere” (r-4 Modelling Section, p623.
Now, if there is an eigenmode then there is an eigenfrequency. But if the mode is driven stochastically the phase of the response will have a random component which will be somewhat confusing.
The question was asked, why does the signal of interest appear to have 2 oscillations in 128 years. Sorry I can’t provide a physics answer – it could be the eigenfrequency – but only the AOGCM.s could answer that question. So I will just comment on the signal processing issues. If you Fourier analyze a time series for a period T then the allowed frequencies are assume to be 0, 1/T, 2/T,……….. up to ½ the sampling rate (Nyquist limit). So with a 128 year record (I just like powers of 2) the frequencies are 0, 1/128, 2/128,……….If the analyzed signal has frequency components between these values then the amplitude will “leak” into nearby allowed frequencies. For example, a signal with period 50 years would leak more or less equally to the frequencies 2/128=1/64 and 3/128. For the data I analyzed the leakage appeared to be very small.
> Hank Roberts suggested that AMO might look similar
Er, no. I suggested you might read up on AMO.
That wasn’t meant to suggest you’d find support in previous discussions, but rather that you’d find what others have been pointing out here. It’s been done.
The discussion of PAber’s contribution is one of the more disappointing I’ve read here. The contributor is hardly a newcomer, nor a serial trouble maker. S/he simply points out that if one least squares fits some time series to a linear combination of three unrelated (but correlated, to the main) series and a linear time function, one shouldn’t be surprised that, upon subtracting the contributions of the extra three, what’s left looks rather more linear. The Tamino I’m used to would already have demonstrated the generality of that with some synthetic data.
The question of data independence is disingenuous. Of course the four (or five) temperature series are independent in the sense that they were developed separately (although basically from just two raw data sets). But they’re surely not statistically independent*, which is obviously PAber’s meaning. They all attempt to measure much the same thing — lower troposphere temperature anomaly — though granted a couple at altitude and the rest at the surface. The fact that they come together somewhat when the “extraneous” three effects are subtracted is comforting, but hardly definitive.
G.
[* If the measurements were perfect, the series would be identical (at least within the two altitude groups) — that is they would be perfectly correlated, the opposite of statistically independent.]
GlennFergus,
First, what you say will be true only to the extent that the measurements reflect the physical quantity being measured. Real measurements have errors, both random and systematic, and in general, both the errors, and the strategies developed to correct for them will be indepencent. Global temperature is not a quantity we can measure by some simple means like sticking a giant thermometer up the tuckus of Mother Earth.
Second, the terrestrial and satellite measurements are completely different datasets with completely different sources of error. You would know this if you had been following the discussion of how the satellite temperature products respond to ENSO.
Third, you seem to have misunderstood the point of the debate and therefore the significance of F&R 2011. If you apply an incorrect model to several independent datasets, you would not expect it to improve agreement between those datasets unless that model is arbitrarily complex. The model used by F&R 2011 uses the simplest description of warming (and one with physical support, as well) plus 3 additional sources of noise that we know are operating in the climate today–about as simple a model as you can hope to come by to describe a global phenomenon. The fact that agreement is improved by application of such a simple model provides very strong evidence. What is more, when the model is applied, lo and behold, the trend becomes quite consistent with what we expect from our knowledge of CO2 forcing and feedback. It puts the lie to the “no warming in X years” argument. It shows that there is probably no additional affect that we can blame warming on–there is no second gunman.
In short, perhaps your disappointment stems more from your ignorance than from the argument itself.
The five-year mean global temperature has been flat for the last decade, which we interpret as a combination of natural variability and a slow down in the growth rate of net climate forcing. – James Hansen et al.
The internet is full of theories about the coming decades being dominated by a solar minimum and La Nina dominance and the cool side of various Pacific modes and the AMO.
All of which, it is implied, can nullify, stand it still, predicted greenhouse warming for decades.
It seems unlikely to me F&R can stave off the political effect of a prolonged standstill.
To a lay person like me if energy in is greater than energy out, something is getting warmer. The usual suspect is the oceans. And they belittle that as being trivial and inconsequential. If one goes to google scholar, the work on consequences of ocean warming is dominated by its effects on sea life. There doesn’t seem to be much there on the effects of ocean warming on ocean dynamics, which appear to have changing the direction of trends in the surface air temperature for a very long time. It would seem impossible to me that an earth system persistently gaining energy can have surface temperature remain flat for decades, but only scientists who are looking at ocean dynamics I can find are led by Tsonis and Swanson and they appear to be saying exactly that.
PAber (#133),
I’ve looked at the paper again, and perhaps you are correct that the residual form is assumed. I think this conclusion though is sound “…any deviations from an unchanging linear warming trend are explained by the influence of ENSO, volcanoes and solar variability.” Their effort is explanatory.
If you are interested in other risidual shapes, you could get the same number of degrees of freedom by modeling the residual as an arc with the radius of curvature as a variable. If you find a better fit with a short radius, that would be interesting.
JCH, F&R 2011 is just one grain of truth with which we can oppose the lies and stupidity of politicians and denialists. The thing is that it is not at all unusual to see “pauses” in the warming trend. I’ve counted 3 in 30 years. It sounds as if you could benefit from looking at the Skeptical Science escalator again.
Ultimately, you have to think about the dynamics of the greenhouse effect. The extra CO2 takes a bite out of the outgoing IR. That means that the temperature must rise until the area under the new chewed up blackbody curve equals energy in. We may approach that equilibrium quickly or slowly–it won’t affect the end result. Physics always wins out eventually.
Ray – Tsonis and Swanson do not show a regime shift at any other point in the escalator. They found a regime shift ~2000. They claim they have found a mechanism, and the say the period after the shift will last for decades and be characterized by a flat surface air temperature and deep ocean warming.
We have had a flattish surface air temperature and deep ocean warming.
I agree physics will win in the end. My question is, how long can a warming ocean provide enough cooling to significantly offset AGW?
JCH,
My problem with Tsonis and Swanson is that they are neglecting several factors in their analysis (albeit ones that would be difficult for them to anticipate). The current solar cycle is one of the wimpiest of the modern space era–the decrease in insolation has not been insignificant. They also suffer from the same malady that plagues the fun-with-fourier crowd–extrapolating from a very limited number of cycles.
As to the oceans,…well, the atmosphere is roughly equivalent to the top 10 meters of the ocean in terms of heat capacity–so if the atmosphere responds on a yearly timescale, the top 700 meters would have a timescale of decades. And if the ocean is involved down to 2000 meters, it could be a centuries. The thing is that the more long-term the response, the greater the sensitivity and the longer the effects of an increase in CO2. A long time constant isn’t necessarily a good thing long term.
The sequestration of CO2 also has a long time constant, so if the ocean heat sink lag was long enough to compensate for the CO2 sequestering time, the overall warming in the pipeline will get reduced.
But I also see your point as building up heat in the system isn’t necessarily a good thing.
137 Tamino said, “AMO is just temperature. So — global temperature is correlated with north Atlantic temperature. What a shocking result.”
So, if the AMO tracked perfectly with global temperature, then that would be evidence that the AMO doesn’t exist, but instead the area is dead average?
WebHubTelescope,
A short time constant also leads to a lower overall sensitivity–that was the key to Schwartz’s one-box model and to everything Lindzen has done for the past 20 years.
> if the AMO tracked perfectly with global temperature
Call it the AMOT:
“Atlantic” “Multidecadal” “Oscillation” in “Temperature”
If anything less than the globe perfectly tracked the global average,
think of the savings in time and equipment — put just one thermometer there!