As we did roughly a year ago (and as we will probably do every year around this time), we can add another data point to a set of reasonably standard model-data comparisons that have proven interesting over the years.
First, here is the update of the graph showing the annual mean anomalies from the IPCC AR4 models plotted against the surface temperature records from the HadCRUT3v, NCDC and GISTEMP products (it really doesn’t matter which). Everything has been baselined to 1980-1999 (as in the 2007 IPCC report) and the envelope in grey encloses 95% of the model runs.
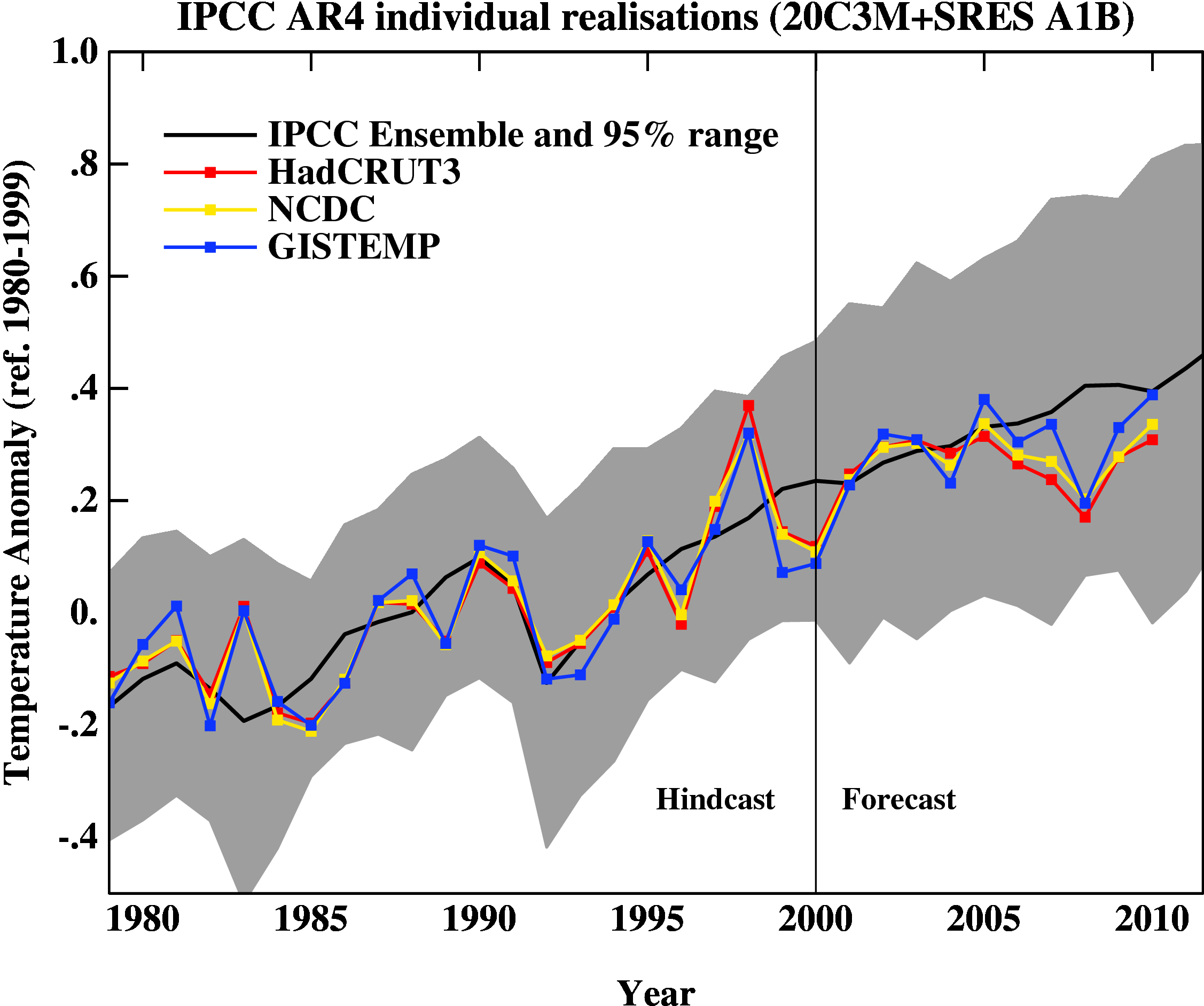
The El Niño event that started off 2010 definitely gave last year a boost, despite the emerging La Niña towards the end of the year. An almost-record summer melt in the Arctic was also important (and probably key in explaining the difference between GISTEMP and the others). Checking up on our predictions from last year, we forecast that 2010 would be warmer than 2009 (because of the ENSO phase last January). Consistent with that, I predict that 2011 will not be quite as warm as 2010, but it will still rank easily amongst the top ten warmest years of the historical record.
The comments on last year’s post (and responses) are worth reading before commenting on this post, and there are a number of points that shouldn’t need to be repeated again:
- Short term (15 years or less) trends in global temperature are not usefully predictable as a function of current forcings. This means you can’t use such short periods to ‘prove’ that global warming has or hasn’t stopped, or that we are really cooling despite this being the warmest decade in centuries.
- The AR4 model simulations are an ‘ensemble of opportunity’ and vary substantially among themselves with the forcings imposed, the magnitude of the internal variability and of course, the sensitivity. Thus while they do span a large range of possible situations, the average of these simulations is not ‘truth’.
- The model simulations use observed forcings up until 2000 (or 2003 in a couple of cases) and use a business-as-usual scenario subsequently (A1B). The models are not tuned to temperature trends pre-2000.
- Differences between the temperature anomaly products is related to: different selections of input data, different methods for assessing urban heating effects, and (most important) different methodologies for estimating temperatures in data-poor regions like the Arctic. GISTEMP assumes that the Arctic is warming as fast as the stations around the Arctic, while HadCRUT and NCDC assume the Arctic is warming as fast as the global mean. The former assumption is more in line with the sea ice results and independent measures from buoys and the reanalysis products.
There is one upcoming development that is worth flagging. Long in development, the new Hadley Centre analysis of sea surface temperatures (HadISST3) will soon become available. This will contain additional newly-digitised data, better corrections for artifacts in the record (such as highlighted by Thompson et al. 2007), and corrections to more recent parts of the record because of better calibrations of some SST measuring devices. Once it is published, the historical HadCRUT global temperature anomalies will also be updated. GISTEMP uses HadISST for the pre-satellite era, and so long-term trends may be affected there too (though not the more recent changes shown above).
The next figure is the comparison of the ocean heat content (OHC) changes in the models compared to the latest data from NODC. As before, I don’t have the post-2003 model output, but the comparison between the 3-monthly data (to the end of Sep) and annual data versus the model output is still useful.
To include the data from the Lyman et al (2010) paper, I am baselining all curves to the period 1975-1989, and using the 1993-2003 period to match the observational data sources a little more consistently. I have linearly extended the ensemble mean model values for the post 2003 period (using a regression from 1993-2002) to get a rough sense of where those runs might have gone.
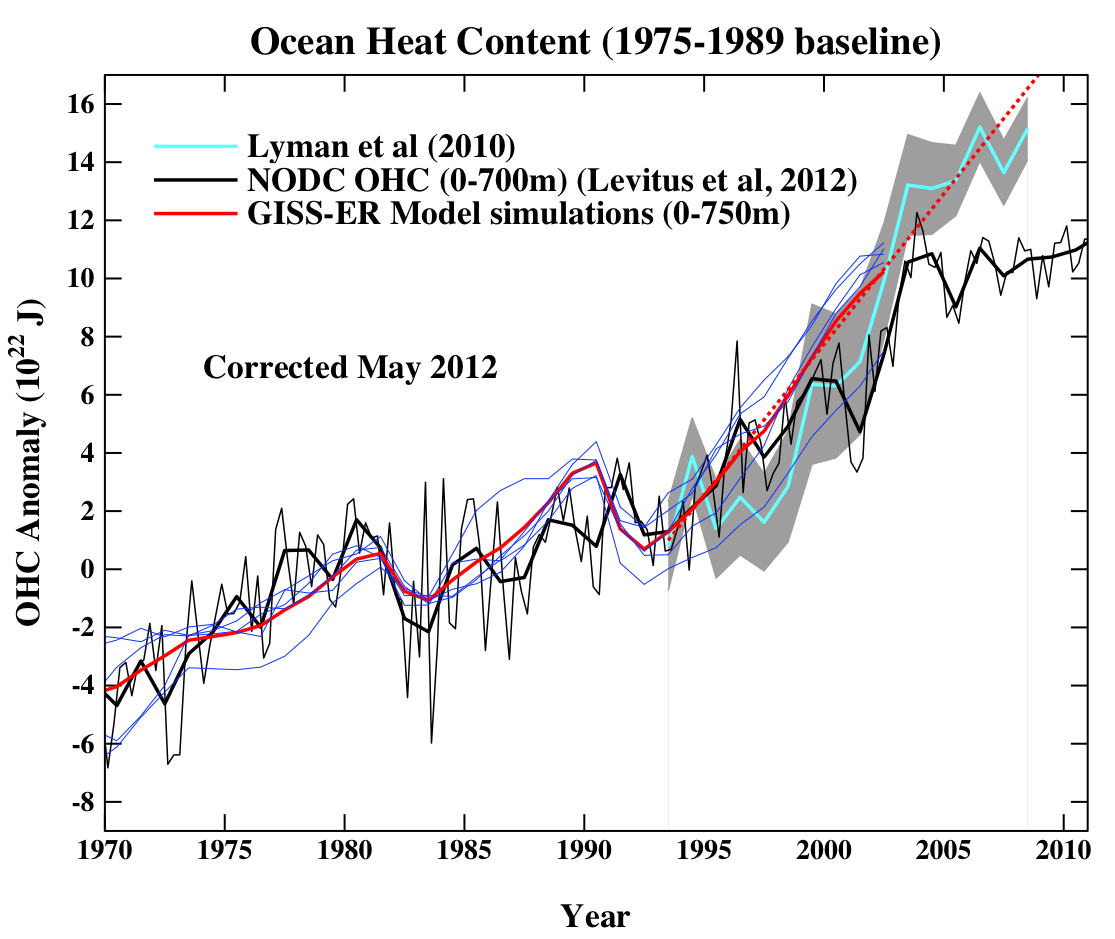
Update (May 2010): The figure has been corrected for an error in the model data scaling. The original image can still be seen here.
As can be seen the long term trends in the models match those in the data, but the short-term fluctuations are both noisy and imprecise.
Looking now to the Arctic, here’s a 2010 update (courtesy of Marika Holland) showing the ongoing decrease in September sea ice extent compared to a selection of the AR4 models, again using the A1B scenario (following Stroeve et al, 2007):
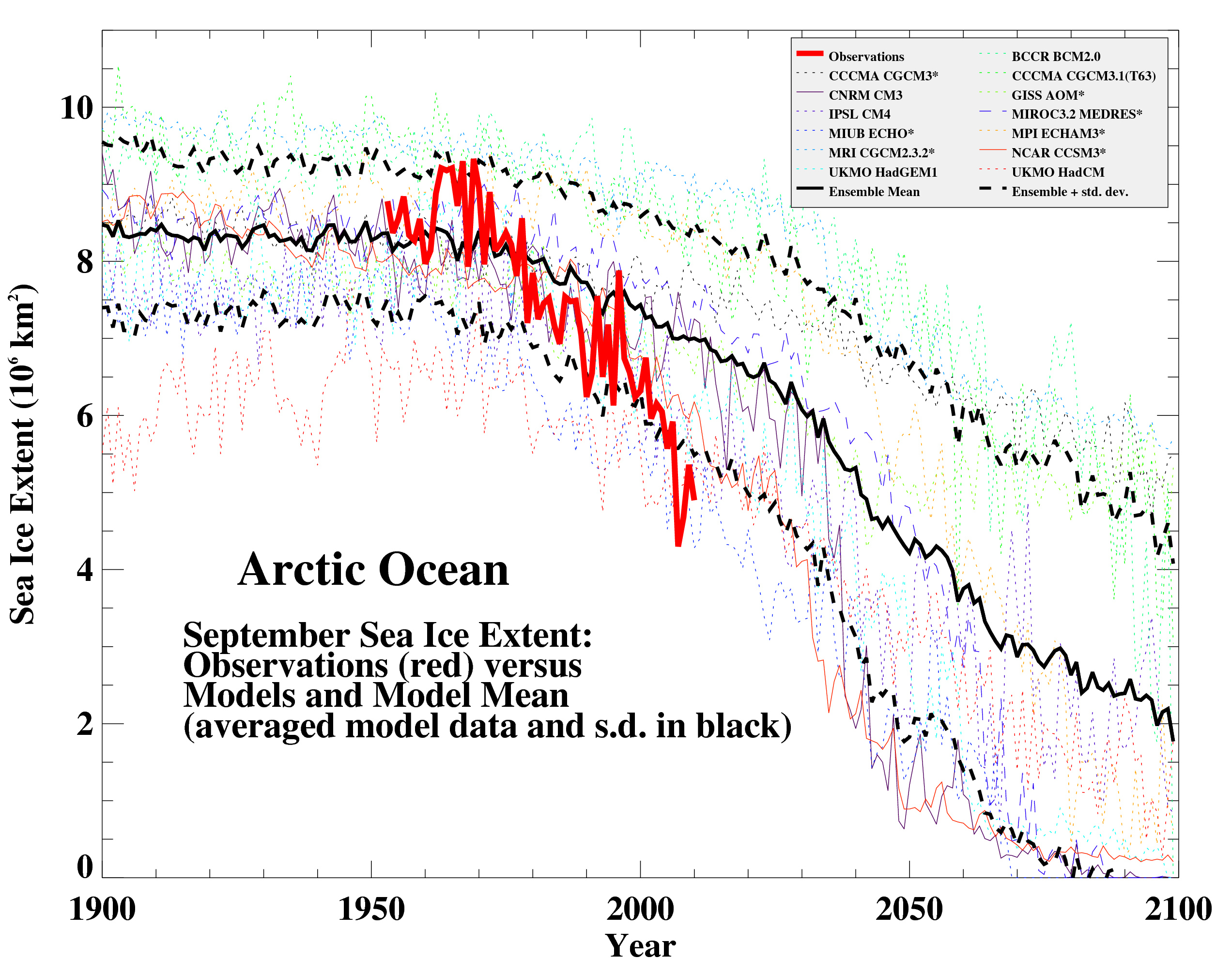
In this case, the match is not very good, and possibly getting worse, but unfortunately it appears that the models are not sensitive enough.
Finally, we update the Hansen et al (1988) comparisons. As stated last year, the Scenario B in that paper is running a little high compared with the actual forcings growth (by about 10%) (and high compared to A1B), and the old GISS model had a climate sensitivity that was a little higher (4.2ºC for a doubling of CO2) than the best estimate (~3ºC).
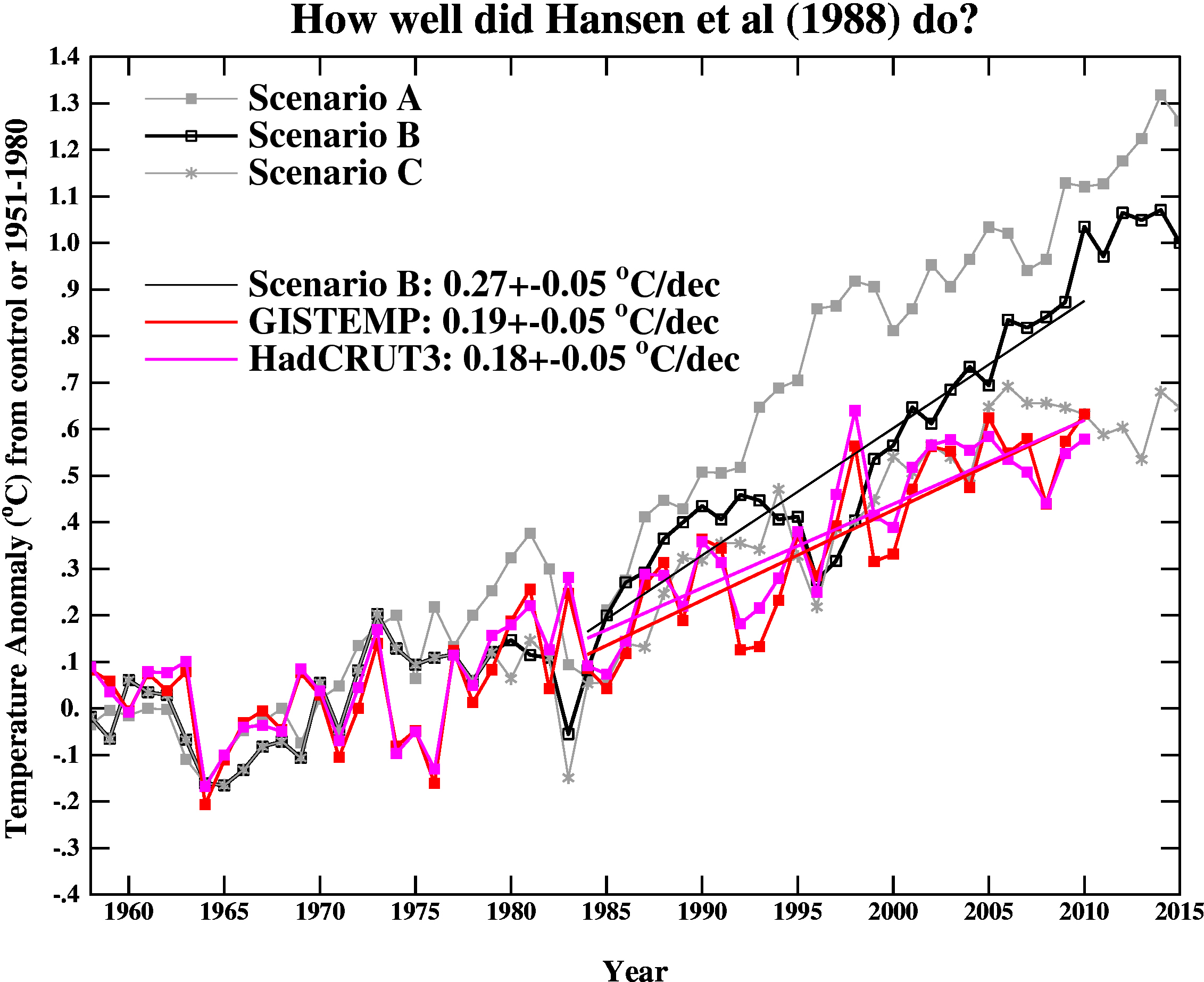
The trends for the period 1984 to 2010 (the 1984 date chosen because that is when these projections started), scenario B has a trend of 0.27+/-0.05ºC/dec (95% uncertainties, no correction for auto-correlation). For the GISTEMP and HadCRUT3, the trends are 0.19+/-0.05 and 0.18+/-0.04ºC/dec (note that the GISTEMP met-station index has 0.23+/-0.06ºC/dec and has 2010 as a clear record high).
As before, it seems that the Hansen et al ‘B’ projection is likely running a little warm compared to the real world. Repeating the calculation from last year, assuming (again, a little recklessly) that the 27 yr trend scales linearly with the sensitivity and the forcing, we could use this mismatch to estimate a sensitivity for the real world. That would give us 4.2/(0.27*0.9) * 0.19=~ 3.3 ºC. And again, it’s interesting to note that the best estimate sensitivity deduced from this projection, is very close to what we think in any case. For reference, the trends in the AR4 models for the same period have a range 0.21+/-0.16 ºC/dec (95%).
So to conclude, global warming continues. Did you really think it wouldn’t?
LOL!
Didactylos, ccpo
“Clean coal” is not a term I invented. It is an oxymoron that is intended to describe coal processes that are cleaner than other options. Greenhouse effect is not very descriptive either, but that is what we work with still describing the gases that regulate global temperature.
Economically, there would be a very low probability that coal will not be used in the future and the best option is that its use be as “clean” as possible. I did not “exclude” any technology in the search for sustainability. I just gave “my” opinion of a logical start in the quest for sustainability.
The tree hugging reference is an example of how not working within the system produces results that go counter to the intent. Rent a huggers, people hired to chain themselves to trees in the Pacific Northwest, were pretty effective in driving some logging companies into other businesses like real estate development. Converting forest into subdivisions was not the desired result. Had the huggers worked with other groups like Ducks Unlimited and other hunting groups for example, more land would have been preserved as natural forest.
Perhaps you two have a less divisive game plan that is better?
> Rent a huggers, people hired …
Got any evidence for this claim? Paying someone to break the law is illegal. You’re accusing someone. Evidence?
captdallas2:
My biggest objection to your compromise is that coal is only cheap because of massive subsidies and failure to count the human and environmental cost. Once regulators pull the rug out from coal, the economic landscape should be very different.
And that’s just taking into account the direct damage from coal. If CO2 is also given a cost, then coal will stay buried.
As for your random shots at “huggers” – environmentalists are not a homogeneous group, and there are plenty of nuts that saner people could do without.
If you want to continue discussing coal, you should probably head over to the open thread.
Coal is still in terms of BTU’s the most efficient energy source per kilogram of anything that we have used or can currently use as an energy source. This is very easy to confirm too. If we need to lower emissions, then yes do two things already recommended: have corporations invest more money into capturing methods and burn coal more efficiently as well. Keep in mind coal is so important to the economy of several states as well.
Captdallas, as soon as someone comes up with a viable “clean coal” strategy that doesn’t negate the cheapness of coal and that doesn’t dump CO2 into the atmosphere, I’ll think about coal. However, having lived in Appalachia, I do not count myself a big fan of what big coal does to:
1)the environment
2)the miners
3)the political process
Coal ain’t pretty.
And even with coal, I think it is a given that standards of living will suffer. Cheap energy is a thing of the past.
Hank Roberts,
This has moved off topic. The classified ads in Portland, Oregon had a few listing for people looking for rent-a-huggers when I was there in the early 90’s. Thought that was common knowledge.
dallas
Ray Ladbury wrote: “Cheap energy is a thing of the past.”
I would say that cheap energy is a thing of the future — once the mass production of inexpensive, high-efficiency photovoltaic materials scales up.
I would say that cheap energy is NOT a thing of the past — the “cheapness” of fossil fuels was an illusion. They were never “cheap”, they only appeared to be cheap because their full costs were hidden.
Ray Ladbury wrote: “And even with coal, I think it is a given that standards of living will suffer. Cheap energy is a thing of the past.”
And even if energy is more expensive in the future, it does not follow that “standards of living will suffer” — if we stop wasting three quarters of the energy we use:
Maximally efficient use of abundant solar energy means that most of humanity’s “standard of living” will improve, not “suffer”, from phasing out fossil fuels.
Ray Ladbury @300 — But glass does not expand more than mercury.
Seeriously now, Annan & Hargreaves write … the lower bound of 0 [degrees Celcius] on the prior is uncontentious: a negative value of sensitivity implies an unstable slimate system … This is the exact opposite for your earlier argument that it implies stabiliity. If there is no agreement now when we know so much about Terra’s climate, surely there would have been none in 1959, so allow some very small subjective probability that it is actually negative for reasons unknown then. [I hasten to add we know have an abundance of evidence that S is not only positive but most likely close to 3 K.]
As for stealing from the upper tail, not necessarily. The smallest of the five calculations gave S=1.6 K. So keep the pdf quite small up to, say, 1.5 K. This steals from the interval [0,1.5) to be distributed over the negative reals, at least up to some rediculously large absolute value.
Complex S? The sensitivity s to be the temperature response to 2xCO2 and nobody has yet suggested complex temperatures. Physics does set some limitations, especially in matters thermodynamical.
If I were attempting to physical justify the possibility of negative S I would have some difficulty coming up, a priori, with some reasons. In 1959 I would simply point out the known glacial cycling and that the correlation of Crowl-Milankovitch cycles was known, it remained in the to-be-demonstrated category.
Also, the determined pdf for S is only to apply over perhaps two doublings as there remain, even today, various unknowns which (probably) apply at high temperatures. As for low ones, Carl Hauser reminded me that if it is cold enough the CO2 snows out, a definite nonlinearity.
David, Actually, if you take the classical definition o senstitivity, Annan and Hargreaves are correct–as it is proportional to 1/(1-f). A negative sensitivity would require f greater than 1–that is more feedback than an infinitely sensitive system. I know that won’t work! I was trying to give you the benefit of the doubt and think how you might trigger a negative response with a positive input.
Regardless of how you look at it, though, a negative sensitivity is unphysical. And CO2 raining out is a positive feedback–as would be vaporization of CO2 with an injection of heat. I can think of lots of ways of gettint a sensitivity greater than zero–just none less than.
And as to swapping around probability–it is certainly desirable that the PDF be smooth. I just don’t see what is gained by entertaining negative sensitivity values that we know will be ruled out by the first likelihood we look at. If all you want is a thick-tailed function, how about a Pareto? Granted, it won’t take you all the way down to zero, but arbitrarily close.
Now a philosophical question. Let’s say that your choice of prior reduces the tail to the point where we can neglect sensitivities greater than 5. Would you trust it enough to base mitigation efforts on it? Are you 100% convinced that the probability of S greater than 5 is negligible?
Somebody back a ways was looking for recent ocean heat content data:
http://www.noaanews.noaa.gov/stories2010/20100920_oceanwarming.html
(hat tip to JCH posting at Tamino’s AMO thread for that)
And there it is:
http://journals.ametsoc.org/doi/abs/10.1175/2010JCLI3682.1
Forgive me if you’ve already answered this, but could the oceans’ absorption of more meltwater than projected (which I presume would tend to cool the upper 700 m, on average) offset some amount of heat absorption from the atmospher and thus contribute to the stasis of measured ocean heat content over the past five years?
DCBob, It’s negligible.
> DCBob … stasis
Citation needed for “stasis” — where did you get that?
Do you know how many data points you need to say whether there’s a trend, for these data sets? Short time spans are wiggles; those don’t tell you anything useful.
I found this:
http://www.skepticalscience.com/images/robust_ohc_trenberth.gif
here: http://www.skepticalscience.com/news.php?p=2&t=78&&n=202
Your source?
Hank, Ray and DCBob: thermodynamic processes consist of two cycles: cooling through refrigeration and energy transfer through heating. DCBob, yes there are contradictory data currently in peer review: some state that the oceans are in stasis, some show warming and some show cooling. The ARGOS floats had some calibration issues on, as best as I can recall more than one occasion. SkepticalScience did a write up on it, I believe it was last year (but could have been 2009) but at any rate, thermodynamics, predicts that there will be times of ocean warming, cooling and stasis, anyways, regardless of where we may, find ourselves now, in terms of ocean temperature changes. Whether natural or artificial, thermodynamic cycles consist of refrigeration and heating processes. Oceans have very high heat capacity and specific heat due to the properties of water and the large amount of water on this planet. SkepticalScience also did a write up on the second law of thermodynamics on October 22, 2010, as well, but it could have been far more in depth, then we could see how oceans are affected by the processes described by immutable laws. All of climate, all of weather, all heating, cooling and temp changes obey the laws of thermodynamics, but it seems, to me, that few in the general public understand what that truly means. I think high school classes should be offered dedicated to the physics of heat flow, a transfer of thermal energy due to temp differences, and temperature, a statistical average of a field, of kinetic motion of molecules. In other words in physics we say temperature is a field, in physical chemistry we tend to add that the averaging of motions leads to a statistical average we call temperature. You can have more heat, say in a larger mass object, but have the same exact heat as a less mass object. Heat does not equal temperature necessarily, but it can lead to a change in temperature.Then of course heat can be used to perform work, and we have latent heat and of course we can apply energy/ perform work, and generate heat loss.
Hank, regarding short time spans, that is oftentimes true, but, not a universal truth. If a Tsunami kills 300,000 people and causes 3 billion dollars in damage, and it is the first of it’s kind in 300 years or more, well, it may indicate a change. Not that we can just attribute that activity to global anything (warming, cooling or stasis) but it would certainly lead to some: speculation, questioning, intuitions, more hypothesis formation, research, testing, potential funding, and some sort of results. Not to mention funding for humanitarian efforts, engineering/construction projects, and so forth. If a few more of similar magnitude and location hit, then we may have a weather trend, and if it is very unusual for the climate, that could lead to further climate research. If the oceans are in stasis, and I do not know that they are, but if they are, for 5 years or a little more, then that is a very significant and telling sign, something is different than previously believed. What that something is, I do not know, but that may mean any number of things: not enough ARGO floats, changing chaotic weather patterns, a conflict in how the data is analyzed and summarized, not enough past decade, measurements to compare with current ones, or any number of human factors.
Correction: meant to say and have the exact same temperature, not same exact heat.
David and Ray, the problem with using any prior is that the robustness of that prior, and its utility in any projection, is to say the least, highly subjective. Any tail we look at: left, right, two tailed, must be analyzed individually, however, and we must make sure we limit our uncertainty only to a point that uses as much data first, prior to statistically analyzing any uncertainty. The basic principles of statistics do work, but just one factor can turn it on its head, like, say a loaded dice, a weighted coin or a far more noisy climate, or complex weather system. This is nothing new, but very basic/fundamental, but I cannot tell you how many times, very smart people, working with statistics/mathematics forget simple, indeispensable data, or principles, including myself in the past.
Oh and I realize that as a rule, in Baysian statistics, we look at past data, at first exclude current or new data and then include it after a statistical analysis, but even so, data analysis is of extreme importance, both past, and present. In medicine if clinical data with good results contradict a Baysian analysis the Baysian analysis is dismissed in that setting and new research must be set up to see what went wrong. For example, some findings in the journal of hypertension, where iatrogenic high BP’s were wrongly linke, not to total probability of developing morbidity/mortality risk factors, but to the bottom line results, by a huge margin.
Those who are interested in OHC should read the Willis-Trenberth-Pileke email exchanges. If nothing else, it will help pass the time until the next OHC paper is completed! Among other things, they discuss the deep-ocean paper to which Hank linked, and they discuss von Schuckmann et al. They’re interesting exchanges. Trenberth refers to an “embargoed” paper – Lyman 10? RC has an update on it here.
For what it is worth, Bob Tisdale claims the ARGO data is now showing warming in the upper 700 meters.
Also, on the Trenberth graph to which Hank linked: the article.
JCH # 321, thanks for the link to the email exchange. I have a problem believing there is missing heat at all. Your thoughts?
Skimming through this incredibly long discussion since – just the 21st of January? – it struck me that Dr. James Hansen’s “Storms of my Grandchildren” really helped to clarify the bigger picture for me. It answered the question of “why 350?” very well and worked to isolate the important from the less so. Instead of getting deeper in the proverbial reeds, my recommendation is to read Dr. Hansen’s recent works (the “Paleoclimate Implications for Human-Made Climate Change” known as the “Milankovic” draft freely available on Hansen’s web site was also very helpful to me as a layperson, http://www.columbia.edu/~jeh1/mailings/2011/20110118_MilankovicPaper.pdf).
Apologies to Dr. Hansen and moderators for unavoidably creating a bald commercial recommendation, but the information it contains would really stand people here on a useful footing. I love RealClimate, wish I had time to really absorb it all. I’ve also purchased Gavin’s beautiful book, “Climate Change: Picturing the Science”, which is absolutely next on my reading list.
Ray Ladbury @310 — Tol & deVos
http://www.springerlink.com/content/x324801281540j8u/
in effect consult 5 experts, 3 from the IPCC SAR group. We chose three of them here and fit a Gumbel prior to the experts’ expectation and standard deviation as most experts point at a right skewed prior, and do not want to exclude greenhouse gas induced global cooling.
The evidence is then entered to form the posterior, one expert at a time and the resulting pdf shifts probability from negative S to the right tail (roughly speaking). As a compleat Bayesian, I object the the empirical Bayesian last step of combining the experts via a weight depending upon Bayes factors for each expert. It looks to be a double use of the evidence to me.
Instead I suggest weighting the 5 values you looked up (thank you again) by how long before 1959 the analysis was done. So ranking from highest weight to lowest, I thiink we have 3.3, 4, 2, 1.6, 5.5. The exact weights have yet to be chosen but I’m sure there is a fairly objective means to do so. The combined prior is then modified by the evidence and the resulting posterior will look about like the posterior in Figure 5 of Tol & deVos; no support for values less than 0, skewed right but not heavy tailed the way starting from a uniform distribution is.
Thanks for participating in quite an interesting (and for me, at least, useful) exchange. Unless you see some unresolved issues, I think we have a sufficiently decent closure.
Jacob Mack @319 — In Bayesian reasoning, one begins with a prior probability, often called subjective to distinguish these from a frequentist approach. However, these prior probabilites can be informed by existing knonwledge, not merely guesses. The choice of
http://www.merriam-webster.com/dictionary/subjective
for Bayesian priors is perhaps unfortunate.
Jacob Mack, Have you read E. T. Jaynes “Probability Theory: The Logic of Science”? It is the probability text he never quite managed to finish in his lifetime, finally published by Oxford University Press. It is truly a gem of a book, and it does an excellent job outlining how to minimize subjectivity in a Bayesian analysis. He has an excellent treatment of Maximum Entropy and minimally informative Priors, and there is at least one priceless nugget of wisdom in each chapter. Check it out if you haven’t.
David,
The values I quoted are all most probable values. Each of those values is the mode of a probability distribution (or likelihood) for S. Will the distribution of modes reflect the uncertainty in S? I don’t think so. The modes wind up pretty close to 3, and the distribution of all 62 modes is roughly Weibull (s=2) but with a somewhat longer positive tail. That is quite a bit different than the sensitivity distributions, which tend to be heavily skewed right. I would contend that the rightward skew is telling us something–that it is easier to make a climate look like Earth with a high S value than a low S value. Should not our Prior reflect that? And if it does not, we have changed the results by our choice of Prior–certainly not in the spirit of minimally informative priors.
I agree that a Gumbel might work, but you get very different values depending on the shape paremeter you choose. A lognormal could also work, and since we are talking ultimately about a feedback, would it not better reflect the physics?
Jacob Mack at 322 JCH # 321, … I have a problem believing there is missing heat at all. Your thoughts?
I think they will find more heat in the deep ocean than both Willis and Pielke seem to think is there during their email exchanges (Willis may have other thoughts now,) but perhaps less than Trenberth is hoping/expects.
Gavin,
This seems like a really rich set of information, now that the record is approaching climate timescales. Is there a way to figure out how much of the difference is due to predicted vs actual forcing, and how much due to a difference between the model and actual response (i.e., sensitivity?). This might be what you are doing in the penultimate paragraph, but if so it was a little too concise for me to follow. Seems like an obvious question to address, so I am thinking someone has done it?
David 325, yes. I am sorry if I was unclear. I realize that it is not just guesswork. I work with Bayesian all the time. When doctors or psychologists use the prior and include newer data, and construct a tree, it is not as if it is useless.I do know though that professional experience and empirical results can at times trump Bayesian predictions based upon constructed trends in any field. I see it happen enough myself, in my work.
Ray 326, I own many books that outline such approaches, but being I have not read that book, I will read it first.
JCH 328: that seems reasonable.
Ray Ladbury @327 — According to Tol & deVos, the orginal Arrhenius estimate of 5.5 K including no information about standard deviation, so they rather celerly did it for Arrhenius.
Following something similar to their procedure for the five estimates available before 1959 leads so something similar in shape to their Figure 5; skewed right but not heavy tailed.
Annan & Hargreaves clearly so that the heavy tail is an artifact of started with a uniform distribution. Starting with the procurude outlined over these several comments, quite similar to the work of Tol & deVos, leads to a more sensible distribution once outdated by the evidence. The entire approach satisfies my sense of what a compleat Bayesian requires (subject to the change in the Tol & deVos procedure) I already mentioned.
Unlike some, for determining a prior distribution I’m perfectly prepared to take a hand drawn estimate; it need not necessarily be drawn from any of the usual (or unusal) families of distributions. After all, to determine the posterior a computation is required.
Since in 1959 little of the physics was understood one has to be quite conservative about allowing what, at first approximation, appear to be outlandish or even physically impossible values; the evidence will resolve the matter provided the total range of the evidence has support in the prior.
David, one could just as easily say that the lack of a heavy tail in the analysis of A&H is due to their choice of Prior. Indeed, since all of the likelihoods (e.g. data) point to a heavy tail, that is precisely why I am a bit leary of forcing it to vanish.
And it is certainly not a valid statement to state that one must be conservative about allowing outlandish values on the negative side when one is using a Prior that makes them go to zero on the positive side!
One of the reasons why I am being very conservative about this issue is that the appropriate risk mitigation approaches are quite different for a sensitivity of 3 and a sensitivity of 8 or even 6. Indeed, I think that is the motivation behind using a Prior that makes the high end vanish! However, if we are wrong, then our mitigation will be totally ineffective.
Do I think sensitivity is 8. No. I think it’s much more likely to be around 3. However, unless we have good physical reasons for the choices we make for our prior, I don’t see how we can do a truly valid Bayesian analysis. As to negative senstitivities, I’m quite satisfied to toss them. They would require fedbacks greater than 1, and if S is negative, our understanding of climate is so screwed we need to start from scratch to begin with.
Ray Ladbury @332 — A compleat Bayesian does not know anything about the evidence (i.e., data) when forming a prior probability distribution. If updating by the evidence produces a heavy tail, so be it, but if heavy tail arises solely by starting from a uniform prior we haven’t done our job as (Bayesian) scientists. That is Annan & Hargreaves point as I take it.
To repeat, a compleat Bayesian isn’t willing to have any unsupported interval without absoutely compeling reasons. Even as late as IPCC SAR some of the experts were not willing to exclude some negative values, so certainly not in 1959.
In 1959 we presumably have 5 “most likely” values from four authors. That’s enough to follow a procedure quite close to that of Tol & DeVos; the resulting prior allows some quite small probability assigned to the negative real line. Now apply all the evidence. The result will look rather similar to that in both Tol & deVos and also in Annan % Hargraves (althugh for both papers, there are still other sources of evidence which should be included, I think).
Now we have a rationally constructed posterior. It has no support for negative S and might, as you state, look similar to a Weibull distribution with shape parameter ~2 and suppose the mode is ~2.8 K. As Bayesian scientists we have done the best we can and hand that over to the risk analysis experts (which certainly does not include me).
We haven’t let economics or risk analysis or anything else such as politics influence our analysis resulting in the determined posterior. We might, however, vary the determination of the prior in various sensible ways (uniform is not one, varying between Gumbel, translated lognormal, normal and Cauchy is) to report some forms of sensitivity; ideally this should be low because the evidence predominates now in 2011.
This exercise determines S, the so-called Charney climate sensitivity. However, looking at longer time scales, a study of the Pliocene suggest ESS is ~5.5 K for 2xCO2. Looking at shorter time scales, we have the transient response for the next century, ~2/3rds of S from AOGCMs.
But whatever, the climate response to the forcings to date has already upped the temperature by ~0.6 K over some sense of normal and that alone is enough to cause serious economic harm to:
Europe in 2003
Russia, Ukraine and Kazakstan in 2010
Southeast Asia in 2010–2011
Queensland in 2011
with various predictions that it will become seriously worse over the next 50 years.
That ought to be enough for risk analysis and policy formation.
David,
The problem with “letting the data tell us whether we have a thick tail is that: 1)we are not at a point where we would be data dominated–especially in the tails; 2)the data may already be telling us that there is a thick tail.
Again, we can by choosing different Priors reach very different conclusions about what sort of mitigation is needed.
Also, we cannot necessarily treat all estimates as imposing equal constraints on the overall distribution. An analysis that produces a very broad probability distribution for sensitivity will not impose as strong a constraint as a sharply peaked distribution. So we need somehow to take the entire probability distribution into account–not just the best-fit values. One way to do this would be to fit both means (or modes or medians) to a distribution and fit widths to another distribution. I’ve been working on something like this for my day job. I wonder if it might work in this application.
One last thought: Given that our result seems to depend critically on the choice of Prior, might we not instead average over the Priors? It might yield a better result.
Ray Ladbury @334 — As I understand it, a compleat Bayesian confronted with several models uses the weighted predictions from the various models; the weighting is somehow related to the Bayes factor. I don’t see that as the same as taking a weighted average over various priors, but I could be persuaded otherwise.
I don’t see the criticality provided one begins with a handful of values from experts; any rational treatment will probably give about the same resulting prior. That prior will lead to something similar to a Weibull distribution, which is not heavy or fat tailed.
What does give a fat tail is using the uniform distribution as a prior. That choice does not appear rational to me, to Carl Hauser, nor, I take it, Annan & Hargreaves; indeed I believe you stated that it has problems.
For those experts not offering advice on the standard deviation of their estimate, somehow the widths have to be estimated. Tol & deVos offers one rational procedure but others could be tried.
David, I believe you could also use a broad lognormal as a Prior and still get a thick tail outto at least 8 or so–or a Pareto.
Model averaging can be done over Priors or Posteriors. One way to do it would be to start with a Prior that is a superposition of simpler Priors: A uniform + a Cauchy + a Lognormal…with each weighted uniformly to begin with, but with weights changing with data. In effect, you start with a uniform Prior over models.
If we are to choose a Prior, that choice must be based on our knowledge of the system we are modeling. It makes no sense to say we know enough to eliminate a uniform Prior while at the same time allowing negative sensitivities, which are in my opinion unphysical for the current understanding of climate (even in 1959).
This still leaves the problem of how to model the entropy (if you will) of each sensitivity estimate. Without that, we wind up giving each estimate equal weight, and we know that is not right. One way we could approach this is essentially by modeling moments separately. The advantage here is that we could use the method of moments to get a best fit for any distribution form and so look at model dependence. Alternatively, we need a way to factor in the full distribution, since, for purposes of risk mitigation, we are interested not just in the mode but also 90 or even 99% WC estimates of sensitivity.
The Cauchy distribution is a fine way to go. I think weighting has to be very well explained in terms of how, why and when. Of course as virtually any statistics book or paper states: “one should always have full access to all raw data, in any field. The reasons given of course are: to replicate findings as many times as possible/needed in a time span, look for any unintentional errors, biases or oversights, and control for the occasional dishonesty, as can happen in any field. The applications of Cauchy are truly incredible in risk assessment and various areas within physics.
Some books to consider, the ones I have actually read, referenced, reviewed, and in many cases applied to my work:
Schaum’s Easy Outline : Probability and Statistics
Spiegel, Murray Schiller, John Srinivasan, Alu
McGraw-Hill Professional Publishing
02/2002.
Information Theory and the Central Limit Theorem
Johnson, Oliver
Imperial College Press
07/2004
Nonlinear Signal Processing : A Statistical Approach
Arce, Gonzalo R.
John Wiley & Sons, Incorporated
2005
Statistical Inference in Science
Sprott, Duncan A. Bickel, Peter J. Diggle, P.
Springer-Verlag New York, Incorporated
06/2000
Mathematical Statistics
Shao, Jun
Springer-Verlag New York, Incorporated
03/1999
Data Analysis : A Bayesian Tutorial
Sivia, D. S. Skilling, John
Oxford University Press
06/2006
Statistical Analysis of Stochastic Processes in Time
Lindsey, J. K. Gill, R. Ripley, B. D.
Cambridge University Press
08/2004
Statistical Problems in Particle Physics, Astrophysics and Cosmology :
Proceedings of PHYSTAT05
Lyons, Louis Ünel, Müge Karagöz
Imperial College Press
2006
Theory of Multivariate Statistics
Brenner, David Fienberg, S. Casella, G.
Springer-Verlag New York, Incorporated
08/1999
Levy Processes and Stochastic Calculus
Applebaum, David Bollobas, B. Fulton, W.
Cambridge University Press
07/2004
Calculus Single Variables
Hughes-Hallet, Gleason and McCallum et al. 4th edition. Wiley.
2005.
However, in statistics and probability one can never really rule out low ends, like in a similar fashion, one can, never really rule out high ends. Thus, mathematically or statistically speaking a 1.5 degree increase from doubling C02 could be possible, and conversely, a 7 degree increase is possible. A wide range of values in a CI could land within a C.R. and have some assigned probability, or they could land in the N.C.R. and still be possible though the N.H. is rejected. The reason why I accept a possible low end temp increase with doubling and reject a high one is due to the actual laws of physics, and nothing more. Thermodynamics does not allow for 2 things: knowing with great certainty where all the heat and refrigeration processes lead to and the predicted cooling/stasis effects that reduces the potential for such high warming. Three things should be the focus when using statistics of any sort and whatever data we do have:
(1.) Apply and use thermodynamics as an interpretive tool.
(2.) Reduce uncertainty with more solid data points.
(3.) Analyze raw data in a wider scope with mathematical/statistical methods.
3 degrees maybe correct. I am not convinced that the clustering shown is going to happen. I cannot see how we can get much more warming with all of the cooling processes witnessed in nature.
Ray Ladbury @336 — From Annan & Hargreaves we known that even a Cauchy prior does not result in a heavy tailed posterior, so it seems unlikely that result would change with a lognormal prior, rationally chosen.
In 1958 we would have the 5 modes you found. That is enough to apply the method in Tol & deVos [where I remind you that even for IPCC SAR at least two of the experts assigned nonzero likelihood to negative S, unphysical or no.] In that method the 5 prior estimates of S are weighted by their Bayes factors to obtain the reported posterior, which clearly is not heavy tailed.
I don’t see any remaining difficulties. The ‘old fashioned’ use of a uniform prior is replaced by the estimates of 5 experts and combined in what I now begin to understand is the compleat Bayesian method employed in Tol & deVos. Thank you.
Jacob Mack @337 — Where any of the 5 experts fail to provide any guidance as to their own estimate of standard deviation, or better, width, Tol & deVos have a senisble way to assign a normal distribution. That same method could be applied to assigning a Cauchy distribution. That certainly appears to be more conservative.
David, A cauchy has the wrong characteristics–for one thing it is symmetric. For another, it supports negative values for S, which is unphysical. I don’t see why you are resistant to a broad Lognormal, for instance.
We also need more than just the best estimates to update whatever Prior or Priors we use.
And finally, again, are you comfortable banking the fate of civilization on a choice of Prior? I think that when the data are not precluding an outcome, it is risky to rely on a Prior to do so.
David B Benson 339. Indeed that method does seem reasonable. I just wonder where the state will be in, when we arrive at doubling.I suspect in the low to mid range.
Ray Ladbury @340 — I meant, of course, translated Cauchy and normal distributions so that the mode agrees with the value of S determined by the expert. Annan & Hargreaves truncated their Cauchy to have support only in the interval [0,100]. Considering the way Bayesian updating is done, I doubt this makes much difference.
I have already explained several times now the two reasons for including negative numbers in the prior for S.
I don’t know what a broad lognormal is, but a lognormal with the same mode is likely to give much the same posterior, although some experimentation or further analysis would be required to decide the matter.
Ideally there is enough evidence that the choice of prior matters little. I opine that any of the various choices we have considered will give much the same result. It is only the extraordinary nature of the uniform distribution (and close relatives) which gives a heavy tailed posterior distribution, as Annan & Hargraves demonstrate.
Civilization is at risk from the ongoing transient response. Its hard enough to persuade decision makers about that over the next 89 years; I fear you’ll run up against the discount rate when attempting to discuss 189 years.
Jacob Mack @341 — Hopefully it is still if, not when, the concentration reaches 550 ppmv. At that point there will continue to be a transient response as actually reaching the equilibrium requires a millennium or so. In any case, the most likely value for S is close to 3 K for 2xCO2.
Jacob #338,
With all your stats references and discussion on this thread, I thought you were building up to something more rigorous than an argument from incredulity (”I am not convinced … I cannot see how…”) based on vague hand-waving about “cooling processes”.
David, do you think that a flat Prior from 0 to 20 would have been an unreasonable choice in 1959? After all, estimates over the next decade or so ranged from 0.1 to 9.6. If not, then perhaps a model-averaged approach would be the best approach. Now as to determining weights, we could take several approaches. One would be to use AIC weights a la Anderson and Burnham (note: if we are going to use a translated Cauchy, that’s another parameter). We could start with Uniform weighting of the Priors and let the data decide which ones have the most support. I would feel more comfortable with this than with selecting a Prior that determines the outcome.
We still have the issue of how well each estimate constrains the distribution and of independence–some of the estimates rely on the same data more or less. When this happens, do we: 1)Average the results, 2)Take the “best”, 3)Take the most recent, or 4)something horribly complicated?
CM 343, I am not done yet:)But then again, the cooling processes are well established. The references just present a background to the discussion. The real answers and evidence of how much we cannot know comes from thermodynamics the first and second law, anyways. Go see the longer posts on the previous page too. No hand waving here.
David B Bension I agree in terms of transient responses, in terms of weather variations, but how equlibrium is treated, I am not so confident in.
Jacob Mack @346 — In the 1979 NRC report on CO2 & Climate
http://books.nap.edu/openbook.php?record_id=12181&page=R1
we find what is now called the Charney equilibrium sensitivity, writen S. It includes only the so-called fast feedbacks. Attempting to take all feedbacks into account produces what is called Earth System Sensitvity, ESS, as in
Earth system sensitivity inferred from Pliocene modelling and data
Daniel J. Lunt, Alan M. Haywood, Gavin A. Schmidt, Ulrich Salzmann, Paul J. Valdes & Harry J. Dowsett
Nature Geoscience 3, 60 – 64 (2010)
http://www.nature.com/ngeo/journal/v3/n1/full/ngeo706.html
Equilibriation time from AOGCMs suggests a millennium and a bit more for S. For ESS takes longer, maybe two or three millennia.
Ray Ladbury @334 — A uniform prior is and always was a cop-out. The method used in Tol & doVos appears to me to be exactly what a compleat Bayesian uses, although I would make two changes: Gumbel to something similar, but heavy tailed; translated normal to translated Cauchy. Their method weights the various expert’s pdfs by the Bayes factor once the envelope of evidence is opened.
To illustrate the use of the Cauchy pdf by doing everything much too simply, start with the 5 available modes of 1.6, 2, 3.3, 4 and 5.5. The unweighted average is 3.28 K; use that as the only mode in this simplified procedure. Now as you say, S less than 0 is unphysical, so the compleat Bayesian simply say it is highly unlikely, the subjective probability that S is less than zero is but 5%. Knowning that value and the mode sufices to determine all the parameters for the translated Cauchy pdf.
One would actually have to read the five papers to determine, as an expert, how to weight the five apriori; otherwise, just directly follow Tol & deVos’s standard Bayesian procedure, which uses goodness-of-fit to do the post facto weighting to produce the resulting posterior pdf. The advantage of the latter is that no judgement is required; the advantage of the former is in discovering that the 5 expert opinions were indeed not all completely independent.
If the real world temperature data is tracking to scenario C and scenario C was developed on the assumption that no more carbon was emitted post 2000 does that not mean that (in terms of the model) the effects we are seeing in the real world are the equivalent of a massive reduction in carbon in the atmosphere (relative to where we actually are). That is the model predicted we would see this kind of temperature trend if we cut all carbon emissions and therefore reduced the carbon in the atmosphere?
What I’m saying is if the assumption for scenario C at 2010 is 2000 level carbon emissions minus yearly reduction (resulting from zero human emissions) and the reality is 2000 emissions plus actual emissions then scenario C was wrong by the difference right? Scenario C overestimated the sensitivity such that we have “x” more carbon in the atmosphere produced a result predicted to occur with significantly less carbon in the atmosphere. So model should have had less sensitivity to carbon. That makes sense to me.
In terms of the other scenarios I dont know what the base assumptions were for them but assuming scenario B most likely matches the carbon emissions we have seen to date it is clealy wrong. I’ll give scenario A the benefit of the doubt and assume it was based on significantly more carbon being emitted.
Elliot,
No, what it means is that the climate sensitivity used by Hansen was higher than current best estimates…as Gavin has pointed ut many a time.